 |
Typical dependence of the forces F,
acting between atoms or molecules in substances, on the
distance r. |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Physics and nuclear medicine |
1.
Nuclear and radiation physics
1.0. Physics - fundamental natural
science
1.1. Atoms and atomic nuclei
1.2. Radioactivity
1.3. Nuclear reactions and nuclear energy
1.4. Radionuclides
1.5. Elementary particles and accelerators
1.6. Ionizing radiation
1.1. Atoms and atomic nuclei
Substance, Fields,
Particles, Interactions
In the introduction to our treatise on atoms, atomic nuclei, and
the physics of the microworld, we make a few preliminary remarks
about the basic building blocks of matter and the nature of the
forces that govern their behavior. All these findings, which are
only outlined here, will always be substantially expanded
and specified in the appropriate places during
the interpretation .
In the physical study of nature, we divide
the whole material world into two basic forms of matter :
Modern physics shows that this division is to some extent conventional - the two forms change with each other; particles of matter can be interpreted as quantum states of specific fields (unitary field and particle theory ) and physical fields can be described using quantum - particles (see "Quantum field theory" below).
Discrete
particle and continuous field model of matter
We model the structure and behavior of matter in physics by the
two different ways mentioned above (forms of matter) :
-> Discrete
particle model , according to
which all bodies and material environments consist of a large
number of small spatially localized objects - particles.
According to classical ideas, particles have a certain non-zero
mass or own energy, have a certain position in space and time, a
certain speed, momentum and kinetic energy. The motion of
particles is governed by the universal laws of mechanics
(idealized "material point") - classical
mechanics (Newton's laws of motion) or relativistic
kinematics and dynamics. Now we know that for a detailed analysis
of particles in the microworld, classical mechanics is not
sufficient, but we must use its generalization - quantum
mechanics.
-> Continuous field model , describing the structure and behavior of matter by
quantities continuously distributed in space. In
modern physics, this field description is used for forces
- interactions - between particles of matter. It
is perfectly elaborated especially for electromagnetic
phenomena between charged bodies and particles -
Faraday-Maxwell electrodynamics (see below "Electromagnetic field and radiation"). Here, too, for a detailed analysis of phenomena
in the microworld, quantum field theory
must be used, not only electromagnetic, but also the field of
strong and weak interactions (see below
"Quantum
field theory", "Strong nuclear
interactions" and "Beta
radioactivity. Weak interactions").
However, the field
description can be used (and especially often used earlier) in continuum
physics for the study of liquids, gases and partly also
solids. The movement of liquids and gases is internally caused by
the movements of their atoms and molecules - a perfectly proven kinetic
theory . However, for the macroscopic description of the
behavior of gases and liquids, the motion of individual atoms or
molecules is not investigated, but the collective motions
of a set of particles. "Averaged" quantities are used,
which are continuously distributed throughout the volume of gas
or liquid. Individual data on the position of individual atoms
are replaced by the average spatial distribution of their number
- the density distribution. In the macroscopic
description , the speed of the disordered motion of individual
atoms is replaced by temperature, and the
ordered motion by flow rate (momentum transfer)
in various places of the material environment. Collisions and
forces between atoms or molecules inside gases and liquids are
expressed by the distribution of pressure.
Important equations of state apply to the
interdependencies between these quantities . The relationship
between the mechanical characteristics of particles (atoms and
molecules) and field state quantities in continuum physics is
derived by the methods of statistical physics.
All properties of material environments and the events observed
in them are an integral manifestation of a
number of chaotic or coordinated simpler movements of the
building blocks of the respective substance.
Basic
building particles of matter
With ever deeper penetration into the microworld of building
matter, physics discovers that atoms (previously considered
indivisible) are composed of particles that can
no longer be decomposed into simpler objects capable of
independent existence. These smallest particles, which are no
longer indivisible, are called elementary particles
and can be considered as the basic "building blocks" of
matter. However, these elementary particles are not static and
immutable, but can undergo mutual changes and
some of them may have a certain internal structure.
In the study of the structure of atoms, we encounter mainly the
three most important particles - the electron,
the proton and the neutron *).
In the study of excitations and radiation of atoms and atomic
nuclei then with a photon - a quantum of
electromagnetic radiation, with radioactivity also with a neutrino
and a positron (antiparticle to an electron) - §1.2, part "Radioactivity
beta".
The properties of these and many other particles are more fully
discussed in §1.5 "Elementary particle
and accelerators" dedicated elementary
particle physics, where it is administered also systematics
of elementary particles (neutrinos is
moreover closely discussed in §1.2, section "Neutrinos - "ghosts"
between particles").
*) The reason why the observed matter is
composed only of electrons, protons and neutrons is that all
other material particles are very unstable.
Four basic
physical interactions
The interaction between particles of matter can be explained by
four basic physical interactions. At the level
of atomic nuclei and elementary particles, two short-range
interactions are dominant :
¨ Strong interaction , important especially by holding atomic nuclei
together (see "Atomic
nucleus" below). It primarily combines quarks into protons and
neutrons, mesons and other hadrons . The inherent strong
interaction between quarks, mediated by gluons, has a long range,
but the nuclear strong interaction, as its
"residual manifestation", is short-range (see "Strong
interaction" below).
¨ Weak interaction , which is applied in mutual transformations of
neutrons and protons with the participation of neutrinos, in
practice mainly in radioactivity b (§1.2, part "Radioactivity
beta", passage "Mechanism of
weak interactions"). It is also short-range.
¨ Certain types of particles,
which we call electrically charged, show a force
interaction described by an electromagnetic
interaction. When these
electrically charged particles are at rest, an attractive or
repulsive electric force acts between them
according to Coulomb's law, when they are in motion, there is
also a magnetic force, in the case of uneven
movements of charges, then there is also the emission of
electromagnetic waves - photon radiation (see
the section "Electromagnetic fields and radiation" below). The electromagnetic
interaction has a long range (more precisely, the range is infinite).
¨ The
fourth interaction, also of long range, is the gravitational interaction, which acts universally between all
particles, is attractive and has a significant
effect on high-mass bodies. Its force manifestations are
described in classical physics by Newton's law of gravitation,
in relativistic physics by Einstein's equations of the
gravitational field - see the book "Gravity,
black holes and space-time physics",
§1.2 "Newton's law of gravitation" and §2.5 "Einstein's equations of the
gravitational field".
The biggest and most
difficult task of contemporary theoretical physics is to find the
so-called unitary field theory, which would unify
the 4 basic interactions and explain them as special cases of a
single general interaction - see the section "Unitary theory
of fields and elementary particles" in
§1.5, more details "Unitary field theory and quantum
gravity" of the above-mentioned
monograph "Gravity, black holes and space-time
physics".
The magnitudes of the force effect of
these basic interactions are diametrically different
and decisively depend on the distances of the
interacting particles. For distances of the order of 10-13 cm corresponding to
the dimensions of atomic nuclei, the relative ratio (or rather, "disproportion") of force effect strong, electromagnetic, weak and
gravitational interaction is about 1 : 10-(2-3) : 10-15 : 10-40. At distances of
the order of 10-8 cm, corresponding to the dimensions of the atomic shell,
short-range strong and weak interactions are practically no
longer act, and the electromagnetic interaction has a decisive
influence.
In our treatise on nuclear and radiation
physics, we will not deal with the gravitational interaction,
which is more pronounced in macroscopic bodies and acquires a
dominant character in bodies of cosmic dimensions and masses. The
strong and weak interaction will be discussed in more detail
below in the relevant passages on the atomic nucleus ("Atomic Nucleus") and in §1.5 on elementary
particles (section "Four types
of interactions"). We will say
some basic information about the electromagnetic interaction here
(below "Electromagnetic fields and radiation"), because we will need it
first to explain it - already in the science of atoms.
Classical
and quantum models in the microworld
In atomic and nuclear physics, we study objects and processes
whose behavior is beyond our imagination based on experience from
the macroscopic world - the behavior of objects composed of a
large set of atoms. Even in the microworld,
controlled by quantum laws (see below), we can
sometimes help out by use illustrative mechanical
comparisons to macroscopic systems known to us. For
example we imagine electrons in atoms as light negatively charged
"globules" orbiting a heavy positively charged small
"sphere" - the nucleus of an atom. Or other times we
imagine the particles as waves or a wave pack. However, we must
always keep in mind that these are just models,
expressing only some selected properties of these microsystems,
not their actual material structure in the usual sense! They are
all just our human models, how to at least roughly understand the
phenomena, that are very foreign to our daily experience.
Importantly, it works in a theory-experiment
relationship; and we believe that it will also help us to
understand the internal mechanisms..?..
An important difference compared to
classical physics is the stochastic
(probabilistic) character of quantum phenomena in the microworld.
For individual processes, we cannot determine exactly when they
will occur, but only their probability. The
individual causality of particle behavior is lost, but a new kind
of stochastic regularity emerges. Chaotic randomness
(apparent or principled?) in the behavior of individual particles
results in a regularity for the statistical set
of these particles as a whole (not for its individual elements).
These aspects of quantum physics will be briefly discussed below ("The Quantum Nature of the
Microworld").
From the philosophical-scientific point of view, the
relations between the macroworld, the microworld and the
megaworld are discussed in §1.0 "Physics - fundamental natural science".
Vacuum - emptiness - nothingness ?
In fundamental physics, phenomena occurring with bodies,
particles and fields are mostly studied in a vacuum. Vacuum
in classical physics means empty space (lat.
Vacuus = empty), approximately
achieved in terrestrial conditions in closed vessels by
exhausting air so that the gas pressure is significantly lower
than at normal atmospheric pressure. An ideal or perfect
vacuum is a state of space in which no particles
of matter (such as electrons, protons, etc.) nor
radiation (photons) are present. Creating such a perfect vacuum
is very difficult, even impossible in practice (it is impossible to get rid of, for example, the
ubiquitous neutrinos or weakly interacting massive WIMP particles
forming hidden matter in space - §1.5).
Even if it succeeds, it will not be an empty space,
where there is nothing and nothing happens - they can reach a
physical fields such as electromagnetic and gravitational (gravitational fields cannot be shielded). Any vacuum is not actually empty - according to quantum
field theory, there are many processes of quantum
fluctuations, virtual pairs of particles and
antiparticles are constantly formed (see
"Quantum field theory"
below).
And in any case no means can a
vacuum (even the "perfect") be considered as "nothingness"!
Nothingness means the absence of anything - matter, energy, even
space and time; it is therefore a synonym for
"non-existence" - a fictitious philosophical concept
without physical content.
From a philosophical point of view, a physical vacuum
is not a state of pure nothingness, but contains potentiality of
all forms of the world of particles (cf. "Anthropic principle or cosmic God"). Vacuum is a "living void"
pulsating in the infinite rhythm of formation and extinction of
structures, virtual and real particles ...
Vacuum energy
In classical (non-quantum) physics is the energy
density of itself vacuum (without fields) zero.
A completely marginal exception here is (non-quantum) relativistic
cosmology, some models of which introduce the so - called cosmological
constant, which generates a certain immanent fundamental
density of vacuum energy in space (§5.2,
part "Cosmological constant" in the above - mentioned book "Gravity,
black holes and space - time physics").
According to quantum field theory,
however, countless processes of spontaneous quantum
fluctuations take place everywhere and constantly in a
vacuum - virtual pairs of particles and antiparticles
are constantly being created and destroyed. The duration of these
fluctuations is too short for us to directly detect these
particles, so they are called virtual. Quantum field
fluctuations have different intensities and spatial dimensions
and interfere with each other. The result of
this wave interference is averaged over time. If the
contributions of individual field fluctuations are canceled on
average, the mean energy of the vacuum will be zero
- this is the so-called "true vacuum".
However, if such a canceled does not occur, the mean energy of
the vacuum will be non-zero - such a state is
called "false vacuum".
According to current cosmology, a
"strongly false" high - energy vacuum could have been
the driving force behind the rapid inflationary expansion
of the very early universe (§5.5 "Microphysics
and cosmology. Inflationary universe." in the book "Gravity, the black hole
..."). The present value of the vacuum
energy is very close to zero, less than about 10-9 J/m3, which corresponds to
the mass density of approximately 10-26
kg/m3. Attempts
have been made explain the vacuum energy through quantum field theory - as a consequence of quantum fluctuations of vacuum. A straightforward computation (resp. dimensional estimation), encompassing all vibrational modes of
energy with a wavelength greater than the Planck length (10-35 meters),
can be in and yet incredibly high density vacuum
energy, corresponding to a mass density of about 1096 kg/m3..!.. In order for the vacuum to
look like an empty space, far-reaching compensations must be applied between the
vacuum fluctuations of the different fields, which cancel out the vast majority of the fluctuations. This "scandalous discrepancy" of the 120
orders has not yet been satisfactorily explained; perhaps the unitary
field theories promise some hope (§B-.6
"Unification of fundamental interactions.
Supergravity. Superstrings."
in the above-mentioned book "Gravity, Black Holes ...")
.
The
movement of microparticles in mass-forming ensembles. Thermals,
thermodynamics.
Before we begin to deal with the properties and composition of
individual microparticles (atoms, molecules, electrons, atomic
nuclei, protons, neutrons, ...), it will be useful to talk
briefly about the general aspects of the movement of these
particles in sets of their large number, forming
macroscopic matter. Each substance and the system or body formed
from it consists of particles - molecules, atoms, ions - which
are composed of smaller "elementary" particles of
electrons, protons, neutrons. These molecules, atoms, or ions,
are in constant disordered (chaotic) movement in different
directions and at different speeds - "thermal"
movement. As the temperature (discussed briefly below) increases,
the speed of particle movement increases. The disordered thermal
movement of atoms and molecules causes several effects in
substances :
-> Diffusion is the process of
spontaneous dispersion of particles into space and penetration of
particles of one substance between particles of another
substance. It takes place willingly mainly in gases and liquids,
during the dissolution of solid substances in liquids (e.g. salt
or sugar in water), to a lesser extent also between solid
substances (observed at the interface of plates of different
metals pressed together). It goes faster at higher temperatures.
-> The pressure of the gas on the walls
of the container is caused by the impact of atoms or molecules
hitting the walls of the container. As the temperature increases,
the gas pressure increases - the particles have a higher speed
and thus a higher kinetic energy.
-> Thermal expansion of solids and
liquids. At a higher temperature, due to the higher speed of the
particles, their mutual distances increase, which leads to an increase
in the volume of the substance.
-> Changes in electrical conductivity of
metals, electrolytes and semiconductors. In metals, at a higher
temperature, the intensity of collisions of electrons with the
atoms of the crystal lattice increases, so the electrical
resistance of the conductor increases slightly with increasing
temperature. The exception is the area of ??very low temperatures
of the °K unit, when in some materials the resistance drops to
zero, to superconductivity. In electrolytes, on the other hand,
the dissociation of molecules into cations and anions increases
at a higher temperature, so the electrical conductivity of the
electrolyte increases with increasing temperature, the electrical
resistance decreases. Semiconductors behave as non-conductors at
low temperatures; with increasing temperature, the electrons gain
energy and (via the "forbidden
band") jump into the conduction band
and can participate in current conduction. As the temperature
increases, the concentration of electrons and holes increases and
thus the electrical resistance of the semiconductor material
decreases.
Particles exert attractive and repulsive forces on each
other, the magnitude of which depends on the distance between the
particles :
 |
Typical dependence of the forces F,
acting between atoms or molecules in substances, on the
distance r. |
The origin of those forces between atoms and
molecules is electrical - Coulomb. Even though atoms and
molecules are generally neutral on the outside, the distribution
of electrons is often asymmetric, electric dipoles are created
here. These are then polarized when the particles approach each
other, and attractive or repulsive electrical forces arise
depending on the mutual configuration of the dipole moments. The
mutual force action of the particles causes the system of
particles to have a certain internal potential energy; in the
case of attractive forces, it is the binding energy (it is the work that we would have to do with external
forces to break down the forces between the particles).
At the usual temperatures of approx. 4÷3000 °K, atoms and
molecules in substances collide elastically, so
that the substance behaves according to the laws of thermals and
thermodynamics outlined here. At very low temperatures near
absolute zero, Bose-Einstein condensation occurs in some
substances, which can lead to superconductivity and superfluidity
(§1.5, passage "Fermions
in the role of bosons; Superconductivity"). At high temperatures
>3000°K, the kinetic energy of the atoms is already high
enough that during their collisions, electrons are ejected from
the atomic shells - to the ionization of the substance and the
formation of plasma. Electromagnetic properties
of electrons and ions are already fundamentally applied here
(JadRadFyzika3.htm#Plasma). And at the highest temperatures
>1012 °K,
even atomic nuclei and protons and neutrons break into quarks and
gluons - a quark-gluon plasma is created for a
moment (JadRadFyzika5.htm#KvarkGluonPlasma). Here the laws of
thermodynamics are already debatable...
Thermics
We call the disordered movement of particles thermal,
because according to the kinetic theory of the structure
of substances, these microscopic movements are the essence of heat
and thermal phenomena. This is what thermals
deals with. The basic physical quantity that describes the
thermal state of matter and its internal energy (specific kinetic energy of the chaotic movement of
atoms and molecules) is temperature.
The absolute - thermodynamic temperature T is
proportional to the mean kinetic energy of the
disordered mechanical movement of matter particles (atoms,
molecules) :
< 1/2 m.v2 > = 3/2 kB . T ,
where m is the mass of the particles, v their speed
of movement, kB is the Boltzmann constant indicating the
relationship between the thermodynamic temperature and the
internal energy of the gas; curly brackets < > indicate
mean value.
Temperature is usually expressed in units called degrees
" o ". The
temperature degrees o are derived from the thermal
state properties of water. One degree represents 1/100
of the temperature difference between the boiling point of water
and its freezing point. So the freezing point of water (melting
of ice) is 0 oC, the boiling point of water is 100 oC (at atmospheric pressure ....).
Mainly two temperature scales are used. In everyday life, the
mentioned degrees Celsius oC are used. In physical thermodynamics, the
absolute temperature scale of Kelvin *) is used, where the
initial-lowest temperature T=0 (oK) is the temperature of "absolute zero",
corresponding to -273.15 oC. Temperature differences in the Celsius and Kelvin
thermodynamic scales are the same (Dt=DT), the difference is at the
origin: -273.15 oC = 0 oK (absolute zero). Negative values in Kelvin are not
possible. Occasionally, we can also encounter some other
temperature scales (oF - degrees Fahrenheit, derived from normal body
temperature, were widespread mainly in the USA, where they are
still used today; or the Réumour scale using the boiling point
of alcohol). Conversion relationships between different scales
are given in physical and chemical tables.
*) Note: For the
absolute temperature in the Kelvin scale, the designations "o
degrees Kelvin oK" are now omitted and expressed
only as "Kelvins K". However, we use the notation oK
in our materials.
The temperature is classically measured using the thermal
expansion of mercury or alcohol in thermometers
- thin glass tubes equipped with a scale, or using the different
thermal expansion of layers of bimetallic strips. For
electronic measurements, the temperature dependence of the
electrical resistance of suitable conductors and
semiconductors in thermistors is used. Another option is
to measure the intensity and spectrum of infrared radiation
emitted by heated bodies.
Thermodynamics
Thermodynamics deals with processes in substances related to
thermal phenomena (thermics), mainly from the point of view of
the dynamics of energy and mass transfers in equilibrium
and non-equilibrium systems, conversions of thermal energy into
other types of energy, thermodynamics of phase transformations,
reversible and irreversible events from the point of view of entropy.
From a principled point of view, the explanation of thermal
regularities using the statistical physics of a large
number of particles using the methods of probability
theory is important here.
In addition to temperature T, heat Q (thermal
energy) is also important here, which in thermodynamics is
the total kinetic energy of all disorderly moving particles -
atoms and molecules - in a system or body. It is part of the
body's internal energy, which includes several
components: above all the mentioned kinetic thermal energy of
particles, potential energy of atoms and molecules, kinetic
and potential energy of oscillating atoms inside molecules,
energy of electrons of the atomic shell, nuclear energy, in
particle physics and astrophysics sometimes even rest energy of
matter according to Einstein's relation E=m.c2.
The basic unit of
thermal energy is the Joule (in general, the
unit of work and energy): 1 J = work done by a force of 1 N
acting along a path of 1 m in the direction of movement.
Sometimes the older unit of calorie is used: 1 cal =
energy required to heat 1 kg of water by 1 oC (under standard conditions, 14.5oC is stated). For small energies in atomic and nuclear
physics, the unit electronvolt is used: 1 eV = 1.602x10-19 J .
Thermodynamics, as a comprehensive science of heat and
its transformations, has developed several basic postulates and
conclusions - laws or principles of thermodynamics, which are
generalizations of observed experimental phenomena :
1. Equilibrium state: Every
isolated system reaches an equilibrium state after a
sufficiently long period of time, in which it will remain
permanently (as long as it is not disturbed by external
influences).
2. Zero thermodynamic law: In
an equilibrium system, the temperature in all places is the
same on average - thermal equilibrium is achieved.
3. First law of thermodynamics:
The energy of a system can be changed only by exchanging heat Q,
mechanical work W, or field or chemical energy. It is therefore
the law of conservation
of energy in a closed system, with the possibility
of work and heat exchange, or transformations caused by
excitations of physical fields. Energy can be transformed from
one form to another, but it cannot be created or destroyed.
4. Second law of thermodynamics:
Heat cannot flow spontaneously from a colder body to a warmer
body. Heat cannot be transferred from a colder body to a hotter
body without a certain amount of work required for this being
changed into heat. Therefore, it is not possible to remove heat
from a body and change it into useful work without a certain
amount of heat passing from a hotter body to a colder body.
5. Third law of thermodynamics: The
thermodynamic temperature of absolute zero T=0 °K
cannot be reached by a finite number of steps.
Entropy
In order to explain and quantify the 2nd law of thermodynamics,
an important quantity of entropy S (Greek en=inside, tropo=change -
change inside) was developed in
thermodynamics. In classical thermodynamics, this
quantity indicates the change in heat Q in relation to
temperature T according to the Clausius formula :
dS = dQ / T ,
where dS
is the change - increase or decrease - in entropy, dQ is the heat
transferred to or removed from the system and T is the
temperature. The 2nd law of thermodynamics states that for heat
transferred by any possible process to any system for the change
in entropy of the system, the inequality dS >= dQ/T holds. A
small (infinitesimal) amount of supplied or removed heat dQ is considered
here, at which the temperature T almost does not change (in the general case, when the temperature would change,
integration over the temperature variable would be performed). From the point of view of thermomechanics, entropy
also expresses the proportion of heat or energy of a system that
does not have the ability to perform work. ......... ........
In statistical thermodynamics, entropy is
defined using the number of microstates that lead to a given
macrostate of the investigated system - see below in the passage
"Statistical thermodynamics". Both of these definitions
of entropy are equivalent in the sense that they lead to the 2nd
law of thermodynamics.
The second law
of thermodynamics can therefore be formulated using entropy
as: In a thermodynamically closed (isolated) system, entropy
cannot decrease.
Statistical thermodynamics
Every system - substance, body - is made up of a large number of
atoms or molecules that oscillate and move chaotically, collide
and reflect each other, penetrate the spaces between them - they
mix. This movement creates heat. From the point of view of
classical physics, every atom and molecule must obey Newton's laws
of mechanics, so their movements and collisions can in
principle be measured and analyzed quantitatively. However, there
are a huge number of atoms and molecules and they cannot be
measured and evaluated individually. Only probability
can be used here - statistical mechanics that
connects and averages microscopic details into macroscopic
behavior and overall outcome.
Microscopic state - in short, the microstate
of the investigated system represents detailed knowledge of the
exact position and speed of each particle (atom, molecule) in
this system at a given moment in time. As the particles move,
collide with each other, change their positions and velocities,
the microstate constantly changes chaotically during the
temperature fluctuations of the system. Each microstate has only
a certain probability of occurrence. Macroscopic thermodynamic
description of the system - temperature, pressure, volume,
represents its macro state. There are many different (mostly only
slightly different) microstates that can globally provide the
thermodynamically identical macrostate of the system. If the
system is in an equilibrium state, despite the constant small
fluctuations of the microstate, there are no changes in its
macroscopic thermodynamic behavior - temperature, pressure,
volume do not change.
In statistical mechanics, the entropy S
of a system is quantified as the number of all microstates that
could provide the resulting macrostate of the investigated
system, according to the probability relation of L.Boltzmann :
S
= kB . ln W ,
where S is the thermodynamic entropy, W is the
number of all microstates that can provide a given thermodynamic
macrostate. The constant kB = 1,38049×10-23 Joules per Kelvin is the Boltzmann constant between the
average thermal energy of the particles in a gas and the
thermodynamic temperature of that gas. The proportionality
constant kB serves to make the entropy value in
statistical mechanics equal to the classical thermodynamic
entropy in the Clausius formula.
Note: The
natural logarithm of ln W is used in mathematical
statistics, where it quantifies the information entropy of a
random variable in a system.
An example of such macroscopic behavior can be imagined
in a simple experiment: We take a container of gas that is
divided into two parts, separated by a partition (similar to the "Maxwell's Demon" picture
below). We fill one part with a gas or
liquid with a higher temperature (molecules
move in it at a higher speed, with a higher kinetic energy) than in the other part. When we remove the partition,
the molecules start to mix - the fast molecules diffuse and
collide with the slower ones. There is an exchange of kinetic
energy and after a certain time the gas or liquid reaches
equilibrium with a constant average temperature. This is a widely
known experience, in practice it never turns out differently.
Newton's equations of motion are invariant with
respect to time reversal. If, in a dynamic system, the
motion of each of its particles is exactly reversed at the same
time, then everything will happen backwards. If we observe the
movements of individual atoms and molecules in microscopic
detail, they behave the same when we watch them forward or
backward in time (similar to when we project a movie forward or
backward). But when we observe a container with gas or liquid,
the mixing process macroscopically becomes unidirectional in
time. We will never see that in a gas or liquid the atoms split
into hot on one side and cold on the other. We cannot separate
them from each other if time runs forward and never turns back.
The reason for such one-way processes is probability
- statistics. In general, the number of disordered states is
incomparably greater than the number of ordered states. The 2nd
law of thermodynamics is therefore a statistical consequence of
the fact that there are much more disordered states than ordered
states.
"Maxwell's demon"
particle sorter ?
In fundamental physics, nothing should in principle prevent
particles from arranging themselves in a variety of uniform and
non-uniform configurations. So nothing should prevent the gas
from splitting into a cold and a warm part, it's just statistical
randomness. J.C. Maxwell proposed the following thought
experiment :
We take two flasks connected by a tube
with a separating partition that can be closed or opened using a
valve (e.g. with a slide). With the partition closed, we pour
into the left bulb a gas consisting of two types of atoms, or
faster (red) and slower (blue) atoms - Fig.a). The right
flask is empty, there is a vacuum. When the partition is then
permanently opened, as a result of the chaotic movement of
diffusion, an average of the same representation of both types of
particles as in the left container (b) penetrates
into the second container as well.
But if there was a valve in the separating partition that could
be alternately opened and closed, it would be possible to
"sort" the particles entering the flask on the right
with it. Let's imagine that this valve would be controlled by
some very fast and observant being with infinitely subtle senses
- a "demon" who would be able to recognize whether the
diffusing particles are fast or slow and could decide whether to
let them pass through the valve (c). He could
only allow faster (red) particles into the second flask, for
example, while he would retain the slower (blue) particles by
closing the partition from which they would bounce back. The
demon thus replaces chance with purpose. Ultimately (after enough
time), only "blue" particles would remain in the left
flask and only "red" particles would remain in the
right flask (d). This would violate the normal
probability that all particles should mix.
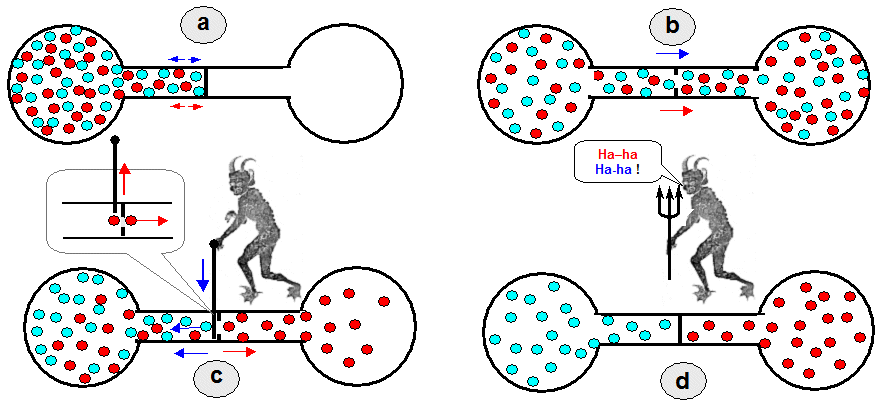 |
| "Maxwell's
demon" able to sort particles. a) Initial situation: two flasks connected by a tube with a separating partition. The flask on the left is filled with a gas or liquid consisting of two types of particles. b) When the partition is opened, as a result of the chaotic movement of diffusion, the same number of both types of particles as in the left container penetrates into the second container as well. c) If there was a valve in the partition, which would alternately open and close a "demon" that is able to recognize diffusing particles, it could only allow e.g. faster (red) particles into the second flask, while it would retain the slower (blue) particles by closing the partition , from which they would bounce back. d) Ultimately (after enough time) only "blue" particles would remain in the left flask and only "red" particles would remain in the right flask. |
In the idealized case, Maxwell's
demon does not have to perform any work in the opening and
closing of the valve when sorting particles, but it uses information
that is not freely available when making decisions - "it's
not free"! Information has a physical nature. This is
information about the speeds and trajectories of individual
particles. Each time the daemon decides between two particles (to
release or retain them), it costs one bit of information.
Each unit of information then brings a corresponding increase in
entropy with the conversion factor kB.log2. This restores compliance with the 2nd law of
thermodynamics.
"Maxwell's Demon" is of course just a fiction
and does not exist in reality. However, its sorting role
for atoms and molecules is performed in nature under certain
circumstances by some physico-chemical and biological processes.
During their function, growth, and reproduction, living cells
create complex, ordered structures - as if they defy the 2nd law
of thermodynamics. However, the cell is not an isolated system,
so part of the energy used for its internal processes turns into
heat, which is dispersed into the surroundings of the cell and
increases its disorder. So the balance of the total entropy of
the cell and the surroundings changes in accordance with the laws
of thermodynamics. Cell membranes often exhibit one-way
permeability and are able to regulate differences in ion
concentrations during energy consumption. Enzymes can also act
unidirectionally and can be metastable - after deactivation,
their energy dissipates, turns into heat and increases entropy in
the surroundings. During metabolism, cells and organisms
successfully get rid of entropy, necessarily created during their
life functioning.
Herbivores and carnivores feed on organic substances
that are in a highly organized state and return them to nature in
a highly degraded state. But not completely, it can also be
partially used by plants, which in addition obtain not only
energy from sunlight, but also negative entropy. In short,
"organisms organize" and at the same time suck
"negative entropy" from their surroundings; and it gets
it from sunlight.
After all, we humans are probably the biggest
"fighters" against entropy and the 2nd law of
thermodynamics. In addition to the biological processes in our
body, we constantly sort something, collect, collect, write
literature, learn about nature and the universe, compose music,
draw pictures, clean the apartment, ... etc. And human
civilization builds colossal creations with a precise structure
...
The relationship between entropy and life is briefly discussed in
the passage "Can the functioning of life and its evolution
violate the 2nd law of thermodynamics?" work "Anthropic Principle or Cosmic
God".
All irreversible processes have the
same physical-mathematical explanation: probability.
The second law of thermodynamics is only probabilistic.
Statistically, everything tends towards the highest entropy. In
purely physical terms, it is not impossible for atoms or
molecules in a container of gas to not mix and remain separate -
it is just extremely unlikely. The improbability of heat passing
spontaneously (without external help) from a colder body to a warmer one is similar to the
improbability of spontaneous arrangement of order out of chaos.
Both of these improbabilities are statistical in nature.
The 2nd thermodynamic law means the tendency of physical systems
of particles to flow from less probable - ordered -
macrostates to more probable - disordered ones.
The laws of thermodynamics play an important role in the
behavior of substances in nature, composed of atoms and molecules
- in our macroscopic world. However, thermodynamic concepts have
been generalized even to other phenomena in the microworld and in
the universe - see e.g. §4.7 "Quantum radiation and thermodynamics of black
holes", or §5.6 "The
future of the universe. Dark matter. Dark energy.", passage "The Arrow of Time" in the monograph "Gravity,
Black Holes and the Physics of Spacetime"... Reflection on causality and randomness in nature and
the universe is in §3.3, the passage "Determinism,
chance, chaos?".
Electromagnetic fields and
radiation
Before we begin to focus on the structure of atoms and the
phenomena taking place inside, it will be useful to say a few
words about one of the most important phenomena in nature - electromagnetic
action and electromagnetic radiation. This is because
all events in atoms and their nuclei are closely connected with
electromagnetic interaction.
Each electric charge Q
excites around it an electric field of intensity
E, proportional (according to Coulomb's law)
to the magnitude of the charge Q and inversely proportional to
the square of the distance r : E = ro . k.
Q/r2,
where ro is the unit vector extending from
the charge Q to the test site and k is the coefficient
expressed in SI in terms of vacuum permittivity eo : k = 1/4p eo . If the charge does
not move (in the given reference system) , it is an electrostatic field. This electric
field causes force effects F = q.E
for every other charge q that enters this space. The electric
field is generally springs, its source is the
electric charges from which it emanates ("springs") and into which the electric
field lines enter. However, even in the absence of electric
charges, if the electric field is excited by electromagnetic
induction with time changes of the magnetic field (as mentioned
below), the electric field may be source-free.
What is the strongest
electric field can be ?
In classical (non-quantum) physics, the electric field in a
vacuum can be arbitrarily strong, almost to infinity (in the material environment, however, this is limited
by the electrical stability of the dielectric). From the point of view of quantum electrodynamics,
however, even in a vacuum there is a fundamental limitation
caused by the existence of mutual antiparticles
of electron and positron : it is not possible to
create an electric field with an intensity stronger than Ee-e+ = me2c3/e.h = 1,32.1016 V/cm, where me is the rest mass of
the electron or positron. When this intensity is exceeded, the
potential gradient is higher than the threshold energy 2me c2 and a pair of
electrons and positrons is formed, which automatically
reduces the intensity of the electric field. Such a strong
electric field has not yet been created, with conventional
electronics this is not possible; strong impulses from extremely
powerful lasers could be a certain possibility in the future ...
If the charge Q moves (electric current), in addition to
the electric, a magnetic field also excites
around itself. The moving charges, forming a current I in
the longitudinal element dl, excite at a
distance r a magnetic field of intensity B (unfortunately called magnetic induction for
historical reasons) according to the Biot-Savart-Laplace
law : dB = k .I .[dl´ro]/r2, where ro is the unit
directional vector of the measured point to the current element
and k a proportionality constant expressed in SI units
called via permeability of vacuum mo: k = mo/4p. The magnetic
field shows force effects on each electric charge q moving at a
speed v : F = q. (B x v);
this so-called Lorentz force acts perpendicular to the
direction of movement of the charge. The magnetic field is (unlike the electric field) always
source-free, the magnetic field lines are closed curves
- there are no so-called magnetic monopolies (magnetic
"charges", similar to electric charges).
During movement or time changes in the
magnetic field, it arises according to Faraday's law of electromagnetic
induction the electric field - in the form of a kind of
"vortex", a rotating electric field around a variable
magnetic field. An induced electric field can cause the movement
of charges, eg electrons in a conductor - induced electric
current. And the time changes of the electric field, in
turn, cause a magnetic field (as if the
so-called Maxwell shear current flowed), again of a vortex character. This dialectical unity of
electric and magnetic fields finds its application in the concept
of electromagnetic field, whose special
manifestations are electric and magnetic fields. This field is
governed by Maxwell's equations of the electromagnetic
field, which were created by merging and generalizing
all the laws of electricity and magnetism. The combined science
of electricity and magnetism, including the dynamics of charge
motions and the time variability of fields, is called electrodynamics.
Note: Details on
the theory of the electromagnetic field can be found, for
example, in §1.5 "Electromagnetic field. Maxwell's equations" of the book "Gravity, Black Holes and the
Physics of Spacetime".
Below, in the section "Atomic
structure of matter" we will see
that electromagnetic forces are decisive for the structure of
atoms and for their properties - they are determining
significance for the structure of matter at the
microscopic and macroscopic level, including all chemical
phenomena. Along with strong interactions, electric forces also
play an important role in the structure of atomic nuclei
(as we will see in the section "Structure
of the atomic nucleus") and in the excitations and deexcitation of their excited
energy states.
The
electromagnetic waves
Maxwell's equations have a number of remarkable properties, but
the following regularity is important to us here: The disturbance
(change) in the electromagnetic field propagates in space at a
finite speed equal to the speed of light. When electric
charges move at a variable speed (unevenly, with
acceleration), they create a time-varying electromagnetic field
around them, which leads to the formation of electromagnetic
waves, which detach from their source and carry some of
its energy into space. The electromagnetic field then further
propagates through space already independently of the source
electric charges and currents in the form of a free
electromagnetic wave - it is derived in
§1.5, part "Electromagnetic waves" already mentioned monography "Gravity,
black holes, and physics of space-time".
From Maxwell's
equations, by a suitable modification can be obtained two partial
differential equations for the vectors E and B
:
¶2E/¶x2 + ¶2E/¶y2
+ ¶2E/¶z2
= e.m .¶2E/¶t2 , ¶2B/¶x2
+ ¶2B/¶y2
+ ¶2B/¶z2
= e.m .¶2B/¶t2 ,
which are wave equations describing the propagation
of a time-varying electric and magnetic field in space at speeds
c = Ö(1/em), where e is the electrical
permittivity and m is the magnetic permeability of the given medium: E(x,
y, z, t) = f(t - x/c) and analogously for B, if
we consider for simplicity the waves propagating in the direction
of the x-axis. The most commonly considered is the harmonic
(sine or cosine) time dependence: E(x,y,z,t) = Eo.cos(w.(t - x/c)) and
analogously for B, where w = 2p.f is the circular
frequency. This is because waves are often caused by periodic
oscillating movements of electric charges (eg in
antennas powered by a high-frequency signal of frequency f); even
in cases where this is not the case (eg braking radiation), the
resulting waves can be decomposed by Fourier into
harmonic components of different frequencies and phases.
The highest speed is reached by
electromagnetic waves in a vacuum, where co = 1/Ö(eo.mo) = 2,998.108 m/s @ 300 000 km/s. In a
material environment whose permittivity and
permeability are greater than for a vacuum, the speed of
electromagnetic waves is somewhat lower - in
light this leads to known optical phenomena of refraction
of light rays when light passes between substances with
different optical densities (see below "Electromagnetic and optical optical properties
substances").
Thus, according to Maxwell's equations of
electrodynamics, electromagnetic waves are transverse
waves of electric and magnetic fields (mutually excited
by their variability), where the vector E of
electric intensity and vector B of magnetic
induction oscillate with amplitude A constantly perpendicular
to each other and perpendicular to the direction of wave
propagation (see upper part of Fig.1.1.1), which in a vacuum
travels at the speed of light c = 300,000 km/s. In practice,
electromagnetic waves most often arise from vibrations of
electric charges - or the vibratory movement of electrically
charged particles such as electrons or ions.
And vice versa, the electromagnetic wave periodically
exerts a force on electrically charged particles - it
sets electrons in motion in conductors and induces
alternating electric current in them; the reception of
electromagnetic waves by the antenna is based on this.
Periodicity in space is given by wavelength, periodicity
in time by frequency. The intensity (strength,
power) of an electromagnetic wave is given by the amplitude
of the oscillating electric intensity E and the
magnetic induction B, energy transfer by the
so-called Poynting vector. There are simple relations
between the speed of light c , the frequency of
oscillation n and the wavelength l
: l = c/n, n = c/l, l.n = c. The higher the oscillation frequency of the
electromagnetic field, the shorter the wavelength. And it is on
this frequency or wavelength
that the properties of electromagnetic waves depend
significantly.
Note: Wave
propagation in material environments and especially physical
fields is a general fundamental natural phenomenon
- it is analyzed in the introductory part of §2.7 "Wave propagation - a general natural phenomenon" of the already mentioned book "Gravity,
black holes and space - time physics".
Electromagnetic waves in atomic
and nuclear physics
The general regularity of
electrodynamics, that the temporal changes of electric and
magnetic fields are capable to propagate in space as
electromagnetic waves transmitting energy, play an
important role in atomic, nuclear and radiation physics. First of
all, it is the electromagnetic radiation of atoms
during the jumps of electrons between the energy levels in the
electric field of the nucleus (see below
"Radiation of atoms"). Furthermore, it is the braking
radiation generated generally during the accelerated
motion of electric charges, in radiation physics especially
during the impact of fast electrons on matter and their rapid
braking during interaction with atoms of matter (§1.6, section "Interaction of charged particles"). The more subtle radiation
effects are Cherenkov radiation and transient
radiation, arising during the passage of fast charged
particles through the material environment (§1.6,
passage "Cherenkov radiation"). In the field of atomic
nuclei, it is the deexcitation of nuclear levels by the
emission of electromagnetic radiation - photons of gamma
radiation (§1.2, part "Gamma
radiation").
Types of
electromagnetic radiation
According to wavelength or frequency, we divide electromagnetic
waves into several groups :
The last two types of shortwave radiation, X and gamma, partially intersect with their spectra (wavelengths or energies) and there are sometimes terminological ambiguities. In the mentioned §1.2, part "Gamma radiation", there is a terminological agreement on the division of shortwave electromagnetic radiation according to its origin - gamma radiation comes from the nucleus, X radiation from other regions of the atom outside the nucleus.
Units of
energy, mass and charge in atomic and nuclear physics
In most areas of physics and natural sciences, a system
of SI units is used, in which the basic units are: meter
[m] as a unit of length, second [s] as a unit of
time and kilogram [kg] for mass; decimal
multiples are often used - centimeter or gram, etc. The basic
unit of work and energy is the joule [J], the
unit of electric charge coulomb [C].
In atomic and nuclear physics, which
examines phenomena at small spatial scales and very small values
of absolute mass, energy and charge, some somewhat different
habits have been established in the units of mass,
energy and charge used. These alternative units are
better "tailored" to the phenomena studied in the microworld
than SI units derived from macroscopic phenomena.
The unit of time second is to
keep, the unit of length, meter or centimeter,
is usually also to keep (of course using decimal fractions 10-xx); sometimes the
unit angstrom is used : 1A° = 10-10 m = 10-8 cm (in atomic physics it is a typical dimension of an
atom), or fermi : 1fm = 10-15 m = 10-13 cm ( femtometer, in nuclear physics it is a
characteristic dimension of the nucleus).
As a unit of energy in atomic
physics it is not used too large 1 Joule, but 1
electron volt, which is the kinetic energy obtained by
the charge of one electron in the electric field at accelerating
potential difference of one volt: 1eV = 1.602x10-19 J.
In nuclear physics, where there are higher energies and energy
differences, then decimal multiples - kiloelenktronvolt (1keV =
103 eV),
megaelectronvolt (1MeV = 106 eV) and gigaelectronvolt (1GeV = 109 eV).
Also the usual unit of weight,
kilogram or gram, is impractically large for
atomic and nuclear physics. In nuclear physics, mass is usually
understood as the rest mass of particles and it
is customary to express it in energy units based
on the Einstein relation E = m.c2
equivalence of mass and energy, ie also in electron volts
: 1eV = 1.783x10-33 grams; and of course in their decimal multiples. The
rest mass of an electron can therefore be
expressed as: me = 9.1x10-28 g = 511 keV. In addition to [MeV], the mass of heavier
elementary particles is sometimes expressed in multiples
of the mass of the electron me - eg the mass of a proton can be
expressed in three different ways: mp = 1.673x10-24 g = 938 MeV = 1836 me .
For an electric charge, instead of
an oversized unit Coulomb, as natural basic units of
charge, the electron charge e is use (resp. the
same size but the opposite charge of the proton),
which is the elementary electric charge: e = 1.602x10-19 Coulomb.
However, the currently used units of dosimetric
quantities, characterizing the effects of ionizing
radiation on matter and living tissue, are based on the SI
system. Because these are cumulative effects of a macroscopic
nature. The basic quantity here is the absorbed radiation
dose, the unit of which is 1Gray =
1J/1kg (for more details see §5.1 "Effects of radiation on the substance. Basic
quantities of dosimetry.").
A note on quantities
and units in nuclear physics
The terminology, quantities and units related to atoms, nuclei,
radioactivity and radioactive radiation have undergone a long and
complex development, which has left some illogicalities and
ambiguities - to be specified below. After all, similar
gnoseological inconsistencies also occur in other physical fields
due to historical development. Recall, for example, the
unfortunate introduction of an electric current as a basic
quantity and its SI unit 1Ampere (using "the force of two
infinite parallel conductors ..."), while the physically
primary electric charge (and the Coulomb unit) is introduced as
derived from current. Or in magnetism the terminological
illogicality of the names "magnetic field intensity"
and "magnetic induction" (for an electric field it is
fine) ...
Excursion
to high velocities - a special theory of relativity
Microparticles, of which matter is
composed, usually move at very high velocities
during processes inside atoms, atomic nuclei and mutual
interactions, often approaching the speed of light. In
experiments with these high velocities, it was found that the
usual laws of classical Newtonian mechanics no longer
apply exactly here. Albert Einstein in his research at the
beginning of the 20th century, followed up on Galileo and
Newton's classical mechanics, Maxwell's electrodynamics and the
research of his predecessors (Lorentz, Michelson-Morley, ...) and
created a new mechanics - the so-called special theory of
relativity, generalizing classical mechanics to
movements at high speeds close to the speed of light. A
systematic interpretation of this certainly interesting theory is
not possible here; it can be found in a number of book
publications (on these pages it is eg §1.6
"Four dimensional spacetime and special theory of
relativity" in the book
"Gravity, black holes and physics of spacetime"). Here we will only briefly
recall some basic phenomena of the special theory of relativity,
which are of fundamental importance in nuclear processes and
interactions of elementary particles.
The special theory of relativity (STR) is based on two
basic postulates :
Relativistic
kinematics
From these two experimentally perfectly verified principles it
follows, that the relationships between positional coordinates
and time intervals of events in different inertial frames of
reference with the laws of classical kinematics control only at
low velocities, while in general they control so-called Lorentz
transformations
x´ = (x - V.t)/Ö(1-V2/c2) , y´ = y , z´ = z
, t´ = (t - x.(V/c2))/Ö(1-V2/c2) ,
indicating the relationship between the spatial coordinates x,y,z
and the time t in the inertial system S and in the
system S´ moving with respect to S speed V
in the direction of the x- axis.
Note: In non-relativistic physics, the
relationship between these coordinates is given by a simple Galileo
transformation x´ = x -V.t, y´ = y, z´ = z, t´ = t
(time t´ here, of course, flows here as fast as t !).
Important kinematic effects of the
special theory of relativity follow from Lorentz transformations
:
Contraction of lengths :
The dimension l of each body of (own) length lo, which moves with
velocity v, appears shortened in the direction of motion
compared to its rest dimension lo: l = lo.Ö(1-v2/c2).
Time dilation :
The time on a moving body flows with respect to the time of the
external resting observer the slower, the faster the body moves: Dt = Dt .Ö(1-v2/c2). Here Dt is the time
measured by the external rest clock, Dt is the actual time
measured by the clock moving together with the body at velocity v
.
Einstein's law of velocity addition :
If one body moves with velocity v1 and the other body with respect to it velocity v2 in the same
direction, then with respect to the initial inertial frame of
reference, the result of the composition of both velocities will
be v = (v1+v2)/(1+v1.v2/c2), and not v1+v2 , as would be was in
classical mechanics.
Of these kinematic effects of special theory of
relativity is considerable importance for nuclear and particle
physics, especially the dilation of time, thanks
to which particles with a short lifetime can live many
times longer if they move at a speed close to the speed
of light. Thanks to this effect, for example, m - mesones (with a
lifetime of 2.10-6 sec) created by the interaction of cosmic rays in the
high layers of the atmosphere, it is enough to reach the surface
of the earth, where we can observe them. Or we can exploit the
mesons p+, p-, created during interactions of high-energy protons
from the accelerator, to come out its in form of the beams and
study their interactions for a time many times longer than their
rest time of life 2.6x10-8 sec.
Relativistic
dynamics
Combining relativistic kinematics STR and (Newton) dynamics of
body motion arises relativistic dynamics, the basic new
finding of which is that the (inertial) mass of bodies m
is not constant, but the mass depends on the velocity
of the body v according to an important relation
m = m 0 / Ö ( 1-v 2 / c 2 ) ,
where m0
is the rest mass of the body *), which it has in
the inertial frame of reference in which it is at rest. The
weight of the body therefore increases with speed,
especially when the speed approaches the speed of light - then
the mass of the body increases theoretically to infinity: limv® c m = ¥ .
Another important result of relativistic dynamics is the
relation for the total energy E of a body of
rest mass mo moving at a velocity v :
E = m o .c 2 / Ö (1-v 2 / c 2 )
and the resulting findings of the equivalence of mass and
energy expressed by the famous by Einstein's relation E
= m.c2 ;
resp. DE
= D
m . c2.
Both these relations of the dependence of mass on
velocity and the equivalence of changes in mass and energy play a
cardinal role in nuclear and particle physics, where there are
mutual transformations of energies and particles moving at high
velocities.
*) This relation cannot be used directly for particles with zero
rest mass (mo = 0) moving at the speed of light v = c - such
particles are mainly quantum of electromagnetic waves - photons.
The photon has energy E = h. n
, given by its frequency n and can be
attributed to the (relativistic) inertial mass m = E/c2 = h.n/c2 .
General
Theory of Relativity
In addition to the special theory of relativity, Einstein also
developed a general theory of relativity, which
is a unified relativistic physics of gravity and
spacetime. We will not deal with this here,
because in atomic and nuclear physics the gravitational
interaction does not manifest (if we omit the unitary field
theory...). This very interesting theory is explained in detail
in the monograph "Gravity, Black Holes and the Physics
of Spacetime", especially in
Chapter 2 "General Theory of Relativity - Physics of Gravity ", along with its implications in astrophysics and
cosmology - Chapter 4 "Black Holes"
and Chapter 5. "Relativistic Cosmology".
Corpuscular-wave
dualism
In classical physics and in everyday life, we observe a
diametrical difference between discrete particles
or bodies with their motions described by mechanics, and between continuous
waves propagating in a certain environment. However, in
a microworld dominated by the laws of quantum physics, this
difference is blurred in certain circumstances !
Corpuscular
properties of waves
At the turn of the 19th and 20th centuries, physics
explained all natural phenomena either using particles,
or by means of an electromagnetic field and its
waves - electromagnetic radiation, a special
kind of which is light. Virtually all the
properties of light known in optics at that time
(laws of propagation, reflection, refraction, difraction of
light, interference) could be very well explained by the wave
concept. Huyghens's wave approach to radiation seemed to triumph
over Newton's corpuscular notion. However, some of the properties
of radiation that were recently discovered at the time could not
be fully satisfactorily explained by the pure wave concept.
Black body
radiation
The first such phenomenon was the spectrum of radiation of a
heated ("absolutely") black body *), which was examined in detail by M.Planck
in 1900. To explain the observed shape of the black body's
radiation spectrum as a function of its temperature, Planck
hypothesized that the emission (and absorption) of
electromagnetic radiation by individual atoms in the body does
not occur smoothly and continuously, but after certain small
precise doses - quanta of energy. Sources of
electromagnetic radiation can be considered as oscillators
that cannot oscillate with any value of frequency and energy, but
radiate or absorb energy only in certain quantities. The
magnitude of the energy E of these quanta depends only on
the frequency of the radiation n and Planck
established for it the relation E = h. n , where the proportionality
constant h @ 6.626x10-34 J/s was called Planck's constant.
Planck himself initially considered this assumption only as an ad
hoc working hypothesis (a kind of
temporary "emergency trick" to explain spectrum
discrepancies), which should later be
replaced by a more acceptable explanation. In reality, however,
this hypothesis proved correct and became the beginning of a new
conception of the microworld - quantum physics.
*) Each body (composed of a substance of
any state), heated to a temperature higher than absolute zero,
emits electromagnetic radiation - thermal radiation,
arising from oscillations and collisions of electrons, atoms and
molecules due to their thermal movements. This radiation carries
away part of the thermal energy supplied to the body from the
outside or generated inside the body. For the model study of
thermal radiation, a so-called absolutely black body is
introduced, which absorbs all the radiation that falls on them.
It can be realized with a closed box with heated inner walls
provided with a small opening through which thermal radiation
escapes into the outer space.
In 1879, Stefan and Boltznan discovered the radiation law for the
intensity of black body radiation as a function of temperature: I
= s . T4, where s = 5.67.10-8 Wm-2.K-4 is the
Stefan-Boltzman constant. However, a satisfactory and uniform law
could not be found to determine the radiated spectrum of thermal
radiation. Two laws were formulated for the radiated spectrum,
which, however, only partially agreed with the experimentally
measured spectral curve: Rayleigh-Jeans's law well
described the spectrum in the long wavelength region, but did not
agree (even diverged) in
the short wavelength region; Wien's law behaved the
other way around. Unify both spectral regions managed to M.
Planck, who discovered a new radiation law that was in full
agreement with experiments in all spectral regions.
Photoelectric
effect
Another phenomenon that resisted satisfactory explanation by the
wave nature of light was the photoelectric effect, abbreviated as
photoeffect. This phenomenon, first observed in
the late 80s of the 19th century A.Stoletov (in experiments with
electric arc radiation) and H.Hertz (in famous spark experiments
demonstrating electromagnetic waves), consist in the fact that
when certain substances, especially metals, light (or
electromagnetic radiation in general) of sufficient frequency
falls on it, electrons are released from its
surface *).
*) We distinguish two types of photo
effect, external and internal. Here we deal with the external
photo effect, when the action of radiation releases
electrons, which escape through the surface from
the substance into the surrounding space - occurs
electron photoemission. This phenomenon is used in
special tubes - photons tubes and photomultipliers.
During the internal photoeffect, the released
electrons remain inside the irradiated material and contribute to
its electrical conductivity (it is used mainly
in semiconductor optoelectric components - photoresistor,
photodiode). In §1.6, part "Interaction of gamma and X-rays", Fig.1.6.3, we will deal with a special type of
photoeffect, where a high-energy quantum of X-rays or g- rays eject
electrons from the inner shells of the atomic envelope; and
mention also the so-called nuclear photoeffect or photonuclear
reaction.

Photoelectric effect
Left: Experimental setup for
the study of the photo effect. Top right:
Irradiation with strong long-wave radiation does not lead to a
photo effect, while irradiation even with weak short-wave
radiation causes a photo effect.
Bottom right: Quantum mechanism of a
photoeffect by absorbing photons of incident radiation and
transferring their energy to electrons.
Detailed experimental tracking (using electron
tubes for the left picture - a prototype of so-called photon
tube) showed that the photoeffect has certain specific
properties, some of which canot be explained by classical wave
concept of electromagnetic radiation :
¨ 1. For
each metal, there is some threshold minimum frequency
nmin
, in which a photo effect occurs; if n < nmin , the photo effect does not occur even at the highest
radiation intensity. On the contrary, even weak radiation with a
higher frequency will cause a photo effect (even
if the number of emitted electrons is lower),
and immediately; according
to the wave idea, the electron would have to "wait"
until a weak wave gradually brought it enough energy to release.
It follows that if an electron is released, it cannot receive
energy gradually and continuously, but must receive the necessary
energy at once.
¨ 2. The
number of emitted electrons is directly proportional to the
intensity of the incident radiation (provided, however, that a
photoeffect occurs).
¨ 3. The
kinetic energy (velocity) of the emitted electrons does
not depend on the intensity of the incident radiation. It depends
somewhat on the irradiated material and is directly
proportional to the frequency of the incident radiation.
The classical wave concept
failed to satisfactorily explain the independence of the energy
of the emitted electrons on the intensity of the incident
radiation and, conversely, its dependence (even direct
proportionality) on the frequency. In 1905, A.Einstein studied in
detail the properties of the photo effect and explained all the
experimentally established facts by assuming that the absorption
of radiant energy takes place not continuously,
but in certain small doses, quantum. The electromagnetic wave of the
frequency n and the wavelength l
= c/n, during the photoefect behaves as a set of particles
- light quanta with a certain energy E
and momentum p : E = h.n, p = E/c = h.n/c = h/l. Thus,
electromagnetic radiation (including light) not only radiates,
but also propagates and interacts (absorbs) in individual
quantities.
The electron on the surface of the plate receives
just the energy Ef = h. n of one light quantum - photon.
Part of this energy is consumed for the work needed to release
the electron from the metal (the output work is equal to the
binding energy Ev the electron in the metal, which is relatively small -
units of electron volts). The residue is converted into kinetic
energy Ek
= (1/2) me.
v2 emitted
electrons of mass me, flying away at speed v. The law of conservation
of energy then leads to Einstein's photoelectric equation
h. n =
Ek + Ev, which quantitatively
describes the properties of the photoelectric effect in perfect
agreement with the experiment. At longer wavelengths, ie
lower frequencies, the energy of the photon is insufficient for
the electron to be released from the bond in the metal (or in the
atom) - no photo effect occurs.
Compton scattering
Particle nature of shortwave
electromagnetic X and gamma radiation is indirectly reflected in
some of their interactions such as Compton scattering of this radiation on electrons.
The experiment shows that the higher the change in the direction
of electromagnetic radiation after scattering on an electron, the
lower its frequency. This dependence of frequency on the
scattering angle is difficult to explain by the electromagnetic
interaction of a plane wave with an electron. On the other hand,
the idea that the interaction occurs by the mechanism of a photon
collision with energy E = h.n with an electron, similar
to the elastic collision of two bodies (such as
"billiard balls"), in which the redistribution of
directions of motion, velocities and energies (and thus
wavelengths and frequencies) is governed by simple laws of
classical mechanics of mass points, explains the observed results
very well Compton scattering - is analyzed
in §1.6, section "Interaction of gamma radiation and X", the passage"Compton Scattering".
The corpuscular-wave dualism of
electromagnetic waves
is illustrated in Fig.1.1.1. At the top of the figure, a common
electromagnetic wave of lower and higher frequency (i.e., larger
and smaller wavelengths) is schematically shown first. If we
increase the frequency n of electromagnetic waves, according to classical physics,
nothing happens other than that the wavelength (l = c/n) will be reduced
proportionally. However, at very high frequencies (of the order
of n»1014 Hz, ie l»10-7 m) we will observe
that the wave will no longer have a constant amplitude, but its
amplitude will fluctuate. This tendency will
increase with increasing frequency and decreasing wavelength. At
extremely high frequencies n»1018 Hz (already corresponding to radiation g) we finally find
that the wave in the classical sense has disappeared - the
radiation will be emitted and propagated in short doses -
quanta (Fig.1.1.1 below) particle character, among which
are relatively long irregular "gaps".

Fig.1.1.1. Schematic representation of
corpuscular-wave dualism in an electromagnetic wave. The upper
part shows an electromagnetic wave with a longer and shorter
wavelength, the lower part shows a quantum image of the
propagation of radiation in quantum - photons.
The quantum of electromagnetic waves
are called photons (this name was proposed by American chemist G.N.Lewis) - we can imagine them as a kind of small
"packages" or "balls" of electromagnetic
waves of a certain frequency, which move at the speed of light c
(lower part of Fig.1.1.1). Each photon contains a certain amount
of energy E, which is greater the greater the frequency n : E = h.n, where h is
the Planck's constant (h = 6.6251x10-34 Js). This constant
plays a fundamental role in all phenomena in the microworld. In
quantum mechanics, the "crossed out" Planck's constant h = h/2p is often used. The
photon is the basic object of the microworld, which has both
particle and wave properties, but strictly speaking, it is
neither a particle nor a wave.
In general, it is observed that in the
long-wave region of the spectrum, wave properties (bending,
interference, scattering, refraction) are more pronounced, while
in the short-wave part of the spectrum, particle properties are
more pronounced (photo effect, Compton scattering, formation of
new particles during interactions). Radiation g, even though it is
inherently an electromagnetic wave, will only behave like a stream
of particles - photons, and we will not prove its
wave properties by any macroscopic experiment; only if we became
"little green dwarfs" in the imaginary experiment,
managed to reduce to the dimensions of the order of picometers
and "entered" inside the photon, we would find out that
the photon is actually an electromagnetic wave inside...
Physical processes of
emission Þ wave or photon character of
radiation
The wave or photon character of
electromagnetic radiation is closely related to the mechanisms
and spatial and temporal scales of the physical processes in
which this radiation is emitted. In electrical
circuits (LC oscillators and antennas) of dimensions millimeters
- meters - hundreds of meters, electromagnetic oscillations of
frequencies of the order of gigahertz, hundreds of MHz or kHz
occur, which leads to the emission of continuous electromagnetic
waves (wavelengths of millimeters, meters or hundreds of meters),
in which the photon character does not manifest.
Light created by deexcitation of the outer electron shells of
atoms with dimensions of ~10-8 cm, already bears significant traces of the quantum
character of transitions between electron levels; it behaves like
a wave as well as a stream of photons. And gamma
radiation, which occurs during very fast quantum deexcitations in
atomic nuclei of ~10-13 cm in size, is already completely photonic in
nature.
Detection of
low-intensity high-energy radiation Þ manifestation of corpuscular character
How can we most easily, in normal laboratory conditions, prove
the corpuscular character of electromagnetic radiation? Above
all, instead of ordinary light, it is appropriate to use high-energy
gamma radiation and to register this radiation with a
sufficiently sensitive one-photon electronic detector
- GM or scintillation detector (§2.3 "Geiger-Muller
detectors", §2.4 "Scintillation
detectors").
When measured in a high intensity beam, the signal at the output
of the detector will be stable and continuous, in accordance with
the idea of a continuous field of radiation. When the radiation
intensity decreases, the output signal fluctuates
- statistical fluctuations (they
are analyzed in §2.11 "Statistical variance and measurement
errors"). If
we reduce the intensity of radiation even more significantly, the
detector will register time-separated discrete pulses
- responses to the passage of individual particles
through the detector.
Another possibility is the detection of
radiation using a sufficiently sensitive photographic emulsion (§2.2 "Photographic detection
of ionizing radiation"). At high radiation intensities, the film will be
continuously blackened after development according to the degree
of total exposure. However, the low intensity of the radiation
will not cause a continuously distributed response in the volume
of the photographic emulsion, but they will see individual separate
traces, as if left by individual flying particles...
Wave
properties of particles
So we see that electromagnetic waves can behave like a stream of
particles - this is one side of corpuscular-wave
dualism. But what about the behavior of (real) particles?
According to classical physics, particles behave like discrete
"pieces of matter" in all circumstances. However,
experiments with the passage of electrons, which are typical
particles in atomic physics, through fine grids *) showed that
the electrons exhibited bending and interference similar
to waves - as if the electron had "bifurcated", passed
simultaneously through two adjacent grating holes at the same
time, and then after bending, the two components interfered with
each other, as is common with waves. Bending interference
phenomena were also observed in other types of particles
(corpuscular radiation). At the same time, these interference
phenomena do not depend on the intensity of the particle flux -
the pattern does not change, even if the intensity of the
electron flux is so small that one electron passes through the
system after another!
*) Davisson-Germer
experiment
A suitable structure for performing diffraction and interference
experiments in the microworld is a crystal lattice,
the nodes of which are individual crystal atoms with typical
mutual distances of about 10-7 cm. Such electron diffraction measurements were first
performed by C.J.Davisson, L.H.Germer, and J.J.Thomson in 1927. A
beam of electrons accelerated by a voltage of U»50V was routed on
the surface of a nickel crystal. The electrons reflected from the
surface layer of the crystal atoms were registered by means of a
detector which was adjustable at different angles
("goniometer"). It was observed that the electrons did
not scatter approximately evenly in all directions, but
significantly more scattered in some directions, significantly
fewer scattered in other directions, and the minima and maxima of
the scattered electrons alternated in the scattering pattern.
When measuring the dependence of the intensity of scattered
electrons on the direction of scattering, they observed distinct
minima and maxima, corresponding to the Bragg condition
of interference, the same as in the diffraction
of X-rays on a crystal grating - that the path angle of two rays
is an integer multiple of the wavelength l: n.l = 2.d.sin J; n = 1,2,3, ..
(order of interference maximum), d is the distance between
two adjacent nodes of the crystal (lattice constant), J is the scattering
angle. The wave radiation scattered on the individual atoms of
the crystal lattice is amplified by interference in directions in
which the path difference of the waves scattered on the
individual atoms is equal to an integer multiple of the
wavelength. And the electrons for which the
"wavelength" l » h/Ö(2me .e.U) was obtained, behaved in the same way, which
corresponds to the so-called Broglie wavelength
(accelerating voltage U gives the electrons of charge e
and mass me
kinetic energy Ek = e.U and momentum p = Ö[2me .e.U], so l = h/p).

Fig.1.1.2. The wave properties of the
particles are manifested in the thought experiment of electron
diffraction at the slit by the formation of interference
patterns.
The essence of these experimental facts is
clearly illustrated in Fig.1.1.2 in an imaginary experiment,
which generalizes the results of many real experiments. The beam
of parallel flying electrons impinges on an impenetrable wall
(screen) with two slits, behind which a photographic plate is
placed. If the electrons were classical particles with
rectilinear propagation, two dark stripes would be displayed on
the photographic plate after development as shadow images of both
slits (Fig.1.1.2 on the left). In reality, however, we obtain an interference
pattern - the alternation of light and darker stripes
(Fig.1.1.1 on the right), exactly as it would occur when a plane wave
with wavelength l = h/p passes, where p = me.v is the momentum of the electron. The interference
pattern does not depend on the intensity of the incident beam, so
it is not due to the interaction of electrons in the beam. If we
attenuated the flow of electrons to such an extent that there
would be only one electron in the system at each pass, each such
passed electron would create its local ("spot")
blackening on the plate. The resulting image, which is the sum of
the spots caused by the individual electrons, would still have
the character shown in Fig.1.1.2 on the right. Thus, the
phenomenon occurs even when the individual electrons fall on the
screen one after the other: as if a single electron passed
through both holes of the screen at the same time - as if a wave
was connected to each individual electron, which interferes with
the two holes. We will return to this experiment briefly below in
the paragraph on quantum mechanics, for the
essence of which is of key importance.
The analysis of these experiments (real and
imaginary) led to the conclusion that any microparticle of mass m
moving at velocity v , can behave as a wave
of wavelength l = h/m.v = h/p, where p is the momentum of the
particle (this wavelength is sometimes
called the Broglie-Compton
wavelength). And this is the other
side of corpuscular-wave dualism. The acquired knowledge can
be summarized in the following way :
| Corpuscular-wave dualism |
Waves
with a frequency n may act as a stream of
particles (quant - photons) of energy E = h. n . |
Gateway to Understanding
Quantum Physics
The duality between waves and particles can be a "gateway"
to understanding quantum physics ! If some
contemporary quantum physicists question this, it is a
misunderstanding in the spirit of the proverb "Everyone
is a general after a battle". Without the exploration
of corpuscular-wave dualism, many newer concepts of quantum
physics would not have emerged, or would have emerged much later,
and would have been difficult to understand. Almost all phenomena
in the microworld can be clearly explained with
the help of this dualism. Particle-wave dualism substantially
alleviates that unpleasant "incomprehensible-incomprehensibility"
of quantum physics, discussed below in the section "Interpretation
of Quantum Physics".
The
quantum nature of the microworld
Classical mechanics, extended and generalized by
Einstein's special theory of relativity, together with classical
Maxwell's electrodynamics, can explain almost all the phenomena
observed in the macroworld of our experience.
Classical physics (especially Newtonian mechanics) is a
generalization of our everyday experience, according to which
material objects exist independently of the observer, have
certain positions and velocities, and move along precisely
defined paths.
However, as we learned in the paragraph on corpuscular-wave
dualism, and as we well'see even more in the next
chapters on atoms, atomic nuclei, nuclear
reactions, radioactivity, elementary particles
and their interactions, the deeper we go into microworld
of the structure of matter, the more the experimental behavior of
microsystems differs from the laws of classical physics. To
understand and describe the atomic and subatomic processes that
take place in very small parts of space and in which particles
with very small masses participate, it was necessary to
fundamentally change or supplement the basic classical ideas and
laws - to build new microworld physics, quantum physics.
Note: This "new
physics" cannot be imagined in such a way that it would
perhaps refute and destroy "old" classical
(non-quantum) physics. In science (and in physics in particular)
the continuity of scientific knowledge applies.
Quantum physics does not refute, but complements, refines, and
generalizes classical physics into phenomena that it is no longer
able to explain; it contains classical physics as a limit
case. The relationship between classical and quantum
physics is formulated as the so-called principle of
correspondence: In the limit of large quantum numbers,
the difference between quantum and classical physics is blurred,
quantum physics becomes classical. Or for large quantum numbers,
quantum physics gives the same results as classical physics (will
be shown below). Thus, although the atoms and subatomic particles
that make up everything are governed by quantum physics, their
large arrays of macroscopic bodies (including us) follow
classical Newtonian mechanics with great precision. The larger
the object, the less clearly its quantum nature...
In the
phenomenological physics of the macroworld, the particles of
which everything is internally composed, such as atoms,
electrons, protons, photons, ..., are considered hard and solid
"small bodies" or material points, moving
according to the laws of mechanics and electrodynamics. Their
sets are governed by the laws of thermodynamics, mechanics and
electrodynamics of the continuum. In addition, in the concept of
field theory, we try to interpret particles as "condensed
densifications" of physical fields.
In quantum mechanics, however, a
particle is no longer a hard and solid body or a precise point,
but only a cloud of blurred probabilities, describing
where we could find the particle during measurement or detection.
These fuzzy probabilities are modeled as quantum states
and wave functions (discussed in
more detail below).
Randomness and Probability in Quantum
Physics
As mentioned above (passage "Classical
and quantum models in the microworld"),
the basic specific feature of the microworld is stochastic
(probabilistic) character of quantum phenomena. The motion of
particles and all other phenomena in the microworld show quantum
fluctuations - chaotic variability in the positions of
particles and their velocities, field intensities, energy values
and other quantities. These physical quantities fluctuate around
their mean values; the magnitude of quantum fluctuations is
limited by the so-called uncertainty relations mentioned
below. During quantum fluctuations, the classical law of
conservation of energy and momentum, as well as other classical
laws that apply exactly in classical physics, can be violated
for a brief moment, or rather interrupted.
Quantum physics is unable to predict with
certainty the specific results of a measurement. It offers only
individual alternatives of values and their probabilities.
And the state of the studied system will change after
the measurement.
According to quantum physics, the result
of a physical process in a given system cannot be accurately and
unambiguously predicted - regardless of how exactly we know the
initial state of the system and how exactly we can solve the
relevant equations of system dynamics. The development of the
system, as well as the result of the experiment, cannot be
determined unambiguously, there are only a number of different
possible results, each of which has a certain probability
*). When we repeat a certain experiment many times, the frequency
of different results corresponds to the probabilities predicted
by quantum physics.
*) A.Einstein metaphorically likened it to
the situation, as if God always threw a dice, and only according
to the result that falls will he decide how the experiment will
turn out. Einstein never came to terms with this idea ...
Quantum theory thus points to a new
form of determinism at a deeper microscopic level: if we
know the state of the system at a given moment, the laws of
physics do not unambiguously determine the future (or the
reconstructed past), but only the probabilities of different
futures (or pasts).
The probabilities and randomities that
occur in everyday life are a reflection of inaccuracies in the
knowledge of initial conditions and other, often complex,
influences. When we shoot an air rifle at a target, shots with
different probabilities hit different places on the target around
the center, depending on the dexterity of the shooter. This
probability is not a property of the shots moving towards the
target, but is caused by ignorance and variability of shooting
circumstances. If we fastened the airgun in the vice, the shots
would fall into one precisely focused place. However,
probabilities in quantum physics express a principled
randomness, that is inherent in the very nature
of phenomena. The microparticles
targeted and transmitted under the same initial conditions will
always fall to a slightly different location around the center of
the target.
To the seemingly
trivial question "Where something is ?" classical
science responds in such a way that "Every thing is in one
particular place", as our common experience in classical
physics based on Newton's foundations shows. In the microworld,
it turns out to be different: subatomic particles can be
"simultaneously in several places". Their exact
coordinates are subject to quantum uncertainty relations (they
fluctuate) and obtain their specific values only at the moment
when we start measuring them (at the moment of interaction). It's
as if something only starts to exist the moment we "look
at" it (discussed below in the section
"Observations and Measurements
in the Microworld") ...
Is quantum stochasticity
fundamental, or is it caused by hidden unknown parameters ?
Anyone who begins to learn about quantum mechanics, upon deeper
reflection, is surprised by a certain "inappropriateness"
of the behavior of particles and systems, contrary to common
sense and natural experience. Is this surprising and
incomprehensible behavior really fundamental, or are
there some other hidden and unknown influences behind it - hidden
parameters ? In such a case, standard quantum physics would
be an incomplete theory, and its stochastic character
would be the result of ignorance of some hidden (yet
unavailable to us) parameters that take on different values. The
behavior of these parameters should be described by some future
more "fundamental" theory, probably within the
unitary "theory of everything".
Let's go back for a moment to the simple
example of shooting an air rifle. If we were to shoot in open
space at a target approx. 50 meters away, we would observe a
relatively large dispersion of hits. If we could not measure the
variable speed and direction of the wind, small variations in the
size and shape of the shots and other possible influences, we
could in principle empirically build a kind of "quantum
mechanics of the movement of the missiles" that would
show the fundamentally stochastic nature of the
trajectory of the shots..?..
No such additional hidden
parameters have been found in the quantum mechanics of microworld
particles. System analysis of the possibility of influencing
measurable quantities in quantum mechanics by hidden parameters
was dealt with by J.Bell in 1964, who established limiting
inequalities for the results of measuring the polarization
of two photons from a quantum "entangled" pair.
Experimental measurements were carried out in the 80s on photon
pairs during cascade transitions in calcium atoms with correlated
polarizations. The experimental results somewhat exceeded the
values of ±2 in Bell's inequalities, which is some indication
against the concept of hidden parameters...
Current quantum physics is generally
inclined to the opinion that the quantum state represents a
complete description of systems, and quantum stochasticity and
uncertainty relations have a fundamental character that
cannot be derived from anything..?.. So it seems that randomness
is somehow incomporated in the deepest essence of our world ?
Other unusual phenomena related to quantum
entanglement are discussed below in the passage "Quantum
entanglement and teleportation. Quantum computers.".
Statistical fluctuations
and noise in imaging
The emission of radiation quantum, as well as its
interaction with atoms of the material environment (and thus the
mechanisms of radiation detection) takes place at the microscopic
level through events governed not by deterministic laws
of classical physics, but by the laws of quantum
mechanics. These quantum regularities are in principle
stochastic, probabilistic. The transitions of electrons
in atoms or the transformation of radioactive atoms is therefore
largely a random process and the resulting
radiation is emitted randomly, uncorrelated, incoherently *).
Therefore, the radiation flow is not smooth, but fluctuating.
The response will be just as fluctuating of any
device detecting and displaying this radiation - these are
fluctuations which cannot be eliminated by any
improvement of the device or method, these fluctuations have
their origin in the very essence of the measured
phenomena.
*) The fact that LASER emits coherent
photons is due to the fact that it is not a spontaneous, but stimulated
production of photons.
Statistical fluctuations (noise) in
measurements and images are therefore a general
phenomenon. They are also hidden in ordinary light
during optical vision and photography, where we do not observe
them due to the large number of photons (of the order of 109), which are available
here. At the top of the image is a photographic portrait exposed
with varying numbers of photons of light. We see that if the
image consists of less than 103 photons, we do not recognize anything at all in the
image except scattered clusters of dots. With the increasing
number of photons, the quality of the image improves (above 105 photons we begin to
recognize the basic motif) and at about 108 photons we get the usual photographic image with all
the details, without noticeable noise.

Influence of registered number of photons on image quality in
terms of statistical fluctuations (noise) - image quality
improves with increasing number of photons.
Above: Photographic portrait exposed
with different number of photons of light (computer
image processing performed by Ing.J.Juryšek) .
Bottom: Gammagraphic image of a phantom
(Jasczak, filled with 99mTc radionuclide) accumulated by a scintillation camera with different
numbers of g- photons in the image.
In practice, statistical
fluctuations are unfavorably applied wherever we do not have
enough number of quanta (photons) displaying radiation. This is
especially true for radiation detection, spectrometric and
imaging measurements. The influence of statistical fluctuations
on the results of these measurements can be expressed simply (but
concisely) by the following rule: If we measure N pulses on a
radiation detector, we actually measured N ± Ö(N) pulses. These
statistical fluctuations are reflected in all cells of the image
and the only way to reduce them is to increase the
accumulated number of pulses - the number of
"useful" photons g, which results in a response in the image. An image is
sharp and clear when it is created by at least 1 million
photons/cm2.
This is difficult to achieve with gamma images, in practice we
often have to settle for about 500-1000 photons/cm2. Therefore,
scintigraphic images tend to be quite "noisy".
Statistical fluctuations degrade image
quality mainly due to the loss of useful structural
details. This can be seen at the bottom of the figure in
the images of the phantom modeling "cold" lesions of
various sizes in a solution of g- radionuclide 99mTc. If the image
consists of less than about 104 photons g, no structure is seen, only statistical fluctuations.
With a larger number of registered photons g of about 105, larger lesions are
visible, and only with 107-8 photons, even the finest structures with small lesions
are shown.
In addition to gammagraphic images,
statistical fluctuations are also reflected in astronomical
images of distant objects, from which very little light
falls on us.
The essence and
interpretation of quantum physics
A systematic interpretation of quantum physics is outside the
thematic scope of this treatise *) and would also take up an enormous amount of space (reference can be made to standard textbooks and
monographs, eg Landau, Lifšic: Quantum Mechanics). We will only take a brief excursion into the ideas and
laws of quantum physics to outline some basic common
principles applied decisively in processes with atoms,
atomic nuclei and elementary particles.
*) After all, fully understanding the essence
of quantum laws and internally identifying with them is
not at all easy - if not impossible! It is said
that the theory of relativity is "understandable -
incomprehensible", but quantum physics is
"incomprehensible - incomprehensible"..!.. Even the
best professional specialists in quantum physics (including its builders such as Bohr, Schrodinger,
Pauli, Feynman, Fermi, Dirac, Heisenberg, ...) admit, that they can very accurately analyze the
results of quantum processes in atoms, nuclei or in particle
interactions, but when someone asks them why it
behaves like that, they don't know..
Quantum physics in the
micro world - but also in the macro world ?
Quantum physics arose during the study of phenomena in the
microworld - at the level of atoms, atomic nuclei, elementary
particles. And it also has its main application there... Quantum
mechanics, however, claims universal validity
not only in the microworld, but also in the macroworld (even in the megaworld, see e.g. §5.5 "Microphysics
and Cosmology. Inflationary Universe."
in the book " Gravitation, black holes and the physics of
spacetime"). The usual idea is that
the application of quantum physics is determined by the size
of the investigated objects: small objects behave quantumly,
large objects classically. In reality, however, it doesn't always
have to be this way. What makes an object quantum or classical is
not so much the geometric size, but the number of degrees
of freedom available to the object. With a small number
of degrees of freedom, the object behaves quantumly. Small
objects such as elementary particles (with
a simple structure, or without structure)
have a small number of degrees of freedom and behave uniquely
quantum. Larger objects, composed of a large number of particles,
have a large number of degrees of freedom and behave classically
because the values of their state variables are averaged over
many degrees of freedom.
Under certain circumstances, even
relatively large macroscopic objects, such as a laser beam of
coherent photons, a laboratory container with superfluid helium,
or a stream of Cooper electron pairs in a superconducting wire
can have a small number of degrees of freedom. An extreme case of
long-range quantum behavior can be states of entangled particles
(see below "Quantum entanglement and teleportation. Quantum
computers."). The specific
situation is with quantum processes involving black holes (it is discussed in detail in §4.7 "Quantum
radiation and thermodynamics of black holes" of the mentioned monograph).
For ordinary bodies of macroscopic masses
and dimensions, quantum effects are completely tiny and
unmeasurable. However, in advanced sensitive experiments, quantum
properties can be observed in increasingly large objects (such as
macromolecules)...
Wave
stochastic description of particles and systems. Interpretation
of quantum physics.
In classical (non-quantum) physics, the state of a physical
system is described using directly measurable quantities, such as
positions and momentum of particles. In quantum physics, the
state of a particle is described by a wave function
(see below), the
square of which indicates the probability that the
particle is in a particular state. The wave function is not a
directly measurable physical quantity, but rather a model idea.
When a particle interacts with another particle, there is a decoherence
(loss of mutual spatial and temporal
connection of phase and amplitude) of the
wave function, leading to the particles acquiring a specific
measurable state as in classical physics. However, this is only a
probability that we measure a certain value of a state
quantity at some place and time. It is not possible to predict in
advance which value will be measured in a specific case, it is
only possible to determine the probability distribution
of the occurrence of different measured values with a larger
number of measurements (under the same conditions).
From a gnoseological point of view,
however, it must be kept in mind that all these are only
mathematical models, enabling the description
and quantification of phenomena in the
microworld. Their physical nature is probably
hidden somewhere deeper ..?..
Simultaneously with the building of its
own quantum mechanics and its mathematical formalism, have been
created several ways of interpretation quantum
laws and heuristic methods of creating a chain of conceptual
structure of quantum physics. We will usually follow an inductive
procedure based on a gradual analysis of experimentally
established facts (we will analyzed it
physically, without debatable philosophical speculations). The most common approach is the so-called Copenhagen
interpretation quantum mechanics, founded by a physics
group led by Niels Bohr. According to her, during the
measurement or interaction, the wave function "collapses"
*) (originally describing the superposition
of possible states) - to reduce quantum
alternatives. This forces the particle to probabilistically
"choose" only one final state and position (which was uncertain until then),
as it is in classical physics. During this collapse, the original
information is not preserved, which can no longer be detected -
the particle is described by a completely new wave function from
the moment of measurement or interaction.
*) "Wave
function collapse" is just a model
mathematical abstraction, it is not a real physical
process! If we were to take seriously the collapse of
the wave function all at once in all space, it would essentially
mean that we "throw away" one universe and replace it
with another universe with a new wave function. Such an idea
would already be close to the many-universe Everett hypothesis.
Of course, nothing like that happens in reality.
And no anthropomorphic
"conscious" observer is necessary; interaction
processes take place in innumerable quantities spontaneously in
inanimate and living nature. Our "observations" are
only rare accidental "probes" into these processes.
In the passage
"Mystical
Quantum Physics? ",
we mention H.Everett's somewhat bizarre multi-cosmic
interpretation, according to which the measurement or
interaction does not collapse the wave function, but creates parallel
realities ("universes") in which all possible
states of the resulting particles exist; these particles can then
no longer interact with each other. At the end of this general
part, we will briefly mention Feynman's approach of quantizing "path integrals", which gives some opportunity to understand the internal
causes of quantum behavior.
Superposition of different states
and collapse of the wave function: sometimes a misinterpretation
of quantum physics ?
However, the concept of "wavefunction collapse"
is only a theoretical model that can be misleading. This
is shown, for example, by a simple (Stern-Gerlach) experiment, in which neutral atoms, vaporized in a
suitable source, are accelerated and allowed to pass through an
inhomogeneous magnetic field formed by two pole extensions placed
one above the other. After passing through, they will hit the
detection plate. Atoms with different spin states will be in mag.
fields behave differently. According to the polarity of the
magnetic field, atoms with spin +1/2 will be deflected upwards,
atoms with spin -1/2 will be deflected downwards. Under normal
conditions, the probability of neutral atoms having spin +1/2 or
-1/2 is 50%/50%, so an equal number of upscattered and
downscattered particles will be detected. We then know with
certainty that atoms absorbed on the upper side have spin +1/2
and those absorbed on the lower side spin -1/2. There was no
"collapse of the wave function", only before the
measurement we did not know the specific spin state of the
particles, we only knew that it could be +1/2 or -1/2. After the
measurement, we know the spin state of the detected particles -
which were already emitted from the source with this state.
The particle is not in all possible states
at once before observation-measurement - it is only in one
state, which we do not know. Before the measurement, we can
only determine the probability of what state it could be
in. And after the measurement, we know the specific condition for
sure. We will discuss the frequently occurring
misinterpretation of quantum mechanics further below in the
passage "Schrodinger's cat".
Wave
function
Let's go back to corpuscular-wave dualism (Fig.1.1.1 and 1.1.2),
which is an important characteristic feature of the quantum
understanding of the microworld - it suggests that the
division of matter into waves and particles is only formal; in
general, we must consider corpuscular and wave properties
simultaneously. The particle does not move along a fixed
localized path, but as if it "waves" along a blurred
path, it behaves like a Broglie wave.
What is the physical significance of
Broglie waves associated with particle motion? The first
straightforward notion that the particles themselves are
waveforms does not hold up, because in some processes, especially
scattering, we could in principle register "parts of the
waves" as "fragments" of the particle, contrary to
experimentation. Even the opposite idea that waves are formations
composed of particles is unsatisfactory (no
particles originating from the wave were observed, only the wave
can behave as a quantum with the properties of the particle when
interacting). A more adequate idea of the
relationship between waves and particle motion can be obtained by
studying the diffraction of electrons, which we register on
photographic film (Fig.1.1.2). If only a small number of
electrons pass, we get an irregular image scattered on the film,
but after passing a large number of electrons, we get a smooth
regular pattern analogous to the diffraction patterns of light
waves. This fact leads to a statistical interpretation
of Broglie waves: that the intensity of Broglie waves at any
place in space is proportional to the probability of the
particle occurring at that place. The classical
trajectory of a particle is replaced by a kind of
"probability cloud", representing a set of places where
a particle occurs with different probabilities.
In quantum mechanics, the state of a particle (or a
set of particles and generally every physical system) is
described by the so-called wave function y(x, y, z) (in the simplest case of an isolated particle, this wave
function is identical to the Broglie wave).
The physical meaning of the wave function is that the square of
the modulus of the wave function ú yú 2 determines the probability dW that the
particle at a given time t is in the element of volume dV
= dx.dy.dz around the point (x, y, z): dW = ú yú 2 .dx.dy.dz. And the mean value of any physical quantity
F(x, y, z), which is a function of the coordinates x, y, z, is
then given by the relation ` F(x, y, z) =ò F(x, y, z).ú yú 2 .dx.dy.dz, where it
integrates over the whole field of variables x, y, z.
Note: The wave
function y is generally introduced as a complex function
(containing both real and imaginary components), so the square of
the modulus ú yú2 = y . y*, where y* is a complex
associated function by y. For the simplest case of a free particle moving in the
direction of the x- axis with momentum px , the wave function
is written in the form y = exp[- i/h (E.t - px.x)], representing a
plane harmonic wave.
Observation and measurement in the
microworld
"Things can
be observed without disturbing them" - this is an experience of everyday life,
especially from visual observation by an "uninvolved
observer". However, the process of observation
or measurement *) in the microworld differs
diametrically in its nature and consequences from the processes
of measurement and observation in classical physics describing
the macroworld.
*) The terms "observation" and
"measurement" are often not distinguished: quantitative
observation is a measurement.
In the physics of classical
systems of the macroworld, it is tacitly assumed that
the process of observation (measurement) does not disrupt
significantly their movement or evolution. The relevant physical
quantities can be measured with sufficient accuracy without
disturbing their values or disturbing the development of the
observed system. Or we assume that any failure caused by the
measurement can be accurately corrected, at
least in principle.
E.g. when measuring the voltage in the electrical
circuit, we use either a voltmeter with a sufficiently large
input resistance, which practically does not affect the measured
value, or if this is not possible, we can know the impedances in
the circuit and the voltmeter to accurately correct the voltage
change. However, experienced electronics experts know that when
measuring extremely weak electrical signals (in which only a few
hundred electrons participate), unremovable noise and
fluctuations are applied, and all correction methods already fail
here.
The most common way to examine the
position of an object is to visually observe it:
we illuminate the observed object with light (unless it is itself a source of light) and our eyes register reflected photons of light. If the
observed body has a macroscopic size and mass (such as an apple or a stone), the
incident and reflected photons of light do not appreciably affect
the position of the body and the basic premise of a "non-participating
observer" is met. However, if the body is of
microscopic size and mass, the impact of each photon can
significantly affect its position and velocity - all the more so
the more accurately we try to determine the position (accurate measurement of the position of a particle can
completely "throw off" its momentum!). For a more accurate localization of the particle
position, the wavelength of the irradiating wave must be short
enough, ie the energy and momentum of the quanta is
correspondingly higher - it causes a more
appreciable disturbance of the observed system
(position and velocity of the particle).
Here we will no longer observe directly with the eyes,
but through an instrument
(eg microscope incl. electron microscope, particle detector,
radiometer, spectrometer), while for
observation of particles of very small dimensions it is necessary
to use radiation with a correspondingly short effective
wavelength. The subjective role of the observer
is often overestimated in connection with
quantum mechanics (it comes from the time
of the origin of quantum physics) and
sometimes even the objective reality as such is questioned. This
is a misunderstanding! Natural processes with innumerable
interactions of particles and fields are constantly taking place
in nature and their results are independent of us.
Only our occasional probes into the events of the microworld are
burdened by fundamental quantum uncertainties. However, this is
not a consequence of our subjective intervention as a conscious
observer, but the influence of the interaction of objectively
existing particles with sensors and instruments used for
observation or measurement (it is briefly
discussed below in the section "Mystical Quantum Physics?").
The oft-cited claim that "observation
creates reality" is misleading and erroneous:
this reality has been there already before, the
observation has only "illuminated" it for us - and may
have changed it, due to quantum influence at the microscopic
level.
So in order to "observe" and
measure a microparticle, we must let it bounce off it
some other particle or quantum of radiation and observe only the
result of this reflection - more generally the result of
the interaction. The inevitable consequence of such a
process is that the collision or interaction
irretrievably changes the state of the monitored
particle - it deviates it, changes its velocity, or even the
internal structure. In general: in order to observe an object or
system, we must interact with it. Only in this
sense can the reality in the micro world be influenced by
mere "observation" !
Thus, the operations (processes) of
observation or measurement necessarily affect the
physical system (disrupt its evolution), while for small
systems *) this
disruption is considerable and irreversible, it has a principled
character and cannot be eliminated or corrected in any
way; and by no improved method - it is the very essence
of things and processes themselves! Quantum mechanics deals with
the behavior of such systems and the processes of measuring their
physical quantities.
*) In the microworld, the term "small"
loses its usual relative character and becomes an objective absolute
attribute determining the quantum behavior of a
given system.
"Observer "
it tends to be one of the most misunderstood concepts in the
interpretation of quantum mechanics (next
to stochasticity, interference of states or collapse of the wave
function...). From an objective point of
view, an observer is some "classical" (non-quantum) object *) that interacts
with a given system, here a quantum one, in order to investigate
some of its properties. Depending on the type of phenomenon being
investigated and the experimental configuration, this
"observer" can be an electronic or optical measuring
device, a mechanical body, or therefore a person (or even another biological organism...). As a result of the interaction, we can then obtain the
proper value of a certain quantum number.
*) Each such "classical" observer
is internally also composed of a huge number of quantum
particles, but their fluctuations are averaged out, so for all
practical purposes they behave like classical...
Quantum theory: ontological physics +
epistemological measurement
In quantum physics, two aspects are closely intertwined, in
feedback, which from a philosophical point of view are called ontological
(what is the actual physical reality) and epistemological (how
to know this reality) :
--> On the basis of experience from classical mechanics and
electrodynamics, we create models of the studied systems,
generalized so that they correspond to the specific laws of
atomic, nuclear and particle physics.
--> We let these particles and fields interact with a
classic measuring system and monitor its response.
This is the only possible method of
measurement, that simultaneously produces the observed stochastic
quantum regularities....
Mystical quantum physics - "quantum
mysticism" ?
Quantum physics is from a
philosophically point of view often falsely interpreted.
From the above fact that reality in the (micro) world can be
influenced by observation, mystical claims are
drawn that "the human mind creates reality",
or "quantum mechanics connects the human mind with the
universe", or "quantum physics creates the
unity of human and cosmic consciousness", is the
essence of "freedom of will" and the like. The
basic mistake or misunderstanding here again results from the
above-mentioned overestimation and misunderstanding of the role
of the subjective "conscious" observer. It is
not our mind that makes observations, but the very interactions
of the basic particles (objectively existing), which take place even
without us. They change the quantum state of systems and
transmit information, our mind only registers and processes it.
In fact, it is an objective reality, whose laws
of which (including quantum ones) determine the behavior of our minds and the functioning
of the entire universe. This approach corresponds to all the
results of our observations so far, it is fully consistent with
them.
The finding that causality and determinism
are disrupted in some phenomena in the
microworld led to a hypothetical connection between quantum
physics and free will. We have a certain
legitimate sense of free will - that we can decide what we will
do today or what we will plan for tomorrow; that it is mainly up
to us, it is not only external circumstances that decide.
However, from the point of view of science, real free will is
only an illusion. Above all, we cannot do
something that is contrary to the laws of nature; and other
things prevented by certain other circumstances... "Freedom
of will" emerges from an inexhaustible number of
interactions and their results, we do not need quantum physics
for it (see also the discussion in the
section "Determinism-chance-chaos?" §3.3 in the book "Gravity,
black holes and space-time physics") ..?..
Infinitely many
parallel universes ?
The stochasticity of the behavior of particles and systems
according to quantum physics also gave rise to H.Everett
's somewhat fantastic hypothesis of an infinite number of
universes : with each attempt to discover reality - with
every interaction of particles - the whole universe splits,
branches or "duplicates" into
two or more "universes" in which the individual
possible results of the interaction take place (with the appropriate probability).
This creates a constantly infinite number of "parallel
worlds", in which all possible alternative futures (and pasts) are
"real"..?..
In some such
universes, for example, an asteroid would have missed our planet
60 million years ago, and dynosaurs would still rule the Earth
(or even create a civilization instead of humans) ..?..
However, available for us (ie "real") is only
the the universe in which we are at the moment; observations can
only be made in "our world". Alternative events in
parallel universes can only be imagined ...
There have also been
sci-fi hypotheses that parallel universes can be influenced
at the quantum micro-level (and therefore also affect
our world). Their quantum (particles) can "seep"
between individual universes and evoke some "bizarre"
effects of quantum mechanics..?.. They are all just
unsubstantiated assumptions ...
On the astronomical
and philosophical context of several universes - multiverse
- see, for example, the work "Anthropic
Principle or Cosmic God",
or §5.7 "Anthropic Principle and Existence of Multiple
Universes" monograph
"Gravity, Black Holes and the Physics of Spacetime".
In the microworld, the order of measurements
is important. E.g. on whether we first measure the position of
the particle (thereby disturbing the momentum) and then only its
existing momentum, or vice versa (by measuring the momentum we
first disturb the position). The more accurately we measure the
position, the less accurately we know the momentum of the
particle - and vice versa. This leads to the principle non-commutativity
of quantum mechanics, expressed in quantum uncertainty
relations (see below).
The term "state"
of a physical system means a situation where
this system is in a configuration (state) with a certain value of
a given physical quantity. In classical physics, for example, the
state of a particle is described by entering the position and
velocity resp. momentum (as a function of time). In quantum
physics, the situation is more complicated, the so-called state
vector, denoted by |y>, is introduced here, where y only symbolically denotes a
state quantity, which, however, does not have a certain value,
but can be a superposition of several
states. E.g. the electron in terms of spin (see
below) may be in the spin state |1> with spin-oriented "up" (z-component spin
projection has a value of + 1/2
h ), or in the state |2> with spin - 1/2 h. However, it can also be
in a more general state |y>, which is a "mixed" superposition of
"pure" states |1> and |2>, which is written in vector: |y> = a1 . |1> + a2 . |2>. This state |y> means that
the probability a12 we measure a value of + 1/2
h and the probability of a22 we can measure the value of - 1/2
h. In general, a superimposed state can be made up of
multiple components: |y> = a1.|1> + a2.|2> + ... + ai.|i> + ... General |y> is therefore a state where a given physical quantity
does not have a certain value, but only the probability
ai2 measurements of individual potential values
"i". Quantum physics is a mathematical algorithm
(computational scheme) that can determine these coefficients ai - but does not
specify the internal physical nature of these phenomena. In the
state |y>, before the measurement, the system has the value of
the given physical quantity indeterminate (potentially
different values are possible) and only the measurement concretizes
this value. Even under the same initial conditions, we always
measure different values of physical quantities,
statistically divided around the mean values determined by
probability coefficients ai2.
Operators.
Uncertainty relation.
Observation or measurement operations are modeled in quantum
mechanics using so-called operators. Each physical
quantity A is assigned in quantum mechanics the operator
A^, which
satisfies certain mathematical conditions (it is linear and
Hermitian). By ^A we mean a rule that assigns to each function u(x) some
other function v(x) - symbolically we write v = ^A u. The operator ^x assigned to the
coordinate x is a simple multiplication of x, while
the momentum operator ^p is given by the derivative according to x
coordinates :
^x ® x, ^p ® - i h . ¶ / ¶ x.
The Planck constant h got here to hold the
relationship between the momentum of a particle and the
corresponding frequency of the Broglie wave in corpuscular-wave
dualism. Other physical quantities - energy and momentum - will
be discussed below.
For operators in quantum mechanics, it is important that
the sequential application of two operators does not have to be
commutative, ie it may depend on the order. For two operators ^A and ^B, the so-called commutator
is defined by the relation [^A, ^B] = ^A ^B - ^B ^A, i.e. the difference between the application of the
operator ^A
and then ^B,
minus the same operators applied in reverse order. This
difference is generally not zero as in classical physics, as each
observation (measurement) in the microworld can cause a system
violation and thus affect the result of the second observation
(measurement), so that the two procedures can provide different
results. The coordinate and momentum operators satisfy an
important commutation relation [^x, ^p] = i . h .
This commutation relation is related to the key
principle of quantum mechanics, the so-called Heisenberg quantum
uncertainty principle, which states that the position x
and momentum p particles cannot be
determined exactly at the same time *), but that the
uncertainties of these two (complementary) quantities are given
by the relation Dx . Dp ³ h. Every
measurement of a particle's position irreversibly perturbs its
momentum - and vice versa. Therefore, it is not possible to
investigate the exact specific path, along which the particle
moves...
*) Quantum "blur",
implied by uncertainty relations, is mostly negligible and
unobservable in the macroscopic world, but on an atomic and
subatomic scale it becomes absolutely decisive!
This quantum uncertainty is an expression of the basic
property of observation and measurement: that it is always an interaction,
irreversibly affecting the parameters of the measured system. The
same uncertainty applies sessions between other dynamically
coupled quantities, eg. between time t and energy
E : DE . Dt ³ h , further
between potential and kinetic energy, etc. This complementarity,
whose "prototype" is corpuscular-wave dualism, is
characteristic of quantum physics.
Characteristic
equations. Discrete values of physical quantities.
When applying operators to wave functions, are especially
important cases where the result of the operator ^A applied to the
function y(x) results again are the same function y(x) multiplied by a
certain number a : ^A y(x) = a. y(x). In general, to each operator ^A belongs a set of numbers an and a set of functions yn, for which the so-called characteristic
equation applies
^A yn (x) = a n . y n (x) .
Numbers (coefficients) an are called proper (characteristic) values
and yn corresponding own (characteristic) function of the
operator ^A.
Eigenvalues an of operator ^A then represent possible values, which
may be a physical quantity a corresponding operator ^A take. Said equation
is a differential equation for the wave function of the state in
which the quantity represented by the operator ^A has the value a.
Eigenvalues satisfying this equation generally do not take on all
possible values, but only certain ones discrete values,
in accordance with experimental knowledge about discrete
(quantum) values of physical quantities in the microworld -
energy of atoms, magnetic moments, spins... It turns out that
energetically (field) bound particles in the microworld belong to
discrete values of energy, momentum and other quantities - we
call them quantum physical quantities. These
discrete characteristic values, expressed as multiples of their
respective elementary value (usually Planck's constant h),
are called quantum numbers.
Quantum
energy. Schrödinger equation.
Similarly to classical mechanics, also in quantum mechanics the
key concept is energy E. Energy E
(consisting of potential energy U and kinetic energy T:
E = T + U) is assigned in quantum mechanics an energy operator
called Hamilton's operator, which for the
simplest the case of a particle of mass m has the form
^ H = - ( h 2 / 2m). D + U,
where D
s ¶2/¶x2
+ ¶2/¶y2
+ ¶2/¶z2
is the so-called Laplace differential operator. The
proper (characteristic) equation of the Hamiltonian operator
^ H y n = E
n . y n
is called the stationary Schrödinger equation.
Its solution for a particle is the wave functions of the
stationary states of the particle in the potential field, in
which the particle acquires discrete energy values En (for continuous and discrete energy values,
see the note below).
The time evolution (motion) of the quantum state of a
microparticle is then described by the nonstationary Schrödinger
equation
^
H y =
i h .
¶y / ¶ t ,
which contains the time derivative of the wave function.
Solutions of the stationary Schrödinger equation
indicates what possible stationary physical states
might particles in a given force field to acquire, via
nonstationary Schrödinger equation can in principle determine
the probability with which the particles pass
from one quantum state to another. It can be said that
Schrödinger's equation has a similar position in quantum
mechanics as Newton's laws in classical mechanics. Among other
things, all the quantum properties of the structure of atoms flow
from it, which will be discussed below (especially discrete
energy levels).
Continuous
and discrete energy - quantized
In classical physics, energy can acquire
all possible values continuously; by doing work, the energy of
bodies in a certain system can be changed arbitrarily. In quantum
physics, the situation is more complicated. The energy values are
the solution of the (stationary) Schrödinger equation given
above. In the simplest case of a free particle
(U = 0), this equation has the form ( h2/2m). Dy + E.y = 0 and its solution are wave functions of the form y = const. e i/h(E.t-p.r), for any energy values E, where E = p2/2m. Each such
function (plane wave) describes a state in which a particle
acquires a certain value of energy E and momentum p
, where the frequency of such a wave is E/h and the wavelength l = 2ph/p is the Broglie wavelength of the particle. The energy
spectrum of a free-moving particle is therefore continuous,
the energy can take values from 0 to ¥ - the energy of a free
particle is not quantized.
If the particle is in the potential field U(x, y, z),
then the motion of the bound particle with
energy E <0 has a discrete spectrum energy
levels, while for positive energies the particle is not bound and
its energy can take on a continuous spectrum. A typical model
case of quantum motion of a bound particle is the motion of a
particle in a potential well - in the simplest
case a one-dimensional motion bound to a line of length L
between two perpendicular walls (infinitely high), from which the
particle reflects perfectly elastically. Such a line-segment
motion of the particle corresponds the Broglie wave, which is
reflected on the walls, while the superposition of the waves
reflected from both walls creates a "standing wave".
Thus, an integral number of half-waves of standing Broglie waves
is formed on the line segment of length L, ie L = n. l/2, where n =
1,2,3, ... The motion of a particle in a potential well therefore
correspond only to certain discrete values of
the wavelengths of Broglie waves ln = 2.L/n , n=1,2,3,... The Broglie wavelength is related
to the momentum of the particle, l = h/p, so that the momentum
of the bound particle pn = h/ln = n.h/L and its energy
En = pn2/2m = n2 .h2/8m.L2 will have discrete
values *). The state of a particle in a potential field,
which corresponds to a standing Broglie wave ln , represents a certain stationary state
of the particle. It is a state with a certain energy En - energy
level of particles in a potential field in a given
steady state. The number n is then called the quantum
number of this steady state. The state corresponding to
n = 1 is called the ground state and corresponds
to the lowest energy level of the particle bound in the potential
field. The change in the energy of a particle is associated with
the transition (jump) to another stationary
state, which is accompanied by the emission or absorption
of a quantum (photon) with energy equal to the
difference of energies of both stationary states (energy levels).
These laws find their application below in Bohr's model
of the atom.
*) At large values of quantum
numbers n, the energy differences of individual
quantum states with quantum numbers n+1 and n are small -
the ratio En+1/En = [(n+1)2-n2]/n2 is close to 1. Thus, the energy changes at individual
higher quantum levels energies are negligible - energy can be
considered continuous here; the results of quantum mechanics at
higher quantum numbers basically correspond to the results of
classical mechanics - the principle of correspondence
.
The actual energy spectrum of particles in
the microworld can be discrete or continuous, depending on the
process by which the particles form, gain energy and are emitted.
The continuous energy spectrum has eg braking
radiation, radiation b, Compton scattered radiation g. Other spectra are discrete,
quantized, line - eg radiation a and g, radiation spectra of
excited atoms, characteristic X-rays, conversion or Auger
electrons. A certain intermediate species between continuous and
discrete spectra are band spectra, where
individual quantum states are separated only by very small energy
intervals and the resulting spectrum appears to be continuous
within the resolution of spectrometric instruments.
The specific mechanisms of particle emission and energy recovery
will be discussed in more detail in the description of the
radiation of atoms and atomic nuclei in radioactivity and other
processes.
Permitted and forbidden
transitions
From the point of view of classical physics, only such events can
take place in which the laws of conservation of
energy, momentum, angular momentum are fulfilled
at all stages. Of course, such processes, called permissible
transitions, can also take place according to quantum
physics in the microworld. They take place very
"willingly", their speed (effective duration of
transition, transformation, interaction) depends on the type of
force that causes it. The fastest are transitions caused by
strong interaction, followed by electromagnetic processes and
finally transformations caused by weak interaction.
However, some such events can take place
in the microworld, in which these classical laws of
conservation are violated at some stages - the so-called
forbidden transitions. We can simply imagine that a
particle (within its permanent quantum
oscillations and fluctuations) constantly
"tries" it again and again until it manages to
"break through" the barrier of prohibition. The wave
function of the particle is spread in the phase space and can
partially interfere with areas where the transition can
"bypass" the violation of the law of conservation.
Prohibited transitions can in principle take place, but with less
probability. A typical case is the tunneling
phenomenon of the passage of a
particle through an energy barrier described below, or forbidden
transitions between the energy levels of electrons in the
envelope (see "Excitation and radiation of atoms" below) or between the energy levels of nucleons
in the nucleus (§1.2, part "Radioactivity gamma", passage "Nuclear isomerism and
metastability") due to higher differences in angular
momentum (multipolarity) than the emitted photon is able to
carry.
Quantum angular momentum. Spin. Magnetic
moment.
One of the important physical characteristics of the motion of
material bodies in space is the angular momentum
- a vector quantity quantifying mainly the rotational motion
of bodies. The law of conservation of angular momentum *)
provides a number of useful data on the properties of motion.
*) The law of conservation of angular
momentum is a consequence of the invariance of physical laws
(Hamiltonian of system) to spatial rotation by
any angle - isotropy of space. This property applies not only in
free space without fields, but also when moving in a centrally
symmetric field, where, however, the invariance to rotation
applies to rotation around the center of the field. The angular
momentum therefore plays an important role in observation the
motion of planets and in analyzing the motion of electrons around
the atomic nucleus in its central field.
The angular momentum of a particle (mass point) in
classical mechanics is a vector quantity L,
which is defined as the vector product of the position vector r
and the momentum vector p : L =
[r x p], or in components in the direction
of the x, y, z axis: Lx= y.pz - z.py, Ly= z.px - x.pz, Lz= x.py - y.px. By replacing the components of coordinates and
momentum with the above mentioned operators, we obtain the
operators of the angular momentum components: ^Lx= h/i (y.¶/¶z - z.¶/¶y), ^Ly=
h/i (z.¶/¶x - x.¶/¶z), ^Lz=
h/i (x.¶/¶y - y.¶/¶x). In vector it can be written ^
L = [^r x ^p] = -i h [r x Ñ],
where Ñ is the vector form of the Hamiltonian differential
operator. The characteristic equation for the angular momentum is
customary (without prejudice to generality) to investigate for
the component z : ^Lz y = lz . y, in spherical
coordinates r, J, j. Her solution is (we cannot break
down mathematical details here) : y = f(r,J). ei. lz.j, where
f(r, J)
is an arbitrary function of the radius r and the angle J. In order for the
characteristic function y to be unambiguous, it must be periodic with respect to j with a period of 2p, so it must be:
l
z
= m. h , where m = 0, ± 1, ± 2, ....
The eigenvalues of the angular momentum lz are therefore quantized- can be equal
to positive and negative integer multiples of the Planck constant
h including
zero. This result is important in that it quantum-mechanically justifies
Bohr's basic postulate model of the atom, which is
discussed below ("Bohr's
model of the atom").
In addition to the components of the angular momentum L,
its absolute magnitude L º |L| = Ö(L2) is also important in
mechanics. The characteristic values K of the angular
momentum square are determined by the equation ^L2 y = K.y. A relatively
complex and lengthy mathematical analysis (again
using here e.g. the requirement of uniqueness of the
characteristic function y leading to the periodicity 2p) can
be used to obtain the formula for the characteristic values of
the square of the angular momentum
K
= h 2 . l (l + 1) ,
l = 0, 1, 2, ...
Characteristic values of the operator of the absolute magnitude
of the angular momentum |L| then they are :
| L |
= h . Ö [l (l + 1)] , l = 0, 1, 2, ...
At a given value of the number L, the angular momentum
component Lz can take the values Lz = L, L-1, L-2, ..., 0, -1, ..., -L, ie a total of 2.L +
1 of different values, corresponding to different orientations of
the angular momentum in space. All these rules apply, among other
things, in the structure of the electron shell of the atom, where
the energy level corresponding to the angular momentum L
is (2.L+1)-times degenerate; in conjunction with Pauli's
principle, this implies occupancy rules for electron levels, as
described below.
S p i n
In classical mechanics, in addition to the mutual angular
momentum of moving bodies, or the angular momentum of a body with
respect to a given point, is also applied the own
(internal) angular momentum
caused by rotation bodies around its own axis.
In quantum mechanics, the angular momentum determines the
symmetry of the state of the system with respect to rotation in
space, ie the way in which wave functions corresponding to
different values of the angular momentum projection are mutually
transformed when the coordinate system is rotated. The origin of
the angular momentum no longer matters here. The analysis of the
properties of particles shows that in quantum mechanics we must
also attribute a certain intrinsic angular momentum
to an elementary particle, which is not related to its motion in
space. Own angular momentum of a particle is called spin
and is denoted by s, while the angular momentum
associated with a particle's motion in space is called the orbital
moment (usually denoted by L or l ). This
property of elementary particles has a specific quantum nature
and cannot be completely explained by classical mechanical
concepts (spin cannot be quantitatively explained, for example,
by the rotation of a particle around its own axis!) *). In the
quantum description of a particle with spin, the wave function
must determine not only the probability of different positions of
its occurrence in space, but also the probability of different
spin orientations. Wave function must therefore depend not only
on the three spatial coordinates, but also on the spin variable
that indicates the value of the projection of the spins in a
particular direction in space (selected axis z ), and
acquires a limited number of discrete values.
*) Difference of spin from
angular momentum
The spin of quantum particles differs
considerably in some of their properties from the usual orbital
or intrinsic rotational angular momentum of bodies :
-> It is quantized,
takes on certain discrete values (mentioned below); however, this
is generally consistent with quantum physics (so
it's not surprising).
-> For a given type of elementary
particle, spin has a precisely given value (in
multiples of the Planck constant); the particle cannot be
"forced" to rotate faster or slower. The spin value
depends only on the type of particle and cannot be changed in any
way (unlike the orbital angular momentum or spin direction) ...
-> The spin of quantum particles
can take values 0, 1/2, 1, 3/2, 2, ... - a multiple of the Planck
constant. In contrast, the orbital angular momentum can only take
on the integer value of a multiple of the Planck constant.
Like the angular momentum in general, spin is
quantized. The eigenvalues of the square of the spin are
equal s2 = h2. s(s + 1), where the spin
number s can be an integer (including zero) or a
half number; is an intrinsic characteristic of a given type of
particle. At a given s, the spin projection can take
values sz
= -s, -s + 1, ...., s-1, s, so a total of 2.s+1 values. In §1.5
"Elementary particles", passage "Indistinguishability
of particles" - "Spin,
symmetry of the wave function and statistical behavior of
particles", we will see that
there are two main groups of particles according to spin s
: particles with half-number spin (most of them
- electrons, protons, neutrons, muons, etc.) and with integer
spin (photons, p and K mesons, hypothetical
gravitons and others). This circumstance is closely related to
the quantum behavior of sets of particles - the
particles behave like fermions or bosons
(§1.5, passage "Fermios-Bosons").
Magnetic moment
Every electrically charged body ("charge",
"charged particle") generates an electric
field in the surrounding space according to Coulomb's
law (if the charged particle is at
rest with respect to the reference system, it is an electrostatic
field). When the charged body moves evenly
in a straight line, it also generates a magnetic field
according to Biot-Savart-Laplace's law. And if the
charge moves unevenly - accelerated or along a curved path, it
excites a time-varying electromagnetic field around itself, part
of which propagates through space as electromagnetic
waves. These basic findings of the unified science of
electricity and magnetism - electrodynamics (see eg §1.5 "Electromagnetic Field. Maxwell's Equations." in the book "Gravity, Black Holes, and
the Physics of Spacetime") work
perfectly not only in classical, but also in relativistic and
quantum physics.
Leaving aside the translational motion (irrelevant here) and the emission
of waves (which we will discuss below), the main mechanism of excitation of a magnetic field
by charged particles is their rotational motion.
The motion of a charged particle in a circular orbit generates a
magnetic field, the direction of which is perpendicular to the
plane of circulation and whose intensity (magnetic induction) is
proportional to the charge of the particle and the angular
momentum of its circulation. This magnetic field behaves like a
fictitious magnetic dipole- miniature "bar
magnet". Its force is quantified by the vector quantity magnetic
moment m, expressing the moment of a pair of forces f,
which would act on this magnetic dipole in the external
homogeneous magnetic field B : f
= [m x B]. A particle with charge q and
rest mass m , which rotates with the angular momentum L,
generates a magnetic dipole moment m = (q/2m).L
according to classical electrodynamics. When exciting a magnetic
field by the rotational motion of charged bodies, the so-called gyromagnetic
ratio g is often introduced, which is the ratio of the excited
magnetic moment and the mechanical angular momentum of the
rotating body. For a classically charged rotating body, g = q/2m.
Rotational motion of a charged particle
excitation magnetic moment, can be of two kinds :
- Orbital (circular) motion
of charged particles in the field of bonding forces with
other particles. This is the case of electrons orbiting an atomic
nucleus. The electron of rest mass me , orbiting with angular momentum L,
behaves like a magnetic dipole with moment m = g . (- e/me). L.
However, it is usually expressed in the form m =
-g . mB .L/h, where mB = e. h /me is the so-called Bohr magneton. The
dimensionless correction factor g indicates the
relationship between the actually observed magnetic moment of the
particle and the theoretical value of the Bohr magneton.
- The proper rotational motion of
a charged particle, rotating around its axis - the
above-mentioned spin of particle. The above
classical relation m = (q/2m).L in principle applies to the
excitation of a magnetic moment even if the angular momentum L
it is created by the rotation of a body with an equally
distributed density of mass and electric charge around its own
axis of symmetry. The spin magnetic moment of an electron can be
expressed as: ms = -gs.mB . S/h,
where S is the spin momentum of the electron (+,
- 1/2 h), the g- factor is approximately equal to 2.
The more complicated situation is
with nucleons - protons and neutrons. By a
straight analogy with electrons, we would obtain the relation mp = gp.mN . S/h for the magnetic
moment of the proton, where mN is the so-called nuclear magneton mN = e. h/mp. However, the correction factor g here has a relatively high
value of gp = 5.58; this suggests
that the determination of the magnetic moment of a proton based
on its spin is problematic (see below). Thus, the proton has a magnetic moment mp = 1,41.10-26
J/T and a gyromagnetic
ratio gp = 2,675.108 rad.s-1.T-1. The gyromagnetic
ratio also indicates the frequency Larmor precession of
the magnetic moment of particles in an external magnetic field;
for protons, the Larmor frequency is 42.577 MHz/T - nuclear
magnetic resonance is used in the analytical and imaging
method (see §3.4, section "Nuclear magnetic resonance"). A neutron,
as an electrically neutral (uncharged) particle, should have no
magnetic moment, it should be mn = 0. In reality,
however, a neutron has a non-zero magnetic moment mn = -0,97.10-26
J/T, which
is only slightly smaller than that of a proton (and has the opposite sign). How
is it possible?
The origin of the magnetic moment of nucleons does not
lie in their rotational angular momentum (spin), but
comes from their internal structure - that they
are composed of quarks "u" and
"d" (§1.5, passage "Quark structure of hadrons"). For hypothetical or model
quarks, the magnetic moment m"u" and m"d" is assumed, which in the first approximation can be
modeled in a similar way as a nuclear magneton: mq = qq . h/mq. The magnetic moment of a nucleon can then be
considered to be composed of the vector sum of the magnetic
moments of three charged quarks and the orbital magnetic moments
caused by the motion of these charged quarks in the nucleon. With
quark model magnetic moment of the proton (composed of two quark "u" of charge +2/3e
and 1 quark "d" having a charge of -(1/3)e) we can then be approximated as mp = 4/3m"u"-1/3m"d" = 2,8.mN = 1,41.10-26 J/T. And the
magnetic moment of a neutron (composed of 2 quarks "d" with charges -1 / 3e
and 1 quark "u" with charge +2/3e) then it is mn = 4/3m"d"-1/3m"u" = -1,9.mN = -0,97.10-26 J/T. Quantum chromodynamics seeks a more detailed
analysis, including gluon fields and virtual particles inside
nucleons (not yet completed).
Quantum
field theory
We have so far dealt with the quantum behavior of the microworld
from the point of view of quantum mechanics of
microparticle motion: probability waves (forming fields) are
assigned to mass particles and specific quantum
properties of particle motion are obtained by solving
relevant wave equations, including discrete values of energy and
other physical quantities. Quantization of this kind is sometimes
referred to as "primary".
In addition to particles, the main subject of the
scientific description is the physical field.
The physical field, which carries energy, momentum and other
physical parameters, as well as particles, must also have a
quantum character in the microworld. In the quantum description
of fields, sometimes called secondary quantization,
on the other hand, the field is expressed using particles
- quantum excitations in the field. The transition from classical
to quantum field theory consists of two basic stages :
The application of this method of
quantization to the electromagnetic field is the basis of quantum
electrodynamics (QED) and leads to the idea of the
electromagnetic field as a set of particles - photons,
each of which has energy h.w and momentum h.w/c; the rest mass of photons is zero, their spin
(intrinsic angular momentum) is equal to 1 (resp. 1.h). At the
same time, these electromagnetic quanta (photons) are interpreted
as particles mediating the interaction of
electrically charged particles. Radiation and absorption of
photons by electric charges (especially electrons) is expressed
by means of so-called creation and annihilation
operators, that generate or take photons in a certain energy
state in an electromagnetic field.
New - quantum concept
of force: intermediate exchangeable particles
In classical physics, each kind of interaction of bodies is
assigned a corresponding field - a space in
which certain forces act on particles. In
classical physics, it is an electric, magnetic, gravitational
field. The magnitude of the field action at each point in space
is expressed by the field intensity (force
acting on the "unit test particle") or by its potential
(work associated with the transfer of particles to a given
place). The changes ("commotion") in this field
propagate at a finite speed from place to place, which is
accompanied by the transfer of energy, momentum, and other
physical quantities. From the point of view of classical physics,
these quantities, such as energy and momentum, are transmitted continuously
during field changes. In quantum physics, it turns out that
during changes (disturbances) in the field, physical quantities
are transmitted discontinuously over certain
"portions" - quanta.
Quantum field theory, in its concept of secondary
quantization, leads to a new concept of the field as a set
of particles - quantum fields. And the interaction of
particles (interactions) is caused not by the field force, but by
the mutual exchange of these quantum field particles - the exchange
of intermediate particles. The particles are constantly
receiving and emitting quantums of fields, which causes them to
interact with each other. This exchange mediating (intermediate)
quantums, we interpret as a quantum particles - carriers
of interactions. This introduces a new concept
of force and interaction in quantum field theory. This
concept plays a key role in the interactions of
"elementary" particles - it is
discussed in more detail in §1.5 "Elementary particles and accelerators", section "Interactions of elementary
particles".
Virtual or real particles ?
Are these intermediate particles mediating the interaction real?
The answer is yes and no ! Let's briefly discuss
this problem in the electromagnetic field - quantum
electrodynamics. According to it (as outlined above), the photons
are quantum of the electromagnetic field, and
the electric force between two charged particles is caused by the
constant exchange of photons. However, if we
looked at the space between two stationary charges, we would not
register any flow of flying photons. It's just a model, those
intermediate photons are virtual here ! In
quantum electrodynamics, the force is only modeled
by using photons: the static field is artificially decomposed
into a superposition of waves (harmonic oscillators), these are
quantized and the resulting photons are designated as the quantum
of the field that mediates the interaction. Rather physically
substantiated is the claim that "photons are a
quantum of the electromagnetic wave", not than
"quantum of the electromagnetic field". In
the static case, nothing is radiated physically!
The actual radiation associated with the transfer of energy and
momentum - with the flow of photons - occurs only in the dynamic
case - during the accelerated motion of the charges.
Then the virtual photons turn into real ones.
The mutual interactions (collisions, scattering) of particles in
the microworld are always dynamic processes (often at
high energies), in which the virtual intermediate particles,
hidden in the vacuum are "liberated", transformed into
real particles and actively participate in the
interaction.
Note: An interesting
exception to the radiation of virtual particles even in the
static case is the so-called Hawking radiation
of quantum evaporation of a black hole. It is created that one of the two particles is
pulled below the horizon of the black hole and absorbed and the
other particle thus becomes a real particle and can be emitted (it is analyzed in detail in §4.7 "Quantum
radiation and thermodynamics of black holes", passage "Mechanism
of quantum evaporation"
monograph "Gravity, black holes and space - time physics").
Quantum
fluctuations of fields
One basic postulate of quantum mechanics is known
Heisenberg uncertainty principle Dx. Dp ³ h , where h º h/2p @ 1,05.10
-27 g cm3/s is the Planck constant. The
relation of uncertainty applies not
only between position and momentum in quantum mechanics, but between every two dynamically coupled -conjugated
quantities, ie also in quantum field theory. If we observe, for example, a magnetic
field in a small spatial region characterized by the dimension L,
there will be energy proportional to B2.L3 and the time required to measure
the field will be L/c; uncertainty relation DE. Dt ³ h then gives (DB)2.L4 l h.c,
or DB l hc/L2.
Thus, it can be said that the quantum
fluctuations of the electromagnetic field in size L are of equal order: DE ~ DB ~ Ö(h.c) / L2.
Thus, the field is constantly
"oscillating" between configurations whose fluctuation
range is greater the smaller the spatial areas we observe. The
influence of these quantum fluctuations on the motion of an
electron around the atomic nucleus (these quantum fluctuations
"overlap" over Broglie waves in Bohr's model of the
atom - see the passage "Bohr's model of
the atom",
Fig.1.1.6) is schematically shown in the
figure :
 |
Schematic representation of the motion of an electron around an atomic nucleus. A closer look at the Kepler trajectory of the electron would reveal small chaotic irregularities caused by quantum fluctuations in the electric field. The mean deviation from the global trajectory is zero, but the standard deviation leads to a small shift in the energy level of the electron. This shift was actually measured as part of the so-called Lamb-Rutheford shift. |
In the above-mentioned quantum field
description - secondary quantization - these quantum
field fluctuations can be considered as quantum - particles.
The vacuum thus becomes a highly dynamic environment
in which virtual particles are constantly created
and destroyed. These particles have an immeasurably
short duration, they are undetectable, we say they are virtual.
In addition, quantum fluctuations and virtual particles arise
everywhere with the same density and impinge on matter from all
directions, so that their force effects are balanced and canceled
on a macroscopic scale. Under certain circumstances, however, the
cumulative effects of a large number of these particles may still
have a slight macroscopic effect.
In addition to the afore mentioned Lamb
shift we managed to measure the so-called Casimir
effect :
We place two horizontal plates (electrically uncharged) right
next to each other in a vacuum. In the gap between the boards may
arise quantums - virtual particles with only short wavelengths (whose integer multiple is given by the width of the
gap), while in the space outside the plates
they can take on any wavelengths. The total density of the
particles is thus lower in the gap and the pressure of the
particles from the outside prevails on the plates. The plates are
thus attracted to each other by a force which is greater the
narrower the gap between the plates.
Furthermore, the observed dipole magnetic
moment of an electron is formed, in addition to the
basic electrodynamic component, also by an anomalous magnetic
moment, created by the interactions of the electron with virtual
photons in quantum electrodynamics.
Assuming the universal validity of the quantum principle
of uncertainty, a similar situation should occur in the general
theory of relativity as the physics of gravity and spacetime:
should quantum fluctuations in the geometry of spacetime
occur..?.. - §B4 "Quantum geometrodynamics". Some paradoxical interpretations of vacuum
quantum microfluctuations are discussed in §B.5, the passage
"The mystery of vacuum quantum energy <->
Cosmological constant".
Feynman quantization of path integrals
At the beginning of our fleeting excursion into quantum physics,
we mentioned that it is by no means easy to understand the intrinsic
causes of quantum behavior of microsystems based on our
experience with classical macroworld behavior. For example, how
is it possible that in the famous double-slit experiment (Fig.1.1.2 ) a particle can pass through both holes at the same
time and then interfere "with itself"?
Feynman's formulation of quantum
theory is characterized by a very close relationship to classical
physics *) expressed by the principle
of least action.
In classical physics (mechanics, electrodynamics, GTR),
between a given initial x1 and final x2
state, of the
investigated systen always make only such a movement
for which the integral of the
action S = x1òx2 L dt is extreme. On the other hand,
in quantum physics, as is well known, such processes also take
place that do not comply with this principle and are impossible
according to classical physics - for example, the tunneling
phenomenon.
*) The transition from
classical to quantum physics is so elegant and straightforward
here, that J.A.Wheeler
used this approach to persuade A.Einstein to revise his
opposition to the stochastic principles of quantum mechanics. But
to no avail: "I don't believe that God would play
dice with the world ",
Einsten persistently objected...
In Feynman's approach, all trajectories leading from the initial state x1 to the final state x2, are
considered equiventally and simultaneously, regardless of whether they are
permissible or not according to classical physics. As if the particle were moving along each imaginary
trajectory at the same time as it traveled
between the two states - it is the set of all virtual
trajectories ("history"). If the integral x1nx2Ldt is calculated for each trajectory, the
probability of transition of the system from the initial state x1
to the final state x2 will be
given by the square of the quantity
 ,
,
obtained as sum and taken through all trajectories - the sum through all possible "histories". It is evident that the largest
contribution to this sum is made by those trajectories that have
a phase coefficient (i/h) ò Ldt almost the same (exponents add up),
while for trajectories with large differences in (i/h) ò Ldt the exponents in the sum
cancel each other out. The most probable trajectory
(corresponding to close values of ò
Ldt) will therefore be a classical trajectory with extreme
behavior of the integral of the action. Trajectory here means
"path" in the space of the given configurations systems; if it is a complex
system described by a large number of parameters, it will be a
trajectory in multidimensional space. Feynman showed that this
formulation is equivalent to the usual Schrödinger and
Heisenberg concept of quantum mechanics. Similarly to about
the classic principle of least action, in practice in not immediately
seek extreme integral ò Ldt, but derive Lagrange
equation of motion, even when using Feynman method, the total
sum over all trajectories is not directly calculated. Feynman's procedure is rather
used as a means for deriving and elaborating quantum theories, as
well as their physical interpretation.
..........- add, edit
Some
gnoseological questions :
Is quantum physics a major obstacle to the knowledge and use of
nature ?
We physicists believe in the recognizability of the
world, and it is our professional duty to work for the
best possible knowledge of the mechanisms and laws
according to which nature "works". From this point of
view, we are "horrified" that randomness,
stochasticity, statistics, which are a reflection of our
ignorance of the exact conditions and states in complex
sets of many interacting particles, are "dabbling" into
fundamental physics !
Quantum physics is often considered a
theory of fundamental constraints, according to
which our observations and measurements are inevitably
inaccurate, natural phenomena are ruled by chance, and we should
give up hope that science can accurately describe our world.
Quantum mechanics is often considered an insurmountable
obstacle to the knowledge of the deepest microworld or
the practical use of microscopic phenomena (eg further
miniaturization of electronic circuits). Already in the early
periods of the development of quantum physics, it turned out that
corpuscular-wave dualism, the randomness of phenomena and their
superposition, discretion and especially the quantum
relation of uncertainty, fundamentally prevent
us understand and use nature in such a way and to such an extent
as we were used to in classical physics (mechanics,
electrodynamics, ...). This somewhat misleading view has its
roots in a time when physicists have developed, perfected and
confronted quantum mechanics with classical theories and
philosophical concepts.
In recent decades, however, a different
perspective has become increasingly common. What does the
uncertainty principle say and what does it not say? They merely
claim that not all observed quantities of a physical system can
take on certain ("sharp") values at the same time. Not
all quantum measurements are limited by the uncertainty
principle. Although the position or velocity is indeterminate and
"blurred", other properties can be quite
"sharply" defined - for example, blurred electrons in
an atom produce a well-defined energy of a given orbital. In some
cases, we can ingeniously circumvent this dreaded obstacle, and
at the quantum level we can use the special properties of
microsystems in new advanced devices such as lasers, integrated
circuits, nanotechnology, new possibilities in informatics and
computers (see below "Quantum
computers").
........ see also the discussion in "Natural laws, models and
physical theories".................
At the deepest level, is the world discrete or
continuous ?
This is an important gnoseological
question on which opinions of physicists differ. In modern
terminology, this question could be paraphrased: “Is the
physical world essentially analog
or digital ?”. The
physical relationship between the continuous
(fluent, smooth) and discrete nature of the
microworld can be essentially twofold :
× Discretion is basic
: ® secondarily generates
continuity (apparent)
This is the most common approach in modern physics, based on
atomistics, thermodynamics and statistical physics. From the
point of view of atomic physics, all substances are composed of
discrete ones atoms that have a specific integer
number of protons in the nucleus and electrons in the envelope.
And the spectrometry of the radiation emitted and absorbed by the
atoms shows that the electrons in the atom occupy discrete
energy levels, determined by integers. Bohr's
model of the atom is based on this (see
"Bohr's model of the atom"
below). In sets of large numbers
of atoms and molecules, the methods of statistical
physics make it possible to derive the laws of gas
kinetics and thermodynamics, which are continuous.
However, the basic "input values" of the theory are discrete
integers. The continuity "emerges" from the
averaged a large number of discrete events. The
water in the glass appears as a continuous medium,
but if we look at it with high magnification, we will see the
molecules and atoms of which it is composed. These atoms also
have the internal structure of electrons, protons and neutrons.
At the most basic level of current knowledge, matter is made up
of fundamental leptons and quarks (§1.5,
part "Standard model -
uniform understanding of elementary particles"), which are considered as discrete
particles that can in principle be "counted
down one after the other" *).
*) Gnoseological note: The role of integers
is called metaphorically in classical mathematics that "God
created only whole numbers, everything else in mathematics is the
invention of humans". However, for modeling nature,
mathematics introduced more general sets, especially real
numbers (see §3.1 "Geometric-topological
properties of spacetime",
section "Sets and representations")
for which it created extensive apparatus of differential and
integral calculus.
× Continuity is
essential : ® secondarily generates
discretions (again only apparent?)
Quantum physics microworld based on a particle-wave
ideas. The wave equation of quantum mechanics (Schrodinger
equation) contain only continuous
quantities. An illustrative example of this concept is Broglie's wave
explanation of Bohr's quantum electron paths around the
nucleus of an atom - see below, Fig.AtomBroglie.gif. Here, the discretion of electron paths is formed by
the continuity of the wave functions of
electrons - their "wave continuity".
In the standard particle model,
it is taught that the basic building blocks of matter are the
basic discrete particles - leptons (especially
electrons) and quarks. However, on a more fundamental level, in unitary
field theory (§B.1 "The
process of unification in physics" in the book "Gravity, black holes
...."), the basic building block of
physical theories is field - a continuous "fluid"
substance distributed in space (the best
known example is the electric and magnetic field). From the point of view of unitary field theory, "fundamental
particles" are not fundamental, but
are composed of continuous fields (and their
waves or quanta) - see below. Particles are
"precipitates" of a unitary field.
Nature is probably a true continuum,
in which we do not find any building elements that are no longer
indivisible at any level of magnification. Physical quantities
are generally not integers, but continuous real
numbers, for which the number of decimal places is
constantly increasing with the gradual refinement of the
measurement. Integers retain only the significance of the number
of types of significant particles in terms of the type
of their interactions (e.g. 3 types of
neutrinos, 6 types of quarks), the
expression of the number of electrons in atomic shells, the
number of protons and neutrons in nuclei, or order and number of
excited states.
Is space and time
continuous or discrete ?
In most disciplines of classical
and quantum physics, space and time are considered to be a
continuous, infinitely divisible continuum - a
kind of "stage or arena", against the background of
which physical processes, interactions of particles and fields
take place. What if, however, the continuity of space-time is the
same illusion as it was until the 19th century continuity of
matter? As modern physics learns about the discrete quantum
structure of matter, it is hypothesized that space-time
is also quantized - it consists of a huge but countable
number of very small already indivisible elementary
"cells", a kind of "space-time dust". If
these hypothetical "quantum geometries"
are small enough, e.g size of the order of the Planck
length 10-33 cm,
spacetime appears to be completely continuous, as no physical
processes studied so far can distinguish finer distances than
about 10-15
cm.
Thus, there is a possibility that
continuous quantities could in fact be discrete in a closer
(enlarged) view: they may lie on a dense grid of
individual separate points, which in the view available to us
gives the illusion of a continuum. It is similar
to the pixels on a computer screen observed at basic
magnification and zoom.
Note: It is interesting that a discretized version
of quantum fields - a lattice field - was
developed in quantum physics, where the continuous space - time
is replaced (modeled) by an evenly arranged set of points, only
in which the quantities of the fields are determined. However, it
is only a model that facilitates quantum calculations, it does
not follow that this is in fact the case.
Thus, in addition to the generally
accepted concept of continuous space, it is
possible to alternatively postulate or axiomatically introduce
the primary discretion of space : space is
formed by individual separate "cells", only in which
field values (potentials, intensities) are defined. These fields
are therefore also discrete in terms of spatial distribution. If
the spatial lattice (matrix) is sufficiently dense or fine (even
in the dimensions of Planck lengths 10-33
cm), space seems to us
"illusory" as a continuum. However deepest
mikromìøítcích the space could primarily be discreet
- "pixellated" or "voxellated"..?..
General relativity conceives gravitational
field as a curved spacetime (see §2.2
"Versatility - a basic property and the key to
understanding the nature of gravity" in the book "Gravity, Black Holes and
the Physics of Spacetime"). If we
want to quantize gravity, it is necessary to "quantize"
spacetime. The combination of the general theory of relativity
and quantum physics thus reveals (or postulates) a discrete
structure in space-time itself, whether
fundamental or induced - see §B4
"Quantum geometrdynamics" and §B5 "Quantization
of the gravitational field",
part "Loop theory of gravity
" in the already mentioned monograph).
Reflection of continuous versus discrete aspects of
nature is probably necessary in creating a unitary theory
of physics - the theory of everything - TOE (§B.6 "Unification of
fundamental interactions . supergravity. Superstrings." monograph "Gravity,
black holes and spacetime physics").
Author's note:
Personally, I slightly prefer the opinion that fundamental
is a continuity (perhaps even causal?), which induces an
apparent discretion (and perhaps also quantum
stochasticity)..?.. However, even the concept of a discrete
super-dense space-time lattice could perhaps be the main idea for
understanding the microworld..?..
Negative
time in the microworld ? - Probably
not..!..
When electromagnetic radiation - photons of suitable energy -
passes through a material environment, they are absorbed by
atoms, which are temporarily excited to higher energy
states. Subsequently, deexcitation occurs, during which
photons of spectral energies are emitted (discussed in more
detail below in the passage "Excitation
and radiation spectra of atoms").
Under normal circumstances, these secondary photons are temporally
consecutive, with a certain (usually
very small) time delay. However,
in highly sensitive experiments with very short (picosecond)
laser pulses, it sometimes surprisingly turns out that some
secondary photons leave the material slightly before
the primary photons enter it! As if "negative
time" had passed between the process of
excitation and deexcitation of atoms..?..
There have been speculations about the
existence of a real "negative time" that could be used
to travel through time into the past ("Time travel -
fantasy or physical reality?")...
However, the real explanation of these paradoxical observations
rejects this as misleading and turns to two physical
circumstances :
1. The phase shift in the photon path, which can
"simulate" small time shifts between the emission and
detection of photons. 2. Quantum uncertainty
relations, to which photons and atoms are also subject, which are
"blurred" in space and time. So in quantum physics,
effectively even time can fluctuate slightly in both positive and
negative directions...
Is the world recognizable ?
This basic gnoseological question is often discussed from a
variety of philosophical perspectives. From the scientific
point of view, the cognition of our world can be reflected in
principle on three levels :
1. Phenomenological cognition
The study of the specific course of individual natural processes
is the basis of scientific knowledge. The accuracy of this
knowledge is given by the level (resolution) of physical
instrumentation, optical observation systems, chemical-analytical
methods. The principal limitations in
phenomenological cognition are imposed on us in
the microworld by quantum relations of uncertainty (see, for example, the section "Quantum physics" above), in the macro- and
megasworld then horizons of events of
relativistic astrophysics (§3.3 "Cauchy's
problem, causality and horizons"
in the monograph "Gravity, black holes ....").
2. Knowledge of internal causes,
mechanisms, laws
This is the main content of advanced scientific research. From a
detailed analysis of the course of natural processes (phenomenological) under different
conditions and comparisons from other processes, general natural
laws are formulated, if possible with universal
validity for a wider class of phenomena. This makes it
possible to understand the functioning of nature (it is discussed in the section "Natural laws,
models and physical theories"
§1.1 in the already mentioned book "Gravity, black
holes ...").
3. Absolute deterministic
recognizability
The maximalist requirement of complete recognizability
of the world would require that for all elementary particles,
atoms, molecules and other structures we can predict their exact
spatial positions at all times, as well as
predict accurate values of fields (potentials,
intensities) in all places of space. Our current knowledge shows
that this is not possible ! In addition to
technical impracticability, quantum relations of
uncertainty prevent this at the microscopic level, and
at all levels special irregularities in the behavior of sets of
particles, called "deterministic chaos", which
generate chance - is discussed in more detail in
the section "Determinism-chance-chaos?" §3.3 in the book "Gravity,
black holes and the physics of space-time". Furthermore, if space is continuous
(see the discussion above "Is space and time continuous or discrete?"), an infinite and even innumerable
set of points would require an infinite amount of
data for each, even the smallest, district of the system under
study!
However, to deduce from the negative message of level 3 a
categorical statement about the unknowability of the
world is not substantiated and can be misleading *)! The
world is basically recognizable in the sense
that we understand the mechanisms of its functioning,
on the basis of which we can often predict the behavior of many
important systems in nature and space in the long run and with
great accuracy. E.g. based on Newton's and Kepler's laws (gravity
and mechanics), astronomers can predict the motions of planets in
the solar system with high accuracy many centuries to come. In
the horizon of millions to billions of years, however, minor
gravitational disturbances will eventually result in chaotic
deviations, which will significantly change the motions of the
planets (some of them may even escape from
the system ...). So it is not apt to say
that "the world is unknowable", but that
"the knowability of the world has its
limitations".
*) Such a sharp statement that "the world
is unknowable"could provoke skepticism,
nihilism, agnosticism. It would also record various
"alternatives" and charlatans who downplay the
impressive achievements of serious scientific knowledge and claim
that only they, thanks to their "miraculous abilities",
have the gift of "true knowledge" and can control the
world (or rather some trusting people...).
Some unusual and
paradoxical consequences of quantum physics
Quantum tunneling phenomenon
If a particle moves in a certain force field, the law of
conservation of energy - the sum of the kinetic energy
of a particle and its potential energy in a given field - is
fulfilled at each point of the trajectory when moving according
to classical physics. An interesting case of particle motion is
the motion in a force field, whose potential has the shape of the
potential barrier - in the simplest case of
movement in the direction of the X axis, such forces act on the
particle that its potential energy Ep is everywhere zero, except for the area x1 <x <x2, where the value Ep = Vo. If the kinetic
energy of the particle Ekin is less than the height Vo potential barrier, according to classical physics the
particle should bounce when moving from the place of the barrier
and move back against the original direction of motion - the
particle is never able to overcome the potential barrier. The
particle can overcome the potential barrier only if it has a
sufficiently large kinetic energy Ekin>Vo.
However, in quantum mechanics, where a
particle is described by a wave function
(according to corpuscular-wave dualism, it is a Broglie wave),
there is a non-zero probability that the wave will "seep
through" the barrier and the particle may suddenly be on the
other side of the barrier. Waves, unlike conventional particles,
can get behind the obstacle due to bending and
then continue to move through space. Analysis of the wave
function using Schrödonger's equation shows that a plane wave
incident on the barrier wall partially bounces off it (and
interferes with the original wave) and partially penetrates
inside the barrier. If the width d = x2 - x1 of the barrier is
small enough compared to the depth of penetration of the wave,
the Broglie wave reaches the second wall of the barrier, where
the potential suddenly decreases - the wave enters free space and
continues to move away from the barrier as a plane wave, with a
lower amplitude (expressing the probability
of the particle passing to the other side of the barrier). The particle has passed potential
barrier even if, according to classical physics, the energy of a
particle is insufficient to overcome the barrier!

Symbolic representation of the quantum tunneling phenomenon.
Left: A ball rolling
with the kinetic energy of Ekin against an elevated terrain wave (hill - gravitational
potential barrier of height Vo) can overcome it only if it has sufficient energy Ekin > Vo. Middle:
If a tunnel is pierced in a terrain obstacle, the body can
overcome it even at a significantly lower energy than the
potential height Vo. Right: Simplified
representation of a rectangular potential barrier of height Vo, through which
particles (~waves) can pass with a certain probability even at a
lower kinetic energy than Vo - as if "hidden tunnels" led across the
barrier.
From an energy point of view,
the described phenomenon can be explained by the quantum
uncertainty relation DE.Dt ³ h between energy
and time (discussed above). The value of the instantaneous energy
of a particle fluctuates in its short time
around its mean size, up and down. Once a particle reaches a
potential barrier, energy can (coincidentally) be momentarily
increased for a short time, allowing it to cross the
barrier. During the act of self-penetration, within the
uncertainty relation, the law of conservation of energy may not
apply. The shorter the moment of fluctuation Dt, the greater its
possible range DE. If the particle does not manage to reach the other
side of the barrier during this duration of sufficiently large
fluctuation, it will return - it will bounce off; this, of
course, happens even if the energy fluctuation is negative at the
moment the barrier is reached. The wider and higher the potential
barrier, the less likely the particle is to penetrate
successfully; most of the particles penetrate the barrier only
partially and eventually bounce off the potential wall. With a
sufficiently narrow barrier, the particle is more likely to
successfully overcome it due to a sufficiently high short-term
energy fluctuation.
This effect, when a particle crosses a
potential barrier higher than the energy of the particle, is
called a tunneling phenomenon - a particle that
does not have sufficient kinetic energy (and therefore cannot
"fly" over the potential barrier) can still penetrate
the barrier with a certain probability, as if a hidden
"tunnel" had been drilled in it. The particle, on the
other side of the barrier, seemed to "tunnel".
The tunneling phenomenon has a probabilistic character. It occurs
either in a large number of incident particles, some of which
manage to "tunnel", or the individual particle must be
able to perform a series of "failed attempts" before it
can "release" from binding in the nucleus (eg alpha-radioactivity) or in the
material (eg thermoemission).
Probability w of quantum tunnel
passage of a particle with kinetic energy Ekin through a potential barrier of height Vo (> Ekin) and width d
is approximately equal to
w
» exp ( - 2d. Ö [2m. (Vo - Ekin) / h 2 ] ) .
This probability decreases exponentially with the width d of
the potential barrier.
One of the basic parameters by which we
characterize physical systems is their energy content. If a
system has a lower energy state available than the current one,
its dynamics (acting forces) tend to bring it to this lower
energy state. However, situations of more complex potential
dependencies often arise, when reaching this lower energy state
first requires a local ascent to a higher energy state - there is
a potential barrier in the way that must be "climbed".
In classical physics, such an obstacle is insurmountable and a
lower state cannot be reached, the higher state is metastable.
We must first "invest" some energy to overcome
the energy barrier and only then can we "profit"
from the released energy. The quantum system makes it possible to
overcome this barrier even without the supply of external energy.
What is impossible in classical physics is only less likely in
quantum physics... When tunneling through a barrier, it is never
possible to observe a system in a transition state with a higher
energy than it had at the beginning, but only before tunneling
with a given initial energy and after tunneling at the resulting
state with lower energy and with the released energy in some
other form (such as radiation, heat, ...). The law of conservation applies exactly to the overall
energy balance!
The tunneling phenomenon, which is
typically a quantum-mechanical effect associated with the wave
properties of particles, is significantly applied in many
phenomena of the microworld - in atoms and atomic nuclei (eg in alpha
radioactivity, nuclear reactions -
especially in thermonuclear fusion), in
electrical phenomena in conductors and semiconductors. In an
electric field, electrons can be emitted from metals
(thermoemission, photoemission) even if the kinetic energy of the
electrons is lower than the corresponding output work; a
tunnel scanning microscope is based on the
quantum tunnel emission of electrons from the surface of
conductive substances. Thanks to the tunnel effect, many
processes at the microscopic level can take place even at
significantly lower energies than would be
necessary according to classical physics. Without it, we wouldn't
have a chance to use natural energy - or a chance to live!
Schrödinger's
cat - a wrong
interpretation of quantum mechanics ?
It is a somewhat morbid *) and absurd thought experiment, which
the Austrian physicist E.Schrödinger formulated in 1935 to show
the paradoxical property of the superposition of states
in quantum physics. We know that when some stochastic phenomenon
is observed - measured in the micro world, it affects its state.
If we have a particle, for example an electron, by measuring its
position or speed we get a certain result. However, we perturbed
its position and velocity a bit during the measurement itself, so
the question is, what did it look like before we measured and
perturbed it? Quantum mechanics offers the interpretation that
when we measure a certain property of an electron (position or
velocity), we get a certain result, but before we measured it,
this electron existed in all possible states at once. And only
the act of measurement is what forces him to accept a certain
state. With this "cat experiment", Schrödinger tried
to point out the absurdity of this interpretation, which,
however, was later mostly accepted in quantum physics...
*) Unfortunately, the virtual
morbidity of this experiment was replaced in a few years by real
morbidity committed by his german compatriots, who used the same
hydrogen cyanide to murder thousands of innocent people in
concentration camps..!.. However, Schrödinger himself was a
staunch opponent of german fascism.
The following objects are placed in a hermetically sealed opaque
box :
1. Live cat; 2. Flask with poisonous gas - hydrogen cyanide (in the first version it was a rifle aimed at a
cat) ;
3. A sample of radioactive material containing one
radionuclide atom with a half-life of 1 hour;
4. A radiation detector electronically coupled to a
mechanism capable open the flask. When the radioactive atom
decays, the detection device registers it, the electrical device
inside the box uncorks the flask of poison, and the cat dies.
Schematic representation of the "Schrödinger's cat"
thought experiment.
The decay of a radioactive atom is a stochastic
quantum phenomenon - we cannot predict the time when the
nucleus will decay, only the appropriate probability;
after one hour, there is about a 50% chance that the nuclide has
decayed. According to the notions of quantum mechanics, a
radionuclide that is not observed, is in a superposition of a
decayed and an undecayed nucleus, as if it were in both states at
the same time. So the whole follow-up system in the box should be
in a superposition of states: [decayed
radionuclide - dead cat] and [undecayded nuclide
- live cat]. However, if we open the box, we
will of course see only one of these states.
The paradox is that in interaction with a
suitable quantum system (radionuclide), a cat can get to a state
where it seems to be alive and dead at the same time. According
to quantum mechanics, the system in the box is described by a
wave function that contains a combination of these two possible
mutually exclusive states - that is, at every point in time, the
cat is alive and dead at the same time. It is only when we make
an observation (by opening the box) that we force the system to
accept one option or the other. So when we open the lid of the
box, external observation decides whether the cat really lives or
not. The imaginary experiment points to the imperfection
(incompleteness) of thid interpretation of quantum mechanics in
the complex understanding of nature, in the transition between
the micro- and macroworld.
This imaginary experiment was popular
especially in the period of building concepts of quantum
mechanics, when it played a certain heuristic role. From today's
point of view, he is no longer very convincing...
Rather than the contradiction of physical reality, it expresses
the paradox of its formal description. It is an erroneous,
frequently occurring interpretation of quantum mechanics (cf. also the above discussion of the Copenhagen
Interpretation of Quantum Mechanics "Wave
functions. An interpretation of quantum physics." and their problems "Superposition
of different states and collapse of the wave function: ever an
erroneous interpretation of quantum physics?" ).
In reality, the particle before observation-measurement is
not in all possible states at once - it is only in one
state that we do not know. Before the measurement,
we can only determine the probability of what state it
could be in. And after the measurement, we know the specific
condition for sure.
Note:
A possible bizarre solution to this
paradox is sometimes considered from the point of view of the
hypothesis of an infinite number of parallel worlds
in which all possibilities are realized (it is discussed in §5.7
"Anthropic principle and existence of multiple
universes", passage
"Concept of multiple universes").
In one universe the cat is dead, in the "neighboring"
universe the experiment survived ...
Quantum entaglement and teleportation.
Quantum computers.
An interesting and for classical physics completely surprising
consequence of the fundamental nonlocality of
the quantum description of particles by means of wave functions
is a phenomenon called quantum entanglement. It
consists in the fact that two particles, whose quantum state is
"intertwined" originally by a common wave function,
remain in a sense still connected by a kind of
"invisible bond", even at any distance. If the state of
one of the entangled particles changes, the state of the other
particle also changes, "immediately" - a kind of "teleportation"
of information occurs, according to some opinions "at
superluminal speed"..?.. (will be
discussed below) .
As mentioned above, the evolution
of a quantum system is described by a wave function. It is a (thought.) wave propagating through space, with the object
("particle") "occurring", in a non-local
sense, everywhere at the head of this wave. When an object
interacts with another quantum object or measuring instrument, a
"wave function collapse" occurs, and the object is
temporarily localized and can be described in
particle form. The collapse of the wave function takes place non
- locally - the wave function, according to this
interpretation, suddenly disappears from the whole space..?.. It
is only a theoretical-hypothetical idea....
According to the usual so-called Copenhagen
interpretation of quantum mechanics, the investigated system
consists of the quantized objects themselves and of classical
measuring instruments or observers. The collapse of the wave
function locates the information that the observer obtained by
measuring.....
If we have a pair of
spatially separated quantum subsystems that form part of a single
system, these subsystems are bound to each other
through a common original wave function. The measurement
(interaction) of one subsystem thus bound forces the other bound
subsystem to immediately go to the corresponding (complementary)
state, regardless of the spatiotemporal distance. This phenomenon
is referred to as EPR-nonlocality
(Einstein-Podolsky-Rosen) or EPR-paradox
.
A.Einstein and his collaborators
B.Podolský and N.Rosen formulated the thought experiment
outlined below to show the internal contradiction and
incompleteness of quantum physics. It seems paradoxical that
without the presence of exchangeable (mediating) particles or
fields, it is possible to immediately influence a particle that
is, for example, at the opposite end of the universe - a kind of
"haunting effect from a distance"!
According to the special theory of relativity, it can be expected
that only places between which the space-time connection is
limited by the speed of light can be in causal contact. However,
quantum mechanics, due to its nonlocality of wave functions, can
in a sense temporarily violate this causal
requirement of relativistic physics. Now, quantum
entanglement is no longer considered paradoxical. By performing
measurements on one particle, no mass or energy is transferred to
the other particle. And as for information, both observers must
use "classical" communication using a signal with
sub-light speed to confront the measured results; this ensures
the STR causality of both measurements (see
also the commentary to Fig.1.1.3 below).
Mutual nonlocal interconnection
or "intertwining" of quantum states is
referred to in English as entanglement. It is a quantum
correlated state of a system of two or more particles, in
which the state of one particle cannot be measured without
influencing the other (and therefore it
makes no sense to talk about the states of individual particles). Both particles have a common non-local wave
function.
This can be illustrated by the example of
a particle initially at rest, with zero momentum, which breaks up
into two identical particles flying apart, each with a spin of
1/2. The law of conservation of the total momentum implies that
if we measure a spin projection 1/2 to a certain axis for one
particle, the other particle must have a spin projection to the
same axis -1/2 (and vice versa). Therefore, if we measure the
spin on one particle, immediately we learn (we judge)
the spin value of the second particle, no matter how far. As if
this information was spreading immediately, contrary to the
special theory of relativity *)! From a quantum-mechanical
non-local point of view, when measured on one particle, the
common wave function "collapses" in the whole space (in imaginary idea?), which is
reflected in the state of the other particle. However, the actual
verification and reconstruction of the measured quantum state of
the second particle is only possible with a classical
communication channel with sublight speed!
*) Therein lies the oft-stated misconception
about the superluminal speed of quantum teleportation.
If we know that both particles are quantum linked and have
oppositely oriented spin, measuring the spin of one particle
naturally implies the opposite spin of the other particle,
without the complexity of its measurement and teleportation of
information. And if we don't know it, it is generally necessary
to transmit information about the state of particles with a
communication signal at sublight or light speed.
Another typical example of "entangled"
particles is a pair of photons generated
simultaneously in a quantum process. It can be a pair of photons
emitted from an atom after its excitation, the polarization of
which can be correlated (in the simplest
case to the opposite, perpendicular to each other). If we measure a single photon polarization e.g. in the
direction of the horizontal X axis, the second photon
polarization is in the direction Y. This may occur with radiation
gamma produced during annihilation particle and antiparticle (see
§1.2 and 1.5). Quantum entangled photons are also formed in
nonlinear optical crystals by the impact of coherent
monochromatic radiation from a laser, where some incident photons
"split" into two bound photons with lower energy, the
polarizations of which are complementary to each other.
Quantum
teleportation
The term "teleportation" (Greek tele = distance , Latin portare =
carry, transfer ; ie transfer, relocation in
distant) often found in science fiction,
generally refers to the process by which a given object (even a person in science fiction) disappears
in its original place and appears in another place (in science fiction, for example, at the other end of
the universe, immediately or at superlight speed). In a more sophisticated embodiment, it is an indirect
relocation : the object is disassembled and analyzed in one
place, the obtained complete information about its
construction is transferred to another remote location, where
then an exact copy is created (reconstructed) using this
information.of the original object. This copy is not created from
the original matter, but from particles of the same kind (eg
atoms) in a new place, which are assembled into the same
structure as the original object - it is not a physical transfer
of objects - their matter (substance), but information
transfer. And it definitely doesn't go through infinite
or superlight speed!
Quantum interconnected (entangled)
particles can in principle be used for the so-called quantum
teleportation of information about the state of another
particle that interacts with one of them. In 1993, Ch.Bennet
proposed the following indirect method (Fig.1.1.3) :
Fig.1.1.3. Simplified arrangement principle
for quantum teleportation.
Let us have an O1 observer (sender's laboratory) and an O2 observer (recipient's
laboratory). At the O1 observer, we create a pair of entangled
particles A and B so that the A particle remains at the
O1 and the B particle
is sent to the O2 observer.
The O1 observer then
realizesthe interaction of particle A with the third particle C carrying
the information (state) to be teleported; measures the
resulting states of particles A and C after interaction. The
original state of particle C is deleted, but thanks to
entanglement, this information appears (in coded form) on the
distant particle B, whose state B´ is measured by the observer O2. In order for the O2 observer correctly determined
the original state of particle C which was in the place O1 , the observer O1 must connect with the observer O2 using a classical (non-quantum,
causal) communication channel (eg electromagnetic signal) and
tell him what result of the states of particle A and C after
measured the interaction. The O2 observer then confronts the result of his measurement of
the state of particle B with the data communicated by the
observer O1 (using
them to decode his result by linear transformations of the type
of rotations in the vector base...), while the final result is to
determine (reconstruct) the original state of particle C in place
O1 - this corresponds
to the teleportation of this information.
Thus, both a nonlocal "EPR"
channel of entangled particles and a normal (causal)
communication channel are required to perform quantum
teleportation. This is the only way to decode teleported
information. It is this necessity of classical communication that
effectively makes it impossible to send information at
super-light speeds. Thus, quantum teleportation does not
violate the principles of causality of the special
theory of relativity - EPR is no longer a paradox...
The process of quantum teleportation in
its current understanding can only work within elementary
particles and cannot be used for teleportation of macroscopic
objects. There is no known way in which a set of quantum-bound
states could interact with a macroscopic object in a targeted
manner. In addition, this method transmits only the value of one
observable quantity, not the complete quantum state.
Quantum teleportation of the polarization
state of UV photons was first performed experimentally in 1997 in
the laboratory of quantum optics and spectrometry in Innsbruck.
Later, quantum teleportation was performed on excited states of
calcium ions 40Ca+ (in the same
laboratory in Innsbruck) and beryllium 9Be+ (at
the National Institute of Standards and Technology in the USA). In 2017, we managed to teleport photons between the
ground station and the Chinese satellite Micius to a distance of
1400 kilometers.
Quantum
electronics, quantum computers
An important quantum property of particles, electrons, protons
and whole atoms is spin - the intrinsic
rotational momentum of a particle. Particles with non-zero spin
can act as magnetic dipoles that respond to an external
magnetic field. The spin of an electron is oriented in two
opposite directions (spin projection) , which are referred to as upward-pointing states |á> and down |â>. When such
a particle passes through a suitably configured (inhomogeneous) magnetic field,
the particles with spin |á> deflects to one side, while particles with spin |â> tilts to
the opposite side. They therefore fall into different places
of electronic detectors. On this principle, the so-called spintronics
develops - electronics, which, in addition to the charge of
electrons, also uses the orientation of their spin.
Digital application of the principles of this quantum electronics
leads to quantum computers.
On these remarkable quantum properties
have therefore recently "rushed" some experts in the
field of computer and cybernetics,
who have reformulated them into their digital terminology and,
together with physicists, have begun to work on the possibilities
practical applications in this area. In current (already classical) digital and
computer technology, the basic unit of information is "bit"
- an electronic signal whose state takes two values (it is digital), which are
expressed as "0" or "1".
It is usually realized by two normalized well-distinguishable
values of voltage in the gate circuit. Groups of
combinations of these bits ("bytes",
groups of 8 bits) then express the codes and numerical values of
all data in the binary system.
In quantum informatics, the so-called quantum
bit or qubit (quantum
bit) is introduced as the
basic unit as a quantum bit version - digital units of
information. While the classical bit is always
in either the |0> or |1> state, the qubit also carries
arbitrary values between 0 and 1 during the
process - it also includes all superpositions of
probabilities of these states. In the wave function, information
about all superposition coefficients is carried in parallel.
Qubit state |q> is written as: |q>
= A . |0> + B
. |1>, where A and B
are complex probability coefficients of states |0> and |1>,
for which A2 + B2 = 1 holds.
The complex superposition state
"between 0 and 1" is implicitly contained only in the
free state, without any interaction. The specific explicit value
|0> or |1> is acquired by qubit only at the moment of measurement
(interaction). During the interaction (when
we "look" at it, detect it, decode it), the state of the qubit "flips" - in quantum
terminology, "collapses" - to one side or the
other, whichever is most likely at that moment.
Quantum computers mainly use three specific phenomena
from the quantum microworld: quantum superposition
of states, quantum interconnectedness and interference (constructive or destructive) of
quantum states. The quantum computer is based on three basic
principles :
1. Technical realization of qubits ; 2. Quantum
entanglement of qubits ; 3. Detection
and decoding of quantum states (logical operations with
qubits) .
Ad 1 :
Suitable two-level quantum-mechanical microsystems can
be used for technical realization of qubits (photons, electrons, atoms). So
far, four methods for realizing qubits have been tested :
¨ Utilization of photon
polarization ;
¨ Use
the spin of particles, especially electrons ;
¨ Use excited atoms, especially
hydrogen atoms ;
¨ Use
of superconducting conductors arranged in
so-called Josephson junctions (they
are described in §2.5, section "Microcalorimetric detectors", passage "SQUID") .
Several other special quantum phenomena
could be used (.....), which have not yet been realized.
Ad 2 :
Quantum entaglement of qubits can be
performed by mutual interaction of particles, atoms or ions.
Interconnected quantum states are often realized by means of a
laser pulse. If we managed quantum interconnected N
qubits, the number of superposition coefficients is 2N. Operations with
these interconnected qubits are parallel (it takes place with all superposition coefficients), which gives the potential for high performance
of electronic storage, transmission and analysis of information.
Ad 3 :
For the recognition and decoding
of quantum states of qubits and for logical operations with them,
use methods depending on the type of qubits used. For polarized
photons, these are optoelectronic
methods. The measurement of the plane of polarization can be
performed by placing a polarization filter in the path of the
photon, through which only photons with a certain plane of
polarization (state |1>) pass, while photons polarized
perpendicular to the plane of the filter do not pass (state
|0>). Photons polarized in other planes will behave as qubits
in the superimposed state - according to the angle of rotation of
the polarization, the amplitude will change the probability that
the photon will pass or not pass through the polarization filter.
Magnetoelectronic methods are used for spin
orientations.
Perspectives of
quantum computers ?
The application of the laws of quantum properties in informatics
and computer technology promises attractive possibilities for quantum
computers that some computational tasks might be able to
solve many times faster than conventional computers. Often
mentioned, but in fact marginal, is the possibility of perfect quantum
cryptography (protection of
transmitted data using quantum keys).
The problem is to build quantum computers
with a large enough number of qubits. Large sets of particles no
longer behave according to the laws of quantum physics and begin
to follow the laws of classical mechanics and electrodynamics.
Possibilities of creating so-called modular quantum systems
are being explored : construction of many small quantum
processors and their interconnection by a small number of nodal
quibits, which would not disturb their quantum properties (the modules themselves remain relatively isolated from
each other). Quantum chips
are developed in "high-tech" microelectronics
laboratories, in which pairs of entangled ions (in ion traps) or entangled
photons (in optical crystals or micro ring
resonators) are generated and analyzed.
These could become essential elements of truly usable quantum
computers.
A big problem is the prevention of quantum
decoherence of qubits, for which it is necessary to completely
isolate the system from the disturbing influences of the
environment, including thermal oscillations. Therefore, the operating
temperature is a significant technical obstacle
to the practical use of the quantum computers being developed so
far. For the correct function of qubit circuits, it is necessary
to cool them to a very low temperature close to absolute
zero (of the order of milliKelvins), which requires a
complex cryogenic technique.
So far, quantum computers are in the stage
of experimental verification and improvement of
basic physical and technical principles. Manipulating qubits is
incomparably more difficult than bits in
electronic computers. There will be a long and
difficult journey to create truly usable and powerful quantum
computers ..!..
After initial enthusiasm, many computer experts are now
somewhat skeptical of quantum computers. They
will definitely not be "self-saving"! They will not be
universal, so they can no replace classic digital electronic
computers (we will probably never have
quantum PCs at home...). They will be
suitable only for some special areas (eg searching for information in large unsorted data
files, factorization decomposition of numbers into coefficients,
fast Fourier transform, ...), where they
can significantly speed up classical algorithms. Due to the
quantum-stochastic nature of qubit states, quantum computers use probabilistic
algorithms (individual processes are
repeated a million times), with an effort
for fast repairability and convergence. Whole pure quantum (100-%) computers they are
not feasible - and it probably wouldn't even make sense.
Rather, they will be quantum coprocessors for
large specialized computing systems.
Brief recap :
What
are the basic differences between classical and quantum physics
Before we start dealing with the
properties of the microstructure of matter - atoms, molecules,
subatomic particles, for the sake of clarity, we will briefly
recap here what the most important differences are between
classical physics and quantum physics and how these differences
affect our understanding of events in nature (both on earth and
in space) :
-> Scales,
sizes :
Classical physics deals with macroscopic objects -
objects around us and their systems, their movement, forces
acting between them, mainly electric and gravitational.
Quantum physics focuses on the behavior of particles on
microscopic scales - molecules, atoms, subatomic particles. Their
movements, mutual interactions, physical fields and their quanta.
-> Duality
between particles and waves :
Classical physics deals with particles as distinct,
localized and separate objects.
In quantum physics, particles can exhibit properties
belonging to both particles and waves. The particles are not
localized. This can cause diffraction and interference.
-> Determinism
- probability :
Classical physics is deterministic - it is assumed that
the future behavior of the system is precisely determined by the
initial conditions in the past, and it is possible to predict
exactly what the outcome will be. Randomness is considered only
as a manifestation of a large number of interactions in sets of
particles, within the framework of statistical physics.
Quantum physics introduces a stochastic nature - quantum
fluctuations - into the description of the movement and
interactions of particles. We can only predict the probability of
a certain outcome, which will basically be slightly different
each time, even given the same starting conditions. With multiple
repetitions or a large number of particles, the various
stochastic results are averaged, the fluctuations are smoothed
out and, on the contrary, a very accurate result is produced.
-> Uncertainty
Principle :
In classical physics, we can measure all physical
quantities of particles, such as position, velocity, momentum,
energy, in principle with absolute precision; apart from
instrumental precision, nothing prevents us from doing so.
In quantum physics, however, the so-called uncertainty
principle (Heisenberg's) is applied, according to which certain pairs of
physical quantities, such as the position and momentum of a
particle, cannot be measured simultaneously with absolute
precision. The more precisely we measure one quantity, the more
uncertain the other quantity becomes. This uncertainty here is a
consequence of the wave nature of the particles.
-> Concept
of physical forces :
In classical physics, each interaction of bodies and
particles is assigned a corresponding field - a space in
which certain forces act on the particles. In classical physics,
it is an electric+magnetic and gravitational field. Changes in
intensity in the field propagate with a finite speed (c), which
is accompanied by a continuous transfer of
energy, momentum, angular momentum.
In quantum theory, the field is modeled as a set of particles
- a quantum field. And mutual force action - particle
interaction - is caused by the mutual exchange of these quanta - intermediate
particles. Particles constantly receive and emit quanta of
intermediate fields, which causes their force action. For
electromagnetic forces, the intermediate quanta are photons.
In the static case, intermediate photons are virtual,
under dynamic action, virtual photons are transformed into real
ones, real radiation occurs. Physical quantities are transmitted discontinuously
in certain "portions - quanta".
On a macroscopic scale, quantum processes are basically
negligible, classical physics remains highly accurate in
the vast majority of phenomena, all mechanical and electrical
machines in industry and households, cars, airplanes, space
rockets work according to it. And natural phenomena on land, in
the sea, in lakes and forests, in the atmosphere, the orbits of
the planets around the Sun, etc.
However, quantum physics has enabled us to
understand the hidden atomic and subatomic phenomena that are the
inner essence of all matter. In space, it participates in
thermonuclear reactions in stars leading to their radiant energy
and the creation of elements ("we are
all descendants of stars"), the
creation of the universe and the primordial cosmic
nucleosynthesis. She also led or assisted in the development of
new technologies such as transistors, integrated circuits,
lasers, for the construction of advanced electronic devices. It
also contributed to the construction of equipment for obtaining
energy - photovoltaics and, above all, nuclear energy.
Quantum and classical physics are thus
increasingly intertwined, for the future a combined approach
will be needed...
Atomic
structure of matter
The question of the structure
and composition of matter is one of the most basic and
important questions that people ask nature - along with questions
about the origin, size and structure of the universe, or
questions of the origin of life. In earlier times, when humans
did not have the means to gain a deeper insight into the
microscopic dimensions of the interior of matter, it was by no
means easy to make any credible claims about the invisible
microstructure of matter. Scholars therefore resorted to various
assumptions and hypotheses, formed by analogy with what was seen
with the naked eye.
In this context, a fundamental question arose: does
matter have a continuous or granular
structure? In other words: matter is infinitely divisible
to smaller and smaller particles, or in this division do we
finally come across the smallest, further indivisible
isolated particles?
Intricate
historical development of the concept of atoms
The Greek ancient philosopher Demokritos (5th century BC, partly followed the views of his
teacher Leukippos of Miletus) was a
supporter of this second possibility of the smallest indivisible
particles, arguing that if matter were indefinitely divisible, it
would not remain in the end, nothing that would carry the
properties of the substance. Therefore, each substance must be
composed of indivisible particles which carry the properties of
that substance. He called these smallest indivisible particles
"atomos" - Greek. "indivisible".
Note: It would be
a complete misunderstanding to consider Demokritos as the
discoverer of atoms or the creator of atomic theory! Demokritos
knew nothing about real atoms, his opinion was just one of many
speculative hypotheses, mutually equivalent at the level of
knowledge at the time; other scholars at the time rightly
considered matter to be infinitely divisible ...
By the way, the above-mentioned philosophical
argument about the bearers of the properties of matter would no
longer stand. We know that an increase in quantity, or a
combination of more quantities, can create a new quality. The
properties of the system are created only by a combination of the
properties of its subcomponents. And it's the same with matter. A
specific substance may not have any elementary carrier of its
properties - these properties are created only by a specific
"construction" of a substance from particles, which
themselves have completely different properties ...
The idea of
atoms then fell into oblivion for a long time. It was not until
the turn of the 17th and 18th centuries, when feudalism and the
church lost their absolute power, that the former alchemists -
charlatan and often fraudulent "goldsmiths" in the
service of the rich and powerful - gradually was replaced serious
scientists who no longer wanted a recipe for making gold or
various elixirs, but they tried to penetrate into the true essence
of the construction of matter. It was then that the idea
of the basic building blocks of matter (Descartes, Hook) began to
appear again in connection with the study of the behavior of
substances, especially gases (the dependence of pressure on the
volume of gas). From the 18th century, with the gradual
liberation from earlier alchemical superstitions and prejudices, chemistry
emerged as an independent discipline. Through a series of
experiments, R.Boyl and A.L.Lavoisier came to terms chemical
element as a substance that can no longer be broken down
into two or more other substances. During chemical experiments,
important laws of chemical processes were determined :
- The law of conservation of mass and energy
of substances entering the reaction and resulting reaction
products in a closed system (M.V.Lomonosov 1748, A.L.Lavoisier
1774) ;
- The law of constant
merging ratios (J.L.Proust and J.Dalton 1799), the law
of multiple merging ratios (J.Dalton 1802) and the law
of constant volume ratios (Gay-Lussac 1805), observed in
reactions in the gaseous state.
These laws became the experimental basis
for clarifying the question of the internal structure of the
elements. J.Dalton gave a natural explanation of all these
important laws in 1808 in his atomic hypothesis,
according to which each element is composed of a large number of
mutually identical atoms, indivisible
particles characterized by a certain characteristic mass and
other properties. The atoms of the same element are the same, the
atoms of different elements differ in mass and other
"chemical" properties. These atoms are the basic
indivisible building block of matter that participates in chemical
reactions - the merging of elements consists in the
joining of two or more atoms. In this concept, the law of
conservation of mass in chemical reactions is an outward
manifestation of the indestructibility (and also the
"uncreatability") of atoms. The new bound whole,
created by merging an integral number of atoms, was called a molecule
(lat. Moles = mass); the name comes from A.Avogadra from 1811, who also
discovered the first relationships between molecular, weight and
volume amount of substances.
Note:
We now know that the law of conservation of mass
and merging ratios differ slightly from ideal values. This is in
connection with the relationship between equivalence of mass and
energy E = mc 2given by the binding energy of the reaction, the mass
defect of atoms and nuclei, the difference between the mass of a
proton and a neutron. These aspects will be discussed below where
appropriate.
Electrolysis
played an important role in understanding the composition of
substances and in discovering a number of elements: the
decomposition of substances (mostly their
aqueous solutions) by the action of an
electric current from Volt electric cells (batteries). First it
was the electrolysis of water into hydrogen and oxygen, then the
electrolysis of various alkalis, acids and salts into hydrogen,
oxygen, sodium, potassium, calcium, copper, zinc, chromium and
other elements. An interesting question arose: "If
electricity can decompose substances into elements, could it even
combine elements into more complex substances?". She
already anticipated later knowledge of electrical origin of
all chemical reactions (see "Atomic interactions" below).
Periodic Table of the
Elements
In 1869, D.I.Mendelev systematically dealt with the chemical
properties of various elements. He found that the chemical
properties of elements periodically depend on
their relative atomic mass (atomic weight). He proposed to
arrange the elements in a table, in order of increasing atomic
weight into horizontal rows (forming periods) so that elements of
similar properties get under each other. The definitive
explanation of this Mendeleev's periodic table of
elements was made possible by the development of the
physics of atoms - see below "Bohr's quantum model of the atom", passage "Occupancy and configuration of
energy levels of atoms" and "Interaction of atoms - Chemical merging atoms - molecules".
A similar story, explaining the essence of the
observed regularity and repetitive structure and
properties at different scales is repeated in other areas of
science :
- In particle physics - §1.5 passage
"Unitary symmetry
and particle multiplets"
and part "Standard model -
unified understanding of elementary particles", passage "Preon hypothesis".
- In astrophysics of stars - §4.1"The
role of gravity in the formation and evolution of stars"- The Hertzprung-Russell diagram, in the book
"Gravity, Black Holes and the Physics of Spacetime".
At the turn of the 19th and 20th centuries, when a
sufficient amount of experimental data from the field of
chemistry and physics was collected, is was realized that pure
elements are composed of "indivisible" basic particles
- atoms (which bear their
properties), which can combine - merge -
into molecules in compounds. Next experiments in
the early 20th century showed that even the atom is not
an indivisible (unstructured) elementary particle, but
has its own complex electro-mechanical structure.
In terms of construction materials, atoms are not the last,
smallest and most fundamental particles of the substance, but
only one of the important hierarchical units of
substance structure.
The structure of atoms
Although physics and chemistry during the 19th century
increasingly convincingly showed that substances consist of atoms
and molecules, the nature and structure of the atoms themselves
practically nothing was known until the end of the 19th century.
Experiments with electrolysis carried out by
M.Faraday in 1836 have already shown that chemical compounds have
a lot in common with electrical phenomena. The
first significant penetration into the structure of the atom was
the discovery of the electron, made in 1895 by
J.J.Thomson in the study of electric discharges in gases *) and
the discovery that all atoms contain electrons.
*) Electric discharges
Electric shocks in the air, known as spark jump among
bodies sufficiently electrified by static electricity, have been
known for a long time (for the development of
knowledge about electrical phenomena, see also §1.1 "Historical
development of knowledge about nature, space, gravity", passage "Electricity and magnetism"
in the book "Gravity, black holes and space-time
physics"). In 1743,
M.Lomonosov suggested that lightning and aurora borealis are
manifestations of electric discharges in the air (he
was right about that lightning; aurora borealis is more about the
interaction of high-energy particles from the Sun with the upper
layers of the Earth's atmosphere). In the last decades of
the 19th century a number of researchers have studied
high-voltage electric discharges in dilute gases (as early as 1838, M. Faraday observed a strange
fluorescent arc between the cathode and the anode, connected to
an electrical voltage in a tube with dilute air). Glass
tubes or flasks with sealed electrodes were used for this - discharge
lamps, filled with air or other gases, diluted by means of a
vacuum pump to a pressure of about 10-3
atmospheric (approx. 100 Pa). The most famous were the so-called Geissler
tubes, used since 1850. These differently shaped lamps,
beautifully lit in different colors (according to the type of gas
charge), were very attractive; they evolved into "neon"
tubes. We now know that the light manifestations of an electric
discharge are caused by ionization and excitation of gas atoms,
caused by the impact of electrons (accelerated in an electric
field), followed by deexcitation with the emission of photons.
 |
|
| Discharge lamps - gas-filled tubes with electrodes to which a high voltage >100 V is applied | Cathode ray tubes - very dilute gas-filled tubes with electrodes (discharge lamps - Crookes tubes), to which a very high voltage > 1-10 kV is applied |
Later, electric discharges were studied in even more dilute gases at a pressure of about 10 -6 atm., when the visible discharge ceases. In 1859-76, J.Plücker, J.Hittorf, and E.Goldstein observed a faint fluorescence of the flask opposite the cathode: as if some radiation came out of the cathode, hence the cathode radiation. In 1880, W.Crookes designed a special glass flask with sealed electrodes, the so-called Crookes cathode ray tube, into which various objects, screens, and minerals were inserted between the cathode and the anode. At voltages of about 1000V and higher, Crookes found that with sufficient dilution of the gas, invisible so-called cathode rays emanate from the direction of the negative electrode, causing the bulb to fluoresce in places opposite the cathode. The objects and screens inserted between the cathode and the anode cast sharp shadows in this luminescence, some of the minerals exposed to the cathode rays fluorescent. Vacuum tubes, screens, and X-rays tubes have evolved from Crookes cathode ray tubes, however, the diluted gas was replaced by a vacuum and the cold cathode by replaced by heated cathode, which thermoemission supplies the necessary electrons ("cathode rays").

1895: J.J.Thomson - discovery of electrons
=> first model of atom
In 1895, J.J.Thomson studied the deflection of
these cathode rays in electric and magnetic fields and found that
cathode rays are made up of very light negatively charged
particles, whose charge corresponded to an elementary electric
charge (roughly determined from Faraday's laws of electrolysis
and later specified by Millikan's experiments). In this way, he
discovered the first elementary particles of the microworld - electrons
- and revealed the corpuscular nature of cathode rays, which are
formed by a stream of fast-flying electrons. We now know that
these electrons came from gas atoms ionized by the impact of
other electrons accelerated in an electric field. Name electron
(Greek electron
= amber; static electricity was
observed on amber objects in ancient Greece) comes from G.J.Stoney, who in 1891 dealt with Faraday's
laws of electrolysis in connection with Dalton's atomic concept
and concluded that the electric charges needed to exclude
individual types of atoms are integral multiples of a certain
small basic, elementary charge, representing a kind of
"atoms" of electricity (electricity was until then
considered a continuous "fluid"). Further experiments
with cathode ray tubes led to the discovery of X-rays (§3.2
"X-rays - X-ray diagnostics").
Note: The
electrical phenomena in discharge lamps and cathode ray tubes
were dealt with by a number of researchers in the given period,
either independently or in mutual connection or cooperation. It
is also probable that researchers "sunken patriots" who
did not penetrate the general consciousness also came to new
discoveries of knowledge in their remote laboratories. Therefore,
arguing about the particular primacy of individual specific
researchers can be problematic - and it is basically useless...
It is important that by joint research they significantly
contributed to revealing the laws of electricity and the
microworld (cf. also the passage "Significant
scientific discoveries - chance or method?" in §1.0).
Electrons have (conventionally) negative electric charge and according to the first
experiments were more than 1000 times lighter than electrically
neutral atoms; we now know that electrons are 1837 times lighter
than a hydrogen atom. Thus, each atom must contain a sufficient
amount of positively charged mass to balance the negative charge
of its electrons, and this positively charged component
represents almost the entire mass of the atom. Based on these
findings, J.J.Thomson proposed in 1898 the idea that atoms are a
miniature homogeneous sphere of positively charged matter, into
which electrons are nested - Fig.1.1.4 on the left. This Thomson
model of the atom was also called the "pudding
model", due to its resemblance to the English pudding
with baked raisins.

Fig.1.1.4. To develop ideas about the structure of atoms.
Left: Thomson's "pudding"
model of the atom. Middle: Rutheford
experimental arrangement of scattering a -particles by metal foil. Right:
Difference of dispersion a particles by atoms for the case of Thomson model and
model of atom with nucleus.
A more detailed experimental investigation of
the structure of atoms was undertaken in 1909-11 by E.Rutheford,
who, together with his collaborators H.Geiger and E.Marsden,
performed important experiments with alpha particle
scattering (a maximum energy of
7.7 MeV emitted by the natural radionuclide 226Ra and its decay products, especially polonium) during their passage through a thin gold foil (thickness about 3.10-4 mm, which corresponds to about 104 atomic layers) - Fig.1.1.4 in the
middle; alpha particles after passage and scattering of the foil
are labeled as a'. These particles were observed visually by Rutheford
and co-workers according to the flashes in the scintillation
layer (zinc sulfide) with which the flask surrounding the
irradiated foil was coated from the inside.
Note :
Scattering experiments (mostly with high-energy
electrons and protons on accelerators) are generally the most
important method of investigating the structure of the microworld
and the properties of particle interactions - see §1.5 "Elementary particles".
According to Thomson's model of the atom,
it was expected that heavy and fast alpha particles would easily
"pierce" the thin gold foil - they would pass through
the foil either directly or with only a small scattering
(Fig.1.1.4 at the top right); the uniformly sparse distribution
of charge and mass inside the "pudding" atom causes
only weak electrical forces when passing heavy alpha particles.
The passed alpha particles should then leave their light traces
only on a small area on the back of the flask, in a direct
direction from the emitter.
However, the experiment showed, that in addition of
this, a number of particles a' scattered by a large angle, some were
even reflected in the opposite direction - Fig.1.1.4 in the
middle *). In order for heavy alpha particles (more than 7,000
times heavier than an electron) moving at high speed (almost 2.107 m/s) to disperse in
this way, large forces had to act on them inside
the atoms, which would not be possible with the Thomson model
with a relatively light, sparsely dispersed positive mass in
which light electrons are embedded. Although most alpha particles
easily penetrated by the fringes of atoms, some of them had to
bounce off "something" small, heavy, and positively
charged inside the atom.
*) Most flashes, as expected, appeared on
the back of the flask in a straight line from the emitter, which
corresponded to the passage of alpha particles through
"gaps" between atoms, far from the nuclei. However, the
particles passing through the inner part of the gold atoms showed
considerable angles of deflection.
To clarify these experimental results,
Rutheford abandoned Thomson's model and proposed an image of an
atom composed of a very small nucleus (less than
ten thousandths of the diameter of the whole atom *), in which
the positive charge and almost the entire mass of the atom are
concentrated, and from electrons located at a certain (relatively
large) distance from the nucleus. Namely nearby of this extremely
small, heavy, and the positively charged nucleus, around which,
according to the Coulomb law, very high electric field
intensities acts, the alpha-particles that fly just around the
nucleus are effectively scattered (Fig.1.1.4 bottom right). If
the alpha particle flew relatively far from the nucleus, it did
not disperse almost at all. The closer the path a- particle
approached the nucleus, the more it dissipated (due to the
greater electrical repulsive forces).
*) Later measurements showed that the
nucleus is even 100,000 times smaller than an atom (!) and
clarified the structure of the atomic nucleus (described below in the "Atomic
Nucleus" section).
However, the electrons in this Rutheford
model of the atom cannot be at rest, because the
electrostatic force would draw them to the nucleus and the atom
would collapse - they must move, orbit the nucleus
*) along paths where the electric attractive force is balanced by
centrifugal force, analogous to this is the case with planets
in the solar system - a planetary model.
*) In quantum mechanics, an alternative
explanation of the structure of atoms is sometimes given
: electrons cannot fall on the nucleus due to quantum-mechanical uncertainty
relations (discussed above in the "" section)
and the fermion character of electrons. Electrons cannot
acquire a smaller distance, or a lower energy level in the
electric field of the nucleus than the lowest basic one; if we
tried to "push" them even closer to the nucleus, they
would "defend" themselves with an intense repulsive
force - electrons as if their wave nature
"did not fit " into such a small space - as if they
suffered from a "claustrophobic effect". The
so-called Fermi pressure of degenerate electrons arises
here, which counteracts the electrical attraction of the nucleus.
Electrons in the atomic shell according to Pauli's exclusion
principle "pair" into pairs with opposite spin in
areas of space called orbitals and the
quantum-mechanical oscillations resulting from corpuscular-wave
dualism prevent them from occupying smaller volumes. In our
interpretation, however, for better comprehensibility and
continuity between classical and quantum physics, we will stick
to the usual "planetary" explanation - the orbit
of electrons around the nucleus.
Only in the quantum model of the atom will we use
corpuscular-wave dualism to explain the quantization of electron
orbits (Fig.1.1.6) and use the "claustrophobic effect"
of quantum uncertainty relations to explain the repulsive forces
in the nucleus at subnuclear scales (see
below "Strong nuclear
interactions").
All nature is almost
absolute emptiness !
Our whole nature is only emptiness, "polluted" by an
almost negligible amount of matter. Everything around us is made
up of only a small amount of real - "solid",
concentrated - matter. This somewhat paradoxical statement
clearly follows from the knowledge of the structure of atoms. An
atom is not some solid mass ball, but it consists of a very dense
nucleus of only 10-13 cm and an almost empty electron package. The nucleus,
bearing more than 99.9% by weight of the atom, is about 100,000
smaller than the whole atom. This can be compared to a large
sports stadium (representing an atom), in the center of which is
a small children's ball representing the core; a few electrons
would circle on the area of the stadium and the rest would be
completely empty. As can be seen from Fig.1.1.4 on the right, the
energy particle, in collision with the atom, in most cases flies
through it as if through empty space; only if it accidentally
hits the nucleus will there be a reflection or interaction.
Thus, an atom is actually an empty space,
"polluted" by several protons, neutrons and electrons.
About 99.98% of each atom is an empty vacuum. Even our body,
which is built of these atoms, is mostly formed by emptiness: the
whole "real" mass of our body could theoretically be
compressed into a ball with a diameter of about 1 mm, the rest would
be emptiness. The same emptiness forms and all objects around us
...
Matter is mainly the
field
Thus, if atoms are predominantly empty space, at the mechanistic
point of view there is a paradoxical question: "How is it
possible that the most individual material objects do not
penetrate with each other? Why do we see clear
boundaries fixed objects?"- why don't we go trough the wall,
or why don't we "penetrate the wood" while sitting and
fall through the chair due to the force of gravity? The answer to
this paradoxical question of why the material normally does not
pass, is the electromagnetic field - a force
evoked by charged protons and electrons in atoms. If the bodies
get close to each other, their atoms (due to the deformation of
the electronic configuration) begin to electrically repel
each other and under normal circumstances there can be no
interpenetration of atoms. When sitting on a chair, we are
actually hovering ("levitating") over the upper layer
of atoms of the chair's material, on the "pillow" of
the electric field. The "penetration" of atoms occurs
only at higher forces and energies, as discussed below in the
section "Interaction of atoms".
It is similar with weight. The sum of the
rest masses of the basic building blocks - quarks and electrons -
of our body would represent only about 1% of the mass of our body
(§1.5, passage "Quark structure of hadrons"). The predominant part of
the mass of our body (and of each material object) is formed by
the kinetic energy of the building particles and the energies of
the fields, according to the relation E = mc2.
| Gnoseolological note : |
| Trajectories
and orbits of particles <-->
quantum states ? Our understanding of nature is largely based on experience, expressed in classical mechanics (and event. the theory of relativity). That is why, even when transitioning to quantum physics, we use the idea of particle movement along certain trajectories and electron orbits along (quantized) orbits in the atom for better understanding. However, according to the opinion of current quantum physics, these trajectories and orbits of particles do not exist, particles only occupy certain quantum states..?.. |
| We will reflect on this dual epistemological view at a number of places in our discussion of atoms, particles and the physics of the microworld. |
Planetary
atomic model
E.Rutheford therefore based on the above-mentioned scattering
experiment with alpha particles during their passage of thin metal foils,
formed the first realistic model of the atom - now commonly known
planetary model according to which the atom
consists of a positively charged core, around
which orbit the negatively charged electrons
(Fig.1.1.5 - where, however, the planetary
model is already draw in an improved version of Bohr's model). The attractive electric force acting under Coulomb's
law between the negative electrons and the positive nucleus is
balanced by the centrifugal force created by the circular
circulation of the electrons.
For the motion of an electron
with charge -e and mass me in the electric Coulomb field of a nucleus with charge
+Z.e (Z is an atomic number, now called a proton number- see
below "Atomic
nucleus"), according to 2.
Newton's law of force and Coulomb's law of electrostatics, the
equation of motion apply
me.d2r/dt2 = F
= -(1/4p.eo).(Z.e2/r2).ro ,
where r is the position vector from the nucleus
to the electron location, r is the instantaneous distance
of the electron from the nucleus, ro is a unit radius-vector pointing from the nucleus to the
electron. The nucleus is considered to be motionless and
infinitely heavy compared to the mass of the electron me . This equation of
motion expresses the motion of an electron in the central field
of the nucleus along Keppler orbits (generally an ellipse,
hyperbola, parabola), similar to the motion of planets in the
central gravitational field (for a detailed mathematical analysis
in §1.2 "Newton's law of gravitation" in book "Gravitation, black holes and space
- time physics"). In the simplest case of a circular orbit
path of radius r we get a simple equation of motion
me.v2/r = (1/4p.eo).Z.e2/r2 ,
indicating the orbital velocity v the electron depending
on the radius of orbit r. This basic equation of the
planetary model of the atom can also be easily obtained as a
condition of the balance of the centrifugal force me .v2/r, acting on the
electron in a circular motion, and the attractive electric force
(1/4p.eo).Z.e2/r2 of nucleus from the Coulomb law.
However, the
original planetary model had the drawback of being in conflict
with classical electrodynamics: According to Maxwell's equations
of electrodynamics, every electric charge moving with
acceleration, emits electromagnetic waves. So every electron
orbiting the nucleus (circular motion is
uneven - the direction of the velocity vector changes -
centripetal acceleration) should generate a
periodically changing electromagnetic
field, which would be manifested by the emission of
electromagnetic waves carrying away the kinetic energy
of the orbiting electron - see §1.5 "Electromagnetic
field. Maxwell's equations.",
Larmor formula (1.61'), monograph "Gravity,
black holes and space-time physics". An electron braked in this way would orbit in a spiral
and fall closer and closer to the nucleus, the intensity and
frequency (equal to the frequency of the
circular motion of the electron) of the radiation would increase, until
the electron finally hit the nucleus *). Such an "electric
collapse" the planetary atom would run very fast,
in about 10-10 seconds for the hydrogen atom.
*) By substituting into the mentioned
Larmor radiation formula -(dE/dt) = (2/3).(1/4p.eo).q2a2/c3 of the charge of the
electron q = e and the acceleration of its circular motion a = v2/r = (1/4p.eo)Z.e2/me.r2 we get for the time change of the radius of circulation
r (decreasing r , descending along a spiral)
differential relation dr/dt = -(4/3).(1/4p.eo).(Z.e4/me2c3r2). By integrating its
inverse form from r(t = 0) = rat - original radius of the atom rat » 10-10 m in the initial
time t = 0, to r (t = tcol ) = rnuc - impact on the nucleus of radius rnuc » 10-14 m, we get for the collapse time tcol
the value tcol = (4p2.eo2me2c3/Z.e4).(rat3 - rnuc3) » 10-10/Z [sec].
Fortunately, we do not observe anything
like that - atoms exist here and are stable! In addition, atoms
with electrons in different orbits would emit different
frequencies of electromagnetic radiation continuously,
in contrast to experimentally observed discrete spectra of atomic
radiation composed of individual spectral lines
of precisely given wavelengths (frequencies
and energies) characteristic of different
atoms (see below "Radiation
of atoms") .
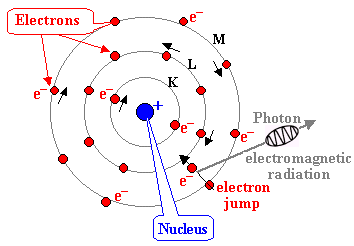 |
Fig.1.1.5. Schematic
ilustration of the planetary structure of an atom in
which negative electrons orbit a positively charged
nucleus. According to Bohr's model, electrons orbit the nucleus only along quantized discrete orbits on which they do not radiate. When an electron jumps from a higher to a lower path, the corresponding energy difference radiates as a quantum (photon) of electromagnetic radiation. |
| Is it
an atom ? Looking at this picture, almost every educated person says that "it is an atom". This answer is only partially correct, because in reality it is only a model of the atom. If we could reduce ourselves in the sci-fi concept to the size of one picometer and penetrate the atom, we would not see any "balls" - electrons orbiting another "ball" - nuclei. At most we could see only fluctuating and rippling fields, with different densities distributed around the orbitals. However, this drawing is quite apt (cf. the passage "Ball Model" in §1.5 "Elementary particles "), can clearly display and understand most important processes in atoms - excitation and deexcitation, emission of photons of characteristic radiation, chemical fusion of atoms, processes of interaction of atoms with ionizing radiation, internal conversion of gamma and X radiation with emission of conversion and Auger electrons, other accompanying phenomena in radioactivity... That's why we will use it often. |
|
Bohr's quantum model of
the atom
The mentioned serious shortcomings of the planetary model of the
atom was repaired in 1913 by the Danish physicist Niels Bohr, who
based on experimental knowledge and in the spirit of the ideas of
the emerging quantum mechanics supplemented the
original planetary model of the atom with three important postulates
:
The planetary model, supplemented by these three postulates, represents the famous Bohr model of the atom (Fig.1.1.5), which successfully explains the most important quantum properties of atomic structure, including discrete line spectra of radiation emitted by atoms (see below). Bohr's model has retained its validity to this day (with the relevant generalizations mentioned below).
The Atom
and the Planetary System: Similarities and Differences
After discovering that the atom is a system of positively charged
nuclei and negatively charged electrons bound by an electric
force, the well-researched solar system bound by gravity became
the inspiration for clarifying the structure of this atomic
system. There is an obvious analogy on three
points :
Based on these analogies, Rutheford's planetary model of the atom was created. However, there are also fundamental differences between the planetary system and the atom :
These differences have forced
Bohr's above-mentioned modification of the planetary model of the
atom. Nevertheless, the planetary concept of the atom is still
used in some illustrative qualitative considerations...
One of the main differences between
the classical electromechanical and quantum understanding of
atoms is the mechanism of radiation of atoms.
Radiation from atoms is not emitted continuously, but after
quantum, and the frequency of the radiation f not given by
the frequency of a periodic electron circulation, but the energy
difference E of stationary orbits of electrons, combined
with the relationship E = h.f between the energy of
electromagnetic quantum (photons) and the frequency f
corresponding electromagnetic waves (cf. above-mentioned "Corpuscular-wave
dualism").
Atoms are very empty !
If we compare the typical size of
an atom 10-8 cm - the orbits of electrons - and the size of a dense
nucleus 10-13 cm, we see how extremely empty the
atom is: as much as 99.9999999999999% of the volume of the atom
is empty space (vacuum)...
Why don't
atoms glow at rest? - wave mechanism of quantization
The mechanism of quantization in Bohr's model of the atom can be
most clearly understood by the idea of the corpuscular-wave
behavior of the electron as it moves in orbit around the atomic
nucleus. We will first consider the simplest case - the hydrogen
atom.
From a corpuscular point of view, an
electron of mass me and charge -e, orbiting a proton of charge +e along a
circular path of radius r with velocity v , is
acted upon by a centrifugal force FC = me.v2/r and Coulomb attractive electrostatic force FE= (1/4p.eo).e2/r2. The condition of equilibrium (stability) of the path
is then FC=FE, e.g. me.v2/r = (1/4p.eo).e2/r2, from which the relations for the radius of the path
and the orbital velocity of the electron follow
| e 2
e
r = ---------------- , v = ----------------- . 4 pe o m e v 2 Ö (4 pe o m e r) |
However, if these relations are fulfilled, the
electron could orbit according to classical ideas at any distance
r from the center of the atom.
From a wave point of view, a circulating electron can
be considered as a wave whose Broglie wavelength is l = h/me.v . In order for such
a "electron wave" to orbit continuously along a path of
radius r , an integral number of
wavelengs l must be "deposites" on this path, ie either
one complete Broglie electron wave l , or 2 wavelengths per
circumference 2pr, 3l/circumference, 4l/circumference, etc. - Fig.1.1.6, in above. Only then do
all the electron waves stack and follow each
other smoothly along the entire circumference of the path. If
less than a few wavelengths occur along the path (Fig.1.1.6 in
below part), the wave continuity is broken and the path is not
stable, there will be discontinuity and disturbing interference,
which is formed into a quantum of electromagnetic radiation - a
photon is emitted, which carries the appropriate amount energy
and the electron goes to the nearest stable orbit with an integer
number of Broglie wavelengths.

Fig.1.1.6. Above: An electron orbits a
nucleus along a stable orbit indefinitely and without radiation,
if its orbit contains an integer number n of Broglie
wavelengths of the electron. Bottom:
With a non-integer number of wavelengths, the "wave
continuity" is broken and the orbit is unstable - a photon
is emitted and the electron goes to a stable orbit with an
integer number of wavelengths.
A circular path of radius r has a
circumference of 2p r, so the condition for the stability of the path is
2
p r n = n. l , n = 1,2,3,4,
..... ,
where rn
denotes the radius of the path which contains n
wavelengths l = h/me.v. Substituting for the orbital velocity from the
planetary model v = e/Ö(4p.eo.mer) we get that only
those electron paths are stable, whose radius is given by the
relation
|
For n = 1 we get the lowest
(basic, unexcited) orbit of an electron in a hydrogen atom with
radius r1
= 0.529.10-8 cm. This value is called the Bohr radius
and is also considered as one of the model values of the electron
radius re (see the
discussion in §1.5, passage "Size of elementary particles ...").
The integer n
is called the main quantum number and determines
not only the order of the "allowed" quantum path, but
also the energy of the electron in a given quantum path: The
total energy E of an electron in orbit is given by the sum
of its kinetic energy Ek = (1/2) me,v2 and the potential energy v = e/Ö(4p.eo. mer) in the Coulomb electric field of the nucleus (we choose the zero potential point at infinity; the
sign "-" means that the force acting on the electron is
attractive). Thus E = Ek + Ep = me.v2/2 - e2/(4p.eor), which after substituting v = e/Ö(4p.eomer)
gives E = e2/(8p.eor). For the allowed
paths of the orbital radius rn they then discrete values of energy En are obtained :
| m
e
e 4
1
E n = - ----------. ---- , n = 1,2,3, ....., 8e o h 2 n 2 |
which are referred to as energy levels
or shells. These levels are all negative (related to the fact that we have chosen the potential
of the electrostatic field to zero at infinity), which means that the kinetic energy of the electron in
the quantum path is not enough to free the electron from the
attractive force of the nucleus and escape from the atom. The
absolute value of electron energy |En| indicates the work
(energy) that we would have to supply the electron to transfer it
from a given quantum path n to infinity, ie to free it
from the attraction of the nucleus, ie to release it from the
atom.
If an electron orbits on the lowest
quantum path n = 1, we say that it is in basic
(unawakened) state. The transition to at higher quantum path is
possible only by supplying energy - excitation
of the atom, which may occur either photon absorption or action
of Coulomb electric forces when passing charged particle impact
or another atom (e.g at higher temperatures). During the
transition from this higher energy level n to the lower
energy level n-1 , ie during deexcitation
, the energy difference is emitted in the form
of a quantum (photon) of electromagnetic waves of energy E = En-1-En and wavelength ... ..
If the energy supplied to the electron is higher than the binding
|En|, the electron is released from the field of the nucleus
and flies out - ionization of the
atom occurs.
An
improved Bohr model ; quantum numbers
The original Bohr model applied to a hydrogen atom and considered
only circular orbits of electrons. With the improvement of
experimental spectrometric methods, it has been shown that the
spectral lines of atoms are not simple, but double and multiple -
the spectra show a fine structure. To explain
this fine structure, Bohr's followers, especially A.Somerfeld,
supplemented and perfected Bohr's original model of the atom.
In addition to circular orbits, elliptic
orbits of electrons with a longer (major) half-axis given by the
principal quantum number n have been proposed, while the
minor (shorter) half-axis is characterized by a second quantum
number l , which can take discrete values from 0£ l £ n-1. This quantum
number 1 , formerly referred to as the minor quantum
number, is now called the orbital quantum number
and determines the magnitude of the angular momentum
M1 of the
electron in a given orbit. Quantum mechanical analysis gives a
quantum value for the angular momentum :
M
l =
(h / 2p) . Ö[ l (l-1) ] , l = 0, 1, 2, ......, n-1 .
The duplication and fine structure of the spectral lines can then
be explained by the transitions between energy levels with
different quantum numbers n to different sub-levelss
differing in the value of l , on which the total energy E
depends only little.
An electron orbiting at a velocity v
along a circular path of radius r represents, from an
electrical point of view, a miniature current loop flowing
through an electric current I = e.v/2p r (the v/2p.r indicates how
many times an electron with charge e has passed through a
given path point per unit time). This current loop generates a magnetic
field and its magnetic moment is me = pr2.I
= r.e.v/2 = (e/2me).me.r.v = (e/2me).M, where M is the orbital angular momentum of
the electron. Since the angular momentum M is quantized (Ml = l.h/2p, l = 0,1,2,
......, n-1), the orbital magnetic moment of the electron me on a given quantum path is
m e = m l . e.h / 2m e = m l . m B , m l = 0, ± 1, ± 2, ....., ± l ,
where ml
is the magnetic quantum number and the constant mB is called the Bohr magneton -
represents the smallest, elementary quantum of magnetic moment.
In addition to the orbital magnetic
moment caused by the movement of an electron in orbit, the
electron also has its own so-called spin magnetic moment
and its own "rotational" angular momentum - spin.
These properties are often simply explained by the rotation of an
electron around its own axis - a rotating electron would have its
rotational angular momentum and corresponding magnetic moment.
However, this explanation is not entirely consistent, as the
"circumferential speed" of the electron would have to
significantly exceed the speed of light (contrary to the special
theory of relativity) and it would not be possible to explain
what force compensates for the enormous centrifugal force and
holds the electron together. Spin must be considered as a purely
quantum property of a particle, for which we do not have an exact
classical model.
For own angular momentum, i.e. the
spin of the electron, then is hold that its projection to the
axis of rotation can take only two values: either -1/2 h , or +1/2 h; the spin magnetic
moment of the electron is then given by the Bohr magneton: ± mB. For the momentum of the electron Ms and the spin magnetic
moment ms the following applies: Ms = s . h , ms = -(e/me).Ms = ±mB, where s = 1/2 or -1/2. The number s is called
the spin number, and in the electron can take
values ±1 / 2 (in §1.5 "elementary
particles" encounter with particles, e.g. mesons p , for which three values of the spin number are
possible: -1, 0, +1).
The interaction between the magnetic
fields excited by the spin and orbital angular momentum of
electrons, the so-called spin-orbital interaction,
leads to the splitting of energy levels of electrons in atoms
into nearby "subsurfaces", which is reflected in the
spectra of radiation from atoms by splitting spectral lines into fine
structure.
E.g. for hydrogen, the lowest energy level
of the electron n = 1 is split into two subsets with the
consensus and dissent spin of the electron and proton. The
transition between these two states corresponds to the absorption
or radiation of electromagnetic radiation with a wavelength of 21
cm. The emission and absorption of this atomic hydrogen radiation
is very important in radio astronomical observations of outer
universe.
a - the constant of
the fine structure
For the construction of atoms (as well as atomic nuclei), the
force with which particles interact with electromagnetic fields
is of particular importance. In general, this force is expressed
by Coulomb's law of electrostatics and Lorentz force acting on a
charge moving in a magnetic field. In quantum physics, where the
electrical charge is quantized in multiples of the elementary
electron charge e , performs an interesting ratio that
represents electrical, quantum and relativistic properties of
electromagnetic interaction of charged particles in a vacuum: it
is called fine structure constant *)
a = e 2 /2 e o h c =
0.0072973525376 = 1 / 137.0359996868 ,
where e is the elementary charge of the electron, h is Planck's
constant (reduced), c is the speed of light, e is the electric
permittivity of the vacuum. The constant of a fine structure is a
dimensionless quantity, its numerical value does
not depend on the choice of units.
*) The name comes from the fact that this
constant appears in the relations for the splitting of spectral
lines of radiation of atoms into a fine structure due to
the so-called spin-orbital interaction.between spin and
orbital angular momentum of electrons, resp. between the magnetic
fields excited by them. This constant was first used in 1916 by
one of the pioneers of atomistics, A. Sommerfeld, in the study of
the fine structure of electron levels in an atom. He extracted
this dimensionless value from earlier Rydberg constants
expressing the wavelengths of spectral lines at electron jumps
between levels in an atom and interpreted it as a measure of
relativistic deviation of spectral lines about Bohr's model
(ratio of velocity v1 electron in the first orbit of Bohr's hydrogen atom in
vacuum a = v1/c).
This important physical constant characterizes
the strength of the electromagnetic interaction,
acting as coupling constant in quantum electrodynamics.
It co-determines the properties of atoms, molecules and
substances composed of them, as well as the properties of atomic
nuclei, including nuclear reactions. Possible variability of
basic natural constants during the evolution of the universe
is sometimes discussed , and the fine structure constant could be
a suitable tool for sensitive spectrometric analysis of radiation
from outer space (see also the passage "Origin
of natural constants" in
§5.5 "Microphysics and cosmology" monography
"Gravity, black holes and space - time physics").
| Gnoseolological note : |
| Trajectories
and orbits of particles <-->
quantum states ? Our understanding of nature is largely based on experience, expressed in classical mechanics (and event. the theory of relativity). That is why, even when transitioning to quantum physics, we use the idea of particle movement along certain trajectories and electron orbits along (quantized) orbits in the atom for better understanding. However, according to the opinion of current quantum physics, these trajectories and orbits of particles do not exist, particles only occupy certain quantum states..?.. |
| We will reflect on this dual epistemological view at a number of places in our discussion of atoms, particles and the physics of the microworld. |
Occupancy and
configuration of electron levels of atoms
Let us now move from a hydrogen atom to more complex atoms with
more electrons. Imagine that we have created a nucleus with Z
protons and we place it in a space containing free electrons. By
electric forces, this nucleus will attract electrons, which will
gradually occupy the individual "allowed" quantum
orbits around the nucleus until an electron shell formed by Z
electrons is formed and the atom becomes electrically neutral.
Electron
orbits, shells, levels, orbitals
The electron orbits are quantized, so from an energetic point of
view it would be most advantageous, if all electrons occupied the
lowest energy level with the main quantum number n = 1. However,
such "crowding" of electrons to one level does not take
place. Conversely, according to the so-called Pauli
exclusion principle *), only one electron can be in the
same quantum state, so if the lowest energy levels are occupied,
other electrons must occupy ever higher and higher levels.
*) This exclusion principle was derived by
the Swiss physicist W.Pauli in 1925 on the basis of a series of
experimental studies of the distribution of electrons in atoms.
Later, this exclusion principle was theoretically justified as a
consequence of the quantum-statistical behavior of particles with
antisymmetric wave functions (relative to particle transposition)
- the so-called fermions, which include also
electrons (see §1.5 "Elementary particles").
Using Pauli's exclusion principle,
we can determine how many electrons can simultaneously orbit in
the paths (subshells) corresponding to the main quantum number n
: there are possible n-1 values of the orbital quantum number l
, with for each l there are 2.1 +1 different values of
magnetic quantum number ml and two possible values of spin magnetic number ms (+1/2, -1/2). Thus,
each subshell can contain a maximum of 2.(2.1 + 1) electrons and
each shell with the main quantum number n a maximum of n-1
of these subshells, ie a maximum total of
l = 0 Sn-1 2. (2.l - 1) = l = 0 S n-1 4.l + 2.n = 4. (n-1) .n / 2 + 2n = 2 n 2
electrons. Said set of electrons forms the n-th
shell (sphere, level) of the atom. These energy levels,
corresponding to the discrete values of the principal quantum
number n , are denoted by letters (in the direction from
the inside of the nucleus): K, L, M, N, O, P. The number of
electrons that can orbit at a given level is therefore not
arbitrary, but is limited by the maximum number
2n2 :
K (n = 1): max. 2 electrons, L
(n = 2): max. 8 electrons, M (n = 3): max. 18
electrons,
N (n = 4): max. 32 electrons, O(n
= 5): max. 50 electrons, P (n = 6): max. 72
electrons.
Electrons occupy paths gradually, starting with
the K shell.
This system of occupying electron
shells and subshells in atoms, together with the analysis of the
binding electric force of electrons, makes it possible to
understand the most important laws of the chemical
behavior of elements. If we sort the chemical elements
in order by atomic number, elements with similar chemical and
physical properties are repeated at regular intervals. This
empirically determined periodic law was formulated by
D.I.Mendelev in 1869 in his periodic table of elements,
which was supplemented by his followers and specified in its
current form (see below the section "Interaction
of atoms", passage "Periodic
chemical properties of atoms").
An analysis of the electron
configuration mainly shows, that the electrons in a fully
occupied shell, termed closed shell, are
strongly bound, because the positive charge of the nucleus
significantly exceeds the negative charge of the internal
electrons causing electrically "shield". Distribution
of the effective charge in of an atom containing only closed
shells is perfectly symmetrical, the atom has no dipole moment,
does not attract other electrons and its own electrons are
strongly bound, such atoms do not enter chemical bonds, are
chemically inert - this manifests itself in
helium 2He,
neon 10Ne,
argon 18Ar,
krypton 36Kr,
xenon 54Xe,
radon 86Rn
*).
*) The fully occupied sphere K is
for helium and the fully occupied sphere K and L
for neon. However, in the case of heavier inert gases Ar, Kr, Xe,
Rn, the filling of the outer shell is only 8 electrons, which is
related to the dependence of the binding energy on the orbital
quantum number, as a result of which the filling of some
subshells can become energetically disadvantageous.
In contrast, atoms with one electron
in the outer shell easily lose this electron because it is weakly
bound: it is relatively far from the nucleus, whose charge is
shielded by internal electrons to an effective value of only +e -
this explains the high chemical reactivity of alkali metals (and
also hydrogen) with valence +1. On the contrary, atoms that lack
one electron in the outer shell for closure try to obtain this
electron by the attractive force of an incompletely shielded
nuclear charge, which explains, for example, the increased
reactivity of halogens. For chemical reactions, see the section
"Interaction of atoms" below, passage "Chemical fusion of atoms
- molecules".
Orbitals
Due to the wave-stochastic laws of quantum physics, electrons in
the atomic shell do not orbit along a predetermined path (precise
orbit), but it is possible to determine only the area in
which the electron is located with a certain probability.
The region in which the electron is most likely to
occur (> 95%) is called the orbital. The
electrons in the shell are grouped into finer spatial
configurations, orbitals, depending on the minor
(orbital) quantum number l , which
determines the type of orbital and the value of the magnetic
moment of the electron (discussed above). In a given shell,
according to the increasing minor quantum number, the orbitals
are denoted sequentially by the letters s, p, d, f.
On the basic shell n = 1 there is only one orbital 1s,
on the shell n = 2 there are orbitals 2s and 2p, ..., on
the shell n = 4 can be orbitals 4s, 4p, 4d,
4f respectively. Due to the quantum exclusion principle,
electrons gradually occupy the s- orbital shell K,
followed by s- and p- orbitals of the shell L, s-
, p- and d- orbitals of the shell M, etc ...
Each orbital is filled with one and then the other electron with
opposite spins. The way orbital is occupied is sometimes called Hund's
rule. Orbitals can be differently oriented in space,
according to the magnetic quantum numbers m
(takes values -l, ..., 0, ... + l). These orbitals of the same
type, which differ only in spatial orientation, have the same
energy - they are energetically degenerate.
When an atom is placed in an
external magnetic field, the originally uniform energy of the
electrons within the orbital spreads to several different (though
close) energy levels, depending on the different orientations of
the orbitals. The motion of each electron inside the shell
creates a magnetic moment (the vector of
which depends on the spatial arrangement of the orbitals), to which a force acts in the external magnetic field.
This interaction leads to a fine splitting of the energy levels
of the electrons. A very fine distribution of energy levels
inside the orbitals also occurs due to the opposite spins
(+1/2, -1/2) of electrons (Stern-Gerlach
experiment).
Designation of atoms
of elements
In connection with the structure of atomic nuclei (see section "Atomic
nuclei" below), atoms are characterized by two basic parameters :
- Proton number Z (formerly called
atomic number A), indicating the number of
protons in the nucleus - and for a neutral (non-ionized) atom,
also the number of electrons in the envelope. This also gives the
position of the element in Mendeleev's periodic table of
elements.
- The nucleon number N (formerly
called the mass number) indicates the total number of
nucleons in the nucleus of an atom - the sum of protons and
neutrons. Characterizes weight of atom (since the
nucleons in the nucleus represent more than 99.99% by weight of
the atom).
A commonly used way to write these
numbers in certain element X is via the upper and lower
index: NXZ. E.g. hydrogen 1H1, nitrogen 14N7,
sodium 23Na11,... It will be
discussed in more detail below in the "Atomic
Nuclei" section.
Excitations
and spectra of atomic radiation
According to Bohr's model, electromagnetic radiation is generated
in the electron shells of atoms when electrons pass from higher
levels to lower ones. Since the energy levels of atoms are
quantized, photons of radiation with very specific energies are
emitted from the shell of the atom - the spectral distribution of
energies and wavelengths is not continuous, but discrete.
Excitation,
deexcitation and ionization of atoms
Excitation
of atoms
In order for an electron to transition from a higher to a lower
level, the atom must first be supplied with energy
leading to its excitation *) - to transition the
electron to a higher energy level. This energy can be supplied
either by a Coulomb electromagnetic interaction of an incoming
charged particle (electron, proton, collision with another atom),
or by photon radiation.
*) We are considering "already
finished" atoms here, not a situation where atoms are just
emerging - the formation of atoms is, of course, also accompanied
by quantum excitations and radiation.
Under normal circumstances, electron
levels in atoms with the principal quantum number n are
mostly excited to values of n+1, n+2 or n+few values of the
principal quantum number. However, with the help of strong pulses
of the electric field, electrons can also reach highly excited
states with values of n~100 and more. Such atoms with highly
excited electrons are sometimes called Rydberg atoms (after J.R.Rydberg, who measured the spectra of excited
atoms, especially hydrogen, at the beginning of the 20th century). The diameter of such atoms already reaches macroscopic
dimensions of the order of micrometers. Using sophisticated
methods with a combination of laser and microwave radiation, it
was possible to prepare excited atoms with dimensions of almost
one millimeter!
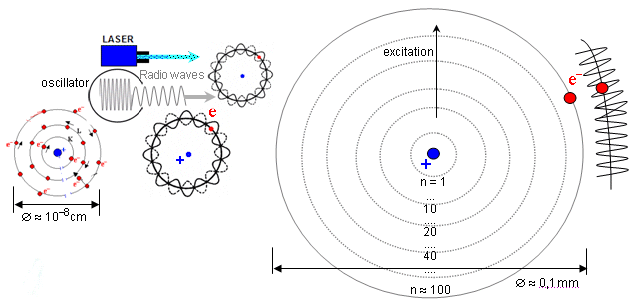
Strong electrical impulses or radiation can cause electrons in
atoms to reach highly excited states - Rydberg atoms are created.
An important property of Rydberg atoms is their
higher sensitivity to the electric field gradient. This makes it
possible to "operatively" manipulate atoms in demanding
atomic and particle experiments - see e.g.
§1.5, passage "Artificial production of antimatter".
Excited atoms
themselves are usually very unstable. They deexcite either
one-time to the ground state with the emission of visible or UV
light, or jumps between higher levels with the emission of
microwave radiation. The Rydberg valence electrons are excited
into high orbitals considerably distant from the nucleus. A
somewhat unexpected consequence of the high excitation of
electrons to large values of the principal quantum number is the extended
lifetime of the atom. This is due to the fact that an
electron can only absorb or emit a photon with an appropriate
energy equal to the difference between the levels (in the case of
Rydberg electrons, these are energies in the deep infrared
region). The lifetime of a Rydberg atom is proportional to n4.
Highly excited
Rydberg atoms can bind to each other by sharing electrons when
they approach and form a regular arrangement into hexagonal
planar clusters, the so-called Rydberg mass.
During the formation of this cluster, valence highly excited
electrons are delocalized and trapped in the potential wells
created between the atomic nuclei. This confinement prevents
electrons from leaving the cluster and causes the Rydberg matter
to have a long lifetime. Another property is the
very weak interaction of this matter with
electromagnetic radiation - its "darkness".
These properties make Rydberg matter a certain candidate for dark
matter in the universe, or for some part of it (§5.6,
section "Future development of the
universe. Dark matter" in
the book "Gravity, black holes ...).
Deexcitation
of atoms
To dexcitation of the atom and emission of
radiation then has mostly occurs spontaneously (according to some concepts of quantum field theory,
spontaneous deexcitations and emission of radiation is initiated
by constant quantum fluctuations of vacuum). Electrons in atoms can only go over between existing discrete
energy levels. Even here, however, there are certain limitations
caused by the law of conservation of angular momentum.
The photon carries the released angular momentum difference
between the respective levels through its spin,
which is equal to 1. The transition between
levels whose angular momentum differs, for example, by 1/2, is
therefore not possible by photon deexcitation - we say that this
transition is "forbidden". If an
electron occupies such a higher energy level, it cannot
spontaneously go into a lower (basic) energy state - it remains
"trapped" at a higher level for a longer time: such a
state is called metastable or isomeric (atoms that are stuck in a metastable state differ from
the original atoms only in the energy state).
Deexcitation can be induced either Coulombically (non-radiation)
by interaction with surrounding atoms or particles, or through a
higher level by radiation.
A similar mechanism of
"allowed" and "forbidden" transitions - gamma-deexcitation
- can be found even in the atomic nucleus in
§1.2, part "Gamma radiation", passage "Nuclear
isomerism and metastability".
Metastable states of atoms are used in some
radiation applications :
- Quantum light generators - LASERs,
by irradiation with light, they "pump" electrons to
metastable levels and also, by means of light, trigger a mass
return transition, avalanche deexcitation,
leading to an intense flash of light.
- Thermoluminescent dosimeters, in the sensitive
substance of which electrons are excited to a metastable state
due to exposure to ionizing radiation, and during later
evaluation, deexcitation is induced by heating (§2.2 "Photographic
detection of ionizing radiation",
passage "Thermoluminescent dosimeters").
The very process of deexcitation of
the excited energy level and formation of the emitted photon is
very fast, but not immediate. According to the laws of quantum
electrodynamics, deexcitation process of the electron in the
atomic packing is about 10-16 seconds.
Ionization
of atoms
If the atom, or any of its electron, energy supplied is higher
than the binding energy of an electron at a certain
energy level, this electron is released from the
atom and wiil fly out - occurs ionization of the
atom, from which it becomes an ion (Greek
ion = pilgrim, going). When an
electron is ejected, the neutral atom becomes a positively
charged particle, a cation. If there are enough
electrons in the environment, the electron will be recaptured -
the electron will recombine with the ion,
creating a neutral atom and photon radiation of the electron's
binding energy. Similarly, a "extra" electron (in an
electric discharge, by another atom) may be passed to a neutral
atom; the result is a predominant negative electric charge, an anion
(negative ion) is formed.
Ionization occurs by the impact of
fast-flying particles - ionizing radiation - into atoms, by
electric discharges, by the collision of fast-moving atoms in a
substance heated to a high temperature (several
thousand degrees), by dissolving salts in
water, by mechanical friction of substances ("static
electricity"). Whenever an atom or molecule loses or gains
an electron and the number of electrons no longer corresponds to
the number of protons in the nucleus, an ion
is formed - the atom or molecule carries a positive or negative
electric charge. Atoms and molecules that have one or more free
or missing electrons have an increased tendency to chemical
reactions(see below "Interaction
of atoms") due to electrical interactions with other atoms. At
this reactions, atoms and molecules can formed, that othewise are
already electrically neutral (they have the
same number of protons and circulating electrons, so they are not
ions), but they have unpaired electrons in
their orbits: they are called radicals
because they are chemically very reactive, with each
other and with others surrounding atoms and molecules (their essential significance for radiation effects on
matter and living tissue is discussed in more detail in Chapter 5
"Biological effects ionizing radiation").
Emitted
radiation
The energy of the emitted photons is given by the energy
difference between the levels of electrons in the atom. The
energy distribution of electron levels is completely characteristic
of the atoms of a given element, so by measuring the
spectrum emitted by a certain substance, we can determine the
element whose atoms are located there - this forms the content of
the atomic spectrometry.
Spectral distribution of
wavelengths, resp. the frequency or energy of the photons of the
electromagnetic radiation emitted by the substances can, in
extreme cases, have diametrically different shapes :
In terms of the positional relationship between the primary energy source, radiating atoms and the spectrometer, we encounter two types of spectra :
Interaction
of atoms
The atomic structure of matter
makes it possible to explain naturally and from a uniform
physical point of view a number of important phenomena at the
atomic and subatomic level, from which all properties and
manifestations of matter are derived - chemical reactions and
molecular properties, structure and properties of solids, liquids
and gases, all thermal phenomena (kinetic theory of heat),
electrical, magnetic and optical properties of substances.
Chemical
fusion of atoms -> molecules
Each atom binds a number of electrons in its electron shell
exactly equal to the number of protons, so that the atom is electrically
neutral. However, this electrical neutrality of the
atoms is fully manifested only at greater distances, where the
field of the positively charged nucleus is perfectly "shielded"
by the negative electrons in the envelope. In the close vicinity
of the atom, however, we can encounter residual
manifestations of electric forces *), caused by vector
folding of electric field intensities from protons in the nucleus
and from electrons located in different places of the electron
configuration of the envelope. When twoo atoms are closely
approached, these electric forces (initially repulsive) can lead
to such a rearrangement of the configuration of electrons on the
outer shells (e.g., to the sharing or transfer of electrons) that
electric attractive forces can arise that
permanently bind the atoms together to form a molecule
- Fig.1.1.7. We say that there has been a chemical fusion
of atoms. The combination of rearranged electron orbitals of
individual atoms creates common molecular orbitals. From
the energetic point of view, chemical bonding results in such a
rearrangement of electrons (electron density) in the outer
valence layers of nearby atoms, which has a lower energy
than isolated atoms and is therefore more stable.
*) Interestingly, although electric forces
have a long (unlimited) range, their "residual
manifestation" - the "chemical" forces between
atoms - are short-range. In the vector
composition of electric forces from protons in the nucleus and
electrons in the envelope, these forces are canceled at greater
distances, but at short distances a non-zero "residue"
remains. A similar mechanism is encountered in the atomic nucleus
in short-range nuclear forces between nucleons, which
are a residual manifestation of long-range strong interactions
between quarks - see below "The structure of the nucleus", part "Strong nuclear interactions".
Due to the energy released during
the chemical bonding of atoms, molecules are formed in an
energetically excited state. Deexcitation occurs
either by emitting infrared radiation or by direct
electromagnetic interaction with surrounding atoms and molecules.
Radiation deexcitations is applied in reactions in thin gaseous
medium, while in the dense medium of liquids and solids is
dominant direct dexcitation with the participation of surrouding
atoms and molecules. In both cases, the energy released during
the chemical fusion is eventually transferred to the surronding
atoms and molecules of the substance in the form of kinetic
energy of motion - the substance is heated,
the heat of reaction is generated (we mean here exothermic
reactions, see below).
When atoms approach each other, they are initially
electrically repelled (eponymous charged
electrons in envelopes). That is, so that the atoms can get close
enough to each other - such that their orbitals blend and a
chemical bond can form - a certain electrical repulsive
barrier must be overcome. Appropriate activation
energy must be supplied to the atoms. This is done by
the kinetic energy of the thermal motion of atoms - a certain
minimum temperature is required to carry out
chemical reactions in reaction mixture. At low temperatures,
chemical reactions practically do not take place *). At high
temperatures, chemical reactions take place faster, but the mean
kinetic energy of atoms and molecules can exceed the binding
energy of atoms in molecules - during collisions, the molecules
break down, the chemical compound again decomposes,
the reaction yield is lower.
*) Stimulation of chemical reactions
by radiation and tunneling effect
Another possibility of stimulating chemical reactions is
irradiation with ionizing radiation. In the irradiated substance,
electrons are released from the atoms and positive ions are
formed. The resulting electric forces allow the merging of atoms
without the need to impart kinetic energy to overcome repulsive
forces. Radiation stimulation of chemical reactions plays an
important role in the cold gas-dust clouds in space (see "Cosmic
radiation"). However, already
"finished" molecules are decomposed by ionization
radiation - occurs radiolysis of compounds.
At low temperatures,
according to classical chemistry, reactions between atoms do not
occur. However, the quantum laws of the microworld also allow
small chemical reactions here due to the mutual penetration of
the wave functions of atoms by the tunneling effect
(this phenomenon was discussed above in the
passage "Tunneling Effect"). A more detailed study of
these reactions is difficult, because in laboratory conditions
they occur very slowly, with a small yield, and they are
difficult to distinguish from the same reactions caused by random
statistically higher speeds of some atoms. However, in large
gas-dust clouds in space, over long periods of time, they can
contribute to the chemical composition of interstellar matter and
planetary atmospheres.
Energy and
the kinetics of chemical reactions
As mentioned above, to effect a merger of two atoms it is
necessary to supply them with certain activation kinetic energy QA. On the contrary,
during the actual merger, the binding energy of the atoms in the
molecule QR
is released. From the point of view of energy balance, their
difference Q = QR -QA - reaction energy is important.
According to the sign of the reaction energy, chemical reactions
are divided into two groups :
¨ Endothermic (endoenergetic)
reactions Q <0 ,
wherein the binding energy of the atoms in the molecule is less
than the kinetic energy of the interacting atoms,
"consumed" to overcome the repulsive electrical forces.
Endothermic reactions cannot be maintained spontaneously, the
activation energy must be supplied continuously from the outside;
the rate of such reactions is then given by the
"supply" of this energy. An example is the formation of
carbon disulphide in the passage of sulfur vapors through a hot
coal: C + 2 S ® CS2.
¨ Exothermic (exoenergic)
reactions Q> 0 , where there is a "release"
and gain of energy, which is drawn from the binding
energy of atoms in molecules. For exothermic reactions,
there are several possibilities for their kinetics. Time course -
kinetics exothermic reactions - decisively depends on the
concentration of interacting atoms in the reaction mixture,
pressure, temperature, the presence of other types of atoms or
molecules.
With a sufficiently high concentration of reacting
atoms, a situation may arise where the released reaction energy
during the merging of two atoms is efficiently transferred by
electromagnetic interaction to the surrounding atoms. These atoms
thus gain kinetic energy, causing them to merge immediately,
releasing more energy - which is passed on and causes other atoms
to merge. Upon delivery of the initial (initiating) activation
energy, a chain chemical reaction is formed *).
If the reaction mixture contains a large number of atoms in a
sufficiently high concentration, this chain reaction has the
character of an explosion: its velocity
increases exponentially, in a small moment (of the order of ms) practically all
atoms in the reaction mixture combine. Suddenly released heat of
reaction heats the mixture to a high temperature (of the order of
thousands of degrees), which causes a rapid expansion - the explosion
of the reaction mixture. A well-known example is the
ignition of a mixture of hydrogen and oxygen, a small spark of
locally elevated temperature is sufficient. If the concentration
of one of the components is lower, or the individual components
are fed to the reaction space gradually, an equilibrium chain
reaction having the character of a continuous combustion
can be established.
*) The nuclear chain reaction
has a similar kinetics, but a different mechanism fission of
heavy nuclei of uranium or plutonium by neutrons - see §1.3,
section "Fission of atomic
nuclei".
At low
concentrations of reacting atoms, the chain reaction does not
occur. When atoms are combined into a molecule, binding energy is
released, which is emitted in the form of infrared photons.
However, these photons fly away, the probability of their
absorption by other distant atoms in a sparse environment is
negligible. For chemical reactions to take place in a sparse
environment, the activation energy must be supplied externally
continuously (the situation is similar to endothermic reactions).
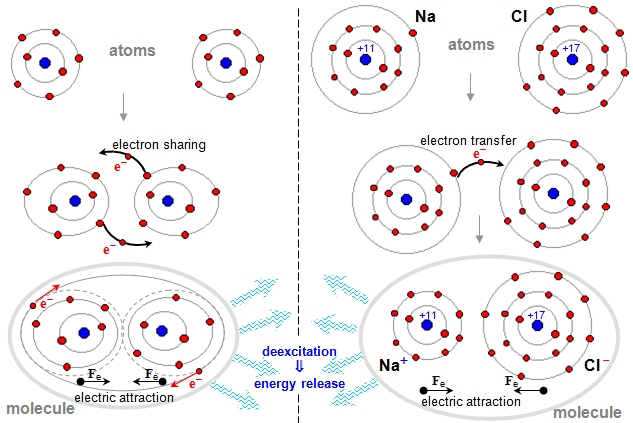
Fig. 1.1.7. Symbolic representation of the mechanism of joining
atoms and their electrical bonds in molecules.
Left: Covalent bond of two atoms caused
by electron sharing. Right: An
ionic bond of atoms caused by the handover of an electron from
one atom to another.
Types of chemical
bonding
When two atoms approach each other, there are basically three
diferent possibilities of their interaction :
In addition to the above-mentioned purely
covalent and purely ionic bonds, many molecules undergo a mixed
type of bond in which the atoms share electrons unequally.
Metal bond
In addition to the covalent and ionic bond between two atoms,
there is another type of bond in which the electrons of the outer
valence layer are not shared by two nuclei or atoms, but by a
large number of atoms. This applies to metals. Metal atoms are
characterized by a small number of electrons in the outer shell,
usually one or two electrons. These external valence electrons
from a larger number of nearby atoms can then form a single
continuous cloud - the so-called electron gas,
in an array of regularly spaced nuclei surrounded by electrons of
the inner layers. A metal crystal is a kind of huge
"molecule", made up of regularly distributed cations,
between which binding electrons move freely. The electrostatic
attractive forces between these cations and the electrons in the
cloud then form a bond called a metal.
From a physical point of view, chemical bonds are described using several parameters, four of which are mentioned here :
In a similar way as atoms, molecules
or atoms with molecules can also react together . A more detailed
analysis of the mechanisms of atomic bonding belongs to the field
of physical chemistry. The merging of specific
types of atoms and the properties of the formed molecules
(reactions of their further merging or decomposition) then form
the main content of chemistry.
Periodic
chemical properties of atoms
In the pre-scientific period, alchemists studied
substances. However, they had no idea about atoms and their
nuclei, but they also did not recognize elements and compounds.
They judged the substances according to their external
manifestations and a few simple "cooking" reactions
that they were able to carry out. In the 18th century, when
earlier errors of alchemy were gradually abandoned and
distinguished by a number of attempts chemical elements
and compounds, classical chemistry arose, as a
science of the combination of elements, the properties of
compounds, their other mutual reactions of compounding and
decomposition. The most important finding was the discovery of
the periodicity of the properties of elements
according to their relative atomic weight (we now know that the
atomic or proton number Z decides): if elements are sorted
sequentially according to their atomic number, their chemical
properties repeat after a certain sequence of elements (see also above part "Atomic
structure of matter",
passage "Periodic table of elements").
The systematic culmination of classical chemistry was the
creation of a periodic table of elements
(Mendeleev compiled its first version in 1869), in which the
elements are arranged according to the ascending atomic number
into horizontal rows (forming periods) so that the elements of
similar properties get under each other (into columns). Mendeleev
left a few blanks in the table and made the bold hypothesis that
new elements would be discovered later to fill these gaps; it
really came true.
In the first
half of the 20th century it was revealed that the periodicity of
elements is based on the quantum behavior of electrons orbiting
the atomic nucleus, in the laws of occupancy of
individual orbitals (explained above in the
section "Planetal and Bohr model of the
atom", passage "Occupancy
and configuration of electron levels").
The first
period has only one type of orbital called "s", which
can be occupied by one (for hydrogen) or two (for helium)
electrons. The atoms of the second and third periods have, in
addition to one orbital "s", three orbitals of type
"p". Each of these 4 orbitals can again be filled with
one or two electrons, with a total possible number of 8
electrons, creating a period of eight elements. The fourth and
fifth periods have, in addition to the orbitals "s" and
"p", a third type "d", which adds another 10
places for electrons - the length of the period is thus extended
to 18 elements. The last two rows of the table contain heavy
atoms with four orbitals of types "s", "p",
"d" and "f" and have a period of length 18 +
14 = 32 elements. The last element with Z = 118 has all orbitals
"s, p, d, f" filled with electrons.- see §1.3, section
"Transurans"),
a completely new table row will have to be created for them. From
element 121, a new, as yet unknown type of orbital "g"
would be added, which would extend the periodicity (number of
columns) up to 50 elements. From the point of view of the
chemical properties of atoms, however, this has only a debatable
significance, superheavy nuclei immediately disintegrate and
possibly their volatile atoms have different properties than
those corresponding to the periodic table :
Violation of
periodicity ?
The exact periodicity of the physico-chemical properties applies
only to lighter elements. The principle of similar behavior of
elements in the same column of the periodic table may be violated
for heavy atoms due to relativistic effects in
an electronic package. With a high number of protons, the
electric charge of the nucleus is high, which also leads to a
high velocity of electrons on the internal orbitals. In heavy
atoms, the internal electrons reach orbital velocities that
partially approach the speed of light (they become
"relativistic"), so the effects of the special theory
of relativity are beginning to apply here. Due to relativistic
contraction, the size (shrinkage) of the internal orbitals
decreases. Reducing the radius of the inner orbitals results in
an increase in the electrical "shielding" of the
positive charge of the nucleus by these electrons, so that more
distant electrons (no longer relativistic) are attracted to the
nucleus by less force. External orbitals, especially valence
ones, are less bound to heavy atoms than would correspond to a
conventional non-relativistic quantum model of an atom. And also
the energy distant between the outer levels is smaller.
This is reflected in the optical properties of the elements and
in some specific chemical reactions. Relativistic quantum
mechanical effects cause atoms of very heavy elements in the
region of transurams to behave chemically differently
than we would assume based on their location in the columns of
Mendeleev's periodic table (will be
discussed in §1.3, at the end of the section "Transurans", in the section "Chemical
properties of transurans") .
Bonds of
atoms and molecules in solids and liquids
In addition to the above-mentioned radiation phenomena and
chemical fusion processes, electrical forces, given by electronic
configurations of atomic shells, are also responsible for tight
clustering of large numbers of atoms and molecules into solids
and liquids as well as their properties -
flexibility, strength, compressibility, electrical, magnetic and
optical properties, thermal properties.
The solids contain primarily the ionic
and covalent bond analogs mentioned above in
connection with the chemical fusion of atoms into molecules. In
addition, significantly weaker so-called van der Waals
forces are applied in liquids (and partly also in
amorphous solids).
Van
der Waals forces
All atoms and molecules (including atoms of inert gases of
helium, argon, xenon, etc.) show a weak short-range mutual
attraction, which is caused by the so-called van der
Waals forces *). The basis of van der Waals forces are
the attractive forces between the electrical dipole
moments of atoms or molecules. For polar molecules that
have a permanent electric dipole moment (such as an H2O molecule, where the
end of a molecule with an oxygen atom has a higher electron
concentration and is more negative than the opposite part of a
molecule with hydrogen atoms), the molecules orient each other
with their ends of opposite polarity, creating an attractive
electrical force.
*) Based on phenomenological considerations in 1873,
J.D. van der Waals introduced these attractive
"cohesive" forces (forces holding together) between
molecules into his well-known equation of state
of imperfect (ie real) gas, generalizing the equation of state
for perfect gases in order to be able to explain gas condensation.
However, the polar molecule can also attract molecules
that do not normally have a permanent dipole moment: the electric
field of the polar molecule when approached causes such a
redistribution of charge in the second molecule that induces
a dipole electric moment in the same direction as the polar
molecule's moment - the result is an attractive force. A more
detailed electrical analysis shows that the magnitude of this
force FW ~ a.d2/r7 is proportional to the square of the dipole moment d
and inversely proportional to the 7th power of the distance r
; a is
a constant indicating the polarizability of the molecule.
However, even for nonpolar molecules
and for closed shell atoms where the electron distribution is
symmetric on average and the mean dipole moment d is zero,
the instantaneous dipole moment shows quantum fluctuations in
magnitude and direction. Although the mean value of the dipole
moment < d > is zero, the mean value of the square of the dipole
moment < d2 > it is not zero, but has
a small finite value - this creates an effective attractive force
between the two fluctuating electric dipole moments, which is
proportional to ~ <d2>/ r7.
Van der Waals forces are much weaker
than the forces of ionic and covalent bonds. In addition, the
high power of their indirect distance dependence, r-7, causes short-range
forces that only apply when molecules or atoms are close together
(doubling the distance between two
molecules will reduce the attractive force acting between them by
more than 120 -times).
Van der Waals forces cause the
condensation of gases into liquids and the solidification of
liquids into solids even when the mechanism of ionic or covalent
bonding does not apply (eg to inert atoms with closed shells).
These forces are also the basis for other properties of
substances, such as viscosity, surface tension, adhesion,
friction.
According to the state, we
divide substances into three well known basic groups :
Thermal
motions of atoms and molecules
Atoms and molecules that make up substances are never at rest
with each other, but perform constant movements. According to the
kinetic theory of heat, the movements of atoms
and molecules in substances are the cause and essence of all
thermal phenomena. In solids, atoms and molecules exhibit oscillating
motion in the crystal lattice. In gases and liquids, a disordered
motion of elastically colliding *) atoms and molecules takes
place (can be observed as the known Brownian motion).
*) At sufficiently high temperatures,
however, these collisions of atoms and molecules are no longer
elastic, the excitation of atoms and molecules
occurs with subsequent deexcitation accompanied by radiation. At
even higher temperatures, atoms are ionized and molecules
decompose, a plasma state is formed, sometimes
called the 4th state (see below the passage "Plasma - 4th
state of matter") .
Mechanical impacts of gas atoms and
molecules on the walls of the vessel cause reaction forces that
cause gas pressure.
The instantaneous velocity of the
individual condensing gas molecules varies and changes
irregularly over time, both in size and direction. In statistical
mechanics, the so-called Maxwell-Boltzmann's law
is derived by the statistical distribution of kinetic energies of
moving molecules in a (ideal) gas ......... In a gas heated to
the (absolute) temperature T, the mean kinetic energy <ek> per molecule is
proportional to the temperature according to the relation: <ek> = (3/2) .kT,
where k is the so-called Boltzmann constant,
whose numerical value is k = 1.380x10-23
Joule/Kelvin. This constant is a kind
of "conversion factor" between the energy
measure of the temperature of a
substance and a phenomenologically established temperature
scale in degrees Kelvin (°K; the relationship between
the absolute Kelvin scale and the "water" Celsius scale
is T [°K] = 273 + t [°C] ).
Since the kinetic energy ek of a molecule of mass
m is related to its velocity v the known relation ek = (1/2) m.v2, for the velocity of molecules (so - called mean square
velocity <vkv> - is the square
root of the mean value of the square of the velocity of
molecules) followed the relation: <vkv> = Ö<v2> = Ö(3kT/m). For ordinary gases at temperatures common in
the Earth's air, these speeds are in the order of hundreds of
meters per second. E.g. for hydrogen at 0 °C (= 273 °K) is <vkv> »
1300 m/s.
Mechanical impacts of atoms and molecules on the walls of the
vessel cause reaction forces that cause gas pressure
. Pressure P is expressed as the force acting per unit
area, this force being given by the rate of change in time of the
momentum of the incident particles. The momentum
p = m.v a molecule of mass m
is related to its kinetic energy by the relation ek = p2/m. With each elastic impact on the wall, the molecule
changes its momentum to the opposite, ie the total change in its
momentum is Dp = 2.p. The momentums of the particles are oriented
chaotically in all three directions in space, so that the number
of particles hitting the wall is on average only 1/3 of their
total number. The number of incident particles is further given
by their number no in volume unit. After taking into account all these
circumstances, the pressure is given by the relation: P =
(1/3).m.no.<v2>, resp. P = (1/3).r .<v2>, where r is the gas
density. The pressure of the gas on the walls of the vessel is
thus directly proportional to the density of the gas and the mean
value of the square of the velocity of its molecules.
............ equation of state .... ...................
Heat propagation
Heat, ie disordered or oscillating motions of atoms and
molecules, spreads in substances from one place
to another in three basic ways :
The dependence between the absorbed amount of
heat (energy) DQ and the temperature increase DT of a heated body of mass m
is important for the thermal properties of substances. This
dependence generally has a complex nonlinear course, but if there
are no phase transitions (changes of state) and we do not move in
a large temperature range (within the limit DT ® 0), this dependence is
approximately linear: DQ = m.C. DT. Coefficient C in this dependence is called the
specific or measure heat given
substance.
................... ..............
A more detailed study of thermal
energy and thermal properties of substances forms the content of
a special area of physics - thermals and thermodynamics.
Electromagnetic
and optical properties of substances
The atomic and molecular structure of matter makes it possible to
explain naturally and from a uniform physical point of view the
interactions of electric and magnetic fields, electromagnetic
waves (and especially light), with substances. All electrical and
magnetic phenomena originate from the basic building blocks of
the atom - electrons, as carriers of the
elementary negative electric charge, and protons
carrying a positive elementary charge. And forces acting - interactions
- electric and magnetic fields with atoms and molecules of
the material environment cause all the peculiarities and
differences of electromagnetic phenomena in comparison with these
phenomena in vacuum. It will be shown below that from a
macroscopic point of view, the electromagnetic field in a
material environment (especially dielectric) can be described by
essentially the same Maxwell's equations as in vacuum, in which
the values of electrical permittivity eo and magnetic permeability mo of vacuum are replaced by respective coefficients e and m for the substance.
From a general theoretical point of view,
it is discussed in §1.5 "Electromagnetic field.
Maxwell's equations" of
the book "Gravity, black holes and the physics of
space-time".
Electrical
phenomena in the material environment
Based on the properties of atoms and molecules, it is possible to
explain electrostatic phenomena, including the
very "formation" of an electric charge. Interactions of
atoms and molecules in substances (in the simplest case by
mechanical friction of two bodies) can release a certain number
of external electrons from atoms. If a large number of these
electrons accumulate on one of the interacting bodies, this body
with an excess of electrons has a negative electric charge, while
in the other body with an excess of protons a positive electric
charge is applied. Such electrically charged
bodies with charges Q1 and Q2, placed in a vacuum at a distance r, will exert
a force on each other according to the known Coulomb's law F
= k. Q1.Q2/r2, where k is a
coefficient expressed in a system of SI units using the so-called
vacuum permittivity eo : k = 1/4peo .
If electrically charged bodies are
placed in a material environment, in addition to
their mutual Coulomb interaction, their electrical interactions
with atoms and molecules of matter will also occur. The basic
nature of this interaction will depend primarily on whether or
not the substance contains freely moving electric charge
carriers.
Solid state physics
describes the electrical properties of these substances using the
so-called band theory, according to which
electrons in matter are combined into energy bands, separated
from each other by unoccupied bands of "forbidden"
energies. Discrete energy states of electrons orbiting individual
atoms in solids in orbits propagate into energy bands
due to interaction with other atoms in the solid, but there are
certain gaps between these bands - the so-called bands of
forbidden energies, which electrons cannot acquire. The
energetically highest occupied band is the valence
band , followed by the forbidden band and above it lies
the so-called conduction band of electrons,
which already behave as free. If the forbidden
band is wide, the conduction band is completely unoccupied
in the equilibrium (basic) state, all electrons are bound and the
substance is electrically non-conductive.
Otherwise, electrons jumping into the conductivity band cause the
electrical conductivity of the substance.
From this electrical point of view,
substances are divided into two extreme groups :
1. Conductors
- substances that contain freely moving electric charges (or
their carriers). The electric field, with its force effects, sets
the carriers of the electric charge in motion -
an electric current is generated, which lasts
until the rearranged electric charges disrupt the electric field;
the charges equalize. According to the nature of moving electric
charge carriers, electrical conductivity is divided into two
types :
-> Electron conductivity
caused by freely moving electrons. The conductivity band is so
close that it overlaps with the valence band and the outer
electrons pass freely into the conduction band. It occurs mainly
in metals, where part of the outer electrons is
not bound in atoms in the crystal lattice, but is freely
dispersed and forms a so-called electron gas. Metals are
therefore very good conductors of electricity and also heat. The
large amount of weakly bound electrons in the metal conduction
band allows relatively easy release of electrons from
their surface. Heating the metal (to a
temperature above about 400 °C) by
increasing the kinetic energy of the electrons causes the thermoemission
of the electrons. Similarly, the impact of
electromagnetic radiation, light and harder radiation leads to
the photoemission of electrons - a photoelectric effect
(it was analyzed in more detail above in
the section "Corpuscular-wave dualism", passage "Photoelectric effect").
-> Ionic conductivity caused
by the movement of positively or negatively charged ions - atoms
with missing or excess electrons in the envelope. This type of
conductivity occurs in solutions with
dissociated molecules - so-called electrolytes,
or in ionized gases (electric
discharges).
The movement of electric charges in
conductors is not completely free, the carriers of electric
charge collide with atoms and molecules in matter, thus
transferring to them part of their electrically obtained kinetic
energy. Electric current generates heat, conductors put resistance
to electric current (expressed in Ohms). The only
exception is the phenomenon of so-called superconductivity,
when electrons (connected in so-called Cooper
pairs forming Bose-Einstein condensate) move completely freely in the conductor and the
electrical resistance drops to zero (§1.5,
passage "Fermions as bosons; Superconductivity").
-> Semiconductivity. A
special group of substances are semiconductors,
substances with a narrow band gap, where electrons
jumping from the valence band to the conduction band (by thermal
motion or photoexcitation) become negative conductivity carriers
and empty spaces in the valence band - so-called holes
- effectively appear as positive conductivity carriers. By
incorporating suitable impurities of elements
that provide conductivity electrons (donors) or accept
electrons from valence band bonds (acceptors) into
semiconductor materials, an increase in their
conductivity and a predominance of free negative
("n") or positive ("p") carriers can be
achieved. Very important electrical phenomena occur at the interface
adjacent semiconductors of type "n" and "p" -
rectifying "diode" effect at the n-p
interface, amplifying "transistor" effect at
the p-n-p or n-p-n interface, as well as optoelectric
phenomena. The most important semiconductor materials are germanium
and silicon.
In addition to wide use in electronics (transistors, diodes, LEDs, integrated circuits,
computer processors, memory chips, optoelectric display chips,
...), germanium and silicon are also used
in semiconductor detectors of ionizing radiation
(§2.5 "Semiconductor
detectors"). For some purposes, a combination of tellurium,
cadmium and zinc is also used here - CZT detectors.
2. Non-conductors (insulators,
dielectrics)
- substances in which no freely moving electric charges are
present (the conduction band is separated
from the valence band by a wide band of forbidden energies, so
that electrons from atoms do not get into it). Here the electric charge of the inserted bodies can
persist, the non - conductive substance is able to separate (isolate)
charges of various sizes and signs. Atoms and molecules remain
generally electrically neutral, but the force of the electric
field leads to a certain rearrangement of the charge distribution
in atoms and molecules - the so-called dielectric
polarization (Fig.1.1.8 on the right). Originally, the
spatially symmetric charge distribution in the time average *) is
slightly deformed due to electric forces - the positive charge is
effectively shifted in the direction of the field, the negative
charge in the opposite direction. The effect of so-called sliding
charges arises.
*) This applies to atoms and so-called non-polar
molecules with a symmetric spatial distribution of positive and
negative charges. In addition, there are polar
molecules, in which the atoms are bound by ionic bonds, with an
asymmetric charge distribution forming a miniature electric
dipole. However, the orientation of these molecular electric
dipoles in the substance is completely disordered due to thermal
movements, so that their electrical effects are canceled outwards
(Fig.1.1.8 in the middle). However, the external electric field
exerts a force on the individual dipoles and partially orients
them in the direction of the field - there is an orientational
polarization of the dielectric (Fig.1.1.8 on the right). In
addition, the force of the field will somewhat increases the
dipole moment of the polar molecules thus oriented.
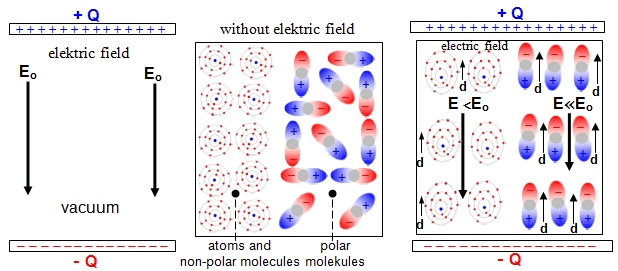
Fig.1.1.8. Polarization of dielectric atoms and molecules and the
formation of sliding charges.
Left: The electric field between two
electrodes of charge +Q and -Q has an intensity Eo in
vacuum. Middle: In the absence of an
external electric field, atoms and non-polar molecules have a
symmetrical charge distribution on average, and polar molecules
have random chaotic orientations of their dipole moments. Right:
The action of an external electric field deforms the originally
symmetrical charge distribution in atoms and non-polar molecules
- they become electric dipoles; for polar molecules, dipole
moments are oriented. In both cases, the dipole moments are
oriented opposite to the electric intensity vector Eo
external field - dielectric polarization effectively reduces the
intensity of the applied field from the maximum vacuum value Eo to
the value E .
The result of electrical interaction with atoms and molecules (non-polar and polar) of the dielectric is the formation of electrical dipoles oriented in the field direction. The electric field of the electric dipoles d induced in this way adds to the original acting field Eo - and since it is in the opposite direction, it effectively reduces the value of the electric field intensity, reduces the electric force to the value E < Eo . For not very strong electric fields, the polarization P is directly proportional to the intensity of the electric field: P = k . E , where the coefficient k is called dielectric succeptibility (polarizability) of the dielectric. Coulomb's law still applies to the force action of electric charges in a substance, but in the proportionality constant, instead of the permittivity of the vacuum eo, performs the permittivity of the substance e, also called the dielectric constant, e : e = eo + k = er . eo, where er = 1 + k is the so-called relative permittivity of substance. The relative permittivity of substances is always greater than 1, for non-polar and dilute substances only slightly (for air only 1.006), for polar substances it can be quite high (for water er = 81).
Magnetic phenomena in the material
environment
Magnetic phenomena are a manifestation of the interactions of
moving electric charges. The moving charges, creating a current I
in the length element dl , generate a
magnetic field of intensity B *) at a distance r
according to the Biot-Savart-Laplace law: d B
= k. I. [dl
´ ro] / r2, where ro is the unit direction vector from the
measured point to the current element and k is the
proportionality constant expressed in the system of SI units
using the so-called vacuum permeability mo : k = mo/4p. The magnetic
field then shows force effects on each electric charge q moving
at a speed v: F = q. [B ´ v];
this so-called Lorentz force acts perpendicular to the
direction of movement of the charge.
*) For historical reasons, the quantity B
is called not intensity but magnetic induction
.
The excitation of the magnetic field in the medium can
again be expressed using the Biot-Savart-Laplace law,
but in the proportionality constant instead of the vacuum
permeability mo, performs the
magnetic permeability of the substance m = mr . mo, where mr = m/mo is the so-called relative
permeability of the substance, indicating the
"amplifying" or "attenuating" effect of the
substance on the magnetic field (here is
mean the "permeability, transmisivity" for the
magnetic field).
For diamagnetic substances is mr <1, the
paramagnetic agent is mr > 1; in both of
these cases, however, the value of mr is very close to 1. But for ferromagnetic substances, mr reaches high values of the order of 103 -105 (here,
however, it is not a constant, but a variable whose value depends
on the intensity of the magnetic field; for strong fields, the
state of magnetization saturation is reached, the hysteresis
effect also manifests itself).
If we insert a substance into a
magnetic field, the atoms and molecules of the substance will
interact with the magnetic field, leading to the magnetization
of the substance. This is because the electrons moving in the
atomic shells generate their elementary electric currents
("current loops"), which excite their
elementary magnetic fields expressed by the so-called magnetic
moment m = I. S , defined
as the product of the current I and the area S
of the current loop. In atoms, elementary current loops and
magnetic moments are caused by two types of electron motion :
a) The cycle of an electron along its path - trajectory or
orbital magnetic moment; b)
Due to electron spin - spin magnetic moment.
The resulting magnetic moment of an atom is the vector sum of the
moments of all its electrons. During this vector addition, three
significant cases can occur :
1.
Diamagnetism
All moments are compensated for each other, the
resulting moment is zero. In such atoms, when
inserted into a magnetic field, the electron paths are deformed
so that additional magnetic moments are induced,
the field of which is directed (in
connection with the so-called Lenc rule of the opposite effect) against the direction of the external
field. Thus, the field weakens, such substances
are called diamagnetic. It is, for
example, carbon, copper, sulfur, water, gold, plastics and most
other substances.
2.
Paramagnetism
Only spin moments are compensated. In the external
magnetic field then occurs twisting the magnetic moments
of the individual atoms in a direction consistent with the
external field, thereby amplifying the resulting
magnetic field. Such substances are called paramagnetic.
However, the tendency of magnetic moments is counteracted by the
thermal motion of atoms, which in turn puts atoms into a state of
chaotic disorder - according to the so-called Curie's law,
the magnetic amplification effect (so-called magnetic
susceptibility) is inversely proportional to absolute
temperature. Paramagnetic substances are e.g. aluminium, oxygen,
calcium, sodium, magnesium, manganese, barium, platinum...
3.
Ferromagnetism
Atoms have uncompensated spin moments (this occurs with
atoms that do not have a fully occupied electron level). In this
case, some substances may occur in certain small areas spontaneous
orientation of all magnetic moments in one direction - the
so-called magnetic domains is created, which is
magnetized to a saturated state (the size of these domains is
about 10-6 -10-2 cm). Under normal
circumstances, these domains in the substance are randomly
distributed and oriented, so that their magnetization is
canceled. However, when an external magnetic field is inserted,
these domains are easily oriented so that the vector of their
magnetization is directed in the direction of the field - there
is a total magnetization of the substance, which significantly amplifies
the applied magnetic field. Such substances with
significant magnetic properties are called ferromagnetic
(according to iron, which is the
oldest known substance of this kind).
Ferromagnetic properties disappear at higher temperatures, when
the domains of spontaneous magnetization decay and the substance
acquires paramagnetic properties (the
relevant boundary temperature, characteristic for a given
substance, is called the Curie temperature ). In addition to iron, ferromagnetic properties are
exhibited by e.g. cobalt, nickel, gadolinium and some metal
alloys, such as the Al-Ni-Co alloy of aluminum, nickel, cobalt,
iron; Sm-Co samarium-cobalt; Sr-Fe strontium with iron; iron,
nickel, molybdenum; iron and chromium; iron, neodymium and boron.
Ferromagnetic substances are
primarily the mentioned metals, which are electrically
conductive. Electrically non-conductive (or high electrical resistance)
ferromagnetic materials called ferrites (ferrimagnetic materials) are
also used in electronics. They are compounds of oxides of
ferromagnetic elements iron, manganese, barium. They are mainly
used as coil cores for high frequency signals.
Magnetically
soft and hard ferromagnetic substances. Magnetic hysteresis.
Permanent magnets. Magnetic recording.
Most ferromagnetic materials, e.g. iron without alloying
additives, become magnetized in a magnetic field, but when
removed from the magnetic field, the atoms in the magnetic
domains return to their original configuration and the material loses
its magnetic properties - it is called a magnetically
soft material.
However, some ferromagnetic materials,
when magnetized when placed in a magnetic field, retain
their magnetization permanently even after the external magnetic
field is removed. Part of the magnetic domains will remain
oriented in the direction of the magnetic field. It exhibits
so-called magnetic hysteresis (Greek:
hysteresis = delay) - the
dependence of the current physical state of magnetism on previous
reactions to the value of the applied magnetic field. These
substances are called magnetically hard. These
properties has iron-steel alloyed with carbon admixture, some
alloys of rare earth metals such as samarium-cobalt,
neodymium-iron-boron ...
Materials showing high high magnetic
hysteresis (large area under the hysteresis
curve) are used to prepare permanent
magnets. These properties has iron-steel alloyed with
carbon admixture, some alloys of rare earth metals such as
samarium-cobalt, neodymium-iron-boron ...
Materials exhibiting high magnetic
hysteresis (large area under the hysteresis
curve) are used for the preparation of permanent
magnets. In addition to high-alloy steel, there are
alloys of samarium-cobalt, iron-nickel, cobalt-nickel-aluminum
and several others. A particularly high intensity of permanent
magnetization (approx. 1.3 Tesla) is achieved with neodymium
magnets, made from an alloy of neodymium, iron and boron -
Nd(2)Fe(4)B.
Thin layers of ferromagnetic materials are
used in electronic recording media. Magnetic
tapes - sound (audio, tape recorder), image (video),
data - are made of a magnetic layer applied to a plastic tape
that moves around the core of the coil. An electrical signal is
fed into this coil, the resulting magnetic field magnetizes the
tape - a magnetic recording is created. During reading,
the recorded tape is moved around the reading coil, in which an
electrical signal is induced, which after amplification is
reproduced or processed.
Computer disks have a
magnetic layer deposited on a plastic or aluminum disk that
rotates and a recording and reading coil moves in close proximity
to the magnetic surface in a radial direction between the center
and the edge. Recording and reading are done in concentric
circles.
Ferromagnetic layers on recording discs or
tapes are usually made of powdered ferrites (Fe2O3,
Cr2O3, ...) with a plastic binder, applied in a micron layer.
Recently, a new read head technology has been used in computer
hard drives, using the spin dependence of electron
scattering in magnetic layers. In two ferromagnetic layers,
excited by an external electromagnetic signal, a different
magnetoresistance *) is manifested depending on the orientation
of the electron spins - an effect called ("giant")
magnetoresistance GMR. Two ferromagnetic layers are
used in the reading head, separated by a non-magnetic layer. This
GMR sensor uses the opposite direction of magnetization
of the respective elements on the magnetic recording medium to
detect the bits that are assigned logic "0" and
"1", which causes changes in the electrical
conductivity (resistance) of the sensor. This causes a modulation
of the electric current in the circuit connected to the GMR
sensor, which is decoded and digitized to produce the resulting
bit information. New technologies enabled a substantial increase
in the capacity of hard drives, from the original approx. 10 MB,
to the 500 GB and later several TB. Spintronics is
trying to use this effect even in MRAM computer memories, which
at a new level could have the advantages of permanent information
retention, which was previously the case with ferrite memories.
*) Magnetoresistance is a
phenomenon observed in multilayer structures, composed of thin
alternating ferromagnetic and non-magnetic layers. It manifests
itself as a change in electrical resistance depending on whether
the magnetizations of adjacent ferromagnetic layers are directed
in parallel or in the opposite direction. The resistance is
relatively lower for parallel orientation and higher for
antiparallel orientation. It is caused by the dependence of
electron scattering on their spin orientation.
Computer recording media
A number of technologies have been developed to record large
amounts of data in computer technology and informatics. Leaving
aside some historical pre-electronic attempts to record
information, we can summarize the gradual development of
information recording in brief as follows :
-> Paper punched cards and tapes
where small holes have been punched in the paper in certain
precise positions. The position of each hole carried a unit (bit)
of information. Rarely, instead of paper, punched tapes were also
made of plastic or metal foil for less wear and tear and a longer
life after frequent repeated use. Computer printers (which at the time were often just modified electric
typewriters) sometimes had tape punches
installed; the information was printed and punched on the tape at
the same time. The punched cards and tapes were then inserted
into an electro-mechanical or opto-electronic reader,
which they passed through, read the code written from them and,
according to it, performed the required function in the machine,
or entered the data or function to be performed by the computer.
Punched cards were mainly used in machine tools, punched tape in
computer science and scientific research, where there was a large
amount of data.
-> A magnetic tape that had a
significantly larger recording capacity and could be erased and
subsequently overwritten with new information. It passed close to
the reading or recording coil, which electromagnetically recorded
the corresponding magnetization on the ferromagnetic layer of the
tape. And during playback (reading), the magnetized tape induced
an electrical voltage as it passed around the reading coil, which
was amplified and processed. It was mostly used for analog
acoustic recording (magnetophon tape, or casette tape), image
recording (videorecorder) and digital data recording.
-> A magnetic removable disc,
also called a floppy disc or diskette. Inside
the square plastic package was a flat plastic circle (disc)
covered with a ferromagnetic layer, on which information was
stored using a recording coil. Data was written on a rotating
floppy disc in circles and read with coils that could be moved
differently along the surface of the disc in a radial direction.
-> A magnetic hard disc (internal
- permanent - disc) is installed in the computer for
long-term storage of information, its operative writing and
reading. They are primarily computer programs and operating
systems, recorded data and files.... It consists of one or
several wheels (discs) on whose magnetic layers information is
written in circular tracks (the same, but with greater density,
as on a floppy disc). In addition to the internal hard drive,
other external discs connected by a connector, now
mostly USB, are sometimes used.
-> An optical disc is a flat
disc with a shiny, light-reflective surface on which
information is stored using tiny protrusions and depressions that
are written in a circular spiral (similar to the circles on
floppy disks and hard drives). They are usually burned with a
laser, with a larger number of copies they are sometimes pressed
mechanically. They are read by a laser directed at the reflective
layer. If the ray hits the raised peak, it is reflected and in
the reading element is converted into an electrical signal
"1". When it hits the depression, it does not bounce,
the reading element does not record anything, which means a
logical "0". Mainly two types of optical discs have
been developed. CD (Compact Disc) with
a capacity of approx. 700 MB and DVD (Digital
Video Disc or Digital Versatile Disc), which can
record up to 7 times more data than a CD. Mainly music and
videos, as well as computer programs and data files are recorded
on these optical discs. A special miniaturized version of the
optical disc is the music so-called MiniDisc (described
in detail in the article "Minidisk.htm").
-> Ferrite memory consists of
a large number of small ferrite ring cores, which are wrapped
around thin wire conductors - miniature "coils" that
write and read magnetic information. Each such ferrite ring
represents one bit. It does not depend on the power supply, so
the data is preserved even after the computer is turned off.
-> RAM (Random Access
Memory) is used as the computer's operating memory. It
consists of semi-conductor elements, into which signals are
conducted using conductive materials, which switch some
semi-conductors and close others. Switched semiconductors charge
capacitors, representing "1", uncharged "0".
It is dependent on a constant power supply, after the computer is
turned off the data is nullified; after switching on, the
operating system and any data from the hard disk will be loaded
again.
-> "Flash disc" is a
compact miniaturized portable memory that does not depend on an
electrical supply after recording. It is used as a memory card to
transfer data between computers and other devices. Data is
electrically written to elementary transistors inside the flash
board. Each cell consists of two transistors separated by a layer
of silicon oxide. If this oxide is conductive, the cell is in the
"1" state, if it is non-conductive, the cell is in the
"0" state. The conductivity of this layer is regulated
by the electric charge. The flash drive is easily connected to a
computer and other digital devices via a USB (Universal
Serial Bus) interface connector, which, in addition to
writing and reading data, also has pins for power supply and
charging of external devices. It is used to connect computer
keyboard and mouse, printer, external memory drives, digital
cameras and camcorders and more.
Note: "Flash
disk" is actually neither "flash"
- lightning (there is no electrical discharge) nor "disc"
- it is shaped like a small rectangular plate. It's just a
metaphorical name. It is customary to call storage media in
computer science "disk", even though they have a
different shape and do not rotate. And the name "flash"
comes from the fact that recording and erasing content is
operational and thus "lightning fast" compared to
earlier memory technologies, where the process of erasing and
rewriting data was gradual and relatively slow.
-> F-RAM (Ferroelectric
Access Memory) is an electrically independent direct access
memory that can retain data even after the power is turned off
power supply, similar to ferrite memory. F-RAM memory cells use
the residual polarization of the ferroelectric material after
exposure to an electric field.
-> M-RAM (Magnetoresistive
Access Memory) is based on so-called ("giant")magnetoresistance
in two ferromagnetic layers, separated by a non-magnetic layer
(it was outlined above in the passage "Magnetic
recording"). It is in the
development stage, it cannot yet compete with F-RAM ...
Spintronics
Classical electronics is based on the electric charge of
electrons and their movement - the electric current
and the magnetic field excited by it. In addition to
this charge, however, electrons have their own rotational moment
of momentum - spin and associated magnetic
moment. In a magnetic field (generated, for example, by a
coil), the electrons move, apart from the action of the basic
Lorentz force, along slightly different trajectories according to
the spin orientation. For free electrons, this is a relatively
subtle effect, detected only in some particle experiments.
In the 80s of the 20th century however, a
new branch of spin electronics, or spintronics
for short, began to develop, which, in addition to the basic
charge of electrons, also uses their spin orientation
and spin-charge coupling for various electromagnetic
behaviors of bodies, primarily ferromagnetic and semiconductor
elements. In practice, it is significantly applied in multiple
ferromagnetic (combined with non-magnetic) layers, excited by an
external electromagnetic signal, as a different magnetoresistance
depending on the orientation of the electron spins (GMR
sensors were mentioned in the previous paragraph about magnetic
recording).
Natural
magnets
The magnetic force action of minerals - permanent
magnets - known since antiquity - has long been
separated from electrical phenomena in the understanding of
science. The mentioned theory of magnetic moments of atoms and
molecules shows that even in permanent and natural magnets the
origin of the magnetic field lies in the interactions of moving
charges. These are so-called magnetically hard
ferromagnetic substances (mostly containing iron), which retain a
certain remanent magnetization even without an external
magnetic field. Even the earth's core (and the cores of some
other planets and the plasma interiors of stars) create a natural
magnetic field - see "...." .....
Electromagnetic waves in matter
Propagation of electromagnetic
waves in matter at the classical level given by Maxwell's
equations (§1.5 "Electromagnetic
field. Maxwell's equations" books "Gravity, black holes and spacetime physics") , in which instead of vacuum
values of electrical permittivity eo and magnetic permeability mo are the respective coefficients e and m for the
given substance (their origin was discussed
above in the passages "Electrical and magnetic
phenomena in the material environment"). If the medium contains free charge carriers, the
non-zero current density j will appear on the
right side of Maxwell's equations, which in the simplest (linear)
case is given by Ohm's law - this expresses a direct
ratio between the specific conductivity of material
s and
the current density j flowing through the
material after application of electric field E :
j = s.E. Using the ohmic resistivity
rohm = 1/s, the current density can be expressed equivalently as: j
= E/rohm.
These Maxwell's equations in the
material environment have a wave solution
¶2 E
/ ¶ x2 + ¶2 E / ¶
y2 + ¶2 E / ¶ z2 = em .¶2 E / ¶
t2 + sm .¶E
/ ¶t ,
which differs from the normal vacuum wave equation in that it
also has a term with the first derivative according to time s.m .¶E/¶t, which describes
losses - damping - absorption of waves in a
given material due to excitation of currents (sometimes called the "telegraph
equation", because the attenuation of the
signal in the telegraph line behaves in an analogous way). The resulting attenuation causes that if an
electromagnetic wave of circular frequency w = 2p f with an input intensity I0 falls into the
substance, with increasing depth d its intensity I will
decrease according to the exponential law
I (d) = I 0 . e - [ Ö
( w.s.m / 2)].
d
with absorption coefficient Ö(w.s.m/2), increasing
with wave frequency and specific conductivity of the material.
Sometimes the value of the effective depth of penetration
of the electromagnetic wave into the substance de = Ö(2/ws.m) = Ö(rohm /p.F.m) is introduced, at which the amplitude of the
electromagnet. waves drop to 1/e. With good dielectrics with low
conductivity (s® 0, rohm®¥), electromagnetic waves pass almost without attenuation
to great depths. On the contrary, in metals with very good
conductivity for free electrons (s®¥, rohm®0) electromagnetic waves almost do not penetrate *), they are reflected from their
surface (in electronics this manifests
itself as the so-called "skin effect" for
conductors through which high-frequency alternating current flows
- it flows only at the surface of the conductors). The space surrounded by a sufficiently dense wire mesh
therefore functions as a so-called Faraday cage,
shielded against external electromagnets. waves.
*) Eg. for copper having a
conductivity s = 5.8x107 S/m, or electrical resistivity rohm = 1.68x 10-8 W.m,
the electromagnetic wave of frequency 1MHz penetrates to a depth
of about 65 micrometers, at a frequency of 300MHz the penetration
depth de is only 3.8 micrometers.
Faraday
cage
The so-called Faraday cage or shielding box
*) is based on the fact that in an electrically conductive
object, electric charges collect on its surface and do not
penetrate inside. If we have a working space surrounded on all
sides by a conductive material - a cavity in a
conductive object - the surrounding electric field causes the
freely moving electric charges in the conductive shell to be
continuously distributed in such a way, that the effect of
the field is canceled inside the cavity.
*) It is named after the
important pioneer of electromagnetism, M.Faraday, who assembled
the first such cage and measured with the help of an electroscope
that the charge applied to the outer wall does not cause any
electric field inside.
A true near-perfect Faraday cage consists
of a continuous envelope of highly conductive material (e.g.
copper sheet), without holes or gaps, around the inner space. In
practice, however, wire grids or nets made of such materials are
mostly used. The Faraday cage shields the interior from the
electric field. It cannot eliminate stable or slowly varying
magnetic fields, but only high frequency ones (f>~300MHz/d, where d is the cage size in
meters). For a permanent magnetic field, a
metal container made of dia- or paramagnetic material is not an
obstacle, for an alternating magnetic field only partially due to
electromagnetic induction. A ferromagnetic metal with high
permeability can partially shield a permanent magnetic field by
"deflecting" its lines of force around the examined
space.
To a large extent, a Faraday cage can also shield the
interior from electromagnetic waves. For effective shielding, it
is necessary that any gaps, openings, "eyes" in the
network are substantially smaller than the wavelength of the
signal we need to shield. E.g. the inside of the car is a very
imperfect Faraday cage, which will impair or make it impossible
to listen to the radio on long and medium waves (without an external antenna), but
mobile phones work satisfactorily there (to
shield the most commonly used frequency of 900 MHz, the windows
in the car would have to be only about 15-20 cm). Coaxial cables used in electronics function
as an effective Faraday cage.
In the case of an electromagnetic wave,
the electric and magnetic components behave somewhat differently
in a Faraday cage. The electric component is eliminated in the
conductor due to electrical induction, while the magnetic
component can locally penetrate a certain depth of the
wall for a small moment and the electromagnetic induction may not
be enough to immediately cancel it out. This may cause some
anomalies of somewhat lower shielding efficiency..?..
The situation is more complicated with the
shielding of very short-wave - photon - X and gamma
radiation. For this radiation, even in the continuous envelope of
the Faraday cage, the very gaps between the atoms create
"eyes" through which the waves~photons can pass. Here,
the shielding ability does not depend on the electrical
conductivity of the shell walls, but on the electron density
of the shell electrons of the atoms of the material from which
the shell is made - on the density and proton number of
the material. The copper sheet would no longer be optimal here,
harder gamma radiation could easily pass through it. A sheet of
lead or uranium (238U) would be better here. It wouldn't even have to be
electrically conductive, it could be barite concrete or
leaded glass. It is briefly discussed below (in more detail in §1.6, passage "Absorption
of radiation in substances") :
Very short wave electromagnetic
radiation
These usual regularities, derived from the classical electrodynamics
of the continuum, apply accurately enough to the
"ordinaryl" electromag. waves of longer wavelengths (much greater than interatomic distances) and not too high frequencies (max.
up to "optical" frequencies of about 1014 Hz, in rare cases
for some optically transparent dielectrics up to 1015 Hz). Due to the very high frequencies and short
wavelengths, the atoms do not "manage" to react so
quickly, the response of the substance is no longer
synchronous. Atoms begin to oscillate
in the crystal lattice and in molecules (where
their vibrational and rotational modes can be excited), for higher energies the electrons in the atoms also
oscillate (excitations and ionizations can
occur). Quantum laws of discrete energy
levels are beginning to be applied, electrons rising from the
valence band to the conduction band are appearing. Radiation
absorption consists in the exchange of energy of penetrating
photons with the environment, in which part of the energy is
converted into the kinetic energy of the atoms of matter - heat.
The passage or absorption of radiation is spectrally
selective, significantly depending on the wavelength
(frequency). And for very high frequencies - high photon
energies - the classical optical laws disappear, discrete
quantum interactions occur (see
§1.6, passage "Gamma radiation interactions"). Depth dependence of
radiation absorption still retains exponential character,
but absorption coefficients are no longer
related to continuum electrodynamics (independent
of permeability and specific conductivity of material), but are given by effective cross sections
of radiation interaction with matter atoms (very
complex functional dependencies arise for different materials and
radiation energies). For electromagnetic
radiation X and gamma, the absorption is discussed in §1.6,
section "Absorption of radiation in
substances", Fig.1.6.5.
Opacity
The ability of a material environment to attenuate the
radiation that passes through it is called opacity
(lat. opacitas = shading, shadow). It expresses the degree of "opacity" of a
substance, quantitatively expressed by the ratio of the intensity
of incident radiation and radiation transmitted through the
substance. For longer wavelengths, the opacity is caused by the
above-mentioned ohmic losses, for shortwave radiation, the
absorption of electromagnetic radiation is the result of
electrons in atoms - excitation and ionization,
or absorption and scattering by free electrons.
Note : Some very good dielectric
(capable of forming a transparent crystal) when they are
heterogeneous and multi-crystalline, can be opaque
due to multiple refractions, reflections and scatterings between
individual crystals.
Ingredients other
("foreign") atoms or molecules in the crystal lattice
form in the regular lattice the local "centers" of different
binding energies of the atoms, which can oscillate into
other energy modes by the electromagnetic wave and thus affect
the optical properties of the substance. This usually leads to
increased absorption of radiation of certain wavelengths ...
Optical properties of substances
As mentioned above in the section "Electromagnetic fields and radiation", light is an electromagnetic wave of short
wavelength (approx. 360-750nm). The optical phenomena of
refraction and reflection of light are described at the
macroscopic level by simple laws of geometric optics.
At the microscopic level, however, these simple laws are the
result of much more complicated interactions of electromagnetic
waves with atoms and molecules of matter. As an electromagnetic
wave passes through a material, the electrons in atoms and
molecules are subjected to electric and magnetic forces, under
the influence of which they move. The reaction to the electrical
component of the wave is an oscillating motion of
electrons in the material, the magnetic field causes a circular
motion. These movements cause periodic polarization
of the atoms and molecules of matter, which affects the
properties of the wave and its propagation. The higher the
effective polarization induced by the wave (depends
on the coefficients e, m and on the difference of the wave frequency from the
natural frequency of oscillations of atoms and molecules in the
substance - will be discussed below), the slower
the electromagnetic waves propagate in a given optical
environment.
It should be noted that the
dimensions of the atoms of matter are significantly smaller
(about 4 orders of magnitude) than the wavelength of visible
light. Such an electromagnetic wave therefore does not
"see" individual atoms and molecules, but interacts
with the "collective" response
of millions of atoms or molecules. From a macroscopic point of
view, therefore, the response of a material to such
"long" electromagnetic waves can be described by two
standard parameters known from the science of electricity and
magnetism :
- electrical permittivity e characterizing the
polarization response to an electric field;
- magnetic permeability m, which expresses the
reaction of orbiting electrons (forming elementary "current
loops") to a magnetic field.
The electromagnetic wave will then
be a wave solution of Maxwell's equations, in which
instead of vacuum values of electrical permittivity eo and magnetic permeability mo the respective coefficients e and m for a given substance will
appear ("Electromagnetic field and radiation"). In a dielectric medium
transparent to electromagnetic waves of the appropriate
wavelength, the velocity c´= 1/Öem of the propagation of this wave will be less
than c = 1/Öeomo in vacuum *). From Huygens' law of waves, it follows
that at the interface of two optical materials
with different velocities c1 and c2 the propagation
of waves will change the direction of propagation - the refraction
of light according to Snell's law sin a/sin b = c1/c2 = n, where the refractive index is given by the
permittivity and permeability n = Öem. The law of reflection follows from
the same Huygens law from an environment into which
electromagnetic waves cannot penetrate (which are mainly
materials with free-moving electrons, such as metals, or some
optical interfaces).
*) Clearly, we can imagine this
slowing down of light in such a way that individual photons are
repeatedly absorbed by atoms or molecules in matter and then
emitted again. This causes them to "delay" in time,
which appears macroscopically to slow down. However, in the
intervals between the radiation by one atom and the absorption by
an adjacent atom, they move at a basic velocity c in a
vacuum!
However, it is only an auxiliary idea, the
interaction here does not occur at the level of individual
photons with atoms, but collectively with many thousands of
atoms. An even coarser example: A classic express train (not a
special express train) and a passenger train, if pulled by the
same type of locomotive, move at the same speed between the
stations. As a result, the passenger train moves more slowly due
to time delays at many stops...
In material optical environments, the
speed of light is slightly lower than in a vacuum and depends
somewhat on the wavelength, ie the frequency of light - the
so-called dispersion *). E.g. in water the speed
of light for red light is (rounded) 226 000 km/s, for violet 223
000 km/s; it is even slower in crystals and glass. Of all natural
materials, diamond has the highest refractive index (n =
2.42), in which the speed of light is only 123,881 km/s - this
leads to significant optical effects of refraction and reflection
of light in diamond crystals, which is the source of its
aesthetic popularity as jewelry.
*) The dispersion phenomenon is caused by the frequency
dependence of the polarization of the dielectrics in the
variable electromagnetic field of the passing wave. Charged
particles (negative electrons and positive nuclei), which are
part of atoms and molecules, are held around their equilibrium
positions by elastic (quasi-elastic) electric forces. In the
field of these forces, each atom or molecule has a certain own
frequency of oscillations fo. Due to the incident electromagnetic wave, the charged
particles in the molecules and atoms perform forced oscillations
with a frequency equal to the frequency of the incident wave f . If this frequency is
far from the frequencies fo of the natural oscillations of atoms or molecules, the
resulting effective polarization is small and light passes
through the medium at a little reduced speed; at the same time
absorption and dispersion are small. If these frequencies are
close, partial resonance occurs and the speed of light differs
significantly from the vacuum value of c , or the
refractive index differs significantly from one. For f <fo the refractive index
will increase with frequency and will be quite high in the
vicinity of fo , for f> fo the refractive index will decrease with frequency
("anomalous" dispersion). Significant resonant
absorption occurs for frequencies f close to fo, the material is
almost opaque to light of this wavelength. In the visible light
range, most materials show a "normal"
dispersion, in which the refractive index increases with
frequency. For other wavelengths (beyond the region of the
resonant frequency) we can also encounter anomalous
dispersion.
When the wavelength
of the electromagnetic wave is shortened, ie
with the growth of the energy of the photons, the individual
interaction with the individual atoms and
molecules of the substance begins - the laws of geometric
optics gradually disappear. For the
area of softer X-rays, the effects of diffraction
on the crystal lattice of the substance are applied, for harder
X-rays and g-rays,
any optical phenomena of reflection and refraction longer do
not show, this ionizing radiation interacts hard
with individual atoms through photo- effect, Compton
scattering and the formation of electron-positron pair (see §1.6 "Ionizing radiation" passage "Interaction of gamma rays" Fig.1.6.3 ).
Electro-mechanical,
electro-thermal, electro-chemical, electro-optical phenomena
Mutual electromagnetic interactions of atoms and molecules and
their interactions with external electric and magnetic fields are
the cause of many other related phenomena on the border of
electricity and mechanics, thermals, chemistry, optics,
biophysics. We can name for example :
¨ Piezoelectric
phenomenon - mechanical deformations of some crystals
(eg quartz) cause the opposite charges on the walls of these
crystals. Conversely, if we apply to the opposite walls of the
crystal electrodes with opposite charges, the crystal is slightly
deformed in this direction (electrostriction). A similar
electrical effect occurs when heating crystals - a pyroelectric
phenomenon.
¨ Magnetostriction-
change in length dimensions and volume caused by magnetization of
ferromagnetic substances.
¨ Thermoelectric
phenomenon - the formation of electrical voltage or
current when heating materials to different temperatures.
Conversely, the formation of thermal gradients in the passage of
electric current. The cause of these phenomena is thermal
movement and diffusion of free carriers of electric charge. These
include the Thomson effect in a conductor with a
temperature gradient, or the Seebeck and Peltier
effects at the interface of two conductors with different Fermi
levels, where a contact potential arises.
¨ Photoelectric
effect- electron emission or change in the electrical
properties of the substance during light irradiation. When
electromagnetic waves hit a substance, it interacts with atoms
and electrons in the valence or conduction band. Upon absorption
of this energy by a weakly bound electron in the conduction band,
its photoemission can occur - an external photoelectric
effect. If the radiant energy is absorbed by an electron in
the valence band, it can jump into the conduction band - an internal
photoelectric effect, which creates free carriers of
electric charge and the conductivity of the material occurs (or
increases).
¨ Electroluminescence-
emission of photons of light by the effect of the passage of an
electric current. Photons of light are created when electrons
jump from a higher energy level of the conduction band to a lower
level of the valence band (the electron recombinates with the
hole), or through the level of a suitable admixture. In the
so-called LED diodes, this phenomenon occurs in the area of the
p-n transition.
¨ Electrochemical
phenomena - change in the chemical composition of
compounds and chemical reactions caused by the passage of an
electric current. It is mainly electrolysis - the
excretion of substances on the electrodes when an electric
current passes through a solution of dissociated compounds (electrolyte).
¨ Electric
discharges in gases- passage of electric current through
ionized gas. The formation of free carriers of electric charge -
electrons and ions, or ionization, occurs either by
heating to a high temperature, or by the absorption of
electromagnetic or corpuscular radiation of sufficient quantum
energy. Ionization can also be caused and maintained by electrons
and ions accelerated by the electric field between the electrodes
during own discharge.
Plasma - 4th state of matter
At high temperatures, in an electric discharge or by the action
of ionizing radiation, electrons are ejected from the gas atoms
and the atoms themselves become positive ions. Such a partially
or fully ionized gas is called plasma (Greek plasma = ductile material; the electric
discharge copies the shape of the tube and its shape is easily
influenced by electric and magnetic fields).
Plasma is sometimes referred to as the 4th state of
matter (1st solid, 2nd liquid, 3rd gas, 4th plasma). In order to
distinguish this ionized substance from other situations with
electrically charged particles, we require two additional
properties in the physical definition of plasma :
- Electrical neutrality on a
macroscopic scale (on average the same number of electrons and
positive ions) - we do not consider charged particle beams to be
plasma;
- Collective behavior caused by a
long-range interaction of sufficiently close charged particles -
it is not a very dilute or weakly ionized gas by plasma.
Thus, the general physical definition of
plasma is: " Plasma is a set of particles with free
charge carriers that is globally neutral and exhibits collective
behavior ". This definition also includes exotic
forms of the substance, such as quark-gluon plasma (§1.5, passage " Quark-gluon plasma -"5th state of
matter" ") .
Plasma has significant electrical
properties: it is electrically conductive, it reacts to
a magnetic field, it can generate electric and magnetic fields on
its own, complex electro- and magneto-dynamic processes take
place in it. It is these phenomena that are very important in
astrophysical processes in hot ionized gases in space.
In ordinary terrestrial nature, plasma occurs
relatively rarely in atmospheric discharges, lightning. From a
global perspective, however, plasma is a very important
form of matter - most of the observed substance in the
universe is in the plasma state. Plasma is of great importance
for achieving thermonuclear fusion - §1.3, part "Fusion of atomic nuclei".
Atomic
nucleus
Let us now look deep into the interior of the atom - directly
into the atomic nucleus itself. Before we deal
with the structure of the atomic nucleus, it is worth noting its size
compared to the size of the atom. "Diameter" of an atom
is of the order of »10-8 centimeters (thus far below the
resolution of the optical microscope - atom is much smaller than
the wavelength of light; even of electron microscopy atoms are
not directly observable). However, the core
is even 100,000 times smaller! - its "diameter" is only
»10-13 cm.
At the same time, almost the entire mass (more than 99.9%) of the
atom is concentrated in the nucleus. The density with which
matter is "crammed" in the atomic nucleus is therefore
unimaginably high - r
» 1014 g/cm3 !
It is not easy
to imagine such a huge density: if, for example, a box of matches
were filled with nuclear matter, it would weigh about a billion
tons (!) - it would break through the table, soil and rock and
fall into the center of the Earth. Apart from atomic nuclei, we
do not encounter such a high density anywhere in the surrounding
nature. However, wonderful bodies called neutron stars have
been discovered in space. They are stars at the end of their
lives with depleted nuclear "fuel", gravitationally
collapsed to the size of only tens of kilometers, they are
composed of neutrons with a density of also »1014 g/cm3 .They rotate quickly and when the charged particles
interact with a strong magnetic field, electromagnetic radiation
is created, which "sweeps" the surrounding space as the
star rotates, similar to the light of a rotating beacon - we
observe them as pulsars. Details can be found in
Chapter 4 "Black Holes", §4.2 of the book "Gravity, Black Holes and the Physics
of Spacetime".
It follows
from the very fact of such small dimensions and fantastic
densities in the atomic nucleus - even without knowledge of the
specific structure of the nucleus, that great forces
will act in the atomic nuclei and there will be "high
energy" in the game (this
will be discussed in §1.3, part "Nuclear energy").
Note: At
the same time, it is quite clear from these facts, that
alchemists trying to transmute elements (eg to turn lead into
gold) had no smallest chance of success! By the
methods at their disposal (grinding, hammering, annealing,
burning, chemical fusion) they only "scraped" atoms
along their uppermost (valence) shells. If they wanted to change
the element, they would have to penetrate a hundred thousand
times deeper into the interior of the atom, change the nucleus,
and only then would they achieve transmutation. Of course, they
did not have the resources, energy or knowledge to do so. Now, in
principle, nuclear physics can do it by methods of
"bombarding" nuclei with elementary particles
accelerated to high energies (or neutrons in reactors) - however,
only a tiny amount of transmuted elements can be prepared in this
way.
Atomic nucleus
structure
The existence of a positively charged, very small and dense
atomic nucleus was convincingly proved by the above-mentioned
scattering experiments of E.Rutheford et al. from 1911 (Fig.1.1.4), but nothing could be
deduced from these experiments about the nature and structure of
the atomic nucleus. The discovery of a proton, a
positively charged heavy particle, also made by Rutheford in
tracking alpha particle traces in the Wilson's clode chamber,
played a key role for revealing the structure of atomic nuclei (a
similar key importance as discovery of eletron for in uncovering
the structure of atoms).
Upon impact of the particles a in the nitrogen
nuclei, a reaction of 4a2 + 14N7 ® 17O8
+ 1p1 occurred. Two traces
emanated from the collision site, one corresponding to the oxygen
nucleus, the other to a positive particle identical to the
hydrogen nucleus - this particle was called a proton.
A proton as an elementary particle is denoted "p", or
alternatively, according to chemical terminology, "H"
or 1H1 as a hydrogen
nucleus. The reality of its positive elementary charge is
sometimes characterized by the index "+", ie p+. Further measurements were used to gradually determine
the properties and physical characteristics of the proton, see
§1.5 "Elementary particles".
The idea was
immediately offered that the nuclei of atoms were composed
of protons. It was also supported by the remarkable
regularity in the masses of the atoms - that the masses of all
the atoms are almost exactly integer multiples of the mass of the
hydrogen atom. However, the model of a nucleus composed of
protons alone encountered two problems :
First, it was the electrical Coulomb repulsion of
uniformly charged protons, which would be extremely strong at
such short distances, and at the time no other forces were known
to counter it and maintain the stability of the
nucleus. Furthermore, the masses of all atoms except hydrogen
were about half that actually observed.
Therefore, models in which protons and electrons combine
in the nucleus were temporarily proposed: the nucleus of an
element with atomic number Z it would consist of
2.Z-protons (ie twice the protons) and Z-electrons, whose
negative charge would compensate for the excess positive charge.
The proton-electron model gave approximately the correct mass
values for light nuclei, but not for heavy nuclei. Radioactivity b , in which
electrons are emitted from nuclei, seemingly supported this
"nuclear electron" model. However, other properties of
the cores were no longer in line with this model (eg the magnetic
moment of the cores would be significantly higher).
The missing article to clarify the
structure of the atomic nucleus was supplemented by the discovery
of the neutron, made by J.Chadwick in 1932 during
experiments with bombardment of beryllium nuclei by particles a. It turned out
that these neutrons, particles about as heavy as protons but
without an electric charge, are probably the mysterious missing
component that is together with the protons in the atomic nuclei.
At the same time, the composition of proton and neutron nuclei
naturally explained the existence of isotopes: isotopes of one
element contain the same number of protons (therefore they have
the same chemical behavior), but different numbers of neutrons,
so they differ only in mass.
The Wilson cloud chamber was after
colliding particles a the core Be observed only one foot, which belonged
carbon nucleus C . When Chadwick performed a detailed
analysis of a and C particle tracesfrom the point of view of
the laws of conservation of energy and momentum, he came to the
conclusion that during the collision, in addition to the carbon
core, another relatively heavy and energetic particle must be
formed, which does not carry an electric charge and therefore
does not create an ionization trace in the nebula. Thus, a
reaction of 4a2 + 9Be4 ® 12C6
+ 1n0 occurs; the newly
discovered neutral particle (slightly more than a proton's mass)
was called a neutron, labeled "n". The
electrical neutrality of a neutron is sometimes characterized by
the index zero "o",
ie no. Other experiments and physical properties of the
neutron were gradually determined by further experiments, see
again §1.5 "Elementary particles".
Thus, it was found that atomic nuclei
consist of two types of heavy particles (nucleons): protons
and neutrons, while these protons and neutrons
are held in the nucleus by a new, hitherto unknown, type of force
- the so-called nuclear forces (see below).
 |
| Fig.1.1.9. Schematic representation of the structure of the atomic nucleus. The right part shows the energy levels of the nucleus, the excited nucleus and its deexcitation by gamma photon emission. |
In Fig.1.1.9, the atomic nucleus is imaginarily
"magnified" a total of about 1014 times and its structure is schematically shown here.
The nucleus consists of particles of two kinds collectively
called nucleons: positively charged protons
p+ and neutrons no without electric charge. The number of protons in the
nucleus, called the proton number Z,
unambiguously determines the configuration of electrons
on the individual shells of the atomic shell (each nucleus
"picks up" so many electrons to be electrically
neutral) and thus the chemical nature of the
atom - proton number Z is also a serial number in
Mendeleev's periodic table of chemical elements. Number Z
is therefore sometimes called an atomic number. The
total number of nucleons, called nucleon number N,
determines the mass of an atomic nucleus in multiples of the mass
of a proton or neutron; mass number N is also sometimes
called the mass number and is denoted A. Nuclei
with the same number of protons, which have different numbers of
neutrons, are called isotopes - the chemical
properties of the respective atoms are the same, differing only
in mass (see the section "Physical
and chemical properties of isotopes" below). We denote nuclei by letters of chemical designation
according to Mendeleev's table of elements (here we generally
denote X), while we add a nucleon number as a superscript and a
proton number as a subscript: NXZ - eg hydrogen 1H1,
helium 4He2, carbon 12C6, uranium 238U92. Since the proton
number is uniquely determined by the name of the element in
Mendeleev's table, the subscript is often omitted (eg instead of 12C 6, only 12C is abbreviated
writed).
The sizes
(diameters) of atomic nuclei (in view of
strong interaction) range from about
1.6 fm (ie 1.6.10-13 cm) for a hydrogen atom -
diameter of 1 proton, up to about 15 fm (ie 1.5.10-12 cm) for the heaviest atoms from the uranium region and
nearby transuranium (for particle size in
the microworld see also §1.5, passage "Size,
dimensions and shape of particles?").
Physical and
chemical properties of isotopes
The different number of neutrons in the nuclei of isotopes
naturally affects their physical and, in part, to a much lesser
extent, their chemical properties. The physical
properties of isotopes can be divided into nuclear
and atomic. Different nuclear properties
of different isotopes of the element lie in three aspects :
- Different courses
(type, cross section) of interactions and nuclear
reactions when bombarded nuclei of different isotopes of
the particles, or when they collide (this
is discussed in detail in §1.3, "Nuclear reactions and nuclear energy") .
- Stability or instability - possible radioactivity
of nuclei, depends on the number of neutrons, due to the number
of protons (§1.2 "Radioactivity",
especially part "Stability
and instability of nuclei"). It is often sufficient if there is only one neutron
more or less in the nucleus and the relevant isotope is already
radioactive (the properties of radioactive
isotopes are studied in detail in §1.4 "Radionuclides").
- Furthermore, there are different values of the magnetic
moment of nuclei, depending on the number of paired and
unpaired protons and neutrons - this may be important in the
analytical method nuclear magnetic resonance (see §3.4, section "Nuclear
magnetic resonance").
A somewhat different atomic properties
of different isotopes are due to differences in atomic
weight, given by different number of neutrons in the
nuclei of the same element. This is more pronounced especially
for light elements with a low proton number. Hydrogen atom 2H1 - deuterium D,
is 2 times heavier than ordinary hydrogen 1H1, and its oxygen
compound, "heavy water" D2O, has a
density about 10% higher than ordinary "light" H2O.
The freezing point of heavy water is (
instead of 0 °C for ordinary water) 3.8
°C, boiling point 101.4 °C.
The chemical properties of atoms - the
ways in which they are bound and reacted with other atoms - are
determined by the configuration of the electrons in the atomic
shells, which depends on the number of protons in the nucleus,
not on the number of neutrons. Thus, different isotopes of the
same element have the same chemical properties.
This is very important in nuclear chemistry and in the
applications of radionuclides in laboratory methods
(§3.5 "Radioisotope
tracking methods"), biology and medicine (especially
in nuclear medicine - Chapter 4 "Radioisotope scintigraphy"). The only way in which the
chemistry of different isotopes of the same element may
differ somewhat is the rate of chemical
reactions. A larger number of neutrons in the nucleus
means that the atoms of such a higher isotope are heavier
and thus move slightly slower
in the reaction mixture than lighter isotopes. Therefore,
chemical reactions with heavier isotopes will proceed somewhat more
slowly under otherwise identical conditions - the kinetic
isotope effect. This is most pronounced in deuterium,
where it even leads to the biological toxicity of this
isotope of otherwise biogenic hydrogen. Replacing ordinary
hydrogen with its heavier isotope deuterium significantly slows
down the rate of biochemical reactions - it acts as a
"brake" on many life processes in cells. This has
negative effects especially in higher organisms (where a higher deuterium content, above about 30%, can
even cause death).
Strong
nuclear interactions
If we look at this model of the nucleus in terms of the laws of
electricity, a fundamental objection or question arises
immediately: How is it possible that the nucleus
holds together? According to Coulomb's law, charged
protons of the same sign will repel, so that they would
immediately "scatter" into the surrounding space, no
nuclei and atoms (except hydrogen) could exist. In reality,
however, (fortunately) nothing like this happens, the cores
usually hold us nicely "together". Therefore, in
addition to the electric repulsive forces, there must be other
forces that are attractive and stronger than the electric ones -
these forces then overcome the electric repulsive forces and keep
the core together. They are called strong nuclear
interactions; their nature will be briefly discussed
below. They are about 100 times stronger than electric forces,
but they have one specific peculiarity - they have a short
range. They work effectively only up to a distance r » 10-13 cm, while for
larger distances they are already negligibly weak - with distance
r they decrease rapidly exponentially. The potential of
these forces is often modeled by the so-called Yukawa
potential
U
(r) = g. e - d . r /
r ,
where g is a constant expressing the strength of the interaction
and the parameter d = 1,6.10-13 cm characterizes the
range of nuclear forces.
Note: The
characteristic length of 10-13 cm, important in nuclear physics, is sometimes called 1
Fermi; it is also 1 femtometer [fm].
Each nucleon can
therefore interact directly only with a limited number of
adjacent nucleons - nuclear forces show saturation.
This is the main reason for the reduced stability of heavy
nuclei, as will be shown below (§1.2, §1.3). Since
electrostatic (Coulomb) proton repulsion is long-range and acts
significantly throughout the nucleus, there is a limit to the
ability of strong nucleon interactions to prevent the decay of
large nuclei. At this boundary is the core of bismuth 209B83,
which is the heaviest stable core *); all heavier nuclei with
Z> 83 and N> 209 are already spontaneously transformed into
lighter nuclei (especially by radioactivity a) - see §1.2 "Radioactivity".
*) Until recently, bismuth-209 was indeed considered the most
heawy stable nuclide. In 2003, however, its weak radioactive
transformation by alpha decay with a very long half-life
of 2.1019
years to 205Tl was demonstrated in the Orsay nuclear laboratories.
With such a long half-life, the radioactive conversion is
practically unobservable and the 209Bi isotope appears to be stable. Lead of 209Pb
is now considered to be the heaviest truly stable isotope.
Nuclear forces do
not depend on the type of nucleons, they are charge
independent. Thus, strong nuclear interactions act both
between protons and protons, and between protons and neutrons or
between neutrons and each other - protons and neutrons belong to
a group of particles called hadrons (see below §1.5 on elementary particles). A more detailed analysis showed that nuclear forces
are spin-dependent (the
interaction between nucleons depends on the angle between the
spin and the junction of both particles) - the
interaction between two nucleons with parallel spins is somewhat
different from the interaction of nucleons with antiparallel
spins.
Influence of weak
interactions on the structure of nuclei
If there were only strong (and
electromagnetic) interactions in the
microworld, there could also be "mononucleon" nuclei
composed only of protons or only neutrons (mono-neutron
nuclei would not have an electron shell).
Nuclear "monsters" composed of thousands of neutrons
could also form. However, we do not observe anything like this in
nature, there are no stable nuclei from either the two protons
themselves or the two neutrons; even the neutron itself is
unstable. In nature, namely, also another kind of force is at
work - a weak interaction, which mercilessly transforms
by beta (- or +) radioactivity any
nucleus in which a certain ratio between the number of protons
and neutrons is violated. The mechanisms of these processes are
discussed in §1.2, section "Radioactivity beta".
The nature of strong
interactions between nucleons
According to an older concept proposed by H.Yukawa in 1935,
nuclear forces are caused by the exchange of p- mesons
between nucleons. Although this idea seemed to explain quite well
some of the then known properties of nuclear forces, further
research has shown that the real cause of nuclear forces (and strong interactions between hadrons in general) is to be found at a deeper level - in the internal
structure of protons, neutrons, p-mezons and other hadrons.
According to today's concept, the primary cause of "strong
interactions" between hadrons is gluons
mediated interactions between quarks inside
the hadrons. The observed "strong" interactions between
hadrons, and thus nuclear forces, are a kind of "residual
manifestation" of these primary interactions
between quarks. Simply put, we can imagine that gluons partially
"seep" from the inside into the immediate
vicinity of protons or neutrons and cause attractive nuclear
forces there.
It is noteworthy that the inherent
strong interactions between quarks are expected to have a long
range, while the observed short range of the
resulting interactions between hadrons (and thus nuclear forces)
is due to the "residual manifestation"
mechanism of these forces (for further
discussion see §1.5 "Elementary Particles") section
"Interaction of elementary particles", "Quark structure of hadrons" and "Four types
of interactions").
Note :
It is interesting that similar mechanisms are seen in
interactions and chemical compounding of atoms:
short range "chemica" forces between the atoms of the residual
speech dlouhodosahových electric forces from protons
and electrons in the envelope, which are added together in
vector: at greater distances it is canceled, at short distances
it remains a non-zero "residue" - see above "Interaction
of atoms".
In the commonly used name "strong nuclear
interaction" the word "nuclear" is inserted,
because we mostly deal with the properties of the atomic nucleus,
in which these interactions apply most significantly. In particle
physics, the name "strong interactions"
sufficed, as these are fundamental forces acting generally
between interacting hadrons - as a
mentioned consequence of a strong interaction between quarks
forming hadrons. Nuclear forces are only a special manifestation
of these strong interactions.

Fig.1.1.10. Graphical ilustration of
nuclear force potentials for neutron and proton as a function of
distance. The right part of the figure shows the discrete
(quantum) energy levels of nucleons in the potential well of the
nucleus.
Figure 1.1.10 graphically shows how the
potentials of the forces acting between the nucleus and the
nucleon depend on the distance. In an imaginary experiment,
imagine that with the nucleon we are slowly approaching toward to
an atomic nucleus. For a neutron no (left) without an electric charge, only the field of
strong interaction acts, so at greater distances the force is
negligible and at distances of the order of 10-13 cm an attractive
force acts, which binds the neutron to the nucleus. For
a positively charged proton p+, an electric repulsive force will act
at greater distances according to Coulomb's law (blue curve in
Fig.1.1.10), and only when we overcome it (we
say that we have overcome the Coulomb barrier) and the proton approaches the nucleus at a distance
close to 10-13 cm (1 fm), an attractive nuclear force
(red curve) begins to act, overcoming the electrical repulsive
force, and "ties" the proton to the nucleus. In both
cases, the resultant force curve is marked in green in the
figure. At even smaller distances (tenths of fm) inside the core,
the attractive force is in both cases effectively replaced by a repulsive
force *), preventing complete shrinkage of the core; its
origin is related to the quantum principle of uncertainty
and to the exclusion principle of fermions.
*) Nuclear interactions at subnuclear
distances At short distances of
the order of tenths of fm, nuclear interactions have a repulsive
character
. This "repulsion" of nucleons as they approach each
other at a distance of <<1 fm is not a specific property of
a nuclear strong interaction (which is a residual manifestation
of a strong interaction between quarks within nucleons) or
"incompressibility" of nucleons, but is only an
"effective force" that it is a consequence of quantum
relations of uncertainty and fermion character of
nucleons (Pauli exclusion principle). Nucleons cannot reach a
smaller distance, or a lower energy level in the field of nuclear
forces than the lowest basic one; if we tried to "push"
them even closer together, they would "defend"
themselves with an intense repulsive force - nucleons as if with
their wave nature did not "fit" into such a small
space...
This effect leads to the
so-called Fermi presure of degenerate fermion gas in the
final stages of stellar evolution, which can stop the
gravitational collapse and balance the massive gravitational
forces (§4.2 "Final Stages of Stellar Evolution. Gravitational
Collapse" in the
monograph "Gravity, Black Holes, and the Space
Physics"). However, only if the mass of the star is not too
large - in that case strong gravity, according to the general
theory of relativity, occurs to create an event horizon
that "overpows" even this quantum counterpressure and a
complete catastrophic gravitational collapse wins and forms a black
hole.
The course of the interaction potential of nucleons
for distances of tenths of fm is largely speculative,
is not implemented in nucleus and cannot be verified
experimentally. We cannot "take two protons in hand",
push them close to each other, and measure the forces by which
they are attached or repelled. This can only be done by collision
experiments at high kinetic energies. At medium energies
(units up to tens of MeV), the dependence according to Fig.1.1.10
is measured in scattering experiments, but only with a part of
the repellent component. For a larger interaction
"approach" of nucleons, it is necessary to use larger
collision energies of hundreds of MeV. Here, however, a new
phenomenon manifests itself from about 300 MeV: the production of
p- mesons (pions). We are already
encountering the fact that short-range nuclear forces are a
residual manifestation of a long-range strong interaction between
quarks within nucleons, mediated by gluons. In
an effort to get as close as possible to the nucleons, we no
longer get any real interaction potential, because the nucleons
"melt" into the quark-gluon plasma,
cease to exist "individually" and we observe a number
of secondary particles reflecting the properties of the new state
of hadron matter (§1.5, "Quark
structure of hadrons"). Nucleons
at higher energies are not incompressible, but
change into new states and particles.
Experimental measurements (with
scattering of high-energy electrons) show that the approximate
relation R = d . N1/3 applies to the radius of the nuclei,
where N is the nucleon number of the nucleus and the
parameter d has the value d = 1.3·10-13 cm - this is the range of strong
interaction. It follows from this relationship that the volume of
the nucleus is directly proportional to the nucleon number N
and thus each nucleon occupies approximately the same volume in
the nucleus. Thus, the nucleus can be considered as a set of
nucleons with an approximately constant density of nuclear mass.
Neutrons without an electric charge show
only attractive nuclear forces - they help to
"stabilize" the nucleus. For each nucleus there is a
certain ratio of protons and neutrons, for which the nucleus is
the most stable (this ratio is close to 1:1 for light nuclei, for
heavy nuclei it is up to about 1:1.5 in favor of neutrons). If we
add or remove some neutrons to a nucleus with a stable
configuration of protons and neutrons, usually such a nucleus
will no longer be stable, but will spontaneously decay (or
transform) - it will be radioactive (the relevant mechanisms will be analyzed in §1.2
"Radioactivity").
Excited states of the
nucleus
Nucleons are located in the nucleus and move in the field
of nuclear forces (strong interactions), in which they
can have different (binding) energy - they move in a kind of
"potential pit". According to the laws
of quantum physics, nucleons cannot have continuously variable
energy in this field, but only certain quantized
energy values. Thus, similar to the electrons in the atomic
shell, the nucleons are located at discrete energy levels
in the nucleus (Fig.1.1.9 and 1.1.10, both on the right). Proton
and neutron levels differ somewhat due to electrical interaction
and are occupied independently, with Pauli's
exclusion principle limiting the occupancy of each such level by
a maximum of two protons and two neutrons with opposite spins.
The lowest energy level of the nucleus corresponds to the ground
state, but the nucleus can (by supplying energy - excitation
) get to a higher energy state - to the so-called excited
energy levels - as if the nucleus were
"inflated", the nucleons are "farther apart"
(Fig.1.1.9), occupy higher levels. The energetically excited
nucleus usually "collapses" very quickly - the levels
are deexcited, while the corresponding energy
difference is emitted in the form of a photon
of electromagnetic radiation - radiation g
(see §1.2, section "Gamma radiation").
In addition to the ground state,
atomic nuclei (except hydrogen) have a number of excited states (energy
levels), only some of which are involved in radioactive
transformations. The other excited states arise during the
bombardment of nuclei by energetic particles from accelerators.
Metastable
levels and nuclear isomerism
The lifetime of excited nuclear levels is usually very short (»10-15-10-6 sec.), but there are
situations where the lifetime of the excited level is in the
order of seconds, minutes and even several hours, days and years
! - such levels are called metastable and we
speak of the isomeric state of the nucleus. Such
a nuclear isomer is often considered to be a separate
nuclide and is denoted by the superscript "m"
at the nucleon number e.g. 99mTc. This phenomenon occurs when there is an energy level
near the ground state of the nucleus, which differs
significantly from the ground state by its angular
momentum - spin (at least 3h , ie DI ³ 3), see the core
shell model below. Then the radiation g emitted at the transition
from such a level to the ground state must have a higher
multipolarity (E3, M3 or higher) - transitions between such
levels are unlikely, they are
"forbidden", so the corresponding lifetimes can take on
large values. Isomerism and metastable states do not occur in
light nuclei (where there are no excited levels with DI ³ 3), but only for nuclei with a nucleon number from 40;
details are explained by the shell model of nucleus. An important
example is the metastable technetium 99mTc, which deexcites with a half-life of 6 hours, see the
following §1.2 "Radioactivity", section "Gamma radiation".
However, some nuclear isomers have such
different quantum properties from the ground state (especially
the spin value) that there is no transition to the ground state
of g- radiation
photon emissions , but to the radioactive conversion of beta- , beta+ or
electron capture, to another neighboring nucleus (§ 1.2, section
"Nuclear isomerism and metastability").
Binding
energy of atomic nuclei
As already mentioned, protons and neutrons are bound in
the nucleus by an attractive strong interaction. Associated with
this binding force of nucleons is a certain potential energy
called the binding energy of the nucleon or the
whole nucleus. The total binding energy of the nucleus
Ev means
the energy required to completely decompose the nucleus into
individual free nucleons *). At the same time, this binding
energy is equal to the energy that would be released when the
nucleus was formed from individual nucleons.
*) For the time being, we are leaving aside the mechanisms by
which such a distribution or composition of nuclei can be carried
out; we will deal with this in §1.3 "Nuclear reactions and nuclear energy".
According to the relativistic concept of
mass-energy equivalence, due to the binding energy, the total
mass of the nucleus m(Z, N) is always somewhat less
than the sum of the masses of its free protons Z.m p and neutrons (N-Z).mn. The difference
between the resulting rest mass of the nucleus and the total rest
mass of the free nucleons of which the nucleus is composed,
D m = Z.m p + (N-Z) .m n - m (Z, N) ,
is called the weight loss or defect.
According to Einstein's equivalence relationship between mass and
energy, the weight loss is related to the total binding energy of
the nucleus by the relation Ev º DE = Dm. c2. If we divide the
total binding energy of the nucleus Ev by the number of nucleons N, we get the average binding
energy per one nucleon` Ev = Ev/N.
Weight loss is expressed either in
grams or in atomic units of mass (1/12 of the mass of a carbon
atom 12C),
binding energy is usually expressed in megaelectronvolts [MeV] in
nuclear physics. E.g. the helium nucleus 4He2 has a mass loss Dm = 0.5061.10-25 g, the binding
energy Ev º DE = 28 MeV, the binding
energy per nucleon is 7 MeV.
Sometimes the rate of weight loss is
expressed by the so-called cogestion coefficient d = (Dm/m), sometimes
multiplied by 10000.
The binding energy
per nucleon (or compression coefficient) with a proton number initially increases rapidly, the
largest is for nuclei around iron, then again slightly decreases
- see Fig.1.3.3 in §1.3 "Nuclear
reactions and nuclear energy".
This dependence is also crucial for the possibilities of
obtaining nuclear energy. Fig.1.3.3 will be
mentioned here for clarity :

Fig.1.3.3. Dependence of the mean binding
energy Ev
per one nucleon on the nucleon number of the nucleus. In the
initial part of the graph, the scale on the horizontal axis is
slightly stretched to better see the differences in binding
energy for the lightest nuclei. The right part of the figure
concerns two ways of releasing bound nuclear energy, which will
be discussed in detail in §1.3 "Nuclear reactions and nuclear
energy".
Binding energy and
stability of atomic nuclei
As with other bound systems, the binding energy of atomic nuclei
can be expected to be closely related to their stability.
It is related to the "external" stability in
the supply of energy to the nucleus from the outside (usually by scattering some particles bombarding the
nucleus), as well as to the "internal"
stability or instability caused by internal mechanisms in
nucleons and their bonds. In the following §1.2 "Radioactivity" we will get acquainted with the processes and
mechanisms by which nuclei can transition from higher energy
configurations to lower energy configurations during radioactive
transformations. In order for every nuclear process (and
every physical process in general) to take place, two basic
conditions must be met: the energy balance and
the existence of the appropriate mechanism by
which the process takes place. The stability of light and
medium-heavy nuclei is determined by the ratio of the
number of protons and neutrons. According to Fig.1.1.10,
the quantum energy levels of protons and
neutrons in the field of nuclear forces are given, which are
occupied independently. If at these levels a situation arises
where the energy of a different configuration of protons and
neutrons is energetically lower enough, "will work" a
mechanism of weak interaction, which is able to
mutually convert protons and neutrons - there is a radioactive
transformation of beta (beta- or beta+ depending on whether
there is an excess of neutrons or protons). For heavy nuclei in
the uranium and transuranic regions, alpha radioactivity
occurs due to the inability of a strong interaction, due to the
short range, to hold such a large number of nucleons together. In
§1.2 "Radioactivity" we will analyze all these
processes in terms of mechanisms and energy balance on a
3-dimensional table of nuclides, mapping the binding energies of
nucleons in nuclei - part "Stability and instability of atomic nuclei", Fig.1.2.8 and 1.2.9 in §1.2.
Atomic
nucleus models
Due to their size of »10-13 cm and quantum character, atomic nuclei are completely
beyond the scope of any direct observation. To understand the
various processes with atomic nuclei, it is necessary to get some
at least approximate ideas about nuclei and their internal
arrangement. Atomic nucleus models are certain
schematic representations, fictitious constructions, and
analogies that explain, with greater or lesser success, certain
properties or processes in light and heavy atomic nuclei. There
are several models, each of which usually explains only some of
the specific nuclear processes for which it was created (with the
exception of the shell model, which is more general).
Here we will only briefly mention some of the more commonly used
models :
Diversity of atomic nuclei
Currently, more than about 2,600 species of different nuclei are
known, differing in the number of protons or neutrons. Of these,
the stable nuclei are 270, the other nuclei are radioactive.
There are 340 nuclides in terrestrial nature - 270 stable and 70
radioactive. Let's list some important specific cores of
elements. The simplest element is hydrogen 1H1 (hydrogenium), whose nucleus consists of only a single
proton p+,
around which a single electron e- orbits. The
addition of one neutron no forms the nucleus of heavy hydrogen 2H1 - deuterium. The heaviest isotope of hydrogen
is tritium 3H1,
containing a proton and 2 neutrons; however, two neutrons per
proton are "a little too much", the equilibrium
configuration is broken, and tritium 3H1
is already decaying radioactively (decaying
b- with a half-life
of 12.6 years to helium 3). Another
important light nucleus is helium 4He2 containing two
protons and two neutrons (there is also a small amount of 3He).
Other important nuclei include
carbon 12C6, nitrogen 14N7, oxygen 16O8, sodium 13Na11, sulfur 33S1 , ....., iron 56Fe26, ...., gold 197Au79 etc. The heavier the
nucleus, the more different isotopes it has, some of which are
stable, but most is radioactive. The last stable cores are lead 208Pb82 and bismuth 209Bi83; all heavier nuclei
are already radioactive - we gradually get into the area of
uranium nuclei (235,238U92 and other isotopes) and transuranic nuclei (plutonium,
americium, californium, einsteinium, fermium, mendelejevium ...).
The heaviest known cores (such as 258Lw103 and higher) are already disintegrating so quickly after
their artificial production, that it is difficult to prove their
existence at all. The preparation of heavy transurans is briefly
mentioned in §1.3 "Nuclear reactions", part "Transurans". The properties of the three important transurans
(plutonium, americium, californium) are given in §1.4, section
"The most important radionuclides".
Stability of atomic nuclei
The temporal stability or instability of atomic nuclei is due to
the complex interplay of strong, electromagnetic
and weak interactions between nucleons (and even
within nucleons). In principle, the nuclei are held together in a
stable configuration by the predominance of the strong attractive
nuclear interaction of nucleons over the weaker electrical
repulsive force between protons. For too large nuclei, a strong
nuclear interaction, due to its short range, is not enough to
bind the nucleus strong enough, which can lead to the emission of
nucleons (alpha radioactivity), or even to the fission
of the nucleus. Within the nucleons themselves, there are
strong and weak interactions between quarks; these weak
interactions can lead to transmutations of quarks within nucleons
and thus to mutual transformation between protons and neutrons -
this results in the instability of the nucleus, in its
transformation into another nucleus (beta radioactivity).
The mechanisms of different types of radioactivity will be dealt
with in §1.2 "Radioactivity".
Strong, electromagnetic and weak interactions determine the energy
conditions in the nucleus according to the number of
protons and neutrons, their mutual ratio and arrangement. From
the energetic point of view, we will analyze the causes of
nuclear instability in §1.2, section "Stability and instability of atomic nuclei".
The
origin of atomic nuclei and the origin of elements - we are the descendants of stars!
Cosmic
alchemy
D.I.Mendeleev and his followers systematized the individual
elements known in nature into the periodic table. Chemists have
studied in great detail the properties of all these elements and
their compounds, which are the cause of the variety and diversity
of the world. But let's ask ourselves a curious
question: Where did the individual elements come from? How
did their atomic nuclei form?
They werw constructed,
metaphorically speaking, by God "with his
hands" already at the creation of the world - ie all
the elements were created already at the creation of the
universe? Or did they originate during the further evolution
of the universe? Contemporary astrophysics and cosmology
clearly lean towards the second possibility - it has developed a
fascinating "scenario" of the chemical
evolution of the universe - cosmic nucleogenesis.
According to the standard
cosmological model, the universe was born before about
13 to 15 billion years ago in a very hot and dense state - when
called "Big Bang".
Within the classical general theory of
relativity, the actual act of the origin of the universe
(the big bang) has the character of a point so-called singularity
with zero volume, infinite curvature of spacetime, infinite
energy density. According to the quantum theory of gravity,
however, spacetime in the microscales of the so-called Planck-Wheeler
lengths »10-33 cm show such large quantum fluctuations in
geometry (metrics) that even the topology of spacetime
fluctuates - spacetime has a "foamy"constantly
spontaneously fluctuating microstructure. According to the
concepts of quantum cosmology, the universe was born of
quantum space-time foam; what's more - together with our
Universe, more universes could have been born
in this way ! (cf. "Anthropic Principle or Cosmic God ").
Individual phases of the evolution
of the universe after the "big bang", accompanied by
rapid expansion and cooling universe,
are divided into 4 significant stages differing in the dominant
physical interactions and processes that took place at that time (described in detail in §5.4 "Standard
Cosmological Model. The Big Bang." of the book "Gravity,
Black Holes and the Space Physics")
:
To recap, at the end of the Lepton
era, all the matter in the universe consisted of only hydrogen
(75%) and helium (25%). This situation lasted
for about 300,000 years throughout the radiation era,
when the universe expanded and the temperature dropped. When the
temperature dropped below about 3000 °K, the hydrogen and helium
atoms already retained their electrons - hydrogen gas and helium
were formed, and the era of matter that lasts so far has
begun. The gas envelope was very thin, but had an inhomogeneous
structure. Local densities began to shrink under their own
gravity, creating nuclei of galaxy clusters and galaxies. There,
the gravitational shrinkage and densification of the gases
continued, increasing the pressure and temperature (adiabatic
compression).
When the temperature inside some of the
thickening clouds reached about 107 degrees, the kinetic energy of the nuclei began to
overcome the repulsive electrical forces between the positively
charged nuclei - thermonuclear reactions ignited. The thermonuclear
reaction is the fusion of atomic nuclei at high
temperatures, with lighter nuclei forming heavier nuclei (§1.3).
High temperature is needed for positively charged nuclei to
overcome electrical (Coulomb) repulsive forces with their kinetic
energy and to approach each other at a distance of »10-13 cm, where due to
attractive strong interactions, both nuclei can merge and combine
to release a considerably large binding energy. This released
energy is then the source of the star's light and heat, and
further shrinkage stops - the gravitational forces are balanced
by the pressure of the radiation and the thermal motion of the
ionized gas due to the released nuclear energy.
Thermonuclear reactions and
nucleosynthesis in stars
(more detailed analysis is in §4.1 "Gravity and
evolution of stars", part "Evolution
of stars" -
"Thermonuclear reactions inside stars" monograph "Gravity,
black holes and space-time physics").
For most of the star's life is thermonuclear
combining hydrogen to helium which is the most energy efficient. After consuming
hydrogen inside the star for some time, gravity prevails, the
star continues to shrink, and the pressure and temperature rise
so much that the helium nuclei begin to coalesce into carbon
(4He + 4He ® 8Be + g , 8Be + 4He ® 12C + g, reactions 3a(=4He )® 12C+g). After depletion of helium, further shrinkage of the
star's interior occurs, and at ever-increasing temperatures,
other thermonuclear reactions accompanied by carbon combustion
take place ( eg 12C + a ® 16O + g, 16O + a ® 20Ne + g, 20Ne + a ® 24Mg +
g, 12C + 12C ® 24Mg, etc . .. ) and at higher temperatures also oxygen (16O + 16O ® 24Si+ a, resp. ® 31P + p, resp. ® 32S + g). The nuclei of silicon and other elements in the hot
thermonuclear plasma capture neutrons, protons and a-particles,
creating other heavier elements. In addition to carbon, many
similar nuclear reactions produce oxygen, nitrogen, ...,
magnesium, ..., ... silicon, ... calcium, ... chromium, ... and
finally iron.
Note: In order for a star to
be able to synthesize heavier elements, it must have enough mass
for gravity to cause sufficiently high pressures and temperatures
inside it. Small stars can only make helium from hydrogen, more
massive stars like our Sun will form nuclei down to magnesium,
and much larger stars will have a whole sequence of thermonuclear
reactions.
How do the thermonuclearly
created heavier elements get away from stars ?
If no other processes took place in the stars apart from
thermonuclear nucleosynthesis, all the heavier elements
"cooked" in this way would remain forever
trapped in the interior of the stars by strong gravity
and would not contribute in any way to the chemical evolution of
the universe, not even life could arise. Fortunately, there are
two processes that release the synthesized heavier elements from
the gravitational grip of the stars and enrich the surrounding
interstellar space with them :
--> Thermoemission of gases
from the upper layers of the "atmosphere" of stars -
the stellar wind (passage
"Stellar wind"), which continuously carries a small amount of the
star's gas, with an admixture of synthesized heavy elements, into
the surrounding space.
--> A supernova explosion that
ejects a substantial amount of the star's material, including a
large amount of thermonuclearly synthesized elements, into the
surrounding space. And during the proper explosion, it will
create many other even heavier elements (see the section "Supernova
explosion. Neutron star. Pulsars."
in the §4.2).
For iron nuclei, the sequence of
thermonuclear reactions ends because the elements around iron
have the highest binding energy, so the nuclear synthesis of
heavier elements is no longer an exothermic reaction (energy must
be supplied). All nuclear reactions releasing energy cease, the
active life of the star ends - the final phase of stellar
evolution occurs.
What happens next? It depends on the
remaining mass of the star. If this mass is not higher than about
1.25 masses of the Sun, the star (compressed by gravity from the
original several hundred thousand kilometers to an average of
several thousand kilometers and a density of the order of
thousands of kilograms per cm3) remains in equilibrium, when gravitational forces are
balanced by the so-called Fermi pressure of degenerate
electron gas in a fully ionized substance. A star in this state
is called a white dwarf (until it glows hot with
the remaining heat; then it becomes a black dwarf );
such a star is not very important for the
chemical evolution of the universe - the heavier elements
synthesized during its evolution remain gravitationally
"trapped" inside the white dwarf and will not enter the
surrounding universe.
If the star has a residual mass
greater than about 1.25 times the mass of the Sun (the so-called Chandrasekhar
limit), the pressure of the electron gas is no longer able
to balance such enormous gravitational forces, gravity will win
and shrinkage will continue. Electrons are "pushed"
into the nuclei and absorbed by them (there is a
massive electron capture); they combine there with protons to
form neutrons and flying neutrinos: e- + p+ ® no + n (inverse b-decay). As a result, the electron content in the star
decreases and their Fermi pressure decreases, making the star's
substance easier to compress - further shrinking and absorption
of electrons. The process continues at an avalanche-increasing
rate: in a fraction of a second, the star will shrink violently,
almost all of which protons and electrons merge into neutrons
(atomic nuclei dissolve and cease to exist). At this stage,
equilibrium can (but does not have to!) re-occur - a neutron
star is formed, which has a diameter of only a few tens
of kilometers and is composed of a neutron "substance"
with a density of »1014 g/cm3 of the same order as the density in atomic nuclei.
The gigantic gravitational forces are balanced by the Fermi
pressure of the degenerate neutron "gas". Fast-rotating
neutron stars are observed in space as so-called pulsars
- they emit a cone of directed electromagnetic radiation as they
rotate, which, like a beacon, we observe as very regular rapid
flashes of radiation.
During the implosion leading to the
formation of a neutron star, a large amount of energy is suddenly
released, which is partially emitted by neutrinos and
electromagnetic radiation (not only infrared and visible light,
but mainly hard X-rays and gamma radiation), while the outer
layers of the star expand rapidly into space and form then a
glowing nebula: the formation of a neutron star is accompanied by
a supernova explosion, which emits a huge amount
of energy and the outer layers of the star are
"scattered" into the surrounding space.
If the burned star has a residual mass more
than twice the mass of the Sun, the gravitational forces are
already so great that they can overcome the Fermi forces between
neutrons, the catastrophic gravitational collapse does not stop
at the neutron star stage and continues until the star, acording
to the general theory of relativity, falls below its
gravitational radius, crosses the horizon and a black
hole is formed (details in Chapter 4 "Black Holes" of the book "Gravity,
Black Holes and the Physics of Spacetime").
A supernova explosion is essential for the chemical evolution of the universe in two ways :
Stars such as our Sun and the
entire solar system formed from clouds of gases "remelted
and boiled" by earlier generations of stars *); these clouds
have already been enriched with heavy elements.
*) The stars of the first generation, which formed in the period of about
300-700 thousand years after the big bang from hydrogen and
helium (other elements were not yet in space at the time),
probably had quite large masses of about 100-300¤. According to the laws of stellar
evolution, therefore, they evolved
very rapidly-
after about 3-5 million years, they exploded like supernovae and
introduced heavier elements into the interstellar matter, which
were formed in them by thermonuclear fusion. The next generation
of stars, which formed from this substance enriched with heavier
elements, no longer reached such masses, and their lifetimes were
hundreds of millions of years to several billion years. Our Sun
probably formed as a 3rd generation
star made
of material enriched after the explosion of 2nd generation stars
(and previously 1st generation).
Stars can be
described as a kind of "alchemical cauldrons" of the universe, in which heavier elements are formed from
lighter elements by thermonuclear synthesis. Alchemists,
who often looked at the stars (also engaged
in astrology ) at night with
religious reverence, called on them and begged for help, had no
idea that these stars had been doing (and still do) on a huge
scale what they did for billions of years before, they tried
unsuccessfully on a small scale - transmutation
- to transform elements. So with a bit of exaggeration, we can
proudly say that “we
are all descendants of the stars!"-
every atom of carbon, oxygen, nitrogen, sulfur, etc. in our body
formed long ago billions of years ago in the "fiery nuclear
furnace" of the interior of an old star, now long extinct.
All elements on Earth, except hydrogen, which is primordial and
helium, come from the "dust" of stars burned out long
before the creation of our solar system. We are the
"ashes" - a kind of 'recycled waste' thermonuclear
fusion of ancient stars ...
An exception are light elements deuterium, lithium,
beryllium and boron are not the direct product of thermonuclear
reactions in stars (on the contrary, in these reactions they are
"burned"), but they were formed by the primordial
nucleosynthesia and interaction of cosmic rays with other nuclei,
especially carbon, nitrogen and oxygen, which are fragmented into
lighter nuclei by high-energy cosmic rays.
Fusion
of neutronon stars
Another way of creating heavier elements in space
occurs with the close orbit of two neutron stars
and their merging - fusion, "collision". In this
process, a large amount of neutron matter is ejected,
which immediately "nucleonizes"
to form atomic nuclei (§4.8, passage "Collisions
and fusions of neutron stars"). This
creates a large number of cores, with a relatively higher
proportion of heavy elements. Due to the huge
number of neutrons, the r-process of rapid
repeated neutron capture by lighter nuclei takes
place intensively, during which very heavy nuclei
are also effectively formed - from the area around iridium,
platinum, gold, to a group of uranium.
The evolution of stars from the point of view of relativistic astrophysics is described in more detail in the book "Gravity, Black Holes and the Physics of Spacetime", §4.1 "The role of gravity in the formation and evolution of stars"; cosmic nucleosynthesis from the point of view of nuclear (astro) physics is outlined in the work "Cosmic Alchemy", a synthetic view of the evolution of the universe in the work "Anthropic Principle or Cosmic God".
Nuclear
astrophysics ® atomic astrochemistry
According to the laws of nuclear astrophysics,
light atomic nuclei were formed at the beginning of the
universe by primordial cosmological nucleosynthesis,
heavier nuclei by thermonuclear synthesis inside stars.
These nuclei are originally "bare", without electron
shells - gamma radiation and sharp collisions at high
temperatures will not allow the formation of a permanent electron
shell, electrons are immediately ejected from the atomic shell,
complete ionization of atoms. No chemical reactions and
compound formation can occur here. In the ejected clouds, these
nuclei enter cold interstellar space, where the nuclei capture
their free electrons with their electrical attraction, filling
them with electron orbits to form complete atoms of
elements. Chemical reactions may already occur between
them.
The
probability of collision and merging of two or more atoms in the
sparse gaseous state of cold interstellar clouds is very small.
However, there are two important mechanisms of chemical reactions
in space :
¨ "Cold"
astrochemistry
For the formation of molecules from atoms in space, solid dust
particles condensed in an ejected nebula are very important.
There, the atoms are close to each other and can exchange
electrons - chemical reactions and the synthesis
of molecules from atoms in interstellar space take place
on grains of dust. They can also be stimulated
by radiation from surrounding stars and cosmic radiation.
By interacting with radiation, neutral atoms become ions,
which, thanks to attractive electrical forces, are able to carry
out reactions and bonds to molecules even at very low
temperatures (at which normal chemical reactions do not take
place).
¨ "Hot"
astrochemistry
Gas envelopes can function as "space chemical
laboratories" around some stars, especially around red
giants rich in carbon and oxygen. There are large differences in
temperature and pressure in the individual areas of the envelope
and there is intense radiation. The kinetic energy of the thermal
motion of atoms overcomes the repulsive electric forces, and the
atoms can approach by sharing the valence electrons and merging
them into molecules. Temperatures are higher in the interior and
compounds of silicon, magnesium, aluminum, sodium, etc. may be
formed. In the lower temperature, compounds with longer carbon
chains may be formed.
Intense chemical reactions then occur in protoplanetary disks
and the planets formed around them around stars,
where there is sufficient density and often favorable
temperature.
Using radio
astronomy spectrometry, a large number of molecules not only
inorganic (water, carbon dioxide, ammonia, ...) but also more
than 100 different types of "organic" molecules
composed of hydrogen, carbon, oxygen, nitrogen were discovered in
interstellar clouds. Some are composed of more than 10 atoms, in
addition to methane, there are also polycyclic aromatic
hydrocarbons, aldehydes, alcohols and the like.
One stellar giant (or several of these
stars) on the inside of one of the spiral arms of the Milky Way,
which exploded as a supernova about 7 billion years ago,
was important to our Earth and solar system - from the cloud
ejected by it, enriched with heavier and biogenic elements, the
germinal nebula for the Sun and our entire solar system
condensed. We don't know where the remnant of this previous star
is, it ended up like a black hole...
Occurence
of elements in nature
Cosmic nucleosynthesis
outlined above - primordial cosmological and stellar - led to the
current average representation of individual elements in space
according to Fig.1.1.12 above. By far the most abundant elements
in the universe are hydrogen and helium. In principle, it can be
said that the element is more abundant in the universe, the
smaller the proton (atomic) number, so the fewer protons it
contains in the nucleus, the simpler it is - the easier it is to
form in nuclear reactions. Exceptions are the light elements
lithium (Li), beryllium (Be) and boron (B), the significantly
lower occurrence of which is due to the fact that they
"burn" to helium inside the stars before the main
conversion of hydrogen to helium takes place. The opposite
exception is a group of very stable elements (with high binding
energy of nuclei, so it is easier to "survive" the
final stages of stellar evolution) around iron (Fe), whose
content is increased. Very slight occurrence of elements, which
do not have stable isotopes - technetium (Tc), promethium (Pm)
and actinides such as polonium (Po) to palladium (Pa), is due to
their radioactivity with a not too long half-life; these elements
can be formed in trace amounts by neutron capture. Thorium (Th)
and uranium (U) are also unstable (radioactive), but with very
long half-lives (of order 108 -1010 years), so after its formation in supernovae, it is
sufficient to persist for a long time in interstellar clouds,
stars and planets.
The regular
"oscillations" in the representation between adjacent
elements, which can be seen in the graph (especially in the areas
between Z = 8-20, 30-40, 45-60 and 62-75), are related to the
slightly higher binding energy of nuclei with an even proton
number than nuclei with an odd number of protons. These even
nuclei are therefore somewhat more stable - they are easier to
form in nuclear reactions and are "more resistant" to
destruction during the turbulent final stages of stellar
evolution. Therefore, they occur a little more abundantly
compared to their "odd" neighbors.
Note: The
chemical evolution of the universe is still ongoing,
so the current representation of the elements will change in the
distant future; there will be mainly a decrease in light
elements, which will merge into heavier elements. See also §5.6
"The future of the universe. The arrow of time.
Hidden matter." the
mentioned monograph "Gravity, black holes ...".
 |
| Fig.1.1.12. Relative representation of
elements in nature depending on their proton (atomic)
number Z, related to hydrogen Z = 1. Above: The current average representation of elements in universe. Bottom: Occurrence of elements on Earth (in the Earth's crust) and terrestrial planets. Due to the large range of values, the relative representation of the elements (relative to hydrogen Z = 1) on the vertical axis is plotted on a logarithmic scale; however, this can optically distort a large difference in the representation of hydrogen and helium compared to heavier elements, especially in the upper graph. |
Representation
of elements in nature - selection mechanisms
The basic representation of
individual elements in global "cosmic" nature is
therefore given primarily by primordial cosmological
nucleosynthesis (see §5.4
"Standard cosmological model. The Big Bang. Shaping the
structure of the universe.",
Passage "Primary nucleosynthesis") - 98 % of light elements of hydrogen
and helium (with trace amounts of lithium) and only 2% of
heavier elements formed by nucleosynthesis
in previous generations of stars (is described in §4.1 "The role of
gravity in the formation and evolution of stars" passage "Thermonuclear reaction inside
star "), which in the final
stages of their lives ejected these stars into interstellar space
(§4.2 "Final stages
of stellar evolution. Gravitational collapse , part "Supernova explosion, neutron stars,
pulsars"). Such is the
approximate representation of elements in existing stars,
interstellar matter, nebulae, gas-dust clouds.
However, in more detail, in different places in the Universe and
at different times, the chemical composition of matter can differ
significantly, the chemical composition is differentiated
- selection mechanisms are applied
"favoring" some elements and suppressing others :
Time selection factor
is given by the degree of stability or instability
(radioactivity) of the elements. When a supernova explodes, they
are ejected and basically all isotopes of all elements
are formed. Soon after this grandiose event, we could find not
only stable elements in the vicinity of the supernova, but also a
number of radioactive elements. In terms of astronomical
distances and time scales, however, only stable nuclei
will be preserved for further development, and of radioactive nuclei,
only those whose half-life of radioactive decay is sufficiently
long, greater than about 108 years. Unstable nuclei with a shorter half-life will decay
billions of years after a supernova explosion (transform into
other, stable nuclei), so we will no longer find them in matter.
Gravitational
selection factor
causes spatial selection of lighter and heavier elements - gravitational
density differentiation, especially in planetary systems
around stars. Heavier elements (such as iron and nickel) descend
towards the center and are concentrated in the cores of the
planets, while lighter substances (such as silicates) float to
the surface - there is a planetary differentiation of
density. Gravity in co-production with radiation pressure and its
thermal effects acts as a "mass separator",
separating light elements and molecules from heavier ones in protoplanetary
disks around emerging stars (§4.1 "The role of
gravity in star formation and evolution"
of the mentioned monograph, part "Planets"). In the inner parts of planetary systems
(such as our solar system), therefore, smaller planets with a
higher content of heavier elements - terrestrial planets
- are formed, while in more distant regions,
large planets composed mainly of light gases - gas giants. The relative representation of elements on Earth and
other terrestrial planets is therefore diametrically different
from the average representation of elements in space - see.
Fig.1.1.12 below. The main difference is the significantly higher
proportion of heavier elements (due to hydrogen) and the
practical absence of helium (see below
"Helium - an element of the sun god").
Chemical selection
factor
related to the different reactivity of the elements and to the
properties of the resulting compounds. It is mainly due to the
difference between dense and refractory compounds of silicon and
many metals, compared to volatile compounds of hydrogen, carbon
and other elements. As well as the inert properties of helium and
other "rare" gases.
Rare
and exotic elements in nature
As mentioned above, during thermonuclear reactions inside stars
and then during a supernova explosion, the nuclei of virtually all
elements of Mendeleev's table are formed, including
heavy nuclei up to transurans. They are thereby different
isotopes of these elements, including radioactive. For
further development, however, only stable nuclei
will be preserved, and of the radioactive ones, those whose
half-life of radioactive decay is sufficiently long,
longer than about 108 years.
Extinct radionuclides
Unstable nuclei with a shorter half-life have already decayed
(transformed into other, stable nuclei) billions of years after
the explosion of our "parent" supernova . These extinct
radionuclides - "burnt out" or
"extinct" - no longer occur in our terrestrial nature (or occur very rarely if they are continuously formed by
natural processes such as cosmic rays or decay chains of
long-lived radionuclides - §1.4 "Radionuclides"). Their earlier existence can be deduced from the
analysis of the representation of their stable decay products
(daughter nuclides). An example is iodine 129I, which decays to a stable xenon 129Xe with a half-life of 15.7.106 years; it was found
in increased concentrations in iodine samples in meteorites.
Furthermore, aluminum 26Al, which decomposes into magnesium 26Mg; or iron 60Fe .......
So-called primary radionuclides
(such as 40K,
232Th, 235,238U) have been
preserved from radioactive nuclei, although their amount is lower
than at the beginning - see §1.4 "Radionuclides". No transurans have been preserved, as well as
radioactive isotopes of other elements with half-lives of less
than about 108 years. In the following §1.2 "Radioactivity" will be
discussed in detail the laws of radioactive transformations.
Virtually all light and medium-heavy elements up to bismuth (ie
with a proton number less than 84) have their stable
isotopes, represented in nature.
A notable exception is technetium Tc43,
which does not have a stable isotope (the most
stable is 98Tc with a half-life of 4.2 million years, ...); about 30
isotopes of technetium are known. Therefore, it practically does
not occur in terrestrial nature, and its place in Mendeleev's
periodic table remained empty for a long time. Artificial
technetium was first found in 1937 by chemists C.Perrier and
E.Segrém in a sample of molybdenum, which had previously been
irradiated by accelerated deuterium nuclei by nuclear physicist
T.Lawrence ( 96Mo+2H®97Tc+n, resp. 98Mo+2H®97Tc+2n). Later (in 1962) a trace amount of technetium was
found in uranium ore (approx. 1 mg Tc per 1 kg U), where it is
formed as one of the fission products during spontaneous fission 235U. A relatively
large amount of technetium is formed in nuclear reactors during
the fission of uranium - in fuel cells about 27 mg of Tc is
produced for every gram of 235U split. Due to the long half-life, technetium is one of
the difficult components of nuclear waste. It is also interesting
that this exotic and practically unknown element, thanks to its
metastable isotope 99mTc, which is a pure g-emitter,
has become a very important radionuclide, on which most methods
of so-called radiosotope scintigraphy in nuclear
medicine are based - see chap. 4 "Scintigraphy".
Another such element from the center of Mendeleev's
periodic table, which does not have a stable isotope and
therefore occurs only in a small proportion, is promethium
(Pm). And of course all the elements heavier than bismuth - actinides
such as polonium, radium, radon, transurans. Thorium and uranium
also do not have stable isotopes, but thorium-232 and
uranium-238,235 are commonly found in nature due to their very
long half-lives (as mentioned above).
Helium -
an element of the sun god
The terrestrial story of the second most abundant element in the
universe - helium 4He2 - is also interesting. Helium is so rare in terrestrial
nature, that it has not been known for a long time and was
surprisingly first discovered not on Earth, but on the
Sun ! This happened in 1868, when the French astronomer
Pierre Janssen examined the spectrum of solar radiation in detail
and noticed that in addition to the spectral lines of hydrogen,
carbon, oxygen and other known elements, there are spectral lines
of a hitherto unknown "solar" element, which was called
helium (Helios = ancient Greek sun god
). Only later was helium found on Earth, first in uranium ores (in 1895 W.Ramsay, P.T.Cleve and N.A.Langley), then in the natural gas from which it is now
mined.
Why is helium, which is abundandly
widespread in space in general, so rare on Earth? This is because
helium is too light and an inert gas
that does not combine with anything (valence electrons He
completely fill the valence orbital 1s and thus prevent chemical
reaction with other elements). Earth's gravity
will not hold it, at Earth's temperature helium
rises in the atmosphere and escapes into space from the upper
layers of the atmosphere. Hydrogen gas behaves in the same way,
but due to its high reactivity, it has combined with oxygen into
heavier water molecules (which the Earth's gravity will sustain)
and has been preserved in large quantities on Earth.
Note: Only
large material planets (such as Jupiter) will retain more helium
in the atmosphere due to stronger gravity.
Thus, helium remained on Earth only in closed
underground spaces, from where it could not escape into
the atmosphere. All this helium on Earth probably comes from radioactive
a-decay natural radioactive substances, uranium
and thorium - the a particles itself is the nucleus of helium, see below
§1.2 "Radioactivity", part of "Radioactivity Alpha". It is estimated that about 3,000 tons of helium
are produced in the Earth's interior per year. Most of the helium
thus formed remains absorbed in the crystal lattice inside the
rocks, some of which is released in the gas phase into the
cavities in the Earth's crust. These closed underground spaces
are also a reservoir of natural gas, from which helium is
isolated by fractional distillation and liquefaction (in natural gas helium is present in a concentration of
up to 7%). The most common use of liquid
helium is as a cooling medium, as it has the
lowest boiling point of all substances 4.22 °K = - 268.9 °C.
Boiling liquid helium can achieve very low temperatures at which
many conductors show superconductivity (§1.5 "Elementary
particles", passage "Fermions as bosons; Superconductivity"). Liquid
helium is therefore used for cooling superconducting
electromagnets (§1.5, passage "Electromagnets in accelerators") in nuclear magnetic
resonance, accelerators, tokamaks (§1.3
"Nuclear reactions", part "Tokamak")
.
| Back: Nuclear physics and physics of ionizing radiation | |||
| Nuclear and radiation physics | Radiation detection and spectrometry | Radiation applications | |
| With cintigraphy | Computer evaluation of scintigraphy | Radiation protection | |
| Gravity, black holes and space - time physics Anthropic principle or cosmic God | |||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | |||