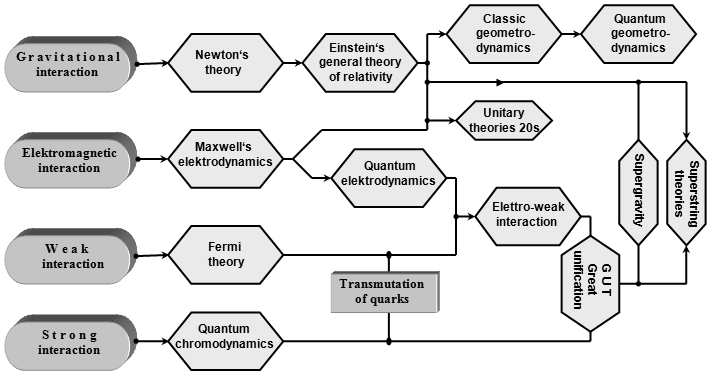
Fig.B.8. Schematic representation of the basic structure of unification of fundamental interactions.
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Appendix B
UNITARY FIELD THEORY
AND QUANTUM GRAVITY
B.1. The process of unification in physics
B.2. Einstein's
visions of geometric unitary field theory
B.3. Wheeler's
geometrodynamics. Gravity and
topology.
B.4. Quantum
geometrodynamics
B.5. Gravitational
field quantization
B.6. Unification of fundamental interactions. Supergravity.
Superstrings.
B.7. General
principles and perspectives of unitary field theory
B.6. Unification of fundamental interactions. Supergravity. Superstrings.
An objective reason why A.Einstein and his followers, despite
all erudition and effort, failed to develop a satisfactory
unitary field theory, was mainly that they did not have
sufficient experimental data on the laws
of the microworld - the properties of elementary particles.
They tried, so to speak, to "invent
nature from your office desk". This is partly true of Wheeler's
quantum geometrodynamics described in §B.4, which although introduces
the quantum principle, but otherwise it
also considers the
properties of only two types of fields - gravitational and
electromagnetic.
Now the situation is
diametrically different. There is a huge amount of experimental
data on the interactions of many types of elementary particles at
different energies. From these experimental data, important
general principles were derived that must be taken into account
when compiling any unitary theory that seeks to claim an adequate
description of reality (§B.7). Besides the gravitational and electromagnetic interactions appear two other
types of interactions that play a fundamental role in the microworld: a strong interaction permitting the existence of atomic nuclei and a weak interactions causing e.g. radioactive b -decay.
Unification of 4 kinds of
interactions
Extensive research in the field of nuclear and particle physics
has resulted in the so-called standard
model of particle physics, in which 25 fundamental
particles and 4 forces (interactions) give a perfectly
functioning explanation for everything in nature
and space - see §1.5, passage "Standard model - uniform understanding of
elementary particles" in
the monograph "Nuclear physics and ionizing
radiation physics".
Nevertheless, even with this great success, fundamental physics
is not satisfied. Firstly, from a fundamental point of view 4
different interactions are bit "too much",
there should be only one! - to achieve the
so-called "theory of everything" TOE (Theory Of Everything).
And another problem: one of the fundamental forces - gravity
- is essentially different from the others in that it has not yet
succeeded in creating a completely consistent quantum theory (discussed above in §B5 "Gravitational
field quantization")...
Strange properties of gravity
The non-linearity of gravity in GTR, "self-gravity",
the curvature of space-time, are properties very different from
other kinds of interactions. This is probably the main gnoseolological
obstacle to complete unitarization. Some experts,
especially in quantum physics, emphasize here (probably
unjustified) even the so-called information paradox
in black holes (this issue is discussed in
the passage "Return of Matter by Quantum Evaporation"). This contradiction
of quantum physics and general relativity here is (in my opinion)
artificial and unfounded, it is just the subjective
opinion of some experts...
Modern unitarization efforts take place
on the ground of quantum field
theory and
their goal is to unify the fundamental
interactions
between elementary particles - strong, weak, electromagnetic and
gravitational interactions. Because this is a very large area,
mostly outside the focus of this book, we summarize only the
basic principles and knowledge of unitarization in the physics of
elementary particles - see Fig.B.8, which is a continuation of
the basic unitarization scheme of Fig.B.1. Before discussing
specific methods of unitarization, however, we will briefly
approach the basic ideas of
unification of fields and the important role played by symmetry and conservation laws.

Fig.B.8. Schematic representation of the basic structure of unification of
fundamental interactions.
Physical
field « physical space ® unification
Already in §B.2 we outlined a very deep and beautiful idea of unitary
field theory:
according to it there should be a single, completely basic and
all-encompassing physical field, the manifestation of which would
then be all observed fields in nature - gravitational,
electromagnetic, fields of strong and weak interactions (and all their
manifestations, even in subnuclear physics). Then there is
nothing in the world but this field, of which everything is
composed - even material formations (eg particles) are a kind of
local "condensation" of this field.
Physical field
is a space in which a certain quantity is distributed in a
certain way - at each point a certain scalar, vector or tensor
describing a given field (potential or force action) is defined.
The time evolution (variability) of the field is expressed in
classical physics by the functional dependence of the field
quantities on time, in the theory of relativity by the
introduction of 4-dimensional spacetime. Several types of fields
can be present in a given space, which in the classical approach
is expressed using several vectors or tensors at each point in
space.
If we want to unify
these fields into one unitary field, we can
proceed in terms of the relationship between space and field in
basically two ways :
Both of these methods may be equivalent to some extent, but the existence of a very sophisticated mathematical apparatus of differential geometry and manifolds topology favors the second approach, which will be applied below to geometric formulations of supergravity and superstring theory.
Symmetries
in Physics
The term symmetry in physics evolved
from symmetries in geometry (and includes these
geometric symmetries as an important special case). In geometry,
symmetries express the regularity of the shape of certain
geometric formations. We have here the central symmetry
of a circle or sphere, the axial symmetry of a
cylinder, chiral symmetry - mirror left-right
symmetry. The symmetry of a geometric shape is manifested by the
fact that with certain changes in the position - the so-called transformations,
the properties of the studied geometric object do not change -
they are invariant with respect to these
transformations.
In physics, it does not have to be
such a simple and illustrative symmetry, but it can also be a
certain abstract symmetry at the level of
mathematical equations.
Symmetry and its
disruption
At the level of basic regularities, nature appears to be
essentially symmetrical, but at the level of
practical phenomena and events, symmetry tends to be more or less
broken. We can illustrate this with a simple example from
everyday life: if we stand a pencil on the table exactly
perpendicular in the tip, is equally likely to fall to either
side due to rotational (cylindrical) symmetry. If it fell preferentially to
one side, it would mean that the symmetry is disturbed
(this could be caused by inhomogeneity of
the pencil material, a slight deviation from the cylindrical
shape, asymmetrical tip trimming; possibly by external influences
such as the presence of an electric field, air flow in the room,
etc.).
When such symmetry disturbances occur in
the region of particle interactions, it indicates the
presence of a certain field causing this
asymmetry and also the existence of some new particle
which is the quantum of that field; this field can also be
understood as a "compensating" field
needed to maintain the basic symmetry, which seems to be
disturbed at the level of the phenomenon. At least that's how we
model it in modern physics...
Symmetry
and conservation laws
In physics, the symmetry of a particular physical system is
understood constancy (invariance) important feature
of this system for transformations of variables that describe it.
The symmetries of the equations of
motion,
describing the dynamics of the system, with respect to the
transformations of their variables, play a very important role here.
Thus, such transformations of quantities describing a given
physical system that leave the shape of the equations of motion
of this system unchanged. These symmetries can (but do not have
to *) respect the solution of these equations.
*) Equations describing the dynamics of the
system have certain symmetries, but the resulting state of the
system, which is the solution of these equations, does not
respect this symmetry - for example, due to asymmetric initial
conditions.
According to E.Noeter's theorem,
the invariance of equations of motion with respect to certain
transformations leads to laws
of conservation of certain physical quantities. In classical
mechanics, the law of conservation of energy can be considered as
a consequence of homogeneity of
time
(independence of time shift), the law of conservation of momentum
as a consequence of space
homogeneity
(invariance to spatial translations) and the law of conservation
of angular momentum as a consequence of space isotropy (symmetry with spatial rotations).
Next important principle of symmetry
in modern physics is the Lorentz
invariance,
originally discovered as a (more or less random) mathematical
property of Maxwell's equations derived from the experimentally
observed laws of electromagnetism. The course of physical
reasoning at the time was roughly as follows
:
| experiment | ® | field equation | ® | symmetry. |
Thanks to A.Einstein and his theory of relativity, physicists realized that the principles of symmetry can be a powerful gnoseological tool; let us just remember that it was from the requirement of symmetry to general transformations of space-time coordinates, together with the principle of equivalence, that the general theory of relativity emerged. Now the method in theoretical physics is more of a scheme :
| principles of symmetry | ® | lagrangian | ® | field equation . |
A physically justified requirement of a certain symmetry can serve as a certain "design principle" or aid in the creation of physical theories and models. And the presence of symmetries in physical models makes it possible to make some important theoretical predictions without having to know specific detailed (and often quite complex) solutions of equations of motion.
Calibration - gauge -
transformations; calibration - gauge - field
The term calibration - gauge -
*) in physical, technical and laboratory fields, means a
procedure in which the exact setting of the
relationship between the measured quantities on measuring
instruments or tools is performed or verified. A typical simple
example is the calibration of a measuring cylinder for liquids,
which is provided with marks (dashes, lines) with a marked volume
[milliliters]. Or calibration of a voltmeter, which is provided
with a scale with marked divisions of voltage values [V, mV].
Calibration is usually performed by comparison with values from
other (more accurate) measuring instruments and standards. A
special field of metrology deals with precise
calibration.
*) The word "calibration,
caliber" comes from French caliper = inner
diameter of mainly rifles or cannons, drilling, caliber of
firearms. Portable - something that has a certain size, diameter,
precise settings, calibration.
The english word "gauge"
comes from old French "jauge" - graduated rod
used for measuring.
Here in field
theory, calibration - gauge is meant as a suitable
setting - transformation, "calibration, gauge"
- of certain quantities (coordinates, field potentials), which
preserves the values of field intensity, but at the same time
allows a more suitable mathematical notation and easier specific
solution in field theory. This certain "freedom" in the
choice of potentials allows you to choose the shape of the
potentials - to perform their "gauge" so that it is as
advantageous as possible for the given problem. The invariance of
the fields under gauge transformation is called gauge
invariance.
We have already
encountered this procedure in our book, for example, in §1.5,
passage "Properties of Maxwell's equations" -
"Field potentials", §2.5 "Einstein's equations of
gravitational field", passage "Linearized theory of
gravity" and §2.7 "Gravitational waves", passage
"Plane gravitational waves in linearized gravity".
This classical concept of invariance to
gauge transformations [Lagrangian -> field equations ->
potential transformations preserving field equations], the
current methods of building unitary field theories are
reversed: the requirement of invariance to a certain gauge
transformation is declared as primary and from
its fulfillment the properties of field are derived. When a local
gauge invariance with respect to specific (physically
more or less justified) symmetries is
required, certain additional terms containing derivatives of
transformation parameters appear in the field equations, to
eliminate which it is necessary to introduce corresponding
compensating terms, which can be interpreted as a some field -
this creates a new gauge field
that could describe a new further interaction..?..
It will be discussed in more detail below. From a
physical-philosophical point of view, this may be a debatable
approach, but it "works"...
The composition of two transformations, in
which the system does not change, also results in an operation
that keeps the system the same - from a mathematical point of
view, the set of all symmetries of a given system is a group
:
Transformation groups
For a better understanding of some of the terms and designations
used below, typical of unitary field theories, it will be useful
to insert a short mathematical nipple outlining the description
of transformations using group theory.
A group is a (non-empty) set G,
between the elements of which a binary operation
"l" is defined, assigning to each two elements a, b Î G a new element c
= a lb
Î G,
which is also an element G. This binary transformation is associative
: (a lb) l c = a l (b l c), has a unit element iÎG: ali = ila = a for each element aÎG, and for each element aÎG there exists an element inverted
a-1ÎG: ala-1=a-1la= i. The most
common example of a group is the set of all positive rational
numbers in a normal multiplication operation ("l" = " .
"). If the binary operation "l" is commutative,
ie a l b = b l a for each element a, b ÎG, is called G the
Abel group. The number of elements g of a group
G is called the order of the group. If g is infinite but
countable, G is called an infinite discrete group.
If the elements of the group form a
continuous set, the order of the group is no longer applicable.
On the other hand, it is possible to introduce certain topological
properties defining a manifold into a
continuous set of group elements (for more information on
topology, see §3.1 "Geometric-topological properties"), or even metrics. The above-introduced binary
operation c = a l b, defining a group, can then be written as a
functional relation c = f(a, b). If all these group operations
(inducing the display of the group G on itself) are continuous,
the set G forms a topological group.
The topological group that is a manifold is called the Lie
group *). A typical example of a Lie group is the
Euclidean space Rn. Also, the set of continuous transformations forms a
Lie group. It is the groups of transformations
in which certain quantities are preserved that play an important
role in the physics of fields and particles. Since physical
transformations are mathematically expressed by matrices of
transformation coefficients (Aij,Aab), the respective transformation groups are matrix
groups.
*) Sets of this kind, which are both groups
and varieties, were first introduced in the 70s of the 19th
century Norwegian mathematician Sophus Lie (1842-1899)
in the analysis of the properties of solutions of differential
equations. Lie groups combine structures from three basic
mathematical areas: algebra, analysis, and geometry. They are
used in solving differential equations, in differential geometry
and algebraic topology, in quantum mechanics, in the theory of
relativity, in describing particle interactions, unitary field
theories (supergravity, superstrings - see below). In physical
applications, they usually appear as Lie groups of
symmetries of the studied system.
The unitary group U(N) is defined as
the group of all transformations x'a = Aabxb (a,b=1,2,....,N), which preserves the scalar product and the
invariance of the unit length of the vector |x| = x*axa - ie
for the transformation matrix the relation A*abAba = 1 applies (asterisk * denotes a component complex
asociation). If another restriction Det A = 1 applies, it is a
so-called unimodular subgroup SU(N) of group
U(N). .
Groups in physics
In physics, groups have found their first application in
crystallography, where they express the symmetry properties of
the crystal lattice of solids. In relativistic physics, groups
first appeared in the work of H.Poincaré, who showed that
Lorentz transformations of spatial and temporal coordinates
between inertial frames of reference form a (Lie) group; this
group of general Lorentz transformations (inhomogeneous,
including translations) is called the Poincaré group.
However, in the further development of the special and especially
the general theory of relativity, we can encounter the use of
groups only sporadically and marginally. From the end of the
1920s and the beginning of the 1930s, group theory began to be
applied more in quantum mechanics in the analysis of
multielectron configurations of atoms and in quantum chemistry.
Unitary symmetry
groups
New horizons for the application of groups have opened up in
nuclear physics since the 1940s and 1950s in describing the
properties of elementary particles. The large
number of elementary particles that were discovered in
high-energy interactions, naturally led to efforts to systematize
them and to introduce unitarization schemes.
In particular, each baryon and lepton is assigned a baryon
number B and a lepton number L
(particle +1, antiparticle -1), which are retained in all
interactions. Significant similarities and symmetries
between some elementary particles, especially hadrons, were
found.
If we look away from the electric charge, protons and
neutrons, for example, can be considered as two states (doublets)
of one particle - a nucleon. Similarly, the pions p+, po, p- form a triplet of similar particles. When studying the
strong interactions themselves, which are charge-independent, we
can disregard the charge. To describe these similarities and
symmetries, a new quantity isotopic spin or isospin
T *) was introduced. Nucleons have an isospin T = 1/2,
with the projection of the isospin T = +1/2 corresponding to a
proton and a T = -1/2 neutron. Pions were assigned isospin T = 1,
with projections -1, 0, +1 for p-, po, p+. In the system of interacting nucleons and pions, the
law of conservation of isospin applies. To express these
symmetries, the SU(2) group was created - a
special, unitary (unimodular) group in a complex 2-dimensional
space; this group is a locally isomorphic group of rotations O(3)
in 3-space, expressing the isotropy of space - symmetry to
spatial rotations, leading to the law of conservation of angular
momentum.
*) It was based on a formal analogy with
ordinary spin, where a particle with spin 1/2 occurs in two
states with spin projection -1/2, +1/2 and a particle with spin 1
in three states with spin projections -1, 0 , +1. Isospin T
is a vector in thought (auxiliary) "isotopic space". In
general, a particle with isospin T can occur in (2T + 1)
states with isospin projections on the reference axis: -T, (-T +
1), (-T + 2), ..., -1, 0, 1, ..., (T-2), (T-1), T.
Another important step was the discovery of some
"strange" (unexpected) properties of the interactions
of mesons K and hyperons in their combined pair
production, which led to the introduction of the concept of strangeness
described by the quantum number S ("Strange").
Later we were introduced general quantum number called hypercharge
Y = B + S, the sum of baryon number B and strangeness S.
It turned out that with strong interactions, both isospin T
and hypercharge Y are preserved. This led to the search
for the group SU(2) ´Y, describing the extended symmetry properties of
hadroms. In 1964, M.Gellman and E.Neeman proposed to use a
minimal Lie group, containing SU(2) ´ Y as a subgroup - the group
of unitary symmetry SU(3). This extended symmetry led to
the construction of a baryon multiplet - a decouplet (3/2+), in which, however,
one place was missing at that time; the hyperon W was thus
predicted, which was soon actually discovered.
The hadron symmetry group is a 4-parameter isospin
and hypercharge conservation group. Further analysis of unitary
symmetry showed that the system of hadrons can be very well
explained by the hypothesis that hadrons are composed of
subparticles - a triplet of quarks. This created quark
chromodynamics as a theory of strong interactions ... (is
described in "Quark structure of hadrons").
........
......... symmetry groups U (1), SU (2), SU (3), ....., SO (...),
... ., Lie algebras ...
............
In the terminology of the theory of groups of unitary
symmetries it can be said that particles are
representations of a group of symmetries. More
precisely, we identify (interpret, assign) the components of the
basis of the irreducible representation of the symmetry group
with a set of physical states - particles (or their ecxitated
states, resonances).
Global and local symmetry; Gauge
field
When studying physical systems, the corresponding symmetries can
be divided into four categories. Depending on the relationship [system] - [environment] it can be :
¨ External symmetry - invariance to changes in the
"position" of the system (or its parts) in space and
time (in addition to the usual
transformations of space-time coordinates, it is eg reversal of
time "T" or spatial inversion "P") ;
¨ Internal symmetry - invariance to transformations
of internal characteristics of the system (eg
exchange of particles for antiparticles, charge association
"C") .
In terms of space-time
"range", constant or variability of transformations,
symmetries of two kinds are applied in physics :
The basic starting point of gauge
theories
is the thesis that all four basic interactions in nature are a
consequence of the requirement of the invariance of the theory to
the respective gauge transformations. Within the gauge
theory it is possible to formulate quantum electrodynamics (where
the electromagnetic field is obtained as a gauge field at the requirement of
lagrangian invariance of free spinor field to local phase
transformations from group U(1)) and Einstein's gravitational
theory (gravitational field arises from
gauge transformations of spacetime - Poincaré group).
Gauge fields in calibration theories
are primarily "intangible" (their quantum has zero rest
mass), which is adequate for electromagnetic and gravitational
fields. Development of theory e.g. weak interactions in gauge
theories but it causes some problems stemming from the fact that
these interactions are mediated intermediate bosons (W+,
W-, Z°), which, due to short range
interaction considerably heavy weight (tens of GeV/c2).
This problem was overcome by the mechanism of the so-called spontaneous symmetry breaking [131], [153], which is a
modification of the Lagrangian, in which both the Lagrangian and
the equations of motion still have the original given symmetry,
but their own physical states no longer have this symmetry (there
is no contradiction - for example, motion in a centrally
symmetric field under asymmetrical initial conditions may not be at all
symmetrical). This spontaneous symmetry breaking then causes, that the
respective gauge field to effectively act as a non-zero
mass field without violating the gauge invariance.
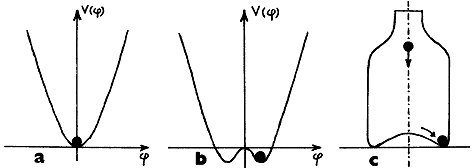
Fig.B.9. Illustration of the mechanism of spontaneous symmetry
breaking in gauge theories.
a) For the effective potential of the
shape of a simple symmetrical pit with a single minimum, the
ground state is also symmetrical.
b) For such a form
of symmetric effective potential, the ground state of the field j no
longer has symmetry.
c) The
movement of a ball released exactly along the axis into a glass
with a dented bottom illustrates the case when, despite the
equation of movement of the ball, initial conditions and shape of
the glass are symmetrical, the final state does not have this
symmetry: the ball always rolls off into the wall recess - previous
symmetry is spontaneously broken.
The essence of the
mechanism of spontaneous symmetry breaking is roughly outlined in
Fig.B.9. On Fig.B.9a shows potential energy (effective
potential) scalar field j of mass m and
the coupling constant l with isngle
(model) Lagrangian L = (1/2) (j,i)2 - (m2/2) j2 - (l/4) j4. The effective potential V(j) = (m2/2)
j2 - (l/4) j4 has (for m2 > 0)
the shape of a symmetrical potential well, in which the most
advantageous energy state corresponds to the field j = 0. If the effective
potential would have
the form V(j) = - (m2/2) j2 - (l/4) j4 (corresponding to the case m2 <0), the
potential well will have the form according to Fig.B .9b, so that the
minimum V(j) will no longer correspond to
the state j = 0, but the field j = j o
= ± m/Öl. Although the potential of V(j) is still symmetrical with respect to the
change of the sign j ® -j, the
basic state of the field j no longer respects this symmetry
(the ball symbolically representing the state of the field always
rolls to one of the minima - Fig.B.9c).
After breaking the symmetry, the
spectrum of particles (mass of excitations) changes. In this
simple case, j = 0, m 2 <0 would be a theory of
tachyons with an imaginary mass m2(j=0) =
d2V/dj2|j=jo= - m2 < 0, while after symmetry
breaking the square of the mass becomes positive by excitation of
the scalar field: m2(j=jo) = d2V/dj2|j=jo= 2.m2.
Thus, the
basic idea of the Higgs-Kibble mechanism *) is to introduce an auxiliary
scalar field (Higgs field) with such an interaction
potential into the Lagrangian of the gauge theory, but the Lagrangian as a
whole would remain gauge invariant. Then the gauge
fields will effectively behave as a field with non-zero mass about you.
In addition, so-called Higgs bosons - scalar particles with non-zero
rest mass, as a quantum of these auxiliary
scalar fields, also
appear in the theory.
*) This hypothesis was first introduced in 1964 by the authors
P.Higgs, F.Englert and R.Brout, G.Guralnik, C.Hagen and T.Kibble.
The Higgs field in 1967 was used by S.Weiberg, A.Salam and
S.Glasshow to build the theory of electroweak interaction
with heavy intermediate bosons W±, Z° (mentioned below).
Thus, it turns out that theories
of all fundamental interactions can be uniformly created within gauge
theories differing mainly by the calibration
group. Gauge
theory thus also forms a suitable basis for
unifying interactions: two types of interactions with the
calibration group G1 and G2 can be united to create the gauge
theory with gauge group G obs and exceeding group G1xG2 as its subgroups. In constructing
unified theories of weak, strong, and electromagnetic
interactions, this basic idea is supplemented by the assumption
that before the symmetry was broken, all vector bosons mediating
interactions were intangible. However, after spontaneous
symmetry breaking (due to the formation of constant scalar fields
in the whole space), some of the vector bosons gain mass and the
corresponding interactions become short-range - the symmetry
between the different types of interactions is broken.
Unification of electromagnetic and weak interactions
The first significant success on this path was recorded in the
unification of electromagnetic interaction and weak interaction
in the so-called electroweak interaction - this is the Weinberg-Salam-Glashow theory. Before the formation of a
constant scalar Higgs field H, this theory has a gauge
symmetry SU(2)xU(1) and describes the
electroweak interactions of particles caused by exchanges of
immaterial vector bosons. After the formation of the scalar field
H, the symmetry is spontaneously broken up
to the subgroup U(1), the corresponding part of the vector bosons
(W+, W-, Z°) acquires a mass (of the
order ~ eH » 102 GeV), the respective interactions become
short-range ® weak interactions, while the
other field Ai remains an intangible ® electromagnetic field. It was thus
possible to unite weak
and electromagnetic interactions into one theory, in
which they appear as
two different aspects of the same phenomenon.
Weinberg-Salam's theory of
electroweak interaction can now be considered experimentally
practically verified, because in 1973 the existence of so-called
weak "neutral currents" (causing reactions of type nm + e ® nm + e was proved at CERN), and especially in 1983, intermediate bosons W±, Z°, whose masses (mW @ 82 GeV, mZ @ 93 GeV) and the decay methods agree very
well with the predictions of the Weinberg-Salam model.
Electro-weak interaction with
intermediate bosons W± very elegantly explains the nature of beta-radioactivity by transmutation
of quarks inside neutrons or protons - it is explained in more detail
in §1.2 "Radioactivity", part "Radioactivity beta" in monograph "Nuclear
physics and ionizing radiation physics" :

Schematic representation of the
mechanism of b- neutron decay (top) and b+
-proton transformation (bottom) within
the standard model of elementary particles.
Strong
interactions and quark model
Before you briefly talk about the next stage of unification -
grandunified theories, mention a few words about the
specific properties of the strong
interaction
(a more detailed explanation in §1.5 "The Elementary
Particles", passage "Quark structure
of hadrons" in book "Nuclear
Physics, ionizing radiation"). On the basis of extensive
experimental material, obtained mainly in the 50s and 60s in the
search for new elementary particles, significant symmetries were observed in the properties of
elementary particles, which in 1964 resulted in the formulation
of a quark model of hadrons, according to which all
hadrons are composed of still "more elementary" quarks (this
name was taken from the literary work of James Joyce with a
significant dose of recession). Quarks are fermions with a spin of 1/2
and a third electric charge. To explain the system of hadrons
within the additive quark model, 6 species (metaphorically used
the word flavor - "smell") of quarks were gradually
introduced, symbolically marked "u" (up), "d"
(down), "s" (strange), "c"(charm), "b" (bottom),"
t "(top - the existence of a t-quark
is indicated by a striking symmetry in the system of leptons and
quarks). For the
same reason, it was necessary to assign quarks a new internal
quantum number - "color", which takes on three discrete
values called "red", "blue",
"yellow"; while baryons are "colorless" ("white") combinations of three colored quarks,
mesons then a combination of quarks and antiquarks. However, the
main difficulty of the quark hypothesis is that no free particles
with quark properties have ever been observed. Therefore, if
quarks exist at all, they must be very
strongly bound in hadrons.
In the late
1960s, the quark
model was to some extent supported by the results of experiments
with high-energy electron scattering on nucleons (deeply
inelastic scattering) showing that in such "hard
bombardment", the nucleon does not behave as a compact
particle, but as a cluster of several (three) more or less free
scattering centers - so-called partons. The quantum
numbers of the partons (charge, spin, isospin) corresponded to
the values expected for quarks. However, the direct
identification of quarks and partons was hindered by a
contradiction: on the one hand, partons in nucleons behaved as
free in experiments, on the other hand, quarks are so strongly
bound that they cannot be released from nucleons.
Quantum chromodynamics
Significant progress in understanding the properties of strong
interaction was achieved in the 1970s, when
the so-called quantum chromodynamics (QCD, Greek chromos
= color ) was formulated and developed [92], [55] as a theory of strong
interaction; the same right can be called "quark chromodynamics". This theory is constructed in a
similar manner as quantum electrodynamics (QED), but is based on non-abel
gauge symmetry physically associated with the color quark. A significal paradoxical feature of QCD is asymptotic
freedom: the
effective coupling constant of the interaction between quark
approaches zero during shrinking distances, but rapidly increases with
increasing distance. Asymptotic freedom allows naturally
understand the seemingly incompatible characteristics quark as
partons: quarks at small distances inside nucleons hardly
interact, while in terms of greater distances are bonded very
strongly. Closely related to asymptotic freedom is the hypothesis
of perfect "imprisonment"
of quarks,
according to which quarks cannot exist as free particles
(infinitely large energy needed for release), but only bound in
hadrons.
The strong interaction between
quarks in QCD is mediated by a vector gauge field, whose zero rest mass
quantum, called gluons, play a similar role here as
photons in QED. Unlike quantum electrodynamics, gluons have a
"color" charge and interact with each other
(they can "emit" each other); due to this nonlinearity,
the vacuum in QCD has a complex structure, especially in the
region of "infrared" (low-energy) vacuum fluctuations.
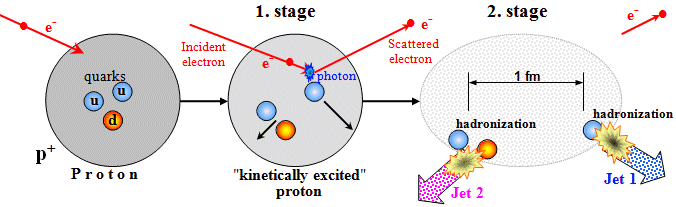
Jets - traces of hadronized quarks
At very high energies, during hard and deeply inelastic
collisions of electrons with protons, a number of secondary
particles are formed, which fly out unisotropically
in some kind of directed "jets". A
detailed analysis of the angular distribution and energy of
particles in jets showed the following mechanism of interaction,
which can be divided into two stages:
During the 1st stage, the high-energy electron, when interacting
with the proton, transfers part of its kinetic energy to one of
the quarks, which after this scattering moves for a short time
practically freely (asymptotic freedom) inside the proton;
similarly, the remainder of the proton formed by the two
remaining quarks. However, the quarks will not be released from
the proton. As soon as the distance between the radiated quark
and the rest of the proton exceeds about 1 fm (= 10-15 m), the 2nd stage
occurs: the forces between them begin to increase sharply and in
the quark-gluon field the quarks and antiquarks are produced,
which are formed into mesons and baryons - the so-called "hadronization"
of the quark-gluon plasma. The result is the emission of two
angularly collimated sprays of particles - jets,
which fly out approximately in the directions of flight of the
quark and the rest of the proton in the first stage. These jets
are actually the traces of quarks.
This mechanism is simply illustrated in the figure, which comes
from §1.5 "Elementary Particles" of
the book "Nuclear Physics and Physics of Ionizing Radiation" :
In quantum chromodynamics,
there is a problem of CP-disruption of the combination of charge
symmetry and parity in quark theory, which is solved by
introducing particles called axions - they are
light (rest mass about 10-5 eV) hypothetical particles with spin 0, which are sometimes
discussed as possible part of the so-called hidden (dark,
non-radiant) matter in the universe (see
§5.6 "The future of the universe. The arrow of time.
Hidden matter.").
Further details on the properties of elementary particles and
their interactions are given in §1.5 "Elementary
particles" of the book
"Nuclear physics and physics of ionizing radiation".
Grand
Unification
If we have the theory of strong interactions (QCD) and the theory
of electroweak interactions (Weinberg-Salam model), which are all
gauge theories, there is naturally an attempt
to combine these theories into one even more general theory of
interactions. This next stage of unitarization is sometimes
refereed to as Grand Unification (GUT - Grand Unification
Theory). The group
of gauge symmetry G in this large unification must
contain subgroups SU(3)colorx[SU(2)xU(1)]electroweak Ì G; the simplest group of this type is
SU(5), but models with gauge groups SO(10), E6 and others are
also used [194].
In grandunification theories,
vector bosons X and Y (also called leptoquarks because they cause transitions
between quarks and leptons) that are intangible before breaking
the symmetry - like all other vector particles; leptons can
easily be converted into quarks and vice versa *). First Higgs
field disturbs the initial symmetry SU(5), into
SU(3)xSU(2)xU(1) - strong interaction
described SU(3) are separated from electroweak described by the group SU(2)xU(1). The X- and Y-mesons gain a large mass
(of the order of mX,Y ~ 1015
GeV), which
strongly suppresses the transformation of quarks into leptons and
makes the proton practically stable. Another Higgs field then
disrupts the symmetry between weak and electromagnetic interractions
as in the Weinberg-Salam model.
*) This circumstance could have been of
great importance in the formation of baryon asymmetry in the very
early stages of the evolution of the universe (it is discussed in
§5.4 "Standard cosmological model. The Big Bang.
Forming the structure of the universe." and also in §5.5).
One of the main predictions of
grandunification theories is the instability
of a proton,
which should decay into muons or positrons and into one neutral
or two charged pions [p ® (m+ or e+) + (po or p++p-)] with
lifetime of the order of tp » 1030 -1033
years. This
decay would be caused by the conversion of a quark to a lepton
via the X boson, and due to the enormous mass of
the X boson, its probability is extremely
small. However, observing proton decay would be very important,
as it would decisively show that grandunification theory is on
the right track. Experiments *) so far give estimates tp > 1030
years.
*) These attempts to observe proton decay
are made deep underground (due to cosmic ray shielding), where
large water tanks are located, equipped with many
photomultipliers that could detect faint flashes caused by the
passage of fast particles formed as proton decay products. The
most perfect device of this kind is Superkamioka-NDE
in Japan, which did not detect any proton decay, but was very
successful in the detection and spectrometry of neutrinos (see
the "Neutrinos"
section in §1.2 of the book "Nuclear
Physics and Ionizing Radiation Physics").
The idea of grand unification is certainly very
attractive and promising. However, there are still many
unresolved issues and problems, e.g. mass hierarchy problem
generated by the mechanism of spontaneous symmetry breaking in
the scalar portion of theory - emerges here too many free
parameters (more than 20), it is not clear how to choose between
them to several alternative models and others; GUT is too
phenomenological. In addition, grandunification theories do not include gravity. Thus, theories attempting great
unification are not yet in such a state that they can be
considered "finite" theories of interactions. However,
their use, for example, in cosmology already leads to new
interesting concepts beneficial for both cosmology and elementary
particle physics - see §5.5.
Superunification
and supergravity
Opinions on the role of gravity in the structure of elementary
particles vary widely; they extend between two extreme positions :
If the universality of
gravity can be extrapolated down to the microscale of elementary
(subnuclear) particles, at least the first part of the second
extreme view b) would certainly apply. The local
densities of matter and energy here reach such values, that the
gravitational interaction would become strong. The view is
growing that at present it is no longer possible to separate the
physics of elementary particles and the physics of gravity; it
even seems that without the inclusion of gravity, a consistent
and uniform theory of the particles that make up matter cannot be
established. It is therefore a natural effort to complete the
unitarization of interactions in quantum field theory by
including the gravitational interaction, its unification with the
other three types of interactions. This ambitious unitarization
program is called superunification
or supergravity.
To unite gravity with other types
of interactions in the spirit of the above-mentioned scheme of unitarization
of gauge theories means to combine internal
symmetries with geometrical ones, ie to find a common group
including both space-time transformation group (eg Poincaré
group) characterizing gravity in GTR and internal (not space)
symmetry of weak, strong and electromagnetic interactions. It
turned out that such a unification (in a non-trivial way, ie not
as a mere direct product) was not possible within Lie groups, but
it was necessary to use new algebraic structures in a generalized
group, often called Lie superalgebras
or graduated Lie
algebras. In generalized groups, the respective algebras are
determined by both commutation and anticommutation relations
between individual generators. Those Lie superalgebras which contain as their subalgebras a goup
of space-time
transformations (e.g. Poincaré groups) are called supersymmetric.
The algebra of supersymmetry is
designed to contain, in addition to ordinary Poincaré group
generators (space-time shifts Pk and rotations Mkj), also spinor generators Qi
with suitable commutation relations. If such an algebra is
realized in the field space, the generators transform Qi tensor fields to spinor fields and vice
versa. Because the quantum theory of tensor fields describing
bosons with integer spin (governed by Bose-Einstein
statistics) and spinor fields describe fermions with half-integer
spin (Fermi-Dirac statistics), operators Q i
actually generates the transformation for transferring fermions
bosons, and vice versa. In supergravity ,
the sharp boundary
between fermions and bosons in current physics is thus removed.
Another characteristic feature of supergravity is that in
addition to the gravitational field, which is a gauge field
against local transformations of spacetime, it also contains a
spinor field - a gauge field with respect to local
supersymmetric transformations generated by Q i;
such a field is denoted as Rarit-Schwinger
and its quantum is called gravitino (it can have spin 3/2 or 5/2 *).
*) In supersymmetric unitary theories of
elementary particles, each particle is assigned its so-called superpartner
- each boson has its fermion superpartner and fermion, on the
other hand, has its boson counterpart. The most frequently
discussed supersymmetric particles are the mentioned gravitin
and also photin - weakly interacting mass
particles with spin 1/2, introduced as a supersymmetric partner
of the photon. Supersymmetric particles to fermions are sometimes
discussed: s-leptons as superpatters to leptons,
eg s-electron , s-muon , s-neutrino (also
called neutralino - it should have a high weight
of dozens of GeV), or quarks - s-quark.
Elementary particles are discussed in more detail in the book "Nuclear
Physics and Physics of Ionizing Radiation" , §5.5 "Elementary Particles".
Supersymmetry means that "force"
and "matter" particles (ie, field and matter) are two
aspects of the same reality. In principle, supersymmetry makes it
possible to solve the infinity problem in such a way that the
closed-loop contributions in Feynman diagrams for virtual bosons
lead to positive infinities and for virtual fermions to negative
infinities, so that they could optimally cancel each other out.
The simplest supergravity theory
- so-called simple supergravity
created in
1976 [89], [66], was more of a model experiment because it
contains a minimal number of fields; it also excludes quarks and
leptons. Physically more realistic variants of supergravity
theories try to expand the number of spinor generators and also
introduce internal symmetry generators. This creates an extended
supergravity, which contains 4N spinor generators Qa i (a =
1,2, ..., N) carrying the internal symmetry index a. If we limit ourselves to particles
(fields) with a spin not exceeding the value 2, in the spacetime
of dimension d = 4, the N-extended supergravity theories
with N = 1,2, ..., 8 are possible. The simplest extended
supergravity theory is the N = 2- supergravity, unifying Maxwell's and
Einstein's theory; two gravitons are assigned to photons and
gravitons here. Maximum extended N = 8 -supergravity contains: one
graviton field, 8 Rarit -Schwinger fields (gravitin), 28
vector fields (bosons) with spin 1, 56 spinor fields (fermions)
with spin 1/2 and 70 scalar fields. Thus, multiplets of extended
supergravity theories have a much richer structure than in simple
supergravity. However, although they contain an excessive number
of fields, they do not contain the fields of some known
particles, e.g. the m- meson...
From the unitarization scheme in
Fig.8, we see two seemingly diametrically different paths:
Einstein's geometric path ending with Wheeler's geometrodynamics
and the path of quantum field gauge theories leading to
supergravity, which has nothing to do with geometric character.
Because Einstein's concept of gravity as a geometric structure of
spacetime is based on very deep and illustrative
principles, the question naturlly arises as to whether the geometric means you
can not construct even a theory and supergravity.
Physically, it would mean that the "charges" in supergravity theories
should have their origin in the generalized geometric structure
of spacetime, similar to the gravitational "charge"
in the GTR has its origins in the curvature of
spacetime *).
*) An interesting variant of
multidimensional unitary theory, which has emerged recently, is
the theory of so-called superstrings. In this theory, particles and quantum
fields are interpreted as excited states of oscillations
(one-dimensional) relativistic strings in multidimensional space (most often d =
10). These superstrings with the characteristic length in the
order Planck »10-33 cm can be both open (free ends) or closed, wherein the interaction string
consists either at the connection of the ends of two strings (a third string is
formed) or in the rupture of
one strings into two parts. The main advantage of string
theory is considered its better renormalization properties - there are no
"ultraviolet" divegens. Superstring theory is briefly
discussed below in a separate passage at the end of this chapter.
Geometric formulation of
supergravity. Multidimensional unitary theories.
Indeed, it has been shown that supergravity can be formulated as
a geometric theory in superspace (the superspace created by the
extension of Minkowski spacetime is generally curved and has
other spinor dimensions) using a differential geometry apparatus
generalized to the situation where some of the coordinates
anticommutate. It is thus a space with torsion, and it has been shown that all
components of curvature can be expressed using torsion and its covariant derivatives. Torsion thus
becomes an important geometric object in supergravity.
Recent attempts at a geometric
formulation of supergravity thus lead to a certain
"renaissance" of Kaluz-Klein's theory (see §B.2):
theories are constructed in multidimensional (d> 4) "spacetime", which with the help of spontaneous
compactification could give a realistic theory in spacetime of the effective dimension d = 4. The mechanism of spontaneous
compaction consists
in finding a special vacuum solution of generalized Einstein's
equations in d-dimensional spacetime, corresponding to the
representation of a d-dimensional manifold in the form ed = e4 ´ Bd-4, where e4 is four-dimensional spacetime
(mostly Minkowski is considered) and Bd-4 is a compact "inner"
space. Excess d-4 dimensions ("extra-dimensions") are "rolled" on
sufficiently small scales (mostly Planck scales of 10-33 cm are considered), as discussed above in
the passage "Physical
field «
physical
space ®
unification".
The total (resulting) d-space in
multidimensional unitary field theories is formed by the outer 3 + 1 dimensional spacetime (generally curved) and other d-4
extradimensions (usually 5-7) of the inner
space. These extradimensions form a special manifold, whose geometric properties,
especially holonomy and connections, suitably model the (unitary) symmetries
of the interactions of elementary particles - thus unifying them with geometric gravity 3 + 1
dimensional spacetime.
The basic idea of
multidimensional unitary theories with compacted dimensions is
that the physical laws we observe depend on the geometric
properties of other, hidden extra-dimensions. There are many solutions in
multidimensional theories, differing for example in the metric
size of compactifications. The compacted dimensions are too small
to be observed or detected in any way. However, different
geometries of additional dimensions imply different types of
particles and forces, which causes different physical phenomena
in the macroscopic world.
Generalized Kaluz-Klein unitary
theories for various dimensions d> 4 have been studied. In
order for such a theory to be complete and realistic, ie to unify
all known particle interactions, it must contain a
phenomenological group of internal symmetry SU(3)xSU(2)xU(1). As Witten [283] recently
showed, in order for the "inner" space Bn to have SU(3)xSU(2)xU(1) - a group of isometries, its minimum
dimension must be equal to n = 7, ie the dimension of the initial
manifold the Kaluz-Klein theory must be d = 11, which coincides with the result for the
maximum N = 8- supergravity in (d = 4) -space-time
obtained in [59].
In Chapter 5 (§5.5 "Microphysics and cosmology.
Inflationary universe.") the cosmological consequences of
grandunification and supergravity theories were discussed. In the
earliest stages of the universe's evolution at high temperatures,
when spontaneous compaction has not yet taken place, spacetime
could have all its 11 dimensions. The spontaneous compaction that
then occurred could, in principle, lead to all possible vacuum
solutions, so that "islands" could be created in which
spacetime could have different topologies, number of dimensions
and metric signatures. The earliest
universe could thus be a kind of "window" into the
higher dimensions of the generalized Kaluz-Klein unitary theory.
Although supergravity is not yet
complete, it is undoubtedly a very promising unitarization
concept. To verify the correctness of the path taken by
supergravity, it would be essential if we could experimentally
prove the existence of gravitins, which are characteristic of
supergravity theories. So far, however, the only
"laboratory" for the indirect verification of
supergravity theories is cosmology - the consequences of
phenomena in the very early universe.
Superstring
theory
One of the basic concepts of physics is the concept of a material
point - an idealized object, whose mass (and other
parameters) are concentrated in a single geometric point of
space. The trajectory through which a material point in space
runs is a curve, each point of which can be characterized by
spatial coordinates and time. The dynamics of a material point in
classical mechanics is given by Newton's equations (§1.2); in
quantum mechanics, particle dynamics is described by the
Schrödinger equation; trajectories connecting the initial and
final state of a particle in space are the starting point for
quantization using Feynman integrals over trajectories (§B5).
In classical mechanics, the notion
of a material point was merely an idealization of
real bodies, useful for the analysis of their motion. However,
the special theory of relativity has reinforced the importance of
the notion of a material point: no elementary (fundamental)
object can have finite spatial dimensions, because no signal or
interaction can propagate at superluminal speeds. When two bodies
of non-zero dimensions collide, not all parts can react
immediately, which means that the body is composed of more
elementary objects: Þ the elementary object must be a point
object.
However, the point nature of
fundamental objects - field sources - leads to serious problems
in field theory: at limit transitions to zero dimensions,
mathematically divergent expressions leading to
infinite values. It is necessary to get rid of these
divergences (basically ad hoc) by methods of renormalization
- to perform a suitable gauge transformation so that the results
of the calculation match the experimental values.
However, it was possible to find a
way to systematically avoid these unfavorable mathematical
divergences - these are theories in which, instead of points, the
elementary objects are one-dimensional lines or
loops of non-zero length - the so-called strings.
If these strings were small enough (microscopic), they might not
be observable - they would look "from a distance" like
points. Thus, the basic building blocks of nature would not be
particles with zero dimensions, but one-dimensional strings that vibrate
different ways, corresponding to different types of particles.
And the particle interactions would correspond to the joining and
uncoupling of the strings. The strings are basically the same,
but they differ in the degree (mode) of their vibrations -
according to which the string can be, simply put, for example, an
electron or a quark.
According to this concept,
everything in the universe - all forces and all matter - is made
up of small vibrating energy lines called superstrings. The
different ways in which the string vibrates resonantly represent
different types of particles. Different types of forces and
particles can come from different vibrations of the same string.
One of the main pitfalls of superstring theory is the question of
their experimental verification. Superstrings, if they exist, are
extremely small (Planck dimensions). Therefore, there is no hope
for their direct experimental demonstration ...
Description of the
motion of a free string
A free (relativistic) particle of rest mass mo in spacetime (d = 4)
is described by the integral of the action (see §1.6) S0 = mo. n ds = mo.nÖ[(dxi/dt)(dxi/dt)] dt , where s
is the space-time interval and t is the proper time of the
particle. This action S0 (index
" 0
" here indicates that it is a point, ie 0-dimensional
particle) is proportional to the length
of the worldline particles (relativistic interval s ) - Fig.B.10
left. The variational principle of the smallest action dS = 0 then leads to
Lagrange's equations, from which follow the equations of motion
of relativistic mechanics in STR (1.100), resp. (2.5b) in GTR.
This procedure can be generalized to a different number of
dimensions than d = 4.
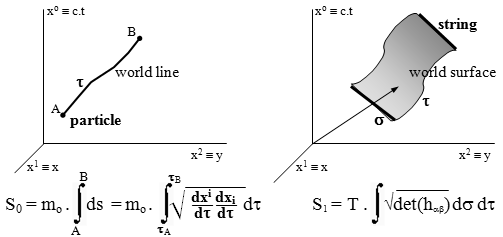
Fig.B.10.
Left: The trajectory
of a "0-dimensional" free particle in space-time is a
1-dimensional worldline that can be parameterized by the length
of the interval s or by the eigenvalue t .
Right: The trajectory through which a
1-dimensional string runs in space-time is a 2-dimensional world
surface, which can be parameterized by its own time t and another
parameter s , characterizing the position of a point on the curve
representing the string.
The natural generalization of the integral of
the action from a material point to a string leads to the fact
that the action of the string will be proportional to the size
of the world surface , which the string
"sweeps" during its movement (evolution) in space-time
- Fig.B.10 right: S1 = T. n Ö[det(hab)] ds dt, where hab (a, b = 1,2) is a two-dimensional metric on the world surface;
T describes the "tension" of
the string, given by the weight of the string
per unit length.
.................. ..... add .......
relativistic and quantum description of the string ....... ......
String Theory in Strong
Interaction
String theory has a complex history. The idea of one-dimensional
objects - strings - was born in the late 60's
during one of the attempts to describe strong interactions. The
study of hadron collisions (especially p- mesons) at high energies
led to the so-called Venezian model, which quantifies
the amplitudes of effective cross sections using products and
proportions of G- functions whose argument is squares of the sums of
4-momentums of interacting particles and resulting particles. It
turned out that the spectrum of Venezian's model is identical
with the spectrum of normal modes of "vibration" of a
one-dimensional quantized object - relativistic strings
(in 1968, M.Virasoro and J.Shapiro noticed
this). And Feynman diagrams describing the
interactions of two particles can be consolidated into one
diagram, in which 4 interacting particles (2 incoming and 2
outgoing) are shown as open strings (linear shapes of a topologically equivalent line); interchangeable particles mediating the interaction
can also be shown. Each string can "vibrate" in
different ways and accordingly appear as particles of a certain
type (electron, photon, ...) - particles are excited
states of "vibration" of the string. More
specifically, different vibrations of the string model
different parent particles.
Note: The size of
the superstrings was considered here in the order of 10-13 cm, corresponding
to the characteristic range of strong interaction.
Detailed
mathematical analysis has shown that the quantum theory of the
boson string is consistent (eg in terms of conformal invariance)
only if the dimension of spacetime is d = 26. This dramatically
exceeds the observed number of dimensions d = 4 of our spacetime.
This discrepancy can be resolved by the hypothesis of
"coiling" or compacting excess
dimensions into small closed (compact) manifolds, as mentioned
above in connection with the generalized Kaluzo-Klein unitary
theories, or in §5.7 in connection with the quantum cosmology of
the very early universe.
Another disadvantage of the original string theory is
that in the spectrum of a free boson string (which contains only
transverse modes) the ground state corresponds to a particle with
a negative square of mass, ie a particle with imaginary mass - tachyon
(for fundamental reasons, especially in terms of
causality, we have already ruled out the possibility of the
existence of tachyons in §1.6). The second excited state is
already more favorable - it corresponds to a quantum with zero
rest mass and spin 2, which can be identified with a graviton,
see below.
In the mid-1970s, quantum
chromodynamics was created (it was briefly mentioned
above), which interprets strong interactions using quarks and
gluons, which act on each other through the so-called "color
charge". The great success of quantum chromodynamics has
pushed existing string models into the background for more than
10 years.
Note: However, some physicists at the time imagined
that the quarks in hadrons were connected by strings (gluon
tubes) that held them together as "rubber fibers" (H.B.Nielsen, Y. Nambu, L.Suskind).
Supersymmetric
String Theory
As outlined above in the section on supergravity,
attempts to unify the gravitational interaction with other types
of interactions within gauge quantum field theories have led to
the notion of supersymmetry. This theory
connects bosons and fermions: for each boson he predicts a
"superpartner" who is a fermion, and vice versa. The
application of these new symmetries, expressed geometrically (by
commutation and anticommutation relations in spacetime) to string
theory, led to a reduction in the required number of dimensions
of spacetime from the original d = 26 to d = 10
(and no longer contained any tachyon). This created a supersymmetric
string theory, or superstring theory.
In addition to the boson string, a fermion string, or
superstring, which has another spinor variable, appears here as
its partner.
In the spectrum of excitations of a
relativistic quantized string, there is a particle with zero rest
mass and spin s = 2, which can be identified with a graviton
- a quantum of gravitational waves. This led J.Sherk and
J.Schwarz in 1974 to the idea that although string theory was not
suitable for describing strong interactions, it could become a
suitable tool for building a quantum theory of gravity.
However, the size of these hypothetical strings must be radically
reduced from the originally considered 10-13
cm to the dimensions of 10-33 cm of Planck-Wheeler
length, characteristic of quantum gravity (introduced in
§B.4).
Strings, or superstrings, are
elementary one-dimensional structures that can - as resonators -
vibrate in different frequency modes. The vibrations, which are
determined by the dimensions of the string and its tension, are
quantized, the corresponding energy takes on discrete values. The
frequency of these vibrations and the number of waves determine
the basic properties of the particles (eg mass or charge). Since
the string has small dimensions, it can oscillate in other
independent "directions", given by extra-dimensions.
Superstring excitations can be
"vibrational", "rotational", and excitations
of "inner degrees of freedom" - internal symmetry,
supersymmetry. Different quantum excitations (normal superstring
modes) are interpreted as a spectrum of elementary particles.
This spectrum proves to be so rich, that it can model not only
all the building blocks of a standard model of elementary
particles, but also quantum gravity. Successful completion of the
superstring concept would thus represent a unified
approach to the diverse world of elementary particles
and all their interactions - the so-called "theory
of everything" TOE (Theory
Of Everything) could be achieved.
A truly perfect unitary theory of "everything" should also explain the origin and concrete values of basic natural constants, resp. ratios of these constants. From a cosmological point of view, this question is briefly discussed in §5.5, passage "Origin of natural constants".
Another dimension, M-theory, 11-dimensional
superstring theory
The further development of superstring theory continued the
research of M.Gren, J.Schwarz and E. Witten, who found such gauge
groups that the theory of superstrings was fully covariant in
space-time (in the spirit of GTR). Five such models of
superstring theory were found, the most interesting of which were
two so-called heterotonic theories with gauge groups
SO(32) and S8xS8.
An important role in the theory of
superstrings in recent years has been played by the analysis of
mathematical (and consequently physical) equivalence or duality
between different superstring models. These dualities
represent new types of symmetries, unifying different models,
which may take different forms at first glance, but lead to
equivalent physical results. Two types of dualities have been
found between existing superstring models. S-duality
is manifested by the equivalence of two superstring models, in
which we replace the coupling constant g with its
inverse value: g ® 1/g. T-duality has a geometric
character: a model with a certain coordinate, compacted on a
circle of radius R, is equivalent to another superstring
model with compactification on a circle ~1/R (more precisely Lstr2/R,
where Lstr is the length of the
superstring). Sometimes the so-called U-duality, created
by a combination of S and T-duality, is also
discussed.
Another consequence of dualities and
unification of superstring models is the extension of the proper
dimension of strings from the original d = 1 to objects with a
different (higher) number p of spatial dimensions, eg
2-dimensional objects - membranes. From this is
derived the abbreviated name "brane".
Such multidimensional objects are no longer called superstrings,
but p-branes: for p = 0 it is a point, for p = 1
it is a string, for p = 2 a membrane, etc.
The study of string dualities has
shown that all existing superstring theories can be combined
into a more general theory, called M-theory (E.Witten, 1995; the designation "M" comes
from the name membrane, some authors link it to the
attributes mystery, magic, etc.) *). Such a unified M-theory can be realized by increasing
the dimension of the manifold to d = 11.
If we compare this with the concepts of supergravity above, we
see that the number of dimensions coincides with 11-dimensional
supergravity; close connections between this two unitary
theories, at least in the low-energy limit case, were also
analytically proven.
*) Another variant was also proposed, the
so-called F-theory (C.Vafa,
1996), using primarily 12 dimensions, but
two of which are immanently twisted (to
2-toroid). It provides a large number of
solutions, potentially usable in models of
particle physics ...
Allegorically, the designation
"M" is sometimes associated with "Mother" and
"F" with "Father"...
The six
extra-dimensions of the general space are compacted into an
internal so-called Calabi-Yau manifold, whose
geometric properties of the SU(n) holonomy suitably model
the symmetries of the interactions and elementary
particles. Elementary superstrings can oscillate in different
dimensions. The geometric structure of inner space determines the
laws of individual interactions between elementary particles and
the values of physical constants (such as charges and masses of
particles) that characterize individual particles - the
"obvious" laws of nature in "outer"
3-dimensional space. However, these basic physical laws, which we
have observed in our nature and the universe, are here a
consequence of the more fundamental internal
laws of the unitary theory of superstrings *).
*) These unitary theories allow many solutions
using different actions (Lagrangians) and also depending on how
the internal space is compacted. There can be a plethora of these
solutions. We can also interpret it asdifferent universes
with different apparent laws in 3 + 1-dimensional spacetime,
which again leads us to think about the "multiversion"
in §5.5 "Microphysics and cosmology. Inflation universe" and in §5.7 "Anthropic
principle and the existence of multiple universes" ...
Briefly summarized :
Everything in the universe is made of small vibrating strings
that can vibrate in different ways and in different directions -
dimensions. Additional "extra-dimensions" are extremely
small, so we cannot observe or measure them. They are coiled into
small loops of the Calabi-Yau magnifold and affect only phenomena
at the smallest sub-sub-microscopic scales. We live on a
3(+1)-dimensional slice of multidimensional space; such slice is
called a brane. All known particles and powers
are located on this brane. Perhaps except for gravity, which
according to some hypotheses can "seep" into other
dimensions (this sometimes explains why it
is so weak)..?..
Astrophysical and cosmological
consequences of superstring theories
As with earlier quantum field theories and multidimensional
unitary theories, interesting hypotheses of astrophysical
and cosmological consequences *) of superstring
theory are offered here.
*) The discussion of some cosmological
consequences of quantum and multidimensional theories has already
been outlined, for example, in §5.5 "Microphysics
and cosmology. Inflationary universe"
and in §5.7 "Anthropic principle and existence of multiple universes". Astrophysical implications for black hole
physics in §4.7 "Quantum radiation and thermodynamics
of black holes".
Different solutions of superstring
theory, as well as other unitary field theories, can predict different
universes with different properties (dimensions, values
of physical constants or mass spectra of elementary particles);
the anthropic principle may also say its own to
the reflection of these possibilities and their selection - see
"Anthropic Principle or the Cosmic God".
It is very difficult to decide
between different versions of the origin of the universe based on
astronomical observations. The only way to test the initial
phases of the universe is to detect relict gravitational
waves (mentioned in §5.5), which as the only type of
radiation could pass through a dense and ionized substance
filling the early universe. These primary (relict) gravitational
waves would have a different spectrum for
different scenarios of initial phases of the evolution of the
universe (eg for the inflation model, the
amplitude of the waves would increase towards long wavelengths,
for the ecpyrotic model, on the contrary, towards short
wavelengths). However, their measurement
will only be possible in the future using large detectors located
in space, such as the forthcoming LISA (§2.7,
section "Detection of gravitational
waves", final passage). Another possibility is a detailed analysis of
fluctuations and polarizations of relic microwave radiation,
which could be "modulated" by primordial gravitational
waves.
Concluding remark:
Superstring theory is currently in the stage of intensive
development. In addition to the pioneers J.Schwarz, M.Green,
E.Witten, several hundred physicists (especially the younger
generation) and a number of research groups work on it.
Superstring theory is considered by
many physicists to be the most promising current candidate for a
complete unitary field theory, unifying all 4 types of
interactions and also quantum physics with the general theory of
relativity, to the long-awaited "theory of
everything". However, many physicists are
skeptical of superstring theory. They point out the
ambiguity of its conclusions, the opacity and excessive
mathematical complexity, especially the difficulty and even the impossibility
of experimental verification in the foreseeable future.
Certain possibilities of indirect
verification could result from experimental measurement of
electric and gravitational force action at microscopically short
distances, where the usual law of inverted squares ~1/r2 could be subtly
modified by the dependence of ~1/r2+d, in which the number of additional (hidden) dimensions d
would manifest..?.. And in general, the measurement of particle
interactions at accelerators at increasingly higher energies, in
which noticeable anomalies from the standard model could manifest
themselves...
| B.5. Gravitational field quantization | B.7. General principles and perspectives of unitary field theory |
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||