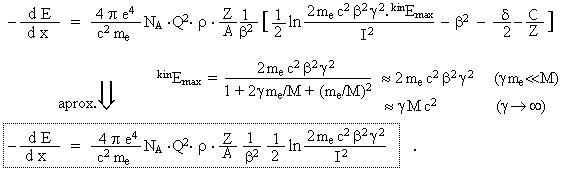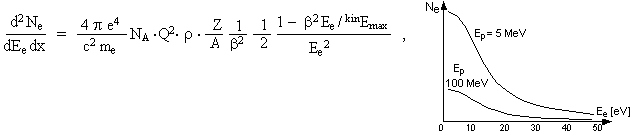Ionizing radiation in space and laboratories for research and
use in medicine and technology
1.
Nuclear and radiation physics
1.0. Physics - fundamental natural
science
1.1. Atoms and atomic nuclei
1.2. Radioactivity
1.3. Nuclear reaction and nuclear energy
1.4. Radionuclides
1.5. Elementary particle and accelerators
1.6. Ionizing radiation
1.6.
Ionizing radiation
Radiation - an
important natural phenomenon
| Radiation
: |
By radiation (rays)
we generally mean processes in which energy
is transferred acros space "at a
distance" through physical fields or microparticles
*).
In addition to energy, radiation also involves the transfer
of matter and information . |
*) Thus, radiation is not the
macroscopic transfer of kinetic energy, for example, by a stone
thrown into the distance or a bullet fired from a rifle.
Radiation is, for example, flying electrons,
protons or neutrons, accelerated nuclei of atoms, flying ions or
whole atoms. And of course electromagnetic waves and their
quantum photons.
This radiative
energy transfer can be performed by two types of mechanisms :
- Time-varying field ,
which is propagating in the form of waves
*) which detach from the source and transfers into a
space part of energy from this source. Examples are
electromagnetic waves or gravitational waves. We are
talking about wave radiation.
*) From a physical point of view, this is primarily due
to the fact that the disturbance in the physical field
(electromagnetic or gravitational) propagates at a finite
speed, so that the field itself has energy
(and momentum). Furthermore, the equations of these
fields have a wave solution (for
physical-mathematical details, see "Maxwell's
equations").
Wave propagation
in material environments and especially in physical
fields is a general fundamental natural
phenomenon - it is analyzed in the introductory
part of §2.7 "Wave propagation - a general natural phenomenon" of the monograph "Gravity,
black holes and space - time physics".
- The moving
particles ,
which are emitted by the source, fly through space at
high speed and thus transfer kinetic energy
(as well as momentum and eventually
also electric charge) from the
source to the surrounding space. An example is radiation b (a stream
of fast-flying electrons) or a (a stream of helium
nuclei). This is corpuscular radiation.
Radiation can spread either :
- In vacuum
- free propagation of waves and free movement of
particles according to the law of inertia; or
- In a material environment
,
where part of the radiation can pass in
the original direction, but more or less part of the
radiation is scattered and absorbed
(with possible subsequent re-emission of part of the
radiation). The degree of scattering and absorption is
usually energetically dependent, as a
result of which the passage of radiation through the
substance not only attenuates the radiation, but often
also changes its spectral distribution
and cause the formation of additional secondary
radiation.
In terms of absorption in
substances, or, conversely, the ability to pass through
substances, a distinction is made between low -
penetrating radiation (a, b), which has a
range of only fractions of a millimeter to millimeters in
materials, and penetrating radiation (X,
g, neutron, muon, neutrino), able to pass through
a layer of substances with a thickness of many
centimeters, meters or more.
Transmission
of information by radiation
The transmission of energy by radiation, owing to its
structuring, is accompanied by the transmission of
information. Radiation carries information about its source
(its nature, composition, "strength", or variability,
etc.), as well as about the material environment
through which the radiation passes (density, thickness, chemical
composition of the substance environment). This information is
"coded" both in the intensity of the radiation
and in the energy spectral distribution. With
the help of detection and spectrometry,
radiation can help us uncover the secrets of the composition
of matter, the structure and the evolution of
the universe (especially stars and galaxies, as well as
global cosmological issues), in the biological field the anatomical
structure and physiological processes in living organisms
(§3.2 "X-ray diagnostics" and chapter 4 "Radioisotope
scintigraphy").
Energy
and effects of radiation
In addition to the type of radiation (the type of particles that
make up radiation), the energy of the radiation
quantum determines its properties of propagation and interaction
with matter. From this point of view, we distinguish :
l "Soft"
radiation ,
the quantum of which has a low energy (< approx. 5keV) and are
not able to eject electrons from atomic shells. They mainly show
mechanical and thermal effects on the substance, in some cases electrical
effects (external and internal photoeffect, changes in electrical
conductivity) and photochemical effects on more complex
or weakly bound molecules (classical photography, photosynthesis
in plants).
l "Hard"
radiation ,
the quantum of which has a sufficiently high energy (tens of keV
and higher) and when passing through a substance, electrons are
ejected from atoms and ionization of the
substance occurs. Ionization then leads not only to electrical
and photochemical effects, but in the case of compounds to a
number of chemical reactions of decomposition of
existing molecules and possibly formation of new compounds.
Energy carried by hard radiation, through the effects of
radiation on matter, can therefore be used in a number
of so-called radiation technologies; in the medical
field, the application of radiation helps to treat
certain diseases, especially tumorous (§3.6 "Radiotherapy").
Electronics
- optoelectronics - photonics
Some special scientific and technical fields deal with the
transmission of energy and information :
¨ Electronics
is a scientific and technical field dealing with the transmission
of energy and information through electrical signals
- especially electrons and the electromagnetic fields and waves
excited by them.
¨ Optoelectronics , also
called photonics, is a scientific and technical
field dealing with the transmission of energy and information
through photons, especially visible light. It
deals with photon sources, especially lasers and
light emitting diodes, light transmission
techniques (eg optical fibers), methods detection of
photons and their conversion into electrical signals
(photodiodes and phototransistors, CCD, photomultipliers) and
processing of these signals in electronic circuits, including
computer software. Emissions, interactions and detection of
photons take place at the quantum level, so there is
sometimes talk of quantum photonics.
Electronics and optoelectronics play a key
role also in the detection of ionizing radiation,
in electronic sources of ionizing radiation (X-rays tubes,
accelerators), as well as in the relevant measurement and control
technology.
Ionizing radiation
In the study of radioactive phenomena and particle interactions,
we have repeatedly recognized that various types of emitted
radiation here usually have a very high energy,
much greater than ordinary light. This high energy of quanta of
"radioactive" radiation, gamma, X-rays and some other
species, is an important property that determines the effects
of radiation on matter - it is ionizing
radiation :
| We call ionizing radiation such
radiation, the quantum of which has such a high energy
that they are able to eject electrons from the atomic
shell and thus ionize the substance . |
To ionize the material environment by pulling
an electron out of the atom, it is necessary to transfer to the
electron energy greater than its binding
energy in the atom - output work, ionization energy. For
the lightest hydrogen atom, whose electron is in the ground state
on the K shell, it is 13.6 eV. For more complex atoms with
the proton number Z, the binding energy of the electrons
on the K shell is Z2 -times greater than hydrogen. For lead (Z=82), the
ionization energy on the K-shell is about 85keV. For atoms with
more electrons, we have different values of ionization energies,
because electrons have different binding energies on different
shells. The value of the binding energy decreases rapidly with
the distance of the electron path from the nucleus - it is
inversely proportional to the square of the main quantum number,
which indicates the order of the electron path. The valence
electrons, which are furthest from the nucleus on the outer
shell, have the smallest binding energy.
For common types of photon (X and
g), electron
(b-) and alpha
radiation, the energy limit of ionizing radiation in practice (for example in radiation protection) is taken as 5 keV. The situation is
more complicated with neutron radiation, where even very
slow neutrons enter the nuclei and can cause secondary ionization
through nuclear reactions (even delayed or longer-term - activation
of nuclei, formation of radionuclides). Similarly, the ionization
threshold energy for b+ radiation is not
defined, where even very slow positrons annihilate with electrons
to form hard ionizing radiation g.
Terminological
note :
The names "nuclear radiation
" or "radioactive radiation"
are also sometimes used for ionizing radiation.
These names are not very appropriate and can be misleading.
"Nuclear radiation" includes only radiation a, b, g emanating
from the nucleus, but not braking and characteristic X-rays,
annihilation g- rays, nor radiation generated by accelerators and
particle interactions. The same is true of "radioactive
radiation", where the word "radioactive" may give
the impression that the quantum of this radiation is radioactive
- this is of course not true (except for neutron radiation (free neutrons are b- radioactive) and some
"exotic" species of radiation, such as muon or pion,
consisting of short-lived decaying particles; but this is not
meant here). The term "radioactive radiation" can only
be understood in the sense of "radiation generated by
radioactivity" and even then includes only certain types of
ionizing radiation. Commonly used name "radiation"
generally includes all types of radiation, not just ionizing
radiation.
Physics of
ionizing radiation - radiation physics - radiology - dosimetry
The physics of ionizing radiation is also known
as radiation physics or radiophysics. It covers
a wide range of issues :
¨ Mechanisms of radiation
formation
¨ Physical
properties of radiation
¨ Interaction of
radiation with matter (including radiobiological
effects)
¨ Detection and
spectrometry of radiation
¨ Mathematical
analysis and evaluation of results
A special area of radiation physics is radiological
physics, dealing with physical aspects of radiation in
medicine. Dosimetry of ionizing radiation is a
field of radiation physics, which deals with the effects of
radiation on substances in relation to the types and properties
of radiation - substance interaction and the amount of radiation
absorbed in the substance (absorbed energy - "dose") -
§5.1 "Effects of radiation on matter". The studied substance is mainly living
tissue, model measurements of doses and dose rates are
performed in water, air and special dosimetric phantoms.
Radiology
-
radiation in biology and medicine
From the etymological point of view, the word radiology
generally means the science of radiation. However, with
historical developments, its importance has narrowed and
specialized. Radiology is now a science of the
importance and use of radiation in medicine and biology,
a medical field that uses ionizing radiation for diagnosis and
therapy. It mainly includes three main special fields :
l X-ray
diagnostics , also called radiodiagnostics *) (§3.2
"X-ray diagnostics")
l Radiotherapy (§3.6
"Radiotherapy")
l Nuclear
medicine (Chapter 4 "Radioisotope
scintigraphy")
*) During the development, they
vere in the field of radiodiagnostics included some other
diagnostic imaging methods, that do not use
ionizing radiation - ultrasonic sonography (see Ultrasound sonography ), nuclear magnetic resonance (Nuclear magnetic resonance ) and thermography ( Thermography ).
Radiobiology deals with the biological
effects of ionizing radiation (see §5.2 "Biological effects of ionizing radiation") - a field on the border of radiation physics and
biology.
Types of ionizing
radiation
Directly
and indirectly ionizing radiation
Ionizing effects are therefore a common property of all types of
ionizing radiation. However, the specific mechanisms of
radiation-mass interaction are specific to each type of
radiation. In this respect, ionizing radiation is divided into
two groups :
- Radiation directly ionizing
- a radiation quanta which carry an electrical
charge and therefore directly
eject or pull electrons from the atoms by Coulombic
electrical forces. These include radiation a, b-
and b+, proton radiation p+ etc .
- Radiation indirectly ionizing
- its quants are not electrically charged; they first
transfer their kinetic energy in the matter to charged
particles (mostly electrons, sometimes to atomic nuclei)
and only these then ionize matter by direct effects on
atoms. This group includes mainly X-ray and g photon
radiation, further also neutron radiation.
In terms of physical, chemical and especially biological
effects of ionizing radiation on the irradiated
substance, especially on living tissue, the radiation is
sometimes divided according to the density of ionization,
which it causes in the substance during its passage :
¨ Sparsely
ionizing radiation - X, gamma, beta radiation. When
passed through water or tissue, it forms about 100 ion pairs /1
micrometer.
¨ Densely
ionizing radiation - alpha radiation, neutron radiation,
proton radiation. It creates up to 2000 ion pairs /1 micrometer
of tissue.
This circumstance is related to the
so-called linear energy transfer (introduced in
§5.1). X-rays, gamma and beta radiation have a relatively long
range in the substance (especially gamma radiation) and
therefore the ions formed are sparsely
distributed along the long path of the particle - low linear
energy transfer. If the radiation in the substance has a short
range (neutrons, protons, alpha radiation), the absorbed
energy is distributed along a short path - the linear energy
transfer is high and the ions formed are distributed very densely
along the path. For the purposes of radiobiology and radiation
protection (Chapter 5 "Biological effects of radiation.
Radiation protection"), a so-called quality factor Q
is introduced for each type of radiation, which
indicates how many times a given radiation is more biologically
effective than photon (X or gamma) radiation. For X, gamma and
beta radiation, the quality factor is Q = 1, for slow neutrons Q
= 2-3, for fast neutrons and for protons Q = 10, for alpha
radiation Q = 20. This issue is discussed in more detail in
Chapter 5 "Biological effects of ionizing radiation.
Radiation protection".
Wave and
corpuscular radiation
In the paragraph on corpuscular-wave dualism, we have
shown that waves can behave like a stream of particles, and
particles, on the other hand, have wave properties. But this does
not mean that the difference between particles and waves is
completely erased! There is one important criterion according to
which we can reliably know whether radiation has a wave or
corpuscular nature: it is the rest mass mo of quantum
of this radiation. The rest mass mo is the mass of the particle measured in the inertial
frame of reference in which the particle is at rest.
- Wave radiation - mo = 0: the
quanta of this radiation do not have a rest mass,
they are the quantum of waves moving at the speed of
light; if we brake them, they give up all their energy
and disappear. In nuclear physics, this
group includes only electromagnetic radiation
whose quantum is photons, in the general
theory of relativity and quantum gravity then gravitational
waves (for example, §2.7
"Gravitational waves"
in the book "Gravity, black holes and
space-time physics") whose quantum are hypothetical gravitons
(gravitational waves has
managed to detect only from the fusion of black holes and
neutron stars in distant universe; there
is no hope for experimental demonstration of gravitons in
the foreseeable future).
- Corpuscular radiation - mo >
0: quantum of this radiation has a non-zero rest
mass, it is a stream of mass particles
moving at a speed less than the speed of light, which
retain their existence even after stopping the movement.
These include radiation a, b-, b+, proton radiation p+, a stream of
deuterons and heavier nuclei ("ions", eg
carbon), neutron radiation no, neutrino radiation n and a number of
other types of radiation generated during high-energy
collisions of elementary particles (m- meson and p- meson
radiation, ...).
In addition to this basic division, specific
types of ionizing radiation are also considered, the names of
which are given by the type of particles or
quanta that make them up, or originated in a historical
context. For photon radiation, it is X
(X-ray) and gamma radiation - depending on the
energy of the photons and the mechanism of formation. Of the
corpuscular radiation, the alpha radiation
(current of fast helium nuclei) and beta
radiation ( b- -
electron radiation, b+ -
positron radiation). All this types of radiation are commonly
known.
Less common and "exotic"
types of radiation
In addition to the usual types of ionizing photon radiation (X, g) and corpuscular (a, b±) in nature and in artificial sources, can sometimes be
found with other less common or even "exotic" types of
radiation :
¨ Neutron
radiation , which occurs mainly during nuclear
reactions, in large quantities especially in nuclear reactors.
Its properties are discussed in more detail below in the section
"Neutron radiation and its interactions".
¨ Proton radiation is a
basic component of primary cosmic radiation in nature and is
artificially produced in accelerators. In addition to research in
particle physics, it is used for the production of artificial
radionuclides (together with accelerated deuterons; §1.4, part
"Production
of artificial radionuclides" and in the
so-called hadron radiotherapy (§3.6,
section "Hadron radiotherapy").
¨ Radiation
of heavier ions , formed by fast-flying nuclei
of heavier elements than helium. They are trace in
primary cosmic rays and are artificially produced on accelerators
for nuclear research, radionuclide production (including
transuranium) and for the purposes of hadron radiotherapy
(eg accelerated 12C carbon nuclei).
¨ Muon radiation (current
of fast muons m+ or m-) is an important component of secondary cosmic
radiation in nature, falling on the earth's surface. It arises in
a number of high-energy interactions of particles in nature and
on accelerators.
¨ Pion
radiation (current of fast pions p+ or p-, or p0) occurs on Earth in the upper layers of the atmosphere,
where it arises from interactions of high-energy primary cosmic
radiation. At large accelerators, pions are formed during nuclear
interactions of protons accelerated to high energies. In addition
to basic research in nuclear physics, it is experimentally tested
as an effective tool in hadron radiotherapy (§3.6, part "Hadron
radiotherapy", passage "Radiotherapy
of meson p- ").
¨ Antiproton radiation,
formed by a stream of fast antiprotons (antiparticles to
protons), arises during nuclear interactions of protons
accelerated to very high energies. In addition to basic research
in particle physics, its use for hadron radiotherapy is
being considered (§3.6, section "Hadron
radiotherapy", passage "Antiproton
radiotherapy").
¨ Neutrinos
radiation is, in terms of particle fluence, one of the
most abundant and most intense radiation in nature
- universe. However, its radiation significance is completely insignificant
(practically zero) and it is usually not even classified
as ionizing radiation. This is due to the extremely
small effective cross-section of the interaction of neutrinos
with the substance. The origin and properties of neutrinos are
discussed in detail in §1.2, section "Neutrinos -
"ghosts" between
particles".
Sources
of ionizing radiation
In §1.2-1.5 we have shown a number of phenomena in which
ionizing radiation is generated. Each object, device, material or
preparation which emits ionizing radiation is referred to as a source
of ionizing radiation or short radiator
or emitter. This radiators can be classified
according to several criteria. The division into natural
and artificial sources is not important to us
here (however, it is stated in §5.2,
passage "Sources of
irradiation by ionizing radiation"). According to the
principle and mechanism of radiation generation,
we can divide the emitters into :
- Electronic
radiation sources ,
in which the ionizing radiation is the result of
electromagnetic acceleration of charged particles. These
are mainly X-ray tubes producing braking
X-rays (§3.2 "X-ray diagnostics") and particle
accelerators (see section
"Charged particle
accelerators" in
§1.5). Accelerators produce either
primary radiation, ie beams of
accelerated particles (mostly protons or electrons), or secondary
radiation, arising from the interaction of the primary
beam with the target, or in the opposite colliding of
particles. Thus, virtually all types of radiation
(including "exotic") mentioned above can be generated. A special
category is electromagnetic synchrotron radiation
generated in electron accelerators ("Synchrotron radiation generators") and neutron
radiation generated in neutron generators ("Neutron generators"). Radiation
produced in accelerators, in addition to research in
nuclear and particle physics, is used for the production
of artificial radionuclides (§1.4
"Radionuclides"), in radiotherapy (§3.6 "Radiotherapy") and in a number of
analytical and technological methods.
Recently, laser sources have been
developed in which the emission of X-rays, g -rays and
particles is generated by a high concentration of energy
from short and very intense laser pulses impinging on a
suitable target.
Note:
Even a vacuum television or computer screen is a weak
source of soft X-rays; they are no longer used.
- Radioactive
sources ,
in which the ionizing radiation (a, b and g, resp.
neutron radiation) arises during the radioactive
nuclei transformations -
see §1.2, "Radioactivity". Radioactive
emitters are used, for example, in radiotherapy - cesium
or cobalt irradiators (§3.6, part
"Isocentric
radiotherapy" and
"Stereotactic
radiotherapy SBRT"-
"Leksell gamma-knife")
and brachytherapy emitters (§3.6, part "Brachyradiotherapy"), in nuclear
medicine - radiopharmaceuticals for diagnostics and
therapy (§4.8 "Radionuclides and
radiopharmaceuticals for scintigraphy"), in a number of
industrial applications (see
chapter 3 "Application of
Ionizing Radiation"). All of these types of radiation (and,
moreover, the proton radiation) also arise during
nuclear reactions, fission and nuclear fusion. A
massive radiation source are nuclear reactors (§1.3, section "Nuclear reactors").
- Radiation
of cosmic origin ,
which arises during stormy and high-energy processes in
universe - thermonuclear reactions inside stars,
explosions of supernovae, processes around black holes,
shock waves in ionized gas, etc. -
is discussed in more detail in the section "Cosmic radiation". The primary
cosmic radiation of high energies falls into the
Earth's atmosphere, where it interacts with air atoms to
form secondary cosmic radiation, which
also hits the Earth's surface.
- Electric
discharges in the atmosphere
Lightning
passes in an electrically conductive "channel"
of ionized gas - plasma, which is temporarily formed in
air (which is normally an electrical insulator) due to ionization
by the impact of electrically accelerated electrons
on air atoms. It is caused by a strong electric
field created by the uneven distribution of
electric charge between storm clouds and between the
ground. A lightning discharge transfers electrons between
different regions of the atmosphere, especially clouds,
or between clouds and the earth. The potential difference
in the electric field here can reach up to 100 million
volts! During a lightning discharge, cascades of
electrons form, which, after being ejected from
their atoms in a strong electric field by storm clouds, accelerate
almost to the speed of light. When these accelerated
electrons strike the air atoms, braking X and
gamma radiation are produced. Furthermore,
electron-positron pairs are formed, and by annihilation
of positrons, another g radiation.
These mechanisms produce short sporadic ossuring weak
flashes of radiation g.
Note:
As initiators of flash the secondary
cosmic ray showers can also may serve - it is mentioned
below "Secondary cosmic radiation", passage "Cosmic
radiation - "ignitors" of atmospheric lightning
?".
According to the energy of
emitted quantum radiation, we can divide sources of ionizing
radiation into two groups :
¨ Low-energy , producing particles or photons with energies of the
order of up to hundreds of keV. In radiological
jargon, they are also called "kilovoltage".
These include X-rays and most radiosotopes.
¨ High-energy , producing quantum radiation with energies of unit,
tens or hundreds of MeV, GeV,
up to TeV. In radiological jargon, they are also
called "megavoltages".
These are mainly high-energy accelerators,
occasionally some radioisotopes (such as 60Co).
According to the technical solution and constructional
arrangement, the sources of ionizing radiation,
especially radioactive emitters, are further divided into two
groups :
- Closed emitters ,
in which the self radiant substance hermetically
encapsulated in a non-radioactive package, so
that under normal circumstances the use of sources the
radioactive material can not escape into the environment
*) - no contamination can occur. When using closed
radionuclide emitters, only radiation passing through the
envelope is used, the radioactive substance itself does
not enter the application.
*) There is a formal clause in the
radiation protection literature, that the tightness of
the hermetic encapsulation must be "tested and
certified"...
From this
point of view, electronic radiation sources automatically
fall into the category of closed emitters. Without
reservations this is true for X-ray tubes. The situation
is more complicated with high-energy accelerators and
electronic neutron generators (§1.5, section "Charged particle
accelerators"),
where high kinetic energy particles or neutrons can
induce nuclear reactions and activate
objects in their vicinity - open emitters can be induced.
- Open sources ,
where it owns a radiated radioactive substance - a
preparation - is freely accessible for
manipulations (for portioning, pipetting, radiochemical
reactions, etc.). They are mainly radioactive solutions,
powders, or gases. An open emitter can be used as a
radiation source similar to a closed emitter. However,
the main use is the direct entry of the radioactive
substance into the application. They are primarily
manufactured and used in radiochemical
technologies. They can serve as radionuclide
"trackers" (radiondicators) to monitor the
spatial or temporal distribution of natural or
technological processes. In medical applications - nuclear
medicine - they are radiopharmaceuticals
applied to the internal environment of the organism. They
are used for radioisotope diagnostics (§4.8 "Radionuclides and
radiopharmaceuticals for scintigraphy") and biologically
targeted radionuclide therapy (§3.6, section "Radioisotope therapy").
When
handling open emitters, there is a possibility of
undesired release of radioactive substances into the
surrounding environment - the risk of radioactive
contamination of persons and the work area or
the environment (it is discussed in more detail in §5.5,
section "Radioactive
contamination").
Note:
In the literature on radiation protection we can find a
somewhat misleading simplistic laconic formal
"definition" of an open emitter: "An
open emitter is one that does not meet the conditions of
a closed emitter", which often means the
aforementioned leak tests and certifications. In our
physically focused treatise we will not consider these
formal aspects, for us the factual
closure or openness of the emitter is important, not
formal norms and regulations. We cannot easily take
samples from inside a well-encapsulated closed source
just because it does not have a "valid
certificate"..!..
Some other aspects of radiation sources from the point of
view of radiation protection are discussed in §5.4-5.6 .
Depending on their geometric shape,
radiation sources can be :
¨ Point sources - their size is much smaller than the distance at which
we examine the emitted radiation or where the irradiated object
is located.
¨ Line sources - the radioactive substance is filled in a thin tube or
contained in a thin wire (inside or applied
to the surface). Line sources can be made linear
(line-shaped) or can be bent into a curve of any shape.
¨ Planar sources - the radioactive substance is applied in a thin layer
on a substrate, usually in the shape of a rectangle or circle.
¨ Volumetric (spatial) sources - radioactive substance is distributed in the material
of a certain body, most often in the shape of a block, cylinder,
sphere, ...
The distribution of the radiator in
length, area or volume can be homogeneous or inhomogeneous.
Point, line and area homogeneous sources are often used as a standard
and calibration emitters for radiometric
instruments, including scintillation cameras (see eg "Phantoms and phantom measurements in nuclear
medicine").
Another more detailed division of sources of ionizing
radiation is according to the type of emitted radiation
(emitter a, b, g, X, neutron source, source of accelerated protons or
heavier ions), according to the application for
which the source is intended (industrial sources - eg
defectoscopic, medical irradiators, etc.), according to its
"strength" and thus the degree of radiation
risk in its use (small source, insignificant,
significant or very significant source), see Chapter 5 "Biological
effects of radiation. Radiation protection".
Physical
quantities characterizing ionizing radiation
Radiation energy
The basic physical quantity characterizing ionizing radiation is
the kinetic energy of its quanta (particles,
photons). The properties of radiation during the interaction with
substances - ionization, range, possible nuclear reactions,
formation of secondary radiation, significantly depend on the
energy of the emitted particles. The basic physical unit of
energy joule [J], generally used in all areas of
macroworld science, is impractically large for measuring the
kinetic energy of microparticles. The electron volt [eV] and its decimal multiples
[keV, MeV, GeV, TeV] are used here - see
§1.1 "Atoms and atomic nuclei", passage "Units
of energy, mass and charge in atomic and nuclear physics". The conversion
relationship is: 1 eV = 1.6.10-19 J.
Sources of ionizing radiation are usually
not completely monoenergetic (they do not
emit radiation of only one energy), but
emit quantum radiation of different energies. In such a
case, we characterize the radiation energy by
the energy spectrum, which indicates the
distribution (relative representation) of emitted particles or
quantum radiation according to their energy (it
is described in detail in Chapter 2 "Detection
and spectrometry of ionizing radiation"). It is expressed
graphically by plotting the energy in [keV or MeV] on the
horizontal axis and the relative number of quantum particles
having the corresponding energy on the vertical axis. The energy
spectrum can have two basic forms :
¨ Continuous spectrum ,
when a radionuclide or electronic source emits particles with all
energies in a certain interval (usually
from zero to a certain maximum energy),
while depending on the energy, their representation changes more
or less continuously. This is the case for beta
radioactivity (§1.2, section "Beta radioactivity",
fig.1.2.3 in the middle), for braking
radiation from an X-ray tube (§3.2
"X-rays - X-ray
diagnostics", Fg.3.2.1 in
the middle), for synchrotron radiation
from accelerators (§1.5, part "") or neutron stars (§4.2 "Final stages of
stellar evolution. Gravitational collapse", part "Neutron stars" in
monograph "The gravity, black holes and the physics of space-time"). Graph is a more or less
smooth continuous curve in some areas of energy
increasing, in others decreasing or zero.
¨ Line spectrum when the source emits
particles of only one or a few specific - discrete
- energy. This is the case with gamma radiation from
radionuclides (§1.2, part "Gamma radiation",
Fig.1.2.7) or with characteristic
X-rays from internal electron orbits of atoms (§3.2, part "Sources of X-rays - X-ray tubes", passage "Characteristic X-rays"). Also in conversion and Auger electrons
(§1.2, part "Internal
conversion of gamma and X-rays"). The line spectrum is formed by sharply expressed
discrete maxima - peaks - for precisely defined
energies; in areas outside the peaks, the values are zero (or in practice significantly lower than in peaks).
Note: In
the past (roughly until the 1960s), the spectrum of photon
radiation, especially X, was sometimes drawn using the wavelength
on the horizontal axis. This method is very unsuitable
and misleading, especially in relation to the mechanisms of the
origin this radiation, where decides the energies
of electron orbits and nuclear levels in [keV], or accelerating
voltage values in [kV]. Now wavelengths long since abandoned
here, radiation spectra are plotted fundamentally in energy
units [keV and MeV] (wavelength is
sometimes still used for soft X-radiation in X-ray
diffractometry).
Radiation
power - source emission, angular emission and radiation
characteristics
Another basic characteristic of each radiation source (not only
ionizing) is its "strength", intensity, radiance or
radiation power - the amount of radiation emitted by the source
per unit time. The quantity emission of
the source is introduced, defined as the number of
particles emitted from the source per unit time - the unit is
[number of quantums /second], abbreviated or dimensionally [s-1] *). For strong
sources, the radiant power of a source is
sometimes expressed in energy units of watts [W], as the total
energy of all quantum radiation emitted by the source per unit
time (1 second). Emitters for therapeutic use are also sometimes
characterized by dosimetric quantities of dose or kerm yield
[Gy.m2 .s-1], which is the dose
or kerm rate at a reference distance of 1 m from the center of
the emitter.
*) The number of particles or energy must
be understood as an average value, time-averaged
over statistical fluctuations radiation flow
from the source - is especially important for weak sources! For
radioactive sources, the emission is given by the activity
of the relevant radionuclide with appropriate coefficients (see below "Intensity
of radiation from radioactive sources"), indicating the number of
emitted particles per 1 radioactive decay, as well as corrections
for self-absorption in the source and in the source housing,
event. formation of secondary particles during various
interactions within the source.
In addition to
the total emission or radiation power of the source, the directional
distribution of the emitted radiation is also important.
Some sources, especially radionuclides, emit radiation almost isotropically
in all directions, others non-isotropically -
different radiation intensities are emitted in different
directions, they can also have a very narrow directional
radiation characteristic *). The quantity angular
emission of the source is introduced, which is the
emission related to the unit solid angle; the unit is [(number of
quantum / second) / 1steradian], dimension [s-1.Sr-1]. The angular
distribution of the radiation emitted by the source - the angular
emission of the source - is expressed by the directional
radiation characteristic, which is a diagram in polar or
spherical coordinates, expressing for each angle the
corresponding flux of emitted quantums from the source to this
direction (angle).
*) Most light sources radiate almost isotropically,
i.e. they have a spherical radiation diagram, eg small light
bulbs (except for the direction of the base), as well as many
stars in universe (if they are in equilibrium and do not rotate
quickly). Strongly non-isotropic is the emission
of lasers or semiconductor LEDs, in the universe of supernovae
and neutron stars, or accretion disks around rotating black holes
(quasars - see §4.8 "Astrophysical
significance of black holes" of
the book "Gravity, black holes and space-time physics",
passage "Accretion disks" - there is also in the lower
right part of Fig.4.28 an example of a strongly non-isotropic
angular radiation characteristic of a thick accretion disk around
a rotating black hole, where the radiation takes place in the
form of jets along the axis of rotation).
At ionizing radiation sources, radionuclide
sources emit isotropically (unless
their geometric configuration or encapsulation causes increased
radiation absorption in some directions). X-rays and generally
braking radiation, which occur when charged particles (electrons)
hit a target, have non-isotropic radiation. Very
narrow radiation characteristics - "pencil" beams - are
present for accelerator particles. Radiation is often
intentionally shaped or collimated into narrow
beams (see below the section "Radiation
beam definition - collimation"), eg on irradiators in radiotherapy (§3.6, section "Modulation
of IMRT, IGRT irradiation beams").
All quantities
characterizing the intensity of radiation sources depend on a
number of circumstances within the sources and are generally functions
of time. For electronic sources, the time dependence is
related to the switching on and off of the source and to the
electronic regulation of energy, power and
intensity. In the case of radioactive emitters, it is mainly an exponential
decrease in activity with time (§1.2,
section "General laws of
transformation of atomic nuclei",
Fig.1.2.1), depending on the half-life
of the relevant radionuclide.
Field and beam of radiation, intensity of
radiation
A quantum of radiation propagating
from a radiation source, creates a so-called field of
radiation (radiant field) in the surrounding space. If
the quantum of radiation in a given place in space moves mainly
in one particular direction, we speak of a beam of
radiation. In addition to the type and energy of
individual quanta of ionizing radiation, another fundamental
characteristic of a field or beam of radiation is the intensity
(strength) of this radiation, which also determines the degree of
effects of radiation on matter at a given location. The intensity
of radiation is quantified by a quantity called fluence
(from Latin fluentum = current, flux). Depending on the physical and application context,
the intensity of radiation (its flow -
fluence) quantifies in principle
in two ways :
- Particle fluence
(particle flow or particle flux density) F is
defined as the number of quantum
radiation passing in 1 second per unit area located at a
given location perpendicular to the direction of quantum
propagation. It is expressed as [(number of particles/s)
/m2].
Note:
This simplified wording applies to a wide parallel beam.
In the general case of radiation propagating in different
directions, the particle flux is defined as the number of
quanta passing per 1 sec. a sphere with
a unit area of the main cross-section centered on a given
point. This definition is independent of the direction of
radiation, it includes all directions.
- Energy fluence (energy flow or energy flow density) W
is defined analogously, but instead of the number of
quanta, their energy is taken. The unit
is [W/m2].
In the general case, the
radiation field is fully described if at each of its points (r, J, j) the energy E
and the number of quanta of radiation N propagating in the
direction (J, j) are known in polar coordinates - energy and angular distribution
of radiation intensity I(E, J, j). However, full knowledge
of this distribution is not necessary in practice (it would be
very difficult to measure it). By integrating the distribution
function over all directions (over all values of angles J, j from 0 to 2p, ie over the full
spatial angle 4p) we obtain a spherical distribution I(E) = 0n2p0n2p I(E,r,J,j) dJdj, expressing the total flow of
particles (or energy flow) passing per 1 second of spheres with a
unit main section in any direction - the fluence.
When using
ionizing radiation, there is usually a typical radiation
situation: we have a certain source of radiation that emits
radiation into its surroundings (creates a radiation field) and
this radiation acts on the substance present, which can be also
living tissue. For some applications of radiation, especially in
radiotherapy (§3.6 "Radiotherapy")
and in radiation protection (§5.1 "Effects of
radiation on matter. Basic quantities of dosimetry."), the radiation field is also quantified using dosimetric
quantities - distribution of the radiation dose
or dose rate in a given irradiated substance, most often
in water or tissue. In practice, the radiation beam is never
homogeneous, so the spatial distribution of radiation intensity
and radiation dose is usually complex course (the highest dose is in the central part of the beam,
decreases towards the edges). The spatial
distribution of the radiation dose is often mapped using
so-called isodose curves - imaginary lines
representing the connections of points with the
same dose. Usually, isodose curves are plotted for certain
percentages from the site with the maximum dose, eg isodose 80%,
50%, 20% and the like (it is reminiscent of
the contours on the map).
Geometric shape of
radiation beams
The spatial distribution of
radiation intensity - the geometric "shape" of the beam
- depends on a number of circumstances of emission and
propagation of radiation quanta in a vacuum or in the material
environment. Under normal circumstances, the radiation beam
generally has a diverging shape *). The primary
cause of this divergence is the different directions of
the velocity vectors with which the individual quantums
of radiation fly from their source to the surrounding spatial
angle. In the vicinity of the source, the divergence of the beam
of radiation is large, decreases with distance, and at great
distances, the radiation eventually becomes practically parallel.
In the case of copuscular charged radiation (alpha, beta,
proton), the mutual electrical repulsion of
consistently charged particles also contributes to the divergence
of the beam. During the passage of radiation through the
matter, the scattering of radiation
quanta on the atoms of matter (in the case
of photon radiation it is Compton scattering) significantly contributes to the divergence and
"blurring" of the beam shape.
*) A certain exception is the parallel
light beams emitted by lasers and the secondary
radiation generated in the target by the impact of high-energy
(ultrarelativistic) particles, which is narrowly directed due to relativistic-kinematic
effects.
For many applications, parallel
or converging (convergent, focused) shape of the
radiation beam is required. In the optical field, this can be
achieved relatively easily by passing light through contact
lenses or by reflecting it from hollow mirrors. Unfortunately, no
refractive or reflective optics work for ionizing radiation. The
desired shape of the radiation beam can (to a limited extent)
only ba achieved by collimation (see "Delimitation
of a radiation beam - collimation'), but at the cost of a large loss
of intensity of the initial radiation.
Intensity of radiation from radioactive
sources
Frequent sources of ionizing radiation in practice are radioactive
emitters (§1.2 "Radioactivity"). The radioactive source emits its radiation isotropically
in all directions, to the full solid angle 4p. With the distance r
from the source, the radiation "dilutes", it is
distributed on an imaginary sphere with an area S = 4p r2. The intensity
of radiation I (fluence of particle-quanta
/s / m2)
emitted from a radioactive source such, is therefore directly
proportional to the activity A in preparation, and
inversely proportional to the square of the distance r
from the source to the measuring point (this
is exactly true for a point emitter in vacuum, approximately in
situations where the distance is significantly greater than the
dimensions of the source) :
I
= G. A / 4p r 2 .

The coefficient G indicates the number of quanta emitted
by the radionuclide in one radioactive conversion. In the
simplest case, G = 1; if only part of the decays lead to excited
nuclear levels (and another part to the
non-radiative ground state of the daughter nucleus), G <1. In the case of cascade deexcitation, G> 1;
similarly for positron b+ radionuclide
preparations G » 2 (simultaneous emission of two
annihilation photons g). To determine the energy
fluence and the radiation dose, the mean energy of
the emitted quanta would be further multiplied (more detailed is derived in §5.1., passage "Radiation dose from radioactivity").
In practice, to determine the
intensity of radiation from radionuclide sources, it is necessary
to take into account the effects of radiation absorption
in the source itself or its envelope, as well as in the environment
between the source and the measured site - the resulting
intensity will be lower : I = G . A/4pr2
. e-m.r , where m is the linear absorption coefficient of the material
medium.
Most often, the radiation intensity is
quantified for photons of gamma radiation, or X-rays. For
radiation a and b, it is problematic to use this relationship, because a
significant part of such radiation is already absorbed in the
source itself and another significant absorption occurs in the
air or other environment lying between the source and the
measured place.
Radiation beam delimitation - collimation
In the vast majority of processes of ionizing radiation, this
radiation is emitted almost isotropically in all
directions *).
*) The exceptions are the interactions of high-energy
particles, where due to the relativistic laws of conservation of
momentum, the emerging secondary particles and radiation are
kinematically directed (collimated) in the
direction of movement of primary high-energy particles.
However, we often need to
direct the radiation (collimate) to a certain angle, or
to concentrate it to a certain place; radiation
in other directions can be undesirable - disruptive or even
harmful and dangerous.
¨ Electromagnetic collimation of
charged particles
In the case of corpuscular radiation of charged particles,
suitable direction - collimation - can be achieved by the action
of electric and magnetic fields, which exert a force on the
charged particles. This deflects the direction of the beam, which
can be directed to the desired location.
¨ Mechanical
absorption collimation of radiation
However, a simpler way, which works both for charged
particles and for g and X radiation, is to use collimators. A collimator
is a mechanical and geometric arrangement of materials absorbing
a given type of radiation, which transmits
radiation only from certain desired directions
(angles), while radiation from other directions absorbs and does not
transmit **).
**) However, such absolutely sharp
collimations cannot always be achieved in practice. For
high-energy penetrating radiation g, partial shine
trough occurs at the peripheral edges of the collimator,
which creates a kind of "half-shadow" in the edge parts
of the collimated beam - a "penumbra".
Collimators are used in virtually all
applications of ionizing radiation. Most of them are simple
collimators in the shape of various tubes or
apertures (as shown, for example, in Fig.2.8.1). Intricately
configured collimators then play a key role, for example, in scintigraphy
(imaging collimators with a large number of holes - §4.2
"Scintillation cameras", section "Collimators"),
in X-ray diagnostics (Bucky-Potter or Lysholm filter - §3.2 "X-ray diagnostics") and in radiotherapy (mainly
multileaf MLC collimators - §3.6 "Radiotherapy",
passage "Modulation of
radiation beams").
Reflective mirror optics work for soft X-rays under certain
circumstances, but only for very small angles of
incidence-reflection - see the appendix "X-ray telescopes" at the
end of §3.2.
Some detection and imaging methods use so-called electronic
collimation of radiation (see eg "PET cameras" or "Compton cameras").
However, this is not a matter of delimitation the beam of
radiation - all the radiation falls into the detector, from which
a certain part is selected only for the purposes
of detection and display on the basis of coincidence detection
and electronic directional reconstruction of particle paths.
Interaction
of ionizing radiation during passage through matter
Under normal natural and laboratory conditions, matter
(substance) is composed of atoms, which are
eventually bound in molecules and can form crystalline
or amorphous structures of solid, liquid or gaseous
state (we do not consider
"exotic" forms of the substance, such as ionized plasma). The interaction of radiation with matter therefore
takes place primarily at the atomic level, or at
higher energies at the nuclear and particle
levels.
Collective and
individual interactions with atoms
Macroscopic bodies when moving in a material environment
(eg a stone thrown into water) interact simultaneously, collectively,
with many billions of atoms and molecules. Similarly, electromagnetic
radiation of longer wavelengths - radio waves, light:
collective electromagnetic interaction with a large number of
atoms leads to the known laws of optics -
reflection, refraction, bending. However, high-energy
quanta of ionizing radiation have such a short
(effective) wavelength that they interact separately with
individual atoms of matter, with electrons, or atomic
nuclei and elementary particles. Therefore, the interaction of
ionizing radiation with matter is fundamentally different from
conventional "soft" radiation such as light.
Before we
begin to describe the ways of interaction of specific types of
radiation with substances of different composition, we will
mention some general mechanisms applies to the
passage of radiation through matter. Above all, in all types of
radiation we encounter cases of radiation passing without
interaction, where the quantum of radiation can freely
pass between the atoms of matter; this case occurs more often for
hard radiation passing through a substance with a lower density.
When different types of ionizing
radiation pass through a substance, quantum radiation generally
interacts with envelope electrons and atomic nuclei. In
principle, all three interactions that are relevant here can
apply - strong, weak and electromagnetic interaction :
- Strong interactions
can evoke scattering caused by nuclear forces, nuclear
reactions, and at high energies also interactions of
elementary particles to form new particles and
antiparticles, such as electrons and positrons, p and K
mesons, hyperons, and combinations thereof.
- Weak interactions
manifest themselves only exceptionally and marginally
during the passage of common types of ionizing radiation
through a substance. They are important for neutron
radiation (due to their beta radioactivity), neutrino
radiation (interaction of neutrinos with nucleons - see
the description of neutrino experiments in §1.2, section
"Neutrinos
- "ghosts"
between particles")
and high-energy cosmic radiation or from accelerators,
where mesons p and K , hyperons and other particles
decaying due to weak interaction.
- Electromagnetic interactions
with charged particles cause Coulomb scattering,
ionization and excitation processes of atoms and nuclei,
radiation processes such as braking radiation and
Cherenkov radiation. For the quantum of gamma radiation,
electromagnetic interactions cause a photoeffect, Compton
scattering, the formation of electron-positron pairs and
their annihilation, photonuclear reactions (see below "Interactions of gamma and X-rays"). It is
characteristic for all these types of processes, that the
interaction of electric charges with the electromagnetic
field in which the charges are located, produces a
quantum of radiation - photons,
depending on their energy and origin, mostly X-ray or
gamma-ray photons. Electromagnetic interactions are the
most common and important processes in the passage of
most types of radiation in practice. They are also most
often used in the detection of ionizing
radiation.
All these interactions and
processes lead to the loss of energy of these
particles during the passage of quantum ionizing radiation
through the substance, their braking and finally
to stopping (if the substance environment is
large enough) - the radiation has a limited range
or outreach in the substance *). Along the path
of their flight, the quantum of radiation leaves an ionization
trace of free negative electrons and positive ions. Some
of these ions and electrons recombine with each
other again, but some of them can cause new chemical
bonds and reactions in the surrounding substance (unless
the substance is an element composed of the same type of atoms),
especially when it is a more complex organic substance. The use
of ionizing effects of radiation for its detection and
spectrometry is discussed in more detail in Chapter 2 "Detection and spectrometry of ionizing radiation", the chemical effects of ionizing radiation on
substances and especially on living tissue in Chapter 5 "Biological effects of ionizing radiation".
*) Range of radiation in matter
Because the individual processes of interaction and collisions of
radiation quanta with atoms of matter have a random character,
the range of radiation particles is not always the same - it is
around a certain mean value called the mean range Rs .
Sometimes the value of the maximum range Rmax is
given. The range of radiation in a substance is often also
described by the effective range R90 ,
which is the distance at which 90% of the original emitted energy
of the particles is absorbed (or the radius of the spherical
space of the substance around the point source at which 90% of
the energy emitted by the source is absorbed).
What happens
to a quantum or particle of radiation after they are braked and
absorbed in matter - what is their ultimate "fate" ? It
depends on the type of radiation :
- In
the case of photon radiation (X,g), the photons
transfer all their energy to the particles of matter, mostly
electrons, and themselves disappear during the photo effect.
-
Electron b- is
gradually braked by collisions with the electrons of the atomic
shells of the substance, then it almost stops (performs only
thermal oscillations) - the substance is "enriched" by
one electron, which remains either free or binds in an atom.
- The positron b+ is also braked by collisions with envelope electrons,
but after stoping it does not remain in the substance - it
annihilates with the electron to form two opposing photons g (and those from
the substance either fly out, or are absorbed).
- The proton
p+, after
its braking, "captures" the electron and the substance
is enriched by one hydrogen atom.
- Neutron
n0 has two
possibilities: Either it is absorbed by some nucleus and causes a
nuclear reaction - in the substance the relevant atom is then
transmutated to another isotope; or the core may cleave into
other elements. If a slow neutron remains in matter for longer,
it spontaneously transforms into a proton, an electron, and an
(anti)neutrino.
- Particles a after braking
"captures" two electrons and the substance is enriched
in one helium atom.
More complex situations occur at high
energies of quantum and radiation particles, where nuclear
reactions and the formation of new particles
can occur. All the various processes are discussed below.
Thermal
and electrical effects of radiation
Another phenomenon little known in common applications
accompanies all interactions of radiation with matter: it is heat.
During the absorption of radiation, part of the energy is
transferred to the substance at the level of the kinetic
energy of the atoms. And the kinetic energy of the
motion of the atoms of matter is nothing but heat. With each
subsequent interaction, the atoms of the substance will oscillate
to greater and greater kinetic energy - the irradiated
substance will heat up. At low radiation fluxes, this
phenomenon is unobservably weak, but during intense irradiation
the substance "warms up" quite clearly - for example,
targets in accelerators must often be cooled.
If the substance is irradiated with quantum carrying electric
charges (radiation a, b-, +, protons), or secondary charged particles fly out of
the substance, the substance will be to charged
electrically. This phenomenon would be observable only
in a vacuum; in the air, ionizing radiation releases free charge
carriers (electrons, ions), which dissipate and neutralize the
charge of the irradiated body.
Effective
cross-section of the interaction of radiation with matter
In §1.6 "Elementary particles" the concept of the
so-called effective cross-section of the
interaction was introduced , which expresses the probability of
particle interactions in a clear geometric way. Even in the study
of the interactions of radiation with a substance, it is possible
to apply the illustrative idea, that each atom of the irradiated
substance behaves as an "absorbing body" of radius r,
which the incident particle either hits and the given interaction
occurs, or does not hit them (passes them, flies around) and the
interaction does not occur. The larger the radius of this body,
resp. its effective area s = p.r2 - effective cross section, the greater
the probability of interaction (probability that the particle
"hits").
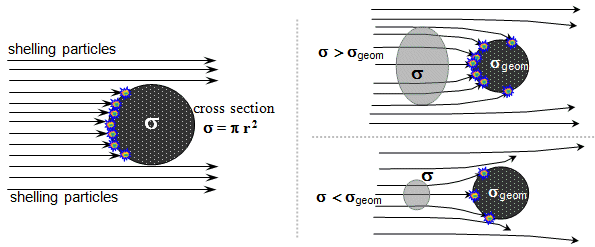
Expression of the probability of interaction of radiation quanta
(firing particles) with a target particle (atom) using an
effective cross section
The cross section may, but need
not be, directly related to the "geometric mean" atoms
rgeom , or
their "geometrical cross section" sgeom = p .r2geom . For "effectively interacting" particles it
is s > sgeom , for weakly
interacting particles is s
< sgeom
. In addition, the same firing particle can cause different
interactions on the same atom, the different probabilities of
which are described by different effective cross sections. These
effective cross sections no longer have anything to do with the
geometric dimensions of atoms - they are the result of the
internal mechanisms of specific types of interactions.
The unit of effective cross section
in the SI system would be m2, which is, however, inadequately large, and therefore
the unit barn (bn) is used in nuclear physics :
1 bn = 10-28 m2, which has the order of magnitude of the geometric
cross section of atomic nuclei.
Note: The slang name "barn"
originated in the early nuclear technology in the 1940s from the
humorous comparison that neutrons hits "nuclei as big as
a barn" - uranium 235 nuclei.
The effective cross section of the interaction
is very closely related to the absorption coefficient, the
so-called linear attenuation coefficient m, in the
exponential law of absorption of ionizing radiation in
substances. This connection will be clarified below in the
section "Absorption of radiation in substances".
Multiple
interactions - cascades of interactions and sprays of particles
When the interaction of high-energy radiation in a sufficiently
voluminous medium environment, the effect of multiple
interactions occurs. The secondary particles released
during the first interaction of the incident primary particle
cause further interactions, producing additional
(tertiary) particles that do the same. From one incident
particle, a whole spray of secondary particles
is formed in a cascade of interactions. As the evolving spray
penetrates to the depth of the material, the number of secondary
particles increases and their average energy decreases. Once this
energy falls below a certain threshold, the multiplication
process will stop and the energy of the particles will be
dissipated by ionization and excitation; the number of particles
in the spray will decrease until the spray finally disappears. In
practice, we distinguish two types of cascade interactions :
¨ Electromagnetic
sprays
arising from the interaction of high-energy photons or electrons
with atoms of matter. Secondary electrons and photons emitted
during the primary interaction, due to paired e- e+ production, Compton
scattering, photoeffect and braking radiation, produce additional
electrons (+ positrons) and photons; etc. ...
¨ Hadron sprays
arising from inelastic interactions of high-energy hadrons with
atomic nuclei of the material. Nuclear fragments are formed and
new secondary particles are produced - p, n, p, K. The number of
these secondary particles is approximately proportional to the
logarithm of the energy n ~ ln E.
In many cases in practice, this spray is not
purely hadron or electromagnetic, but mixed. The
hadron spray includes pions that immediately
disintegrate: p+,-®m+,-+nm , po®g+g; this leads to
the formation of an electromagnetic electron-photon-muon
spray that accompanies the hadron cascade. Thus, each
hadron shower also has an electromagnetic component. And with the
interaction of high-energy photon or electron radiation, photonuclear
reactions emit protons and neutrons, which can enrich the
electromagnetic spray with a hadron component.
Cascades of interactions and sprays of secondary particles are
observed in cosmic rays (Fig.1.6.7) and in particle interactions on
accelerators (in bubble chambers, trackers and calorimeters).
Secondary radiation generated by radiation
interactions with matter
Any object that is irradiated with (primary) radiation generally
becomes a source of weaker secondary radiation. During the
interaction of ionizing radiation with matter, processes occurs
in which secondary radiation of various kinds is
generated :
¨ Braking
radiation (bremsstrahlung) generated during the movement of mainly electrons and
positrons in matter
¨ Compton-scattered g-radiation
or X-radiation
¨ Diffracted neutrons
¨ Photoelectrons released
from the atomic packaging due to the photoeffect of primary
radiation
¨ Characteristic X-rays
following after the photoeffect of primary radiation
¨ Auger electrons
generated by internal conversion of characteristic X-rays
¨ Electron
and positron radiation arising from primary high-energy
radiation in the formation of electron-positron pairs
¨ Annihilation g -radiation
of 511keV energy, arising by annihilation of positrons formed by
electron-positron pairs
¨ Protons and neutrons
generated by nuclear interactions of primary radiation
¨ Mesons p and K, muons, or
hyperons, formed by particle interactions of high-energy quanta
of primary radiation
¨ Light radiation
generated by deexcitation of electrons on the outer shells of the
atomic envelope, during Cherenkov's radiation of
secondary electrons, or during deexcitation in the luminescent
centers of certain substances (scintillators).
Photoelectrons, Auger electrons and
electron-positron pairs are mostly absorbed in the substance,
only a very small part of them can fly out of the layers at the
surface of the irradiated substance. However, Compton-scattered g -radiation,
characteristic X-rays, braking radiation, and annihilation g- rays can easily fly
out of the irradiated substance and thus enrich the original
radiation field. Similarly, neutrons produced by scattering or
nuclear reactions. The mechanisms of secondary radiation creation
will be discussed in more detail below.
Albedo
The name albedo is sometimes used for the amount
of secondary radiation emitted by the irradiated body (lat. albus = white; albedo = whiteness). In natural sciences, the term albedo
generally means light reflectance diffusely reflecting
matte surface and is quantified as the ratio of the intensity of
the reflected light to the incident light; it is usually
expressed in %. It depends on the frequency, or wavelength or
energy, ie on the spectrum of the considered radiation and also
on the angle of incidence of the radiation. Albedo is often used
in astronomy, where the light reflectance of planets or asteroids
irradiated by sunlight suggests the composition of their surface,
such as the proportion of ice. The average albedo of the planet
Earth is about 30%, for the Moon it reaches only 12%. Here on
Earth, fresh snow has an albedo of about 90%, a grass area of
15-25%, a coniferous forest of about 10%, the water surface of
the sea only about 4% (light easily penetrates into the water and
is absorbed in depth). Of the chemicals, high albedo 96-98% has
magnesium oxide and barium sulphate, and very low (less than 1%)
amorphous carbon.
Albedo can be determined not only for light,
but for any electromagnetic radiation, and also for other types
of radiation (ionizing, corpuscular). In the case of ionizing
radiation, however, it is not reflected radiation, but secondary
radiation caused by scattering and other interactions of quantum
primary radiation with atoms of matter - with electrons in the
envelope or with atomic nuclei. For X and g radiation, the albedo of
common substances (such as water or living tissue) is very low,
below 1%. Is caused mainly by Compton scattering, partly also by
X-ray fluorescence radiation. Higher albedo, up to 40%, may be at
neutrons.
Interaction
of charged particles - directly ionizing radiation
First we will deal directly ionizing radiation, wherein the first
mention common features of the interaction of this radiation at
it passes through the substance, then we analyze the specific
features of the interaction of radiation a, b+, - and
proton radiation.
Excitation
and ionization
The charged particle, as it passes through the substance, loses
its kinetic energy mainly by electrical Coulomb interaction with
electrons in the atoms of the substance. If the energy
transferred to an electron in the atomic shell is relatively
small and is only enough to "raise" the electron to a
higher energy level, it is a process of excitation
of atoms. The excited state of the atom is not stable - the
electron immediately jumps back to the original level - dexcitation
occurs, and the energy difference is radiated in the form of a photon
of electromagnetic radiation. During the excitation of electrons
on the outer shells, visible light is emitted, on medium shells
UV radiation, during excitation on the inner shells, then photons
of characteristic X-rays (with spectral
lines Ka,b).
If an electron receives enough
energy to be completely released from its bond to the parent
atom, it moves away from it permanently - the atom is
ionized, divided into a negative electron and a positive
ion. By primary ionization is meant the number
of ion pairs formed by the ejection of electrons by the primary
particle. Some electrons punched out during ionization have so
much energy that they can ionize further along their path - this
is a secondary ionization (such
electrons were formerly called delta
rays because their trace in a nuclear emulsion or nebula chamber
has a characteristic branched shape).
Linear energy transfer LET
During ionization and excitation, a fast charged particle loses
its kinetic energy by imparting momentum to electrons by the
action of electric Coulomb forces. The magnitude of the momentum
transmitted to the electrons is proportional to the magnitude of
the Coulomb forces and the time for which these forces act
(interaction time). Coulomb forces are proportional to the charge
of the particle q and the electron density of the
substance. The interaction time is inversely proportional to the
velocity of the particle v, so that the energy transferred
to the electrons is proportional to 1/v2. The amount of energy loss per unit path of a particle
- linear energy transfer LET *) - is therefore
directly proportional to the electron density of the substance
(this is given by the density r
and the proton number Z) and
inversely proportional to the square of the particle velocity: -
dE/dx ~ q.r.Z/v2 (the exact value is given by the
so-called Bethe-Bloch formula below, which also includes
the mean excitation potential of the atoms of the substance,
approximately proportional to the proton number Z).
*) Linear Energy Transfer (LET) expresses the amount
of energy transferred by an ionizing particle per unit length of
its path to a given environment. In practice, it is usually
expressed in [keV/mm] or [MeV/cm]. For alpha particles with energies of
4-8MeV, LET in water is about 100keV/micrometer, at the end of
the path in the Bragg maximum it can increase locally up to
300keV/mm.
For beta-particles with typical energies of hundreds of keV, LET
is only about 0.2 keV/micrometer.
Energy transfer
charged particles by interaction with electrons
Dissipation (or "braking power") of the -dE/dx charged
particles when passing through the substance is given by the
co-called Bethe-Bloch formula (whose simpler variant derived N.Bohr (1913) - in the
lower part of the formula in frame, complete more accurated
variant then H.Bethe and F.Bloch (1930-33) - the upper part of
the formula) :
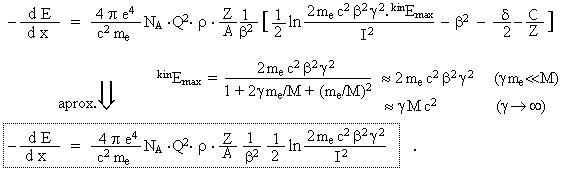
This is here a primary particle with charge Q and mass M
(M >> me ), flying at instantaneous velocity v
[relativistic designation b=v/c, g=1/Ö(1-v2/c2)] trough material medium of density r, whose atoms have
a proton number Z and a mass number A , I is
the mean excitation (ionization) energy of the atoms of the
substance [eV]. N A = 6,022.1023 is the Avogadro's constant, me is the rest mass of the electron, e is the
elementary charge of the electron. kinEmax is the maximum value of energy that can be
kinematically transferred from the flying primary particle (mass
M) to the free electron (mass me) in one collision. Parameter d(b) is the density
correction caused by polarization (applied at high energies), C/Z
is the correction for slow particles with velocities comparable
to the velocity of bound electrons. The mean excitation
(ionization) energy I is approximately proportional to the
proton number: I = 10[eV].Z; for lighter atoms (Z <20) the
empirical dependence I = 10[eV].Z0,9 was measured.
The energy of the secondary
electrons ejected from the atoms of matter during the
passage of the heavy charged particle, was derived in an
analogous manner to the energy return of the primary charged
particle according to the Bethe-Bloch formula. The number of
these secondary electrons is the proportional Q2/b2 and their energy distribution (spectrum) is :
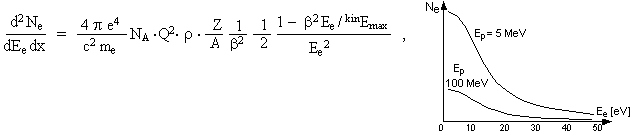
where d2
Ne is the number of kinetic energy electrons Ee (Ee >> I) in the
energy interval dE e released on the path d x . The curves to the
right of the formula show the approximate energy spectrum
of secondary electrons released during the passage of protons
with an energy of the order of hundreds of MeV and units of MeV
through water (roughly corresponds to the
situation around the site of the Bragg maximum). The average energy of secondary electrons increases
with the energy of primary charged particles, but for proton
radiation of units up to hundreds of MeV it is generally very
low (during their rapid flight
through the atomic envelope, the protons are enough to transfer
only a small amount of energy to the electrons) - in the order of tens of eV. However, the number
of secondary electrons increases significantly at low proton
energies, leading to the existence of a Bragg maximum,
as discussed below.
Depth dependence of
ionization - Bragg curves
Specific or linear ionization is the number of
ion pairs formed per unit length of the path of the interacting
particle. In Fig.1.6.1 at the bottom right are the so-called Bragg
curves of the dependence of specific ionization on the
depth of penetration of a charged particle into matter. As the
particle slows down and decreases in velocity,
the ionizing effects increase - slower motion
leads to a longer time of action of the Coulomb
interaction, which is enough to transfer more energy and pull out
more electrons; the transmitted energy is inversely proportional
to the square of the particle velocity. Just before full braking
- stopping the heavy charged particle,
the greatest energy is transferred - the curve of the depth
dependence of the specific ionization has a significant so-called
Bragg maximum. After stopping, further
ionization does not continue; if the particle has been positively
charged, it is neutralized by trapping electrons to form neutral
atoms. The possibilities of using this
depth dependence of ionization in the so-called hadron
radiotherapy are discussed in §3.6
"Radiotherapy", part "Hadron radiotherapy".
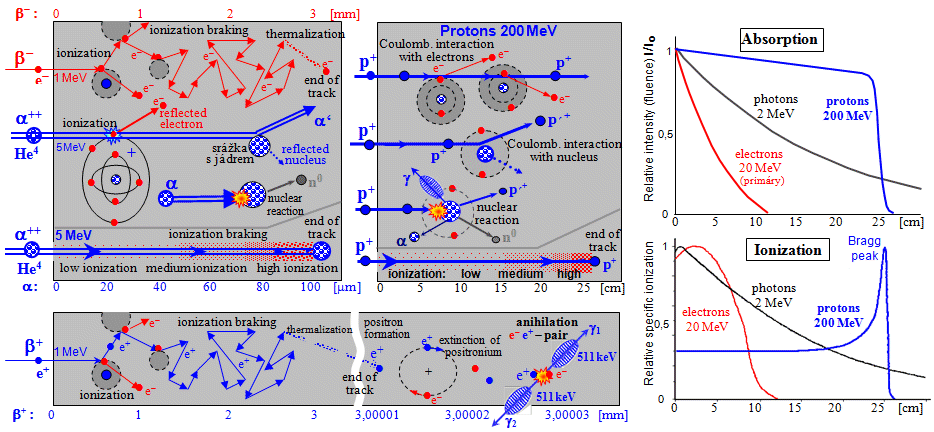 |
Fig.1.6.1. Interaction
of fast charged particles with matter.
Top left: Schematic
representation of ionization mechanisms in the passage of
beta- and alpha particles .
Top middle: Three basic
mechanisms of proton radiation interaction with matter.
Bottom: Interaction of positron
beta+ radiation with a substance ending in
annihilation of a positron with an electron.
Right: Bragg curves of depth
dependence of absorption and specific ionization along
the path of gamma photons, accelerated electrons and
protons. |
The ionizing and excitatory effects of
high-energy radiation described above are the most important
effects we encounter when ionizing radiation passes through
matter. We will also mention here some accompanying
phenomena (which, however, can
play an important role in certain situations), in which secondary radiation is
usually emitted :
Scattering
When particles interact with atoms and atomic nuclei, they are
subjected to electric and nuclear forces, which can change
the direction of movement of particles - causing them to
scatter. Scattering is mainly applied to light
particles (electrons) and lower kinetic energies. During the
passage of charged particles through the material environment,
the interaction with the electric Coulomb field of atoms and
their nuclei manifests itself. In terms of energy balance, the
scattering is divided into two categories :
- Elastic scattering
If the kinetic energy does not change into another type
of energy during scattering, it is elastic
scattering. Elastic scattering occurs mainly at lower
energies, below the threshold of more complex
processes such as excitation, ionization, formation of
other particles. In the case of elastic scattering, the
law of conservation of energy and momentum of the
arriving particle and scattering center (atom or nucleus)
is fulfilled. The particle continues to move in a
generally different direction and with lower energy and
momentum, part of which has been transmitted to the
scattering body.
With the simplest
case of scattering of charged particles on a single
scattering center - the atomic nucleus - dealt
E.Rutheford in 1911 during his famous experiments with
scattering a particles (see Fig.1.1.4 in §1.1. "The
atoms and atomic nuclei", part "Atom
structure"), in
which the atomic nucleus was discovered. In this simple
case, an electric force acts according to Coulomb's law
and it is a motion in a central-symmetric field, for
which Kepler's laws apply similarly to the motion of
planets in the solar system (see eg §1.2 "Newton's
law of gravitation",
relations (1.1) - (1.18c) in the book "Gravity,
Black Holes and the Physics of
Spacetime") with the difference that in the case of
charges of the same name it is a repulsive force and the
trajectory of the particle is a hyperbola. Based on these
laws, Rutheford derived his known relation for the
angular distribution of scattered particles.
- Inelastic
scattering
If the kinetic energy of a particle is converted to other
types of energy in processes other than mechanical motion
(eg emission of radiation quanta, changes in the internal
structure - excitation, deexcitation), it is inelastic
scattering. Inelastic scattering occurs at
energies higher than the excitation or ionization
energies of atoms or atomic nuclei and is accompanied by excitation
or ionization of atoms (an example of multiple ionization for
beta-radiation is shown in the upper left of Fig.1.6.1), or excitation of the atomic nucleus. At high
energies tens and hundreds of MeV may be accompanied by nuclear
reactions - see §1.3 "Nuclear reactions", at very high energies as well production
of new particles and antiparticles (muons, mesons p and K,
baryons) - §1.5 "Elementary
particles". From the
viewpoint of radiation, it is important that in the
process of inelastic scattering of the primary radiation
arises secondary ionizing radiation (as was discussed above in the section "Secondary
radiation generated by radiation-substance interactions").
When charged particles pass
through a substance medium that contains a large number of atoms,
the particle after one scattering is usually subject to further
collisions and scattering on other atoms - there is multiple
scattering (as shown in Fig.1.6.1
at the top left); individual scatterings
can be elastic or inelastic.
Interaction of positron ( beta+
) radiation
Very specific way interacts with the substance the b+ i.e. positron e+ radiation - in lower part fig.1.6.1. As long as the
positron has a high velocity, it pulls electrons out of the shell
with its electric forces as it passes around the atoms, and thus ionizes,
similarly to the beta- electron. However, after sufficient braking (in water
or tissue after about 1-4 mm), the positron e+ meets the electron e-,
and since they are "antagonistic" antiparticles, they
destroy each other ("eaten"): their annihilattion
e+ + e-
® 2g occurs - they are converted
into two quantums of hard radiation g
with energies 511 keV *).
*) It is interesting that, according to the laws of quantum
electrodynamics, there should be also the opposite
process to annihilation of a positron with an
electron e+
+ e- ® 2 g, the so-called Breit-Wheeler
production of e+ e- pairs. In this
process, on the other hand, electron-positron pairs could
theoretically be formed by the collision of two photons g1 + g2 ® e+
+ e-. However, this two-photon process has a very low
probability (slight effective cross section), to demonstrate it
would require an extremely intense collimated beam of gamma
photons with energy higher than 511keV - has not succeeded yet...
Some possibilities of realization of multiphoton pair production
are briefly discussed in §1.5, passage "Electrons and positrons".
Both photons
of annihilation radiation fly out from the annihilation site
exactly in opposite directions - at an angle of
180o (in the center of gravity
system). This fact is used in the
scintigraphic method of positron emission tomography PET (as described in detail in §4.3, section "Positron emission tomography PET"). Thus, if we have a sample of the radioactive substance
b+, positrons with
electrons annihilate already inside this sample, so that we do
not register practically any positrons in its vicinity, but such
a sample will be a source of intense hard radiation g with an energy of
511 keV. And just the same, when we apply a radioidicator labeled
with b+ radionuclide to
the body - each positron at a distance of about 1-3mm from the
place of its origin annihilates with an electron in the tissue,
and we can detect in coincidence two quanta of g radiation with
energy 511keV flying in opposite directions - this is the basis
of PET scintigraphy (see also "PET
cameras" in chapter 4
"Radioisotope scintigraphy").
In terms of the classification of different types of radiation,
positron radiation interactions are discussed once again in the
section "Beta+ radiation interactions" below.
Positrons
e+ are
actually a kind of "visitors from the anti-world"
- particles of antimatter. The
properties of antiparticles, antimatter, antiworlds or
"antiuniverses" are discussed in §1.5 "Elementary
particles and accelerators", passage "Antiparticles
- antiatoms - antimatter - antiworlds" (including the possibility
of "production" and use of antimatter, with a bit of
humorous sci-fi story about the meeting of a "earthly girl"
with a cosmic "anti-boy"...).
Braking radiation (bremsstrahlung)
During the passage of fast charged particles through matter, due
to the Coulomb interaction with electron shells and nuclei of
atoms, the velocities and direction of motion of the particles
change - their scattering occur. The scattering of a charged
particle on atoms at a large angle causes a large and rapid
change of the velocity vector with time, ie a large
"acceleration" of the particle, which according to
Maxwell's electrodynamics leads to the emission of
electromagnetic radiation - photons called braking
radiation X or g with continuous spectrum. This type of scattering occurs
on the one hand in the field of electrons, but especially during
the passage of a charged particle near the nucleus with charge Z
(Fig.1.6.2 in the middle), during which they will be on a
particle with mass m and the charge q exerts
electric Coulomb forces proportional to the product q.Z, so that
they will impart to the particle an acceleration proportional to
q.Z/m. According to the laws of electrodynamics, each accelerated
charge emits electromagnetic radiation, the intensity of which is
proportional to the square of acceleration *), ie Z2.q2/m2. It follows that
energy losses by braking radiation will be significantly greater
in heavy substances with a large proton number Z and that
braking radiation will be applied mainly to light charged
particles, ie electrons (protons lose a
million times less energy to braking radiation than electrons). The effective cross section for excitation of braking
radiation is larger in the field of the atomic nucleus, than in
the field of envelope electrons.
*) The physical-mathematical
derivation is given in §1.5 "Electromagnetic
field. Maxwell's equations.",
Larmor's formula (1.61'), monograph " ravity,
black holes and space-time physics".
The effective cross section for the production
of braking radiation in matter is generally given by the highly
complicated Bethe-Heitler formula (derived
from quantum radiation theory, corrected by the Sauter
and Elwert factors of the Coulomb shielding of the
electron shell). For a not very wide range
of energies of incident electrons Ee (tens to hundreds of keV) and proton numbers Z
target material (medium to heavy materials), the overall efficiency
of braking radiation production h can be approximated by a
simplified formula :
h = Ee [kev] . Z . 10-6 [photons / 1
electron] .
Only a relatively small part (only about 1%) of
the original kinetic energy of the incident particle changes to
braking radiation when braked in the substance. Most of the
energy is eventually transferred to the kinetic energy of the
atoms of matter by multiple Coulomb scattering - it is converted
into heat.
The
graphical shape of the energy spectrum I(E) of
continuous braking X-rays is described in the first approximation
by the so-called Kramers formula :
I(E)
= K. I. Z . (Emax - E) ,
where I(E) is the relative intensity of photons of energy E
, K is a constant, Z is the proton (atomic) number
of the target material, Emax is the maximum energy of X-ray photons, given by the
kinetic energy of the incident electrons. For E = Emax , is I(Emax) = 0 and the
formula applies only to E <Emax .
It is logical that the efficiency of brake
radiation production is higher for high Z - large electric
Coulomb forces act around such nuclei, causing abrupt changes in
the velocity vector of the incident electrons that get close to
the nucleus. The efficiency of braking radiation production
[number of photons / 1electron] increases with energy Ee incident electrons.
However, the overall energy efficiency - the ratio of
the total energy of the emitted photons to the energy of the
incident electrons - is lower for higher energies (due to the
higher percentage of low-energy photons). And the heat production
in the target material is higher.
Braking radiation
has a continuous spectrum from energies close to
zero to the maximum energy given almost by the value of the
kinetic energy of the incident particles. The energy of the brake
radiation photons depends on the speed (acceleration) at which
the electrons are braked when interacting with the substance. The
individual electrons penetrate differently close to the nuclei of
the material, thus emitting different wavelengths or energies of
photons. Those electrons, which "softly" slow down with
repeated multiple scattering on the outer electron shells of
atoms, emit low-energy X-rays. The deeper the electrons penetrate
into the interior of the atoms of matter, the closer to the
nucleus, the faster the intense Coulomb forces change velocity
vector of electrons, and the harder the braking radiation is
produced. The shortest wavelengths arise for electrons that have
penetrated close to the nucleus to the level of the shell K
or closer and were braked at once. Depending on the impact factor
of the individual electrons relative to the atoms of the
substance, all possibilities are continuously realized. Such a
different degree of braking of electrons causes a mixture of
radiation of different wavelengths or energies of photons - the
result is continuous spectrum of braking
radiation (see eg Fig.3.2.5 at the top
right in §3.2 "X-rays - X-ray
diagnostics").
The angular distribution
of the emitted photons of braking radiation depends on the energy
of the primary charged particles. The mean angle J of the emission of the
quantities of braking radiation excited by the electrons with
kinetic energy Ee is approximately given by the relation J = m0e .c2/Ee (= 0,511 /Ee for the energy in MeV). At low
energies, the braking radiation is emitted practically isotropically
in all directions from the point of interaction. With increasing
energy Ee
of the electron exciting the braking radiation, the mean angle J of the emitted
quanta g is ever smaller - at high energies of the incident
charged particles, the braking radiation is preferably emitted in
a narrow cone "forward" in the
direction of incidence of the primary particles. The directional
radiation pattern of high-energy braking radiation has the shape
of a sharp "lobe" in the direction of the primary beam (see, for example, the figure "Radiotherapy-HomogFiltr.gif " at the top left in §3.6 "Radiotherapy").
Braking radiation finds significant
use in the excitation of X-rays by the impact of
electrically accelerated electrons on the anode in X- ray tubes- see §3.2 "X-rays - X-ray
diagnostics"), or when exciting hard g- radiation
by the impact of high-energy electrons from a linear accelerator (see §1.5 "Elementary particles", part "Charged
particle accelerators") on a suitable target; it is often used in radiotherapy
(§3.6 "Radiotherapy").
Terminological
note :
For braking radiation or deceleration radiation,
for historical reasons the German name "bremsstrahlung"
often occurs.
The very term "braking" is
somewhat misleading, as it gives the impression that it is
radiation generated only when the speed
reduction (deceleration, braking) of charged particles. The
same radiation but also arises when accelerating of
charged particles. However, in nature and in the laboratory, the
particles do not accelerate sufficiently fast, so that the
"acceleration radiation" is negligible and is not
observed. On the other hand, the braking of fast charged
particles, especially light electrons, in substances is quite
rapid, so that the braking radiation can be very significant.
Braking radiation arises not only during the actual
"braking" of a charged particle (perhaps in a strong
electric field of a uniformly charged particle), but also during
a curved motion in an electric or magnetic field (see the
following paragraph - synchrotron radiation), which does
not primarily involve braking. However, braking nevertheless
occurs here secondarily, because the electromagnetic radiation
carries away the kinetic energy and thus effectively inhibits
the movement of the charged particle.
Cyclotron and
synchrotron radiation
A special type of "braking" radiation is the so-called cyclotron
and synchrotron radiation *). It arises during
the movement of charged particles in a magnetic field,
where these particles are acted upon by a Lorentz force
curving their paths - forcing them to move in a circle or spiral
(helix) with an axis parallel to the magnetic induction vector.
Due to the uneven movement of electrically charged particles
during the circular orbit under the influence of the magnetic
field, braking radiation is generated. According to the
well-known Larmor formula of electrodynamics, the intensity of
this radiation is proportional to the electric charge and the
square of the acceleration of the particle motion, here it is a centripetal
acceleration of the circular motion. Thus, for a given
kinetic energy of a particle, the intensity of synchrotron
radiation is inversely proportional to the square of the mass of
the particle. This phenomenon therefore applies almost
exclusively to the motion of light particles, electrons,
with high kinetic energies (and thus high velocities), which move
in the strong magnetic field with high radial accelerations. Due
to their high mass, protons emit cyclotron or synchrotron
radiation a million times smaller.
*) The names derive from the
fact that these radiations occur in the respective circular
accelerators (§1.5, section "Circular accelerators"). Synchrotron radiation was first observed in
1947 on a large (for that time) accelerator - 70MeV GE
synchrotron.
Cyclotron
radiation emitted by slower (non-relativistic)
electrons is monochromatic with a frequency
corresponding to the Larmor cyclotron frequency f =
e.B/(2p me), where e is
the charge and me the rest mass of the electron, B is the magnetic
induction; falls into the field of radio or microwave
radiation.
Synchrotron
radiation is emitted by high-energy (ultra)relativistic
electrons in a magnetic field. The radiation is emitted in a
narrow cone in the direction of electron movement. Multiples of
the Larmor frequency also appear in its spectrum. For
relativistic electrons, there is a blurring of the cyclotron
(Larmor) frequency due to different relativistic time dilation at
different points in the circular orbit relative to the observed
location. The emitted synchrotron radiation therefore has a continuous
spectrum. Synchrotron radiation takes place in the visible
region of the spectrum, in strong magnetic fields also in
the field of X-rays. In circular high-energy
accelerators, synchrotron radiation can be disruptive -
causing unwanted energy losses of the accelerated particles. On
the other hand, it can be used to intentionally create intense sources
of radiation with advantageous properties for some
laboratory applications (see §1.5, section
"Synchrotron radiation
generators").
Cyclotron and especially synchrotron
radiation also occurs in a number of processes in
universe - in hot corona of stars, in nebulae, around
neutron stars, in massive quasar jets - where fast electrons move
in magnetic fields (see eg §4.2 "Final
stellar phases. Gravitational collapse..." in book "Gravity, Black Holes and the
Physics of Spacetime").
Photoeffect
and characteristic X-radiation
In addition to braking X-rays with a continuous spectrum, a
certain smaller amount of characteristic X-rays
with a line spectrum is emitted (characteristic pair of peaks Ka, Kb, or weaker and
lower peaks of the L series), whose energy does not depend on the
energy of incident particles, but it is given by the material
- the type of atoms of which the irradiated substance is composed
(it is characteristic of it). This characteristic
radiation manifests itself as "peaks" on a continuous
curve of the braking radiation spectrum. The characteristic X-ray
is caused by two processes :
¨ Direct process of the impact photo effect
at the internal energy levels of the envelope in the atoms of the
irradiated substance (left part of Fig.1.6.2) - fast charged
particles penetrate into the interior of the atoms and eject
bound electrons from the K and L shells. When
electrons jump from the L shell to the emptied K
shell (K-series), or from the M shell to the L
(L-series), a characteristic X-radiation is then emitted (cf.
also with Fig.1.1.3 in §1.1).
¨ Indirect
process of photoelectric absorption of braking radiation -
braking X-rays, produced by the above-mentioned mechanism during
the passage of a charged particle, interacts with other atoms
inside the substance, e.g a photon photoeffect (described below "Interaction
of gamma and X-rays", Fig.1.6.3
left), with the ejection electrons from the
inner shells, followed by an electron jump and the emission of
characteristic X-rays.
The impact photoeffect of charged
particles and the emission of photons also occurs when electrons
jump in the outer shells, but the energy of these photons is low
and this radiation is overlaid by continuous braking radiation at
the beginning of the spectrum.
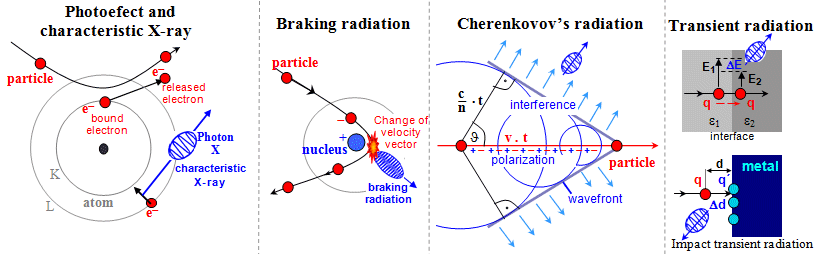
Fig.1.6.2. Mechanisms of characteristic X-rays, braking
radiation, Cherenkov radiation and transient radiation
Cherenkov
radiation
When an electrically charged particle passes through the medium,
the electric field of the particle causes local
polarization of atoms and molecules of the medium along
the path - small electric dipoles are formed. After the
passage of the particle, the atoms of the environment depolarize
rapidly, while the obtained energy is radiated in the form of
electromagnetic waves - light. This electromagnetic wave emitted
along the path of the particle is subject to interference,
the effect of which depends on the velocity of the
particle. During the slow movement of the charged
particle, the polarization energy is elastically transferred back
to the particle. During the rapid
movement of the particle, a limited rate of depolarization will
manifest, the particle "runs away" from a given place,
and "delayed" depolarization occurs by the emission of
an electromagnetic wave. If the velocity of the charged particle
in the environment is greater than the phase velocity of
light (in this medium), the light waves emitted during
depolarization at various points in the path may enter the phase
and "constructive" interference and observable
radiation may occur at a suitable angle J. In other words, a coherent
emission of dipoles formed by polarization occurs as a charged
particle rapidly passes.
Geometric
analysis particle motion, propagation of emitted light
and interference properties is shown in Fig.1.6.2, the second
picture from the right. Due to the depolarization of the medium,
each part of the particle path becomes a source of a weak
electromagnetic signal, which propagates in the material
environment at a speed of c/n. During the elementary time t
, this signal propagates into a spherical wavefront of radius
(c/n) .t , during which time the particles travel the distance
v.t. During this time interval, spherical wavefronts
gradually escape from all other points of the path, which during
this time t they reach smaller radii than v.t. The common envelope of these wavefronts forms the
mantle of the cone, in the section in Fig.1.6.2 on the right the
hinge of a right triangle. Into these sites the individual
partial signals arrive in the same phase and positive
interference may occur. Such an analysis can be done for each
point of the particle path and time interval t . It
follows that the "constructive" (positive, amplifying)
interference will occur at the angle J given by the mentioned
right triangle, whose cosine cos J = (v/c) .n .
The resulting radiation thus conically
diverges from the path of the particle flying at
velocity v at an angle J
given by the relation cos J = 1/b.n, where b = v/c, n = c/c' is the refractive index
of the optical medium (c is the speed of light in a
vacuum, c' the speed of light in a given optical medium).
The refractive index of optical media depends somewhat on the
wavelength of light, n = n(l) - light dispersion.
Thus, if a charged particle passes
through a substance medium with a velocity exceeding the
speed of light c' in this medium (this
is given by the electrical permittivity e and magnetic permeability m of the substance: c' = Ö(e.m), otherwise also
the refractive index n of the substance: c' = c/n), occurs electromagnetic shock waves (similar to the formation of acoustic shock waves when a
body passes through air at supersonic speed),
at which visible light called Cherenkov radiation
is emitted.
This radiation
was first observed in 1934 by the Soviet physicist P.A.Cerenkov
in water exposed to ionizing radiation. Together with S.I.Vavilov
*), they performed a number of experiments to elucidate the
properties of this radiation, reaching a partial explanation that
the observed radiation is caused by fast electrons.
The definitive explanation of the mechanism of this phenomenon on
the basis of the laws of electrodynamics in the material
environment was given in 1937 by their other colleagues
I.M.Frank and I.J.Tamm.
*) His brother was an excellent botanist,
establishing the word Seed Bank of All Plants, including exotic,
rare and little-known species.
The condition for the formation of Cherenkov radiation
is therefore the movement of a charged particle at a speed at
least equal to the threshold speed vmin = c' = c/n,
exceeding the speed of light c' in a given environment. From the
relativistic relation for kinetic energy (Ekin= moc2/Ö(1 - v2/c2) - moc2
- see formula (1.79) in §1.6 "Four
dimensional spacetime and special theory of relativity" of the book "Gravity ,
black holes and space - time physics")
then it follows, that the (kinetic) threshold
energy corresponding to this velocity vmin charged particles
for the formation of Cherenkov radiation when passing through a
medium with a refractive index n is: Emin = mo.c2[1/Ö(1-1/n2)
- 1]. For this case of the threshold velocity, cos Jmin = 1, ie Jmin = 0 - the radiation
goes in the direction of particle motion. At lower speeds or
energy, no radiation occurs.
For ultrarelativistic particles moving at the maximum possible
velocity vmax = c, the maximum radiation angle cosJmax = 1/n. In the water with a refractive index n = 1.33,
the threshold velocity for the formation of Cherenkov radiation
is vmin =
0.75c, which for the electron corresponds to the threshold
kinetic energy Emin = 0.26MeV; the ultrarelativistic electron flying
through water (cosJmax = 0.75) will then emit Cherenkov
at an angle Jmax = 41.5 °. The
threshold energies of some particles for the formation of
Cherenkov radiation in plexiglass, water and air (at normal atmospheric pressure) are
given in the following table :
| Substance |
electron e - |
mion m -, + |
pion p -, + |
proton p + |
| plexiglass (n = 1.5) |
0.173 MeV |
36 MeV |
49 MeV |
320 MeV |
| water (n = 1.33) |
0.26 MeV |
50 MeV |
68 MeV |
460 MeV |
| air (n = 1,0003) |
20.35 MeV |
|
|
|
The energy dW emitted along the path dl
by a particle with charge q, flying at velocity v (b = v/c), by
radiation with angular frequency w = 2p.f and in frequency interval
dw, is
given by Frank-Tamm equation
d2W = (q2.e/4p).w.[1 - 1/b2n2(l)] dl dw .
The total amount of energy *) dW emitted by the particle
per unit dl of the path is then given by the relation
after integration
dW/dl
= (q2/4p) n
[1 - 1/b2n2(l)] e.w dw ,
which integrates over a circular radiation frequency w = 2p.f = 2p/l (the boundary
condition v > c/e). It follows from this expression that the number of
Cherenkov photons dN with energy hf = h .
w emitted
per unit of path dl is
dN2/dl = (dW/dl).(l/hc) = (4p2q2/h.c).n
[1 - 1/b2n2(l)]/l2 dl .
The spectrum of Cherenkov radiation, ie the
number of photons dN emitted along the path of a charged
particle per unit path dl and per unit energy interval, or
equivalent wavelength dl , is thus given by the formula :
dN2/dl dl = (4p2q2/h.c).
[1 - 1/b2n2(l)]/l2 .
Or equally, the number of photons Nl2¸l1 in the spectral region between the wavelengths l1¸l2 emitted along the path l makes :
Nl2¸l1 = (4p2q2.l/h.c). (1/l2 - 1/l1).[1 - 1/b2n2(l)] .
It follows that the intensity of Cherenkov radiation
increases with the refractive index n of the material
environment, its spectrum is continuous and is
the same for all particles with the same charge q, the number of
photons decreases with the square of the wavelength l. The relative
intensity of Cherenkov radiation increases with frequency, so
higher frequencies (shorter wavelengths) are more intensely
represented. That is why in the optical field Cherenkov radiation
appears to us as bright blue; we do not see with
our eyes most of it, lies in the ultraviolet region. The maximum
in the continuous spectrum is usually around 330 nm.
*) Cherenkov radiation in principle
contributes to energy losses and braking of the particle during
flight through the environment, but in comparison with other
mechanisms (ionization, excitation, braking radiation) this
effect is negligible.
 |
Cherenkov radiation generated in an
aqueous phantom during irradiation with electron and
photon radiation beams.
Left: A cylindrical phantom (diameter 20 cm and height 18 cm) filled
with water was irradiated with a wide (magnetically
scattered) beam of electrons with energy 9MeV from
a linear accelerator.
Middle: During passing through the upper
part of the phantom, fast electrons generated Cherenkov
radiation to a depth of about 4.5 cm, when the energy of
the electrons fell below the threshold level of 260 kV.
Right: When irradiating the same phantom
with a beam of photon radiation (max.
energy 6MeV, beam with a diameter of 4cm), the
secondary electrons along the g
beam form the Cherenkov radiation - with a deep decrease
in intensity, as the primary photon beam attenuates as it
passes through water (just below the
surface, a slight increase in intensity is initially seen
- build-up effect to a depth of about 1 cm,
discussed below) "Secondary radiation generated by X and g interactions") .
Note: In the upper and lower part, optical
reflections of light from the cover and from the bottom
of the phantom are visible. Due to the relatively weaker
intensity of the images, the images contain a higher
amount of disturbing noise. .. |
If the material environment for light radiation
is transparent, ie it is an optical environment,
Cherenkov radiation can be visible - bluish
fluorescence observed at stronger particle flux - see phantom
measurement on the accelerator from above in Fig. "Cherenkov radiation of irradiation
beams.." (known
is blue fluorescence around highly radioactive nuclear reactor
fuel elements). This radiation can also be
used with the help of photomultipliers to detect fast
charged particles, whether primary or secondary, caused
by the interactions of primary radiation with a substance - see
§2.4 "Scintillation detectors" , section "Cherenkov detectors". These detection methods find their application in
accelerators, in the detection of neutrinos and cosmic radiation (see also the passage "Neutrinos" in §1.2 "Radioactivity" or below "Cosmic radiation").
Minor interest:
Cherenkov radiation can also occur in our eye
during the interaction of high-energy particles. Faint bluish
flashes of light caused by cosmic rays, indeed are occasionally
observed with astronauts with their eyes closed.
Askaryan radiation
In addition to the above-described classical light Cherenkov
radiation, which arises during the passage of electrically
charged particles, in dielectric environment even at the passage
of high-energy uncharged particles create a spray of
fast secondary charged particles, which by the Cherenkov effect
emit a cone of electromagnetic waves at radio or
microwave frequency 5 GHz), so-called Askaryan radiation.
If this phenomenon occurs in an environment permeable to radio
waves - such as ice, salt, quartz, sand, the atmosphere - this
radiation, generated in the form of short pulses, can be detected
by radio antennas.
Askaryan radiation is tested for neutrino
detection, especially in Antarctica, where high - energy
neutrinos pass through a layer of ice. The ANITA (....) antenna,
located on a balloon above Antarctica, detects these radio
pulses. It works in collaboration with photomultipliers detecting
Cherenkov radiation in Antarctic ice in the IceCube system. ....
Transition radiation
Another radiation-optical effect during the
passage of fast charged particles through an inhomogeneous
medium, is the emission of so-called transition radiation.
This radiation is generated when a charged particle passes
through the optical interface of material media
with different refractive indices, especially if the electrical
permittivities e1 and e2 of this two media differ. During the transition
(rapid passage) of a charged particle through such an interface,
according to Coulomb's law E = (1/4p.e ) .q r2 the intensity of the
electric field around the particle changes very quickly
from the value of E1(r) to E2(r), which according to Maxwell's equations of
electrodynamics evokes electromagnetic waves,
called according to the mechanism of their formation transient
radiation *) - Fig.1.6.2 on the right. The
intensity of this radiation is approximately proportional to the
energy of the charged particle and is generally very
small. ........ add:
Frank-Ginzburg equation ....? ..
*) The mechanism of transient radiation was elucidated on the
basis of the laws of electrodynamics in the material
environment in 1945 I.Frank and V.Ginzburg.
For fast charged particles, both Cherenkov and transient
radiation are generated in the material environment. However,
transient radiation differs from Cherenkov
radiation in two aspects :
¨ Transient radiation is in principle also generated for
charged particles moving at a speed less than the speed
of light in a given environment, it is sufficient that
the environment is optically (electrically) inhomogeneous.
However, at lower velocities (energies) of charged particles, or
a gradual change of the dielectric constant e of the medium, transient radiation
is very weak and long-wave - in the optical field
(an optically transparent environment is a prerequisite here), or
in the field of infrared radiation or radio waves. Such radiation
is usually not detectable.
¨ The passage of
relativistic high-energy particles (especially
electrons) through the interface with a step change in the
refractive index creates short-wave transient X-ray
radiation- soft X-rays, photons with an energy of several keV,
which can be detected by methods for ionizing radiation (TRD - Transition
Radiation Detector), eg proportional ionization chambers.
In general, transient radiation is
the least significant of all types of secondary
radiation generated by the interaction of charged particles with
matter. Since it is very weak (often only less than one photon per particle to pass
through the interface), is usually drouwn
out by much more intense braking radiation and radiation from
atom deexcitation. X-ray transient radiation is sometimes used in
high-energy radiation analysis to detect electrons (TRDs) and
separate them from heavier particles (pions or protons), which
emit X-ray transient radiation only at many times higher energies
than electrons.
Impact transition
radiation
Transition radiation arises also when the impact
of fast charged particles on the surface of bodies. If they are
bodies made of non-conductive material (dielectric), the
formation of transient radiation can be explained by the
above-mentioned mechanism of sudden change of electric field of a
particle when passing from vacuum with permittivity eo to environment with permittivity e > eo . However, transient radiation also arises when a
charged particle hits an metal surface, eg when
electrons hit an anode at X-ray tube. It arises from the fact
that when a fast charged particle approaches a metal surface, the
dipole moment d of the pair [incoming
charged particle q « electron or cation on the
metal surface q´] changes rapidly over time,
which effectively forms an electric dipole (which disappears at the impact).
And according to the laws of electrodynamics, the time change of
the dipole moment of the charges leads to the emission of
electromagnetic waves *) - Fig.1.6.2 at the bottom
right, in this case the impact transient radiation.
This radiation can be observed as a faint bluish fluorescence (it is polarized) at the anodes of
high-voltage vacuum tubes (perhaps first
observed already in 1919 by J.E.Lilienfeld at the anode of the
cathode ray tube - but it was not proven...).
It also occurs at the anode of the X-ray tube (where it is not possible to observe them, as it is
completely drown out with light from a hot cathode) .
*) See §1.5 "Electromagnetic
field. Maxwell's equations.",
formula (1.61), in the book "Gravity, black holes and
space-time physics".
Electric
charging
An obvious, but mostly completely neglected phenomenon in the
interaction of electrically charged particles with matter, is the
electric charging of the originally neutral
substance environment. According to the law of
conservation of electric charge, the electric charge of
each place where the electrically charged particle is absorbed
and braked, increases by the value of the charge of the particle.
At low radiation fluxes, or if the irradiated body is at least
partially conductively connected to earth, this phenomenon is
negligible. However, if we irradiate an electrically insulated
body with an intense flux of radiation a or b, it will gradually be
positively or negatively charged even to a high electrical
potential of up to hundreds of kV (depending on its electrical
capacity). This phenomenon is fully manifested only in a vacuum,
because in the air the radiation causes ionization, the
environment becomes partially electrically conductive and the
charge is continuously led off from the irradiated body.
Self radioactive emitter a or b (if is
electrically isolated) is also electrically
charging, because these particles carry an electric charge and in
the substance of the emitter then dominates the opposite charges
than the sign of the charge of the emitted particles.
We can now turn to the specific properties of
the interactions of specific particles of directly
ionizing radiation :
The interaction of
heavy charged particles - alpha, proton and deuteron radiation,
heavier ions
a - radiation ,
which is a current of fast-flying helium nuclei 4He 2 (2p+, 2no), is characterized by the fact
that of all common quantum radiation they have a- particles the largest
mass and especially the largest electric charge
- it is the positive charge of two protons p+. If the a-particle enters into substance, it exerts a
considerable electric (Coulomb) force on the electrons as it
passes around the atoms, which it very effectively pulls
out of the atomic shells - Fig.1.6.1 at the top left.
Due to these strong ionizing effects, the
particle a, although usually having a high kinetic energy, brakes
very quickly in the substance, so that its range
is very small - at an energy of the order of MeV, the
range is about 0.1 mm in water density substances. The strongest
ionizing effects arise at the end of the particle's range - the Bragg
maximum.
If the particles a have sufficiently high
energy (several MeV), as they pass through the substance
they can overcome the repulsive electrical forces of the nuclei
and enter into nuclear reactions with the atoms
of the irradiated substance. Most often it is the reactions (a, n) in which they
emitted the neutrons. This process is used in radioisotope
neutron sources : a -radioactive substance (most often americium 241Am) is mixed with a
suitable material containing light atoms (most often beryllium),
from the nuclei of which energetic a-particles eject neutrons.
Proton and deuteron
radiation
Largely similar properties of interaction with matter has proton
radiation - stream of fast protons p+ (hydrogen nuclei) and
deuteron rays (which is the current of fast
deuterium nuclei D = 2H1
composed of proton p+ and neutron n0) - Fig.1.6.1 top center. Fast-flying protons or
deuterons interact mainly with atomic shells, from which secondary
electrons knock-out. To a lesser extent, there are
interactions with atomic nuclei - mostly elastic
scattering, but also nuclear reactions in which
secondary protons, neutrons, deuterons, gamma photons are formed.
All these interactions are discussed in more detail in §1.6,
passage "Proton
radiotherapy".
We do not encounter this radiation
in terrestrial nature, but in the upper atmosphere and in
universe, high-energy proton radiation is a major component of
primary cosmic radiation (see
"Cosmic radiation" below). Proton and deuteron
radiation of artificial origin are generated in accelerators (§1.5, section "Charged
particle accelerators"). It is used for the production of radionuclides (especially positron - §1.4, part "Production
of artificial radionuclides"), proton radiation in the so-called hadron
radiotherapy (§3.6, part "Hadron
radiotherapy").
Radiation of heavier ions
Fast-flying nuclei of heavier elements than
helium, also called heavier ions, produce analogous
ionization effects as radiation a or D, but
proportionally higher ionization densities due
to its larger charge. Even heavier nuclei with high kinetic
energies are contained in a smaller percentage in cosmic rays.
They are produced on accelerators for research purposes (study of
nucleus structure and strong interactions, formation of
quark-gluon plasma - §1.5, part "Quark
structure of hadrons"),
formation of heavy transuranic nuclei (§1.4, part "Transurans") and for hadron radiotherapy
(accelerated carbon nuclei are mainly used here, see §3.6,
section "Hadron radiotherapy").
Muon radiation
Muon radiation, which is a current
of fast muons m+ or m-, can also be found on the earth's surface. Is part
secondary cosmic rays, caused by interactions of
high-energy particles of primary cosmic rays in atmosphere (see
"Cosmic rays" below). The muon radiation is highly penetrating,
in addition to its own ionization, the muons m± eventually decay into electrons e± (which is
actually beta± ionizing radiation ) and neutrinos.
Pion radiation ,
which is the current of fast pi-mesons p+ or p-, occurs
on Earth in the upper atmosphere, where it is formed by
interactions of high - energy primary cosmic rays. At large
accelerators, pions are formed during nuclear interactions of
protons accelerated to high energies (> 300MeV). In addition
to basic research in nuclear physics, p- experimental testing is being performed as an effective
tool in hadron radiotherapy
(§1.6, section "Hadron radiotherapy", but it is quite problematic .!..) .
Antiproton radiation ,
formed by a stream of fast antiprotons (antiparticles to
protons), arises during nuclear interactions of protons
accelerated to very high energies (> min.6GeV, for higher
yields > 20GeV). It is being tested experimentally for antiproton
radiotherapy (radiation efficiency is
about 3 times greater than that of protons, but debatable, apart
from the extreme complexity and cost, is the problem of
production of secondary pion radiation - see also §1.6, passage
"Hadron radiotherapy").
For better illustration, we will again present
the important figure 1.6.1 of the interaction of charged
particles with matter :
 |
Fig.1.6.1. Interaction
of fast charged particles with matter.
Top left: Schematic
representation of ionization mechanisms in the passage of
beta- and alpha particles .
Top middle: Three basic mechanisms of
proton radiation interaction with matter.
Bottom: Interaction of positron beta+ radiation
with a substance ending in annihilation of a positron
with an electron.
Right: Bragg curves of depth
dependence of absorption and specific ionization along
the path of gamma photons, accelerated electrons and
protons. |
Interaction of electrons - beta- radiation and
high-energy electrons
Electrons interact with matter primarily through the electron-electron
interaction: incoming primary electron electric forces
acting on the electrons in the atomic packing - causing
excitation and ionization of bound electrons. The primary
electrons thus transfer part of their energy to the secondary
electrons, originally bound in the atoms of the
irradiated matter environment. In addition to this "collision"
electron-electron interaction, primary electrons can lose their
energy by radiation, emitting braking radiation.
Quantum electrodynamics (QED) describes the general
mechanism of electron interaction. Two basic properties apply
here (which result from the general
analysis of the interaction of charged particles outlined above) :
¨ The
stronger electrical action between the electrons is in the case
of a "tighter" their collision. The transmitted energy
(energy loss) and the scattering angle (electron deflection after
interaction) are therefore inversely proportional to the
collision parameter b.
¨ The
time for which electrons are in electrical interaction with each
other (for which they "pass" each other) is shorter the
higher the velocity of the incident electron (its energy) *).
With a time-shorter force action, the arriving electron
"manages" to transfer less energy to the target
electron and also deviates less from the original direction.
*) At energies of the order of MeV, the speed of electrons is
already very close to the speed of light, so a further increase
in energy should no longer seem to cause a shortening of the
interaction time. However, in the center of gravity system of
interacting relativistic electrons, the interaction time
continues to decrease with respect to the energy increase
(relative to the laboratory system) due to the effect of relativistic
time dilation. Therefore, even in the field of relativistic
electron energies, energy loss and scattering angle decrease with
increasing energy.
These two mechanisms lead to the regularity, that the energy
DE
transmitted during the electron-electron interaction and the scattering
angle J are inversely proportional to the energy E
of the flying electron and the value of the collision
parameter b : DE ~ 1/b.E , J ~ 1/b.E .
First we will approach what happens in matter during the
interaction of medium and lower energy electrons (radiation b- from
radioactivity), then we will look at the interaction of
high-energy electrons.
If the particle b-, which is a negatively charged electron e- from
the radioactivity of beta with kinetic energy of the order of
hundreds of keV, penetrates into the substance, then during its
passage around atoms it acts by electric repulsive forces on
electrons, which eject from the atomic shell and
thus ionize atoms. Since electrons are very
light particles, with each such ionization of the atom, the
electron b abruptly changes the direction of its
motion - it is reflected by the repulsive
electric forces from the atom. And then immediately from the next
and next atom - the electron b
will "zigzag" move and reflect
between the atoms, which it ionizes and at the same time loses
energy - Fig.1.6.1 top left. Depending on its energy, it brakes
to a depth of up to 1-4 mm in the water density substance, and in
heavy metals it does not fly deeper than about 0.1 mm. The mean
range (outreach) Rs of radiation b in a substance *) depends on the energy of the radiation
and on the density and proton number of the substance (.......... -empirical formula? ). For energies in the range of
approx. 0.6-3 MeV, the range depends approximately linearly on
energy, for lower energies the dependence is somewhat flattened.
The mean range of 3 mm, given as an example in the scale in
Fig.1.6.1 on the left, corresponds to approximately harder
radiation b with an energy of about 1.5 MeV (as it has, for example,
32P) in
water. For medium energies around 500keV the average range in
water is less than 1 mm, for soft b (as has 3H) the range is very
small, of the order of hundredths of a mm.
*) Due to collisions and scattering, the
trace of the particle b in the matter is it is very winding, so that even two
electrons of the same initial energy, emitted from the same place
and in the same direction, can brake at considerably different
depths. Those electrons that moved in a more direct direction and
suffered fewer collisions with less energy loss penetrate
further, while electrons that have changed direction many times
and lost more energy in collisions slow down. In addition,
particles b from radioactive sources have a continuous spectrum of
energies, which further "blurs" the actual range length
around the value of the mean range Rs . For radiation b, therefore, the value of the maximum range Rmax is
more appropriate. The range of radiation in a substance is often
also described by the effective range R90,
which is the distance at which 90% of the original emitted energy
of the particles is absorbed (or the radius of the spherical
space of the substance around the point source at which 90% of
the energy emitted by the source is absorbed).
Towards the end of the path, when the energy of
the electron is no longer sufficient for ionization, the electron b will lose energy
by exciting the electrons in the atoms. If this
electron is not the trapped in some of the atoms, then its
kinetic energy decreases to a thermal value of » 3/2 k.T (k is the Boltzmann constant), which at room
temperature is only about 0.04eV.
High energy electrons from an
accelerator (betatron or linear accelerator) with energies of
unit up to tens of MeV, after entering the material environment,
they initially move almost in the original straight direction and
only brake slowly. The higher the electron energy,
the smaller the effective interaction cross
section, energy loss and scattering angle. Towards the depth,
along the path of the braked electron, as the energy decreases,
the mean free path shortens, the number of collisions increases,
the proportion of transmitted energy increases and the number of
significant changes in the direction of electron movement
increases (scattering to larger angles). Originally a straight
path of a high-energy electron, it gradually becomes a devious,
ionization thickens and in the final section, before the complete
stop of the electron, a very dense chaotic cluster of
ionization is formed in the matter by ionization and
excitation of atoms (as described above for
the beta radiation interaction).
The curve of the depth dependence of the radiation dose
of a high-energy electron beam shows an initial slight
rise (corresponding to a lower effective cross-section
of high-energy interactions), after reaching a maximum in a few
centimeters followed by a steep drop to zero
(corresponds to complete braking of electrons in matter) - red
curve in Fig.1.6.1 bottom right.
During the passage of electron
radiation through a substance, as already mentioned above, secondary
electromagnetic radiation is generated: braking
X-radiation with a continuous spectrum, characteristic
X-radiation with a line spectrum determined by the type
of substance; when high-energy electron radiation passes through
an optically transparent substance (eg water), visible Cherenkov
radiation is also generated (bluish
fluorescence is visible around strong b- emitters), in inhomogeneous optical environments event. weak transient
radiation.
These optical effects
were discussed above in the section "Cherenkov radiation", including the image from the our measurement
with electron and photon irradiation beams.
Interaction of beta+ radiation
If a particles b+, which is positively charged positron e+, enter the substance, it will initially - as long as it
has a high energy and moves at high speed - like b- during its fly by around atoms by Coulomb electric
forces, pulling electrons from atoms, and due to
its as small mass like an electron, it will again
"zigzag" move and bounce between the atoms, which it
will ionize while losing energy. It brakes
and stops, depending on its energy, similar to the electrons from
radioactivity b-, also
at a depth of about 0.5-4 mm in the substance of water density,
the process of braking and thermalization is similar to that of b-. Only after almost complete braking of the positron (at "thermal" energy) does
its "close" interaction with the electrons occur.
After complete braking, however, the fate of the
positron is completely different from that of the electron b- (Fig.1.6.1 below): upon encounter with the electron,
the electron and positron e+ + e- ® 2 g mutual annihilate,
during which the positron and electron disappear
and transform to two photons of hard radiation g with energies of
511keV, which fly from the point of annihilation in exactly in
opposite directions - at an angle of 180° *). This
perfect angular correlation is widely used in positron
emission tomography imaging in nuclear medicine (§4.3, section "Positron emission tomography PET").
*) These regularities apply exactly in the center
of gravity frame of the positron and electron. The
energy of photons 2 x 511keV is a
consequence of the law of conservation of energy
(rest energy of electron and positron is m0e .c2 = 511keV), the opposite direction 180° is a
consequence of the law of conservation of momentum.
In the case of collisions of positrons of higher energies with
electrons, the angle of flight of annihilation photons would
differ from 180°. However, in the matter, the positron already
have relatively low velocities at the moment of annihilation with
the electron, so that the emitted quanta actually fly in almost
opposite directions.
Positronium
Just before the actual annihilation, the electron e- and the positron e+ can circulate each
other (they orbit the common center of gravity) - they form a
special bound system (similar to a hydrogen
atom) called positronium (Ps). The dimension of
the "atom" of the positronium is twice the hydrogen
atom, the binding energy of the positron is 6.8 eV. Depending on
the mutual orientation of the electron and positron spins, the
positron can be either in the singlet state 1S 0 with oppositely oriented spins -
so-called parapositon p-Ps (1/4 cases), or in triplet
state 3S 1
with concordantly oriented spins - so-called orthopozitronium
o-Ps (3/4 cases).
However, this
system of positronium is unstable, the two
particles approaching each other in a spiral under the emission
of electromagnetic waves; in p-Ps in about 120 ps they
"fall" on each other and there is a self-annihilation
on two photons g. In the case of o-Ps,
annihilation into two photons is prohibited by quantum selection
rules (related to the law of conservation of the spin momentum -
each of the photons has spin 1), so o-Ps would decay in a vacuum
by emitting 3 photons with a relatively long lifetime of about
140 ns.; in the substance, however, the positron bound in o-Ps
much earlier is enough to annihilate with some
"foreign" electron from the surrounding environment,
which has the opposite spin orientation - again two photons g are formed.
The
annihilation of a positron with an electron produces 2 gamma
photons in the vast majority of cases, as mentioned above.
Sometimes, however, more of them can occur, but with a
very small probability (the probability that 2 + n photons will
be formed during e-
e+ -annihilation is proportional an, where a = 1/137 is the fine structure
constant). If a positron interacts with an electron bound in an
atomic shell, the extinction of such a pair may be accompanied by
the emission of only a single photon, and some of the
energy and momentum may be transferred to either the atomic
nucleus or one of the other electrons; however, the probability
of this process is very small and does not apply in practice.
The lifetime
of positrons in substances is in the order of hundreds
of picoseconds. However, the exact value depends on local
electron densities and configurations, which is used in the PLS
(Positron Lifetime Spectroscopy) spectroscopic method. The
investigated material is locally irradiated with a b+- g emitter (most often 22
Na), wherein the positron lifetime is determined by measuring
the delayed coincidence between the detection of photon radiation g of irradiating radionuclides (from 22Na it is g
1274 keV) and detecting the annihilation photons g 511 keV.
When
b+-radiation
passes through the substance, braking and characteristic
X-radiation and Cherenkov radiation are generated in a manner
analogous to b- radiation.
In terms of
the general properties of the interactions of different types of
radiation, positron radiation was also discussed above in the
section "Interactions of positron radiation".
Interactions
of indirectly ionizing radiation
Interactions
of gamma and X radiation
Photons of g
radiation and X-rays
*) do not have an electric charge, so they cannot ionize atoms by
direct electric forces. However, a photon is a quantum of a
rapidly oscillating electric and magnetic field, so when an
electron comes in "close proximity" to this oscillating
field, it can receive electromagnetic energy and
be accelerated by the photon. If this happens to
the envelope electron in the atom, the atom may be excited
or ionized. A photon can also electromagnetically
interact with nucleons in the core - the atomic nucleus
can be excited.
*) Both these X and gamma rays have the
same physical nature (electromagnetic photon radiation) and
largely similar properties, they may differ in the way they
originate. In §1.2 "Radioactivity", part "Radioactivity gamma",
we introduced a terminological agreement, that photon radiation
emitted from atomic nuclei is called radiation g
(even if it has a low energy of a few keV), while radiation
arising from electron jumps in the atomic shell and the braking
radiation of electrons is called X- rays
(even if it has a higher energy of tens and hundreds of keV).
However, photon radiation with very high energies (of the order
of MeV and more) is usually called gamma radiation,
regardless of the way it is generated. Quantum of X and g -radiation moves exactly at the speed of light
in vacuum c (for
interest, however, see below the theoretical note "Is high-energy g
-radiation moving slower than
light?") .
Ordinary photons of gamma and X of lower energies (tens or hundreds of keV) interact
almost exclusively with the electron shell of
atoms. Their interaction with the nucleus is very unlikely (with some exception being the Mösbauer resonant
nuclear absorption described below). Only
at the energies above 5MeV begin to take noticeably manifests the
interactions with nuclei - photonuclear reactions (see below).
The way photon radiation interacts
with matter is determined primarily by its kinetic energy
(wavelength). "Soft" electromagnetic radiation of
longer wavelengths (low energies) behaves mainly like a wave
that interacts collectively with a larger number
of electrons or atoms (which oscillates) in the material
environment, which in the case of light leads to known optical
phenomena of light reflection and refraction. During the
interaction with the atom, the oscillating electromagnetic field
hits either the whole electron shell or most of it, whereas due
to the slower course of the interaction of the binding force of
the electrons, it is enough to "redirected" the
excitation to the whole atom.
As the frequency-energy increases,
the radiation acquires a photon character, wherein the
photons have the properties of free point particles of relatively
high energy. Such photons then interact - collide - individually
with individual electrons, whether free or bound in atoms. At
higher energies, therefore, direct collisions of
photons with electrons are applied ("point-located"
photons can strike individual electrons in atoms directly,
without affecting the surrounding orbitals in the atomic shell). Due to the very short time that the photon is "in
contact" with the electron, the binding forces of the
electrons it is not enough "convert" the excitation to
the rest of the atom.
On the electron side, the mode of
interaction depends on whether the electron is free or how
strongly it is bound in the atomic shell. For free or
weakly bound electrons, the interaction usually has the character
of a direct "collision" of the photon with the electron
and the result is scattering - the photon
"bounces" in another direction and its energy is
reduced by the value passed to the electron (Compton
scatering). However, with electrons
strongly bound in the atomic shell, the photon can interact to
some extent "collectively": the primary photon is first
absorbed by the electron shell, creating a transient excitation
state that then decays spontaneously and emits the received
energy - either again as a secondary photon, or in the form of
kinetic energy of the released electron.
Non-ionization
processes
Without further analysis, we will only mention here the non-ionization
processes that occur during the interaction of
electromagnetic radiation with matter :
- Without interaction - the
quantum of radiation can "free-fly" between the
atoms of matter. This often occurs especially with hard
radiation when passing through light materials
- The Thompson-Rayleigh coherent
scattering of radiation on electrons bound in an
atomic shell occurs in the low energy region. Only
momentum is transmitted, not energy (a light photon is
reflected from the whole atom, whose mass is many times
greater). The interaction with the electromagnetic wave
causes oscillations in the electron shell and the
oscillating electrons then emit back secondary
electromagnetic radiation of the same wavelength but in a
different direction (elastic scattering). All the energy
of the primary photon is transferred to the secondary
photon.
- Thomson scattering on
free electrons is mainly manifests in metals and ionized
plasma, where there are a large number of free electrons.
- Excitation of electrons
on the outer shells of atoms, after which visible or
infrared radiation is emitted during deexcitation.
From
the point of view of the physics of ionizing radiation itself,
these processes have almost no significance - for gamma radiation
they occur only with a very small effective cross section and do
not lead to ionizing effects. However, they are important from
the point of view of atomic physics, the interaction of softer
radiation with atoms. X-ray interference in coherent scattering
on atoms in crystal lattices is used in X-ray
diffraction analysis of the structure of solids
substances (see §3.3 "Radiation
measurement of mechanical properties of materials").
Thomson scattering on electrons is important in plasma physics
and in astrophysics, the excitation and subsequent deexcitation
of atoms is the source of much of the visible, infrared and UV
electromagnetic radiation that we observe in nature.
Ionization
processes
The interaction of g and
X radiation (for short we will in
the next write only g, for X-radiation the situation is analogous) with the substance, leading to ionization effects, can
take place in four different ways marked in Fig.1.6.3 (fifth method, resonant nuclear absorption - the
Mösbauer effect, not shown here, but described in detail below) :

Fig.1.6.3. Four ways of gamma radiation interaction with matter.
- Photo
effect
The photon of radiation g or X here
interacts with the electron e- bound in
the atomic shell, transfers all its energy to it
and disappears (Fig.1.6.3 left) *). The
energy of the photon in this absorption process is
consumed to release the electron from
the atomic shell and to the kinetic energy
of the knocked out photoelectron. The electron that
obtained this energy, is released from the bond in the
atom and flies out with the kinetic
energy Ee = Eg - Eb , given by the difference between the radiation
energy Eg and the binding energy Eb of electron
in the atom. The photoeffect only occurs when the energy
of the incident photon Eg is
higher than the binding energy Eb of the electron on the respective shell.
*) Photoeffect - a complex
radiation-atomic process
The mechanism of the photoeffect is interpreted in the
literature in a rather simplified way, as the direct
ejection of an electron from an atom. In fact, the photo
effect is a relatively complex radiation-atomic
process. This is not a direct
"collision" of a photon with a bound electron.
The electromagnetic field of an incoming photon interacts
with the atomic shell "collectively",
oscillates one or more orbits, giving up all its energy Eg
= h.n and the g photon disappears. The
delivered energy is then concentrated on one electron,
bound in the respective energetically close shell, whose
bond is broken and the electron is released - it is emitted
with a kinetic energy Ee = h.n - Eb .
Another behavior of this emitted
photoelectron e- is the same as for radiation b: it will
"zigzag" move and bounce between atoms, ionize
it is until it finally brakes (and eventually recombines
with some atom). In the place of "vacant" after
the electron that flew out through the photo effect,
immediately jumps the electron from the higher shell in
the atomic envelope, while the energy difference of the
binding energy on the higher and lower shell radiates
in the form of a quantum (photon) of electromagnetic
radiation - emits characteristic X-rays (if it is a shell K, these are lines Ka,b
with energies of about 20-80keV for heavier elements, for
the shell L these are lines La,b
with significantly lower energies).
During this process, however, characteristic
electromagnetic radiation may not be emitted, but as an
alternative phenomenon, energy may be transferred to an
electron on a higher shell, which is then released and
emitted as a so-called Auger electron.
This phenomenon is sometimes interpreted as a process of internal
conversion of characteristic X-rays, although
similarly to the internal conversion of g- radiation,
it is an alternative effect in which energy is
transmitted by electromagnetic interaction directly,
without actual emission of photon -
see Fig.1.2.7 in § 1.2 "Radioactivity", passage "Internal conversion of
gamma radiation".
The efficiency of the
photoeffect depends on the energy of the photons
and the properties of the irradiated material.
Due to its wave properties, the primary photon interacts
collectively with the atomic shell; as the energy
increases, the particle character of the photon becomes
more pronounced and the probability of the photo effect
decreases. In terms of material, the efficiency of the
photo effect, of course, depends on the electron density
- it increases with the proton number Z. The
"bigger" the atom, the greater the probability
of its "hitting" by the photon. With the number
of electrons in the atomic shell, the probability of
absorption of photon energy during the formation of a
transient excited state and the probability of
concentration of this energy on one of the internal
electrons and its subsequent release also increases.
For an effective cross
section sK photo effect
of radiation g with wavelength l and energy Eg ,
running on the K shell of an atom with proton
number Z, an approximate dependence sK ~ Z5.l7/2 ~ Z5/Eg3 (applies provided that
the energy Eg is higher than the binding energy of the
electron on this shell). The
probability of the photoeffect is therefore proportional
to the 5th power of the proton number of the irradiated
atoms and indirectly proportional to the 3rd power of the
energy of the photons g or X. And for a substance overall, this
probability increases with the density of target atoms,
ie with the density of the substance r.
Therefore, the photoeffect occurs most often in g- radiation
with lower energies and in substances with a large proton
number Z. The highest effective cross section for
the photoeffect is when the g- radiation has an
energy only slightly higher than the binding energy of
electrons EK on the shell K or EL on shell L in the atoms of the substance
- resonance phenomenon (bound
electron absorbs electromagnetic energy the more
efficiently its value is closer to the binding energy in
the respective shell). On the graph
of the energy dependence of the effective cross section
for the photoeffect, a characteristic raised
"tooth" appears (see Fig.1.6.4), the almost
perpendicular ascending part of which is sometimes called
the K-edge; analogously, at lower
energies, a less pronounced L-edge appears. The
energy dependence of the photoeffect is an overall
rapidly decreasing curve, interrupted (modulated) by sharp
edges corresponding to the individual energy
levels of electrons in the atomic shell (in more detailed measurements a slight
"splitting" of the absorption edges is observed
due to the fine structure of energy levels in the atom). In general, the photo effect dominates the
area lower energies of photon radiation
- units up to tens of keV. At energies g above
1-2MeV, the probability of a photo effect is already
minimal.
Note:
In visible light, the release of electrons during
interaction with a material (metal or semiconductor - see
§1.1, section "Particle-wave dualism", Fig. "Photoelectric effect
") is referred to as a classical photoeffect
or photoelectric effect. For ionizing radiation,
however, this is an "atomic" photoeffect
taking place at the level of the internal bound electrons
in the atomic shell.
- Compton scattering
If a photon of g or X radiation "collides" with an
electron either free (as in metals
or in the plasma state of matter) or
only weakly bound in an atom (the
energy of the incident photon must be significantly
greater than the binding energy of the electron in the
atom - this weak bond is then not able to transfer the
received energy quickly enough to the whole atom, so the
energy of the interaction is divided only between the
photon and the hit electron),
transfers only part of its energy to it,
flexibly "bounces" away from this electron and
will continue its movemend in a changed direction
and with lower energy - Fig.1.6.3 in the
middle. By kinematic analysis of the collision of a
photon g with a free electron, in which the laws of
conservation of energy and momentum of classical
mechanics of mass points apply (photons
with an electron behave like two "billiard
spheres"), for the energy Eg ' of quantum g', scattered by angle J with respect to the
direction of the primary incident photon g with
energy Eg , the Compton formula can be derived :
E
g ' = E g
/ [ 1 + (Eg
/ moe.c2). (1 - cos J) ] ,
where moe is the rest mass of the electron. The energy of
the scattered photon is thus dependent on the scattering
angle - the larger the scattering angle, the more energy
the photon loses (and the more the reflected electron
gains it) - for backscattering
(ie J = 180°, cos J
= -1) is Eg ' = Eg / [1 + (Eg
/ 0.256) ] - in MeV. Photon radiation is Compton - scattered
randomly in all directions.
The electron bound in the
atom will be released from the atom by this
"collision", will fly out with the
corresponding kinetic energy Eg - Eg' - Eb and will ionize like any other beta radiation.
The probability of Compton
scattering increases with the density of target electrons
in the substance, ie with the mass density of the
substance r and the proton number Z; decreases with
increasing energy of photons. Compton scattering is relatively
most common in g radiation of medium and higher energy and in
substances with low proton number Z (water,
tissue).
Note:
Compton scattering can in principle also take place on
atomic nuclei; however, it has a very low effective cross
section and, due to the large weight of the nuclei, the
change in the energy of the reflected quantum g is also
relatively small. This phenomenon is not applied in
practice, it manifests only corrections material
parameters characterizing the passage of radiation g rays trough
substances.
Compton
scattering can be repeated several times, until the
photon either leaves the substance or loses so much
energy, that it disappears with a photo effect on some of
the electron levels of the atoms.
Compton scattering of photon
radiation is crucial in astrophysical processes in
space. Multiple scattering of high-energy photons on
electrons causes radiation pressure to
maintain the balance of stars against its own gravity and
"carries" energy produced by thermonuclear
reactions from the interior to the surface of stars, into
the photosphere (§4.1 "Gravity
and evolution of stars"
monograph "Gravity, black holes and space-time
physics"). At the
beginning of the evolution of the universe, in the era of
radiation, the scattering of photons on electrons caused
a balance between matter (plasma) and radiation (§5.4 "Standard Cosmological
Model. The Big Bang"
of the above book).
Inverse
Compton effect
The standard Compton scattering of photon radiation
(gamma or X) in substances takes place on electrons that
are essentially at rest, while the
energy of the scattered photons decreases.
In the plasma state, however, there are often free
electrons moving at high velocities (often relativistic). When
scattering photons on fast electrons,
the energy of some photons may increase
if the scattering occurs approximately in the direction
of electron movement. When a fast electron collides with
a photon, the electron transfers part of its energy to
the photon, which therefore has a higher energy
after the collision (higher
frequency - shorter wavelength).
This process is sometimes referred to as the inverse
Compton effect.
In addition to laboratory
plasma experiments, this process takes place on large
astrophysical scales in interstellar space with
multiple interactions of relativistic cosmic ray
electrons with photons of cosmic relic radiation (whose energy can increase up to the level of
gamma radiation). It is also
manifest in high-energy astrophysical
processes, such as accretion disks of black holes in quasars
- see eg §4.8, passage "Quasars as standard
candles".
Both basic phenomena - the photo effect and
Compton scattering - are often combined in the
interaction of photon radiation in matter. In most cases, Compton
scattering occurs first, often multiple, and scattered photons
with lower energy then interact with the photo effect.
- Electron-positron
pair formation
At high energies of gamma photons, interaction may occur
not only with "real" electrons in atomic shells
(or free),
but also with "virtual" electrons
hidden in a quantum vacuum. If a photon of radiation g with a
sufficiently high energy (greater than
2.meo .c2 = 1.022 MeV - the sum of
the rest energies of an electron and a positron, which
are the same) flies into the
substance, then as it passes around the atomic nucleus,
with electromagnetic interaction with a strong
Coulomb field of nuclei, the photon g can convert *) into
a pair particles electron +
positron : g
® e- + e+. The energy of the primary photon is consumed
to form an electron-positron pair, the rest is manifested
as the kinetic energy of the formed e-
and e+ particles. Of this pair, only an electron
remains (after ionization braking
by the same mechanism as b-) in the substance as a
permanent particle. After braking and stopping in the
substance, the positron annihilates with
some of the other electron, to produce two photons of
radiation g with an energy of 511keV, as already described
above for radiation b+.
The process of electron-positron pair formation is most
applied at high radiation energies g and in substances
with a high proton (atomic) number.
*) Spontaneous conversion of a high-energy photon of
radiation g during its movement in a vacuum into an
electron-positron pair is not possible due to
the law of conservation of momentum: the
sum of the momentums of the resulting electron and
positron is less than the momentum delivered by the
primary photon. Therefore, a third particle is needed to
carry away the excess momentum; the particle that takes
over this excess in the momentum balance of the
electron-positron pair is the atomic nucleus, in whose
strong Coulomb field an e- e+ pair were
formed.
The
conversion of a photon to an electron-positron pair takes
place in the immediate vicinity of the atomic nucleus
under the influence of its electric field, so the larger
the charge of the nucleus, the greater the probability of
the formation of an electron-positron pair. A more
detailed analysis shows that the effective cross section
of electron-positron pair formation is proportional to
the Z2 - square of the proton number of the atoms of
the substance.
The formation of
electron-positron pairs can also occurs in the field
of electrons in the atomic shell, but with
significantly lower efficiency (small effective cross
section); it manifests itself more noticeably only at
high energies of gamma radiation (> 30MeV) - see small
dotted red curves at the bottom right in the graphs in
Fig.1.6.4.
For the highest
energies of g
radiation
- hundreds of MeV, GeV, TeV (they occur in cosmic
radiation and in particle interactions at large
accelerators) - the effective cross section for the photo
effect is already very small and also the efficiency of
Compton scattering is significantly reduced. The primary
interaction of this radiation with matter takes place
mainly through the process of electron-positron
pair formation. These generated electrons and
positrons, due to their high energy, can cause a whole
cascade of further interactions to form a large
electromagnetic and hadron particle spray
(discussed above in the section
"Multiple
Interactions - Cascades of Interactions and Particle
Sprays").
The formation of
electron-positron pairs from high-energy photon radiation
is decisively applied in astrophysical processes
in space. At the beginning of the evolution of the
universe, in the Lepton era, the universe was
filled with a dense and hot electron-positron plasma, in
which the equilibrium of annihilation was e-
+ e+ ® 2g and the formation
of g ® e-
+ e+ electron-positron pairs (§5.4
"Standard cosmological model. The Big
Bang" in
monograph "Gravity, black holes and space-time
physics"). In the later
phases of the universe, an interesting effect in the
evolution of stars is the e-
e+- instability of the inner parts of
very massive stars at the end of their lives, which can
cause their thermonuclear explosion and
complete scattering into a cloud of rapidly expanding
gases (passage "Formation of
electron-positron pairs"
in §4.1" Gravity and evolution of stars"
monograph "Gravity, black holes and space-time
physics") and thus
prevent the otherwise inevitable formation of a neutron
star or black hole.
Effective
cross-section of gamma radiation absorption in matter
The total effective cross-section of
the interaction of photon (X, gamma) radiation with matter is given by the sum for
photoeffect, Compton scattering and electron-positron pair
formation (nuclear photoeffect and
formation of heavier particles (pions,
hyperons) has an effective cross section
significantly lower). A typical dependence
of the effective cross section of the interaction on the energy
of gamma radiation Eg is graphically shown in Fig.1.6.4 for light material (water), medium-heavy (iron) and heavy material (lead). The overall trend in the
field of low and medium energy (units up to
hundreds of keV) is a significant
decrease in the resultant ("Total")
effective cross section with an increase in
energy Eg (except for smaller "teeth" - the edges of the
local increase in the vicinity of the binding energy of electrons
on the shells K, L, M). For high energies (MeV), this decrease gradually
stops and is replaced by a slight increase in the effective cross
section due to the formation of electron-positron pairs e-e+.

Fig.1.6.4. The energy dependence of the effective cross section
of the interaction of photon radiation (gamma, X) with the
substance for the photoeffect, Compton scattering and
electron-positron pair formation - is expressed by appropriate
contributions to the linear absorption coefficient m (normalized to
density r). In the area of lower energies, resonantly increased
"teeth" of the photoeffect efficiency can be seen in
the vicinity of the binding energy of EK electrons on the K shell - K-edge ,
analogously L and M edge.
Due to the large range of energy values and
effective cross sections, it is necessary to use a logarithmic
scale - graph [log-log] for a clear display.
- Nuclear
photoeffect ( photonuclear
reaction )
If the quantum of radiation g has a sufficiently
high energy - greater than the binding
energy of nucleons in the nucleus, they can cause a nuclear
reaction directly in the nucleus (see §1.3), in which a
neutron or proton is ejected from the nucleus (Fig.1.6.3
right): photonuclear reactions (g, n), (g, p); at
high energies g (tens of MeV) or even more particles: (g, 2n), (g, np), (g, 2p), (g, a). The
simplest photonuclear reaction is the ejection of a
neutron from the deuterium nucleus g + 2H1
® p + n (ie
its fission into a proton and neutron), which has a threshold energy of 2.23 MeV. For
heavier nuclei, a substantially higher radiation energy g, higher
than about 8-10 MeV, is usually required to produce a
photonuclear reaction. The resulting nucleus after the
photonuclear reaction can be radioactive - we
say that the so-called gamma-activation
occurs.
When irradiating heavy
nuclei in the uranium region (such as 238U) and
transurans with hard radiation g with an energy
higher than 15MeV, such nuclei can be photofission
into two fragments - medium-heavy nuclei from the middle
of the Mendeleev table, similar to their cleavage by
spontaneous or neutron action.
At very high gamma radiation
energies exceeding »150 MeV, then are already new elementary
particles produced (such as p- mesons,
at even higher energies also K-mesons and hyperons), as
mentioned in more detail in §1.5 "Elementary
particles".
- Resonant Nuclear
Absorption - Mössbauer effect
If the quantun of radiation g has an energy
exactly equal to the energy of a certain excited nuclear
level, such a g -photon can be absorbed by the nucleus,
thereby the core is excited to the
appropriate energy level. Immediately, deexcitation
occurs, emitting a photon g of the same energy
(which, of course, generally flies out in a different
direction than the incident photon); it is therefore nuclear
fluorescence. While excitation of resonant
fluorescence is common in the atomic shell, resonant
nuclear absorption does not normally occur and can only
be performed in a special experimental
arrangement. The reason is that the nuclear
absorption lines are very narrow (about
10-5-10-9 eV), so it is very difficult to "hit -
tune" energetically into such a narrow range. Even
when we irradiate with radiation g the same energy,
emitted by certain (daughter) excited nuclei, a substance
composed of the same isotope of the element which
radiation g emits, there is no nuclear absorption, because
the actual energy of the quantum differs somewhat from
the energy of the nuclear level for the following reason:
When the nucleus passes from the excited state, the
energy Eexcit given by the difference between the initial
(excited) and final (ground) state is emitted. However,
all this energy is not carried away by the photon g, but
according to the law of action and reaction this energy
is divided between the energy Eg of the
emitted quantum g and the kinetic energy Ek
of the
reflected nucleus,
ie Eg = Eexcit - Ek < Eexcit .
Conversely, upon the impact of the photon and its
absorption, part of its energy is also converted into the
kinetic energy of the reflected nucleus, so that a higher
energy Eg of incident radiation is required to excite the
nucleus to the energy Eexcit (by this value Ek). The energies of the emitted and absorbed
radiation g are thus shifted relative to
each other by the value DE = 2.Ek . The kinetic
energy of the reflected nucleus follows from the law of
conservation of momentum, ie when the original nucleus is
at rest, the momentum pg of the
photon g must be equal to the momentum pnucl reflected
nucleus, so Ek = p2nucl/2mnucl = p2g /2mnucl = E2g /(2mnucl.c2) » E2excit/(2mnucl.c2). For transitions with energy Eexcit approx.
100 keV in medium-heavy nuclei value Ek is several
hundredths of an eV, which significantly exceeds the
energy width of the nuclear level. In order for resonant
nuclear absorption to occur, it is necessary to replace
this lost energy of the reflected emitting and absorbing
nuclei in a suitable experimental arrangement - to compensate
with the Doppler effect. This can be achieved in
three ways :
¨ 1. By mechanically moving the
source towards the absorber (eg by shifting, placing the
source on a rotating disk, by electro-mechanical
oscillation) to increase the frequency (and therefore
energy) of the emitted radiation by the Doppler effect.
The required speed v this movement is given by the
relation v/c = Ek/Eg . In this way, in 1951, P.B.Moon was able to
observe the resonant scattering of radiation g of 412keV
energy emitted by the daughter nucleus of 198Hg of the
radioisotope 198Au. In 1958, R.L.Mössbauer demonstrated the resonant
absorption of radiation g of energy
129keV emitted by the daughter nucleus 191Ir of the
radioisotope 198Os *); according to him, the relevant phenomenon
was called Mössbauer's.
*) In the Mössbauer experiment,
the source and absorber were also cooled to a temperature
of 88 °K (lower than the so-called Debye temperature of
the material), which increased the probability of
radiation emissiong without reflection of the emitting core, and
similarly absorption. If the energy of the reflected
nucleus E k is not sufficient to excite the crystal lattice
in which the atom is bound from the ground state to the
first excited state, no energy can be transferred to the
crystal lattice and the emission of radiation g occurs
without reflection of the nucleus. Nuclear resonance
absorption then has its maximum around the zero speed of
movement of the source relative to the absorber.
¨ 2. By heating
the radioactive source so that the Doppler effect
"sweeps" the frequencies and thus increases the
line width of the emitted radiation g.
¨ 3. Using the
previous decay b or nuclear reaction to obtain a suitable
velocity of the emitting core to achieve a Doppler
frequency shift.
The method of Mössbauer
spectroscopy, mentioned in §3.3, is based on
the Mössbauer phenomenon of resonant nuclear absorption
of g radiation using method 1.
The most suitable conditions for the
realization of the Mössbauer phenomenon are for nuclei
of the iron isotope 57Fe. The radionuclide 57
Co is used as the radiation source g, which
decays to an excited nucleus 57Fe with a half-life of 270 days by electron
capture. This nucleus emits 692keV (0.14%), 136keV (11%),
122keV (87%) and 14.4keV (9%) g radiation when
deexcited. It is the radiation g of the partial
transition from the excited level with an energy of 14.4
keV that is suitable for excitation of resonant nuclear
absorption due to its low energy. Due to the high Debye
temperature Fe (360 °K), the Mössbauer effect occurs
even at normal laboratory temperatures, while the Doppler
frequency shift required to compensate for the reflection
of the 57Fe core is achieved by mechanical displacement
of the source at speeds of only the order of 1 mm/s.
Note: High sensitivity Mössbauer effect of resonant
nuclear absorption g -radiation 14.4keV 57Fe was used in 1960 by R.V.Pound and G.A.Rebka
to measure the gravitational frequency shift
in the Earth's gravitational field, which was an
important test of Einstein's general theory of relativity
as a physics of gravity and spacetime - see §2.4 "Physical
laws in curved spacetime",
passage "Gravitational frequency
shift" in the
book "Gravity, Black Holes and the
Physics of Spacetime".
Secondary radiation generated by
interactions of X and g with matter
In the interactions of primary radiation g and X with matter discussed
above, there are processes in which secondary particlres
and radiation is generated :
- Electrons released from the atomic shell due to the photo
effect and Compton scattering of primary g- radiation.
At higher energies of g- photons (several MeV), these
secondary electrons move in largely the same
direction as the primary gamma-beam. This leads
to a specific depth dependence of the
ionizing effects of hard gamma radiation in matter:
Secondary electrons, which usually have the direction of
the primary beam and also high energy, cause more and
more ionization. Thus, as high-energy radiation passes
through the substance in depth, the number of secondary
electrons increases and ionization
increases. For hard photon radiation, therefore,
the maximum radiation dose is no longer on the surface (as is the case with soft radiation), but shifts somewhat to a depth,
depending on the radiation energy (depths
of the maximum dose in water or tissue for different
photon radiation energies are approximately: 1MeV ...
4mm; 5MeV ... 1cm; 10MeV ... 2.5cm; 25MeV ... 5cm). In radiotherapeutic terminology, this
phenomenon is called the build-up
effect - the onset of the dose with depth (§1.6, passage "External irradiation
with gamma, X and electron radiation (teleradiotherapy )").
- Compton scatered g and X-ray is the most important
component of the secondary radiation, which is also
reflected in practical applications.
- Characteristic
X-radiation following
after deexcitations in the atomic shell after the photo
effect of primary g- radiation.
- Auger electrons formed by internal conversion of characteristic
X-rays.
- Braking radiation generated during the movement of secondary
electrons and positrons in matter by changing their
velocity during the Coulomb interaction in atoms.
- Electron and positron
radiation arising from
primary high-energy g-
radiation during the formation of
electron-positron pairs.
- Annihilation g-radiation with an energy of 511 kV, arising from the
annihilation of positrons formed during the formation of
electron-positron pairs.
- Light radiation
generated during deexcitation of
electrons on the outer shells of the atomic envelope,
during Cherenkov emission of secondary electrons (it was discussed above in the passage "Cherenkov radiation"), or during
deexcitation in the luminescent centers of certain
substances (scintillators). It is visibly manifested
mainly in optically transparent substances.
Photoelectrons, Auger
electrons and electron-positron pairs are mostly absorbed in the
substance, only a very small part of them can fly out of the
layers at the surface of the irradiated substance. However,
Compton-scattered g -radiation, characteristic X-radiation, braking
radiation, and annihilation g
-radiation can easily fly out of the
irradiated substance and thus enrich the original field of g- radiation.
Secondary light radiation can be used in the case of
optically transparent substances; has an important use in scintillation
detection and spectrometry of g - rays - see §2.4 "Scintillation detection
and spectrometry of gamma rays",
or in the detection of Cherenkov radiation using
photomultipliers. As stated above in the passage "Secondary radiation generated by
radiation-substance interactions", for the amount of secondary radiation emitted by
an irradiated body, is sometimes called albedo.
For X and g radiation, the albedo of common substances (such as
water or living tissue) is very low, below 1%. Is caused mainly
by Compton scattering, partly also by X-ray fluorescence.
Theoretical
curiosity:
Is high-energy g-radiation moving slower than light ?
All electromagnetic radiation
propagates in a vacuum at exactly the speed of light c ,
independent of the movement of the source and the observer. This
is a basic finding, firmly rooted in the special theory of
relativity. Regardless of the wavelength - speed c
propagates radio waves, visible light *), X and gamma radiation.
*) The classical dispersion
observed in light in the matter's optical environment originates
in the (collective) interactions of the electromagnetic wave with
the atoms of matter; does not occur in a vacuum. This is
something else ..!..

Influence of fluctuations in space-time geometry on the speed of
motion of high-energy photons of gamma radiation.
However, in connection with
quantum-gravitational effects leading to fluctuations in
space-time geometry (see §B.4
"Quantum Geometrodynamics" of the book "Gravity, Black Holes and Space-
Time Physics") , there may be
phenomena that may somewhat call this basic statement into
question in certain circumstances. The figure shows a situation
where two photons are emitted from a certain source at the same
time: one photon with lower energy, ie longer wavelength, the
other photon of high-energy gamma radiation with a very short
wavelength. For radiation with a longer wavelength, the
quantum fluctuations of the metrics are averaged
and completely smoothed out in the corresponding longer scale, so
that this radiation will move in the classical vacuum exactly at
the speed of light v = c. Photons of high-energy radiation g however, with a
very short wavelength, they will be "more sensitive" to
fine fluctuations in space-time metrics than low-energy photons.
Such waves will move along a slightly undulating geodetic path,
photons will in a sense "penetrate - copy" the
irregularities in the path, caused by subtle metric
perturbations, and their effective velocity vef will be slightly less
than c . We can compare this to the movement of a car with
small wheels and large wheels on a bumpy road: when driving the
wheels at the same circumferential speed, a car with small wheels
will travel a little slower than a car with a large wheel
diameter.
*) This phenomenon cannot
be considered as a violation or failure of a special theory of
relativity, which is exactly valid in flat spacetime without
metric defects.
These differences are manifested
only at very high energy g, in the area of GeV and TeV. Here, too, the differences
in speed are very small (of the order of 10-20), without the possibility of laboratory measurements.
In the future, they could only be demonstrated by a time
comparison of the detection of light and flashes of hard g- radiation from
catastrophic processes in outer space. At cosmological distances
of billions of light-years, even these slight differences in
speed could "accumulate" and have measurable effects
(the problem, however, is to distinguish these differences from
the differences in emission times in the sources themselves.?..).
Interactions with
quantum-gravitational fluctuations of space can lead to
dissipative phenomena and slight modification of
kinematics not only for hard photon radiation, but also
for high-energy particles in universe.
Neutron radiation and its interactions
Under neutron radiation means a stream of moving neutrons.
Neutrons are normally bound in nuclei by a strong interaction,
along with protons. They are released from the nuclei by nuclear
reactions, which arise during irradiation with
high-energy particles from accelerators and during the fission of
heavy nuclei. Intensive sources of neutron radiation
are nuclear reactors, whether fission or experimental
fusion thermonuclear (§1.3, part "Fission
of atomic nuclei" and "Fusion
of atomic nuclei"). Specific small charged particle accelerators (mostly
deuterons, with a tritium target) called neutron generators
(§1.5, section "Charged particle
accelerators", section "Neutron generators")
are constructed as laboratory sources of
neutrons. However, the most common are radioisotope neutron
sources consisting of a mixture of a- emitter with a light
element such as beryllium (a mixture of 241Am + Be, 239Pu + Be, 226Ra + Be, 210Po + Be). Energetic alpha radiation ejects neutrons from
beryllium nuclei by the reaction 9Be (a, n) 12C. Heavy transuranic radionuclides are rarely
used, most often californium-252, during the spontaneous fission
of which neutrons are released (§1.3,
"Transurans").
In a vacuum, neutrons move freely
and without resistance, but their "range as neutrons"
is not unlimited as might be expected: free neutrons
spontaneously decay by radioactivity b- with a half-life of about 13 minutes into protons,
electrons and (anti)neutrinos. Since neutrons do not have an
electric charge, they do not ionize themselves as they pass
through the substance (this is indirectly ionizing radiation).
The ionization of the environment is caused only by secondary
particles, which are formed during the interaction of
neutrons with the nuclei of atoms (reflected light nuclei, g radiation,
protons, alpha particles, etc.).
After entering the substance,
neutrons interact almost exclusively with atomic nuclei (not with
electrons in the shell), in four ways :
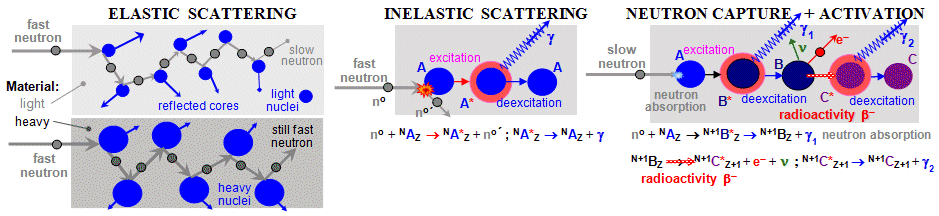
Basic ways of neutron interaction with
matter
- Elastic scattering
neutrons on nuclei is the most common way of interacting
fast neutrons as they pass through the environment,
especially with light nuclei. The flying neutron hits the
nucleus, transfers part of its kinetic energy to it,
bounces off it (similar to billiard balls) and continues
to move with a changed direction and reduced energy. Due
to its positive charge, the reflected nucleus causes
ionization and excitation of the surrounding atoms during
its movement, thus losing its energy. The energy
transferred by elastic neutron scattering is greatest for
hydrogen nuclei (almost half of the energy is transferred
here in a single collision) and decreases with increasing
mass (nucleon number) of the nuclei. Therefore, fast
neutrons are slowed down the most by substances
containing light elements (hydrogen, beryllium, carbon,
etc.); such substances may serve as effective neutron
moderators (top left in the
image; scattering on heavy nuclei slows down neutrons
only slightly - bottom left).
- Inelastic scattering , in
which the neutron again transfers part of its energy to
the nucleus A, but this energy is used to increase
the internal energy of the nucleus rather than the
mechanical motion of the nucleus - excitation of
the nucleus A* occurs (in
the picture in the middle). When
the nucleus returns to its original state (deexcitation
of the excited nuclear levels), a gamma photon
is emitted A* ® A + g, which already induces ionization by the
mechanisms described in the previous paragraph (photo
effect, Compton scattering, ...). This secondary gamma
radiation is used in some analytical methods (see eg §4.3., part "Neutron
- stimulated emission computed tomography (NSECT )").
- Radiation capture , in
which the neutron is absorbed by the nucleus and remains
bound in it - it is a nuclear reaction no + NA Z
® N+1B*Z ; subsequently, one or more photons of gamma
radiation are emitted (during deexcitation of nuclear
levels aroused by neutron absorption) B* ® B + g1 . Gamma radiation then already induces
ionization. Further ionization can then occur
subsequently and in the long term: the nuclei absorbed by
the neutron are often radioactive and
decay with the emission of other ionizing radiation,
especially beta- and gamma: N+1BZ®N+1C*Z+1+e-+n, C*®C+g2 . Radiation
capture of neutrons is most effective for slow,
low-energy neutrons, especially for "thermal"
neutrons with an energy of only about 0.025eV
(corresponding to the thermal motion of atoms) and has a
very different effective cross section for different
nuclei. The most effective neutron scavengers include
boron and cadmium, which are therefore used as shielding
materials for neutron radiation and for neutron flux
control in nuclear reactors. Neutron capture in nuclei is
used in a very sensitive analytical method neutron
activation analysis (§3.4,
section "Neutron activation analysis").
- Nuclear reactions in
which, after the neutron enters the nucleus, another
particle is emitted, such as a proton or an alpha
particle (the previous method
actually belongs to the category of nuclear reactions,
but without the emission of a heavy particle), which ionize. The same applies to the
subsequent activation as mentioned in the previous point.
Nuclear reactions induced by neutrons are mentioned in
more detail in §1.3 "Nuclear reactions". Radiation capture and other
neutron-induced reactions are used for the production of
artificial radionuclides, especially b-, in
nuclear reactors (see §1.4,
section "Production of
artificial radionuclides").
In practice, the individual
mechanisms of interaction of neutron radiation with matter are
often combined. E.g. fast neutrons easily penetrate the
substance, they quickly lose their energy during elastic or
inelastic collisions, especially with light nuclei; these
reflected nuclei then ionize and excite the surrounding atoms.
After slowing down, neutrons enter the nuclei and cause nuclear
reactions there with the formation of radioisotopes - neutron
activation, which can become a long-term source of
ionizing radiation. We do not mention here the interactions of
neutrons with very heavy nuclei in the area of uranium and
transuranium, leading to nuclear fission, which
is discussed in more detail in §1.3 "Nuclear
reactions", part "Fission
of atomic nuclei".
Neutrinous
radiation
Although in terms of particle fluency, neutrino radiation is one
of the most abundant and most intense radiation in nature,
its radiation significance is negligible
(practically zero) and usually does not even classified as
ionizing radiation. This is due to the extremely small effective
cross-section of the interaction of neutrinos with the substance.
The origin and properties of neutrinos are discussed in detail in
§1.2, section "Neutrinos-"ghosts"
between particles".
"Vizualize"
of invisible ionizing radiation ?
Ionizing radiation is invisible to our eyes, we
can only register it using special methods of detection
and spectrometry (Chapter
2 "Detection and spectrometry of ionizing radiation"). For better clarity,
however, it would be appropriate to somehow directly "make
visible" this radiation, respectively its
interaction with the substance. One of the methods is described
in §2.2 - 3-D gel dosimeters; however, it is a relatively complicated and demanding
method, it is used very rarely. There are two other ways to
directly and easily "make visible" the passage of
ionizing radiation through a substance: Cherenkov
radiation in an optically transparent environment (even in water ) and
scintillation radiation (preferably
in a liquid scintillator).
We used these methods experimentally for electron and photon
beams at our workplace and for proton beams at PTC :


The results of these measurements are discussed in more detail in
§3.6, passage "Make the invisible
visible" - display of
radiation beams").
Radiation
absorption in substances. Shielding.
All of the above-described
mechanisms of the interaction of radiation with matter cause a
certain part of the quantum of ionizing radiation to be absorbed
as it passes through the substance. With low-penetrating
radiation, practically everything is absorbed, with penetrating
radiation, part of the quanta is absorbed and part passes. We
will deal mainly with the absorption of g- radiation, which is
penetrating.
Different absorption of ionizing
radiation depending on the type and energy of radiation,
thickness and density of irradiated material is used in a number
of radiation analytical methods, described in more detail in
Chapter 3. It is mainly X-ray diagnostics (§3.2
"X-rays - X-ray diagnostics"), defectoscopy, measurement
of thicknesses and densities of materials or height of levels (§3.3 "Radiation
measurement of mechanical properties of materials"). The absorbed radiation
energy is used in radiation technologies, especially in
radiotherapy (§3.6 "Radiotherapy"). And on the phenomenon of absorption in suitable
materials is based shielding and collimation of ionizing
radiation (see below "Ionizing
radiation schielding').
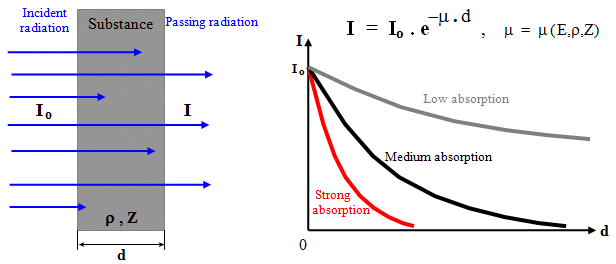
Fig.1.6.5. Basic regularities of absorption of ionizing radiation
in matter of density r, proton number Z and thickness d
.
In the exponential graph on the right,
"low-medium-strong" absorption is meant only
ideologically and unspecified: "strong" absorption
occurs either for low-energy gamma radiation and / or for heavy
shielding material; "low" absorption can be caused by
either high radiation energy and / or light material.
Fig.1.6.5 on the left shows the basic situation
where we place a layer of absorbing substance
(with density r and proton number Z) of thickness d
in the path of a parallel beam of radiation g of initial intensity Io. Part of the
radiation is absorbed, the intensity of the transmitted radiation
is denoted I. On what will depend the amount of absorbed
and passed radiation? Of course, primarily on the thickness
of the material d, where the dependence will be exponential
(it is derived below) :
where the absorption coefficient m is called the linear
attenuation factor. Its value depends on the density
and proton number of the absorbent material and
significantly also on the radiation energy Eg : m = m(r, Z, Eg). The
linear attenuation factor is higher the higher the density r and the proton
number Z of a given substance and the lower the higher the
radiation energy Eg .
The total linear attenuation coefficient m is the sum of the
individual partial absorption coefficients for
photon radiation (gamma, X) for the photo effect mf , the Compton scattering mC and the formation of electron-positron pairs me : m = mf + mC + me . The relative
proportion of these subcomponents depends on the material and
very significantly on the energy of the radiation g (see Fig.1.6.4 of
the section "Effective cross section of the absorption of
gamma radiation in substances").
In addition to
the linear attenuation factor m, a mass attenuation
coefficient m/r is sometimes introduced which is independent of
density. Furthermore, especially for technical purposes (such as
shielding design - see below), instead of the linear attenuation
coefficient m, the values of the so-called
absorption half - layer (half-thickness) d1/2 = ln2 /m @ 0.693/m are often
given in the tables, which is such the thickness of a layer of a
given material, which halves the intensity of that radiation. And sometimes the mass half-layer
of absorption r/d1/2 [g/cm2] is given, which depends mainly
on the energy and the type of radiation.
Note: The basic property of
an exponential function with a negative exponent is that it
approaches zero up to the limit at infinity. After passing the
layer d = d1/2, exactly half of the particle-quantum is absorbed: I(d1/2) = Io /2. At the end of the
next half-layer, half of the half of the particles remain, ie a
quarter: I(2.d1/2) = Io /4. And so on to infinity, so only in the limit d ® ¥ will the limit be I(d®¥) = 0 and all
particles will really be absorbed.
This would mean that the radiation can practically never be
completely shielded. However, this is only theoretically the
case. In fact, each emitter emits only a finite number
quantum particles. After passing through a sufficient thickness
(tens or hundreds of d1/2) in practice, the last quantum is
always finally absorbed ...
Attenuation of a wide
beam of radiation
The exponential law applies exactly to a parallel narrowly
collimated beam of radiation, where is takes into account only
the photons that have passed through the absorber without
scattering. In the case of a wide beam of
radiation without collimation, the detector in the space behind
the absorbing material can also be affected by scattered
radiation, so that the intensity I will be somewhat
higher. This circumstance is expressed in the exponential law of
absorption by introduction of the so-called growth factor
B: I = Io.B.e-m .d. The magnitude of the growth factor (B ³ 1) depends on the
thickness and type of substance, the energy of the radiation, as
well as on the geometric arrangement of the radiation source, the
translucend layer and the detector.
Effective
cross-section of interaction and linear attenuation coefficient
In §1.3 "Nuclear reactions" and §1.5 "Elementary
particles" the concept of effective cross-section
of interaction s was introduced, which geometrically expresses the
probability of a given type of interaction. This is the effective
cross-section of the interaction of radiation, eg g, with the atoms of
the substance (either the total effective cross-section of the
interaction, or individual partial effective cross-sections for
photoeffect, Compton scattering and electron-positron pair
formation). In the interaction of a parallel beam of radiation of
intensity I , 1 cm2 of the substance passes every second I particles,
which interact with the atoms of the substance with an effective
cross section s. The number of atoms in 1cm3 is L » r.mp/N, where r is the density of the material and N is the
nucleon number of the atoms of the substance. The layer dx of
thickness dx contains in 1cm2 of L.dx atoms, each of which represents an
radiation-effective shielding surface of the interaction of size s, so that the
intensity I of the beam is attenuated by -dI = I. s .L.dx. By
integrating this differential relation, we obtain for the
intensity I (x) of the beam at depth x the relation I(x) =
Io.e-s.L.x = Io.e-m .x, where Io is the original intensity of the beam on the surface
and the coefficient m = s .L = s . r .mp /N represents the linear attenuation factor.
The linear attenuation factor is proportional to the density r of the absorbing material
and, thanks to the effective cross section s, significantly depends on
the radiation energy and also on the proton number of the atoms
of the substance (because the proton number also determines the
electron density of atoms).
In addition to the linear attenuation factor m, a mass
attenuation coefficient m/r is sometime introduced, which is independent of density.
Absorption of
polyenergetic beams of radiation - "spectrum hardening"
The beams used in X-ray diagnostics and radiotherapy usually have
a continuous spectrum covering a relatively wide
range of photon energies. Here we observe deviations
from the exponential course of attenuation. The initial layer of
material here weakens mainly low energies, while leaving high
energies almost without absorption. In the depth of the material,
this increases the proportion of higher energies - the beam
becomes more penetrating, its spectrum "hardens".
Due to this spectral shift, the course of attenuation of
polyenergetic beams at depth is no longer exactly
(mono)exponential, but the rate of absorption gradually decreases
with depth.
The "spectrum hardening" effect is used to filter
the X-ray beam spectrum (§3.2. "X-rays - X-ray diagnostics", passage "Sources of X-rays - X-ray tubes").
Shielding
of ionizing radiation
In many applications of ionizing radiation, it is necessary to
prevent ionizing radiation from penetrating to certain
places or from certain directions - it is therefore necessary to
shield a certain part of the radiation. This need
arises, for example, for protection against
ionizing radiation (§5.3, section "Factors of radiation protection"), for detection of ionizing
radiation (where the detector needs to be
shielded from the background, or to detect only radiation from
certain directions - §2.1, passage "Shielding, collimation and
filtration of detected radiation"), in imaging methods such as
scintigraphy (where by collimation we detect only radiation from
precisely defined directions - §4.2, part "Scintigraphic collimators"), in radiotherapy
where by collimation we define a narrow beam of radiation
affecting only the target tumor tissue (§3.6,
part "Isocentric
radiotherapy"), etc. With reference to the above-mentioned mechanisms
of the interaction of radiation with matter ("Interaction of ionizing
radiation in the passage of matter") we will briefly mention
here some general principles for achieving optimal
shielding for individual types of radiation.
Gamma
radiation shielding
The shielding properties of light, medium and heavy materials
depending on the energy of gamma radiation are plotted above in
Fig.1.6.4 in the section "Effective cross section of gamma radiation
absorption in substances". For gamma and
X radiation, the most effective shielding materials are substances
with a high
specific gravity (density) and a proton number, ie with a high electron density - especially lead, tungsten, or uranium *). Lead
containers for the transport and storage of g-radiators, lead sheet metal screens,
shaped lead bricks, etc. are used.
A layer of 2 mm thick lead is sufficient for effective shielding
of gamma radiation with an energy of approx. 100 keV; the higher
the energy of the gamma radiation photons, the thicker the
shielding layer must be used. If is the need to maintain the optical
visibility, used lead glass
with a high content of lead oxide in the melt.
*) Due to its high density (19g/cm3 ) and proton number
(Z = 92), uranium is a very good shielding
material for hard radiation g. In addition to the high price, its main disadvantage
is that uranium itself is radioactive (see
§1.4, passage "Radioactive
decay series"). Its
specific activity can be reduced by removing the isotope 235U, which (despite
its low proportion of 0.7%) forms a significant component of the
radioactivity of natural uranium. The so-called "depleted
uranium" - 238U, thus formed, has a
specific activity of approx. 12 kBq/g and is suitable for
shielding preparations with high activity and small dimensions.
Uranium is not suitable for shielding and collimation of low
activities and weak radiation fluxes, where the own radioactivity
of the shielding material is undesirable.
For economic reasons, it is sometimes more
advantageous to use larger material thicknesses with lower
specific shielding capabilities, if the configuration of the
radiator, irradiated substances and detector allows it. This is
usually the case with the construction solution of workplaces
with ionizing radiation, where, in addition to brick masonry, denser building materials are used - concrete with event. barite admixture, barite plasters, etc.
Absorption
half- thickness
The thickness of the shield required depends on the density
(and nucleon number) of the shielding material, the radiation
energy g and the attenuation required. In addition to the linear attenuation factor m, the
tables often give the values of the so-called absorption half - layer
(half-thickness) d1/2 = ln2
/m @
0.693 /m, which is the
thickness of the layer of shielding material that attenuates the
intensity of the radiation by half (2 half-layers then to 1/4 , 3 half-thickness to
1/8 etc. - the
shielding effect increases exponentially with the shielding
thickness according to the above formula). For some common
materials and radiation energies g (resp. X), the half-layers are as follows
:
|
| E g
[keV] |
water |
concrete |
iron |
lead |
| 100 |
42 |
17 |
4.8 |
0.15 |
| 200 |
51 |
21 |
6.6 |
1.4 |
| 500 |
74 |
32 |
11.1 |
4.2 |
| 1000 |
102 |
45 |
15.6 |
9.2 |
| 2000 |
144 |
59 |
21 |
13.5 |
| 5000 |
231 |
905 |
28.8 |
14.7 |
The attenuation of the radiation
intensity by the absorption layer of thickness d can be expressed by means of a half
-thickness d1/2 by a simple relation I / Io = 2 -d/d1/2
. A shield with a thickness
corresponding to 7 half-thicknesses attenuates the radiation to about 1%, and 10 half-thicknesses below 0.1%.
Beta
radiation shielding
To shield radiation b- are
sufficient lightweight materials (such as plexiglas or aluminum) with a
thickness of about 5-10 mm. For harder beta radiation, it is best
combined with a subsequent thin
layer of lead to shield the braking electromagnetic
radiation generated by the braking of
electrons b in the shielding material. Lead itself is not
the optimal shielding material for energetic radiation b, because it
produces hard and intense braking radiation, for the shielding of
which it is necessary to use an need thick layer of lead.
For shielding positron
radiation b+
in addition to the layer of light material, it is necessary to
use relatively thick layers of lead (approx. 3 cm), or tungsten
to shield hard gamma radiation with an energy of 511keV, arising
from the annihilation of positrons b+ with electrons e-.
Alpha radiation shielding
Radiation a,
due to its low penetration , can be shielded
very easily. A thin (millimeter) layer of light material, such as
plastic, is enough. It is often not necessary to shield against
alpha radiation at all, because even in the air there is a range
of particles a only a few
centimeters, at higher energies max. tens of centimeters. If the
emitter is mixed a+ g, the gamma shield automatically
completely shields the alpha radiation as well.
Neutron
radiation shielding
Neutron shielding is generally a more complex problem than beta
or gamma radiation. Neutrons are the only common types of
particles that do not interact with the electron shell of atoms
of matter, but only with the nuclei of atoms, through a strong
interaction (the interaction of neutrons
with matter has been discussed in more detail in the section
"Neutron radiation and its
interactions"). In the case of fast neutrons, they
must first be slowed down so that they can be
effectively absorbed by a suitable absorber.
Neutrons are most effectively slowed down by the passage of
substances from lighter atoms, e.g. such as those rich in
hydrogen, where they lose energy during elastic scattering on
hydrogen nuclei (protons). To reduce the number of fast neutrons
about 10 times, a layer of about 20 cm of paraffin or plastic is
needed. For the absorption of such slowed neutrons, their capture
by suitable atomic nuclei is then used. The most effective
absorption takes place in cadmium, boron or indium. The
absorption of neutrons in the nuclei of cadmium or boron is
accompanied by the emission of gamma radiation (these are reactions (n, g) of neutron radiation
capture), which also need to be shielded,
by a heavy material - lead. Thus, neutron shielding generally
must consist of three layers: a layer of light
hydrogen-rich material (eg polyethylene), a layer of cadmium or
boron, and finally a layer of lead.
Note: When shielding neutrons, it is
necessary to keep in mind that radionuclides are formed
during the capture of neutrons in some nuclei, when originally
inactive materials can become emitters b and g. These radionuclides then
"internally" contaminate the shielding
and construction materials. E.g. if cobalt-alloyed steel 59Co is exposed to
neutrons, the known radionuclide 60Co is formed by neutron capture, with a half-life of
over 5 years !
Cosmic
radiation
High-speed - high-energy - particles moving through space are
called cosmic rays. They are mostly protons, a
small amount of alpha particles, trace amounts of heavier nuclei,
and from light particles electrons, photons and neutrinos. It is omnipresent
in the present universe, albeit in different areas with varying
intensity and energy. As a rule, cosmic rays falling on us on
Earth are considered (cosmic rays in the
distant universe, interacting with interstellar gas and falling
on exoplanets, will be briefly mentioned below "....").
Discovery of cosmic rays
Light of cosmic origin from the Sun and
stars has been observed by humans since time immemorial. The
first indication that invisible ionizing radiation was
coming to us from universe, was the observation of the Austrian
researcher Viktor Hess in 1912 during a bold ascent on a balloon,
that the level of radiation indicated on the electroscope
increases with altitude *). Further measurements during altitude
flights into the stratosphere, terrestrial measurements with more
advanced detectors and later measurements on space probes, not
only reliably confirmed the existence of this cosmic
radiation, but also measured its properties in detail.
*) This finding was quite surprising
at the time, as experts at the time believed that all natural
radiation, causing ionizing discharging of
electroscopes, has its origin in the emission of radioactive
substances contained in the earth's crust. The radiation level
should therefore decrease with height above the
ground. This was partly indicated by the observation of T.Wulf,
who brought the electrometer to the top of the Eiffel Tower,
where at a height of 330 m he measured about half the ionization
than at ground. However, even this decrease was much smaller than
if it were only radiation (g) coming from the earth's surface. During the balloon
ascents of V.Hess (the flight took place in
Ústí nad Labem, the balloon was filled with hydrogen from the
local chemical factory) and his followers,
airtight electrometers were used so that the rate of discharge
could not be affected by changes in air pressure. When ascending
to the first 800m, the ionization actually decreased, but more
slowly than expected; on the contrary, the ionization then increased
with a further ascending, which at a height of about 3 km was
already quite steep; at a height of 5 km, the ionization was 3
times greater than at the Earth's surface. The only explanation
was: "from above", from outer space, comes penetrating
radiation of extraterrestrial origin, which partially
passes through the atmosphere and contributes to other natural
radiation and ionization even at the Earth's surface. These experiments were then
confirmed in 1925 by R.Milikan using an electrometer with
automatic recording of measurements on film, which could ascend
to far greater heights on a balloon without a human crew; he
called this radiation "cosmic radiation".
The electrometers were only able to show if the
radiation was present and what its approximate intensity was. The
use of particle detectors, especially the
Geiger-Müller detector (see §2.3) and also particle
trace detectors - fog chambers and nuclear photographic
emulsions (see §2.2), has brought great progress in
understanding the nature of cosmic rays. The first trace of a
cosmic ray particle in the nebula chamber was recorded by
D.Skobelcyn in 1922. With the help of coincidence
measurements by G.-M. detectors have been found to
contain cosmic rays charged particles with high
energies exceeding 1GeV. In 1938, Pierre Auger detected
the coincidence of impulses coming from sprays of
particles of (secondary) cosmic radiation generated in
the atmosphere. Using traces of cosmic radiation in fog chambers
and photographic emulsions, not only was the composition of
cosmic radiation revealed, but a number of new particles,
hitherto unknown to physics were discovered - positron e+, muon m, mesons p and K, and finally
some heavy hadrons (hyperons), see §1.5 "Elementary
particles". The study of cosmic rays thus played an very
important role in understanding the laws of the
microworld (after all, we cannot yet achieve such high
energies as occur in cosmic rays in terrestrial accelerators, see
below).
Cosmic
radiation that comes from space is called primary;
we will deal with this first. During the passage of primary
cosmic radiation through the Earth's atmosphere, secondary
cosmic radiation is created (we will mention it in the
second part of this chapter on cosmic radiation). But first,
let's briefly mention the ionizing radiation that comes to us
from the nearest source in the universe :
Stelar
- Solar - "wind"
Inside the stars, the hot gases are held firmly by
gravity. Nevertheless, by thermoemission and the pressure
of the radiation release a smaller amount of gas
particles (plasma) from the hot surface of the star, which are
carried to the surrounding space. This stream of charged
particles, especially protons, electrons and alpha-particles
(helium nuclei), flowing from the star's surface into
interstellar space, is called the stellar "wind".
 |
Left:
Protuberances and eruptions occur in the surface layers
of stars. From the hot atmosphere of the star, plasma
particles are released by thermoemission and radiation
pressure. A stream of these charged particles flies away
from the star like a "stellar wind".
Right: The stellar wind from
the Sun - the solar wind - also flows towards our Earth,
where the absolute majority of it is deflected by the
Earth's magnetic field, goes around the Earth's
magnetosphere and does not penetrate the Earth's surface. |
This phenomenon is well known in our Sun - the solar "wind".
Solar wind particles (with kinetic energy of about 0.5-10 eV)
also hit our Earth. If the clouds of the solar wind hit the
earth's surface fully, it would be dangerous for life. The
long-term impact of solar wind particles on an unprotected planet
would gradually "blow off" the atmosphere, with the
subsequent evaporation of water from the surface - the planet
would become inhospitable, without life (cf part "Stars-Planets-Life"
in treatise "Antropic
principle and/or cosmic Got").
Fortunately,
our planet Earth has an atmosphere and a magnetic field. The
trajectories of charged particles become curved in the Earth's
magnetic field, and most particles deflect or bounce further into
space - clouds of charged particles seem to "flows
around" us along the curves of magnetic field lines. Only a
small part of them enter the atmosphere, especially in the polar
regions, where magnetic field lines approach the Earth's surface.
In the upper layers of the atmosphere, a stream of solar wind
particles interacts with nitrogen and oxygen atoms, causing their
excitation and ionization. During deexcitation, light is then
emitted, observed as aurora borealis.
Radiation from
the Sun, the so-called solar component (consisting
mainly of protons, electrons and 5-10% of helium ions), is
usually not classified as cosmic radiation, due
to its local importance and low energy. Exceptionally, however,
during strong eruptions - "solar storms", solar wind
protons can be accelerated to extremely high speeds and reach
considerably high energies of tens or hundreds of MeV. It may be
caused by successive impacts of ejected particles outwards during
coronal mass ejections. In such a case, the solar wind can behave
for a short time like other full-fledged cosmic
radiation from space, including the creation of cosmogenic
radionuclides (see the passage "Cosmogenic radionuclides" below).
Modulation
of the intensity of incident cosmic radiation by solar activity ?
Primary cosmic rays, coming from distant space, have a long-term
average constant intensity. However, on its way
to Earth, this cosmic radiation also passes through regions of
the nearby universe that are intensively irradiated by
the Sun. Cosmic radiation particles from space do not
pass through an absolute vacuum here, but can interact with
.protons, alpha particles and electrons of the solar wind. The
solar wind somewhat "thickens" the environment of the
solar system, including the around-earth space. A small fraction
of protons from space can interact here and be absorbed. The
variable solar wind can, even with a small effective
cross-section, somewhat modulate the intensity
of incoming cosmic rays. A weak anti-coincidence is
observed between the intensity of cosmic rays falling into the
Earth's atmosphere and solar activity - sunspots and eruptions,
leading to a more intense solar wind (with the
exception of the possibility of a short-term increase in the
production of cosmogenic radionuclides during strong solar
storms).
Primary cosmic rays
Composition and energy of cosmic radiation
By cosmic radiation (primary) we mean
high-energy radiation of cosmic origin, which consists mostly of protons
(88%), helium nuclei (10%) and other elements (1%); the content
of the various nuclei in cosmic rays roughly corresponds to the
representation of elements in the universe, as established as a
result of primordial and stellar nucleosynthesis. From light
particles then fast electrons and neutrinos. High-energy photons
of gamma radiation are also part of cosmic radiation. The energy
of particles of (primary) cosmic radiation varies in a wide
range. The lower limit is about 109 eV - charged particles with low
energies have difficulty penetrating the Earth due to the
magnetic field of Earth. The upper energy
limit of the cosmic rays registered so far is about 1020 eV; if we compare
this with the highest particle energies of about 1012 eV achieved at Earth
accelerators so far, cosmic rays contain by far the highest
particle energies we know *) - they exceed by 8 orders
of magnitude (ie one hundred million
times!) the highest energies achieved so
far in large terrestrial accelerators.
*) In 1991, a particle of cosmic radiation
with an energy of 3.1020 eV was recorded, which in common units
corresponds to about 50 Joules. So the microparticle - the proton
- has "macroscopic" energy !
With increasing
energy E the number of cosmic ray particles decreases
rapidly (is proportional to about E-3), so while the flow of particles with energies around
1GeV is relatively intense (about 104 /sec./m2), there are very few high-energy particles - for
energies of 1016 eV we observe only a few particles per 1 m2 in 1 year, for the
highest energy around 1019 eV it is only about 1 particle /1km2 per year. Particles with the highest energies 1020 eV are detected only
rarely in a few years.
The energy
distribution of particles, ie the spectrum of primary
cosmic radiation, is schematically shown in the left
half of Fig.1.6.6 on a logarithmic scale. The shape of this
spectrum is sometimes compared to the shape of an outstretched
human foot: after a more or less uniform decrease in the number
of particles to energies of about 1015-16
eV, there is a bend in the curve
apears as if the shape of "knee", after which the
decrease in the number of particles with energy begins to be
slightly faster up to very high energies of about1018-19 eV, where the
loss of particles starts to be a bit slower again - a kind of
"ankle" and "instep" appear on the shape of
the curve. This slowdown is somewhat surprising, as from an
astrophysical point of view, an even faster decrease in frequency
of occurence could be expected in the highest energy region,
partly due to pionic interactions of energy protons with
cosmological relic radiation (GZK-limit, see below). However, the
frequency of these highest energy particles is very small and the
quantification of energy is difficult here, so that due to
statistical fluctuations the frequency and energy in this region
may be overestimated. The problem remains open for the time
being, with decisive results expected from measurements of a
large number of cosmic ray showers at the AUGER observatory (see
below).
 |
Fig.1.6.6.
Left: Energy spectrum of
primary
cosmic rays. |
Right:
Reduction of the energy of high-energy
proton radiation by interactions with relic photon
radiation depending on the gread distances traveled in
space. |
Cosmic ray
propagation; GZK limit
The directional distribution of cosmic rays is almost isotropic,
which is related to the complex curved orbits of charged
particles in magnetic fields within the galaxy and in
intergalactic space. The curvature of the path is directly
proportional to the charge of the particle and the intensity of
the magnetic field and indirectly proportional to the mass of the
particle and thus its energy - the so-called Larmor
radius of the circle along which the motion takes place.
The particles we detect have undergone very complex
curved orbits on their way to Earth, which unfortunately
loses directional information about the source
in which they formed *). Only the most energetic particles (above
1019 eV)
have a sufficiently large Larmor radius of curvature (of the
order of kiloparsecs) and largely retain their direction to allow
their approximate location; since no increased
number of such particles are observed coming from around the
plane of our Galaxy, these high-energy particles are probably of extragalactic
origin.
*) We can compare it to an arrow
fired at a greater distance in a strong wind. During the flight,
the wind "plays" with the arrow and changes the
direction of its flight. So at the point of impact, it can be
difficult to determine the direction from which it was originally
fired. If the charged particles of cosmic radiation have low
energy, also in a short time of flight in the cosmic magnetic
field, they can arrive even in the opposite direction than they
were sent. At very high energies, the curvature of the trajectory
is small, the particle keeps its direction - just like a bullet
fired from a rifle, compared to an arrow, it is only slightly
affected by the wind.
In addition to
the curved orbit, there is also a gradual loss of energy
during the propagation of charged particles of cosmic radiation
through space by interactions of photons with relic microwave
radiation (Fig.1.6.6 on the right), in which these particles lose
energy by inverted Compton scattering. At
sufficiently high energies - higher than the so-called GZK
energy limit *), which for protons is about 5.1019 eV, a collision with
a photon of relic radiation even leads to the production
of a pion by reactions p + g2.7 °K ® p + po , p + g2.7 °K ® n + p+ (the neutron then changes again to a proton + electron +
neutrino by b- conversion ) **). These processes,
associated with a significant loss of kinetic energy
(approximately 2.108 eV per interaction), are more intense the higher the
energy of the particle, which means that no matter how high the
energy of the particle was at the beginning (for example 1020 -1022 eV), after
overcoming a distance of about 100-200 Mpc, with gradual
collisions with relic photons to form p-mesons will reduce the
energy to the value of GZK-energy (» 5.1019
eV); below this limit, the effective
cross section for pion formation is already very small and the
braking of charged particles by relic radiation is considerably
slower - it takes place only by inverted Compton scattering.
*) This energy limit is so named after K.Greisen,
G.T.Zacepin and V.A. Kuzmin,
who studied the interactions of high-energy protons of cosmic
radiation with photons and determined the energy above which p- mesons
are efficiently produced in this interaction by
the reaction p + g2.7 °K
® p + po , resp. by an
analogous reaction to the formation of a neutron (Fig.1.6.6 on
the right).
**) Microwave relic radiation gamma? It
may seem strange that the photon of relic radiation, which is a
relatively long-wave microwave radiation corresponding to a
temperature of 2.7 °K, has been termed "gamma
radiation" ( g2.7 °K)! However, this
is justified by the effects of the special theory of relativity.
The cosmic ray particle moves at a relativistic speed, so that
the photons of relic radiation from the point of view of its rest
frame of reference have such a large blue Doppler shift that they
become gamma-photons, which interact with the
"photonuclear" reaction to form a pion. The reaction
occurs via D+ : p + g2.7 °K ® D+ ® p + po (analogous for neutron), where the GZK limit is given
by the threshold energy for the formation of D+ and subsequently pions: it is the energy of the primary
proton at which in the resting system of the proton (or the
center of gravity system) the photons of relic radiation reach
this threshold energy.
Thus, a large
portion of high-energy particles gradually "brakes
againt a relic radiation" - when such a particle
has an initial energy higher than about 5.1019 eV, it loses this
high energy very quickly.
Note: On the one
hand, it is a great pity for the "astronomy of
cosmic rays", which thus loses an interesting
observation "window" into turbulent processes in outer
space. On the other hand, relic radiation perhaps may protect
us from high-energy particles from outer space (see also
the section "Cosmic radiation and life"
below).
This analysis also shows, that the
cosmic ray particles that have energy higher than » 5.1019 eV must come from an
area closer than » 50¸100 Mpc; and explain this
is difficult, suitable nearby sources capable of producing
particles about such a large energy, we do not know
(apart from the unproven hypothetical
possibilities mentioned in point 3. "Energy
interactions of exotic particles" of the following
paragraph on the formation of cosmic rays)...
How does
cosmic radiation arise ?
Due to the above-mentioned facts about the energy spectrum and
the nature of propagation, the explanation of the mechanism of
cosmic ray formation is very difficult and encounters
considerable problems. Potential sources of cosmic
radiation and the mechanisms of its formation can be
divided into three categories :
1. Continuous acceleration
Since normal particle interactions do not produce as high energy
particles as observed, the relevant "cosmic
accelerator" must be uncover. E.Fermi proposed the
mechanism of a certain continuous or diffuse acceleration
during repeated interaction of particles with moving large clouds
of ionized gas (either within the galaxy or intergalactic gas, or
in galaxy collisions), with the interaction of magnetic and
electric fields. The magnetic field must be either very strong
(for neutron stars) or very extensive (radio lobes of active
galaxies).
2. Catastrophic astrophysical processes
The high energies of cosmic ray-forming particles suggest that
this radiation probably does not arise during the normal
equilibrium processes of star and galaxy evolution, but rather
during the cataclysmic processes associated to the sudden release
of extreme amounts of energy. During these processes, an electric
field with a high potential of the order of up to 1019 V can be generated.
The particles are usually accelerated here one-time.
Two types of such "catastrophic" processes could be the
source of cosmic ray energy :
- A supernova
explosion ,
in which a star of sufficient mass in the final stages of
its evolution reaches such temperatures and pressures
inside, that electrons are "pushed" into the
nucleus and thus combine with protons to form neutrons.
At the same time, the core of the star shrinks sharply
and a neutron star is formed. This
process releases a huge amount of energy - a supernova
explodes, scattering the outer layers of the star into
the surrounding space (see Figures
4.2 and 4.3 in the "Black
Holes" chapter of "Gravity,
Black Holes, and the Space Physics"). The rapidly
rotating neutron star has an extremely strong magnetic
field, in which the so-called synchrotron effect
produces radiation emitted in a cone which, like the
light of a beacon, periodically strikes the surrounding
space, including the Earth - such a neutron star is
observed as a pulsar. In the
magnetosphere of neutron stars (where a change in the
magnetic field can induce strong accelerating electric
fields), charged particles can accelerate to tens of GeV
energies. During a supernova explosion, the outer parts
of the star expand at a speed close to the speed of
light, with the resulting shock wave protons
in the rapidly expanding ionized mass can be accelerated
to energies of up to hundreds of TeV by the Fermi
mechanism.
Note: Furthermore,
the interaction of these protons with the shell material
produces (via pions and muons), among other things, high
energy neutrinos (1¸1000 TeV), which
are then part of the primary cosmic rays. At present,
large-scale systems are being built for the detection of
high-energy neutrinos in anarctic glaciers and in the sea
depths (see Chapter 1.2 "Radioactivity",
passage "Neutrinos",
final part).
- Absorption of
matter by a black hole ,
when a large amount of matter attracted by a black hole
creates a so-called accretion disk
around it, in the lowest central area of which there is
an extremely strong heating of the absorbed substance
descending in a spiral into the black hole. Along the
axis of symmetry of this thick rotating disk, a
"funnel" then escapes from the inner part a
stream of particles and radiation - the so-called jets,
which contains particles accelerated to very high (relativistic) energies.
Cosmic ray acceleration mechanisms could work in black
hole jets. Turbulence in the accretion disk can lead to shock
waves*), in which the conditions for
accelerating particles to very high energies arise. Jets
from the interior of rotating accretion disks of black
holes could thus be (in addition to supernovae) a
significant source of cosmic radiation -
high-energy charged particles, especially protons,
spreading over long distances in space.
*) In the ionized
environment of the jet, in the plasma, behind the
relativistically moving commotion, waves of oscillating
electrons and protons are formed - plasma waves. They
generate an oscillating longitudinal electromagnetic
field, which under suitable conditions (synchronization
of particle velocities and the phase of the accelerating
field) can accelerate charged particles even to very high
energies over 1020 eV ("plasma acceleration").
With a suitable orientation
of the disk's rotational axis, the electromagnetic
component of this radiation can also be observed on
Earth. Massive black holes (weighing 104 -108 the masses of
our Sun) are probably found in the cores of many
galaxies; if a massive accretion disk forms around this
black hole, such an active galactic nucleus
is observed from the direction of the disk's axis of
rotation as a so-called quasar - see
§4.8 "Astrophysical significance of black holes" in the monograph "Gravity, black
holes and space-time physics".
For
"exotic" processes around black holes and for
the unrivaled ability of black holes to
"squeeze" energy from matter, see Chapter 4
"Black Holes",
§4.4 and §4.8 in the book "Gravity,
Black Holes and the Physics of Spacetime".
3. Energetic interactions of exotic
particles
There has also been speculation about the possible formation of
high-energy cosmic radiation during the decay of hitherto unknown
very heavy particles with a long lifetime. Occasionally, such a
particle disintegrates (spontaneously or by interaction with
another particle), emitting high-energy particles. The possible
existence of these hypothetical superheavy particles
with rest masses up to 1024 eV is predicted by some so-called supersymmetric
theories (magnetic monopoles, domain walls, cosmic strings
...). According to some hypotheses, there could be extremely
energetic neutrinos in the universe (perhaps also of
relict origin after stormy processes during the Big Bang), which
could form Zo bosons during collisions with other (slow) neutrinos
weak interactions, the decay of which could also form protons and
electrons with high energies up to 1021
eV.
Processes of this kind could take
place everywhere in space, including near Earth. These
hypothetical mechanisms could then explain the observed cosmic
ray particles with the highest energies, which
due to interactions with relic radiation (see the above-mentioned
GZK limit) could not retain this energy during a journey
from distant space.
Particles with very high energies
could also form in the final phase of quantum evaporation of a
black hole (Hawking effect), with a hypothetical quantum
explosion of a black mini-hole - see §4.7 "Quantum
radiation and thermodynamics of black holes" of the book "Gravity, black holes and
space-time physics".
The whole third category of possible
sources of cosmic radiation is so far completely hypothetical, it
has no support in theory or in the results of
observation or experiment.
Unfortunatelly, it must to
admit that the question of the origin of cosmic radiation,
particularly its components with the highest energies, has not
yet been definitively clarified (some
light into this issue could bring new complex method of
measurement of cosmic rays, mainly extensive facilities AUGER
- see below).
Cosmic X
and gamma radiation
In addition to corpuscular ionizing radiation, radiation of a
wave nature also comes from space - electromagnetic X-rays and
gamma rays.
Using X-ray satellite detection ("X-ray telescopes"), a large number of X-ray
sources have been observed in space. X-rays are created
in space during various processes. It can be synchrotron
radiation emitted by relativistic electrons moving in a strong
magnetic field, braking radiation, radiant recombination of atoms
in an ionized gas. Flashes of X-rays can occur when thermonuclear
ignites of hydrogen accumulated by accretion from a red giant to
a white dwarf in a tight binary system. A large amount of X-rays
is created during the accretion of matter to neutron stars and
black holes, when in the inner parts of the accretion disk the
gas is heated to such a high temperature that it also emits
X-rays. Due to turbulence and shock waves in the accretion disks,
this X-ray radiation has an irregular, rapidly changing
intensity. A certain amount of X-rays comes from all directions
in space and is referred to as the X-ray cosmic background.
Previously, it was thought to be scattered, diffuse, continuous
radiation of a similar type to microwave relic radiation.
However, improvements in the resolution of X-ray telescopes have
shown that it is not a continuous cosmic background, but a set of
millions of separate individual sources spread across
the sky (which earlier instruments could
not distinguish from each other). According
to astronomers, these sources are probably the active
nuclei of galaxies, in the center of which is a
supermassive black hole with a massive accretion disk, from which
radiation is emitted even in the X-ray region of the spectrum.
Gamma radiation comes from space
(each time from a different place) in the form of relatively
short flashes of g radiation,
abbreviated GRB (Gamma Ray Burts),
whose duration ranges from tenths of a second, through units and
tens of seconds, sometimes to minutes. Short and long flashes
differ spectroscopically. The radiation energy g is observed in the
range of about 100 keV to several MeV; it is interesting that
short flashes of radiation g with a duration of less than about 2sec. they contain
relatively more high-energy radiation than long flashes. Flashes
of g radiation
are usually accompanied by "afterglow",
in which the energy is reduced to X-rays, then to visible light
and finally to radio waves.
Origin of flashes of radiation g has not yet been
clarified with complete certainty. The most likely sources of
GRBs could be "catastrophic" processes - supernova or
hypernova explosions, black hole accretion, or collisions and
fusions of compact structures such as neutron stars
(these would probably be short flashes of g). The mechanisms of these high-energy processes in space
are briefly discussed in §4.8 "Astrophysical
significance of black holes",
passage "Binary
systems of gravitationally bound black holes. Collisions and
fusion of black holes" of
the book Gravity, Black Holes and the Physics of Spacetime. Self radiation g it does not arise directly in the inner region of a
black hole or a neutron star, but in a surrounding disk of
remaining (or ejected) material in which jets with a velocity
close to the speed of light cause shock waves. Gradual
deceleration of the jet wave when interaction with the
surrounding material can then lead to the emission of
"afterglow" with gradual degradation of energy from g- radiation to X-ray,
visible light and finally to radio waves. It is likely that every
time an intense gamma-ray burst took place in space, a stormy
"catastrophic" event occurred somewhere in the depths
of outer space - a supernova exploded, a black
hole was born, or two neutron stars in
a wild circulation collided and merged.
Next to g radiation must occur in such processes also issue
massive amounts of high-energy particles, i.e. cosmic radiation
in the truest sense. However, no flashes of
corpuscular radiation following the g- flash with an appropriate
time delay were observed. This is because that the paths of
charged particles are deflected and scattered in all possible
directions by galactic and intergalactic magnetic fields, so that
they either do not penetrate us at all or their
"diluted" flux merges with the overall cosmic
background.
The possible threat
to life on Earth by an intense flash of g- radiation and a
subsequent spray of corpuscular radiation from a nearby cosmic
source is discussed in the passage "Cosmic radiation and life" at the end of this §1.6.
Cosmic X and g radiation do not
penetrate trough the Earth's atmosphere and must therefore be
detected in space, using instruments placed on satellites (see below "Cosmic radiation detection") *). Although this radiation is weaker than other
components of the primary cosmic radiation, especially than the
proton component, provides important information about turbulent
processes in outer space (see also the
above mention of the possibilities of testing
quantum-gravitational effects "Is high-energy g- radiation moving slower than light?").
*) In hard g interactions-radiation with
the upper layers of the atmosphere, however, produces sprays of
electrons which propagate in the atmosphere at a speed higher
than the speed of light in this environment. This creates bluish
flashes of Cherenkov radiation, which can be detected by
sensitive photomultipliers placed in the focus of large mirror
telescopes. If there is a whole matrix of photomultipliers in the
focus of the parabolic mirror, it is possible to display the
place in the atmosphere where the Cherenkov radiation originated,
to reconstruct the electron spray and possibly determine the
source of primary radiation from space; cosmic g- radiation
propagates straight through space (as opposed to charged
particles), so that by reconstructing the direction of the
electron spray on the basis of Cherenkov radiation, it is
possible to determine the place (direction) from which the cosmic
g-
radiation originate. Since 2004, the MAGIC (Major Atmospheric
Gamma Imaging Cherenkov) telescope with a segment mirror
diameter of 17 m has been in operation on the Canary Island of La
Palma at an altitude of 2200 m , in the fosus of with is an
imaging system of 576 photomultipliers.
Secondary
cosmic radiation
As primary cosmic rays pass through the Earth's
atmosphere, there are a number of interactions
with air particles, creating secondary cosmic
radiation. Photons of braking radiation are formed, and fragmentary
reactions of atomic nuclei occur. The interaction of
high-energy primary protons p with nucleons N (in the nuclei of nitrogen,
oxygen, carbon) creates energy protons, neutrons, p- mesons: p + N ® p + N + p+ + p- + po + .... The resulting p± - mesons are unstable, they immediately decay (with a
half-life of »2.5.10-8 s) into muons m± and
neutrino: p-® m- + n'm , p+ ® m+ + nm
(neutral po -mesons with a very
short half - life »10-16 s they decay into two quantum gamma: po ® g + g).
Muons are also unstable, but their
half-lives are »2.10-6 s is 100 times longer than pions, so many muons fall to
the earth's surface (this allows the effect
of relativistic time dilation - see passage "Muons"
§1.5 "Elementary particles").
Muons m± decay into
electrons e± and neutrinos *): m- ® e- + n'e+ nm , m+ ® e+ + ne+ n'm , while the resulting electrons and positrons have a
kinetic energy up to 50 MeV.
*) During the decay of pions and
muons, the muon and electron neutrinos are formed; they are
sometimes referred to as "atmospheric neutrinos".
The total balance of neutrinos arising from the
decay of pions p± and
subsequently mions m± leads
to the ratio of the number of muon and electron neutrinos n(nm) : n(ne) = 2 : 1.
Confrontation of this expected ratio of "atmospheric"
neutrinos with the actually measured proportion of neutrinos in
experiments Super KamiokaNDE made it
possible to experimentally prove the so-called neutrino
oscillation - see §1.2, part "Radioactivity
beta", passage "Neutrino".
Interactions
of primary cosmic radiation with the atmosphere most often occur
at a height of about 30 km. The released particles often still
have high energies, so they are able to further fragment the
nuclei. With the collisions, more and more particles are formed
in cascades, the reaction branches off, until
the energy of the secondary particles falls below about 80 MeV,
when the interactions no longer lead to the formation of new
particles, but only to their absorption. The whole spray
of cosmic secondary radiation, most often containing
electrons e±, photons g, muons m± and a
smaller number of high-energy protons and neutrons, hits the
Earth's sutface (Fig.1.6.7). Tens of thousands to millions of
secondary radiation particles can be formed from a single
high-energy proton of primary cosmic radiation. A significant
part of electrons, positrons and gamma photons at low altitudes
is formed by the decay of muons m. Secondary cosmic
radiation is sometimes divided into a soft component
(e±, g with energy up to 100MeV - electron-photon spray)
and a hard component (m±, smaller amount p±, p+, with
energy higher than 500 MeV - muon and hadron spray). At
the Earth's surface, a spray of cosmic rays often covers a large
area of many square kilometers.
Note: The
high permeability of muons is due to the fact
that they have about 200 times higher rest mass than electrons
and show only electromagnetic and weak interaction (unlike
protons or pions, which can interact strongly with atomic
nuclei).
These large sprays of secondary
cosmic radiation in the atmosphere were first detected by Pierre
Auger in 1938 in the Alps at an altitude of around 3 000 m.

Fig.1.6.7. By interaction of high-energy particles of primary
cosmic radiation with the Earth's atmosphere creates sprays of
secondary cosmic radiation.
Cosmogenic
radionuclides
One of the side effects of cosmic radiation is the activation
of some nuclei with the formation of natural cosmogenic
radionuclides (eg 14C, 3H) - Fig.1.6.7 on the right.
--> The most important
here is radiocarbon 14C, whis is formed by the effect of
neutrons, ejected by cosmic radiation from the nuclei of atoms of
nitrogen in the higher-layer Earth's atmosphere: no + 14N7 ® 14C6
+ p+. Its
production is the highest of all cosmogenic radionuclides, as
nitrogen is the most abundant element in the atmosphere and has a
high effective absorption cross section for slow neutrons. This
creates about 2 atoms of 14C per second per 1 cm2 of atmosphere. Carbon 14C, as a long-term radionuclide (T1/2 = 5730 years, pure b-, energy 158keV) constantly contaminates
the biosphere, oxidizes to 14CO2 in the atmosphere, enters into biocycle (by
photosynthesis enters plants from the atmosphere, then by food
into animal bodies) and is therefore contained in all living
organisms. The concentration of 1 atom of 14C is established at about 8.1013 atoms of ordinary 12C; one gram of natural carbon in all living organisms
contains an activity of about 0.25 Bq 14C. After the death of the organism, its metabolic
contact with the atmosphere and the supply of 14C interrupts, so that
the concentration of radiocarbon begins to decrease by its
radioactive b- decay with a half-life of 5730 years. This also changes
the relative proportion between the carbon isotopes 14C, 13C and 12C. The radio-carbon
dating method (also called carbon
chronometry) is based on this :
From the ratio between the relative proportion of 14C radioactive isotope
and stable carbon isotopes in the studied historical subject
biological origin (for example wood, remains of organisms, etc.)
we can approximately determine the age of this
object - the time that has elapsed since the death of the
organisms from which the object originated. The radiocarbon
dating method and other dating methods in geology (using other
long-term natural radionuclides) are described in more detail in
§1.4 "Radionuclides",
section "Natural radionuclides", passage
"Radioisotope (radiometric)
dating".
--> Less represented is cosmogenic
tritium 3H (T1/2 = 12.3 years, pure b-, energy only 18keV). It is formed from deuterium 2H by neutron
absorption (no + 2H1 ® 3H1) in the amount of about 0.25 atom /cm2/s). Tritium in the
atmosphere oxidizes to "heavy" water 1H3HO, which reaches the earth's surface with rainfall.
Similar to 14C, it enters all living organisms in trace amounts (due to its short half-life, however, it is not suitable
for dating).
Some other cosmogenic radionuclides
are also formed in very small amounts :
--> Beryllium 7Be
(electron capture, T1/2 53 days) is used to investigate some
shorter-term transport events in the atmosphere.
Beryllium
10Be (beta-, T1/2 1.6
million years). Measurement of 10Be deposition (using mass
spectrometry), due to its long
half-life, is used to monitor some geological and
oceanographic processes. Its use for the reconstruction of the
power of solar eruptions in the distant past is interesting - it
is mentioned below.
Beryllium
isotopes are briefly described in §1.4, passage "Lithium,
Beryllium, Boron".
--> Chlorine 36Cl
(radioactivity beta- and electron capture, T1/2 300,000 years). Due to its
considerably long half-life, it is suitable for dating samples of
an age of approx. 50x104 -106 years, sometimes in co-production with 10Be (see below).
--> Phosphorus 32P
(beta-, T1/2 14 days) and sulfur 35S
(beta-, T1/2 87 days), due to their trace presence and short
half-lives, have no significance in cosmogenic radionuclides
(artificially produced ones are rarely used in bioanalytical
laboratory methods - 32P, 35S).
Primary cosmic radiation, coming
from distant space, has a long-term average constant
intensity and shows a stable production of cosmogenic
radionuclides. Here on Earth, however, the rate of formation of
cosmogenic radionuclides is somewhat modulated by
variability in the intensity of cosmic rays entering the
atmosphere, due to variability in solar activity (discussed above in the passage "Stellar -
Solar - "wind""). In general, a slight anti-coincidence of the
formation of cosmogenic radionuclides is observed, versus to
solar activity - the intensity of the solar "wind". But
sometimes the opposite: intense solar eruptions
- solar storms - can produce protons with considerably high
energies of tens or hundreds of MeV. These can by nuclear
reactions in the upper atmosphere, for a short time,
produce cosmogenic radionuclides such as 14-C, 3-H,
10-Be, 36-Cl, similar to how energetic protons of cosmic rays
from distant space continuously produce them :
The production
rate ratios of 10Be and 36Cl are very
sensitive to the energy spectrum of the protons that hit the
Earth. 10Be production is maximal at proton energy
~200MeV, while 36Cl production is greatest at ~30MeV
(due to the resonance effect of the 36Cl production
rate when protons interact with 40Ar). This leaves
characteristic traces in short-term increases in the
concentrations of these radionuclides in natural samples (eg in
glacier layers). In principle, it makes it possible to
reconstruct the character - strength - of ancient solar eruptions
(the reliability of these analyzes can sometimes be questionable,
as temporary increases in the concentration of cosmogenic
radionuclides can also be caused by natural anomalies in the
atmosphere, leading to increased contact of the stratosphere with
the Earth's surface...?..) .
--> Under the earth's
surface, the formation of cosmogenic radionuclides can occur by trapping
muons. A negatively charged muon is absorbed by a proton
to form a neutron, a muon neutrino and possibly of a gamma
photon: µ- + p+ -> nµ + n0 + g. This leads to a nuclear reaction in the affected
nucleus, during which neutrons or protons are emitted. Neutrons
can be captured by surrounding nuclei. Impacted atomic nuclei and
possibly even surrounding nuclei can thereby be transformed into radioactive
nuclei - cosmogenic radionuclides contained in underground
substances....
Cosmic radiation - "igniters"
of atmospheric lightning ?
Strong electrostatic spark discharges in the atmosphere - lightning
- are caused by the accumulation of a large number of
electrically charged particles in the clouds, with separated
positive and negative polarities. These electric charges on the
water droplets and ice crystals in the clouds are created by friction,
electrical polarization and electrostatic induction during the
precipitation and fragmentation of water droplets and ice
crystals, during phase transitions of water. The necessary
mechanical energy is supplied by the thermal convection
of air, which also causes the separation of electric
charges. When a sufficiently large amount of separated positive
and negative charges accumulate, the electric field can become so
strong that the breakdown voltage (jump distance) is
exceeded and an avalanche electric shock, lightning,
occurs between two clouds, or between cloud and ground. Electrons
are rapidly accelerated in a strong electric field and, on
impact, ionize air atoms and molecules to form more and more
secondary electrons - the air in this ionization channel
becomes electrically conductive.
However, measurements have shown
that the electric fields in storm clouds are usually too low in
intensity to fire a flash (often only a tenth). The formation of
the initial weak ionization, which can result in the formation of
an avalanche ionization channel of lightning, can also be initiated
by a spray of secondary cosmic radiation, containing a
large amount of charged ionizing particles, especially electrons (this hypothesis was proposed in 1992 by A.Gurevic). This mechanism of radiation initiation of
spark discharges works very well in laboratory conditions at
small jumping distances of the order of millimeters - it is used
in spark chambers (§2.3 "Ionization
detectors", passage "Spark
detectors"). However, it is not
verified in real atmospheric conditions of kilometers
distances. There is a very variable distribution of electric
charges, inhomogeneity of the atmosphere, different amounts and
proportions of charged particles in secondary cosmic ray showers.
The research
is carried out here by analyzing radio waves from atmospheric
discharges, received by a system of antennas, in co-production
with data from the detection of cosmic ray showers.
Cosmic
radiation detection and spectrometry
The motivation for detecting and analyzing cosmic rays comes from
three different areas :
¨ Astrophysics :
Cosmic rays provide us with useful information about processes
in outer space, often the most tumultuous processes in
star death by gravitational collapse (supernova explosions) or
accretion of matter to a black hole (in quasars).
¨ Nuclear and particle physics :
In cosmic rays we encounter particles of the highest
energies, by many orders of magnitude higher than the
energies that we will be able to create on Earth 's accelerators
in the foreseeable future. The interactions of these high-energy
particles can provide important insights into the internal
structure of particles and the properties of their interactions.
During proton interactions at very high energies, for example, new
states of quark-gluon plasma
may appear (which do not implement at
energies unit and tens of TeVs in terrestrial accelerators)..?..
¨ Influence of cosmic radiation on
nature and life :
Cosmic radiation is the most important a natural source
of permanent ionizing radiation to humans, animals and
other living creatures. It also probably played an important role
in the processes of chemical development of the universe, the origin
and evolution of life (see "Cosmic Radiation and Life" below).
The detection and spectrometry of
individual types of ionizing radiation is systematically
discussed from a physical point of view in Chapter 2 "Detection
and spectrometry of ionizing radiation".
However, the detection of cosmic radiation has some significant
specifics, which are more appropriate to discuss at this point in
the treatise on cosmic radiation. From the global point of view,
the issue of cosmic ray detection can be divided into two areas :
1. Direct detection of
primary cosmic radiation ; 2. Detection of secondary cosmic radiation
.
Depending on where we perform the
detection, we have three options:
a) Terestrial detection ; b)
Atmospheric detection
; c) Detection
in universe .
The individual methods of cosmic ray
detection will be briefly discussed below.
Detection
of primary cosmic radiation
The possibilities of direct detection of primary cosmic
radiation, especially particles with the highest energies, are
very limited for us, for three reasons: 1.
Cosmic radiation already interacts with atoms in the upper
atmosphere; 2. Low flux density of high energy
particles; 3. Low effective cross section of the
interaction of high-energy particles with the detector material.
From the standpoint of methodology
of detection, for primary cosmic ray particles are
suitable two types of detectors :
× Photographic
emulsions, mist and bubble chamber
,
stored in the magnetic field, recorded tracks of particles (described in §2.2, the "Track detectors particles'). In particular, photographic
emulsions were handed out balloons to great heights, then caused
a trace particle analysis to obtain a series of important
information about the composition of the primary cosmic radiation
and partly also energy particles.
× Comprehensive electronic
detection systems of particles ,
including semiconductor or ionization trackers,
spectrometers and calorimeters (see §2.1,
section "Arrangement and
configuration of radiation detectors"). This spectrometric system
is located in a magnetic field, the charge and momentum of the
particles can be determined from the curvature of the charged
particle tracks. They are basically similar to particle detectors
on large accelerators, but must be smaller
and significantly lighter so that they can be brought
into orbit. On the other hand, this requirement significantly
reduces the detection efficiency and spectrometry possibilities,
especially for the highest energy particles. This limits the
detected energy range to a maximum of hundreds of GeV; there are
still relatively many such particles and they are able to lose
the necessary part of the energy in a not very massive detector.
If such an electronic detection system is located on a space
satellite (Fig.1.6.8 on the left), it can transmit data on the
type, energy and interactions of cosmic ray particles for a long
time. X-ray telescopes are used
to image X-ray sources (section "X-ray telescopes" at the end of §3.2). To
identify sources of hard gamma radiation from
outer space are used special Compton telescopes (see §4.2, section "High energy gamma cameras").
From the point of view of the
detection site, primary cosmic radiation can be detected in two
ways :
l Detectors placed
on balloons ,
able to ascend to a height of tens of kilometers, perform
measurements there and then descend to the ground again
(Fig.1.6.8 left). Mostly special film emulsions were installed in
the balloons, later also electronic detectors.
l Detectors in
universe on cosmic probes (satellites)
Compared to balloons, detectors on cosmic probes have two main
advantages :
1. Detect the real primary particles, without affecting
by interactions with the atmosphere; 2. They can
work for a long time. The most suitable are the above-mentioned
electronic multidetector systems (Fig.1.6.8
left), with automatic radio sending of measured
signals to the terrestrial coordination center.
The Russian-Italian
project PAMELA spacecraft (Payload for
Antimatter-Matter Exploration and Light-nuclei Astrophysics) for
the detection of particles and antiparticles in cosmic rays and
the measurement of their energies. It contains a magnetic
particle spectrometer (magnetic induction 0,4T) with a silicon
pixel tracker, an absorption spectrometer
("calorimeter") consisting of absorption layers of
tungsten interspersed with silicon secondary radiation detectors
and also hadron detector consisting of helium
ionization tubes for the detection of neutrons and protons (there
is a 3He
isotope in the tubes, which has a high effective cross section
for neutron capture, slowed down in a polyethylene moderator
surrounding the tubes).
The issue of direct detection of
primary cosmic radiation outside the Earth is complex, but future
detection systems will certainly yield interesting results.
However, our terrestrial nature provides us with an effective
"tool" for detecting cosmic radiation: such an
"detector" is the Earth's atmosphere.
By interacting with atmospheric atoms, the high and
difficult-to-detect energy of a primary particle is
"comminuted" into a large number of secondary particles
with lower energies that are easier to detect, even by terestrial
detectors. Furthermore, high-energy radiation (primary particles,
but mainly secondary particles in the spray) as it passes through
the atmosphere, causes light effects (Cherenkov radiation,
fluorescent radiation of excited atoms) that can be detected -
the atmosphere can serve as a huge "scintillation
detector" of primary cosmic radiation. Thanks to
these two mechanisms, the detection of secondary cosmic
radiation, discussed in the following paragraph, can also say a
lot about the properties of primary cosmic radiation - it can
serve as an indirect detection of primary cosmic
radiation.
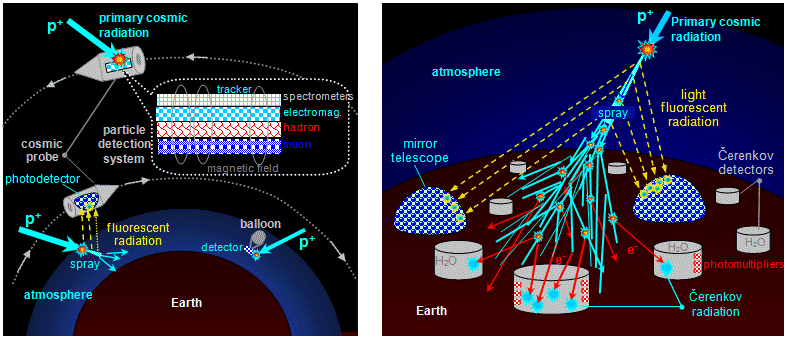
Fig.1.6.8. Possibilities of cosmic ray detection.
Left: Detection by cosmic
probes and balloons. Right: Ground
detection of secondary cosmic rays.
Detection
of secondary cosmic radiation
Individual quanta of secondary cosmic radiation are commonly
detected by ionization, scintillation and semiconductor
detectors, they form part of the natural radiation
background (often undesirable). However, one simple
detector is not enough for a more complex analysis of entire
secondary cosmic ray showers, more complex detection
systems are needed. There are basically two ways to
proceed (according to Fig.1.6.8 on the right) :
- Terestrial
detection of particles
using a large network of a large number of detectors,
spread over several tens of km2. They can be either scintillation
detectors or water Cherenkov detectors.
Flashes of scintillation or Cherenkov radiation are
registered by photomultipliers (see above "Cherenkov radiation"
and §2.4 "Scintillation
detection and spectrometry"). Individual detectors
detect spray particles in a matter of microseconds. From
the time analysis of the pulses from the individual
detectors, it is possible to approximately determine the direction
of arrival sprays. From the number of registered
particles in various detectors, it is possible to
determine the total energy of the spray,
and thus the primary particles (however,
energy calibration is complex, it is based on geometric
analysis and effective cross-sections of interactions).
The first such
detection system was built in New Mexico under the name
"Volcano Ranch Array" in 1960,
consisting of 19 scintillation detectors on an area of 8
km2.
Furthermore, it was the Soviet "Yakutsk"
(working since 1970), where an area of 20km2 are in placed
15 scintillation detectors and 25 Cherenkov detectors,
ingeniously electronically interconnected to determine
the horizon angles of arrival of the spray. The British Haverah
Park (worked from 1968-1987) consisted of a system
of water Cherenkov detectors, supplemented by
scintillation detectors (trigger) on an area of 12 km2. The
Australian SUGAR (Sydney University
Giant Air Shower Recorder), operating in 1968-79,
consisted of an array of 54 scintillation detectors (with
liquid scintillators) on an area of 100 km2; recorded a
series of sprays with energies of 1019-1020 eV. Japanese experiment AGASA (Akeno
Gigant Air Shower Array) worked for Akeno from 1990-2004;
contained 111 scintillation detectors on an area of about
100km2 and recorded a number of sprays with energies
around 1020 eV.
- Detection of
fluorescent radiation from the atmosphere
Ionizing particles of a spray of secondary cosmic
radiation when passing through the atmosphere cause
ionization and excitation of air
molecules, especially nitrogen, after which they return
to their original state (deexcitation) emits
photons in the visible field of light - fluorescent
radiation. The intensity of this fluorescent
flash is directly proportional to the energy of the
primary particle (which has been converted to the energy
of the spray particles). Fast charged particles also
generate Cherenkov radiation as they
pass through the atmosphere.
Fluorescence detectors
consist of a system of mirrors (it's
actually a telescope), concentrating light on cameras
composed of a large number of photomultipliers
(even several hundred). Of course, these detectors can
only operate during a clear moonless night so that the
background light level does not overheat the faint
fluorescent light. The total height of the pulses from
the photomultipliers is proportional to the energy of the
spray. Positional analysis of impulses from individual
photomultipliers can determine the place
(direction) in the sky, where the spray comes from. By
time analysis of signals from photomultipliers, the
gradual development of the spray in the atmosphere can be
observed in principle. In addition to the energy of the
particle, this partly allows independent detection of the
species the primary particle that caused
the spray: protons penetrate deeper into the atmosphere
and the spray begins lower, while the heavier nuclei
interact more strongly and the spray begins in the higher
atmosphere.
The first
functional detector of this type, called "Fly's
Eye", was built in 1982 in Utah. It
consisted of 67 mirrors (1.5 meters in diameter) and 880
photomultipliers. Here in 1991 is managed to detect a
spray of the most energetic particle yet, whose energy
was estimated at about 3.1020 electron
volts! Near this first type, a more advanced detector
with a higher resolution, called HIRes,
was constructed in 1998 (High Resolution Fly's Eye). In
Namibia, in the area of good atmospheric conditions, a
system of 4 telescopes detecting atmospheric Cherenkov
radiation was built in 2002-4, called HESS
(High Energy Stereoscopic System); will focus mainly on
the detection of sprays originating from the interaction
of high-energy cosmic g- radiation.
Fluorescent radiation, which arises during the
passage of cosmic radiation through the atmosphere, can in
principle be detected even from the "opposite side"
(from above) - from space, using space probes,
whose sensitive light flash detector, photodetector, is directed
into the Earth's atmosphere (schematically shown in Fig.1.6.8
left).
AUGER
detection system
For efficient and comprehensive detection of (secondary) cosmic
radiation showers was now built in the Argentine steppe in the
province of Mendoza an extensive detector system called Pierre
AUGER (according to French
physicist Pierre Auger, who first detected cosmic ray showers in
1938 and who also discovered electrons emitted during the
internal conversion of characteristic X-rays in excited atoms). In international cooperation (led
by J.Chronin and A.Watson), a large number
of cosmic ray spray detectors it was deployed here on an area of
about 3,000 km2. The northern branch is in the preparation
stage AUGER project in Colorado, USA. The northern and southern
branches of the observatory will allow the observation of almost
the entire sky, especially the core of the Galaxy from the
southern hemisphere and the extragalactic structure observable
rather from the northern hemisphere.
The AUGER Observatory is a substantial improvement and extension
of the basic scheme according to Fig.1.6.8 on the right. It works
as a hybrid detection system : cosmic ray
showers record systems of two different types of
detectors (all of these detectors are electronically
interconnected) :
Cherenkov's
detectors of fast charged particle
incident on the earth's surface, formed by tanks with water,
where flashes from the passage of particles are captured by
photomultipliers. A ground network of 1600 of these detectors is
created with distances of 1.5 km. Each contains 1200 liters of
high purity water and 3 photomultipliers.
Atmospheric
fluorescent telescopes
detect flashes of fluorescent radiation that are generated when
secondary cosmic ray spray particles pass through the Earth's
atmosphere. Charged particles of cosmic radiation ionize
and excite molecules in the atmosphere (especially nitrogen) as
they pass, and they emit visible light and UV radiation as they
return to their ground state. These flashes of fluorescent
radiation, lasting on the order of microseconds, are detected optical telescopes with a high luminosity and a viewing
angle of 180-360 ° (they have the shape of a "fly's
eye" from many mirror segments), equipped with
photomultipliers or CCD detectors. 24 of these detectors is
deployed, each with a collection area of 3.6 x 3.6 m2 and 440
photomultipliers.
The Pierre Auger
Observatory detects secondary
cosmic radiation, but with the main goal of analyzing
primary cosmic radiation, especially those with the
highest energies. Analysis of data from a number of telescopes
located at different locations in the system, in correlation with
data from Cherenkov detectors, could provide geometric
(stereoscopic) and energetic reconstruction of the spray,
which could also contribute to the kinematic reconstruction of
the direction of the primary high-energy quanta
of cosmic rays - and thus find out where they come
from space.
Does cosmic radiation come randomly
from all directions, or are there any significant directions
corresponding to certain specific sources in space? As mentioned
above, low and medium energy cosmic ray paths are very
curvilinear (curved by magnetic fields) and it is impossible to
determine the direction of their source. Only particles with very
high energies above 1019 eV are able to maintain their direction; the AUGER
project focuses on these.
It is hoped that a significant
number of high-energy particles will be able to find their
direction of arrival and identify it towards one of the
observed supernovae or a galaxy with an active nucleus (quasar -
a massive black hole) inside it. Such observations could
significantly move us to finding sources and
explaining the mechanisms of cosmic ray formation.
At the same time, high-energy cosmic rays could become a new
"observation window" into turbulent
processes in space. In addition to optical, radio, infrared,
X-ray and gamma astronomy, a new branch of particle
astronomy is gradually emerging - cosmic ray
astronomy.
Detection and spectrometry of
secondary cosmic radiation, derived from the interaction of the
highest energy primary protons, can also be useful for nuclear
and particle physics. It can reveal new mechanisms of
high-energy interactions of protons (with the participation of
quarks and gluons), unattainable in terrestrial accelerators in
the foreseeable future.
Cosmic
radiation and life
Cosmic radiation, as high-energy ionizing
radiation, can exhibit the biological effects on
living organisms (the effect of ionizing radiation on life
is generally discussed in detail in §5.2., the treatise "Biological effects of ionizing radiation"). So, in addition to the
important information that cosmic radiation carries about the
properties of elementary particles and phenomena in outer
universe, cosmic radiation is also interesting for its
relationship to the phenomenon of life - its biological
significance. It probably played an important role in
the origin and evolution of life, in at least
two ways :
- Synthesis of
biogenic compounds
Primary cosmic radiation, when interacting with
interstellar matter, especially with particles of
interstellar dust, stimulated chemical reactions between
carbon, hydrogen, oxygen and nitrogen atoms, during which
some important biogenic compounds (simple and complex
hydrocarbons, amino acids,. ..) were created, which
reached Earth and later served as a starting
"building material" for the origin and
development of living matter.
- Mutagenic effects
of cosmic rays
Secondary cosmic rays in the early stages of life on
Earth caused a diverse spectrum of mutations,
from which "positive" mutations have been
transmitted by natural selection as carriers of
evolution.
Cosmic radiation, together
with previously high levels of radiation from natural
radionuclides, has also contributed to the development of
effective cells repair mechanisms against
radiation damage (see §5.2. "Repair
processes").
Cosmic radiation forms an important
part of the natural radiation background to
which life on Earth is exposed *) from its inception to the
present day. The flow of cosmic ray particles is about 200
particles /m2 per second (at low altitudes), the average annual
effective cosmic radiation dose for humans is about 0.4 mSv.
However, the dose rate from cosmic radiation depends on the
altitude - at sea level it is about 0.3 mSv /year, at 1000 meters
above sea level 0.45 mSv /year, at a height of 5 km about 2
mSv/year, in 8 km it is already about 10 mSv/year. It also
depends on latitude - due to the magnetic field of the Earth, it
is larger in the region of the poles and smaller at the equator.
*) Protection
of the biosphere from external ionizing radiation
Some mechanisms that protect life from the
adverse effects of ionizing radiation are important for life on
Earth. Ozone in the upper atmosphere protects us
from ultraviolet radiation from the Sun. A massive layer of the atmosphere
does not transmit X-rays and gamma rays; strongly slows down and
absorbs even high-energy quantum. The Earth's magnetic
field protects us from particles of the "solar
wind" (these have energies significantly less than
"true" cosmic rays, but high intensity - they could,
among other things, destroy the ozone layer). Microwave relic
radiation in space may protect life from high-energy
particles of primary cosmic radiation coming from outer space
(this protection by relic radiation would only be more important
if cosmic rays with the highest energies above 1019 eV were sufficiently
frequent - which is not expected...).
Deadly
cosmic rays ?
So far, we have focused on the "peaceful" cosmic rays
that come from space with an almost constant average intensity
for millions of years. However, in the passage on cosmic X and
gamma rays, we have already mentioned the intense flashes
of g- rays that we observe coming from space
(fortunately distant). These flashes, as well as other
astronomical observations and theoretical analyzes (see Chapter 4 "Black Holes" in the book "Gravity,
Black Holes and the Physics of Spacetime"), show that very turbulent and catastrophic
processes are taking place in universe, during which a
huge amount of radiant energy suddenly released. These are supernova
explosions, gravitational collapse and formation of
black holes, collisions or fusions of neutron stars and black
holes. These processes, through their massive radiant
manifestations, are astronomically observed only in the distant
universe, which on one hand makes it difficult to
analyze and correct understanding, but on the other hand, the
enomous attenuation of radiation intensity by long distances and
scattering effect of intergalactic and galactic magnetic fields
on charged particles, protects us here on Earth
from the dangerous effects of hard radiation.
But what would happen if a similar
energy process took place in our Galaxy in one of the relatively nearby
star (several tens or hundreds of light-years away)? The
immense amount of radiant energy that would strike the Earth
would probably be a huge natural disaster that
could seriously jeopardize the very existence of life here on
Earth! At first we would be struck by a short-lasting but
powerful flash of g- radiation, which would decompose a large part of the
molecules in the upper layers of the Earth's atmosphere with its
ionizing effects; subsequent chemical reactions would produce
large amounts of nitrogen oxides, which, by their light-absorbing
properties, would darken the sky on the side facing the flash. In
addition, the ozone layer would be destroyed. Already these
atmospheric effects would have very serious ecological
consequences for plants, animals and the overall climate on
Earth.
Behind the flash of gamma radiation,
however, an even more destructive massive stream of corpuscular
cosmic rays would reach Earth in a few days, from which,
due to its relatively short trajectory through space, a weak
galactic magnetic field would not be enough to protect us; it
would take tens of days. Each such particle with an energy of the
order of GeV would cascade by interacting with atoms in the
atmosphere to cause a spray of energetic secondary radiation,
including muons. This radiation would penetrate the earth's
surface and even deep below the water surface and below the
earth's surface. The radiation dose would be many times higher
than the lethal dose for humans and other higher
organisms; only highly radiation-resistant species could survive.
High energy particles would further cause nuclear
reactions in the atmosphere and on the earth's surface,
with radioactive nuclei forming , many of which
would have half-lives of many years (eg tritium), some even
millions of years. The earth's land, surface and groundwater
would remain radioactively contaminated for a
long time and uninhabitable.
It is possible that such a "cosmic
radiation catastrophe" has already affected the
Earth in the distant past and may have caused the sudden extinction
of species *), or, conversely, the accelerated
development of new species by increased mutations. Some estimates
of the number of massive stars at the end of their evolution
(which then explode as supernovae) and the occurrence of close
pairs of neutron stars (which will
gradually approach each other due to losses of orbital energy by
gravitational waves and they finally merge to emit a massive
flash) show that such catastrophic events
in the vicinity of about hundreds of light-years around the Solar
System could occur about once every 100 million years. This
estimate remarkably corresponds to the mean time (but again only
estimated) among the largest paleontological changes in the early
prehistory of the Earth.
*) However, there could have
been several reasons for the mass extinction of animal species
during the evolution of life on Earth, and some of them are
considered even more likely or more frequent - Earth collisions
with asteroids, tectonic crustal movements, volcanic eruptions.
The same applies to the possible threat to life
on Earth in the future - even here, a
destructive flash of cosmic radiation is a potential risk only in
the distant future.
A relatively
early supernova explosion, over a time horizon of millions of
years, can be expected in very massive stars observed in the
so-called red giant phase. Such "old" stars,
at the end of their lives, have already burned all the hydrogen
inside, their envelope has heavily "inflated" and
cooled (the "red giant"), and thermonuclear
"burning" of helium and other heavier elements occurs
in the shrinking nucleus (for the evolution
of stars, see "Black Holes"). This less energy-intensive "fuel" is only
enough for a few million years. Once everything is burned, the
star collapses rapidly into a neutron star or black hole, with a
huge explosion supernova of type II (one
such "endangered" relatively close very massive stars
is the red giant Betelgeuse in the constellation Orion,
weighing about 20 Suns masses, about 600 light-years distant from
Earth; a supernova explosion can be expected here within
about 1 million years...). The largest amount of
radiation is emitted in the direction of the supernova's axis of
rotation; potentially the most dangerous are those nearby
supernovae, that face us at one of their "poles".
How to protect
yourself from the deadly cosmic rays ?
However, the question arises, how
can we protect ourselves from this danger ?
Unlike the impact of an asteroid, where the development of
observation methods and rocket technology in the near future will
hopefully avert such "local incidents", it will
probably never be in our power to prevent such massive processes
as a supernova explosion or neutron star collisions, moreover of
tens or hundreds of light-years away! The only way to save life
on Earth would be shielding cosmic ray beam.
Shielding by terrain barriers on Earth (mountains, canyons,
opposite hemisphere in the event of an explosion in the direction
of the North or South Pole) would not be very effective in the
long run due to the spread of the already mentioned radioactivity
by atmospheric flow. A suitable solution would be to shield
the entire Earth with a sufficiently thick shield
(thickness of at least hundreds of meters) placed in a suitable
orbit in outer space above the ground, in the direction of the
intended radiation source. Such a shield could perhaps be
assembled from asteroids that otherwise threaten us locally. At
present, such a project belongs more to the field of science
fiction. However, unlike asteroids, which can appear suddenly in
Earth's orbit, a supernova explosion or neutron star collision is
a "prepared" process that is predictable several
million years ahead. For the advanced civilization of the
future, which will certainly have in detail a
"mapped" of all potentially dangerous objects in the
surrounding parts of our galaxy, this could be a technically and
temporally feasible task. Another option would be to relocate
humanity to another part of the universe, hundreds or thousands
of light years away - but here we are already entirely in field
of sci-fi....
A brief
reflection on the global perspectives of life in
universe is in the passage "Astrophysics and Cosmology: - Human
hopelessness?" §5.6
"The future of the universe. The arrow of time." in monograph "Gravity, black holes and
the physics of spacetime".
Cosmic radiation in distant space
In the present universe the (primary) cosmic radiation is ubiquitous,
only its intensity and spectral composition are different. In
intergalactic space, especially in the area of large
"voids", it apparently has very little intensity.
On the contrary, in the regions near the center of large
galaxies, a considerably high intensity of cosmic rays
can be expected, with a considerable representation of
high-energy particles. The greatest intensity of cosmic radiation
is apparently in the vicinity of exploding supernovae or
accretion disks around black holes - especially in the
direction of their axis of rotation ("Deadly
cosmic radiation" above).
Cosmic radiation in interstellar galactic space can interact with
gas and dust particles in nebulae, which can lead to the
synthesis of a number of compounds, including biogenic ones (as mentioned above "Cosmic
radiation and life"). Interactions of primary cosmic radiation with matter
further produce secondary cosmic radiation,
which can also produced at in other planets and exoplanets in a
small way :
Secondary cosmic rays and cosmogenic
radionuclides on planets
Cosmic radiation (primary) in space affects not only the Earth,
but also other planets in the Solar System and in around
other stars - extrasolar planets (exoplanets). Similar
to here on Earth, nuclear reactions take place here with
the material there - with the atmosphere (if the planet
has one) or with the gaseous or solid matter of the
planet itself. Among other things, cosmogenic
radionuclides are also created. What they will be
depends on the composition of the atmosphere (or the surface of the planet in the absence of an
atmosphere). In most cases, tritium 3H
will probably occur, due to the omnipresent deuterium.
Radiocarbon 14C may be more rare. If there is no life on the planet,
secondary cosmic rays and the occurrence of cosmogenic
radionuclides are only of minor astrophysical interest...
Cosmogenic
radionuclides in meteorites
Direct analysis of cosmogenic radionuclides on other planets is
still difficult to access. Fortunately, even here on Earth we
have a number of found meteorites, some of which
come from the Moon and Mars. In them, it is possible to analyze
the content of cosmogenic nuclides (some of
their parts may come from the period before the formation of the
solar system - the fate of these samples can be complicated
during cataclysmic cosmic events..?.. ).
Vojtech Ullmann