| (2.2a) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 2
GENERAL THEORY OF
RELATIVITY
- PHYSICS OF GRAVITY
2.1. Acceleration
and gravity from the point of view of special theory of
relativity
2.2. Versatility - a basic property
and the key to understanding the nature of gravity
2.3. The
local principle of equivalence and its consequences
2.4. Physical
laws in curved spacetime
2.5. Einstein's
equations of the gravitational field
2.6. Deviation
and focus of geodesics
2.7. Gravitational
waves
2.8. Specific
properties of gravitational energy
2.9.Geometrodynamic system of units
2.10. Experimental
verification of the theory of relativity and gravity
Brief introduction to
Chapter 2 :
The general theory of relativity (GTR) is a theory
of gravity
developed by A. Einstein as a continuation and generalization of
his special theory of relativity (STR). GTR describes how massive
objects, such as stars and planets, cause spacetime
to curve
around them, causing other objects to move in curved paths. We perceive this curvature of spacetime
as gravity. In general, the presence of matter and energy
determines the curvature of spacetime. Einstein's field
equations, generalizing Newton's classical law of gravity, relate
this curvature to the distribution of matter and energy. The
dialectic of GTR can be simply expressed by the sentence: "Matter dictates how spacetime should curve, and
curved spacetime dictates how matter should move".
Physical laws in the curved spacetime of
the gravitational field are studied - the motion of particles and
the propagation of light, gravitational time dilation, the
entrainment of local inertial systems by the angular momentum of
rotating bodies, gravitational electrodynamics and optics.
Excitation of the gravitational field by matter~energy, specific
properties of gravitational energy. The speed of propagation of
gravity, the emission of gravitational waves during accelerated
motion (primarily orbital), the detection of gravitational waves
and their astrophysical significance.
2.1. Acceleration and gravity from the point of view of special theory of relativity
Before we begin to deal in more detail with the relativistic concept of gravity, let us first consider how gravity is included among the basic types of interactions in nature :
What keeps the world together? -
and/or: 4 types of interactions in nature
All the results of previous
physical and scientific research show that all structures and
phenomena in nature and universe are conditioned by the action of
four basic types of interactions :
Relative strengths of
fundamental interactions
The magnitudes of the force effects *) of these fundamental
interactions are diametrically different and
depend decisively on the distance between the
interacting particles. For distances of the order of 10-13 cm, corresponding
to the dimensions of atomic nuclei, the relative force ratio (or better said "disproportion"!) of the action of the strong ("1"),
electromagnetic, weak and gravitational interactions is
approximately 1 : 10-2 : 10-15 : 10-40. At distances of
the order of 10-8 cm, corresponding to the dimensions of the atomic shell,
and for all larger distances, the short-range strong and weak
interactions are practically no longer applied and the
electromagnetic interaction has the decisive influence. The ratio
of the electrostatic and gravitational force between two protons
is 1 : 1.24×10-36, between electrons 1 : 4.17×10-42, between electron and proton is 1
: 2.36×10-39.
*) Comparing "forces"
between different types of interactions is not as easy and
unambiguous as for common classical forces acting between
macroscopic bodies. The relations for forces contain constants
(such as G for gravity and e0 for electricity), whose numerical values depend on the
used system of units (for mass and charge); when comparing, we
then get different values. In particle physics, the values of the
so-called coupling constants a are used to
compare the relative force and for individual interactions, which
are dimensionless. For the strong and weak interactions, the
coupling constants and effective forces also depend on the
momentum at which they are evaluated in collision experiments. In
the above relations, we considered zero momentum transfer (for
the strong interaction, however, in collision experiments ....).
There is no experimental data available for the
gravitational interaction on its effects on microscopic scales,
it is all just extrapolations from the macro world... The
relationship between the gravitational and electric force is
usually determined as the ratio of the gravitational and electric
attractive force between an electron and a proton.
Why can the weakest
interaction - gravity - be dominant ?
The above ratio between the 4 basic types of interactions shows
that from this point of view, gravity is absolutely the weakest
interaction - about 1040 -times weaker than the electric forces for electrons
and protons. So why can this weakest force often win
over other types of interactions and become dominant
in the universe? This is because gravity has 3 important
properties :
-> Long-range extending to infinity,
decreases quadratically with distance 1/r2. This of course globally wins over the short-range
strong and weak interactions. However, the electromagnetic
interaction is equally long-range. However, gravity has another
significant property in contrast to it :
-> Gravity is always an attractive force.
Unlike the electric force, which is attractive only between
opposite charges, but repulsive between like charges. All matter
consists of positive protons and negative electrons, so that the
attractive and repulsive electric forces cancel each other out in
most situations in nature. However, the gravitational force
always acts attractively between all types of matter, regardless
of the number of electrons, protons and neutrons. It has a cumulative
character, the contributions from all material structures are added
up (vectorially).
-> Universality of gravity - it acts
equally on all types of matter and is also created ("excited") by all types
of matter. It does not matter the representation of protons,
electrons, neutrons; even antimatter gravitates in the same way
as (kiono)matter ("Antiparticles, antimatter,
antiworlds"). The general theory of relativity further strengthens
the universality of gravity by generalizing it from material
objects and particles even to all physical fields and all
energy.
These specific properties favor gravity
in most situations in the universe. Gravity is weak at the atomic
and subatomic level, because the masses of atoms and elementary
particles are small. It is more pronounced in macroscopic bodies
and becomes dominant in bodies of cosmic
dimensions with large masses - planets, stars, galaxies.
Acceleration and gravity from the point
of view of special theory of relativity
The special
theory of relativity, despite its enormous contribution to almost
all areas of fundamental physics, has two essential limitations
(which, as we shall see below, are interrelated) :
In practice, we are often forced to observe physical processes from non-inertial frames of reference. It turns out that only formal natural generalization can be made under the special theory of relativity to study the laws of physics as well as in non-inertial systems, so the first shortage would not be so serious. The second disadvantage is more serious: in the presence of gravity, there are no inertial frames of reference, and the special theory of relativity is globally inapplicable here. But as we will see below, due to the close connection between gravity and inertia, the special theory of relativity in the gravitational field retains local validity; this makes it possible to build a relativistic physics of gravity and spacetime - Einstein's general theory of relativity.
All physical measurements and observations of natural phenomena in general are essentially based on the determination of spatial and temporal relations, ie on the determination of spatio-temporal coincidences between events. Each elementary event (spacetime point) is assigned four numbers - the coordinates of that point - this assignment mutually unambiguous and continuous. The coincidence of two spacetime events will then be expressed by the equality of their coordinates. If two spacetime events thus coincide in one coordinate system, these events must be identical in any other coordinate system. The system of space-time coordinates is a matter of choice and therefore has no relation to the physical content of the theory. We can thus express the natural requirement that the laws of physics valid in one frame of reference also apply to every other frame of reference: "all the laws of physics have the same form in any frame of reference". This is Einstein's general principle of relativity (generalization of the special principle of relativity), which expressed mathematically reads: "All physical laws can be writen in the form invariant (covariant) with respect to transformations of spacetime coordinates".
The special theory of
relativity, which operates mostly with inertial frames of
reference, is able to describe the properties also of unevenly
moving objects (relativistic dynamics). The reference systems
associated with non-uniformly (accelerated) moving bodies are not
inertial, so the Lorentz transformation is not directly
applicable between them. However, the "ideal" *)
(sufficiently strong and durable) clock with which the observer in such a
non-inertial system, it measures time, does not change its
structure and properties due to acceleration, so that this clock
will go as fast as an inertial clock moving at a given moment
with the observer. Similarly, the "ideal" (sufficiently
rigid) measuring rods of a non-inertial observer will show the
same lengths as the rods currently moving inertially with it.
Thus space and time intervals measured in the same location by
different observers depends on their (immediate) relative speeds,
not on their acceleration. From the point of view of the
observer in the inertial system, the non-inertial (accelerated)
frame of reference can be considered as a continuous
sequence of
individual inertial systems, so that the relationship between
space-time coordinates will be given by Lorentz transformations
with continuously variable
velocities.
*) By ideal clocks and measuring rods we mean
that the clock "ticking" speed and the length of the
rods are not affected by non-universal influences such
as temperature or applied forces, or a correction is
made to these non-universal influences.
The fact that the laws of special theory of relativity apply even at enormous accelerations higher than about 1030 cm/s2, ie that spacetime relations, mass, energy, momentum, etc., do not depend on instantaneous acceleration, but only on instantaneous velocity, with high accuracy is confirmed experimentally in the scattering of high energy particles [229].
General
principle of relativity, curvilinear coordinates, metric tensor
The general principle of relativity therefore states that not
only systems of (pseudo)Cartesian spacetime coordinates connected
with inertial frames of reference, but also any other systems of
spacetime coordinates, are completely equivalent for the
formulation of physical laws. At first glance it seems that the
principle of relativity contradicts the experience, because in
non-inertial reference frames appear "fictitious"
forces of inertia, affecting the movement of bodies and course of
physical processes. However, the origin of such forces can be
easily explained within STR, and the properties of these apparent
forces (their effect on physical phenomena) can be expressed by
generally invariant equations.
In the inertial frame of reference S~ in Cartesian coordinates x~ i , the space-time interval element has the form
ds 2 = h ik dx~ i dx~ k .
If we move to any system of space-time coordinates xi in a generally non-inertial frame of reference S using the transformation xi = xi (x~ k ), in these new coordinates xi the space-time interval will have the form
| ds 2 = gik(x j) dx i dx k , | (2.1) |
where
| gik(x j) = (¶x~l/¶xi).(¶x~m/¶xk) hlm . | (2.1 ') |
Since the reference
systems S~ and S move with respect to each other
with acceleration, the transformation S ® S~
will not be a fixed Lorentz transformation and the quantities ¶ x~ m / ¶ x k
will generally be functions of place and time. From a
mathematical point of view, non-inertial reference systems are
actually systems of curvilinear
spacetime coordinates. Instead of the constants hik, new quantities gik(xj) appear here, whose functional
dependences on the coordinates xj characterize the relationship of
the system S with the new coordinates xj to the original inertial system S~
with Cartesian coordinates x~ j. Because these quantities gik give a formula for measuring actual distances
in space-time using coordinate differences, they are
called metric tensor in differential geometry.
The metric tensor is of key importance in
the general theory of relativity - it describes
gravity as the geometry of curved spacetime.
Essentially the same applies to it as was stated in §1.6 (note
in the section "Geometry of spacetime. Four-tensors")
about the spacetime interval: If we know the spacetime interval,
ie the dependence of the element ds2 on coordinates, we know "everything" about
space-time, and we can use it to study how bodies (particles)
will move in it and light (photons) will propagate. In other
words, we know the metric tensor gik and the equations of
geodetic lines - trajectories of free particles in the
gravitational field (§2.4 "Physical
laws in curved spacetime").
The equation of motion of a free test particle in the inertial system S~ : d2 x~ i / ds2 = 0, expressed in the general reference system S (ie in curvilinear space-time coordinates x i ) has the form
d2xi/dt2 + (¶xi/¶x~m).(¶2x~m/¶xk¶xl).(dxk/dt).(dxl/dt) = 0 .
This equation is invariant with respect to any transformation of the coordinates xi ® x' i (when using the system of coordinates x'i we get an equation of the same form, in which x are replaced by x'). The equation of motion of a free mass particle using general (curvilinear) space-time coordinates x i (in a generally non-inertial frame of reference) therefore has the form
| (2.2a) |
where the quantities G ik l can be expressed using the metric tensor :
| (2.2b) |
These quantities (describing the effect of "apparent" inertial forces on the motion of a particle) contain the components of the metric tensor and its derivatives; they are called Christoffel coefficients of affine connection (their meaning will be shown in §2.4). Equation (2.2a) is called the equation of geodesy (here, of course, it is a line expressed only in curvilinear coordinates).
Thus we see that using the value gik (i.e. with the help of metric) can be captured even apparent forces acting on the material body in non-inertial reference systems S. Similarly, all other laws of physics (eg the laws of electrodynamics) can be expressed in a generally invariant form valid in any frame of reference S - see §2.4. In the equations written in this way, the components of the metric tensor gik and their derivatives according to the coordinates also explicitly appear. The presence of components gik in the laws of physics it expresses the influence of apparent inertial forces, such as their action on the motion of bodies or on electromagnetic phenomena. Within the special theory of relativity, it is possible to build a generally invariant theory of apparent inertial forces and their influence on all general laws of physics (except gravity).
However, the general principle of relativity taken in isolation is physically meaningless, because any physical law can be formally rewritten to conform to the general principle of relativity (it has the same form in all reference frames) without extending or deepening the physical meaning of this law. Only connection with the principle of equivalence, which put fictitious inertial forces in non-inertial systems on the same level as the actually existing gravitation forces, gives the general principle of relativity profound physical meaning: it leads from the generally invariant theory of apparent inertial forces to Einstein's theory of gravitation.
After the emergence of a special theory of relativity, it became clear that every physical law that wants to claim generality and correctness must comply with the principles of STR. Einstein reformulated the fundamental laws of classical Newtonian dynamics right when compiling his special theory of relativity; in addition to such phenomena as time dilation and and lengths contraction, appeared next interesting effects - the dependence of mass on velocity, the relationship between equivalence of mass and energy, and other related consequences. The laws of electrodynamics did not need any reformulation, Maxwell's equations already in his classic form are Lorentz-invariant (based on electrodynamics actually STR was formed...). However, the special theory of relativity has made it possible to better understand the deep connections between the various laws of electrodynamics (see §1.5 and 1.6).
Relativistic
generalization of Newton's gravity ?
Another situation is with Newton's law of gravitation, which
first is not relativistically invariant, but is also in direct
conflict with the second basic principle of STR - the principle
of the existence of a finite maximum possible velocity of
interactions. Newton's law of gravitation expressed by Poisson's
equation Dj = 4p G r does not contain any time
derivatives. According to this law, the gravitational field j(x, y, z, t) at some point (x, y, z) at
time t is given by the instantaneous
distribution of matter r(x, y, z, t) in the whole space
at the same time t . A change in the distribution
of matter at some point is immediately reflected in the
gravitational field throughout space - the commotion in Newton's
gravitational field spreads infinitely fast. Newton's law of
gravitation is based on the idea of instantaneous
action at a distance and is therefore necessarily only an
approximate law applicable only at low speeds and not too high
masses (so that the gravitational field is weak).
Efforts to relativist reformulation of Newton's theory of gravitation date back to the beginnings of the theory of relativity. Naturally, this was based on Maxwell's electrodynamics, which was (and is still to this day) a model of consistent, perfectly elaborated and comprehensive relativistic invariant field theory, moreover, well verified in practice. In §1.4 we have shown a close analogy between Newton's law of gravitation and Coulomb's law of electrostatics. Since Maxwell's electrodynamics is a generalization of Coulomb's electrostatics, it can be expected that a similar generalization of Newton's law will lead to a correct relativistic theory of gravitation. All attempts to include gravitational phenomena in the special theory of relativity are more or less based on this assumption.
A straightforward way of relativistic rewriting of Newton's law of gravitation is a modification (generalization) of Poisson's equation (1.28 '). The simplest version tries to preserve of the scalar character of Poisson equations: the gravitational field is describeds by the space-time scalar potential j(x), while its source there will also be a scalar quantity characterizing the distribution of the rest mass. The density of the rest mass distribution ro(x) is equal to ro = T i i / c2 in the special theory of relativity, so that the gravitational field will be excited in scalar theory of gravity according to the equation G(j, j, k , j, k, l) = K.T i i . The shape of the function G is determined from the Lorentz invariance requirement, the validity of the superposition principle and the validity of Newton's law for the static case. The law of gravitation in this Nordström theory of gravity [191] has the form of d'Alembert's equation
oj = - ( 4p G / c2 ) . T j j ,
(where oº hik ¶2 / ¶ xi ¶ xk is d'Alembert's differential operator), which is a generalization of Poisson's equation (1.28 '). The solution to this d'Alembert equation is therefore the retarded potential
![]()
with time variable not t , but t-r'/c , expressing the final speed of propagation of the gravitational field, equal to the speed of light, similarly to electrodynamics - let's compare with relation (1.47) in §1.5.
The inapplicability of Nordtröm's scalar theory of gravity stems mainly from the fact that the gravitational field is excited in it only by the rest mass ro = T i i , which contradicts the principle of equivalence. We know that, for example, the electromagnetic energy contained in a body contributes to its gravity (Eötvös's experiment - see the following paragraph). Also the known observation of the bending of light rays in a gravitational field shows that photons with zero rest mass (having only electromagnetic energy) have a non-zero gravitational mass and show a gravitational interaction. Furthermore, the equations of motion in scalar theory lead to the twisting of Mercury's perihelion, but this twisting is about six times smaller and mainly in the opposite direction than observed [16].
Another way of generalizing Newton's law of gravitation comes from Lorentz, who developed it even before the emergence of a special theory of relativity. This vector theory of gravitation is an almost exact copy of electrodynamics and is sometimes referred to as the "Maxwell's theory of gravity". The gravitational field is described herein by the gravitation 4-potential yi = (j, y) containing normal gravitational potential j as one of the components, which are similarly tied electrodynamics Lorentz calibration conditions yk ,k = 0. From this 4-potential is forming antisymmetric tensor intensity of the gravitational field Gik = ( ¶y k / ¶x i ) - ( ¶y i / ¶x k ). The source of this gravitational field is incoherent mass dust, in which the density of rest mass is described by a scalar field ro(x j) and the distribution of motion by a field of four velocities Vi (x j). Four-vector (density) of the mass flow is then j i (x) = r0 .V i = ( r , r.v), where r(x) = r0 / Ö(1-v2/c2) is the mass density, v(x) the velocity at a given point x . In vector theory, the gravitational field is excited by a four-stream of mass j i according to the equations
¶ G ik / ¶ x k = (4p G / c) j i .
From these equations, as in electrodynamics, follow d'Alembert's wave equations yi = (4p G/c) j i and thus the existence of gravitational waves propagating at velocity c . The equations of motion of the test particle d2x i / dt2 = (G / c) Gik dxk / dt show, that all material bodies move in the given gravitational field with the same acceleration.
The outlined vector theory of the gravitational field has two major disadvantages. The first is that only incoherent material dust can be used as a source of gravitational field, or point material resources; for other models of sources (eg fields) it is not possible to define the four-vector mass flow j i well and unambiguously. Even more serious is the second drawback: formulate if the laws of conservation of energy and momentum of the system composed of the material excited by it, and the dust (according to the equations above) density of energy of the gravitational field is negative; the same goes for the energy transmitted by gravitational waves. Even apart from the logical difficulties and inconsistencies already occurring at the classical level, this result is unacceptable from the point of view of relativistic quantum field theory, which requires a positive energy definite of tensor fields describing particles with integer spins.
The common cause of the failure of the scalar and vector theory of gravitation was mainly that only a part of the energy-momentum tensor was taken as the source. If we take the whole energy-momentum tensor Tik as the source of the gravitational field and put it on the right side of the generalized Poisson equation (1.28 ''), the excited gravitational field should also be described by the symmetric tensor yik. In such a tensor theory of gravity (still within STR) the gravitational field will be excited according to an invariant system of tensor equations
| y ik, l , l º y i = (4p G / c) T ik (m) , | (2.3a) |
where Tik (m) is the energy-momentum tensor of all bodies, substances and fields with the exception of the gravitational field itself. As in electrodynamics, additional conditions y ik , k = 0 analogous to the Lorentz condition are introduced. The equations of motion of the test particle are
| d2xi/dt2 = (G/c2) [2.d/dt(yikdxk/dt) - (dxk/dt).(dxl/dt).(¶ykl/¶xi)] . | (2.3b) |
Even the specially relativistic tensor theory of gravity is not yet perfect and correct: it implies the differential conservation law Tik (m), k = 0, which does not take into account the gravitational field and could only apply if there were no gravitational action. In reality, however, the law of conservation (Tik (m) + Tik (g) ), k = 0 must apply for the total energy-momentum tensor, which also includes the energy and momentum of the gravitational field. Thus, the source on the right side of equation (2.3b) should be the total energy-momentum tensor including the gravitational field. Gupta [111] showed that this path can already lead to a satisfactory relativistic theory of gravitation. Since the exact expression for the energy-momentum tensor of the gravitational field could be determined only on the basis of exact field equations, which are not known in the given theory, it is necessary to use methods of successive approximations. Energy-momentum tensor of the gravitational field oTik (g), calculated from equation (2.3a) in the zero approximation, is added to the right side of (2.3a), the following equation in first approximation, to calculate a new (advanced) tenzor energy-momentum 1Tik (g), using which in equations (2.3a) gives a second approximation with an even more accurate energy-momentum tensor of the gravitational field 2Tik (g) and so on. By this procedure it is possible to obtain (although there are problems with uniqueness) the correct Einstein equations of the gravitational field, which are - in contrast to the initial equations (2.3a) - already nonlinear (see §2.5).
However, this does not mean that gravitational phenomena can be satisfactorily described in the special theory of relativity. The equation of motion of test particles in the gravitational field (2.3b) shows here that the special relativistic condition hik (dxi / dt) (dxk / dt) = - c2 is not met on these world lines and the actual time is no longer related here with space-time coordinates by the relation d t 2 = - (1 / c) .h ik dx i dx k . The element of the space-time interval (and thus the actual time) is given by the relation ds2 = -c2dt2 = gik(x)dxidxk , where g ik = hik - (2G / c2 ) yik . Thus, the time (running of standard clocks) at a given place depends not only on the speed of their movement, but also on the potentials of the gravitational field at that place; similarly, the gravitational field is affected by length scales. In geometric terminology, this means that the gravitational field affects the geometric properties of spacetime - spacetime becomes a generally curved Riemannian one. We come to the conclusion that a satisfactory interpretation of gravitational phenomena requires a revision of the basic physical concepts of the special theory of relativity, including a new view of the structure of space and time [247].
In the next we will see that this conclusion (which follows from a relatively complicated analysis of especially relativistic theory of gravity) can be reached directly on the basis of simple considerations of the universality of gravity and only then derive the correct equations of the gravitational field - Einstein's equations.
Non-inertial
frames of reference - "bridge" between special and
general theory of relativity
Let's go back to non-inertial systems. From the point of view of
the inertial frame of reference, STR has space
(three-dimensional) of Euclidean geometry. However, even in
Minkowski's pseudo-Euclidean spacetime, the special theory of
relativity becomes non-Euclidean in non-inertial reference
systems of the geometry of three-dimensional space! It can easily
be shown on a rotating reference frame (Fig.2.1). Let us
initially have a non-rotating straight disk, the center O of
which forms the beginning of the inertial frame of reference S.
An observer who measures the dimensions of this circular disk
with (sufficiently short) ideal measuring rods, measures its radius r and circumference l = 2pr in accordance
with Euclidean geometry. Then we rotate the disk around its
center with an angular velocity w with respect to the
inertial frame of reference. If the measuring rods and the disk
itself are sufficiently rigid ("ideal"), the
centrifugal expansion can be neglected and the observer can
measure the same radius r of the disk on the rotating disk
using radially applied measuring rods as if there were no
rotation. However, if the inertial observer from S~
observes a measuring rods, which the experimenter attached on a
rotating disc to the periphery in order to measure the length of
circumferece l , then these rods are moved in the
direction of its length with circumferential speed w.r . According to
the special theory of relativity, each such rod Ö(1- w2 r2 / c2) - times shorter than at rest.
The observer on the rotating disk therefore finds that there is a
relationship between the radius and the circumference of the
circular disk
2 p r
l = ----------------------- .
Ö(1 - w
2r 2/c 2)
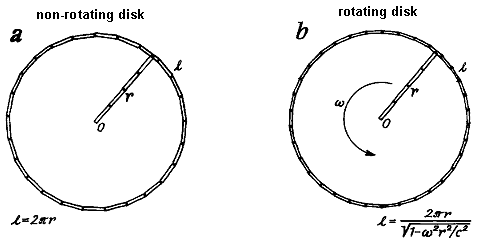
Fig.2.1. Origin of non-Euclidean geometry of space in a
non-inertial frame of reference.
a) The usual
relation l = 2p r between the radius and the circumference
of a circular non-rotating disk .
b) When measuring
on a rotating disk, the circumferential measuring rods (unlike
unchanged radial rods) are shortened due to Lorentz contraction
of lengths; therefore more of them "fit" on the
circumference and the ratio between
the length of the circle and its radius will be greater than
2p - the spatial measurement shows a
non-Euclidean geometry.
The ratio between the length of the circle and its radius is different from 2p, the spatial geometry of the rotating disk is non-Euclidean. The outer inertial observer explains this kinematically using Lorentz contractions of the special theory of relativity, while the inner observer rotating with the disk (for which all parts of the disk will be at rest) will consider it a consequence of "inertial" forces acting on all bodies. Declares that these inertial forces deviate the geometry of space from Euclidean, while the degre of this non-eucleidicity (curvature) of the space is given by the magnitude of these inertial forces, i.e. the centrifugal force w2 r.
Thus, spatial geometry in non-inertial frame of reference is not generally Euclidean, it is not possible to construct a Cartesian system of spatial coordinates. However, the geometry of four-dimensional space-time here remains Euclidean - with a suitable transformation it is always possible to return to an inertial system with (psedo) Cartesian space-time coordinates. Even in the special theory of the relativity of non-inertial systems, spacetime remains a fixed "scene" in which physical processes take place, while these physical processes do not affect the properties of spacetime itself.
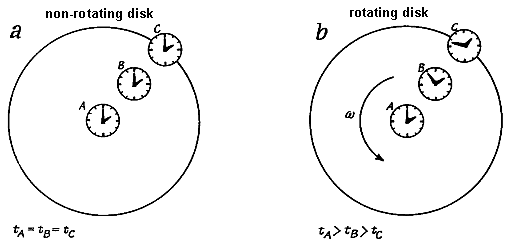
Fig.2.2. Dependence of the speed of the passage of time at the
different places in non-inertial systems.
a) Clocks located in different places of the
non-rotating disk go at the same speed and show the same time.
b) If (identical) clocks are mounted at
different distances from the center of the rotating disk, they
will move at different circumferential speeds and show different
relativistic time dilation (clock A will go as without
rotation, clock B will go slower and C even slower)
- from the point of view ot the inner observer, time in different
places flows at different speeds.
In order for two hours
of identical construction to go at different speeds in an
inertial system, they need to move relative to each other.
However, in a non-inertial frame of reference, clocks *) located
in different places can move at different speeds even when they
are at rest relative to each other.
*) We mean here the so-called ideal
clocks, the operation of which is not affected by any non-universal
influences. Thus, a pendulum or hourglass clock would be
completely unusable here (whose running speed is directly
determined by gravity, it stops in a weightless state);
similarly, other mechanical clocks could be affected by
mechanical deformations of their components. Atomic clocks
are considered to be the most suitable in this respect .
Again, this can be clearly seen in the
example of a rotating reference system (Fig.2.2). Consider a disk
rotating speed w (which will be non-inertial
reference frame S ) on which are mounted at the
center of rotation of clocks A , at the distance rB
clock B and an even greater distance rC
from the center of the next clock C. From the point of view of the
inertial system S~ (starting at the center of rotation),
clock A will be at rest, clock B
will have velocity w .r B and clock C
will have an even
higher velocity w .r C .
According to Lorentz transformation (time dilation) , the clock B
will go slower (and the clock C even slower) than clock A :
t = tA . Ö(1-w2r2/c2). From the point of view of the
rotating reference system S , all three clocks will be at
rest with respect to each other, but each clock will run at such
a speed, as the corresponding inertial clocks, moving at a given
moment together with the clock being examined.
Therefore, the same will apply to the operation of clocks A, B, C as from the point of view of the inertial system - with respect to clock A, clock B will go slower and clock C will go even slower. The observer in the inertial system S~ explains this by the dilation of time caused by their different motion, while the observer in the rotating system (where all three hours are at rest) must consider this as a consequence of the field of inertial forces with universal effects, which he observes in his system.
By applying STR to a rotating disk, we obtain
non-Euclidean spatial geometry (and different course of time in
different places) and at the same time centrifugal forces will
arise - the non-Euclidean geometry and the field of centrifugal
forces have a common cause in disk rotation. The
internal observer, if he did not know about the rotation of the
disk, could consider these anomalous phenomena in the geometry of
space and the passage of time as a consequence of the field of
centrifugal forces; or he could reverse it and consider the field
of centrifugal forces as a manifestation of curved geometry of
space and inhomogeneity of time. This imaginary experiment thus
induces a new way of thinking about the
connections between space and time with motion and gravity, which
resulted in the general theory of relativity
(GTR) as the physics of spacetime and gravity.
Analysis of imaginary experiments with non-inertial
systems - with rotating (Fig. 2.1 and
2.2) and with accelerated rockets (Fig. 2.2 and 2.3 in the following §2.2) - shows that in order for the relevant kinematic
effects to occur, gravity must affect time and space in
the same way, how the speed of movement in STR affects
them. This means that gravity can be described as the geometry
of time and space, combined in 4-dimensional spacetime.
And that is the filling of GTR...
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||