Quantum fluctuating foamy topology of spacetime

Appendix B
UNITARY FIELD THEORY AND QUANTUM GRAVITY
B.1. The process of unification in physics
B.2. Einstein's visions of geometric unitary field theory
B.3. Classical geometrodynamics. Gravity and topology.
B.4. Quantum geometrodynamics
B.5. Gravitational field quantization
B.6. Unification of fundamental interactions. Supergravity. Superstrings.
B.7. General principles and perspectives of unitary field theory

B.4. Quantum geometrodynamics

To recap, the geometrodynamic view of the world of classical (non-quantum) physics is admirably uniform: there is nothing but empty space-time, all matter, fields, and charges are a manifestation of the geometric and topological properties of empty space. Classical physics could thus be fully unitarianized.

However, we know that nature is much more diverse - more than 300 types of "elementary" particles are known, the charge is quantized, etc. Geons with their large mass and overall classical structure cannot be directly related to elementary particles. Similar to geometrodynamic electric charges generated in a curved a multiply connected space are not directly related to quantized charges of elementary particles. From this point of view, the whole classical geometrodynamics appears only as an interesting physical-mathematical prank...
   To harmonize geometrodynamics with the world of elementary particles it would be possible to try to implant appropriate quantum fields and particles (meson, neutrino, etc.) into "pure" geometrodynamics. Then it would be necessary to introduce appropriate phenomenological coupling constants and would appear other shortcomings of the existing apparatus of quantum field theory (difficulty renormalizations), so that in fact the appealing features of geometrodynamics as a perfectly unitary theory woul be disapperared.
   Wheeler went a different way: he tried a quantum formulation of his classical geometrodynamics in the hope that the resulting quantum geometrodynamics could explain the properties of elementary particles. He mainly researched the consequences of quantum uncertainty relations in geometrodynamics.

Quantum field fluctuations and space-time geometry
The basic postulate of quantum mechanics is the well-known Heisenberg uncertainty principle Dx. Dp ³ h , where h º h/2 p @ 1,05.10^-27 g cm³/s is the Planck constant. The relation of uncertainty DA. DB ³ h holds between every two dynamically coupled quantities A and B; for example

If we observe, for example, a magnetic field in a small spatial region characterized by the dimension L, there will contain the energy proportional to B² .L³ and the time required to measure the field will be L/c; uncertainty relation DE. Dt ³ h then gives (DB)² .L⁴ ³ h .c, or DB ³ h.c/L². It can therefore be said, that the quantum fluctuations of the electromagnetic field in size L, are of the order of magnitude

Thus, the field is constantly "oscillating" between configurations whose fluctuation range is greater the smaller the spatial areas we observe. Effect of these quantum fluctuation of the motion of the electron around the atomic nucleus is shown schematically in Fig.B.5 (these quantum fluctuation "overlap" Broglie waves through the Bohr model of the atom - see "Bohr model of the atom" in §1.1 "Atoms and atomic nuclei" monograph "Nuclear physics and physics of ionizing radiation", Fig.1.1.6) .

Fig.B.5. Schematic drawing of the motion of an electron around an atomic nucleus. A closer look at the Kepler trajectory of the electron would reveal the chaotic irregularities caused by quantum fluctuations in the electric field. The mean deviation from the global trajectory is zero, but the mean square deviation leads to a small shift in the energy level. This shift was actually measured as part of the Lamb-Rutheford shift.

Assuming the universal validity of the quantum uncertainty principle, a similar situation must occur even in geometrodynamics: quantum fluctuations in the space-time geometry will be expected. In the spatial region with characteristic L dimensions (investigated in a locally inertial system with diagonal metric coefficients -1,1,1,1), the fluctuations of the space-time geometry, ie metrics, connections and curvatures, will be of the order of equal

where

is the so-called Planck-Wheeler length, which was formally introduced as early as 1899 by M.Planck and whose fundamental significance was clarified by J.A.Wheeler in 1955.

Fluctuations in geometry and topology of spacetime
In the scales L » 10^-8 cm, with which atomic physics works, Dg ~ 10^-25; even for the scales L » 10^-13 cm of nuclear physics, the quantum fluctuations of the metric Dg » 10^-20 are completely negligible. Therefore, in all the situations we face so far, we can rightly consider space-time as a smooth continuum. The basic postulate of classical (non-quantum) physics - special and general theories of relativity, that space is locally Euclidean, is very well fulfilled.

Fig.B.6. At very small scales, the spontaneous quantum fluctuations of space metrics increase (a, b). In the area of Planck lengths, these fluctuations may eventually increase to such an extent that the space becomes multiple continuous (c) - they grow into bizarre fluctuations in the topology (enlarged sections in Fig.d).

However, if we go to ever smaller scales (Fig.B.6a,b), quantum fluctuations gradually increase, when in areas of size L » 10^-33 cm, where according to (B.9) Dg ~ 1, the fluctuations of the metric already so strong that the overgrowth melts in topology fluctuations - Fig.B.6c,d. The dynamic evolution of curved empty space in connection with the quantum principle thus leads to specific laws at very small distances: in microscales of the order of ~10^-33 cm not only the geometry, but also the topology of space fluctuates very strongly (Dg » 1).

From a normal point of view, spacetime appears to us as a continuous smooth continuum. Similarly, when we look at the surface of the ocean from a high-flying plane, we see a completely smooth surface, only slightly globally curved (in the shape of a globe) - Fig.B.7a. If the observer jumps with a parachute and gradually approaches the surface, he can see more and more clearly that it is rippled (Fig.B.7b). When he finally lands on the water with a rubber dinghy, he realizes how far the surface is to an perfectly flat and smooth surface - the surface ripples sharply, spraying foam.
   In meter scales, the local curvature of the surface (waves) fluctuates strongly, in centimeter and millimeter scales even the topological structure of the surface fluctuates - drops separate, foam bubbles are formed (Fig.B.7c).
   

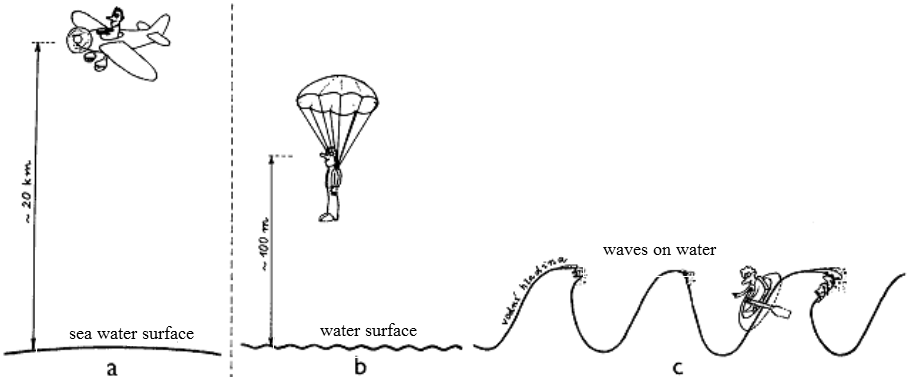
Fig.B.7. The analogy between the geometric-topological structure of spacetime and the structure of the sea surface .
a) When viewed from a height of several kilometers, the sea level appears to be an ideally smooth surface.
b) From a height of several tens of meters, the surface appears wavy, but otherwise smooth.
c) It can be seen from the immediate vicinity that not only the curvature of the surface, but also its topological structure (bubbles, drops) fluctuates strongly.

Similarly, in our spatiotemporal "continuum" the smaller the microareas we observe, the more pronounced the quantum fluctuations of the geometry will be manifested, until finally the space topology itself will fluctuate strongly in the Planck length l_p » 10^-33 cm. For example, topological tunnels will be formed and destroyed, closed areas will be created (virtual "black micro-holes" that will evaporate immediately quantum - see §4.7 "Quantum radiation and thermodynamics of black holes"), even new "micro-univers" ("bubbles" may separate which then disappear; but with randomly generated fluctuations of sufficient magnitude, they are likely to expand in inflation and create a "new" macroscopic "universe" - §5.5, part "Chaotic inflation and quantum cosmology", passage "The emergence of more universes"). According to quantum geometrodynamics, therefore, this seemingly empty vacuum is the scene of the most turbulent microevents - spacetime has a kind of "foamy" constantly spontaneously fluctuating microstructure.
   If an idealized point *) test particle enters such a place, it will be mercilessly thrown left-right, up-down, and chaotically here and there in all directions, until it loses any idea of temporal sequence and spatial proportions — space and time cease to exist for it.
*) If the test particle had non-zero dimensions, it would be immediately torn apart by fluctuating tidal forces.

Quantum fluctuations of spacetime: reality, or maybe forever just a hypothesis ?
To some extent, by formally combining the laws of quantum physics and general theory of relativity, it can be concluded that in areas around the Planck's length » 10^-33 cm, quantum vacuum fluctuations are so large that not only the geometry fluctuates, but also spacetime topology - spacetime here "boils" like a bubbling "quantum foam". In these Planck-Wheeler microscales, quantum foam is ubiquitous : it is not only in singularities inside black holes, but also in interstellar space, around us, inside the cells of our brain, inside atomic nuclei and particles. Under normal conditions, however, the quantum fluctuations of the spacetime metric are so slight, that no experiment has yet revealed them. To "see" them, we would have to have a hypothetical "supermicroscope" providing a magnification of »10³² times and higher *).
*) A more high-quality optical microscope is able to provide a maximum magnification of about 3.10³ times. The fundamental limitation here is given by the wavelength of visible light. The electron microscope can give a magnification of up to » 10⁵-x. Tunneling microscopes and electrostatic microscopes are under development, which will make it possible to image even heavier atoms. However, it is unimaginably far from Planck's details!
   If we on the imaginary virtual experiments on this "supermikroskopu" gradually increased magnification on »10⁸ x, we observed atoms at a magnification »10¹³ x would be able to "see" the atomic nuclei, the nucleons and quarks inside them. But even with further growth of magnification, the space would remain completely smooth, with only a slight continuous curvature given the gravitational mass. Only if we increased the magnification by another incredible 20 orders of magnitude to see the dimensions »10^-32 cm, we would first observe small, but gradually larger and larger fluctuations in the curvature of space. And at a magnification of about 10³³ times, the space would resemble bubbling stochastic-quantum "foam" (Fig.B.6d).
   Directly achieving such an magnification is of course impossible not only for technical, but mainly for principal (quantum-physical) reasons. Even complex and ingenious indirect experiments will not be able to prove quantum fluctuations of space-time in the foreseeable future (but see the following passage on the possible influence of quantum fluctuations of space on the speed of high-energy photons...). They will remain for a long time (maybe forever?) only at the level of an interesting hypothesis ..!..

Possible practical consequence :
Is high-energy g- radiation moving slower than light ?
All electromagnetic radiation propagates in a vacuum at exactly the speed of light c , independent of the movement of the source and the observer. This is a basic finding, firmly rooted in the special theory of relativity. Regardless of the wavelength - speed c propagates radio waves, visible light *), X and gamma radiation.
*) The classical dispersion, observed with light in the matter's optical environment, originates in the (collective) interactions of the electromagnetic wave with the atoms of matter; does not occur in a vacuum.

Fig.B.7d) Influence of quantum micro-fluctuations of space-time geometry on the speed of motion of high-energy photons of gamma radiation.

However, in connection with the mentioned quantum-gravitational fluctuations of spacetime, there may be phenomena which may, in certain circumstances, call this basic initial statement of theory of relativity into question somewhat *). Fig.B.7.d shows a situation where two photons are emitted from a certain source at the same time: one photon with a lower energy, ie a longer wavelength, the other photon of high-energy gamma radiation with a very short wavelength. For radiation with a longer wavelength, the quantum fluctuations of the metrics are averaged and completely smoothed out in the respective longer scale, so that this radiation in the classical vacuum will move exactly at the speed of light v = c. However, photons of high-energy radiation g with a very short wavelength will be "more sensitive" to fluctuations in the space-time metric on a fine scale than low-energy photons. Such waves will travel along a slightly undulating geodetic path, photons will in a sense "intertwine" the unevenness of the path, caused by subtle metric perturbations, and their effective velocity v_ef will be slightly less than c . Locally, such a photon travels a slightly longer trajectory than would correspond to a smooth space. We can compare this to the movement of a car with small wheels and large wheels on a bumpy road: when driving the wheels at the same circumferential speed, a car with small wheels (copying a bumpy surface) will drive a little slower than a car with a large wheel diameter (whose circumference extends beyond small depressions).
* ) This phenomenon cannot be considered as a violation or failure of a special theory of relativity, which is exactly valid in flat spacetime without metric defects (or in a locally inertial systems in GTR).
   These differences in propagation speed are reflected only at the very high energy radiation g, in the field of GeV and TeV. Here, too, the differences in speed are very small (of the order of 10^-20), without the possibility of laboratory measurements. In the future, they could only be demonstrated by a temporal comparison of the detection of light and flashes of hard g-radiation from catastrophic processes in outer space. At cosmological distances of billions of light-years, even these slight differences in speed could "accumulate" and have measurable effects (the problem, however, is to distinguish these differences from the differences in emission times in the sources themselves ...).
   Interactions with quantum-gravitational fluctuations of space can lead to dissipative phenomena and a slight modification of the kinematics not only of hard photon radiation, but also of high-energy particles in space.

Huge quantum microfluctuations
Quantum fluctuations cause the space to have, in addition to macroscopic (gravitational, cosmic) curvature, also "microcurvature" of radius of the order of L*»10^-33 cm and that the necks of topological tunnels are formed everywhere, whose dimensions and mutual distances are also of the order of ~L*. If we have a topological tunnel of size L (and thus areas ~L²), there will be quantum fluctuations of electric field intensity of the order of Ö(h.c)/L², so that the total field strength flow indicating the effective electric charge will be of order of q ~ Ö(h.c) » 10.e, regardless of the dimensions of the tunnel. The typical charge in geometrodynamice but not directly related to the charge of elementary particles, because it is an order of magnitude larger than the elementary quantum of charge e and is not quantized. The energy density E²/8p field in a typical tunnel reaches enormous values ~ h.c/L*⁴ » 5.10⁹³ g/cm³ and characterized by mass-energy per one topological tunnel makes m ~ Ö(h.c/G) @ 2.2.10^-5 g » 10¹⁹ GeV, which is at least 20 orders of magnitude more than the rest mass of elementary particles (and about 9 orders of magnitude more than the maximum energy registered in cosmic rays).
   These huge values are obviously at odds with the very low mean energy density that we observe in space. However, if we take into account the contribution of gravity to the density of energy and mass, then two typical tunnel mouths with masses m₁ » m₂ ~ Ö(h.c/G) = ~10^-5 g, spaced r_1,2 » L* @ 10^-33 cm, will have a binding energy E_gr = -G.m₁.m₂/r_1,2 » - c²Ö(h.c/G) during mutual gravitational interaction. Mass defect of two adjacent mouths of topological tunnels Dm_gr = E_g /c² ~ -Ö(h.c/G) @ -10^-5 g, which is negative and of the same order as the (positive) electromagnetic mass of both structures, can therefore locally to compensate for the energies of the respective fluctuations. Such locally compensated fluctuations no longer show gravitational attraction with more distant concentrations of matter and energy. After such a total compensation of the huge picofluctuations, the vacuum may look as if we observe it.
   However, the observed elementary particles, which are probably not elementary at all, have dimensions of the order of 10²⁰ times larger than the Planck length, and thus could perhaps be a kind of "collective excitations" (involving a large number of elementary fluctuations ) in a sea of strong microgeometry fluctuations, which are canceles everywhere else on average and macroscopically form the usual "vacuum". Whether this is the case and how it is going, no one knows yet ...
   Different interpretation of the quantum microfluctuations of the vacuum is in §B.5, the passage "The Mystery of the Quantum Energy of the Vacuum <-> Cosmological Constant".

Fundamental micro-values of physical quantities - Planck units
Even though quantum geometrodynamics has not yet succeeded in explaining the structure of elementary particles, it provides important limiting fundamental values of some basic physical quantities. Already in §2.9 ("Geometrodynamic system of units"), for a clearer and more economical notation of relativistic formulas, we introduced the so-called geometrodynamic units, in which the speed of light c and the gravitational constant G are assumed to be equal to 1. In the spirit of the idea of a unified relationship of space, time, gravity and matter in the general theory of relarivity. However, quantum phenomena were not taken into account here.
   To include quantum phenomena in the special and general theory of relativity, it is useful to express basic physical quantities using a combination of universal constants c, G, h in the so-called Planck units :

These combinations of c, h, G were formally introduced in 1899 by M. Planck in order to obtain quantities with the dimensions of length, time, mass, which would be composed only of basic natural constants, independent of standard bodies. Their significance for the quantum-relativistic concept of space, time, gravity, and field theory was clarified in 1955 by J.A. Wheeler.

The values of Planck units are very small, beyond the possibility of measuring anything on these scales in the foreseeable future (or maybe never..?..) :
-> The Planck length of 10^-33 cm represents approximately 10^-20 times the diameter of a proton. The size of the Planck length would be a hypothetical particle condensed so that its quantum Compton wavelength is the size of its Schwarzschild radius - a black hole. Below the Planck length, the quantum fluctuations of the spacetime metric are predicted to be so large that the notion of distance is no longer applicable. The Planck length is therefore the smallest physically measurable distance. Any attempt to explore even shorter distances using extremely high energy particle collisions (about 10¹⁹ GeV) would lead to the production of black (micro)holes. On the order of the Planck length, however, superstrings and d-gates are theoretically modeled in attempts at unitary superstring theory.
-> Planck time 10^-43 s is the time it takes for light (in a vacuum) to travel the Planck distance. In the cosmology of the very early universe, it is assumed that it is the first moment after the hypothetical singularity of the big bang, from which the laws of physics begin to operate (§5.4, passage "Stages of the evolution of the universe"). The structure of time at these scales is apparently no longer continuous in these intervals.
-> The Planck mass, with its value of ~22 micrograms, could resemble macroscopic objects (such as cells). However, compared to subatomic elementary particles, this is an extremely large value. Multiplying by c², this corresponds to an energy of 2×10⁹ J - 2 billion joules concentrated in a single elementary particle!
-> Planck's temperature uses Boltzman's constant k_B in addition to h,c,G. At the value of the Planck temperature of 10³² degrees, the emitted thermal radiation would have an extremely short wavelength corresponding to the Planck length of 10^-33cm. In systems of particles at the Planck temperature, black microholes of Planck dimensions could be created and then destroyed by Hawking radiation.
   Quantum spacetime structure here shows, that a smaller distance than L*»10^-33 cm and shorter time intervals than t*»10^-43 s are irrelevant, because the spatial relations and time relations lose their meaning here due to quantum fluctuation in topology (discussed above in the passage "Geometry and Topology Fluctuation", formula B.10). So from a quantum point of view, space and time are not a smooth infinitely divisible continuum, but effectively have a "grainy" discrete structure of some "atoms" or "elementary particles" of space and time - it decays into elementary Planck lengths ("quantum of space") and Planck times ("quantum of time", also sometimes called chronons).
   From the point of view of nuclear physics, the issues of continuous or discrete internal structure of space and time are discussed in the passage "Is the world continuous or discrete at the deepest level?" in §1.1 of the book "Nuclear Physics and Physics of Ionizing Radiation".
   We can imagine the following illustrative justification for the smallest possible length: Visual resolution of two nearby points in space requires the use of a wavelength of light shorter than the distance of the points. The energy of photons is inversely proportional to the wavelength, so the closer the points are, the more photon energy we need. According to GTR, this photon energy causes the curvature of spacetime. At Planck's distance »10^-33 cm the curvature of spacetime (caused by the necessary high-energy photons) would increase so much, that the points would be inside the horizon of a (virtual) black hole - measuring such a small distance becomes fundamentally impossible, spacetime is no longer continuous here. At the Planck length, the GTR loses validity, and the physical processes are controlled by the quantum theory of gravity (§B.5 "Quantization of the gravitational field"). Quantum geometrodynamics suggests that in the smallest microscales there is a kind of "quantum of space" on the background of a general manifold without a metric structure, space can be likened to "quantum foam". This idea could be important for quantum field theory in general, since the energy of the quanta is inversely proportional to the wavelength of the respective "wave ball". If the wavelengths cannot be less than a certain lower limit (in our case »10^-33 cm), because a shorter length simply does not exist, then the energy of the quanta is limited from above - quanta with infinite energy, which causes such problems in quantum field theories, are in advance excluded...
   Planck-Wheeler units are natural units for the description and modeling of natural laws based on the properties of spacetime and quantum physics. The fact that there is the smallest length and shortest time interval in space and time, about which it still makes sense to talk about, is a knowledge that is beyond the scope of geometrodynamics and perhaps even the whole of physics..!..
   

B.3. Classical geometrodynamics. Gravity and topology.		B.5. Gravitational field quantization

Vojtech Ullmann