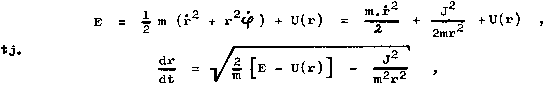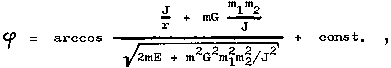The law of general gravity
Chapter 1
GRAVITATION AND ITS PLACE IN PHYSICS
1.1. Development of knowledge about nature,
the universe, gravity
1.2. Newton's law of gravitation
1.3. Mechanical LeSage hypothesis
of the nature of gravity
1.4. Analogy
between gravity and electrostatics
1.5. Electromagnetic
field. Maxwell's equations.
1.6. Four-dimensional
spacetime and special theory of relativity
1.2. Newton's law of
gravitation and its
modifications
Until the middle of the
17th century, there were two completely different and seemingly
unrelated doctrines of motion side by side: terrestrial
mechanics
dealing with the motion of ordinary bodies and celestial mechanics studying the motion of planets
and stars.
I. Newton followed Galileo's kinematics and built the dynamics of
motion of bodies summarized in three well-known Newton's laws (see §1.6 "Four-dimensional spacetime and special
theory of relativity", passage
"Newton's
classical mechanics") . The resulting classical mechanics was (and is still to this day)
able to explain all the movements of bodies that we encounter in
everyday life.
Newton's predecessor, J.Kepler,
summarized a large number of astronomical observations to date
and traced the general laws governing the motion of planets in
the solar system :
I. The
planets orbit the Sun in elliptical orbits (with a small
eccentricity), in the common focus of which is the Sun.
- II. The
areas circumscribed by the planet's guide at the same
time are the same.
III. The
cubes of the large half-axes are directly proportional to
the squares of the orbit periods of the planets.
These empirical Kepler's laws served I.Newton as a starting point for
establishing an even more fundamental law that governs not only the
planets, but all bodies "in heaven and on Earth".
Above all, Newton realized that
the motion of the planets did not conform to the law of inertia.
The planets move in curved orbits (ellipses) around the Sun, so
they must be subjected to a force directed at the Sun - an
attractive force emanating from the Sun. Kepler's third law
applied to the special case of circular orbit says that the
squares of periods 4p2
. r2 / v2 are proportional to the squares
of the radius r. Then centripetal acceleration v2/r must be proportional to 1/r2
. A similar lead can be shown for elliptical movement. Due to
Newton's second law, the force causing such
centripetal acceleration in a planet mass m, must be therefore proportional to the m /
r2. According to the law of action and
reaction, however, the planet must act with a force of the same
magnitude as the Sun acts on the planet, and this force will be
proportional to the mass M of the Sun. The mutual attractive force
between the planet and the Sun will therefore be proportional to m.M / r2 .
The law of general
gravitation
By analyzing Kepler's laws, Newton found that the motion of
planets in the solar system can be easily explained by the
hypothesis that each two bodies are
attracted to each other by a force directly proportional to the mass ml
and m2 of each and indirectly proportional
to the square of the distance r
among them - Newton's law of gravitation :
ml . m2
F
=
G .
------------ . r° , r°
= r / r ,
r2
|
(1.1) |
where r° is a unit vector indicating the direction
from the body ml to the body m2 . The coefficient of proportionality G -
the gravitational constant - must be determined empirically
(from observation or experiment); the value
was measured G » 6.67384×10-11 kg-1 m3 s-2 , see below.
In addition to deriving the form
of the law of attraction between celestial bodies, Newton showed
that this force has the same nature as the gravity
of the earth, forcing all free bodies to fall to the
ground with acceleration. Newton, by comparing the acceleration
of the Moon's motion as it orbits at the appropriate distance
around earth and by the acceleration of free-moving
bodies at the earth's surface, he found that the magnitudes of
these accelerations correspond to the law of inverted squares and
therefore agree with the law (1.1), provided that both the fall
of bodies and the orbit of the Moon around the Earth are
conditioned by the Earth's gravity.
The finding that the force that
compels the orbit of the planet around the sun or moon around the
planet is the same force that causes the fall of bodies to the
ground and called weight, or gravity, united on a common basis before
completely different phenomena and areas:
mechanics, the force
of gravity and "heavenly "mechanics. Equation (1.1) is
therefore called Newton's law of
general gravity.
Gravitational field
For force action in space "at a
distance",
the concept of a physical field is introduced in physics, which
is a space in which forces of a given type act
on (test) particles. Here, it is a gravitational
field
excited by material bodies, which then act on material test
particles. The strength of the gravitational field can be
quantified by the field intensity vector Egr , indicating the gravitational force
acting on a test particle of unit mass. A particle of mass m
will therefore be acted upon by the gravitational force
The gravitational force
and intensity Egr are generally functions of the location - coordinates in the studied space. For the
sake of brevity of notation, instead of the individual
coordinates x,y,z, we will use the position
vector r (radius vector) - the line connecting the origin
of the coordinate system and the investigated point, where the
body is located or where we determine the intensities Egr(r) and potentials jgr(r) of the fields.
In addition to the intensity Egr(r), in the gravitational field
also introduces the gravitational
potential jgr(r). It is a scalar quantity
describing the potential energy of a material body in a
gravitational field - the amount of work required to transfer a unit mass
from a reference (default) point, where the potential is
considered to be zero, to a given point r in the gravitational field. The
reference point with zero potential is usually taken to be a
point infinitely distant from the system of charges, where no
electric field is acting (at least in the
limit). The
potential jgr(r) of the gravitational field is
related to its intensity Egr(r) by the relation
where grad f = [¶f/¶x, ¶f/¶y, ¶f/¶z] is a vector differential
operator quantifying the "steepness of the slope"
- gradient - of the scalar field f in
the direction of the coordinates x,y,z.
Newton's law can then be
expressed in terms of the intensity of the gravitational field Egr excited in space around a point
body of mass M :
| Egr (r)
= G . M / r2 . r°
. |
|
The excited
gravitational potential here is then
| jgr (r)
= G . M / | r | . |
|
The potential depends
only on the distance |r|, not on the direction relative to the
exciting body M.
Analogies between
gravitational and electric fields are discussed in §1.4.
Gravity - an
irremovable all-pervading force
The electrical action between charged bodies (which can be
attractive or repulsive according to the signs of charges)
depends on the material environment and can in principle be shielded (even by
an alternating electromagnetic field using a Faraday cage)
. Gravity, which is
always attractive, however, is an all-pervading
force that
cannot be removed in any way. Gravity cannot be "blocked the
way" by anything, it cannot be
shielded.
If we inserted some massive material between two gravitational
bodies, we would only achieve an amplification
of the total
gravitational action: the gravitational force of the inserted
material would add up in vector to the original gravity.
Universal action of
gravity
Since the attractive force acting on each
body is proportional to the mass of that body, Newton's law is
also consistent with Galileo's law of free fall, according to
which all bodies fall to the ground with equal
acceleration regardless of their mass and composition (for the equality of inertial and gravitational mass,
see §2.2).
According to 2.Newton's law of classical
mechanics - the law of force and acceleration -
the force F needed to set a body in motion is proportional
to its mass m and acceleration a : F = m . a.
If this force is gravity, then for a test body of mass m
moving under the influence of gravity of the central body of mass
M (eg Earth)
at a distance r , we can write Newton's law of gravitation
on the other side of the equation: m . a = G.
M.m / r2 .
On the left and right side of the equation there is a mass m
of the test body, which can be shortened, so the
acceleration no longer depends on the mass of the observed body -
it depends only on the mass of the central gravitational body and
the mutual distance: a = G. M / r2 . As a result, the gravitational force gives
all bodies the same gravitational acceleration, which
explains Galileo's law of free fall. Although a heavier body is
subjected to a greater gravitational force, which at the same
time must do more "work" to accelerate it - this
heavier body puts more "resistance" to acceleration.
Further physical research has shown that
this property of the same - universal - action
of gravity applies not only to ordinary matter,
but also to their building particles such as
electrons, protons, neutrons, as well as to electromagnetic fields
and waves such as light and its quantum. photons
(undoubtedly also applies to other particles
and antiparticles ) . It was this fact universal action on all
matter~energy that proved to be the most important
property of gravity and the key to its new understanding within general
theory of relativity (§2.1-2.4 of
Chapter 2, especially §2.2 "Universality
- a basic property and the key to understanding the nature of
gravity").
Gravitating
bodies
Fig.1.0
shows three situations in which this law of gravity applies
exactly. The basic theoretical situation according to
the upper part of the figure consists in the gravitational action
between two "point" bodies,
in practice bodies whose dimensions are negligibly small in
comparison with their mutual distance.

Fig.1.0. Newton's law of general gravity.
Above: Basic situation of gravitational
action between two (idealized) point bodies with masses m 1 and m 2 .
Middle: Newton's law of
gravitation also applies to the gravitational action between
spherically symmetric bodies of finite dimensions.
Bottom: A spherically
symmetric hollow body (spherical layer or shell) has zero
gravitational force inside the cavity, outside the body the
gravitational force is given by the standard Newton's law.
However, Newton's law of gravitation also
applies exactly to the gravitational action between bodies of finite
dimensions with a spherically symmetric
distribution of mass density (middle part of the
figure). And not only in the outer space around the body, but
also inside the spherically symmetric body - the
gravitational force F(r) at a distance r from the center
is given by the amount of mass m(r) = 4p 0 ò
rr(r). r2 dr, contained
in an imaginary sphere of radius r : F(r) = G.m(r) /
r2 ; matter in the outer shells is not applied, its gravity
acting from different directions is canceled (this situation is also discussed in §2.4, passage
"Time dilation inside
gravitational bodies"). In the lower part of Fig.1.0 there is a curious
theoretical case of a spherically symmetric hollow body
- a spherical layer or shell (it does not
occur in nature). The test specimens
located inside the cavity are not subjected to any
gravitational force (the gravitational
field inside has zero intensity, there is a
constant gravitational potential, gravitational forces from
different directions are canceled), but
outside the body the gravitational force is exactly given by
Newton's law.
In all other configurations of asymmetric
inhomogeneous mass density distribution in bodies of finite
dimensions, the law of inverted squares applies only approximately,
these bodies cannot be completely replaced by their center of
gravity (due to the quadratic nonlinearity
of the law of gravitation). In the general
case of a source of volume V, in which the mass
distribution is given by a function of the local density r(r),
the gravitational force acting on the test particle m
given by the vector volume integral F = -G.m òV r(r´). |r - r|-2 (r - r´)0 dV´
of the vector sum of
contributions from individual material elements of different
density r(r) in the source.
Deviations from homogeneity and spherical symmetry
For large material bodies in universe (with a diameter greater
than about 1000 km), strong gravity automatically ensures an
approximately spherical shape with an almost spherically
symmetrical density distribution. However, if such a body rotates,
it will not be spherical, but only axial symmetry
(cf. §3.6 "Kerr
and Kerr-Newman geometry"
and §4.4 "Rotating and electrically charged Kerr-Newman
black holes").
However, within terrestrial-type planets, there are
certain local inhomogeneities in the mass
density distribution that cause minor anomalies and fluctuations
in the surrounding gravitational field. This is manifested by
minor irregularities and deviations from the Kepler orbits (see below "Motion in Newton's
gravitational field") orbiting
satellites. These irregularities are more pronounced in the low
orbits of the satellites, decreasing at greater distances until
they practically disappear. Gravimetric measurements on the
Earth's surface and analysis of deviations in the orbits of
satellites can be used in geology to detect the internal
inhomogeneities of the structure of our planet - and
thus to identify possible mineral deposits.
Gravitational
constant
For the universal constant G , acting as
a coefficient of proportionality in the law of gravity (1.1) - Newton's gravitational constant - was experimentally determined the value
| G
» 6.67384 . 10-11 kg -1 m 3 s -2 . |
(1.2) |
A very small value of
the gravitational constant G indicates, that the gravitational action is
relatively weak and can only be more pronounced
if at least one of the interacting bodies has a considerably
large mass. Therefore, the mutual gravitational attraction of
ordinary macroscopic bodies is not applied in practice, we do not
observe it in everyday life and it can be demonstrated and
measured only by highly sensitive methods (such
as Cavendish and Eötvös measurements). Gravity is the domain of very material bodies in the universe.
The weakness of the gravitational
interaction, among other things, makes it very difficult
to accurately measure the gravitational constant. The
first measurement of the gravitational constant was made as early
as 1798 by H.Cavendish, who used two lead balls weighing 730 g,
mounted on a horizontal arm suspended on a thin fiber. This
mechanical system functioned as a torsion scales, which
was fitted with a mirror from which a beam of light was reflected
indicating the deflection of the arm. Cavendish approached a pair
of larger lead balls (160kg) on either side of the torsion scales
and measured the torsion arm deflection using a mirror.
Cavendish's experiment was originally designed to determine the
mass and density of the Earth; later analyzes of its results
determined the value of the gravitational constant G » 6,74.10-11 kg-1 m3 s-2 ,which
differs by only 1% from the current value.
Despite the fact that the gravitational
constant G is one of the most important
and most basic natural constants, in comparison with other
physical constants we know its value with only a relatively small
accuracy of about 10-4 (to 4 decimal places). The reason for this
"lousy" accuracy is the above-mentioned weakness
of the gravitational interaction. Perhaps future planned
highly sensitive quantum-radiation measurements using
excited atoms in various quantum states, subjected to the
gravitational action of test masses, can provide some hope for refining
the value of the gravitational constant .
Surface
gravity
For mechanical processes on gravitational bodies (hydrodynamic,
tectonic, atmospheric, ...) and for other events, including
possibly life, on Earth and other planets (especially
terrestrial) are important gravitational forces acting on their
surface. The intensity of gravity on the surface of a
gravitational body, called surface gravity, is
the gravitational force acting on bodies at a given point on the
surface, or the gravitational acceleration of bodies in
a free fall. It is marked with the Greek letter k (kappa). On spherical bodies with a spherically
symmetric mass density, it is given by Newton's basic law :
k = G. M / R2
and is the same at all points on the surface. Due to the
non-spherical shape or inhomogeneous distribution of matter, the
surface gravity varies in different places, mostly by relatively
small values. By gravimetric measurements of these derogations
can be detect anomalies of geological composition, larger
underground spaces, or, in perspective, mineral deposits.
Surface gravity k is also introduced for black
holes, that do not have a surface, but an event horizon
- formula (4.24) in §4.3 "Schwarzschild static black holes"
and (4.47) in §4.4 "Rotating
and electrically charged Kerr-Newman black holes".
This value of surface gravity is (surprisingly) the same
in all places of the horizon, even with a rotating black hole ("0. law of dynamics of black holes"
- §4.6 "Laws of dynamics of black holes").
Gradients of gravitational forces - tidal
forces
The gravitational field, excited
around bodies according to the law of gravity, is inhomogeneous,
in the vicinity of a gravitational body it is significantly
stronger than at greater distances. Thus, when a finite-sized
body is affected by the gravity of another body, the
gravitational force on the near and far sides may be slightly different
- a gravitational force gradient is created,
given by the vector difference in gravitational force
(acceleration) between the two locations. If this body is not
absolutely rigid (in §1.6 we will see that
the theory of relativity "forbids" absolute rigidity), it leads to deformation body shape
(eg, originally a spherical shape strtches into an ellipsoid).
Gravitational gradients causing this effect are called tidal
forces (tide = rapids,
slapping, swelling of water), or ebb
forces. Thus, tidal forces are created due to the non-zero
dimensions of mutually attractive objects: when these
two bodies are attracted, a greater attractive force will act on
each of them on the side closest to the other body than on the
opposite (averted) side.
The name comes from the fact that these
forces are well known from our ordinary earthly life - they cause
sea tide and outflow. This is the gravitational
action of the Moon (to a lesser extent the Sun). During the daily
rotation of the Earth around its axis, its individual regions
move to the Earth-Moon line and tidal forces cause deformations
in this direction. The Earth's crust deforms relatively little (but see below), but large masses
of ocean water can respond to the Moon's attractive gravitational
forces almost instantly - they can move around the Earth's
surface and ocean levels periodically deform
with daily regulrity, rising and faling by several meters. The
Moon attracts water more strongly in the oceans that are closest
to it - a small "bulge" forms on the surface of the
ocean, which manifests itself as a tide at the coast.
The magnitude of tidal forces
can be determined from the law of gravity (1.1) as vector
difference of gravitational force between two given places
around a gravitational body *). If we have a (spherical)
gravitational body of mass M , in whose gravitational
field there is another (test) spherical body of diameter r
and mass m at a distance R , then a tidal force Fgrad will act on the
edges of this body in the direction of the joint
(with the basic body M ) :
« Fgrad = F(R+r) - F(R-r) = G. [m.M /
(R+r)2] - G. [m.M / (R-r)2 ] » - 2
G.m.M.r / R3 .
This tidal force acts outwardly and stretched
body in the direction towards the connector gravitated body M
. In an analogous manner, the tidal force acting on a body of
diameter r in the direction perpendicular
to the junction of the two bodies can be determined as a vector
difference :
áâ Fgrad = G. [m.M / R2] .sin (2r / R) » G.m.M.r / R3 .
In the direction perpendicular, the tidal force is about half and
points inwards - in this direction it compresses
the body. Thus, tidal forces "stretch"
the bodies in the direction of their joint and at the same time
"compress" them in the perpendicular
direction.
*) The resulting simplified expressions ( » ) are created by linearization
- in algebraic expressions or in Taylor power expansion
only members with first powers r , R are left ,
while members with higher powers are neglected.
Tidal forces are more pronounced in principle in three basic
situations (and their combinations) :
1. Close circulation of
two bodies, such as tight binary stars. Tidal forces periodically
deform the partially elastic material of both bodies, with
viscous friction generating heat therein. As a
result, part of the kinetic energy of the orbital motion is
converted into thermal energy, the orbits approaching,
the circulation time is shortened ...
2. A rotating body orbiting near another
gravitational body. This is the case of the rotating Earth,
around which the Moon orbits, mentioned above. In addition to the
deformation of ocean levels (tides), there are also periodic
deformations of the earth's crust and mantle, which are
transformed by viscous friction into heat
heating the planet's interior. It is estimated that approximately
40% of geothermal energy comes from this
gravitational-tidal mechanism inside the Earth (most geothermal energy comes from the radioactive decay
of natural isotopes - see §1.4 "Radionuclides",
passage "Geological significance of
natural radioactivity"
in the book "Nuclear Physics and Physics ionizing
radiation"). This tidal
"warm-up" mechanism also takes place on some moons
around the outer planets of the solar system, which would
otherwise be very cold. An example is Jupiter's moon Io,
in which heating by intense tidal influences leads to strong
volcanic activity.
Interestingly, the tidal
dissipation of rotational energy has apparently slowed and stopped
the earlier rotation of the Moon, which is now facing the
same side of the Earth. Furthermore, since the Moon orbits the
Earth in the same direction as the Earth's rotation about its
axis, tidal forces in the Earth's material cause a gradual transmission.
the rotational angular momentum of the Earth to the orbital
angular momentum of the Moon, whose orbit, as a result, moves
away from the Earth by about 40 mm per year. And the Earth's
rotation slows down slightly. In the
hypothetical case of a counter-rotating orbit, the Moon would
approach the Earth.
3. Compact gravitationally
collapsed bodies with an extremely strong gravitational
field - neutron stars and especially black holes - cause such
strong gravitational gradients and enormous tidal forces
in their vicinity, that even free-falling bodies are intensely
stretched in the radial direction and compressed in the vertical
direction (there is a kind of
"spaghetti") so that in the end
they end up as a "string" of atoms or elementary
particles (§4.2, passage "An
observer falling into a black hole").
In tidal phenomena,
the laws of conservation of energy
and angular momentum apply. The kinetic
energy of the rotation of bodies and their circulation is
partially converted into thermal energy in the material of
bodies. The angular momentum is "redistributed" between
the rotational motion around its own axis and the orbital motion
of bodies around a common center of gravity. The
intensity and character of these transformations depend on the
individual geometric, kinetic and material configuration of the
bodies involved.
Body
motion in Newton's gravitational field
Within classical physics motion of bodies in Newtonian
gravitational field controls the basic second
Newton's law
of force F and acceleration a : a º d2 y / dt2 = F , where after the force F is substituted gravitational force by
inverse square law (1.1). Newton's law of gravitation naturally
follows not only the original Kepler's
laws, but also
other observed properties and possibilities of planetary motion,
star motion in binary and multiple systems and within galaxies,
hydrostatic equilibrium in stars (except
for the final stages). and other effects.
Motion of a body in a
centrally symmetric gravitational field. Escape
velocity.
In addition to the idealized and simple case of a homogeneous
gravitational field (such as free fall and
throw of bodies in the Earth's gravitational field), the simplest and basic task for
moving a body in a gravitational field is when we have one point (or centrally
symmetric) gravitational
body of mass M and investigate the motion of a small test particle m in its gravitational field. It is therefore important to investigate the movement of
the test particle mass m in a centrally symmetric field
excited Newtonian gravitujícím body M. On the test
particle m at a distance r
from the center of the body M , according to (1.1), a gravitational
force F = G.m.M / r2
will act, which according to the law of force and acceleration will give it acceleration a
according to the equation m . a
= G. m.M / r2. The mass of the test body m is
shortened here, so that the gravitational
acceleration
will be
| a º d2 r / dt2 = G. M
/ r2 ; |
(1.3a) |
has a centripetal direction and does not depend
on the mass m - all bodies fall with the same
acceleration. At the point source, in place r = 0, the
gravitational acceleration of the test particle would be
theoretically infinite.
If the spherical gravitational body M
is of finite radius R (situation
according to Fig. 1.0 in the middle), the
simple dependence (1.3a) will apply only outside the body for
r> R, while inside for r <R the dependence will be more
complex, depending on the density r(r) mass distribution. The
gravitational force F(r) at a distance r from the center
is given by the amount of mass m(r) = 4p 0 ò
r r(r). r 2 dr, contained
in an imaginary sphere of radius r : F(r) = G.m(r) / r2 (the mass in the outer shells does not
apply, its gravity acting from different directions is canceled). The gravitational acceleration of the test particle m
for a spherical gravitational body M of radius R is
therefore:
| a(r) = G. M / r2 for r>
R ; a(r) = G. [4p 0 ò r r(r). r2 dr]
/ r2 for r <R . |
(1.3b) |
The gravitational acceleration for an extended
body M is finite everywhere, in the center r = 0 it is zero
(the gravitational force is zero there) .
It is also useful to determine the potential
energy U(r) of the test particle m in the
gravitational field in place r. It is the work done
against the gravitational force F(r) = G.m.M / r2 , necessary to
"pull" a particle of mass m from the point r
of the gravitational field to an infinite distance r ® ¥, where gravity no longer acts and the potential energy
is there already zero. It is therefore given by the integral U(r)
= G.m r ò
¥ (M / r2) dr = - G.m.M / r. The gravitational potential j(r),
which is the potential energy of the body m per unit of
its mass U(r) / m , is
| j(r) = - G. M / r . |
(1.4a) |
This simple relation applies for all distances r
only for the point source M ; in its
place r = 0 the potential acquires an infinite value (similar to the gravitational force F) . If the spherical body M is of finite radius R
(situation according to Fig.1.0 in the
middle), a simple dependence will apply
only outside the body for r> R, while inside for r <R the
dependence will be more complex, depending on the density profile
r(r) of
mass distribution :
The amount of mass contained in an imaginary sphere of radius r
is mr = 4p 0 ò r r(r). r2
dr , so the gravitational force per unit
mass of the test particle will be F(r) = G. (
0 ò
r 4p r(r) r2 dr) / r2 and the potential
will be the integral of this force j(r) = - r ò ¥ F(r) dr. If we divide the space around the body M
into the outside r> R and the inside r <R, the
gravitational potential will be formed by two components :
| j (r) = - G. M / r for r> R; j (r) = -G
.M / R - G. [ 0
ò R
F(r) dr ....... ] for r <R. ... (....
divorce ....) |
(1.4b) |
The gravitational potential for an continuously
spread body M is finite everywhere (if,
of course, the mass density is finite), at
the center r = 0 it has a maximum value (even
if the gravitational force is zero there);
somewhat lower on the surface r = R: j (R) = -GM / R.
The gravitational potential j plays an important
role in the general theory of relativity, as the physics
of gravity and spacetime (starting with
§2.4 "Physical laws in curved spacetime", formula (2.27), and others).
(Please do not confuse the designation
"phi" with the coordinate "j" in the polar
coordinate system!)
The simplest motion of a body in
the central field is radial motion
in the direction of
the body M , or in the opposite direction,
"away" from the gravitational body. The result of this movement will depend on the radial velocity
v of movement
of the body in the place of the distance r from the center
of the central body M .
As it moves outwards from the body M
, the velocity of the body v gradually decreases with
increasing r due to gravitational attraction. According to
the law of conservation, occurs converting the kinetic energy of
motion m.v2
/2 into the potential energy G.m.M / R in gravitational field. If
m.v2/2 =
G.m.M / r, ie the sum of the kinetic and potential energy of the
particle is zero, the particle continues to move to infinity (where there is zero potential energy) and stops there.
Thus, the so-called escape
velocity v2 is very important, which is the smallest radial
velocity needed for the body m to leave the gravitational
field of the central body M from a distance r
forever and move away to infinity :
| v2 (r)
= Ö (2 G M / r)
. |
(1.5) |
The escape velocity does not depend on the mass m
or the composition
of the escaping body (universality of
gravity), it depends
only on the mass M of the gravitational body and the
radius r from which the escaping body starts (for a body starting from the Earth's surface the escape
velocity is about 11.2 km/s - the so-called second
cosmic velocity, which is why we mark it v2 , the escape velocity
from the "surface" of the Sun is significantly higher,
about 617 km/s). In §4.2 (section "Complete gravitational collapse.
Black hole.") we will see that in the gravitational collapse of
massive stars, the escape velocity can reach the speed of light -
thus creating black hole.
Another important "cosmic"
velocity in the central gravitational field is the velocity
of the circular orbit v1 , which a body of mass m must reach in the
azimuthal direction in order to balance the centrifugal force Frot = mv2 /r with the
attractive force Fg = G.m.M/r2 of the gravitational
of a body M, so that the body can orbit in a
circular path of radius r :
| v1 (r)
= Ö ( G M / r) . |
(1.6) |
Again, it does not depend on the mass m
or the composition
of the orbiting body (universality of
gravity) , it
depends only on the mass M of the gravitational body and the
radius r along which the body orbits (for satellites orbiting the Earth in low orbit near the
planet 7.9 km/s - the so-called first cosmic velocity,
that's why we mark it v1).
By comparing equations (1.5) and (1.6) we see that the escape
velocity v2
is Ö2 (= 1.414) - multiple of the
circular orbital velocity v1 .
Note:
The additional cosmic velocities (3.-6.) mentioned in
cosmonautics are given by the specific situation of the Earth and
its orbit around the Sun. They are therefore not of universal
significance and will not be considered in our general treatise
on astrophysics and gravity.
We will analyze more complex types of
movements below using the so-called in the reduced motion of
two bodies method :
Gravitational
motion of two bodies
In the case of Newton's gravitational field, it turns out (will be shown below) that the motion of two bodies can also be converted (reduced) to
the task of moving one test body. So let's have two
bodies with masses m1 and m2 , which act on each other by
gravity according to Newton's law (and are otherwise free). The
equations of motion of these bodies will then be
d2r1
m1m2 r1r2
d2r2
m1m2 r1r2
m1 ------ = -G
--------- ----- , m2 ------- = -G --------- ----- ,
dt2
r2
r
dt2
r2
r |
where r1, r2
are the position vectors of the bodies m1 and m2 with respect to the given
reference point O (origin of the reference
system), r12 = r2
- r1 is the position vector of the
body m2 with respect to the body m1
(ie r21 = - r12) and r = |r12| = |r21| is the distance between the two
bodies. Subtracting both equations gives an equation describing
the relative motion of the body m2 relative to the body m1
:
d2 r
m2 ( m1 + m2 ) r
m 2 ------
= -G ---------------- -----,
dt2
r2
r |
(1.10) |
where r = r12 is the position vector of the body m2
with respect to the body m1 .
It is advantageous to
place the origin of the O coordinates in the common center of gravity of both bodies. Then applies m1.r1 + m2.r2
= 0, so that the position vectors of the individual particles are
to their distance vector r associated relationships
| r 1 =
[m2
/ (m1 + m2] r , r2 =
[-m1 / (m1 +m 2] r . |
(1.11a) |
If we introduce a
quantity
m1 . m2
m = ------------
m1 + m2 |
(1.11b) |
called reduced mass, the equation of motion (1.10) can be
written in the form
| m. d2 r
/ dt2 = F
(r) , F (r) = -G (m1 m2 / r2 ). r
/ r . |
(1.12) |
This relationship has
the form of equation of motion of a single
particle of
mass m moving in an external field F(r) which is formed by the m1
and m2 and is symmetrical relative to the origin
of the coordinate r = 0. The determination of the motion of two
interacting bodies is thus reduced to the problem of the movement
of a single imaginary body m in
a centrally symmetric field around a fixed center of
gravity. If this problem has a solution r = r(t), it is easy to determine the
individual trajectories r1
= r1(t) and r2
= r2(t) on the basis of relations (1.11a)
of the original bodies m1 and m2 .
If we
multiplies equation
(1.12) the scalar vector v = r.
, we
can write them in the form after editing
| d/dt [1/2
m v2 + U(r)] = 0 ; U(r) = -G.m1m2 / r , |
|
here 1/2mv2
is the kinetic energy and U(r) is the potential energy of the body m, related to the field strength
in the relation
| F
= - ¶ U(r) / ¶ r = - dU / dr. r
/ r . |
|
It follows that the
total energy E of a particle is a constant
independent of time:
| 1/2 m.v2 + U(r) = E = const. , |
(1.13) |
which expresses the law of conservation of energy during the motion of a body of
mass m in Newton's central field.
Trajectories of bodies
If we introduce the polar coordinates r, j in
the path plane (motion in the central field is planar) , it is
possible to divide the equation of motion (1.12) into radial and
tangent components :
d2r/dt2 -
r.(dj/dt)2 = -(1/m) . dU/dr =
-(G/m) . m1m2/r2 ,
(1/r) . d/dt
(r2.dj/dt)
= 0 . |
|
(1.14) |
Solution of the second
equation
| r 2 .dj / dt = L = const. |
(1.15) |
expresses the law of conservation of the angular momentum when moving in the central field
and at the same time Kepler's law of surfaces (area speed (1/2)
r2 j. is constant over time), where
the quantity L is the angular momentum per unit mass of the
particle ("specific angular momentum") L = J/m.
Equation (1.14) can then
be written in the form with respect to (1.13)
| m. d2r / dt2 =
m.L2 / r3 + U(r) . |
(1.16a) |
However, it is easier to startfrom the law of
conservation of energy (1.13 ) rewritten in polar coordinates
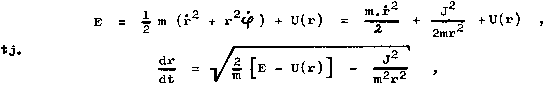 |
(1.16b)
|
which is an equation
describing the radial component of motion. From the law of
conservation of angular momentum (1.15) rewritten in the
form dj
= (J/mr2)dt and from equation (1.16b) further follows the
equation between r and j
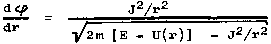 |
(1.17) |
expressing the shape of
the trajectory.
Equation (1.16a), resp.
(1.16b) shows that the radial part of the motion corresponds to a
one-dimensional motion in a central field with an " effective potential "
composed of both the
gravitational potential energy U(r) and the centrifugal potential
energy J2/2m.r2. Values of r at which
is Vef (r) = E, and thus
according to (1.16b) r. = 0, correspond to the turning
points of the path, at which the distance function from
the center r(t) transitions from increase (distance) to decrease
(approach) or vice versa. These turning points determine the
range of distances from the center at which the particle m
can move. A graphical representation of the course of the
effective potential for the motion of a body in the Newton
gravitational field of a central body is shown in Fig. 1.1a. If
there is only one turning point r = rmin, it is the movement of unrestricted (infinite), begining and terminating at infinity. If
there are two turning points r = rmin (r ..
<0) and r = rmax (r .. >0), then the whole
trajectory lies inside the annulus rmin <r <
rmax - this is a limited
movement (finite), in this case after the ellipse. The idea of the effective
potential is a very useful tool in the study of the motion of
bodies in centrally (or axially) symmetrical fields, as we will
see in §3.4,4.3 and §4.4 in the analysis of the motion of
bodies in the gravitational fields of black holes.
The shape of the path is
obtained by solving equation (1.17). For a Newtonian
gravitational field with U(r) = -G.m1 m2 / r (as well as for any central
field with a potential proportional to 1/r or 1/r2
) the integration can be performed analytically :
where the integration
constant can be canceled by a suitable choice of the beginning of
the reading of the angle j ( j = 0
in perihelion). The trajectory equation can then be rewritten in
the form
This is the equation of
a conic section with a focus at the origin of
the O coordinates, ie in the common center of
gravity of both bodies, p is a parameter and e is the eccentricity of the orbit determining
what kind of conic :
E <0,
Þ e <1 - ellipse
E = 0, Þ e = 1 -
parabola
E> 0,
Þ e> 1 - hyperbola. |
|
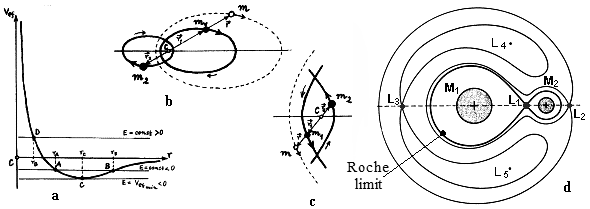 |
Fig.1.1. Motion of
bodies under the influence of Newton's gravitational
field.
a) The course of the "effective
potential" Vef(r) controlling the radial component of the
motion in the central Newtonian gravitational field.
Intersections with the energy line E = const. they
determine the turning points at which the radial
component of the motion changes direction. Lines E =
const. <0 (if they are permissible, ie E> min (Vef)) correspond
to finite motion either elliptical (radial component
oscillates between r = rA and r = rB ) or circular (constantly r = rC ) motion. If
E > = 0, the motion is infinite - it starts and ends
at infinity; point D corresponds to the closest
approach of the body to the center.
b) Finite movement (E <0) of the two
bodies interacting gravitationally m1 and m2 happens ellipses having the same eccentricity
with the focus in a common centroid C . The
problem of two bodies is equivalent to the problem of
motion of a body with a reduced mass m in the
gravitational field centrally symmetrically to the common
center of gravity C .
c) Analogously infinite motion (E> 0)
occurs after hyperbolách around the center C .
d) Cross section of some equipotential
surfaces of a system of two bodies M1 and M2 orbiting a common center of gravity. The bold
line indicates the first common equipotential of both
bodies - the Roche limit. Furthermore, the intersections
of equipotential surfaces are marked - Lagrange libration
points L1 , L2 , ..., L5 . |
Since the position
vectors r1
and r2
of both bodies m 1 and m 2 are proportional to the vector r , each of them also describes a conic
with a focus in a common center of gravity. As can be seen from
(1.11), the ratio r 1 / r 2 is the same for any point of the
path, so that the bodies move relative to the center of gravity
along paths that have the same shape (orbiting, for example,
ellipses generally of different sizes but the same eccentricity )
- see Fig.1.1b, c.
The most important case
is the gravitationally coupled
motion along an ellipse, whose longer half-axis a
and shorter half-axis b are given by
It is obvious that the
longer semiaxis not depend on the angular
momentum, but only
for the energy E . The turning points rmin = a (1-e) and rmax = a (1 + e), ie, the
"perihelion" and the "aphelium" of orbit, are
also the roots of the equation Vef(r) = E. The time of one orbit
along an elliptical orbit , i.e. the period T , can be easily determined from
(1.15) and (1.17) by integration according to time from t = 0 to T
and according to j from j = 0
to 2p. After the adjustment, we get the
relationship
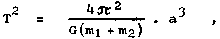 |
(1.18a) |
which is the exact
wording of Kepler's third law. If m1 >> m2, as is the case, for example, in
the solar system, then 3. Kepler's law has the usual form
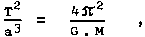 |
(1.18b) |
where M = m1
denotes the mass of the central body (eg the Sun). The ratio of
the squares of the orbital periods and the third powers of the
large half-axes is thus approximately the same for all planets,
but the relation (1.18a) holds exactly. In the special case of circular circulation (e = 0) it is finally possible
that 3.Kepler's law (1.18b) can be expressed in the form
If Newton's law (1.1)
applies, then a closed trajectory is created for finite motion (in a
frame of reference firmly connected to the center of gravity). In order for the trajectory of the finite motion to be closed,
the angle Dj by which the position vector r rotates
over the time between the two turning points rmin and rmax must be a rational
multiple of 2p, i.e. Dj = 2p. m/n, where m
and n are integers. Then, for n
periods of the radial component of the motion, the body performs m
circulates and returns to the starting position. However, in the
case of a deviation from the law of inverted squares in Newton's
law, this condition is no longer met and the
"elliptical" trajectory is not closed. If the deviation
is not too large, such a path can be imagined again as an
ellipse, which, however, is no longer fixed, but the whole
rotates slowly (performs a precessional movement) around the
center of gravity. Such precession causes perihelion and
aphelium to be in a slightly different place in each cycle. The
elliptical orbits of the planets around the Sun actually perform
the above-mentioned precessional motion, while the deviation from
the law of inverted squares is due to the fact that it is not
exactly the central field (gravitational influence of other
planets, the Sun and planets are not point). The general theory
of relativity shows, that Newton's law is not accurate even
for the exact centrally symmetric case for strong
gravitational fields; the resulting precessional
motion and anomalous
perihelion shift have actually been demonstrated in Mercury (see §4.3).
The problem of motion of
several bodies
In fact, there are a large number of individual bodies and
formations of different masses in outer space, which are affected
by gravity. Therefore, the motion of planets, moons, and stars in
binary or multiple systems actually differs from the
above-derived simple laws of motion of two bodies in a common
central gravitational field. The study of the motion of more
gravitationally influencing bodies is called the n-body
problem. This problem is very difficult even for the
case of only 3 bodies, it is generally not analytically solvable.
Only in some special cases is it analytically solvable. As early
as 1772, J.L.Lagrange showed that for each system of two orbiting
bodies, 5 significant points can be found in the coordinate
system rotating together with the connection of both bodies, the
so-called libration points. If we place a third body in
one of them, at suitable speeds the movement of all three bodies
will take place again in conic sections.
The problem of movement of the three bodies is well solved if the
weight of the third body is negligibly small with respect to the
two basic bodies, circulating undisturbed around the common
center of gravity. Then, in fact, the general problem of motion
of three bodies breaks down into the motion of two bodies
discussed above and into a separate problem of motion of one
"test" body in the resulting gravitational and
centrifugal field of two basic bodies - see the following passage
:
Binary
system: equipotential surfaces, Roche limit, libration points
So far we have dealt with the mutual motion of two bodies under
the influence of their own gravitational field. The most
important such case is the so-called binary system
- a system of two gravitationally coupled bodies orbiting a
common center of gravity. An example is the binary systems o twoo
stars, that often occur in space. The binary system of
bodies M1
and M2 is
schematically shown in Fig.1.1d. To analyze the motion of a small
particle (such as gas atoms in the space of a binary system) in
the gravitational and centrifugal field of a binary system, it is
useful to determine the shape of surfaces that are places of a
certain gravitational potential - equipotential surfaces. For
a system of two bodies of masses M1 and M2 rotating around a common center of gravity at an
angular velocity w according to Fig.1.1d, we choose the coordinate system
x, y, z rotating together with the bodies so that the x-
axis is identical with the line connecting M1 and M2 and the origin is in the center of gravity of both
bodies. The gravitational potential j for any point P(x, y, z)
will then be
j(x, y, z) = - G M1 / r1 - G M2 / R2 - ro2 w2
/2,
where r1 and r2 are the distances of the point P(x, y, z) from the
centers of the bodies M1 and M2 , ro the distance from the center of gravity of both bodies.
The gradient of the first two terms indicates the gravitational
acceleration that both masses M1 and M2 cause at the point P(x, y, z), the third term expresses
the centrifugal acceleration caused by the rotation of the
system.
Selected equipotential levels are shown in
cross section perpendicular to the axis of rotation in Fig.1.1d.
In the vicinity of each of the bodies, the equipotential surfaces
have a slightly deformed spherical shape and are enclosed around
each of them separately. At greater distances, the deformation
increases until these surfaces touch both bodies, and at even
greater distances, both bodies already have common
equipotential surfaces.
The equipotential surfaces, which touch at
one point, in the inner libration point L1, form the so-called
critical Roche limit - it is the first common
equipotential surface of both bodies. Within this limit, each
particle moves under the predominant gravitational influence of
one or the other body. At the libration point L1, the test particle
can pass from the gravitational sphere of influence of one body
to the area of gravity of the other body.
An interesting and astrophysically important
phenomenon occurs when, for example, the body M1 of the gaseous state
fills (or exceeds) the entire space defined by the Roche
boundary. In such a case, the gravitational action of the second
body "draws" or "sucks out" the gas from the
upper layers M1, which overflows around the inner
libration point L1 onto the second body M2. This phenomenon often occurs in close binary
stars and can lead to dramatic astrophysical processes,
as will be shown in Chapter 4 on the evolution of stars and black
holes - §4.1, 4.2, 4.8, illustrated in Figure 4.26. In the orbit
of solid bodies, the Roche limit can manifest itself when a
smaller body (eg the moon) approaches during its revolution
around a more massive body (eg a planet) so much, that the
libration point L1 finds itself inside this smaller body. In this case,
opposing gravitational force gradients (additionally having a
time-varying tidal force character) can cause this lighter body
to rupture (however, for smaller compact bodies,
the strength of the body material can prevent this).
In space (in the gravitational and
centrifugal field) around a system of two bodies rotating around
a common center of gravity, there are a total of 5 significant
points L1
, L2 ,
..., L5 -
the so-called Lagrange libration points
(Fig.1.1d). The libration points are the points where the
attractive and centrifugal forces acting on the test particle are
balanced. The body located at these points in
them can remain at rest against the junction of the two bodies M1 and M2. The most important
libration point is the already mentioned internal libration point
L1, which
is located on the connection between the bodies. The outer
libration points L2 and L3 lie outside the system on a line
passing through both bodies. The exact positions of all these 3
points depend on the specific weights M1 and M2 , their distance and speed of rotation. The libration
points L4
and L5 lie
symmetrically outside the line and form isosceles triangles with
the centers of the bodies M1 and M2 .
We will not deal with a
detailed analysis of the motion of bodies under the influence of
Newton's gravitational force here, it is a matter of
"celestial" mechanics (for a more
general case of motion in the gravitational field of a black
hole, however, the relevant analysis is performed in §3.4,4.3
and §4.4).
Astronomical
significance of Newton's law of gravitation
Newton's law of gravitation proved to be very successful in
elucidating all the motions of planets, moons, comets and other
bodies in the solar system. A great triumph was the use of
Newton's law of gravitation to accurately analyze some of the
anomalies in the motion of planets from Kepler's laws, which at
first seemed against the law of gravity. In 1840, astronomers
discovered that the last known planet in the solar system at the
time, Uranus, deviated slightly from the calculated orbit as it
moved. Therefore, there were temporary doubts about the validity
of Newton's law at such great distances from the Sun. However,
further calculations have shown that the anomalous behavior of
Uranus can be fully explained by the gravitational pull of an
even more distant, as yet undiscovered planet, which slightly
diverts the motion of Uranus from its ideal orbit; the position
of a hypothetical planet in the sky was also determined. This theoretically predicted planet was indeed soon
discovered and was named Neptune.
The
Atom and the Planetary System: Similarities and Differences
After discovering that the atom is a system of positively charged
nuclei and negatively charged electrons bound by an electric
force, the already well-researched solar system, bound by
gravitational force, became the inspiration for clarifying the
structure of this system. There is an obvious analogy
at three points :
¨ The electric and gravitational forces
decrease with the square of the distance;
¨ The attractive gravitational force and
the attractive electric force (between charges of opposite sign)
can be permanently compensated in a vacuum by centrifugal force
during orbital motion;
¨ The same Kepler's laws apply to motion
in central gravitational and electric fields.
Based on these analogies,
Rutheford's planetary model of the atom was created (see eg
"Nuclear physics and physics of ionizing radiation",
§1.1 "Atoms and atomic nuclei", section "Atom structure"). However, there are also fundamental
differences between the planetary system and the atom :
¨ The
difference in the properties and strength of electric and
gravitational forces. While the orbits of the planets are stable
for a long time *), the orbiting motion of an electron in an atom
according to Maxwell's electrodynamics would result in intense
radiation of electromagnetic waves, which quickly carry away the
kinetic energy of the orbit.
*) According to the general theory of
relativity, gravitational waves are emitted even during the orbit
of the planets, but their energy is completely negligible and
does not affect the orbits for many millions of years.
¨Huge
difference in size and weight. The planetary system (masses » 1030 kg, diameter » 108 km) can be fully
described by Newton's classical mechanics, while the atom
(diameter » 10-8 cm) is typically a quantum system.
These differences forced Bohr's
quantum modification of the planetary model of the atom.
Nevertheless, the planetary idea of the atom is used in
illustrative qualitative considerations.
"Cosmographic
Mystery" ?
In addition to Kepler's basic laws, astronomers have
tried to explain the specific distances of planets
(radii of orbit) and other bodies in the solar system. Already
Kepler in the work "Mysterium Cosmographicum"
tried to explain the distances of planets from the Sun using
"Platon's polyhedra" circumscribed by the spheres of
individual planets. More recently, inspired by Bohr's
model of the atom (and Balmer's series of spectral lines of the
hydrogen atom), Titus, Bode, and Mohorovic (and other authors)
have sought to find a "quantum law" for the distances
(radii of orbit) of planets in the solar system. We
now know that these laws are only apparent - the
structure of the solar system is, in addition to the laws of
gravity and mechanics, the product of complex and often random
processes of its formation (including collisions and
various resonant phenomena) and has nothing to do with quantum
laws. None "fundamental law" for distances or radii of
planetary orbit it does not exist, efforts to
find it result in mere "numerology". "Cosmographic
mystery" is just fiction..!..
Regular
and chaotic motion in gravitationally coupled systems
The above analysis of motion in Newton's gravitational field was
performed for simplified cases that could be converted to motion
in the central field. A high degree of symmetry
leads to an integrable task with a regular
solution, the laws of conservation of motion integrals
will apply. Two gravitationally bound bodies will orbit
around the common center of gravity along stable elliptical
orbits (here we neglect the emission of gravitational waves, in
the case of the solar system also, for example, the pressure of
radiation from the Sun, etc.). In more complex cases of three or
more bodies, the orbits will interact with gravitational
perturbations- the symmetry is broken. Calculations and
computer simulations show that in such complex systems a small
change do
of the initial conditions causes the
initially close trajectories to diverge exponentially from time t
: d = do .e- l .t . After a long enough
time, the system eventually becomes chaotic. The
degree of linear stability or instability -
"chaoticity" of such a system can be characterized by
the so-called Lyapunov time TL = 1/l , for which the system deviates 2.7 times (this factor
increases each initial deviation); the parameter l = 1/TL is sometimes called Lyapunov's
exponent. For the inner planets of the solar system
(excluding Mercury), the Lyapunov time is estimated to be T L » 5.106 years. The high value of this time explains the
extraordinary accuracy of astronomical predictions of planetary
motions over time horizons of hundreds and thousands of years.
However, at intervals of hundreds of millions to billions of
years, the chaotic nature of the planet's orbits would already be
decisive; some of the planets could even leave the bound system
of the solar system. From a general point of view, the behavior
of chaotic systems is outlined in §3.3, section "Determinism - chance - chaos?".
Physical
significance of Newton 's law of gravitation
Before Newton's law, physics encountered the force acting between
bodies only during their mechanical contact -
impact or friction.
With his law of gravity, Newton first introduced into physics the
concept of direct action of bodies
at a distance ("actio in distans")
in empty space *). However, both Newton himself and his followers
were not satisfied with this
idea and tried to find an "environment" transmitting
gravitational force effects and thus explain the nature of
gravity (§1.3). Later developments in physics have shown that
the idea of direct action at a distance through empty space is
correct, no environment is needed, but it cannot be an immediate
action (as Newton's law assumes), but always properly retarded (see §2.1).
*) The development of the concept of the physical
field has shown that even though two bodies do not
physically touch, they "touch" or even intersect
their fields. And that causes their force interaction.
In addition to its immediate
practical contribution, Newton's law of gravitation is also of
great importance for unitarization. The law of gravity equaly describes
the fall of a stone to the earth, the motion of a planet around
the Sun, or perhaps the motion of a star in a galaxy. This, for
the first time, bridged the gap that (in the understanding of
humans) previously existed between the Earth and the universe.
The same physical laws
have been shown to
apply in the Earth, solar system, and probably throughout the
universe. Newton synthesis a Kepler's kinematics of planetary
motions with her and Galileo dynamics of movement earthly bodies
is so in the history of the first case of process, which later in the
development of science many times repeated, and that continues
today: the unification of formerly independent branches of
physics, showing that the laws of nature are
consistent and mutually articulated - see
Appendix B "Unitary field theory and quantum gravity".
Despite all the successes of Newton's
theory, however, one anomaly remained unexplained under Newton's
law of gravitation. It was a peculiarity of the orbit of the
planet closest to the Sun, Mercury. The orbit of this planet,
whose orbit is considerably eccentric (and therefore perihelium ir relatively well determined), is noticeably differs from Kepler's laws. If it were a
motion of a single body in Newton's centrally symmetric
gravitational field, Mercury would have to orbit along an ideal
constant ellipse with the Sun in focus. The observed rate of
perihelion precession is about 5600" for 100 years, but the decisive part (approx. 5026")
has a kinematic
origin - is caused by the movement of the reference system. The
remaining 575"/100 years is the true precessional motion of
the perihelion, shows that Mercury's elliptical
orbit of slowly rotates. Almost all of this shift can be explained by the disruptive
influence of other planets, especially Venus. After subtracting the
gravitational influence of all known planets from observed orbit of
Mercury, however, it does not get an ideal ellipse, but some very
small anomalous perihelion
displacement
remains about 43"/100 years. This anomalous shift of
perihelion remained unexplained in Newton 's
theory (efforts to explain it, for example, by the influence of
another unknown planet between Mercury and the Sun were not
successful); this was explained only later
by general theory of relativity.
Distribution of kinetic and potential
energy. Viral theorem.
If a system of bodies or particles moves in a force field, the kinetic
energy Ekin of motion
and the potential energy Epot in the force field acquire certain values; the internal energy U is given by the
sum of the kinetic and potential energy of the system. If this force field is a gravitational attraction, where the interacting
force between the individual particles is inversely proportional
to the square of their distance F ~ r –2
, then between the mean value of the total kinetic energy <Ekin > and the mean
value of the potential energy <Epot > the relationship applies :
2 <Ekin > + <Epot > = 0, or
<U> = <Ekin > + <Epot > = 1/2 <Epot > = - <Ekin > .
Thus, the sum of the potential
energy and twice the kinetic energy of the stationary system of
bodies is equal to zero. Or the total energy of the
gravitationally coupled system (at
equilibrium) is equal to half
the mean value of the potential energy of the system (or negatively taken total mean kinetic energy). These important laws, which can be derived in the
framework of classical mechanics [165] is called theorem
virial or virial theorem (lat. vires, virium = power, energy). This knowledge plays an important role in astrophysics
- the formation and evolution of stars (§4.1,
passage "Star formation"), the behavior of galaxies
and galaxy clusters (§5.6, the passage
"Hidden-dark matter in galaxies and galaxy
clusters").
Modifications of Newton's Law of Gravity
Minor difficulties in celestial mechanics (whether
real or apparent) raised
various doubts about the accuracy of the law of inverted squares
in Newton's law of gravitation (1.1). Therefore, during the 18th
and 19th centuries, attempts were made to "refine" and
modify Newton's law of gravitation by introducing various small corrections in the law of inverted squares, e.g.
m.
M a
m. M
F = - G -------- (1 + ----) ro , n = 1 or 2 ;
F = - G
-------- r o ,
r2
r
n
r
2+ b
(Clairaut's law)
(Hall's law) |
|
where a and b are small constants
(corrections) correspondingly modifying the original law of
inverted squares to correspond to the observed anomalies. Another
modification of the law of gravitation has its origin in
Seeliger's well-known "gravitational cosmological
paradox" arising from an attempt to use Newton's law of
gravitation in an infinite Euclidean space (universe) filled with
matter with a constant non-zero density. The law of gravity in
the form (1.1) in such a case gives an infinite value of the gravitational
potential and infinite gravitational force (a
satisfactory solution is obtained only if the mass distribution
density in all directions from a given point decreases faster
than r-2). In order to make the law of
gravity compatible with the idea of an infinite space
homogeneously filled with cosmic matter, a modification of
Newton's law was proposed using an additional exponential factor :
m.
M
F = - G ---------. e - e .
r . ro ,
r2 |
(1.19) |
where e is a small positive constant. This
modification can be related to the hypothesis of "absorption" of gravity by the environment lying between
gravitational bodies. The law of gravitation considering the
absorption of gravity would indeed have the form F = -G (m.M / r2). e - m.r
r , where r is
the density of the environment between the bodies M
and m (homogeneous is assumed for simplicity)
and m is the absorption coefficient.
Attempts to demonstrate gravity absorption have not yielded
convincing results. In addition, the absorption of gravity would
lead to a violation of the proportionality between inertial and
gravitational mass, which would lead to an inadmissible violation
of the 3rd Kepler's law. Furthermore, the effect of gravity
absorption on the Earth's surface would cause appropriate
variations in gravity and acceleration (with a period of 24
hours), caused by shielding the gravitational action of the Sun
and Moon by the the Earth. In experiments with pendulums
no similar effect was observed, as well as properties of the
marine tide caused by the Moon and Sun do
not show any
observable abnormalities which could be attributed to changes in
tidal acceleration stemming from absorbing gravity.
All similar attempts to modify
Newton's law were in the nature of formal ad
hoc hypotheses,
were not substantiated by deeper physical reasons, and ultimately
failed to satisfactorily explain one of the observed anomalies
without other side effects and anomalies contradicting the
results of the observations.
The difficulty in shifting
Mercury's perihelion was not serious enough to threaten Newton's
theory more seriously; some hypotheses, such as that the Sun is
slightly flattened and the gravitational field is therefore not
exactly spherically symmetrical, could explain similar effects.
However, Newton's theory has some more serious conceptual shortcomings, which manifested themselves in
confrontation with a newer knowledge of the laws of nature. From
the point of view of the depth of knowledge, it can be considered
a shortcoming that Newton's law of gravitation does not explain
the exact equality (proportionality) of gravity and inertia. This
equality is purely empirical here and has the character of chance
(for more details see §2.1).
Velocity of gravitation
The main weakness of Newton's theory of
gravitation, however, is the already mentioned assumption of instant and immediate gravitational action "at a distance". In Newton's law of gravitation
(1.1) time does not appear in any way; according to him, a change
in the position of one body is gravitationally reflected
immediately on other bodies, even very distant - gravity
has infinite speed.
This assumption has proved to be
incompatible with the findings obtained during research of
electromagnetic phenomena and generalized in Einstein's
special relativity (see §1.6 and 2.1). The need arose to modify Newton's
law by introducing a time factor - retardation reflecting the final velocity of the gravitational interaction *).
Indeed, this approach leads to a satisfactory and consistent
theory of gravity - Einstein's general
theory of relativity (Chapter 2) - which not only incorporated
gravity into the context of modern physics, but even came up with
the idea of the determining role of
gravity for
all the laws of physics, to identify gravity with the properties
of space and time. In addition to its profound conceptual
significance, the general theory of relativity quite naturally
explains the equality of inertia and gravity, the anomalous shift
of Mercury's perihelion, the curvature of light rays in the
gravitational field, and other phenomena and facts beyond the capabilities of Newton's theory. According
to the general theory of relativity, the commotion in a
gravitational field propagates at the speed of light c
, in the form of gravitational waves ( §2.7 "Gravitational
waves") .
*) The velocity of the gravitational interaction will be dealt
with in §2.5 "Einstein's equations of the gravitational field" and mainly
in §2.7 "Gravitational waves",
where in the passage "How fast is gravity?" general questions of the speed of propagation of
changes in the gravitational field and the possibilities of its
experimental determination will also be discussed.
Galactic
Modifications of Newton's Law of Gravitation - MOND
Newton's law of gravitation, in co-production with the
other 3 laws of mechanics, is phenomenally successful
in analyzing all mechanical processes here on Earth, planetary
motions and other bodies in the solar system, star formation and
evolution dynamics (except final stages), stellar motions in
binary and multiple systems. It fails only in extreme situations
of strong gravitational fields in
gravitationally collapsed compact objects in the final stages of
massive star evolution (§4.2 "Final
stages of stellar evolution. Gravitational collapse. Black hole
formation."). And
in analyzing the structure and evolution of the universe on
cosmological scales (§5.4 "Standard
cosmological model. Big Bang. Forming the structure of the
universe. "). Here
it must be generalized by Einstein's law of gravitation
in the general theory of relativity (§2.5 ' Einstein's gravitational field equations").
Surprising
mismatch, however, appeared at astronomical measurements
of the the velocities of movement - circulation - of stars and
gas in the peripheral part of galaxies and speed
of galaxies in galactic clusters: these velocities
appeared to be higher than expected based on Newtonian
mechanics and gravity (while doing so the
velocities of motion and intensity of the gravitational field are
relatively small here - non-relativistic).
The visible matter in galaxies and their clusters is insufficient
for the dynamics of motion in Newton's law analysis. This paradox
was solved in astrophysics by the hypothesis that the dynamics of
galaxies is determined by an additional massive invisible -
hidden dark matter (§5.6,
section "Future
evolution of the universe. Hidden-dark matter.") .
However, the
hypothetical dark matter has not yet been explicitly discovered -
to clarify what it is composed of, to detect its particles. An alternative
hypothesis to explain the observed dynamics of motion in
galaxies is a suitable modification of Newton's theory (and possibly its relativistic generalization) -
the so-called MOND (Modified
Newtonian Dynamics). The observed astronomical measurements
of the dynamics of the motion of stars in galaxies and galaxies
in galaxy clusters, which are generally attributed to the
gravitational effect of dark matter, try to explain with the modified
form of the law of gravitation. Such a modification of
MOND was proposed in 1983 by M.Milgrom, in which Newton's law of
gravitation F = G.M .m /
r2 is modified by the hypothesis
that in addition to mass and distance, the gravitational force FMOND also
depends on the value of acceleration :
FMOND = G . M . m /[f
(a/ao) . r2] ,
where G is the gravitational constant, M is the
gravitational mass, m is the mass of the test body, r
is the distance. The modification of the classical Newton's law
is given by the empirical function f
depending on the value a acceleration of
the test body, in relation to a certain empirical constant ao (indicating the scale transition between Newtonian and
MOND dynamics). The function f is usually chosen in
the form f(a/ao) = 1/(1+ao/a), or f(a/ao) = 1/Ö[1+(ao/a)2]. In order
to explain the observed velocity curves in galaxies by the thus
modified law of gravitation, for the constant ao by the
fitation were determined value ao »
1.2 × 10-10 m-2
.
Note: In MOND, this is a
different (and otherwise motivated) modification
of the law of gravity than the "Modifications of Newton's law of gravitation" mentioned above!
MOND is thus an ad
hoc empirical formula that purposefully
adjusts the Newtonian dynamics for very small
accelerations, to match the measured rotation curves of spiral
galaxies. The opinions of experts differ on these efforts - both
the concept of dark matter and MOND are ad hoc
hypotheses. Milgrom's MOND with its acceleration
dependence is an artificial and not very convincing
theory of gravity. Why should
the gravitational force depend on the acceleration - and even on
a very small acceleration? It has no
physical logic... Most astrophysicists are more inclined to
the concept of dark matter, in which the dynamics of galaxies can
be explained in more physically justified ways (it is not even excluded that it may be just a mistake
to model the distribution of standard baryonic matter in galaxies
and galaxy clusters..?..) .
Entropic
hypothesis of the origin of gravity (Verlinde)
Originally, this is another newer attempt at an alternative
clarification - exclusion - of dark matter. In this hypothesis (dating from 2016), E.Verlinde declared entropy
to be the primary very basic quantity, the growth of
which causes the "entropic force" that
is the essence of gravity. So there is
no gravity! - we observe it only as an apparent
force, a macroscopic manifestation of entropy growth
with random statistical behavior of microscopic particle-quantum
field systems. This entropic force causes the bodies to move and
performs mechanical work. This rather bizarre and definitely very
unlikely hypothesis is described in §B-5, passage
"Entropic
hypothesis of the nature of gravity".
Mechanistic hypothesis of the
origin of gravity (LeSage)
is the oldest attempt to simply explain the origin of gravity,
long abandoned - see the following §1.3 "LeSage's hypothesis".
Einstein's law of gravitation -
general theory of relativity
The most perfect and by far the most successful improvement and
generalization of Newton's law is Einstein's law of
gravitation within the general theory of relativity
- §2.5 "Einstein's
equations of the gravitational field". We will
use it in the vast majority of interpretations of this book.
In the final
chapters B-1 to B-7 we will also mention some attempts at unitary
and quantum generalizations (eg "Loop
theory of gravity" or "Unification of
fundamental interactions. Supergravity. Superstrings.").
Vojtech
Ullmann