Hawking's quantum evaporation of black holes
Chapter 4
B L A C K H O L E S
4.1. The
role of gravity in the formation and evolution of stars
4.2. The
final stages of stellar evolution. Gravitational
collapse
4.3. Schwarzschild
static black holes
4.4. Rotating
and electrically charged Kerr-Newman black holes
4.5. The
"black hole has no hair" theorem 4.6.
Laws of black hole dynamics
4.7. Quantum radiation and thermodynamics of black holes
4.8. Astrophysical
significance of black holes
4.9. Total
gravitational collapse - the biggest catastrophe in nature
4.7. Quantum radiation
and thermodynamics of black holes
Thermodynamic
phenomena in a black hole
In the previous §4.6 we showed a very close analogy between the
laws of black hole mechanics and the laws of thermodynamics. But
if we wanted to on the basis of this analogy in the context of
classical (non-quantum) physics black holes attributed to the
actual temperature (proportional to the surface
gravity) and the actual entropy (proportional to the surface
horizon) - to build thus a sort of "thermodynamics
of black holes" - this thermodynamics would not be consistent. According to classical
physics, a black hole can absorb bodies and radiation, but it
cannot emit anything; its temperature must therefore be absolute
zero regardless of the magnitude of the surface gravity.
Similarly, the entropy of a black hole according to classic physics
should be infinite regardless of the size of the horizon surface,
because a black hole can theoretically be formed by the collapse
of an infinitely large number of infinitesimal particles. In
classical physics, therefore, the analogy between the laws of
black hole mechanics and the laws of thermodynamics would
remain only an external (and essentially random) similarity
without a deeper physical meaning.
So far, however, we have
investigated the properties of black holes only in terms of the
classical general theory of relativity, without taking into
account quantum phenomena. A completely consistent quantum
approach is not yet feasible, because a complete quantum theory
of gravity has not yet been developed. We must therefore be
content with a kind of "semi-quantum" approach: we will
leave gravity unquantited, we will only quantize other
physical fields. In other words, we will use quantum
physics to describe the motion of matter and the behavior of
non-gravitational fields in curved spacetime (against the
background of unquantited geometry of spacetime - in the
unquantited gravitational field). Because the
effects of quantition of spacetime itself can be significantly applied in
microscales of the order of ~10-33 cm (see §B.3), while in the
scales of ordinary physics (ie above 10-13
cm) they are
very small, it can be expected that this semiquantum
approximation will be to describe reality
well in practically all situations, except for phenomena in the
immediate vicinity of singularities.
Before proceeding to
Hawking's own effect of quantum evaporation of black holes, let
us illustrate the contribution of the quantum approach to the
thermodynamics of black holes in the imaginary experiment
according to Fig.4.22 (designed by J.Bekenstein [11]). Let
us have an empty box thermally insulated from the surroundings,
whose inner walls are heated to a temperature Tm and the
inside of the box contains thermal radiation of a temperature Tm . Let a
black hole (for simplicity Schwarzschild's) of mass M be
at a sufficient distance, on which we will slowly lower the box
with thermal radiation (so that there is no noticeable radiation
of gravitational waves) on a perfectly strong rope *) using a
winch. The potential energy of the box in the gravitational field
of a black hole turns into work spinning a winch; by means of a
dynamo, it is converted into electrical energy, which is stored
in the accumulator. We will assume that the efficiency of
conversion and accumulation is 100%.
*) This is an imaginary
experiment ! A rope of any
material known in physics would necessarily have to break quite
far from the horizon; the same goes for the locker.
It is not a question of materials engineering, but the
limitations are imposed by the laws of nature themselves. The
strength of all known (also in the future) materials is formed by
the electromagnetic interaction between the electronic shells of
the atoms of the material; and it is completely insufficient in
the gravitational field near the horizon. Even hypothetical
materials held, albeit by strong interaction, would not work: the
basic physical boundary is determined by the laws of the special
theory of relativity. The tension of the rope can never be
greater than the mass per unit length multiplied by c2.
Note also that the whole analysis of the
imaginary experiment has only a heuristic character and does not serve to accurately
derive the quantum-thermodynamic laws of black holes.
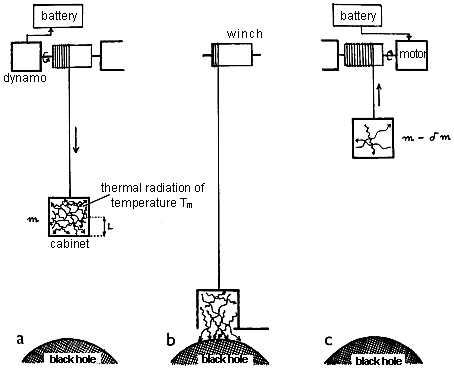
Fig.4.22. An imaginary experiment for studying the thermodynamic
properties of a black hole - a heat engine with a black hole as a
cooler.
a ) Slow
lowering of the thermal radiation box to the black hole; the
energy obtained is stored in the battery.
b ) At the
horizon, part of the thermal radiation is absorbed by a black
hole -> cooling of the box.
c ) The
cooled and unloaded box is pulled back using energy from the battery, the remaining energy
coming from the thermal radiation absorbed by the hole.
In order to be able to
pull the cabinet back again, we can lower it as deep as
possible, so that its bottom just touches the
horizon. Thus, its center of gravity can reach a maximum distance of L (half the height of the box) from the
horizon of the black hole. The total work that is released and
stored in the battery when lowering the box from infinity to a
distance L from the horizon is equal to the binding
energy
| E 1
= m (1 - k .L)
, |
(4.57) |
where m is
the mass of the box and k is the surface gravity on the
horizon of the black hole. Now we open the bottom of the cabinet, so
that part of the thermal radiation of mass dm
escapes and is absorbed by the black hole. Close the bottom again
and slowly pull the lightweight and cooled box (weighing m- dm) back by replacing the dynamo with a
motor powered by battery energy, previously accumulated when lowering the
cabinet. To pull the lightweight box back
to infinity, it will take work
| E 2
= (m - d m) (1 - k .L)
. |
(4.58) |
The energy E1 - E2 remains
in the accumulator, so we can say that the amount of heat dm was converted into the work E1 -E2 . The
arrangement in Fig.4.22 is thus, from the point of view of
thermodynamics, a "heat
engine"
converting heat in the cabinet into work, the role of the
"cooler" being played by a black hole. The efficiency h of heat conversion dm for
the obtained work E1 -E2 is equal to
| h = (E 1 - E 2 ) / d m = 1 - k .L . |
(4.59) |
This efficiency is
always less than one; approaching the ideal unit efficiency would
only be possible if the box size L was close to zero.
And here comes the word quantum
physics,
according to which this is not possible, because the box must be
greater than the characteristic wavelength of thermal radiation
corresponding to a given temperature Tm (in
order for this thermal radiation to "fit" into box) : L ³ h / k.Tm , where h is
the Planck constant ("crossed out": h = h/2p) and k is the Boltzman constant. The
efficiency of heat conversion at work is therefore limited by
inequality
| h
£ 1 - ( k . h / k) / T
m .
|
(4.60) |
According to the 2nd Act
of Thermodynamics, the well-known Carnot
theorem applies
to the thermal-energy process in Fig.4.22
| h £ 1 - Tcoolers / Theaters , |
(4.61) |
where equality applies
only to the reversible action. If we compare both inequalities
(4.60) and (4.61), where the Theater is equal to the original
temperature T m of
the box and the
cooler is a black hole, we see that from a thermodynamic point of
view the black hole should have a thermodynamic
temperature
(TH = h/k.r g for the Schwarzschild black
hole), which is proportional to the surface gravity k. Let's look further at the entropy balance
in this process according to Fig.4.22; let us admit that a black hole
has some finite entropy in the usual way related to mass and
temperature, even if it is not in accordance with classical
physics. The entropy that the box loses when it passes part of
its thermal radiation to the black hole is equal to dSbox = dm/Tm. The
black hole acquires an entropy dSH
= dM/TH, where the weight gain of the
black hole dM according
to the law of conservation of energy (1st law of black hole
mechanics), is equal to the difference between the transferred
mass dm and the energy remaining in the
accumulator : dM = dm -
(E1 -E2 ) = dm - dm (1 - k
.L) = dm. k .L. The entropy of a black hole
thus increases by dSH = dm. K. L/TH; if we substitute here for TH
from (4.62) and if we use quantum conditions L
³ h/k.Tm for the box, we get an inequality
for the total entropy balance
dSH ³ dScabinets . Thus, in accordance with the
2nd theorem, a thermodynamic black hole gains more entropy than a
box loses. Substituting into the relation dSH
= dM/TH to change the entropy of a black
hole for dM from the first law of black
hole mechanics (4.50) and for TH from (4.62), we get
d S H = (k / 8 p h ) d A
;
since it is natural to
assume that a non-existent black hole of zero mass has zero
entropy, ie limA®0SH(A) = 0, integration leads to the
relation
| S H = (k / 8 p h ) A . |
(4.63) |
We get
the result, according to which the entropy
of a black hole is proportional to the area of its
horizon; it is in full accordance with the analogy between the
laws of black hole mechanics and the laws of thermodynamics (discussed in the previous §4.6
"Laws of black hole dynamics").
At the beginning of this
paragraph, we said that according to classical physics, the
entropy of a black hole should be infinite, because a black hole
can theoretically be caused by the collapse of an infinitely
large number of particles of infinitely small mass. According to
quantum physics (the uncertainty principle), however this is not
possible, the Compton length h/mc
of black hole-forming particles must be limited by gravitational
radius of the horizon 2M, so that the number of
configurations, from which a black hole of
a given mass can form is finite. According to quantum mechanics, the entropy of a black hole is very large, but finite.
Loss of information in a black
hole. Holographic principle.
From wiewpoint of statistical physics (and information
theory), entropy is a
measure of the disorder of a given system [167].
When a black
hole is formed by gravity collapse, all information about the
individual properties of the collapsing mass is lost to the outside world except for the total
mass, charge and rotational angular momentum - "a black hole has
no hair", a black hole has no microscopic structure. This
unusual situation is referred to as the "information loss paradox" - see also the discussion in the final
section of this chapter, "Quantum
Evaporation: The Return of Matter from a Black Hole?". This vast amount of lost information is
then a measure of the entropy of a black hole. Due to the
proportionality between the surface of the horizon and the
entropy of the absorbed matter, the somewhat misleading name
"holographic principle" was later adopted :
Holographic principle
Holographic image in optics it is created by
dividing a beam of coherent light (from a laser) into two parts,
one of which impinges on the photographic layer directly, the
other part after reflection from the displayed object. Both of
these beams interfere, and a structure of thin interference
fringes is formed on the photographic emulsion, carrying
information about the phase differences of the two beams. If we
then illuminate this two-dimensional image with coherent light
(again from a laser), the reflected rays reconstruct the same
phase differences as the image they created - the impression of a
three-dimensional image of the original object is created. The
holographic image has the interesting property, that even from a
fragment of the hologram we can see the whole three-dimensional
image, albeit with a lower resolution.
The two-dimensional surface of the horizon of the black hole
carries everything (correspondingly reduced
- "black hole has no hair") information
about three-dimensional configurations of absorbed matter in a
black hole, similar to a two-dimensional hologram carrying
information about a three-dimensional object. However, this ends
the similarity with holography, as detailed information
about the absorbed matter (except M, J, Q) is lost and cannot be
reconstructed in any way.
The "holographic principle" was
further generalized in connection with the construction of
quantum theories of gravity: "Information (degrees of
freedom) about the system within the volume V can be located
(encoded) on the surface ¶V this volume, the density of information does not
exceed one bit per Planck surface l p2 ".
The holographic principle is generally the
statement that information about the N-dimensional
region (its interior) is encoded on N-1 dimensional
boundary of this area. Theoretically, it is justified
only on the horizons of black holes (but M, J, Q only). In other
cases, these are just extrapolations and analogies - unconfirmed hypotheses
....
When capturing an
elementary particle with a black hole, to an outside observer loses the
ability to identify this particle. Expressing ourselves
in computer terminology, one "bit" of information has
been lost: the yes-no particle. The entropy of the black hole
thus increases by a value proportional to the Boltzman constant k (dSH = k.ln2) and at the same time
the area of the horizon A of the black hole increases accordingly. Bekenstein
[11], [13] calculated that when a mass of mass m (m
<< M) and size d is absorbed by a black hole, the
area of its horizon increases by at least 8p m.d. In
quantum mechanics, each particle has an effective diameter of the
order of the Compton wavelength, so if we take the size of an
elementary particle as its Compton diameter h/mc
(but we work in units where c = 1), the area of the horizon
increases by at least 8p h . The ratio between the increase in
entropy of a black hole and the increase in the area of its
horizon when capturing an elementary particle is thus
d S H / d A ~ k / 8 p h .
According to quantum
mechanics and statistical physics, we again get the relation
(4.63), according to which the entropy of a black hole is
proportional to the area of its horizon. The coefficient of this
proportionality then follows from the relation (4.62) for the
temperature of a black hole under the Hawking effect of quantum
evaporation and from the 1st Law of Black Hole Mechanics (4.50),
see below.
In the thermodynamics of gases,
liquids and solids, the entropy is directly proportional to the
number of particles, ie the volume filled with matter. In the
quantum physics of gravity, however, the entropy is directly
proportional to the surface, so that significantly less
information can be "encoded" into a given volume than
would correspond to the classical idea. Equation (4.63) for black
hole entropy can be rewritten in equivalent form
| S H = k. A / 4 l p 2
, |
(4.63´) |
where lp
= Ö(G h
c-3) is the Planck
length (B.10)
introduced in §B.4. We see that the entropy of a black hole is
given by the number of Planck
surfaces lp2, which can cover the horizon of
a black hole (with a coefficient of 1/4). Black hole entropy
(4.63) is also the maximum entropy could be "squeezed"
into the volume enclosed inside the area sizes A .
In other words, a black hole represents the object that most
effectively concentrates the entropy - the area of its
horizon A is the smallest possible surface of the
spatial area in which the mass of a given entropy SH can be located.
Quantum
evaporation of black holes
We still have one last contradiction, preventing the thermodynamics
of black holes from being consistent: a black hole can absorb
anything, but it cannot "in return" radiate anything.
Therefore, a black hole cannot be in thermodynamic equilibrium
with anything, its "temperature" should be absolute
zero according to classical physics.
This missing link in the chain of
black hole thermodynamics was supplemented by S.Hawking, who in
1974 expressed the hypothesis of quantum
radiation of black holes [123], [126], according to which each black
hole spontaneously emits radiation exactly as if it were ordinary
(absolutely) black body heated to a temperature of TH
= k.h/k proportional to the surface
gravity k on the horizon.
A certain harbinger of Hawking's effect of
quantum evaporation was the quantum analysis of superradiation
in the ergosphere of a rotating black hole (mentioned in §4.4)
by Zeldovich and Starobinsky [286], [234]. From the point of view
of quantum physics, the amplification of waves is a kind of
"induced" radiation, so the existence of spontaneous
radiation can also be expected.
The Hawking effect of quantum evaporation
is often discussed in connection with thermodynymics, but it has
its fundamentally independent significance, even
if there was no connection with thermodynamics. Its mechanism
(discussed below) is particularly important. It can serve as a connecting
bridge between general theory of relativity as the physics
of gravity and quantum physics - a "window" to quantum
gravity.
Mechanism of quantum evaporation (the illustrative popular explanation - it may
just be incomplete !)
The basic idea of quantum field theory in curved spacetime
(semiquant approach) leading to spontaneous formation of
radiation particles by quantum effects in an inhomogeneous
gravitational field can be clearly summarized as follows.
According to quantum field theory (see eg
§1.1 "Atoms and atomic nuclei", passage
"Quantum field theory" in the monograph "Nuclear
physics and physics of ionizing radiation"),
the vacuum is filled by fluctuating pairs of particles and
antiparticles, which are constantly formed and then immediately annihilated (recombined). The
most common such pairs are electron-positron
pairs and photon pairs (a photon is
its own antiparticle).
According to quantum uncertainity relations
dE.dt l h, a pair of particles with a mass m
and energy m.c2 is virtual, if their recombination lifetime does not exceed
the Compton time ~h/mc2.
In a strongly inhomogeneous
gravitational field (eg black holes), the gravitational forces at
the particle and antiparticle locations can vary considerably (large gravitational gradients - tidal forces), so that due to the deviation of
geodesics, the two originally virtual particles can
move away from each other in the Comptonian
period to a distance significantly
exceeding h/mc. In this case, recombination
may no longer occur and the originally virtual pair becomes a true particle-antiparticle pair, with the
corresponding energy being supplied by the gravitational field.
Let's go back for a moment to the effect of superradiation
(§4.4., part "Penrose
process", passage "Superradiation"). If the quantum process
described above releases an originally virtual pair in the
ergosphere of a rotating black hole and one of the particles
enters an orbit with negative energy with respect to infinity and
is captured by the black hole, its partner, as in the Penrose
process, may have enouch energy to fly out of the ergosphere like
a real particle and move away from the black hole. By this
mechanism, the rotating black hole will spontaneously emit
radiation, gradually carrying away its rotational energy. Surface
horizon of a black hole with the same time, in accordance with
the classical 2.law dynamics of black holes, increases.
As we said in §4.4, rotating black holes are non-static and
"alive", so the possibility of their quantum radiation
is not so surprising.
Hawking's discovery (so far it is a hypothesis) that even static Schwarzschild
black hole emits radiation that leads to a gradual reduction ("evaporation") of the mass
of the black holes, however
but was completely
unexpected! This is in clear contradiction with the second law of black
hole mechanics (§4.6 "Laws
of black hole dynamics",
Theorem 4.7) ,
according to which the horizon of a black hole cannot be reduced.
However, for the validity of this law (see §4.6) it is necessary
to assume that the intrinsic energy density Too cannot be negative. However, in the
scales corresponding to quantum fluctuations, this assumption may
no longer be met *) and thus the 2nd law of Black Hole Dynamics may be
violated here. Second law of dynamics black holes must
therefore be generalized, so that it
also applies in the case of quantum evaporation; below we show ("Unification of thermodynamics and
quantum evaporation of black holes") that such a generalization also
leads to its unification with the second law of thermodynamics.
*) In addition to the
positive density of local energy for each observer, a
"strong" energy condition also requires an energy flow
of only a temporal nature (§2.6). In creating a virtual pair,
two particles "materialize" with a spatial interval, so
that they are locally a stream of spatial-type energy; this
disrupts the energy condition necessary for the 2nd Law of Black Hole Dynamics.
The laws of quantum physics applied
in curved spacetime around the horizon of a black hole provide
four basic ways to imagine the mechanism of black hole radiation :
1. Absorption of one of the members of a virtual
particle-antiparticle pair below the horizon and emission of the
other member as real particles.
2. Quantum tunneling phenomenon allowing virtual particles
from below the horizon to penetrate into outer space and become
real.
3. Production of particle pairs induced by gradients of
gravitational forces - deviations of geodesics - in curved
spacetime.
4. Quantum theory of gravity (not yet developed).
Basic idea of the mechanism of the Hawking
effect of quantum radiation (according to point 1.) is schematically shown in Fig. 4.23 left.
According to quantum physics, every vacuum is populated by
virtual pairs of particles (and antiparticles), which are
constantly spontaneously created and subsequently annihilated on
microscales. In a strong inhomogeneous gravitational
field with universal effects, a certain "polarization"
of the vacuum of fluctuating virtual pairs of particles and
antiparticles occurs around the black hole.
Virtual particles can sometimes to break away from each other by
large gradients of gravitational forces over distances longer
than the Compton distance. In regions close to the horizon, then there
is a certain probability that one member of a pair of particles and particles
will penetrate below the horizon and be absorbed, while the other
member escapes into outer space like a real particle which "can no longer
annihilate with anything" - it is emitted. In such a case, the negative energy needed to release the originally virtual
pair, is actually brought below the horizon. From a certain
point of view, the particle-antiparticle relationship and vice
versa are related to the inversion of time, so the opposite of
the second law of black hole dynamics will apply to the given
process, ie the horizon will shrink...
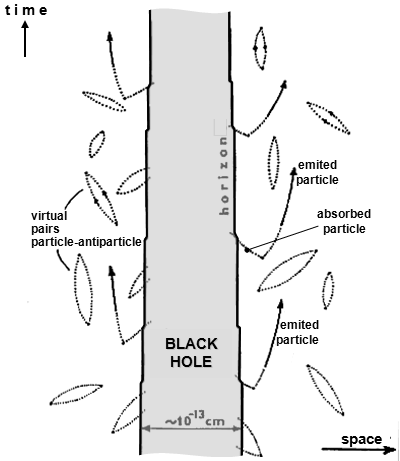 |
Fig.4.23. Left:
Illustration
of Hawking's mechanism of quantum black hole radiation by
absorbing one part of a virtual particle-antiparticle
pair and radiating the other part as a real emitted
particle. The horizon gradually decreases.
However, this illustrative popular explanation of the
quantum evaporation mechanism is somewhat not entirely
accurate, as discussed below.
Right: Below is a schematic representation of
quantum creation, annihilation, absorption, escape, and
emission of quantum radiation particles. Above
right is a
graph of the radial profile of the number of quantum
particles produced at various distances from the source
object and escaping into outer space. |
A misleading illustrative
explanation of the mechanism of quantum evaporation ?
Hawking's original illustrative explanation of the mechanism of
quantum evaporation from 1974, with the aim of understanding it
for the wider public and beyond experts in the general theory of
relativity and quantum physics, we tried to show in Fig. 4.23 left.
However, upon closer inspection, this simplified explanation
appears to be somewhat misleading, and has difficulty explaining the
expected objective facts. The basic mechanism is certainly the
polarization of the vacuum in the strong inhomogeneous
gravitational field around the black hole. Mostly, however, tiny
high-energy particles are not produced near the event horizon as
shown in the figure, but the source of radiation is the entire
wider vicinity of the black hole, roughly 20 times larger than
the horizon; so is the maximum wavelength of the emitted
radiation. And the minimum wavelength of radiation corresponds to
the diameter of the horizon. In addition, Hawking radiation is
dependent on the relativistic effect of the observed frame of
reference, similar to the Unruh effect of accelerated frames of
reference.
A more concise
explanation might perhaps be the generalized mechanism of quantum
evaporation outlined below "Quantum
radiation of curved spacetime - even without horizons?".
Intensity of the quantum emission of a black
hole
The result of quantum analysis (we will not
provide technical details of quantum calculations here, see eg
[123], [117], [280]) is the conclusion that a black hole will
thus produce radiation whose total intensity (power)
will be proportional to
| W ~ h.c 2 / r g 2 . |
(4.64) |
For a general
Kerr-Newman black hole with surface gravity k , the angular velocity of horizon WH
and the electric potential of horizon FH, is the
probability of emission of particles with the energy E (=
h.w where w
is the frequency of
the wave), the angular momentum L (at a looking at the axis of rotation
of the black hole) and an electric charge q, equal to
e -2p(E-L.WH-q.FH)/h.k . G(E,L,q) ,
where G indicates the probability of absorbing a
particle with energy E , the angular
momentum L
and the charge q by this black hole. The mean number of
<N> particles radiated (as a wave -
quantum) with frequency w, angular momentum L and electric charge q, is
then given by
G
d<N> = ------------------------------- dw.dL.dq ;
e-2p(E-LWH-qFH)/h.k ± 1
|
(4.65) |
the "+" sign applies to fermions, the
"-" sign to bosons. The surface gravity k, the angular
velocity WH and the electric potential FH of the
black hole horizon are given by the relations (4.44-4.47 in
§4.4). The absorption coefficient G is a
slowly variable function of w and depends on the type of particles or
radiation; is of the order of one (especially for wavelengths
significantly exceeding the size of the horizon given by M).
For Kerr black hole, this radiation will have the
spectrum of thermal radiation *) of black-body with temperature
TH = k.h/k
= h(rg+-rg-)/8pk.Mg+
; for
non-rotating uncharged Schwarzschild black hole is TH
= h/4pkrg (= hc3/8p.M.G @ 10-7M¤/M [°K]. Distant observer while this
spectrum observed through the "filter" formed
potentials of the field around the black hole.
*) By thermal radiation of
temperature Tm we will next understand the radiation of
an absolutely black body with temperature Tm. It is radiation in a broader sense than
conventional thermal radiation means; this radiation may comprise not only photons (electromagnetic waves), but
also gravitons (gravitation waves), and at a sufficiently high
temperature Tm will be present also the particles with
nonzero rest mass (electrons, protons, and the like.), together
with the respective antiparticles.
It can be seen from Equation
(4.65) that at the same w, the emission intensity of
particles with a positive angular momentum L
is higher than with
a negative angular momentum, so quantum radiation carries
away the rotational angular momentum of a black hole (similar to electrons and positrons they can carry away
with an electric charge). If w
< L. WH , the denominator (4.65) will be
negative (for boson fields); however, this
inequality is a condition of superradiation, so G will also be negative. For black holes of
larger masses (i.e. very low temperature TH)
then the quantum emission can noticeably occur only for radiation
with w < L.WH , and it with intensity G, which is in accordance with the quantum
analysis of superradiation performed by Starobinský [234] and
Unruh [258].
Quantum radiation of black holes
consists mainly of photons (electromagnetic waves whose
wavelength will be comparable to the size of the horizon, l ~ rg /2); electrons, positrons, and
other particles with a non-zero rest mass can only emit black
mini-holes (see the "Quantum Evolution of a Black Hole" section below) .
The Hawking effect of quantum radiation is the
result of the application of quantum field theory in curved
spacetime. In general, there are problems in defining the states
of vacuum and the presence of a particle in a strong
gravitational field. For example, in the field of full extension
of Schwarzschild geometry (Kruskal's diagram in Fig.3.19,
describes an "eternal" black hole), the final result of
the flow of quantum radiation at infinity will be influenced by
the choice of initial vacuum and particle states on the horizon
of the past [25], [259]; by appropriate selection of these
states, it can be achieved that there will be no radiation.
Problems of this kind do not arise for a black hole created by
gravitational collapse in asymptotically planar spacetime,
because all particles here begin (in the past) and end (in the
future) their motion in areas where the influence of the field
can be neglected. For such asymptotically free particles, a
quantity of asymptotic energy can be used and only asymptotic
field shapes can be used in quantization. In this way Hawking
arrived at his result [123]; the final result is completely
independent of the details of the course of the collapse, so it
seems that the result will be valid even without the assumption
that the black hole was created by collapse (the
"eternal" black hole?). Some
other methods of deriving quantum black hole radiation [117],
[280] do show this without the assumption of gravitational
collapse.
In connection with this, it is
interesting to ask the question, where
they actually arise particles forming that make up the quantum
radiation of a black hole? There are basically two diametrically
opposed possibilities. According to the first of them, the
formation of particles is caused by a variable component of the
gravitational field during a gravitational collapse [27], [63],
ie they are formed by collapsing matter before the formation of
the horizon. The collapsing mass remains out of the horizon for
the outside observer, while the radiation takes away its
kinetic energy. The surface of the collapsing object (the area of
the "horizon") is thus reduced. The resulting particles
are then held by the gravitational field for various lengths of
time near the horizon and gradually escape (to infinity).
However, a serious problem arises here: the particles would have
to be formed with ever-higher self-energy in order to compensate
for the growing redshift on their way to infinity. According to
this mechanism, quantum radiation would only occur in black holes
caused by collapse, while "eternal" black holes would
not emit quantum.
The second possibility on which
Hawking was based (and which we also used above in the
explanation) is that particles are constantly formed in pairs
from a polarized vacuum in an inhomogeneous (even static) field
outside the horizon. The energy going to infinity is compensated
by the flow of negative energy of particles falling below the
horizon. All physical arguments testify to the correctness of this
second possibility [260], [280], from which follows directly the independence
of radiation on individual properties and
the course of previous collapse,
as wel as the thermal
shape of the spectrum. According to this, the
"eternal" black hole will radiate quantum in the same
way as a hole created by collapse; quantum effects thus mean that
a truly "eternal" black hole can no longer exist.
Unruh's
accelerating quantum radiation
From the point of view of quantum-gravitational analysis in GTR,
quantum radiation is a more general dynamic effect,
taking place in a vacuum not only in the presence of real
gravity, but also inertial forces in non-inertial systems.
In 1973-76 S.Fulling, P.Davies and especially W.Unruh [259]
showed, that radiation with a thermal spectrum (such as radiation of an absolutely black body) will be generated in an accelerating
moving reference frame in a vacuum. In an inertial
system in a vacuum, no such radiation is manifested, while a
accelerated-moving observer will register radiation in a vacuum
with a thermal spectrum corresponding to the temperature
T a = h .a / (4 p c.k)
@ 10 -19 .a [° K] ,
where a is the instantaneous acceleration, k is
the Boltzman constant, h is Plank's
constant (reduced). It is analogous to the Hawking radiation of temperature TH = h.g/(4pc.k) of a black hole, on the horizon of
radius rg is the gravitational acceleration g .
In terms of the mechanism of
quantum radiation, Hawking evaporation
is due to the
existence of the gravitational horizon
of the black hole, while Unruh's
radiation is
related to the existence of the kinematic so-called Rindler's
horizon in
the accelerating frame of reference. This analogy fully
corresponds to the principle of
equivalence
between gravity and the acceleration of a non-inertial system.
The concept of Unruh radiation also shows that, from the point of
view of the quantum concept, a vacuum filled with virtual
fluctuating quantum fields appears in different states for
different reference frames - depending on the state of motion of
the observer.
Like Hawking's radiation of
quantum evaporation of a black hole, Unruh's acceleration
radiation is still completely hypothetical, without the possibility of
experimental verification *) .
*) During high-energy collisions of
particles in accelerators, very high values of acceleration
occur, at which several quants of Unruh radiation could arise.
However, it is quite impossible to distinguish
this faint radiation from the huge background of very strong
radiation (arising from particle interactions) ! It remains only
as a theoretical interest ...
General quantum radiation of curved spacetime (even
without horizons?)
The hypothesis of quantum radiation from black holes and other
gravitating objects is based on the co-production of three
mechanisms :
1.
Quantum fluctuations of the vacuum - the constant spontaneous creation of virtual pairs of
particles and antiparticles, which annihilate almost instantly
without the presence of an external field.
According to quantum physics, the vacuum is populated by
virtual pairs of particles (and antiparticles), which are
constantly spontaneously created and annihilated on microscales -
space appears as an empty vacuum on larger scales. ........
2. Separation
of virtual particles, which
prevents them from annihilating and leads to the creation of real
quantum particles forming the resulting radiation.
In the Hawking process, this separator is the event
horizon of a black hole in the GTR. However, virtual
particles can also be effectively separated from each other using
gradients of gravitational forces - tidal
forces, curved spacetime of the gravitational field excited
in the vicinity of gravitating bodies. Not only in close
proximity to the horizon, but basically everywhere -
Fig.4.23 right. This would be the general principle of particle
formation from the curvature of spacetime, even without
the presence of an event horizon.
Therefore, if there is a sufficiently strong field
that interacts with the particles - gravitational or electric *),
the particles of the spontaneously formed virtual pair are
locally accelerated in opposite directions by
this field. If the particles are thus sufficiently
separated from each other by the Compton wavelength in a
sufficiently short time provided by the quantum uncertainty
principle (they gain sufficient speed to
satisfy the relativistic relation E2 = m2 + p2 between energy and
momentum), they will not annihilate and
will become real. In sufficiently strong
gravitational fields - in curved spacetime - the virtual pairs
are separated from each other by local tidal forces
(gravitational field gradients) and become real. Gravitational production of
particles occurs in curved spacetime. The energy of the
particles produced comes from the gravitational field, through
its coupling with quantum fields creating virtual particles; in
practice it would almost always be an electromagnetic field.
*) For an electric field, the process of
the possibility of creating real electron-positron pairs was
analyzed by J.S.Schwinger in 1951. However, for such an effect to
be measurable, a local electric field intensity >~1016 V/cm would be
needed, which has not yet been achieved. The question of quantum
production of e-e+
pairs in an electric field is briefly discussed in §1.5, the
passage "What is the strongest electric
field?".
The effective intensity density of
particle production by this mechanism would then be dNef /dt ~ (K . G.M)-1, where the coefficient K is given by
the coproduction of the gradients of gravitational forces in the
GTR and the creation and annihilation of virtual
particle-antiparticle pairs in the quantum field theory. Analysis
in semi-quantum gravity gives a value of K ~ 400÷700, depending
on the model used.
3. The escape of the particles
produced from the vicinity of the
gravitating object, which allows the released particles to
overcome the gravitational barrier and escape outside ("to infinity") as real
radiation.
Most of the released pairs of particles and
antiparticles are created in the close proximity of the
gravitating object where the tidal forces are the greatest (for a black hole it is near the event horizon r~2 GM), but there is also a high probability that they will be
reabsorbed by the gravitating body. With increasing distance, the
intensity of production decreases, but at the same time the
probability that one (rarely both) of the produced particles can escape increases. The
opening angle fesc of the exit
cone for the escape of particles to infinity from a location
at a distance r according to Fig.4.8 in §4.3 (passage "Propagation
of light in the field of a Schwarzschild black hole") is given by the relation
sin2 fesc = 27 (G.M)2 (1 - 2 G.M/r)/r2
.
The probability of particle escape is then (1 + cos fesc) / 2. By multiplying the intensity
of particle production and the probability of their escape, we
obtain the curve of the radial profile of the intensity of
emitted particles coming from different distances from the
gravitating object - the graph in Fig.4.23 on the top right. The
maximum production of escaping particles at a Schwarzschild black
hole can be expected at a distance of around r~2.4 GM .
The total fluence of particles
observed at infinity is then d N../dt ~ (6 ÷ 12)×10-4 (G.M)-1.
The total radiated energy output would then be dE/dt ~
(7 ÷ 13)×10-5 h (G.M)-1. The numerical values of the coefficients
are model-dependent. The lower values given here are
used in works based on the Hawking horizon mechanism, the higher
values are based on analyses according to the generalized quantum
radiation mechanism of curved spacetime, due to the deviation of
the geodesics of virtual particles (not
only in the horizon region).
| For clarity, we will display Figure 4.23 again, here
we are interested in its right part : |
 |
Fig.4.23. Left:
Illustration
of Hawking's mechanism of quantum black hole radiation by
absorbing one part of a virtual particle-antiparticle
pair and radiating the other part as a real emitted
particle. The horizon gradually decreases.
However, this illustrative popular explanation of the
quantum evaporation mechanism is somewhat not entirely
accurate, as discussed below.
Right: Below is a schematic representation of
quantum creation, annihilation, absorption, escape, and
emission of quantum radiation particles. Above
right is a
graph of the radial profile of the number of quantum
particles produced at various distances from the source
object and escaping into outer space. |
This generalized approach unifies the now
classical Hawking radiation of a black hole, Unruh's acceleration
radiation (and by analogy Schwiger's
electric radiation), as different aspects
of the essentially same mechanism of action of quantum
fields in curved spacetime. As a consequence of the production of
real particles, induced by gradients of gravitational forces
- deviations of geodesics of virtual particles - in curved
spacetime. And it also leads to the hypothesis that in principle every
gravitating material structure that curves spacetime should emit
quantum radiation..?.. Of course, this would vary in intensity
according to the degree of curvature of spacetime in their
surroundings (this depends on the density
of the object). And also by
"where" the released particles can fly away,
or what part of them is reabsorbed back in the source
object. Not only black holes, but also neutron stars, white
dwarfs, planets, etc. could emit a small amount of quantum
radiation in space.
For black holes of stellar masses,
practically only photons are emitted. Only in black miniholes
with a subatomic horizon size <10-8 cm and a mass < 1014 kg ~10-16 M¤ could heavier particles such as electrons and
positrons, and later also baryons, be more efficiently created
and emitted. Most photon pairs are created near the event horizon
(r~2 GM), but there is also a high
probability that they will be reabsorbed by the black hole. With
increasing distance from the horizon, the intensity of production
decreases, but at the same time the probability that one (and occasionally both) of the
created photons can escape increases (the
maximum production of escaping particles can be expected at a
distance of around r~2.4 GM - graph in Fig. 4.23, top right). According to the extended concept of gravitational
particle production considered here, it can be expected that
black holes would radiate somewhat more strongly than
corresponds to the classical Hawking mechanism, since quantum
radiation would occur in a somewhat wider area than just in the
vicinity of the horizon..?..
This
hypothetical intuitive idea outlined above was recently analyzed
in detail quantumly by M.F.Wondrak, W.D.Suijlekom, H.Falcke in
the paper "https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.221502". They showed that all the above-mentioned hypothetical
possibilities can be realized in principle and they preliminarily
calculated some specific details :
- The quantum radiation of black holes should be roughly
2× stronger than predicted by the classical Hawking model (this
seems plausible).
- Stellar mass black holes and neutron stars will quantum
evaporate in about 1067 years.
- Macroscopic bodies such as planets (and us humans) will
quantum evaporate in about 1090 years (however, realistically,
they will disappear much earlier by other mechanisms...).
There is debate about the
reliability of these data, but this is an interesting pilot study
on how to newly understand and generalize the phenomenon of
quantum radiation from black holes and possibly other
objects..?..
However, it is still necessary to
keep in mind that the entire hypothetical concept of quantum
evaporation of black holes or other gravitating objects does
not apply in present nature and the universe! There is
no sufficiently rarefied vacuum anywhere that would not contain
far more quanta of cosmic radiation than would be produced by
quantum radiation of astronomical objects. All black holes grow
by accretion, and other gravitating objects also grow by
absorbing surrounding matter, or shrink by ejecting matter and
radiation. It could only apply in the very distant future of an
open expanding universe (as discussed in
§5.6, the passage "Open
Universe" and "Dark
Energy") - in the infinite void of the "heat death of
the universe".
Nonlocality of quantum
evaporation
Is important to reflect fundamental spatial nonlocality process quantum evaporation: the
characteristic wavelength of the quantum radiation is comparable
to the size of the black hole. Each quantum of radiation is
formed in a spatial region of a size comparable to a black hole,
so it is not possible to locate more precisely in space the
location of this quantum. An observer falling into a black hole
would not observe any radiation locally at the horizon...
The black hole shrinks during
quantum evaporation not so much by the escape of positive energy
particles from below the horizon (the horizon is impenetrable
outwards *), but as a result of bombardment and
absorption of negative energy particles from surrounding area.
Hawking's quantum mechanism evaporation is actually a process
of "external liquidation" of a black hole by a
polarized vacuum.
*) In quantum physics (in connection with quantum relations of
uncertainty), however, the processes of "tunneling"
particles from places below the horizon to places outside the
horizon are possible - a particle that is just below the horizon
has a non-zero probability of occurrence outside the horizon (for the nature of the tunneling phenomenon, see §1.1,
passage "Quantum tunneling
phenomenon" in the
monograph "Nuclear physics and physics of ionizing radiation"). The originally virtual
particle can then become a real particle above the horizon,
carrying the appropriate energy from the black hole. These
different interpretations lead to the same
observable consequences for the quantum evaporation of black
holes.
Stochastic character
of quantum radiation
The thermal shape of the spectrum, ie that the quantum radiation
from a black hole is completely random and uncorrelated, is related to
the "black hole has no hair" theorem. Quantum radiation
comes from an region, about which the outside observer has no
other information than knowledge of the total mass, charge, and angular momentum.
Therefore, all configurations of emitted particles that have the
same energy, charge, and angular momentum are equally likely. With
regard to such beyond the horizons of "hidden" areas (hypersurfaces),
about which the external observer has only limited available
information, S.Hawking expressed the so-called "principle of ignorance" [125]: All configurations in "hidden" areas,
consistent with the limited principle observable information, are
equally probable. It leads to a violation
of the predictability of the evolution of these systems (discussed below the passage "Quantum
evaporation: the return of materials and information from black
holes ?").
The black hole will therefore
radiate with equal probability *) any configuration of the
particles, compatible with the conservation of
energy, angular momentum and charge. In principle, therefore, it
is possible for a black hole to emit a
material formation
of any structure. Hawking states [125] that a black hole could
quantumly emit, for example, even
a television or even
humans, but all such complicated and "exotic" modes of
radiation have very neglible chance (and will never
materialize). By far the most likely is the emission of particles
with a thermal spectrum.
*) However, not every such particle or set of particles may come
to infinity with the same probability, because when interacting
with the field of a black hole, there is a certain potential
barrier for the emitted particles, on which some particles can
"bounce" back into the black hole. Only some of the
particles released at the horizon or tunneling below the horizon
have enough energy to overcome the gravity of the black hole and
escape to infinity (escape velocity
directed vertically upwards). Most of these
particles are then captured by the gravitational field and
re-absorbed by the black hole. We can therefore imagine that a
black hole has a kind of " quantum-particle atmosphere
" just around its horizon (this could
only be registered by a hypothetical observer
"descending" slowly to the horizon according to Fig.
4.22; a free-falling observer would not observe it due to the
principle of equivalence) . However, in the
case of macroscopic black holes, such an "atmosphere"
is in any case negligibly sparse, it can only occur significantly
in the case of black micro-holes (see below
"Quantum explosion of a black micro-hole") .
Some possibilities of quantum
evaporation of black holes are further discussed below in the
section "Quantum
evaporation: mass return and information from a black hole?".
A non-astrophysical
analogies to Hawking radiation ?
The general semiquantum mechanism of Hawking radiation in black
holes has inspired the investigation of similar phenomena in
other areas as well. It turned out that a similar theoretical
situation, when waves propagate through a certain medium with
some finite velocity and there are regions separated by horizons
for these velocities, can also occur during the propagation of
light in a dielectric material (e.g. in optical fibers) or
acoustic waves in a flowing liquid...
Unification of thermodynamics and
quantum evaporation of black holes
We said that at in quantum radiation is violated
the second law of dynamics of black holes.
Conversely, in the presence of a black hole, the second
thermodynamic theorem is violated - a black hole (for which
entropy is not defined in the classical case) absorbs matter and
thus draws entropy from the surroundings. However, the absorption
of matter is always accompanied by an increase in the surface of
the black hole and quantum radiation in turn by a decrease in the
surface of the horizon. Offers therefore "save" both the 2nd theorem of
thermodynamics and the 2nd law of dynamics of black holes: to
combine the entropy of matter outside the black hole Sm with the size of the surface A
of the black hole and create from them a quantity S, which
could never decrease with time. Thermodynamic analysis (performed by Bekenstein yet before the discovery of the
Hawking effect)
shows, that such a quantity should be the sum of
entropy outside the horizon and a certain
multiple of the area of the horizon: S = Sm + a.A, where a is a constant. Since we consider k/2p as a temperature, the 1st law of
black hole mechanics can be considered as the 1st theorem
thermodynamic for a black hole, it can be integrated, which gives
a.A = SH = (k/8p h).A + const., where however const.
= 0, because we require that the entropy of a black hole with a
mass approaching zero also go to zero. We can therefore make a
statement that generalizes the second law of black hole dynamics
and at the same time the second thermodynamic theorem :
| Theorem 4.10 ("generalized 2nd
law of black hole dynamics") |
| The sum (k/8p h) -times
of the horizon area A of the
black hole and the entropy Sm of the mass
outside the black hole cannot decrease with time . |
(in the system of units,
where h = k = 1 is a = 1/4). Bekenstein [11]
postulated this generalized law even before Hawking's discovery
of quantum evaporation. However, without quantum radiation,
generalized Second Law 4.10 could be violated in certain
situations, such as when a black hole is in a field of thermal
radiation below the "temperature" of a black hole;
then, when the thermal radiation accretes, the entropy of the
black hole SH increases by a smaller value
than the entropy of the surrounding thermal radiation decreases
(and "heat" passes from the colder environment to the
warmer black hole). Quantum evaporation is therefore a necessary
prerequisite for the validity of the generalized 2nd Law of
Black Hole Dynanics. With the existence of quantum radiation, the
thermodynamics of black holes becomes completely consistent - a
black hole can be in equilibrium with thermal radiation (see the
stability of such an equilibrium, however, below). A black
hole behaves like any other body heated to a certain
temperature TH
and having a certain entropy SH, which, when on interacting with the environment, governed
by basic laws of thermodynamics. All four laws of black hole
mechanics can be equivalently formulated in thermodynamic
terminology and then talk about the laws
of black hole thermodynamics :
| 0 . Law of thermodynamics of
black holes : |
| Temperature TH = k.h/k of stationary black hole is
the same in all places of the horizon. |
| 1. Law
of thermodynamics of black holes : |
The law of conservation of total
energy~ matter applies, where two close equilibrium
states of a black hole are connected by the relation
dMH = TH dSH + WH dJ + FH dQ .
ëwork ì
|
| 2nd law of
thermodynamics of black holes : |
| The
total entropy S = SH + Sm of the
black hole SH and the mass outside the black
hole Sm cannot decrease with time . |
| 3rd law of
thermodynamics of black holes : |
| With a
finite number of steps, the black hole cannot be cooled
to a temperature TH = 0 of absolute zero . |
Let's now look at the
properties of the interaction of a black hole with thermal
radiation. As the weight of the black hole increases, its
temperature decreases. If a black hole absorbs a certain amount
of thermal radiation, its weight will increase, causing its
temperature TH = h /4M to decrease. The black
hole therefore has a negative heat
capacity
(dM/dTH = -4 M2/h) - by supplying energy to the
black hole, its temperature is reduced. Thermodynamically
speaking: by supplying heat (~energy, ie heating), a black hole does not
heat up, but cools down! The more energy (heat) a black hole
absorbs, the colder it becomes, and the more energy it radiates,
the more it heats up.
Let us have a Schwarzschild black
hole *) surrounded by radiation of an absolutely black body with
temperature Tm the same as the temperature of
the black hole Tm = TH. Due to quantum evaporation,
there will be a thermal equilibrium between the absorbed and
emitted radiation, and this balance will, of course, show
statistical fluctuations.
*) Because, to be precise,
only a non-rotating and electrically neutral black hole can be in
equilibrium with thermal radiation. The charged and rotating
black hole preferentially emits particles with an electric charge
and a angular momentum of the
same "sign" as the black hole, so that this radiation
will not have exactly the Planck spectrum of thermal radiation.
Let the black hole absorb at a
certain moment, due to statistical fluctuation, absorb a litle more heat radiation than it radiated.
Because a black hole has a negative heat capacity, its
temperature decreases, thereby reducing the intensity of quantum
radiation; on the contrary, the intensity of radiation absorption
increases somewhat. If the temperature of thermal radiation is
kept constant (this will be the case if the whole universe is
filled with this thermal radiation, or if the black hole is
located inside a thermostat powered by a sufficiently large
energy storage - Fig.4.24a), it will lead to increasingly
significant uimbalance between thermal radiation
accretion and quantum evaporation: the emission of a black hole
will constantly slow down (the black hole will constantly cool)
and the absorption of thermal radiation will constantly
accelerate. The weight of the black hole will increase
indefinitely. If, on the other hand, as a result of a statistical
fluctuation, a black hole radiates a little more energy for a
while than it has absorbed, its temperature (due to its negative
heat capacity) will rise, thus radiating even more intensely and
absorbing less; this imbalance process will increase avalanche. Finally,
the black hole radiates out completely and disappears.

Fig.4.24. To the thermodynamic equilibrium between the quantum
evaporation of a black hole and the surrounding thermal
radiation.
a) Black hole enclosed in a cabinet with heat
radiation, the temperature is thermostatically maintained at a
constant value Tm = TH. If the energy storage is able to provide
and receive an unlimited amount of energy (which models a
situation where the whole universe is filled with thermal
radiation of temperature Tm), the thermodynamic balance between the
black hole and the thermal radiation cannot be stable.
b) A stable
thermal balance between radiation and a black hole is established
only when the black hole interacts with an environment that is
able to release and receive only a limited amount of energy (such
as the thermally insulated box in the figure).
Thus, the negative heat
capacity of a black hole means that the black hole cannot be in
stable thermodynamic equilibrium with an environment that can
emit or receive an unlimited amount of heat radiation; such a
thermal balance is only unstable. A stable thermal equilibrium
between a black hole and thermal radiation is possible only in
the situation shown in Fig.4.24b, where the black hole is
enclosed in a thermally insulated box of final volume. In this
case, a thermal equilibrium is always established, regardless of
possibly the difference between the original temperature of the
black hole and the thermal radiation in the cabinet. If, under
this equilibrium, as a result of statistical fluctuations, the
black hole warms up by emitting more energy than it absorbs, the
temperature of the thermal radiation in the box increases,
accretion prevails and the black hole cools down again. By
analogy, by randomly absorbing more radiation, the black hole
cools down, but the heat radiation in the box decreases and the
temperature drops, quantum evaporation prevails, and the black
hole warms up again.
Quantum evolution and the lifetime of a
black hole
The effect on the radiant
emission of black holes, as a result, somewhat changes the classic image we created in §4.2-4.6 - that
the gravitational collapse creates a black hole, which is the
absolute end product of the evolution of sufficiently massive
stars. Quantum effects mean that even in empty space no black
hole can be exactly stationary, but only quasi-stationary,
because mass, angular momentum and charge gradually decrease as a
result of quantum evaporation. Fig.4.25 schematically shown the basic features thus supplemented
idea of the final stages of evolution of a sufficiently massive
star in empty asymptotically plane space-time. The gravitational
collapse creates a black hole, which at first begins to evaporate
extremely slowly, but with ever-increasing speed. The thickness
of the barrier that the particles have to cross over the tunnel
effect during quantum evaporation is proportional to the
gravitational radius of the black hole. In the case of large
black holes of stellar masses (with dimensions of the order of
kilometers), quantum evaporation is negligible and in practice it
is many times covered by the accretion of gases, particles and
radiation from the surrounding space into a black hole *); here, however, we
assume that the black hole is in a vacuum.
The temperature of a black hole of mass M
TH
= h c3/8pGM.kB @
10-7 M¤ / M [°K]
will be very close to absolute zero for stellar
mass collapsors. In a vacuum, there may be a slight emission of
very weak electromagnetic waves with long wavelengths (many
kilometers). The radiant power-luminosity of the
quantum radiation of a black hole by the Hawking mechanism is
given by
P = h c6/15360 pG2 M2 .
*) The situation would be the opposite for
hypothetic small primordial black
holes with dimensions of the order of 10-13 cm, which will appear very
"hot" and whose quantum radiation will already be very
intense (of the order of 109 W), see §4.8
"Astrophysical significance of black holes", the passage "Primordial Black Holes?". In the case of an open expanding
universe, the temperature of the relic radiation would far
below the temperature of the black
holes of stellar masses after a sufficiently long time, so that eventually all black holes could
evaporate quantum (see §5.6 "The Future of
the Universe. The Arrow of Time. Hidden Matter ") .
The time it takes for a black hole of mass
M to evaporate due to Hawking radiation is
tevap = 5120
p G2 M3
/h c4 ~ 2.1067. (M/M¤)3 years
.
So the time it takes for a black hole of
mass e.g. 3 M¤ (a common
stellar-mass black hole) to quantumly evaporate in a vacuum would
be about 3.6×1068 years. However, in the present universe, no evaporation of black holes occurs. All present black
holes are growing larger by accretion of surrounding
interstellar matter and cosmic radiation (we
are not considering rare processes of collision and merger of
black holes here yet).
Quantum evaporation could perhaps hypothetically come into play
only in the very distant future of an open expanding universe (as discussed in §5.6, the passage "Open
Universe" and "Dark
Energy") - in the infinite emptiness of the "heat death" of the universe..?.
. Quantum explosion of a black
microhole
With
gradual evaporation (decreasing rg) the intensity of radiation and
energy of emitted particles is constantly increasing - a smaller black hole glows more - and not only photons but also
electrons (+ positrons) and later heavy particles (protons,
neutrons, ...) and antiparticles will be
emitted. After
reduction to microscopic dimensions, quantum evaporation
eventually acquires the avalanche character of a kind of quantum black hole explosion. The black hole thus ends its
existence with a massive explosion, during which energy of the
order of 1023 J is
released in the last about 0.1 second. The
speed of the final phase of quantum evaporation (i.e. power of quantum
explosion) depends on how many different types of elementary
particles exists, because in the final stage the
temperature of the black hole increases indefinitely and is capable of
emitting all types of elementary particles. The above value
corresponds to the spectrum of elementary particles as we know
them now (particles composed of 6 types of quarks); if there were
other elementary particles of higher masses, the final quantum
explosion could be several orders of magnitude stronger.
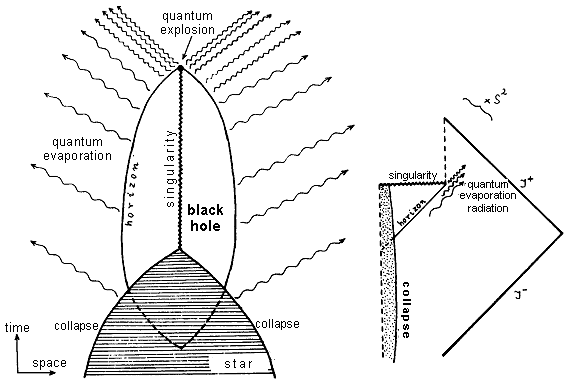
Fig.4.25. Schematic representation of the space-time diagram of
the collapse with the formation of a black hole, the gradual
quantum evaporation of this black hole up to its quantum explosion and complete
radiation away - exhaustion and disappearance.
Basically, a black hole
has only two behaviorals options - depending on its size and the
content of the environment. Either it is an
"all-destructive cannibal" - that is, when a black hole is sufficiently massive and its strong gravitational field literally
"sucks" all matter from the surrounding space and
irreversibly absorbs every body that gets near her. Or, conversely, when
the black hole is very small, it will be a "self-destructive
dealer" - it will glow brightly until it radiates all its
mass and finally ceases
to exist.
Quantum
evaporation: mass and information return from a black hole ?
The effect of quantum evaporation could lead to the idea that
matter (and related information) absorbed by a black hole during
collapse and accretion is only temporarily "trapped" in a black
hole and eventually returns to its original space..?.. This
straightforward view would be however misleading. In quantum
evaporation, only the value of
the gravitational mass - energy equivalent to the substance that formed
the black hole is "returned". The
substance itself, absorbed by the black hole, irreversibly
"melted" in the field - including all its atoms and
particles, all its structure disappeared. What
is emitted from the black hole during quantum evaporation is not
the original absorbed particles, but completely different
"new" particles and radiation, creating from the
gravitational field gradient. Even by more careful analysis of
particles emitted by a black hole during quantum evaporation,
therefore, nothing can be found about objects previously absorbed
by the black hole - it is not possible to "reconstruct"
their composition and structure! Even if we "collected"
all the photons, electrons and other particles and antiparticles
emitted during the whole evaporation process and measured their
energies and other characteristics in the imaginary experiment,
it would not tell us anything about the matter
from which the black hole was previously formed.
Thus, it cannot be expected that the
quantum evaporation of a black hole is a reverse process to the
formation of a black hole by collapse *), and that perhaps some
individual characteristics of the object before collapse could
reappear. All characteristics except weight, charge and rotational angular momentum, the black hole is irreversibly and permanently "forgoten" already when the horizon is created.
For example, the probability of the emission of particles and
antiparticles does not depend on whether the black hole
originated from ordinary matter or antimatter.
*) That Hawking's process of
quantum evaporation would be a time-reversed collapse cannot be
expected anymore because completely different physical theories
are responsible for both processes: classical GTR for collapse and quantum field theory
(against a given background of curved spacetime) for quantum
evaporation.
The process of collapse and
subsequent quantum evaporation also completely violates the law of conservation of the byryon
number (which is considered
unshakable in nuclear physics!). For most of the time, a black hole (which was formed mainly from baryons by its mass) emits almost exclusively photons
and other particles with zero rest mass, thus radiates the vast
majority of its mass. Electrons, positrons and other leptons will be emited by the black hole until it
shrinks enough (and thus "warms
up"), and only at the very
end, will it begins to emit also baryons. However, the weight of
the black hole is already very small at this time, so in
principle it could emit only a very small
percentage of baryons compared to the number of baryons from
which it formed during collapse. And even then, the black hole
will emit on average the same number of baryons and
antibaryons...
The paradox of information loss ?
In §4.5 "Black hole has
no hair" it was shown that when a
black hole absorbs a matter-substance below its horizon, it absorbs
and irreversibly bury all information about it (except only the total mass, charge and rotational
angular momentum). This individual
information about the particles and structures of the absorbed
matter is definitely "forgotten"
for the outside world, it can no longer be ascertained in any
way. It is not recognizable whether the black hole was formed by
the gravitational collapse of hydrogen, helium or iron, ordinary
matter or antimatter, such as the representation of electrons,
protons, neutrons, various types of fields. In this context, it
is sometimes referred to as the "paradox of
information loss" - from the point of view of the
general theory of relativity was discussed in §4.5, passage
"Loss
of determinism? - An information paradox?". Here we will briefly continue this discussion
from the point of view of quantum physics
(and event. the possibility of combining
gravity with quantum physics) :
Determinism
in quantum physics is applied at the level of wave
functions whose future state is determined by quantum
operators that are time inverse; so even the past state of wave
functions is retrospectively determined - wave functions are unambiguous,
unitary, it is assumed here that information
should be preserved. This
"law of information conservation" in quantum
physics (its Copenhagen
interpretation), however, is in fact
fulfilled only at the most basic model level:
when we have the wave function of a particle without any
interaction with the "surrounding world". Then we
actually have a particle with a permanently described wave
function y(t, x, y, z), whose quadrate IyI2 indicates the probability density of
finding a particle at a given place (x, y, z) at time t.
The probability of finding a particle in a certain volume V,
is given by the integral of VnIyI2dxdzdy through the
volume V. And when we add (integrate)
values IyI2 across the whole
space, we should get the number "1",
ie the certainty that the particle "is somewhere".
That is the principle of unitarity: the idea
that the sum of the probabilities of all possible outcomes must
be "1". No information is lost during
the existence of the particle. However, in reality, during the
formation and extinction of particles, information
is constantly lost countless times...
However, when an interaction occurs,
or when the position or momentum of a particle is measured, the
wave function "collapses". And in quantum field theory,
the formation of particles and their extinction commonly occurs,
ie the formation and extinction of the respective wave functions.
So "information" about the existence or non-existence
of particles is constantly appearing and losing
......
Physics of black holes in GTR shows loss
of information about all structural details of matter
collapsed into a black hole, except weight, el. charge and
rotational angular momentum (§4.5 "Black
hole has no hair"). Some quantum physicists see this as a fundamental contradiction
(violation of the principle of
unitarity of wave functions)..?..
Why is it a problem at the theoretical level
?
If there was no quantum radiation from black holes and black
holes persisted forever, we could "alibistically" claim
that information continues to secretly exist inside the black
hole, just inaccessible to us. And many would believe it...
However, black holes slowly evaporate due to Hawking radiation,
which does not carry any specific information about the matter
that created the black hole. So this information is actually -
physically - lost !
One of the proposed solutions could be the hypothesis of
quantum perturbations-fluctuations of the horizon:
any particle that is absorbed by a black hole would leave a
certain quantum "trace" on the horizon ... So a kind of
micro-deformed "wrinkled-hairy" horizon..?..
Hawking radiation of quantum evaporation of a black hole could
then carry information from these quantum deformations of the
horizon..?.. But the problem is the instability
of these hypothetical quantum micro-deformations of the
horizon..?.. Both at the quantum level and also from the point of
view of the general theory of relativity, where all gravitational
and electromagnetic asymmetries radiate in the
form of gravitational and electromagnetic waves - and thus smooth
out...
"Wall of fire" ?
No !
The effort to solve the information paradox also motivated the
bizarre hypothesis of a kind of "fire wall"
from high-energy quanta and radiation (already
mentioned in §4.2, passage "Observer
falling into black hole"),
which could be located just below the horizon of a black hole (A.Almheiri, D.Marolf, J.Polchinski, J.Sully, 2012).
It could allegedly arise from Hawking's quantum radiation, whose
pairs of quanta below and above the horizon could remain
"quantum entangled" even after radiation. Such quantum
effects perhaps could occur in black mini-holes, but not in black
holes of stellar masses (or even larger ones). The presence of a
"fire wall" contradicts Einstein's principle of
equivalence, on which the general theory of relativity is based.
Therefore, the "fire wall"
hypothesis is eroneous undoubtedly, so we did not
consider it when analyzing the properties of black holes.
There is no
"wall of fire" at a black hole, which is consistent
both with the general theory of relativity and, in principle,
with quantum physics.
From a factual scientific point of
view, this "information paradox" is perhaps
only an insignificant detail (its astrophysical significance is probably zero...). However, it may be one of the theoretical obstacles in
some approaches to unifying gravity with quantum physics..?..
Just as general relativity had to
come to reconcile with space-time singularities (where it loses validity) inside
black holes and at the origin of the universe, quantum mechanics should
come reconcile with the possibility of information loss,
when event horizons occur. Nothing important will be
affected! This contradiction could be resolved by a
future unitary field theory, within the framework of the
unification of all interactions and the organic connection of
quantum physics with the general theory of relativity (§B.6 "Unification of
fundamental interactions. Supergravity. Superstrings.").
Objective analysis thus shows, that
in strongly curved spacetime with event horizons the
law of conservation of information generally does not
apply (similar to the
above-discussed law of conservation of baryon number) ! This seemingly padadox loss of information is
not, in fact, a contradiction, but a
physical reality: the
laws of space-time "rule" even
informations !
Violation
of determinism ?
The space-time event of complete evaporation and disappearance of
a black hole (quantum explosion) is actually a naked singularity that appears for a moment, so that
quantum evaporation leads to a violation of the principle of
cosmic censorship discussed in §3.9. In fact, there is no need
to wait for the complete evaporation of a black hole, because, as
Hawking [125] has shown, the principle of cosmic censorship is in
some sense violated during even in "peaceful" quantum
radiation. This is because the emitted particles had an external
observer can be considered as particles originating from a
singularity, that tunnel across
the horizon along
the trajectory of the spatial type. In any case, we are affected
by quantum radiation from areas, about which we have no available
informations (except mass,
charge and angular momentum). The effect of quantum radiation thus
reduce "shielding ability" of the horizon
agains the singularity and thus leads to a fundamental violation of the determinism of the evolution of
spacetime [125]. In §4.5, we have shown that the "black hole has no hair" theorem limits our ability to
reconstruct the past, because a black hole irretrievably
"buries" all information about the structure of matter
from which it originated. Quantum radiation deprives us but
also the possibility of predicting the future, because for quantum
radiation emanating from a black holes (and affecting physical events in the
future), we are only able to determine the probabilities of
individual radiated configurations. The uncertainty and
"randomness" emanating from quantum mechanics is
combined here with the classical uncertainty caused by causal
relationships in strongly curved spacetime - the horizon of a black hole and its property "not to have hair".
Albert
Einstein, who never
internally accepted quantum mechanics (despite
his significant contribution to its construction), as the main argument against
its indeterminism, cited the metaphorical statement "I don't believe God plays dice with the world" *). S.Hawking, on the other hand,
characterized quantum processes in black holes with the words:
"God not only plays dice with
the world, but sometimes throws them even where they are not
visible".
*) The game of dice
here symbolizes complete chance and the
unpredictability of what number will fall in each litter.
Einstein was convinced of the causal and deterministic nature of
the laws of physics, whose "creator and designer" is
symbolically God. He did not believe that the behavior of
individual microparticles is in principle random and
"chaotic" and only with a large number of interactions
will a certain exact regularity "break out" from
different probabilities. Hawking, on the other hand, believed in
the principled nature of stochastic quantum laws (the "dice
game") and, as a quantum astrophysicist, emphasized the fact
that some particles came below the horizon of a black hole where
they were "not visible" from outer space. And the
effect of quantum evaporation of a black hole by this
"hidden stochasticity" can uncontrollably affect the
surrounding universe..!?..
Is it
possible to return information from a black hole ?
The paradox of information
loss in the black hole discussed above arouses
some displeasure among some experts, especially in the field of
quantum physics; all information should be
retained!
Recently, even its author S.Hawking he was
questioned by these opinions and came up with a controversial attitude,
which received wide publicity - there were articles with
sensational headlines such as "Hawking
returns from a black hole".!. :
Allegorical sci-fi depiction of the (non-)possibility
of returning information during quantum radiation of a black
hole.
Imagine that S.Hawhing decides to "jump" into a black
hole. During his fall, his body is "spaghetti" near the
black hole and then even atomized, all structures are destroyed.
In this state, it is absorbed by a black hole (part of its mass is radiated by gravitational waves) .
The question arises whether S.Hawking, resp. information about
it, is present in that black hole (perhaps
in the form of quantum fluctuations of the horizon)? And whether, based on the analysis of all quantum
particles of Hawking radiation during the process of quantum
evaporation and black hole explosion (in an
unimaginably long period of about 1080 years) S.Hawking could perhaps be
"reconstructed" - a kind of his "return from the
black hole"..?..
What is it about from a
sober physical point of view? It is an idea (or
a wish?), that all information (except
mass, charge, and angular momentum - which is retained) about matter that collapses and
accretes to create a black hole may
not be irretrievably lost, but some may be re-radiated back in the Hawking's process of quantum
evaporation..?.. But by what mechanism could this information
escape from a black hole? Two variants in particular were
discussed :
- Quantum teleportation
One of the notable new consequences of quantum physics is
the phenomenon in which the properties of two or more
systems, via the originally common wave function, may
remain in relation to each other over large regions of
space and time. This "entanglement" enables
so-called teleportation (see §1.1 "Nuclear and radiation
physics", passage "Quantum teleportation" in the treatise "Nuclear
physics and ionizing radiation physics"), in which
information is transmitted in space and time
independently of horizons or other space - time
obstacles. A similar mechanism could work for black
holes. Pairs of virtual particles form on the horizon of
events in the entangled state, one of the particles flies
out like Hawking radiation, the other falls into a black
hole and merges with the matter that originally created
the black hole in a singularity. During this interaction,
the quantum state can be transferred from the internal
matter to the absorbed particle, and since the emitted
and absorbed particles are still in an entangled
connection with each other, the information
contained inside the black hole can be transferred
to the outgoing Hawking radiation. The problem here,
however, is thatthe absence of a causal information
channel from the inside of the black hole outwards makes
it impossible to decode this information from
the set of individual quantum states of the radiated
particle.
- Superstring description of a black
hole
According to the theory of superstrings (see §5.6 "Unification
of fundamental interactions. Supergravity. Superstrings."), black holes are a
kind of huge "tangle" of strings or membranes.
The name fuzzballs is used for this
concept. Information about the mass (whose particles have
a string structure) falling into a black hole is stored
in the waves and excitations of these strings, and during
quantum evaporation it may perhaps be radiated back..?..
S.Hawking recently pointed out, that quantum fluctuations could prevent
the creation of a well-defined event horizon, the "ability
to shield" against the information inside the black hole
would not be as perfect as foreseen in the framework of general
relativity..?..
The whole
thing the possibility of radiating information from a
black hole (other than those related to the
"black hole has no hair" theorem, ie mass, charge and
angular momentum) is still completely
unclear, it is only a hypothesis on which
experts do not have a unified opinion. In light of the above
discussion in the passage "Quantum Evaporation: The Return of Mass and
Information from a Black Hole?", this hypothesis is not very
likely. Quantum proponents of the "Law of conservation of
information", even if they "stand on their
ears", do not extract any such information from below the
horizon of events..!..
Arguing "law of information
conservation" is probably out of place here, because a
complete gravitational collapse is so universal and everything
affecting event, that even the usual notion of information
(used in classical physics and standard
quantum mechanics) loses its meaning here,
becomes illusory... (here everything
can be "different "- cf. the above-discussed violation
of the law of conservation of the number of baryons, in
nuclear physics unacceptable..!..) ...
With a bit of exaggeration, we can say that: The properties of
spacetime “boss“ also informations !
Vojtech
Ullmann




