 |
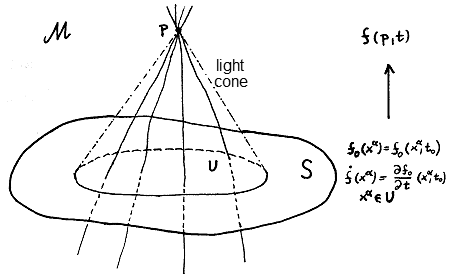
Fig.3.8. The field values f at a point p are uniquely determined by the initial values of the fields fo (and their derivatives `f) in a points x of subset U spatial hypersurface S . |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 3
GEOMETRY AND
TOPOLOGY OF SPATIAL TIME
3.1. Geometric-topological properties of
spacetime
3.2. Minkowski
planar spacetime and asymptotic structure
3.3. Cauchy's problem, causality and horizons
3.4. Schwarzschild
geometry
3.5. Reissner-Nordström
geometry
3.6. Kerr
and Kerr-Newman geometry
3.7. Spatio-temporal
singularities
3.8. Hawking's
and Penrose's theorems on singularities
3.9. Naked
singularities and the principle of "cosmic censorship"
3.3. Cauchy's problem, causality and horizons
The causal
relationships between events in space and time are the basis
of our knowledge of objective reality. We know from the special
theory of relativity, that the motion of matter and the
transfer of energy and information can take place only within the
space-time light cone (see §1.6). Because everything that applies
in the special theory of relativity is true
even in general
relativity, but locally - the flow of matter, energy and information
will always take place inside the local space-time light
cone, as we postulated in §3.1. Local causality is thus given by
the requirement of local validity of the special theory of
relativity (STR). Questions of global causality are no
longer so trivial and must be answered by the analysis of global
geometric and topological properties of a given epecific spacetime,
which is the solution of Einstein's
equations.
The shape and inclination of the light
cones is given by a metric tensor at a given point in space-time. Gravity is thus the force that determines the
causal structure of the universe *) - it defines which events of
space-time can be causally related and which cannot. As we will be
see below, with a sufficiently strong gravitational field (curvature of
space) occur event horizon and region of
space-time appear, which are causally separated from other parts of space-time.
*) Which events are really causally related to each other depends
on the specific situation. The properties of space and time give
us only certain limitations - they determine which events in
principle can be related, or which cannot be causally related.
Local causality in spacetime M can also be expressed as follows according
to Fig.3.8. Let a point pÎM, such that every world line of the time or light type
passing through this point intersects the hyperplate S
(spatial type). As UÌ S we denote the set of all points on S ,
in which it can be intersected by world lines of temporal or
light character passing through the point p. In
other words, U is the set of those points on S, from which the point p can be reached by moving along temporal or isotropic worldlines.
The causality requirement then means that the values of all
fields at point p will be anambiguously determined by the values of the fields
and their derivatives (up to a certain finite order) just in the
set U . Knowledge of fields (and their
derivatives) only in part U is generally not enough to
unambiguously determine the fields in point p. Such
a formulation of the causality principle is already closely
related to so called Cauchy's problem, see below.
 |
Fig.3.8. The field values f at a point p are uniquely determined by the initial values of the fields fo (and their derivatives `f) in a points x of subset U spatial hypersurface S . |
Cauchy's problem in mathematical analysis generally represents a task - procedure for finding a solution for a differential equation under given initial conditions (eg at a given point x the default values of the function fo are entered, as is simplified indicated in Fig.3.8 on the right). These procedures were developed in 1842 by the French mathematician A.L.Cauchy. In our context of particle trajectories and field evolution in space-time, we will focus on how the initial conditions on certain sections (hyperpaces) in space-time can affect field evolution and metrics in other areas of space-time, according to Einstein's GTR differential equations.
Geometry and causality in
spacetime
But before we formulate our own Cauchy
problem, we will analyze the geometric aspects of causal
relationships in spacetime. We will assume that spacetime is
time-oriented, which means
| Definition 3.1 (time-oriented spacetime) |
| Spacetime M is called
time-oriented if, at
each point in spacetime, all vectors of the time or
isotropic type can be divided into two groups: vectors heading to the future and vectors heading to the past . |
In practice, this
distinction can be made with the help of irreversible
physical processes such as the growth of entropy of isolated
thermodynamics systems, radiation of energy by electromagnetic or
gravitational waves, expansion of universe (which is,
however, a very
problematic indicator of the direction of
the flow of time) -
see §5.6, passage "Arrow
time").
In time-oriented space-time, we
can already establish a number of causal relationships
between individual events and entire areas of space-time :
| Definition 3.2 (causal relationships in spacetime) |
|
It should be noted that the statement "event B causally follows event A" does not mean that B must necessarily be a direct consequence of the events A, but only that event B could be principally influenced by the event A .
Closed
World Lines and Time Travel
In §3.1, we saw
that different kinds of "identification" in spatial
dimensions can lead to different kinds of global topology of
space, without affecting the local geometric structure, the local
course of physical phenomena. If we performed a similar
"identification" in time (time scale), closed time curves would appear in spacetime -
closed world lines of the time type; however, they seem inadmissible for physical reasons because they are in conflict with the principle of causality. If we took two points
(t1, x, y, z)
and (t2, x, y, z) on the time axis such
that t1<t2 and these
identified (t1, x, y, z) º (t2, x, y,
z), then an intervention in some physical phenomenon at (x, y, z)
at time t2 would cause at this point changes at time
t1, ie in the past.
Fictitious possibility of creating closed time loops we will show
using the concept of
the so-called wormhole (described in more detail in the
conclusion of §4.4, passage "Black holes: bridges to other universes?
Time machines?") .
Thus, the existence of closed time-type worldlines
probably leads to logical paradoxes
of the kind that along the
closed time worldline, we could go back in time and kill our
grandmother before she could conceive your mother (and she then you
...); or kill one's own parents before you
were born (the paradox can be formulated through various family
relationships). Your
very existence, necessary to carry out such a murder,
would then become inconsistent with the result of that crime. Or the astronaut in the
rocket could, after such a closed time world
line, return to
space and time to its launch, damage the rocket and prevent
itself from this original launch :
| The Astronaut Paradox - A failed launch and a space flight | |
 |
The astronaut launches into space in a rocket and flies into the mouth of a "wormhole", which acts as a "time machine". After a closed time worldline, he could then return in space and time to his launch, damage the rocket and prevent himself from this original launch . |
We have changed the past
- first what we wanted to do happened and then we decide to do it
- or not. Haw, then, would it be possible to reconcile two controversial alternatives in the future: our existence, when we could not be born ?;
or the flight of an astronaut in a rocket when he prevented
himself from taking off ? Therefore,
such a traveler
could not even go back in time and carry out the interventions
mentioned. A traveler through time into the past could prevent
himself from traveling to it... How would it be
possible for an event to happen without happening? A situation
where a future reaction cancels a
previous action has no logical solution. Such logical
paradoxes should be avoided!
These strange, even
"pathological" consequences of time travel naturally
lead to an attempt to find mechanisms that would prevent
space-time events from "doing such nonsense". S.Hawking
put forward a hypothesis called the "principle
of protection of chronology" - the protection
of chronological order, which would forbid causal loops (cf. Penrose's "principle of cosmic censorship"
forbidding nude singularities in §3.9 "Naked
singularities and the principle of "cosmic censorship"").
Some mechanisms of this kind will be discussed here and also at
the end of §4.4, the passage "Black
holes: bridges to other universes? Time machines?".
It would seem that such logical
paradoxes and disputes with the principle of causality in time
travel arise only if "freedom
of will" - that the
relevant subject may, at its
discretion, in
principle take any intervention in ongoing events. In the event that
freedom will not exist (and in classical
physics is really no such thing), may not cause a conflict with the
principle of causality: a time traveler past unchanged, because
it has always been an immanent part of it (it can fill the past,
not change it). The universe can be imagined as a
"finished" and unique 4-dimensional manifold
into which the individual worldlines are already
"incorporated". From this point
of view, all events on closed world lines could already
be
"synchronized" so that they would
interact with each other indisputably in a closed cycle - they
would be self-consistent. However, if we take into account irreversibility evolution of the universe (existence of
dissipative processes, 2nd law of thermodynamics), the existence
of closed time curves is physically unlikely, because the situation at a
later time t2 cannot be identical with the situation at
an earlier time t1. Thus, closed curves leading to a
"time machine" could perhaps function at most in the region of elementary particles.
The picture below - "The billiard ball paradox", however, shows an example of
contradictory behavior, where there is no
subjective decision-making and "freedom of will", it is
a purely mechanical experiment..!..
| The paradox of billiard balls - conflicting trajectories of bodies | |
 |
From a certain
starting position, by tapping the cue, a billiard ball is
sent as a suitable speed toward the right mouth of the
wormhole, functioning as a "time machine" -
along trajectory A. This sphere flies through a
wormhole, goes back in time and flies out of the left
mouth, before it has flown into trajectory A into
the right mouth. It can then crash "into
itself" (into its
"younger version") ,
divert runway A into an alternative trajectory B
, outside the wormhole. However, this prevents it from
flying into the right mouth - and thus hitting itself. When moving, starting with exactly the same initial conditions (from the same position and at the same speed), thus creating two conflicting trajectories A and B, along which the ball would move simultaneously. With proper orientation, the ball can fly through the wormhole several times - there are an infinite number of trajectories, differing in the number of passes through the wormhole... |
Logical lessons learned from
paradoxes :
No macroscopic object - the observer - can retroactively
influence what has already happened. Apparently, there can be no
"pilgrims over time" who could jeopardize the course of
history. We can observe the past as witnesses, not as active
participants. When we look into a distant universe, we actually
see a distant past that has been brought to us by light during
its journey of hundreds of thousands, millions, or even billions
of years. However, we cannot turn
the future behind the past !
Many universes?
Everett's and Wheeler's quantum-mechanical hypothesis of "many
worlds" [79] (discussed in §5.7 "The Anthropic
Principle and the Existence of Multiple Universes") could also provide a sci-fi way to circumvent
disputes and logical paradoxes in time travel; according to which
the universe contains not only a unique history of the world, but
many histories parallel. Whenever there is an
interaction (or, from the observer's point of view, a
"decision" or a random event), there is a
"branching of history" into different universes. If the
time-traveler eventually flies back to the past and changes his
history there (for example, kills his mother before his birth),
there will be a "turn" to another history in the
universe, which will coexist with the original universe - the
traveler will it will actually move to another universe
where it will be part of a changed history. There will be no
unacceptable influence on the future of the present - our,
default, original - universe.
Physical
time travel?
The idea of time travel excites human
imagination and evokes age-old dreams of eternal youth and
overcoming death, correcting or averting past mistakes or
predicting the future consequences of our decisions - an insight
into what fate is preparing for us, or his prevention. Within Newtonian
physics, due to its concept of absolute time,
"time travel" was completely impossible
*). It appeared only in the then beginning science fiction
literature, especially in the famous sci-fi novel by H.G.Wells:
"Time Machine" from 1895.
*) Note: Of
course they have nothing to do with time
traveltime shifts of several hours when traveling by plane, for
example between Europe and America. Here, this is only related to
the rapid flight between the agreed time zones, which
are the result of our measurement of time of day by rotating the
Earth around the axis. We do not move in time, but only in the indication
of time by agreed numbers - daily hours, which are shifted
according to longitude.
It was
only within the special theory of relativity,
which allows influencing the speed of time flow by motion, or the
general theory of relativity showing the
influence of gravity on the course of time, that time travel
began to be considered in a sense a physically
real possibility. If a body approaches the speed of
light or resides in a strong gravitational field (perhaps near a
black hole), time will slow down for it from the point of view of
others, so it actually travels to the future. But neither of
these ways makes it possible to go back to the starting time -
the path to the future is one-way.
The relativistic time
dilation in STR makes it relatively easy to travel
to the future in principle. An observer moving at a high
speed close to the speed of light passes time slower
than a reference "rest" observer, so that even a large
time interval in the rest frame can span a substantially shorter
interval of its own time, ie "travel to the future"
resting reference system; while it is observer still moving
inside his space-light cone (see Minkowski diagram on fig.1.6).
However, to travel into the past, the oserver's
word-line would have to bend and turn back downwards and create a
loop, which at some points would have to be tilted at an
angle greater than 45° with respect to the vertical - it would
be necessary to exceed the speed of light, which
is not possible within STR (Minkowski
spacetime with the usual Euclidean topology).
 |
| The kinematic effects
of the theory of relativity offer - at least formally -
two possibilities of time travel to the past : 1. In the planar spacetime STR by moving the superlight speed (pictured left); 2. In the curved spacetime of the general theory of relativity by moving at a locally sublight speed within a sequence of suitably inclined light cones in an area with a strongly curved geometry of spacetime (Fig. Right). Another hypothetical possibility is the complex topological structure of spacetime - "abbreviations, tunnels, wormholes" ( discussed below) . |
The general theory of relativity,
as the physics of gravity and curved spacetime, basically opens
up the possibility of traveling to the future and the past.
Traveling to the future is again relatively easy in principle: it
is enough for the observer to stay long enough in a place with
strong gravity (high gravitational potential), where the time
according to relation (2.36) passes more slowly, to return to the
starting point at a time, when a significantly longer time
interval has elapsed in the meantime. The §4.3 describes an
interesting phenomenon in the propagation of light in the field
of a massive compact object - the effect of a gravitational
lens. Such light propagation along curved paths leads
not only to interesting optical effects of multiple images, but
also to different time shifts along different
beam paths. An observer moving along a suitable shorter path at a
speed close to c could in principle "overtake"
light photons moving along another (longer) path around a
gravitational body; in extreme cases of motions close to c
around a supermassive body (or even around a rotating Kerr black
hole), these time differences could in principle be used to
travel in time...
Gravity affects both the
passage of time and spatial scales and proportions. In such
globally curved spacetime, there may be some "shortcuts
over spacetime" - hypothetical "wormholes",
which allow the observer in a sense to" overtake "the
light beam and "travel" back to the past. At the same
time locally everything runs according to STR, the speed of light
is not exceeded anywhere. It's similar, that a sailor sailing
here on Earth across the ocean, still facing forward, may
eventually find that he has returned to the place from which he
sailed. When moving in curved spacetime, the observer can in
principle find out over time that he has not only reached the
starting point, but that he has "visited" an event from
his past, albeit locally from his gaze all the time his time
flowed towards the future..?..
A
topologically complex, multiple connected universe ?
The local geometry of spacetime is determined by
the distribution of matter in space - matter~energy curves the
spacetime, in which bodies and particles then move along
geotedics, representing the straightest possible trajectories.
The curvature of space-time is described by Einstein's equations,
whose application to the universe under appropriate simplifying
assumptions leads to Fridman's equations (5.23) describing a
universe whose space can have positive, negative or zero
curvature, see §5.3.
However, this local geometry
generally says nothing about the global shape, ie the overall
topology space. In standard relativistic cosmology, a
simply continuous universe (with a sphere topology) is
considered, on which Einstein's, DeSitter's or Fridman's
cosmological models work. Theoretically, however, the universe
could have a more complex, multi-connected topology,
with different topological tunnels or identifications of
different parts; such a universe might even look like a kind of
"emmental".
The complex multiple connected
topological structure of the space of the finite universe would
have interesting implications for what the observer sees in such
a universe: in principle, he could see multiple
images of galaxies, stars, and even himself, as in a
mirror maze. And in the time at different stages of
development. It could not be ruled out, that when we
observe a distant galaxy, it could be our own galaxy, billions of
years ago! However, it would be very difficult, if not hopeless,
to astronomically recognize that the two galaxies observed are
actually one and the same galaxy, represented by the passage of
light through the complex topological structure of the universe.
We would see them from different angles and, most importantly,
due to the spatial scales of many billions of light-years, in
completely different stages of development, changed beyond
recognition.
A
detailed way to obtain at least partial indications for certain
topological structures of the universe could be a detailed
measurement of the properties of microwave relic
radiation.- its homogeneity, fluctuations (depending on
the angular distance and wavelength), polarization. Already at
the time of the separation of radiation from matter, there were
nuclei of future structures in the universe, so these photons
passed through places with different gravitational potentials,
which led to small changes in their energy and wavelength - a
slight cooling or heating. These fluctuations
should be visible even now, as slightly warmer and colder
"spots" in the otherwise isotropic distribution of
relic radiation - they represent a kind of "paleontological
imprint" of the structures of the early universe. The
temperature difference is very small, of the order of 10-5 degrees, but a
detailed "temperature map" of the early universe has
already been measured using sensitive satellite apparatus -
§5.4, passage "Microwave relic radiation - messenger of
early space messages").
All
these theoretical speculations have no justification
in astronomical observations, so in interpreting of relativistic
cosmology in Chapter 5, we will stick to the simplest and, from
the current point of view, the natural assumption of a simply
continuous topological structure of the universe.
Perhaps the only exception will be
discussions about the possibility of multiple universes;
however, even here it will not be a matter of introducing some a
priori complex topology, but of hypothetical topological
properties "induced" by turbulent quantum-gravitational
processes at the beginning of the universe.
GTR in certain special solutions of Einstein's
gravitational equations allows causal loops from
a mathematical point of view. This is the case, for example, in
Gödel's solution describing the rotating universe [104], or in
spacetime around a long massive cylinder rotating at high speed
(greater than c/2). The rotation of spacetime in such solutions
carries with it light, and thus causal relationships between
objects, in such a way that it allows the material object to move
through a closed time worldline by suitable circulation without
exceeding the speed of light around the object. However, such
solutions are only certain mathematical curiosities that
are not realized anywhere in nature. The same
probably applies to the ring singularities in Kerr's geometry (§3.6 "Kerr and
Kerr-Newman geometry") inside the rotating black holes, or to
geometric-topological constructions involving so-called "wormholes"
in spacetime - see §4.4.
Geometric-topological
possibilities of "travel" in space and time in
connection with the properties of space-time of black holes will
be discussed in §4.4., Passage "Black holes: bridges to other universes?
Time machines?", systematically in work (syllabus) "Journeys
through time : fantasy or physical reality?". Some related
considerations about the direction of time flow are further
outlined in §5.6, passage "Arrow of time". For the topology "time
travel" are important so-called Cauchy's
horizonts (discussed in more
detail below) ,
which, among other things, define and separate the space-time
areas, in which time travel
into future and past
is and is not possible.
Cauchy region and
horizon. Event horizon.
In the
following, we will assume that in real space-time, closed
worldlines of temporal or isotropic nature do not occur, that is,
as it is sometimes said, a reasonable chronological
condition is
met. Then, in the spacetime for each hyperarea-hypersurface S
of the spatial type,
there is a certain maximum region of spacetime, in which
it is possible to unambiguously and completely predict physical
phenomena on the basis of knowledge of the initial conditions on S (Fig.3.9) :
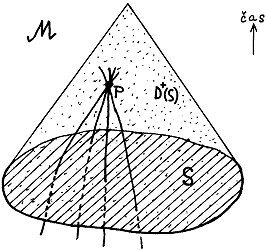 |
Fig.3.9. Based on knowledge of the initial conditions on the spatial hypersurface S , the future can be unambiguously predict in the Cauchy region D+(S), if the world-lines of time or isotropic type passing through any point p Î D+(S) in the past previously intersected the hypersurface S . |
| Definition 3.3 (Cauchy region *): |
| Cauchy's region of the future D+(S), resp. past D-(S), of hypersurface S of the spatial type, are called the set of all such points p Î M , for which each worldline of time or isotropic type passing through the point p intersects S in the past (resp. in the future). |
| Definition 3.4 (Cauchy hypersurface *): |
| Hypersurface S , which intersects each non-extendable worldline of the time or isotropic type, ie. for which D+(S) È D-(S) = M, is called the global Cauchy hypersurface . |
Thus, if there is a
global Cauchy hypersurface in space-time M, then based on the required set of
initial conditions on this hypersuface it is possible to
unambiguously determine the physical
situation in the whole M, ie predict
values of fields and positions and motions of all particles at
any point in time in the future or past. Such is the situation, such as, in
the flat Minkowski spacetime STR, where, for example, each hyperspace
t=const. is Cauchy's hypersurface. In §3.5 "Reissner-Nordström
geometry" and 3.6
"Kerr and Kerr-Newman geometry",
however, we show that this "deterministic ideal of classical
physics" is not fulfilled in some more complex cases, global
Cauchy hypersurfaces do not exist there.
*) A task which, based on a
set of initial conditions on a hyperplane S with the help of field equations it
extends the solution further into the future (or into the past)
is called Cauchy's problem (according to the French mathematician A.L.Cauchy,
who dealt with the mathematical side of these solutions in the
19th century); hence the names "Cauchy region", "Cauchy
hypersurface" and
"Cauchy horizon".
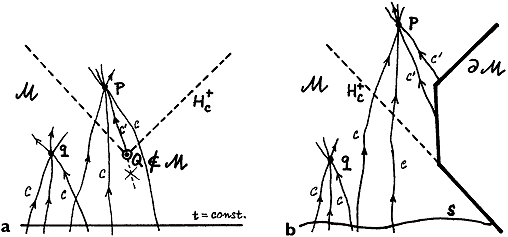
Fig.3.10. Examples of situations where there are no global Cauchy
hypersurfaces in spacetime M (and therefore Cauchy horizons H+C are
present ).
a ) A certain point Q
is "cut out" from the manifold M; then
we can imagine a worldline C '
passing through the point p, which, when
viewed into the past, ends at the place where Q was, and thus
does not continue to the hypersurface t = const.
b ) Manifold with "angled" conformal
boundary ¶M (eg Kerr or Reissner-Nordström
geometry has a similar structure).
In addition to the worldlines C
intersecting S, they can go
to point p (uncontrollably from S) also
world lines C ' from border areas ¶M .
The fact, that some hypersurface S is Cauchy hypersurface, is a property not only the hypersurface S, but also of the whole surrounding spacetime M. Examples of situations, where there are no global Cauchy hyperssurfaces in space-time are shown in Fig.3.10. In Fig.3.10a there is an ordinary Minkowski spacetime, from which only a single point Q is "cut out". If it wheren't for that, each hypersurface S = (x, y, z, t | t = const.) would be a global Cauchy hypersurface. The state, for example, at point q is really unambigously determined by the initial conditions on S . However, if we take any point p inside the cone with the vertex at the cut-out point Q, then most of the worldlines passing through the point p will be intersect hypersurface S, but there also exis world lines which, when the extension of the point p in time to the past, encountered and hit the deleted point Q and thus can not be extended up to S. If we inverse this in time, we can say that from the cut-off point Q, additional "disturbing" influences (information) can come uncontrollably (by world lines not continuing into the past) to point p, which violates the prediction made from the hypersurface S for point p on the basis of knowledge of the complete set of initial conditions on S. There is no Cauchy hypersurface in such spacetime. A conical hypersurface diverging from the removed point Q separates the region of spacetime, in which evolution can be predicted based on the data on S from the region, where this is not possible; such an area is called the Cauchy horizon :
| Definition 3.5 (Cauchy horizon) |
| Cauchy's
horizon of the future H+C(S), resp. of the past H-C(S) of the hypersurface S
is called the boundary of the Cauchy region D+(S) in the future, resp.
boundaries of the area D-(S) in the past, ie H+C(S) = { p | pÎD+(S), I+(P) Ç D+(S) = 0 } , H-C(S) = { p | pÎD-(S), I-(P) Ç D-(S) = 0 } · |
It is obvious that the hypersurface S, which does not have a Cauchy horizon H+C(S) or H-C(S) is a global Cauchy hypersurface. Each bounded hypersurface has a Cauchy horizon (see Fig.3.9), so Cauchy horizons of this origin can be considered "trivial" - they do not tell us anything about the causal structure of a given spacetime. Only non-trivial Cauchy horizons are important, eg those that are for them for every (even unbounded) spatial hypersurface lying in a certain part of spacetime. Such non-trivial Cauchy horizons will be shown in §3.5 "Reissner-Nordström geometry" and 3.6 "Kerr and Kerr-Newman geometry".
 |
Fig.3.11. The horizon of the particles of the observer O (moving along the worldline C ) in the event p separates the particles which the observer O can see from the world point p from those particles which are hitherto unobservable from there. |
Let us have an observer O , which moves in space-time M along the world-line C (of a temporal nature). Let us imagine that the spacetime M is filled with a system of test particles moving along time worldlines. An observer O located at worldpoint (event) p can see some of these particles (those that intersect the light cone past point p ); however, there may be particles in M whose light lines do not intersect this light cone and therefore the observer O cannot see them from the point p (some of them will see later) - Fig.3.11. We say that for the observer O in the event p exists the particles horizont, separating region of space-time, in which the particles are observable geodesics from p, from a region of spacetime in which the moving particles cannot be observed from p. The particle horizon arises, for example, when the infinity of the past J- is of a spatial character, as in Fig.3.11.
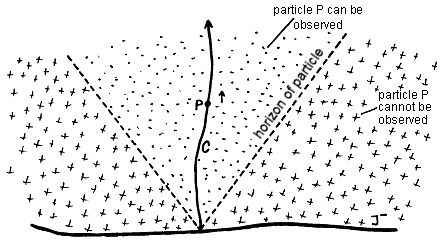 |
Fig.3.12. The horizon of the particle P moving along the worldline C separates the regions of space-time from which the particle P can in principle be observed during its movement along the worldline C, from the areas from which it can never be seen. |
Particles moving along
the world line C can be observed from certain
areas of space-time, but in general there can be areas in M from which it cannot be observed in
principle (Fig.3.12). The boundary separating these two regions of spacetime is called the horizon of
particle, moving along the
world line C.
As can be seen from Fig. 3.13, in general
spacetime for an observer O moving along the world line C, there may be events that he can never see
- we say that these events are hidden
behind the horizon of events for the observer O. Event
horizon (the future) for observer O, traveling along the world-line C,
we call the area separating those areas of space-time whose
worldpoints (events) can be seen by the observer O as
he moves along the world C, from the areas that the
observer O can never see from C.
From Fig.3.13 we see
that the event horizon for a geodetic observer arises, for
example, when J+ is of a spatial character. In
Minkowski spacetime, no geodetically moving observer has an event
horizon, because his light cone gradually runs through spacetime.
However, an observer moving, for example, uniformly accelerated
has a horizon of future events (the so-called Rindler's horizon).
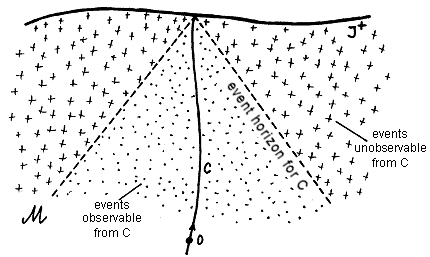 |
Fig.3.13. The event horizon for an observer O moving along the worldline C separates those events that are observable to O during his movement along the C worldline, from the events that he can never observe from the worldline C. |
The event horizon for observer O depends on its specific movement and therefore does not provide completely unambiguous and objective information about the causal structure of a given spacetime. We can make more specific judgments about the causal structure of spacetime, when we find in it a horizon of events that will be for a certain wider class of observers, for example, for all observers moving in a certain area of spacetime. As we will see below (§3.5-3.6 and Chapter 4), the most important are the event horizons, which are them for every observer located in a certain external asymptotically planar region, ie for all observers distant at infinity. It is horizons of this kind that we will keep in mind when we talk about the horizons of events in the next :
| Definition 3.6 (event horizon) |
| Event
horizon (future) is the boundary of the space-time region, from
which worldlines
can be led to the isotropic infinity of the future J+, which at each of their points lie inside or on the mantle of the
light cone of the future (i.e. causal curves) : horizon = ¶ J-(J+) - is the boundary of the past of the area J+ . Anologously, the horizon of past events is ¶ J+(J-) . |
The event horizon thus separates the regions of spacetime from which particles can reach infinity J+ from the regions from which no particle can escape to infinity (Fig.3.14).
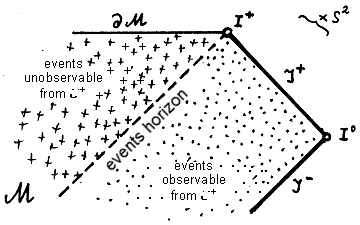 |
Fig.3.14. The event horizon is the boundary dividing those space-time regions, in which events can be observable from infinity J+, and regions from J+ in principle unobservable. |
The reasons why event
horizons arise will be explained below on specific solutions of
Einstein's equations; this is most often because in certain areas
gravity is so strong, that it does not let any body or
light out. Here we will notice only some geometric-topological
properties of the event horizon.
Horizon
generators are
called those isotropic geodesics, that lie in the horizon (at
least for a certain finite interval of the affine parameter). It
can be imagined that the escape velocity on the horizon is equal
to the speed of light and therefore the photons are constantly
"floating" on the horizon. R.Penrose [203] proved an
important theorem on the structure of the horizon of future
events :
| Theorem 3.1 (horizon generators) |
| The
event horizon is generated by isotropic geodesics,
that do not have endpoints in the future. The generating geodetic, that enters the horizon already remains there and cannot intersect with any other generator. Every event on the horizon, which is not the world point of the generator input, goes through exactly one generating zero geodetic. |
The properties of spacetime horizons play a key role in the physics of black holes , as we will see several times in Chapter 4.
Cauchy's problem and the
evolution of spacetime
So much in brief on general issues of causality in spacetime (further details can be found especially in the
monograph [127]).
The specific realization of these causal links, is expressed in
the so-called Cauchy task, which consists roughly of the
following:
Consider the Cauchy hypersurface spatial type
S on which
known (measure) the initial value of the field; if the field is
described by second-order differential equations, the initial
conditions for them must include the distribution of the field
potentials and their first time derivatives. These Cauchy initial
values satisfy certain binding conditions resulting from the
field equations (to be consistent with the field equations). Then
we can use field equations to extend this initial solution to the
immediate future (or past), ie to the infinitely close hypersurface S'.
By repeatedly continuing this procedure, it is then possible to extend the solution further and further into the
future (and past) and thus determine the field values in the
entire Cauchy space-time region D+(S); if S
is a global Cauchy
hypersurface, the field in the whole
spacetime M can be determined.
Cauchy's problem expresses the deterministic character of the whole state of physics: the
evolution of each physical system (field) is unambiguously
determined by the equations of motion (field equations) only when
the appropriate initial conditions are given. This can be
seen in the simplest case of Newton's classical equations mechanics that completely determine the trajectory
of a particle only by entering the appropriate initial
conditions, such as the position of the particle and its velocity
at a certain point in time (eg t = 0). Electrodynamics has a similar character , where
it is necessary to :
a ) In space-time choose a spatial-type
hypersurface ;
b ) On this
initial hypersurfaced, enter the intensities
of the electric field E and the magnetic field B so
that they are consistent with the Maxwell equations div B
= 0, div E =
4 pr, which play the role of binding conditions for the initial values ;
c ) Then, using the second pair of
Maxwell's equations rot E = - ¶B/¶t, rot B = j
+ ¶E/¶t,
the whole evolution of the electromagnetic field in the
future (and in the past) can be determined.
The actual initial conditions are
obtained by measurement; they are the results of observations and
cannot be obtained or derived from equations of motion (these
equations impose only certain limitations on them). There is so far no
theory (nor does anyone know if such a
theory can exist at all..?..), which together with the equations of
motion would determine the initial values *).
*) A new interesting approach
to the problem of initial conditions is now emerging in quantum
cosmology in connection with the concept of inflationary expansion of the very
early universe. According to this concept, the structure and
evolution of the universe is not determined by the initial
conditions during the Big Bang, but is the product of only the
very fundamental laws of physics - see §5.5, passage
"A
complete cosmological theory ?".
When applying the Cauchy problem to Einstein's gravitational equations, it is useful to divide this system of equations into two groups. The first group consists of four equations
| Ri° - 1/2 di° R = 8p Ti° , | (3.8) |
which contain time derivatives of the metric tensor only of the 1st order and do not contain its second time derivatives. These equations are the binding conditions for the initial values . The second group consists of six equations
| Rab - 1/2 dab R = 8p Tab , | (3.9) |
which contain the second
time derivatives of the metric tensor and
thus describe the evolution of the field. Cauchy's problem here is that :
a ) We
have (enter, measure) the values of the metric and its first
derivatives on suitable initial hypersurface of spatial character, which must
satisfy the binding conditions (3.8) ;
b ) By
integrating equations (3.9) we can then extend the initial
solution further, ie obtain the values of
the metric tensor on other spatial hypersurfaces .
However, Cauchy's
problem for the gravitational field (ie for GTR) is somewhat different from
the corresponding problem for other physical fields. If we have
two metrics g1 and g2 between which there is a
diffeomorphism converting to each other, these metrics are
physically equivalent. Thus, there are whole classes of
equivalent metrics, so the solution of gravitational equations
can be found with only precision to diffeomorphism. In order
to eliminate this ambiguity, it is necessary to prescribe certain
conditions, similarly to the introduction in electrodynamics
of Lorentz conditions for the elimination of arbitrariness in
calibration transformations. The equations of most physical
fields are linear; the nonlinear equation appears
only when several fields interact with each other. However, due
to its universality, the gravitational field
exhibits self-gravity (interacts "with
itself"), and Einstein's equations of the gravitational
field are nonlinear with and about ourselves, even without the
presence of other fields. The gravitational field also determines
the metric and thus the structure of spacetime, in which
we solve Cauchy's problem. Therefore, we generally do not know in
advance what the Cauchy region of evolution of the initial hypesurface
will be - we do not know the space-time region, in which the solution is to be
determined (evolution can give us "surprises", perhaps
in the form of horizon or singularity).
It can be proved that if the
initial values satisfy the coupling equations and if the
postulate of local causality is satisfied for a possible
non-gravitational field (see §3.1), Cauchy's problem for
Einstein's equations (and non-gravitational mass equations of
motion) has an unambiguous solution (with
diffeomorphism accuracy). Moreover, this solution depends
in a sense continuously on the initial conditions, as
claimed in the sentence, the simplified wording of which is as
follows [127]:
| Theorem 3.2 (continuity and stability of the solution of the Cauchy problem) |
| Let g represents in U solution
Cauchy problem for the initial condition w to spatial hypersurface S . Then for changed initial conditions w + Dw such that their change Dw will be small in the region J-(U) Ç S, we get in the region U a new solution g ', which will be close to the original solution g . |
This theorem justifies
the use of perturbation analysis of
the solution of
gravitational equations mentioned in §2.5, where from a known
solution under certain initial conditions (eg solution for the
case of exact symmetry) we try to obtain information about a new
solution under slightly changed initial conditions (eg slight
symmetry violation). These methods are of considerable
importance especially in the analysis of the gravitational
collapse, in which the known course of collapse in the case of a
spherically symmetric infer the course of real collapse without
exact symmetry, see Chapter 4.
However, a truly consistent use
of Cauchy's problem to determine the evolution of physical
systems in nature is not possible, Cauchy's problem is only a
theoretical model and a guide on how to find such a solution in
principle. The reason is that it is not
possible to determine the complete set of initial values of
physical quantities on the Cauchy hypersurface
of spatial type sufficiently
densely and precisely, partly due to the finite speed of
propagation of interactions would have been necessary to get into
the future at all (even very distant) points, which is also
practically impossible. When solving the Cauchy problem,
the initial condition for the Cauchy hypersurface are only
awarded on the basis of certain theoretical model (e.g. everywhere vacuum or homogeneous distribution of a
certain density, etc.) and we follow the evolution of this model.
In addition, there may be (at least theoretically, see §3.5-3.9) situations where the considered
spacetime does not have global Cauchy hyperfields, and even the
best knowledge of the complete set of initial conditions is not
sufficient to determine its evolution. Furthermore, the Cauchy
problem is the epitome of classical deterministic spirit of the classical physics; quantum
processes
preserve deterministic relations only at the level of wave
functions, while globally the exact determinism of classical
physics is already disturbed (see the
following passage "Determinism, radomnesss,
chaos" and also §4.7).
Determinism
in principle, randomness and chaos in practice ?
Cauchy problem embodies Laplace mechanistic conception of the
universe as a "clockwork" :
"A perfect reason, knowing at given
moment all the forces governing nature and the relative positions
of objects in it, and that would be powerful enough to analyze
this data, could be summarized into a single system the motion of
the largest cosmic bodies and the lightest atoms: for such a mind
there would be nothing uncertain and the future as well as the
past would be present before his sight" (Pierre Simon
Laplace, 1812) - a mechanistic
conception of the world.
Is our universe deterministic,
as Laplace claimed, or is ruled by chance, how
often does this seem to us in everyday life? The first weakness
of Laplace's idea is that we can never measure the initial state
of a system absolutely accurately, so even
future deductions from it cannot be completely accurate. However,
it was assumed that if we perform the initial measurement with an
accuracy of, for example, 12 decimal places, then all subsequent
predictions will also have an accuracy of 12 decimal places - the
initial error does not disappear, but it does not increase
either. Unfortunately, it turned out that the error or deviation
actually increases - at each step of the
evolution of the system, the prediction error increases by a
certain percentage, so after a few steps or tens of steps, we can
no longer predict practically anything ...
From a thermodynamic point
of view, statistical chaotic phenomena in dynamic ensembles of
microparticles are discussed in §1.1 "Nuclear Physics",
passage "Thermodynamics".
This amplification of errors is the second
weakness, negating the perfect Lapace determinism. Sensitivity to
initial conditions makes the behavior of the system irregular and
unpredictable - chaotic (Greek
cháos = empty, gaping abyss, formless state; it means a
state without order and laws). The individual elementary stages of the system's
behavior are governed by deterministic laws, but result in such
irregularities that they appear to be completely random. Such
(apparent) chaos is thus a complex and (seemingly) irregular
behavior, which in fact has a simple deterministic basis. Because
this chaos is generated by systems themselves governed by
deterministic laws, it is often referred to as "deterministic
chaos". This chaos is probably the main reason that
our nature is so varied, diverse, variable. And perhaps also the
"driving force" of mental activity and our human
"freedom will"..?..
Everywhere in the universe, matter behaves according to the
same laws of physics and chemistry. However, the
specific behavior, the course of events and their outcome, depend
on current conditions - these have also evolved
according to these exact laws, but often through a complex
combination of circumstances, that already have the character of chance.
The role of chance
in the origin and evolution of life is discussed in the work "Anthropic principle and/or cosmic God", passage "Origin
and evolution of life".
Quantum physics also shows that at the
microscales of space and time, nature is truly and principally controlled
by chance, for example, whether or not a particular
elementary particle or radioactive nucleus decays at a given
moment is a purely coincidental matter; between the nucleus which
is to disintegrate immediately and the one which does not (or
only after a long time) can not be found absolutely no
difference. Only file a large number of particles or radioactive
nuclei appear accurate statistical regularity.
After all, a fundamental question arises as to where these
statistical regularities come from; are they traces of some hidden
determinism on a more fundamental level? Quantum physics
resolutely denies this ...
It turns out that the deterministic idea works only in
the simplest idealized cases - determinism can
be considered only "in principle", not in
practice. In real systems of many bodies, which follow
not only the laws of classical but also quantum mechanics, we
observe that the slightest uncertainty in determining the state
of a system at a given initial time usually leads to a complete
loss of the ability to accurately determine its state even after
a relatively short period of time. Small differences in the
initial conditions can cause large changes in the resulting
phenomena. In other words, almost identical states of presence
can evolve towards very different futures - any prediction
becomes impossible, the phenomenon effectively becomes random;
we are talking about the chaotic behavior of the
system *).
*) On this instability and
indeterminism the behavior of complex systems is
often encountered by meteorologists in their efforts to forecast
the weather for a longer period of time (which usually fails).
They refer to it metaphorically as the "butterfly
wing effect" - that the mere flutter of a butterfly
wing, causing a slight swirl of air in Europe, for example, can
"cause" a storm or cyclone on the other side of the
Earth - in America or Australia.
However, it should be borne in mind that the "butterfly wing
effect" is just an ad-absurdum of increased mystification!
In fact, atmospheric events are constantly influenced by local
fluctuations in the surrounding natural conditions,
which are many orders of magnitude greater than that distant
butterfly effect ...
Lyapunov instability
Calculations and computer simulations show that in such unstable
systems a small change do of the initial
conditions causes, that the initially close trajectories to
diverge exponentially with time t : d = do .e -l .t . After a long
enough time, the system eventually becomes chaotic.
The degree of linear stability or instability -
"chaoticism" of such a system can be characterized by
the so-called Lyapunov time TL = 1/l , for which the
system deviates 2.7 times (by this factor is increases each
initial deviation); parameter l= 1/TL is sometimes called Lyapunov exponent.
Interestingly, even seemingly stable
systems such as the solar system are probably chaotic. The
orbits of the planets are mutually affected by gravitational
perturbations - the symmetry of Kepler's orbits is
slowly broken. For the inner planets of the solar
system (excluding Mercury), the Lyapunov time is estimated at TL » 5.106 years. The high value of this time explains the
extraordinary accuracy of astronomical predictions of planetary
motions over time horizons of hundreds and thousands of years.
However, at intervals of hundreds of millions to billions of
years, the chaotic nature of the planet's orbits would already be
decisive; some of the planets could even leave the bound system
of the solar system.
Until recently, it was assumed in classical
physics that simple systems behave simply, and that therefore
every complex behavior must have "complex causes."
However, the analysis of the behavior of the systems in recent
years has shown some surprising findings. That the behavior of
even simple systems can be very complex, seemingly chaotic. And
again, some complex systems can behave surprisingly simply - for
example, due to self-regulatory or synergistic mechanisms. Within
this new theory of chaos, the chaos and order
are like connected vessels: under certain circumstances, order
changes into chaos, under other conditions chaos turns into
ordered structures. And even (seemingly) chaotic behavior leaves
traces albeit of complex and seemingly disordered, but the theory
of chaos often finds a surprising order in them - a kind of
"organized chaos". These traces
chaotic behavior usually have a complex geometrical structure,
for a description of which is no longer suitable classical
Euclidean geometry, demonstrates, however, that it can be well
modeled with a new type of so-called fractal geometry
(see below).
To describe the behavior of dynamic systems is often
used so-called phase space (introduced
by H.Poincaré) - an imaginary mathematical
space whose points represent all possible states of a dynamic
system. The behavior of the system is then expressed by a certain
phase trajectory - a curve in this phase
space.The dynamics of the system can be represented by geometric
shapes in the phase space. If we start a dynamic system from some
initial state (point in phase space) and observe its long-term
behavior, it often happens that its trajectory in phase
space will converge to some defined geometric shape, sometimes
even with different choices of initial conditions. Such an end
formation in phase space, to which the dynamic behavior of the
system is directed, is called the attractor
(lat. Atractio = to attract) - this structure
seems to "attract" the trajectories of the system in
phase space, so that the system either rests in it, or
"orbits" around it.
A system that settles in a constant quiescent state has
only one point as an attractor. In a system that stabilizes by
repeating its state periodically, the attractor will be a closed
loop around which the system revolves. Systems with
quasi-periodic motion have more complex attractors with multiple
and split loops. Chaotically behaving systems describe in phase
space very complex trajectories around special formations called strange
attractors, which have a fractal structure
:
Fractals -
infinitely segmented formations
Objects in nature, although mostly irregular and complex, are
usually modeled using simple geometric shapes
such as line, triangle, square and rectangle, circle or ellipse,
plane, cube, sphere and other shapes described by Euclidean
geometry. Formulas for calculating their length, area or volume
are also well known for these basic structures. Similarly, in
other more complex shapes, which can be composed as a combination
of finite or infinite (but countable) number of basic geometric
shapes.
We can assign a certain integer to all such formations -
the number of dimensions or the (topological) dimension
of a given shape, determined by the number of numbers,
coordinates or parameters determining the position of points in
these shapes: a line or curve (albeit heavily bent) has dimension
1, the surface has dimension 2, cubes, spheres and all spatial
shapes have dimension 3 (because the position of each point in
them it is uniquely determined by 3 numbers - coordinates).
However, it turns out that very articulated,
"rough" and irregular shapes in nature
(as well as the behavior of chaotic systems) better than
classical Euclidean geometry models the so-called fractal
geometry (lat. Fractus = broken,
break ), which allows to describe even
infinitely segmented shapes. Euclidean geometry is a kind of
abstraction of real shapes, while fractal geometry reflects the
real complexity and articulation of shapes: fractal shapes are no
longer a simple combination of ideal geometric shapes, but are of
infinite complexity - the more detailed we examine them, the more
complex details appear. Fractal geometry tries to capture all the
holes, bumps, distortions, entanglements that occur in natural
formations. Despite this bizarre complexity of fractal geometry,
it reveals certain regularities of so-called self-similarity,
where each part of the object is similar to the whole (see below)
- in nature there are often branching fractal structures. It
turns out that fractal geometry is a suitable mathematical tool
for describing the structures and dynamics of natural processes.
For
readers who do not come into contact with sets more
often, it may be useful to read in §3.1 "Geometric-topological
properties of spacetime",
the introductory part "Topology", the passage "Sets
and representations" and also the section "Infinity in space and time", passage "Infinity in mathematics".
From
the history of fractals
The roots of these concepts go back in a way to the founder of
set theory G.Cantor, who in 1883 built a peculiar purely
speculative set - the so-called Cantor's discontinuum.
Cantor's discontinuum arises from a line segment of unit length
by first removing the middle third, then in the remaining two
third segments always the middle third again, etc., to infinity.
Then a set of isolated points remains, Cantor's discontinuum or
Cantor's dust. The sum of the lengths of all omitted
intervals is exactly equal to 1. Cantor's dust is, at first
glance, a negligible group of points. However, Cantor proved that
there are exactly as many of these "dust grains" as
there were points on the original line segment (!) - they can be
unambiguously assigned to each other. The part is, in a sense, as
numerous as the whole - compare with the discussion of the
concept of infinity in mathematics in §3.1 "Geometry and
topology of spacetime", the passage "Infinity in space
and time". If we stack all the omitted
third sections from the previous structure on top of each other
in steps (the same height as the width), a so-called devil's
staircase will be created. This "staircase",
despite its complex fractal structure of infinitely many degrees,
has a finite length of 2.
Other features of unusual internal structure, such as
the Koch flake or the Sierpinic rug, will be discussed below in
connection with fractal geometry and the Hausdorff dimension. The
paradoxical properties of these artificially constructed objects
or structures with the mathematicians of the time,
"bred" by classical algebra and mathematical analysis,
seemed so bizarre and contrary to intuition and common sense,
that they called them a kind of perverted "mathematical
monsters".
However, the main founder of modern
fractal geometry is Benoit Mandelbrot, who revealed new and
unexpected structural properties of geometrically complex shapes
and sets - the anomalous dimension and periodicity
of structures in different scales. In the 1960s, Mandelbrot analyzed
noise and errors in electronic signal transmission. He observed
that alternating time intervals of correct and erroneous
transmission occur on different time scales - a kind of
"self-similarity". Coincidentally, he linked this
knowledge to empirical data on the measurement of the length of
sea coasts (specifically the coast of the island of Corsica),
collected by L.Richardson. He found that the determination of the
length of such a coast depends significantly on the scale, ie on
the "length of the rod" with which we perform the
measurement. On a larger scale, on the map, we do not see all the
real irregularities, bends, protrusions and other intricacies of
the coast, which will "bridge" the larger scale - we
will measure the length shorter. In smaller and smaller
scales of a more detailed view, we have to copy smaller and
smaller fragments when measuring with a short rod, so with a
finer scale, the detected length of the coast will become larger
and larger - theoretically to infinity (the so-called
Richardson effect). For the length of the coast L
measured by a rod of length e , Richardson determined the empirical dependence L(e) = K. e
1 - DR
, where the constant K is a certain "normal"
length of a particular coast and the constant DR (called Richardson's
constant ) characterizes the fragmentation from
about 1.05-1.3; the average value of the Richardson constant is
taken to be 1.26. Mandelbrod analyzed Richardson's empirical
formula by of a given coast. For different coasts, the value of DR ranged Mandelbrod
analyzed Richardson's empirical formula by introducing another
parameter of the number of intersections of the measuring rod
N(e),
so that L(e) = e .N(e). He thus adjusted the equation to the form K = L(e). e DR -
1
= e
.N(e). e DR - 1 = N(e). e DR
, from which it follows that K can
be considered as a Hausdorff measure and DR as a Hausdorff
dimension of a set of points describing the coast.
Furthermore, Mandelbrod analyzed and supplemented the so-called
Julius sets. By elaborating and generalizing these findings,
Mandelbrod came to the concept of fractal .
Properties of fractals
Fractal formations (fractals) have two basic remarkable
properties (which can also serve as definitions of fractals) :
From a mathematical point of view, a self-similar
set A from the n-dimensional Euclidean space En is a set for which
there are finally many so-called contracting representations
f1 , f2 , ..., fn (these are such imaging En to En, which reduce the distance between two points lying in
En), such
that A arises as a unification of A = i=1Cn fi(A). Such self-like
sets are created by repeating "myself" in a certain
transformation, such as scaling, rotation or shifting.
Self-similar sets are invariant to scaling - they look similar
when zoomed in or out. It can be said that a self-like set arises
"from itself" - it arises by repeating the same basic
motif. E.g. Cantor's discontinuum consists of its repeating exact
copies, reduced to 1/3.
We can
simplified say that a fractal is a geometric
shape (or set) that consists of a certain number of its suitably
reduced "copies". Such a principle of repeating
similar shapes in reduced or enlarged form we can often
observe in nature, where many complicated and complex formations
are created by repeating simple structures and rules. It is, for
example, the growth of tree branches, coral reefs in the sea,
snowflakes, weathered rocks, or branching of the vascular system
in the body from large aortic vessels to the finest capillaries.
Structures of this kind are very effective in packing a large
surface area into a small volume.
Topological dimension
The usual dimension - the number of dimensions -
of an object, also called the topological dimension
(see §3.1 "Geometry and topology of spacetime") is an integer D indicating the number of
parameters which unambiguously define the position of individual
points of this object. A line, line fragment, a circle, a
parabola, a sine wave, and any other curve have the dimension D =
1 (it is one-dimensional), because the position of a point on it
can be parameterized by a single number (coordinate). Each smooth
surface - plane, triangle, circle, spherical or cylindrical
surface, has the dimension D = 2, because the position of the
point here must be defined using two coordinates. Bodies such as
a cube, cylinder, a pyramid, a sphere, as well as the entire
usual space around us, have the dimension D = 3, because the
position of each point in them is uniquely determined by 3
coordinates. By analogy, we can formally construct formations
with higher dimensions, even if we have no direct experience with
them and cannot imagine them; in our treatise we often use
4-dimensional spacetime.
Fractal
dimension
Hausdorff's dimension
However, we can look at the dimension from a
non-topological point of view - from the metric
point of view, which models the process of measuring
a given geometric shape - determining its length, area, volume, measure
in general. Let us first consider the measurement of a line
fragment (dimension D = 1) of total length L, which we
cover N with equally long intrervals ("scales")
of length e. The number of intervals N(e) that cover the whole line
fragment depends on the length of the intervals according to the
relation N(e) = L. (1/e) and the length of the line segment can be calculated
based on the number of coverage L = N(e). e . If we measure the length
of the curve in a similar way, we will refine
the coverage, so that the length will be expressed by
the relation L = lime®0N(e). e . Similarly, in
the case of dimension D = 2, the area of a square of side L
can be covered by the number N(e) of squares of side e , and for the
total area of the square we get S º L(2) = N(e). e2. For a general planar
shape, its area L(2) can be expressed as L(2) = lime®0N(e).e2. In general, for a D-dimensional structure, the
relationship between its size (measure) L(D) and the number of coverage N(e) is a measure of length e : L(D) = lime®0N(e).eD. By logarithmization,
this makes it possible to express the dimension D of a
shape of "volume" L(D) using the relation D = lime®0[ln N(e)]/[ln L(D)+ ln(1/e)]. By normalizing to the unit volume, we get a relation
for the dimension, which we can consider as an alternative independent
metric definition of the dimension
- so-called Hausdorff-
Kolmogorov dimensions DH :
D H = lim e® 0 [ln N ( e )] / [ln (1 / e )] ,
where N(e) is the number of coverage of the measured structure by
scales (lines segments) of length e .
If the formation is regular, it is not necessary to
calculate the limit for infinite refinement of the scale; it is
enough to compare which resultant factor will change the
determined length of the examined unit when the scale is refined
by a given certain factor. The relation for determining the
Hausdorff dimension is then simplified to:
D H = ln N / ln (1 / e ) ,
where N
is the change factor of the determined length, e is the length of
one newly formed scale fraction when the original shape is
divided by the scale change factor 1/e .
If we calculate the
Hausdorff-Besikov dimension for any smooth one-dimensional shape
(line or curve), we get DH = 1, for a smooth area shape we get DH = 2, for ordinary
three-dimensional geometric shapes DH = 3. For geometrically smooth shapes in general always
holds DH =
D - Hausdorff's dimension is equal to the topological dimension.
However, for complex articulated formations - fractals
- their Hausdorff dimension is higher than the
topological dimension and is usually given by a non-integer
value. The Hausdorff dimension can be considered as a certain generalization
of the usual (topological) dimension, which better captures the
behavior of complex articulated formations than the topological
dimension. The fractal dimension quantifies the degree of
complexity or articulation of an object by how fast its measured
length, content, or volume increases depending on the size of the
scale by which we measure (a generalized Richardson
effect is used).
Similarity dimension
For self-similar sets, another alternative definition of
dimension can be expressed - the similarity dimension.
This dimension quantifies how many copies of itself, reduced by
an appropriate factor, are contained in a given set. If the
examined object contains N copies of themselves, reduced
by factors 1/ki (i = 1,2, ...,
N) , the similarity dimension DS is given by the
relation
i
= 1S N (1 / k i ) D S = 1 .
For the most common case that the factors k i are the same (k i = k), we obtain a similarity dimension by solving the
equation i=1SN(1/k)DS = 1, which gives DS = ln N / ln k = DH. It can be proved that the similarity dimension is
equal to the Hausdorff dimension. The concept of similarity
dimension thus
making it easy to determine the fractal dimension of symmetrical
fractals of geometric origin. It is enough to find out how many
"copies of itself" and to what extent the structure
contains, and its fractal dimension will be given by the
proportion of logarithms of these values - see below.
Grid dimension
For more complex fractal features whose structures do not show
self-similarity, the fractal dimension can be determined
empirically by grid counting - "box-counting".
A grid (of the dimension given by the
topological dimension of the studied formation) of cell size d
is overlaid over the given formation and the number of cells
containing some points of the observed formation is calculated.
This gives the number N , which depends on the size d
grid cells N = N(d) - the denser grid (smaller d), the
larger the N. We gradually refine the grid (reduce d)
and analyze the function N(d) by plotting it in the log/log
graph [ln N(d) « ln (1/d)]. We use the obtained points to intersect a
line, the direction of which then indicates the
fractal dimension of the investigated formation.
In the simplest case, when the test grid is refined by a factor
of 2 (twice as thick), the number of cells counted between two
consecutive coats is multiplied by 2D, where D is the fractal dimension.
For self-similar objects, this method gives the same
values as the similarity and Hausdorff dimensions; however, it is
easy to algorithmize and works even for complicated fractal
formations.
Examples
of fractal formations
Koch's flake
One of the simplest and most interesting examples of how a
complex fractal formation can be created from an originally
Euclidean-shaped geometric construction is the so-called Koch's
curve ; this curve was constructed in 1904 by the
Swedish mathematician H. van Koch as a geometric model
approximation of the perimeter of a snowflake - hence the name
"Koch snowflake". We can construct the Koch
snowflake by a series of successive triangular iterations as
shown in the figure. We start from an equilateral triangle with
unit side length (1st iteration); the perimeter therefore
consists of three sections of unit length. In the 2nd
iteration, we connect to the middle third of each side another
equilateral triangle with a third length of the side - a
6-pointed star is formed, the circumference of which consists of
12 sections of length 1/3. In the next iteration
we add another smaller triangle to each middle third of each of
the 12 sides. The length of the curve will be extended by 1/3 at
each step (four parts of the line will form four of the same
length.) In the infinite limit of the number of steps n®¥ we get a curve
whose length 3.(4/3)n is infinite, but the content of the
area bounded by this infinite line remains finite
(less than the area of the circle circumscribed by the original
triangle, since the Koch curve does not intersect the
circumscribed circle anywhere; at each iteration of e®e/3, 4
(self-similar) parts are formed, ie N(e/3)®4.N(e). According to the above
definition formula (in the simplified version), the Hausdorff
dimension of the Koch curve comes out : DH = ln4/ln[1/(1/3)] =
ln4/ln3 @ 1.261, ie higher than
the topological dimension D = 1. Thus, such a curve
"fills" a space (plane) somewhat more than a mere line
or line segment with dimension D = DH = 1- it is a set or shape metric
"denser" than would be expected from
its topological dimension D = 1.
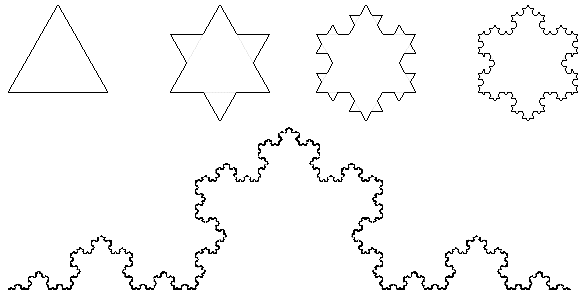 |
| Construction and structure of Koch
fractal curve. Above: 1., 2., 3. and 4. iteration of the curve. Bottom: Enlarged view of the rugged structure of the curve. |
Such "dense" fractal formations with
a Hausdorff dimension higher than the topological one are created
by adding infinitely many refining parts into
geometrically smooth formations .
Cantor's discontinuum
By removing infinitely many
infinitely decreasing parts, on the contrary, "thinner"
sets are created, whose Hausdorff dimension is smaller
than the topological dimension. The oldest example is the already
mentioned Cantor's discontinuum with D = 1 and DH = ln2 / ln3 @ 0.63 (Cantor's
discontinuum is the unification of its two copies reduced by a
coefficient of 1/3).
Sierpinski triangle
it is created by cutting an inner smaller triangle formed by the
middle bars of the original triangle from the initial triangular
area (D=2). We repeat this procedure in the three remaining
triangles, etc. - an infinitely many infinitely small triangles
are created. This formation consists of three of its copies
reduced in half, so that D H = ln3 / ln2 @ 1.58.
The Sierpinski carpet
is created by an analogous carving procedure from a square area,
which we always divide into 9 identical squares (using
perpendicular partitions in 1/3 and 2/3 of each side) and cut out
the middle one. Repeat the same procedure with the remaining 8
squares, etc. The Sierpinski square with the default D = 2
consists of 8 of its copies reduced to 1/3, so DH = ln8 / ln3 @ 1.89.
Menger's sponge
Generalizing to three-dimensional objects creates a Menger's
sponge : Divide the cube into 27 identical smaller cubes and
remove the middle 7 (whose edge is not part of the edge of the
original large cube). We repeat this procedure with the remaining
20 smaller cubes, etc. In the end, an infinitely segmented
three-dimensional grid with an infinite surface is created (each
wall of the Menger sponge is also a Sierpinski carpet), but with
a zero (infinitesimal small) volume. Interestingly, in addition
to fractal properties, it also contains topological equivalents
of all curves existing in space. Since this formation (with the
initial topological dimension D = 3) consists of 20 copies of the
original cube reduced to 1/3, the fractal dimension of the Menger
sponge DH
= ln20 / ln3 @ 2.73.
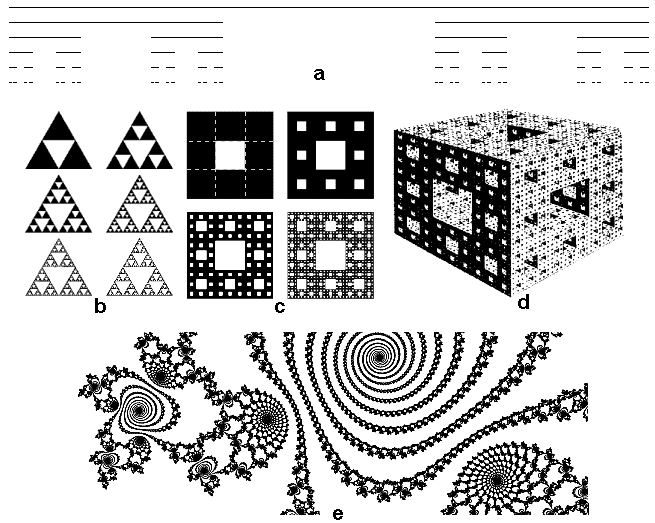 |
| Some typical fractal sets and
formations. a: Cantor's discontinuum (first 6 iterations). b: Sierpinsky triangle (first 7 iterations). c: Sierpinsky carpet (first 5 iterations). d: Menger's sponge (after about 5 iterations). e: Example of a polynomial Julius-Mandelbrot fractal (detail - cut-out from a complex plane). |
Polynomial fractals
Other interesting fractal shapes arise as a geometric place of
points in the Gaussian plane of complex numbers z = x + y.i (
i is an imaginary unit), for which iterative methods for
solving some algebraic equations converge. The simplest example
is a gradual iteration of the function of a complex parabola
zn+1 = zn2
+ c, where a set of all complex numbers z0 is drawn into the
complex plane, for which the sequence zn converges (zn is finite for n®¥). These so-called
Julius- Mandelbrot sets
forms a great variety of often beautiful patterns,
depending on the value of the constant c ; they can be
continuous or discrete. They are now popularly
rendered using computer graphics , including spectacular
color modulations *). However, most fractals are
"invented" by nature itself ..!..
*) The color representation of individual
points of a bit-map is modulated, for example, by the number of
iterations needed to reach a certain value | z |.
Fractals in nature
For complex fractal sets, the calculation of the Hausdorff
dimension cannot usually be performed directly algebraically
according to the above formula. It is necessary to proceed
"experimentally" or empirically - to construct a graph
[ln N(e)
« ln
(1/e)]
and determine the dimension by extrapolating the graph directive
for 1/e®¥ ; or use lattice methods to determine the
fractal dimension. In nature, we also encounter complex objects
whose shape or behavior cannot be described by a single fractal
dimension; such "multifractals" are
characterized by two or more dimensions (manifested by different
linear segments on a log / log graph).
From the fractal formations
occurring in nature, values were empirically determined for the
Hausdorff dimension: seashore DH @ 1.26
(Richardson's constant); rock surface DH @ 2.3; human brain
membrane surface DH @ 2.76.
Theory of
relativity, quantum physics + chaos theory ® new conception of
reality ?
As mentioned above, in nature we encounter a number of phenomena
leading to the formation of fractal structures *). In the field
of astrophysics and cosmology, it is possible that groups or
clusters of galaxies and galaxies arising from germinal
inhomogeneities spread by expansions of the universe to different
sizes (§5.4) have a fractal structure. In §5.5
"Microphysics and Cosmology. Inflation Universe", the
passage "Chaotic Inflation and Quantum Cosmology", we
will see that the presumed set of spontaneously emerging
universes from quantum fluctuations creates a "fractal
tree" of new and new "universes"...
*) Even fractal geometry is just a model,
to some extent idealized. The fragmentation of natural formations
and the complexity of the behavior of dynamical systems is
colossal, but not infinite. The fractal model
loses its validity at the level of atomic dimensions,
where the idea of self-similarity ceases to apply (atoms do not
have a fractal structure) and the determination of the metric
dimension loses the possibility of realization.
The behavior of nonequilibrium
and nonlinear dynamical systems is dealt with by synergetics,
which can be described with a bit of exaggeration as the doctrine
of organized chaos - against the background of
seemingly chaotic behavior, hidden patterns are sought, which are
often very non-trivial and remarkable. The self-similarity of
fractals corresponding to strange attractors of chaotic systems
is a kind of hidden order that is a symptom of some kind of
"deterministic chaos".
It turns out that the theory
of chaos and infinite arcticulation of formations is
probably a new fundamental idea of the
surrounding world, complementing two already elaborated and
proven fundamental conceptions of modern physics: the theory
of relativity and quantum physics. All
three fundamental theories, on the one hand, lead to the
enrichment and deepening of our understanding of nature and the
universe, but at the same time, unfortunately, they set our
knowledge at the same time universal limit restrictions, a kind of
"gnoseological barriers", through
which we fundamentally can not get :
¨ The theory of relativity
shows an impassable limit the spread of fields and information
given speed of light in vacuum and then in combination with
gravity as a theory of curved spacetime, the existence of the
event horizons, which are repeatedly discussed in our
book.
¨ Quantum physics,
with its relations of uncertainty and stochastic character, sets
the limits of recognizability of the course of
individual processes in the microworld (the
individuality of particles and processes is actually blurred).
¨ Chaos
and nonlinear dynamics fundamentally limit the
possibilities of long-term predictability of the exact behavior
of all systems, even seemingly simple processes (the most powerful computer or the most accurate
numerical methods will not help us in this, it is a fundamental
limitation!) .
However, we will not deal with
these last aspects of the behavior of physical systems; in our
book we will deal with a deterministic analysis of
gravity and the structure of spacetime - that is, deterministic,
at least in principle, within the general theory
of relativity.
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||