| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Physics and nuclear medicine |
1.
Nuclear and radiation physics
1.0. Physics - fundamental natural
science
1.1. Atoms and atomic nuclei
1.2. Radioactivity
1.3. Nuclear reactions and nuclear energy
1.4. Radionuclides
1.5. Elementary particles and accelerators
1.6. Ionizing radiation
1.7. Neutrinos - ghosts
between particles
1.2. Radioactivity
Experience with the substance of which the
surrounding world is composed shows that most substances are
relatively stable over time and change only over longer time
scales. However, these changes are mostly of a chemical
nature, the atoms of the commonly occurring
elements themselves are almost always stable.
Practically until the end of the 19th century physicists and
chemists firmly believed that atoms are immutable and
eternal.
Discovery
of radioactivity
At the turn of the 19th and 20th centuries however, phenomena
have been discovered in which some substances emit
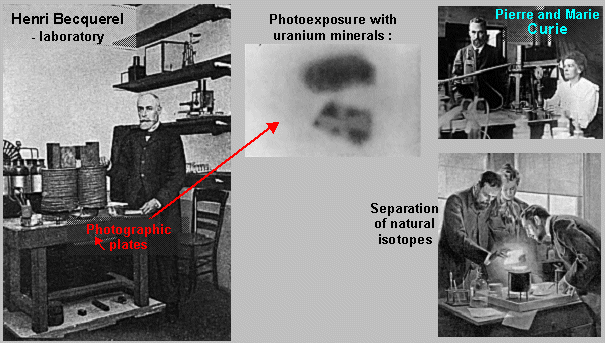
invisible penetrating radiation. As early as 1896,
during experiments with the luminescence of minerals and
crystals, H.Becquerel observed that even without exposure to
external light, some minerals (uranium compounds) emit special
invisible radiation (Becquerel initially called them
"uranium radiation"), which penetrates the light-tight
envelope of photographic plates and causes them to blacken.
Henry Becquerel experimented with the luminescence of various
minerals in Paris, including the uranium minerals he had from his
father. He exposed the minerals to the sun's rays and judged
their luminescence by blackening the photographic plates. One
day, with the minerals ready for the exposition, the sky overcast
and Becquerel, disappointed, placed the minerals in a drawer on
the photo plates. After a few days, he called up the photographic
plate (accidentally, perhaps to compare or check the quality of
the plate, or whether the minerals have a chemical effect on the
photographic plate..?..) and to his surprise he saw a black image
of the minerals on the plate. No external light or any
luminescence could cause this image, as the plate was still
wrapped in black paper and the mineral was not in the sunlight,
it was still in the darkness of the drawer. After further
experiments, he come to an opiniont, hat a kind of invisible
radiation emanated directly from the interior of some minerals,
which penetrated the cover paper and exposed the photographic
plates.
Note: A brief
reflection on the extent to which the discovery of radioactivity
was the result of chance or methodological procedure is given in
§1.0 "Physics - fundamental natural science",
passage "Significant
scientific discoveries - chance or method?".

This phenomenon was then dealt with by Marie
Sklodowska-Curie, her husband Pierre Curie and G.Bemont, who
found other "glowing" elements, polonium and radium, in
uranium ore. This phenomenon was called radioactivity (these substances "actively emitted
radiation"). It was later found that
radioactive elements change their chemical nature when emitting
this radiation - radioactivity is accompanied by the transformation
(transmutation) of the nuclei of atoms of one element to another
element. In 1899 with the properties of radioactive ("uranium") radiation
was dealt with by E.Rutheford, who found two different components
in this radiation :
- soft
component , which is absorbed by a sheet of paper and
whose range in the air is only a few centimeters; he called it rays
a.
- harder component , about
100 times more penetrating than a , which passes through a
thin aluminum sheet; here he called radiation b .
Shortly afterwards, in 1900, P.Villard observed that radium
emitted even more penetrating radiation, which
is able to penetrate tens of centimeters of concrete; he called
them radiation g. Later it
turned out to be electromagnetic radiation with
a very short wavelength, shorter than X-rays.
Furthermore, at this time, Mr and
Mrs Curie and A.Beckerel discovered that b- rays have a negative
electric charge, the specific value of which is close to an
electron (these results were then refined
by W.Kaufmann in 1902) - it turned out that
radiation b
is a stream of electrons.
In the years 1903-1908, E.Rutheford performed a number of
experiments with the passage of radioactive radiation in the
field of strong magnets. He found that the deviation of the rays a in the transverse
magnetic field is significantly smaller and is directed to the
opposite side than in the case of negatively charged radiation b. Finally, he
showed that radiation a is a
current of doubly ionized helium atoms, i.e.flow of
helium nuclei. He found that the radiation g did not deflect in
the magnetic field.
In 1908, E.Rutheford and his
co-workers discovered by spectroscopy that two new gases appeared
in a closed tube with a sample of radium (RaCl 2 chloride ) that had
not been there before: one had spectral lines of helium, the
other was then unknown and was called radio emanation,
now radon. It turned out that radioactivity is a
spontaneous decay of the atomic nucleus, in
which the starting element changes to another - the element is transmutated.
In 1919, the same Rutheford first achieved artificial
transmutation of a non-radioactive nucleus: by bombarding nitrogen with particles a from a
radioactive source (radium) it caused the reaction 14N7 + 4He2 ® 17O8
+ 1H1, which he first
observed in a chamber filled with various gases, by means of a
fluorescent screen recording the flying protons 1H1. The transformation of the nitrogen nucleus after the
impact of the particle a was confirmed in 1923 by Rutheford's collaborator
P.M.S.Blackett in a Wilson nebula chamber filled with nitrogen,
where between a large number of "free" a particle
trajectories in nitrogen cases where the trajectory of the
particle a ended in "branching" into two new tracks: the
long and narrow path of the proton and the wide short track
belonging to the oxygen nucleus.
Artificial radioactivity
All these basic findings have been made on natural
radioactivity, observed mainly in the heaviest elements. In 1934,
F.Joliot-Curie and I.Joliot-Curie first created artificial
radioactivity.
It happened when they irradiated aluminum with rays a. They observed
that the aluminum thus irradiated, emits radiation even when the
irradiation with the rays a was stopped, while the intensity of the radiation
gradually decreases. By nuclear reaction with particles a, aluminum was
converted to radioactive phosphorus 30P, which was emitted by the positron e+ decays into silicon :
a + 27Al13® 30P15 + n ; 30P15®(b+;2,5min)® 30Si14 + e+ .
Positron radiation was observed by J.-Curie in the ionization
chamber. §1.3 "Nuclear reactions" is devoted to
nuclear reactions.
For some artificially created radioactive substances (eg already at the first 30P) they then observed a new type
of radioactivity b+, where instead of negative electrons, positively
charged positrons are emitted. Gradually, a
number of artificial radioisotopes were created, which showed all
kinds of radioactivity - b-,+, g, a. In 1940, G.N.Flerov and K.A.Petržak discovered
that uranium, in addition to radioactivity a in a very small number of
cases, also decays by spontaneous fission into
pairs of medium-heavy nuclei, releasing neutrons; this
spontaneous cleavage is characteristic of all transurans, where
it is even more pronounced.
As in other
fields of physics, terminology, quantities, and units related to
radioactivity and radiation have undergone a long and complex
development that has left some illogicalities and ambiguities -
to be specified below.
We will not
describe in more detail the next historical development of
knowledge about radioactivity (and the heroic efforts of
researchers) and we will enter directly into current physical
knowledge about these phenomena.
General regularities of atomic nucleus
transformations
Nuclear transformation
means a change in the composition or energy state of a nucleus.
In this chapter we will be interested in the spontaneous
transition of nuclei to a more stable state with lower
energy. First, we give a brief definition of
radioactivity :
| Radioactivity
is a phenomenon in which a spontaneous internal
transformation of the composition or energy state of
atomic nuclei occurs, while high-energy radiation is
emitted. Nuclei exhibiting this property are called radionuclides. |
In this process, part of the binding energy of the nucleus is released in the form of kinetic energy of decay products (and often also in the form of electromagnetic radiation) - high-energy (ionizing) radiation is emitted. There is either a transformation of the nuclei of one element into the nuclei of another element - transmutation (for radioactivity a and b ), or energy deexcitation of the levels of the same nucleus (radioactivity g - isomeric transition). Radioactive transmutation is also called radioactive decay. In addition to the name radionuclides, the name radioisotopes is often used (these are certain specific isotopes of nuclei, showing radioactivity). Substances and articles containing radionuclides are referred to as radioactive emitters. The properties of specific radionuclides are detailed devoted to §1.4 "Radionuclides", the resulting radiation is then discussed in detail in §1.3 "Ionizing radiation".
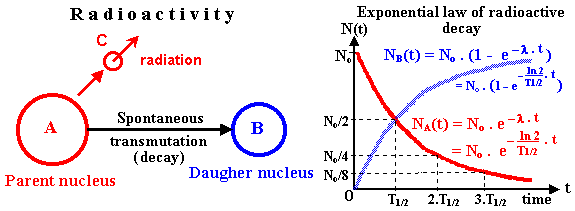
Fig.1.2.1. Basic general scheme of
radioactive transformation and exponential law of radioactive
decay.
The most basic general scheme of radioactive
transformation is shown in the left part of Fig.1.2.1. The
nucleus A, called the parent, spontaneously
(ie without external intervention - only
due to internal forces and mechanisms acting in
the nucleus *) transforms
into a "slightly smaller" nucleus B
called the daughter, while the particle C
called radiation flies out. This particle
radiation carries energy and the composition difference
between nuclei A and B. The law
of conservation of energy and baryon number
(symbolically A = C + B
for both of these characteristics) must be met. In order for
radioactive transformation to take place, the mass-energy
condition m(B) + m(C) < m(A) must be met according to the law
of energy conservation, where m(A) is the mass of the parent
nucleus A (analogously to the daughter nucleus B), m(C) is
the rest mass of the emitted particle C. When nuclear
transformation is released kinetic energy DE =
[m(A)-m(B)-m(C)].c2, which carries most of the emitted particles C,
a small portion also resulting core B reflected due to the
law of action and reaction. The energy difference between the
basic states of the parent and daughter systems is called the energy
of transformation Q.
*) Cause of radioactivity
The mechanisms of each type of radioactivity will be discussed in
detail below. Here we can only give a brief summary of the causes
of spontaneous nucleus transformation :
Radioactivity a is caused
by quite understandable instability of too heavy nuclei (which
strong short-range interaction ceases to be able to sustain), on
whose "periphery" a very stable helium nucleus is
formed, which can be emitted under certain circumstances by the
contribution of a quantum tunneling phenomenon
(Fig.1.2.2). Even simpler is the cause of radioactivity g -
it is a mere "reorganization" of nucleons during
deexcitation of an energetically excited nucleus, the energy
difference of which is emitted by a photon g (this is analogous
to the deexcitation of electrons in the atomic shell).
The cause of radioactivity b is more
complex: it lies deep in the subnuclear region - in the quark
structure of nucleons, where weak interaction can
cause mutual transformations of quarks "u" and
"d", and thus transformations of protons and neutrons
(see below "Mechanism of decay b; weak
interactions", Fig.1.2.5).
From an energy point of view, we will analyze the causes of
radioactivity below in the section "Stability
and instability of atomic nuclei". Here we can only state, that out of more than
1,800 known nuclides (natural and artificial), only 266 are
stable, while others are radioactive - they spontaneously
transforms themselves more or less rapidly into other nuclei (for
more details see §1.4 "Radionuclides").
Before we will
describe the individual specific types of radioactivity, we will
mention those aspects that all types of radioactivity have in common:
these are mainly units of radioactivity and the exponential law
of radioactive decay.
Units of radioactivity
As with any physical phenomenon that we want to quantify, it is
necessary to determine the quantities and units
of radioactivity in which we will measure its
"strength", "intensity" or magnitude. The
relevant quantity is called the activity (of
emitter, preparation or set of nuclei in general) and is defined
as the number of nuclei that is converted
per unit time, or equivalent as the decrease in the
number of nuclei (not yet converted) per unit time. The activity
of a radionuclide is not a constant, but decreases with
time as the original nuclei gradually disintegrate. The
instantaneous value of A(t) activity at time t is
therefore :
A (t)
= - d N (t) / d t
,
where N(t) is the number of nuclei not yet converted at a given
time t. The number of emitted particles per unit time, ie
the intensity of radioactive radiation, is also proportional to
this activity.
Since radioactivity is a
phenomenon in which the atomic nuclei of one element transform
into the nuclei of another element over time, wherein
the time is measuring in seconds, the natural
unit of activity is 1 decay per 1 second. This unit was
named 1 Becquerel in honor of the French pioneer
in the field of radioactivity Henri Becquerel : 1 Bq = 1
decay / 1 second (on average *). And its
decimal multiples: kilobecquerel (1kBq = 103 Bq), megabecquerel
(1MBq = 106 Bq), gigabecquerel (1GBq = 109 Bq). The greater the
radioactivity of a given substance (sample) in Bq, the more
nuclei per second are transformed by us and the more intense
radiation the substance emits to its surroundings.
*) In the definition of a unit of
radioactivity, the word "on average"
(is given in brackets); under the influence of stochastic laws of
quantum physics, radioactive decay does not take place evenly,
but shows irregular statistical fluctuations.
Therefore, we would measure a slightly different number of
decayed nuclei every second - the results should be averaged, or
measured for a longer time and the results normalized to 1
second.
Old units of activity - Ci, mCi, mCi
At the beginning of the radioactivity research, one of the heroic
acts was the separation of 1 gram of pure 226Ra radium
from several tons of uranium ore by Marie-Sklodowska-Curie and
her husband Pier Curie. Since it was the first known pure
radioisotope, 1 gram of radium 226 was taken in
their honor as a standard and the basic unit of radioactivity,
which was called 1 Curie (1 Ci). The respective
decimal fractions were then milicurie (1 mCi = 10-3
Ci) and microcurie (1 mCi
= 10-6 Ci). Later, when many other radionuclides were
discovered or prepared and the very nature of radioactivity was
known (as shown in Fig.1.2.1), disadvantages of
this randomly generated unit were seen. Conversion
between the old and the current unit of activity is: 1Ci @ 37
GBq (i.e. 1 mCi @ 37 MBq and 1 mCi @ 37 kBq).
In addition to the total activity of
the emitter, in many cases it is necessary to know the specific
(normalized) activity of the relevant
preparation or sample. The specific activity is usually given as mass
activity, which is the activity of the mass unit
of the emitter - 1 kg, but in practice usually 1 gram: A1g = A/M [Bq/g], where A is the total activity and M
is the weight of the preparation. For liquids (or gaseous) preparations, volume
activity is often used, ie activity per unit volume - liter, in
practice mostly milliliters: A1ml = A/V [Bq/ml], where
A is the total activity and V is the volume of the
preparation.
The higher the activity of the
emitter, the more intense it glows. The total energy
output P[W] of the emitter
of activity A [Bq] is:
P = A.DE,
where DE
is the energy released during one decay (converted
to Joules: 1eV = 1.6x10-19 J), ie the difference between the
energies of the parent and daughter nuclei, reduced by the
resting energy of the emitted particle formed during the decay (as mentioned above). E.g. a
emitter with an activity of 1GBq, formed by a radionuclide with
energy DE
= 1MeV/decay, will have an energy output of approx. 1.6x10-4 W = 0.16 mW. Part of
the energy performance of the radiator is converted into heat
(kinetic energy scattered nuclei and the absorbed energy of
radiation already at source), the residue carries ionizing
radiation - constitutes the actual radiation power
of radiator; in absorbing radiation in the substance, then the
dose rate (see §5.1, "The effects of radiation on substance. Basic quantities
dosimetry.").
The exponential law of
radioactive decay
Radioactive transformation of nuclei is a stochastic
quantum-mechanical phenomenon, so it is not possible to predict
the time in which a particular nucleus will transform. Only the probability
l with which the core of a given species transforms per
unit time (1 second) can be determined. Let us have a radioactive
substance (sample), in which at the initial time t = 0 there is a
total of No of the same radioactive nuclei A, which will be
gradually transformed into nuclei B (according to the
diagram in Fig.1.2.1). We are interested in how fast the number
of parent cores A will decrease (and thus
also increase the number of daughter cores B) - in other
words we want to determine the functional dependence of N(t) of
the instantaneous number of N (remaining) parent nuclei on
time t. The number of nuclei DN, that decay in a short
time Dt,
will be proportional to the current (instantaneous) number of
nuclei N(t) and the probability factor l called the decay
or transformation constant;
in a sufficiently short time interval Dt, a fixed part of the
present number of N radioactive nuclei is always
converted. Thus, the original number of nuclei changes over time Dt by :
D N(t) =
- l . N
(t). D t
.
If we go from finite differences to
infinitesimal differentials (D-->d), we can
write the differential equation after dividing by dt :
dN(t) / dt = - l . N (t) ,
whose integration gives the function N(t) = const. e-l.t,
where e @ 2,718 is the transcendent so-called Euler number
- the basis of natural (Napier) logarithms. The boundary
condition N(t=0) = No then gives the value
of const = No for the integration constant, so we can write the
resulting time law of radioactive decay :
| Exponential law of radioactive decay : |
| N (t) = N o . e - l . t |
The graph is a descending
curve called an exponential (red curve in
Fig.1.2.1 on the right). On the contrary, the number of nuclei of
the daughter element B increases
according to the exponential law NB(t) = No. (1 - e-l .t) - blue curve in Fig.1.2.1 on the right.
An important quantity is the value of the
time in which exactly half of the original
number of nuclei is transformed: it is called
the half-life of transformation (decay) and is
denoted by T1/2
. Thus N(T1/2) = No/2, which after
substituting into the above derived exponential law: No/2 = No.e-l.T1/2 and
logarithmization, gives l = ln2/T1/2 @ 0,693/T1/2. The exponential law of radioactive decay can therefore
be written in the most commonly used form :
| N (t) = N o . e -( ln2 / T1/2 ) . t @ N o . e - ( 0.693 / T 1/2 ) . t |
After the time t = T1/2 has elapsed, exactly half of the nuclei are converted:
N(T1/2) =
No/2.
After the next half-time elapsing, the half of the half of nuclei
number will remain, ie a quarter : N(2.T1/2) = No/4. And so on to infinity, so only in the limit t®¥ will the limit be N(t®¥) = 0 and all
nuclei will really transform *).
*) This is only theoretically. In fact, there is only
a finite number of parent radioactive nuclei in
each radioactive emitter or preparation. After a sufficient
number of half-lives (tens or hundreds of T1/2 ) have elapsed, in practice the last
the parent nucleus will always eventually disintegrate
(transform) and the sample will be non-radioactive.
In addition to the
decay constant l and the half-life T1/2, the mean lifetime of the nucleus t =
1/l = T1/2/ln2 is sometimes
introduced, which is the time (t = t) for which the activity
drops to 1/e @ 0.3679 of its original value. All three of these
variables (half-life T1/2, conversion constant l and mean lifetime t) indicate how fast
a radionuclide transforms or decays.
The relationship between half-life
and activity
The number of atomic nuclei decaying per unit time (1s) is equal
to -dn(t)/dt
= l.n(t)
= n(t). ln2/T1/2; and this is by definition the activity
in Bq (the value of T1/2 must be given in seconds; for the number of nuclei we
use the symbol small n so that it does not confuse with
the nucleon number large N).
Therefore, if we currently have n radioactive nuclei in
the preparation at time t, its immediate activity will be
A
[Bq] = n. l = n. ln2 / T1/2 ;
it will therefore be directly proportional to the number of
radioactive nuclei n, indirectly proportional to the
half-life T1/2 and will decrease with time according to the
exponential law n(t) = no.e-l.t = no.e-(ln2/T1/2).t
.
If we have a radionuclide with nucleon
number N, then the mass unit of 1 gram contains
approximately n @ 1/(N.mn) @ 6.1023/N atoms (mn is the mass of the nucleon; a binding energy that is
less than 1% can be neglected here; the constant 6.1023 is the known Avogadro
number expressing the number of atoms in one gram
molecule of the isotope). The specific
activity A1g [Bq] (mass activity)
of 1 gram of pure radionuclide with nucleon
number N and half-life T1/2
[sec.] is thus given by the relation
A
1g @ (6.10 23 /N).ln2/T 1/2 @ 4.16.10 23 / (N.T 1/2) .
The radionuclide is thus the "stronger radioactive",
the shorter its half-life and the smaller its nucleon number. For
some known long-term radionuclides there is a specific activity :
| Radionuclide | 3 H | 14 C | 60 Co | 137 Cs | 226 Ra | 235 U | 238 U |
| T 1/2 [years] | 12.3 | 5730 | 5.27 | 30 | 1602 | 7,1.10 8 | 4,5.10 9 |
| A 1g [Bq] | 3.6.10 14 | 165 GBq | 4.2.10 13 | 3.2.10 12 | 36.6 GBq | 79 kBq | 12 kBq |
The total activity A[Bq]
of the mass M[g]
of pure radionuclide with nucleon
number N and half-life T1/2
[sec.] is then determined by the
relation
A
= M.A1g @ 4,16.10 23 .M / (N.T 1/2 ) .
In practice, pure carrier-free radionuclides are usually not
present *), on the contrary, in most preparations they are very dilute,
their concentration is small; the specific activity usually does
not exceed a few GBq/gram, in some samples it does not even reach
the level of 1Bq/g.
*) After all, pure carrier-free radionuclides with high activity
would often melt or evaporate with the heat released
- see "Thermal effects of radioactivity" below. E.g. 1
g of pure radioiodine 131I (T1/2 = 8
days) would have a colossal activity of 4,600,000 GBq, its energy
output would be almost 750 W - by the heat released would
evaporate immediately of it! Exceptions are radionuclides with a long
half-life, which may well exist concentrated in larger
quantities of many grams and kilograms - eg radium or uranium
(for uranium 235 and plutonium, however, beware of critical mass
and ignition of the chain fission reaction! - see the section
"Nuclear fission" in §1.3
"Nuclear reactions").
Different
decay rates and half-lives of radioactive decays
Each radionuclide has its very definite,
specific and characteristic half-life *). The
shorter the half-life T1/2, the faster the radionuclide transforms (decays).
However, the half-life values are very different
for different radionuclides. We know radionuclides with unusually
long half-lives of the order of billions of years (these include
some natural radionuclides such as 40K with T1/2 =
1.3.109 years or 238U with a half-life of 4.5.109 years), hundreds of
thousands of years, thousands of years (eg 14C radiocarbon with T1/2= 5730 years), hundreds and tens of years (eg 137Cs with a half-life
of 30 years), medium-long half-lives of years and tens or units
of days (eg 57Co with T1/2 =
270 days, radioiodine 131I with a half-life of 8 days), several hours or minutes
(eg 99mTc
with T1/2 = 6 hours, 18F with T1/2 = 110min., 15O with a half-life of
2.2 minutes), even very "short-term" radionuclides with
half-lives of the order of seconds or fractions of seconds (eg 81mKr with T1/2 = 13sec., heavy transurans
Z> 111 with half-lives sometimes of the order of
milliseconds).
*) Rarely, however, are radionuclides that
have two different half- lives in the same
nucleus. This is because some nuclei can decay by two
different mechanisms, each with a different probability
and thus a different half-life. An example is the core 80Br35, which with a
half-life of 17.6 min. disintegrates b- decay to 80Kr36, and on the other hand with a half-life of 4.38 hours
by b+ decay and
electron capture transforms into a nucleus 80Se34. Another interesting example from the field of
transurans is Californium 252Cf98, which, on the one hand, decays with a half-life of
2.65 years a-decays to 250Bk (and then to the whole decay series), on the other
hand, with a half-life of 85 years, it disintegrates by
spontaneous fission into cores from the center of Mendeleev's
table; while neutrons are emitted.
These huge differences in half-lives
are due to the different probabilities with
which, according to quantum laws, the relevant processes take
place inside the nuclei, which will eventually result in
radioactive transformation. A number of factors in its
construction determine whether a nucleus is stable or will
disintegrate and at what rate (probability). Above all, these are
configurations of energy levels of protons and
neutrons in the field of nuclear forces, related to the relative number of protons and neutrons
and the total number of nucleons. The higher the energy levels in
the field of nuclear forces occupy protons and neutrons (an important circumstance here is that the proton and
neutron levels occupy independently), the
greater the likelihood of converting the nucleus to a lower
energy configuration. Therefore, nuclei with a large excess
of protons or neutrons, as well as nuclei with an
enormously high total number of nucleons, usually decay
considerably rapidly, ie with a short half-life, by radioactive
decay by the mechanisms discussed in the next passages of this
chapter.
Enormous differences in the
half-lives of radioactive nuclei raise the question of the limit
values of half-lives that are still of physical
significance, ie the question of what is the shortest and
longest half-life values can in principle occur :
Radioactive transformation takes place in
atomic nuclei, which are hidden deep inside atoms, whose electron
shell effectively shields all chemical,
mechanical and thermal influences, as well as the action of
external fields. Radioactive decay is therefore independent
of external normal physical and chemical influences and
conditions (pressure, temperature, state, chemical form, external
field, etc.) - there is no way to speed it up or slow it down.
However, this statement is not entirely absolute. Below in the
section "Independence of radioactive decay on external
conditions", radiation or
chemical influences, that may to some extent change the
course of radioactive transformations in nuclei, will be
discussed.
Long-term stable rates or half-lives of
some natural radionuclides are used to determine the ages
of objects of organic origin and mineral rocks - it is described in more detail in §1.4, section "Radioisotope (radiometric) dating".
Mixtures of radionuclides, decay
series, radioactive equilibrium
The (mono-) exponential law of decay derived from above applies
only to a radioactive substance consisting of radioactive nuclei
of the same species with a precise half-life
value, whose daughter nuclei are already stable and do not decay
further. However, if the preparation contains two
or more species of radionuclides with different
half- lives, the dependence of immediate activity on
time will no longer be a (mono) exponential function, but will be
a combination of two or more exponential dependences with
different half-lives corresponding to represented radionuclides -
it will be biexponential or multiexponential
dependence in general - Fig.2.1.B (a).
Specific situation in the time regularity of decay
occurs when it is a radionuclide X, whose daughter
nuclei are not stable, but continue to decay - it is
generally a so-called decay series of
"generically" related radionuclides - Fig.2.1.B (b,
c). Disintegration dynamics here will depend on
the ratio of half-lives of the parent radionuclide primary X and
subsidiaries, further decaying radionuclides Y.
If the half-life of the primary radionuclide is significantly
longer than the half-lives of the daughter radionuclides, the
rate of decay will be established at this longest (control)
half-life - the decay series will be in radioactive
equilibrium, at which the ratio of the activity
of the parent and daughter radionuclides will be kept constant.
By radioactive equilibrium we generally
mean a situation where - despite radioactive decay - the relative
number of nuclei of a certain radionuclide remains constant
because these radioactive nuclei are constantly supplemented
by some production mechanism, while the production rate of the
daughter radionuclide is equal to its decay rate. This production
mechanism can be :
l Nuclear reactions
This is the case in nature with cosmogenic radionuclides,
which are constantly produced in the atmosphere by cosmic
radiation (§1.6 "Ionizing radiation", part "Cosmic
radiation", Fig.1.6.7). Also in the
artificial production of radionuclides by a constant
flow of neutrons in the reactor or protons in a cyclotron, a
radioactive balance can be achieved between the production
nuclear reaction and the decay of the resulting radionuclide
(§1.4 "Radionuclides", section "Production
of artificial radionuclides").
l Radioactive decay of the parent
radionuclide having a longer half-life to daughter radionuclide
with a shorter half-life.
In terms of time can recognize two types of radioactive
equilibrium of "generationally connected" radionuclides
X and Y (as well as situation when the balance does not occur) :
¨ Long time
equilibrium ,
also called secular equilibrium (lat.
saecularis = centennial, permanent, long-lasting, secular).
The already mentioned equilibrium concentration of cosmogenic
radionuclides has this character. In the decay radioactive
series, it occurs when the default parent radionuclide X has
a much longer half-life than the daughter radionuclide Y;
then, in terms of the time horizon of the half-life of the
daughter radionuclide, we can consider its activity to be
constant - Fig.2.1.B (c). In the long run, even
the secular equilibrium is only approximate; overall, in fact,
the "equilibrium" amount of the daughter radionuclide
slowly decreases with the half-life of the parent radionuclide.
Secular equilibrium occurs, for example, in the decay series of
primary long-term radionuclides 232Th, 235,238U (§1.4 "Radionuclides").
¨ Temporary equilibrium (passing, fleeting, unsteady),
also called transient equilibrium (lat.
transitivus = transient, short-lived) is established
when the half-life of the parent radionuclide X is
only slightly longer than the daughter Y - Fig.2.1.B
(b).
¨ No
equilibrium
In a situation where the parent radionuclide X
has a shorter half-life than the daughter Y, no
radioactive equilibrium can be established at any time.
If the parent radionuclide X was at the initial time t = 0 is prepared without the
content of daughter radionuclides, then when its decay the amount
of daughter radionuclides Y first increases, goes through a maximum and then
decreases with the half-life of daughter Y.
Time dynamics of
radioactive equilibrium
In the simplest case of subsequent conversion of two
"generationally bound" radionuclides X(lX)®Y(lY)®Z(stable),
the rate of change of nuclei of parent radionuclide X
and daughter radionuclide Y will be given by a system of two differential
equations: dNX/dt = - lX.NX , dNY/dt = lX.NX - lY.NY . By integrating it
[under boundary conditions at t=0: NX=NX(0), NY=NY(0)] we obtain a biexponential time law
for the daughter radionuclide Y :
NY(t)
= NX(0).[lX/(lY-lX)] . (e-lX.t - e-lY.t ) + NY(0).e-lY.t ;
for the parent radionuclide X, of course, the classical monoexponential law NX(t) = NX(0) .
e-lX.t remains.
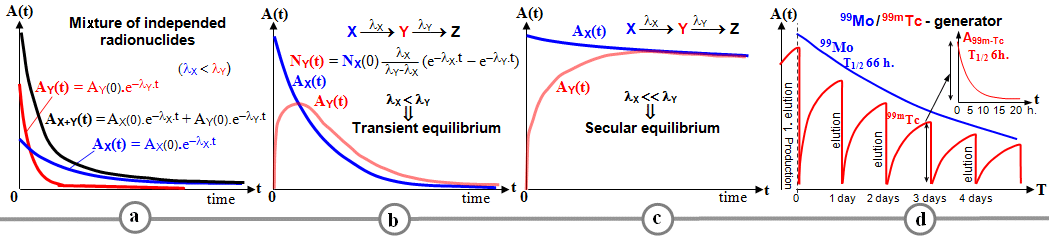
Fig.2.1.B. Time dynamics of radioactivity in a mixture of two
radionuclides.
a) In a mixture of two independent radionuclides
X , Y, each of them is
converted according to its own half-life and the total activity
of the preparation is given by the sum of both exponential
functions.
b), c) In the decay series of two
generically related radionuclides X --> Y, the decay dynamics
depends on the ratio of the half-lives of the primary parent
radionuclide X and the daughter, further decaying radionuclide Y; depending on this
relation lX and lY a transient or secular equilibrium of both
radionuclides can then be established.
d) Specific radioactive dynamics of the
radionuclide molybdenum-technetium generator during repeated
elutions of the daughter 99mTc, emerging from the conversion of the parent 99Mo.
If lX < lY, then after a sufficiently long time is exponential
element e-lY.t
negligibly small compared with e-lX.t. The law of time for the daughter
radionuclide is then simplified to: NY(t) = NX(0).[lX/(lY-lX)].e-lX.t = NX(t).lX/(lY-lX) - after a
sufficiently long time, the equilibrium ratio
between the daughter and the parent radionuclide is established, transient
equilibrium (Fig. b), at which the
activity of the daughter radionuclide decreases with the
half-life of the parent radionuclide. The activity of the
daughter radionuclide AY = lY.NY = NX(t).lY/(lY-lX) is maintained
slightly higher than the instantaneous activity of the
parent radionuclide (at lX < lY the ratio lX /(lY - lX) is greater than 1), in the ratio AY/AX = lY/(lY-lX).
If lX << lY, then for short times compared to the half-life of the
radionuclide X is lX .t << 1 and the
first exponential term e-l
X .t
can be approximated by 1; after several half-lives of the daughter radionuclide Y (when
the second exponential term is close to 0) an equilibrium
amount of this radionuclide is then established NY = (lY/lX).NX - secular
equilibrium (Fig. c). The
equilibrium activity AY = lY.NY = lX.NX = AX will be equal to the activity
of the parent radionuclide X.
In the long run, however, even this "equilibrium"
amount decreases with the half-life of the parent radionuclide X.
These
regularities will be illustrated below in the case of the
so-called radionuclide generator - part "Radioactivity
gamma", passage "Pure gamma-radionuclides; technetium 99m Tc; radionuclide generators". Specific types of generators for obtaining
short-term radionuclides are described in §1.4, section "Radionuclide
generators".
Note: The
relationships given in this paragraph apply exactly provided that
all disintegrations of the X ® Y ® Z chain take place in 100% of cases. If this is not the
case, appropriate correction factors should be
introduced and the resulting activity of the daughter isotopes
will be lower.. This is the case with decay
chains (b) -> (metastable g), if a certain percentage of decays do not take place
at the excited metastable level, but at the ground state of the
daughter core (an example is the mentioned Mo-Tc generator).
For a decay series of a larger number of generically
coupled radionuclides, their decay time dynamics is given by a
system of a corresponding larger number of linear differential
equations. E.g. for series 3 radionuclides X(lX)®Y(lY)®Z(lZ)®W(stable)
it will be a system of three equations: dNX/dt = - lX.NX, dNY/dt = lX.NX - lY.NY, dNZ/dt = lX.NX - lY.NY - lZ.NZ . Under the initial conditions NX(0)=NXo, NY(0)=NZ(0)=0 we get the usual monoexponential decay law for the
parent radionuclide X, for Y the above biexponential law, for the third member of
the series Z it will be a combination of 3 exponential terms :
NZ(t)
= NXo.lX.lY . {e-lX.t/[(lY-lX)(lZ-lX)] - e-lY.t/[(lY-lX)(lZ-lY)] - e-lZ.t/[(lZ-lX)(lY-lZ)]} .
For more complex decay series, additional exponential terms with
corresponding exponents and coefficients are present.
Particularly complex decay series with many
secondary radionuclides occur in heavy uranium
and transuranic nuclei; these decay series will
be discussed in §1.4 "Radionuclides", Fig.1.4.1.
Some together phenomena accompanying
radioactivity
Backscattering of nuclei
Due to the emission of particles and quants of radioactive
radiation, due to the law of conservation of momentum
- action and reaction - backs bounce of
the daughter nucleus occurs, which takes over a certain small
part of the kinetic energy of decay. This phenomenon of "hot"
daughter nuclei is essentially reflected at each
radioactive decay, but with most of the radioactivity alpha,
as a particles
capable have high weight and are usually emitted with high
kinetic energy - with high momentum. For conventional
alpha radionuclides with nucleon number N @
220-240 that emit a particles capable
of energy of about 4-7 MeV, the kinetic energy of the reflected
daughter nuclei is around 100keV. The nuclei reflected in this
way brake very quickly in the material on a path of approx. 500
nm, along which they cause ionization. The energy of chemical
bonding of atoms in compounds is only about 50-100 eV.
The back reflection of nuclei can thus
lead to the release of atoms from the crystal
lattice of minerals, or from chemical bonding in molecules *).
The kinetic energy of the reflected nuclei will also have ionizing
and thermal effects (see
below). In common nuclear applications,
core rebound is usually not physically manifested. However, for
some accurate spectrometric measurements, it can have a
significant effect, along with the thermal movements of atoms.
Examples are Mössbauer spectrometry (see §1.6, section "Interaction of gamma and X-rays", passage "Mössbauer
effect" and §3.4, section "Mössbauer spectroscopy"), or measuring the exact
shape of spectrum b to determine the rest mass of neutrinos (see section below "Neutrinos",
passage "Resting mass of
neutrinos").
However, it can manifest itself significantly chemically
:
*) (radio) Chemical effects of reflection
When a radioactive atom is bound in a molecule of a compound, the
reflection of nuclei can have a significant chemical
effect. The kinetic energy of the reflection of nuclei,
and thus of the respective atoms, is usually significantly higher
than their chemical binding energy in the molecules of the
compounds. Therefore, after radioactive transformation, the atom
of the daughter nuclide is usually "ejected" - dissociated
- from the chemical bond in the original molecule. This may have
an adverse effect on the reduced radiochemical stability
of radioactive preparations, especially radiopharmaceuticals (see §1.4, section "" In vivo
generators "in nuclear medicine" or §3.6, part "Radioisotope therapy", passage "Physical and
biological factors"). If
alpha-transformation occurs in the organism, especially inside
the cell, the ionizing effects of reflected nuclei may contribute
to radiobiological effects (§3.6,
passage" Beta and alpha radionuclides for
therapy ") .
Thermal
effects of radioactivity
A logical but little-known phenomenon in common applications
accompanies all types of radioactivity: it is heat.
During radioactive transformation, particles (quantum) of
radiation fly out of the nucleus at high speed. According to the
law of action and reaction, this will "throw" the
nucleus (and in fact the whole atom) in the opposite direction -
it will be given the kinetic energy of motion. Similarly, in the
absorption of radiation, energy is transferred to the substance
at the level of the kinetic energy of the atoms. And the kinetic
energy of the motion of the atoms of matter is nothing but heat.
With each further and further radioactive transformation, the
atoms of the substance will thus oscillate to greater and greater
kinetic energy - the radioactive substance will heat up.
At low activities used mostly in practice, this phenomenon is
unobservably weak, but strong emitters "warm up" quite
clearly (eg in radiators for radiotherapy); the strongest emitters must even be cooled to prevent
thermal damage (or even melting or
evaporation) - this is especially the case
for spent fuel cells from fission nuclear reactors (§.1.3, section "Nuclear reactors", section "Problem of cooling of
nuclear reactors").
Note: The energy use of nuclear reactors
in power plants is also based on similar thermal effects.
The heat released by the radioactive decay of natural
radionuclides, uranium 235,238U, thorium 232Th and potassium 40K, is probably an important source of geothermal
energy, heating the Earth's interior - see §1.4 "Radionuclides", part
"Natural radionuclides", passage "Geologic significance of natural
radioactivity".
Electrical
effects of radioactivity
Charged particles a or b (see below) carry away the electric charges from the
radioactive emitter and according to the law of
conservation of electric charge in the emitter
substance, then predominated the opposite charge than the sign of
the charge emitted particles. The actual radioactive emitter a or b is therefore
gradually electrically charged. At low flows
radiation, or if the emitter is least partially conductivelly
electrically connected to the earth, this effect is negligible.
However, electrically insulated radiator with intense flux of
radiation b or a will gradually be positively or negatively charged to a
high electrical potential of up to hundreds of kV (depending on
the electrical capacity of the radiator body). This phenomenon is
fully manifested only in a vacuum, because in the air the
radiation causes ionization, the environment becomes partially
electrically conductive and the charge is continuously removed
from the radiator body.
The electrical and thermal effects of radioactivity are
used in small electrical sources - see §1.3,
section "Radionuclide volta cells ("atomic" batteries )".
Independence of radioactive decay
on external conditions
Radioactive decay is a spontaneous process - it
is caused by the internal mechanisms of the atomic nucleus. It is
independent of external normal physical and
chemical influences and conditions (pressure, temperature, state,
chemical form, external field, etc.), there is nothing to
accelerate or slow down this disintegration. This is because the
nucleus is hidden deep inside the atom, whose electron
shell effectively shields all chemical,
mechanical and thermal influences, as well as the action of
external fields. However, this proven statement is not
entirely absolute.
Above all, it may not apply under extreme conditions. If
we heat the radioactive substance to a very high
temperature tens or hundreds of millions of degrees, the
nuclei in an already completely ionized plasma will acquire such
a high kinetic energy, that they will overcome the Coulomb
repulsive force during collisions and nuclear reactions
will occur, changing the speed and nature of
radioactive decay (see §1.3 "Nuclear reactions"). Extremely strong
electromagnetic or gravitational fields would have a similar
effect (not yet available here on Earth,
but they probably occur in universe around compact
gravitationally collapsed objects, see eg Chapter 4 "Black
Holes" of the book "Gravity,
Black Holes and Space-Time Physics"). The Electron capture can be
affected (slowed down or completely stopped) by heating
the substance to about 104 degrees, when the complete ionization
of atoms, including the L and K shells, from which electron
capture occurs; in addition, the rate of electron capture can be
very slightly affected by chemical bonds (see "Specifics
of electron capture" below). The rate of decay by electron capture can also be
affected by the action of external pressure on
radioactive atoms (higher pressure leads to
an increase in electron density and thus to an increase in the
probability of electron capture by the nucleus, but only at very
high pressures). Complete ionization of
atoms can significantly affect the half-life of beta - decay
of some (isolated) radionuclides by the effect of so - called b-decay into bound electronic states. Gamma-radioactivity can be affected by the external
environment through the effect of internal conversion of radiation g , which depends on the electronic configuration of the
atomic shell. For fully ionized atoms, the internal conversion
coefficient would become zero.
The structure of nuclei, and thus
radioactive decay, can be altered by irradiation with
neutrons, fast protons or other particles *) causing nuclear
reactions. Furthermore, the chemical bonding of
the radionuclide may to some extent affect the electron capture
and the process of internal conversion of gamma radiation (see
below).
*) Even neutrinos can alter the course of
beta radioactivity in nuclei: the capture of an (electron)
neutrino induces the transmutation of a neutron to a proton,
which is beta- radioactivity, analogously the
interaction of an antineutrinos with a proton induces a beta+
radioactive conversion. In practice, however, this phenomenon is
not observed due to the very small effective cross section of the
neutrino interaction (it could only be applied in a huge flow of
neutrinos during a supernova
explosion ).
But these are all special or
"exotic" situations. However, in almost all situations
occurring in practice in the application of
nuclear and radiation methods (Chapter 3), we can consider the course and half-life of radioactive
decay to be completely independent of external conditions.
What
happens to the atom during the radioactive transformation of the
nucleus? Chemical properties of radioactive substances
Nuclei are in most circumstances part of atoms, for the structure
of which they play a decisive role (the
nucleus is the "boss" of the atom).
The chemical properties of radioactive elements are, until the
moment of radioactive decay, completely identical
to the properties of their non-radioactive isotopes *). Thus,
radioactive atoms (before their radioactive transformation) can
enter the same compounds as the same non-radioactive atoms. This
is used in a number of radiochemical technologies, including
medical applications of radionuclides (see §3.5 "Radioisotope tracking methods", §3.6 "Radiotherapy",
section "Radioisotope
therapy" and §4.8 "Radionuclides and
radiopharmaceuticals for scintigraphy").
*) Slight differences in kinetics
(rate) during the chemical reactions caused by the different
weight of isotope atoms (with different number of neutrons
in the nucleus) are chemically usually insignificant. However,
they can be used for isotope separation.
However,
during the radioactive transformation of the nucleus, changes in
the atomic shell necessarily also occur *). When
the radioactivity a the charge of the nucleus is reduced by 2 protons, which
resultis in the release of two electrons from an atom envelope.
For b + the charge of
the nucleus decreases by one proton, so that one electron is
released from the shell. During electron capture, the inner
electron is absorbed by the nucleus, followed by a series of
deexcitation jumps of electrons in the envelope, accompanied by
the emission of characteristic X-rays and other soft radiation
photons. Conversely, during the conversion of b-, the charge of the nucleus increases by one proton, so
that the resulting daughter atom takes up one electron from the
surroundings. During this reconfiguration of the electron
shell, following immediately after the radioactive
transformation of the nucleus, the energy levels of the electrons
are also shifted from the original levels of the parent atom to
the new levels of the daughter atom, when emitting of soft
electromagnetic radiation. The reconfiguration of the electron
shell results in a change in the number of valence electrons and
thus change in the chemical properties of the
atom (its oxidation number). If the original parent atom was part
of the compound, after the radioactive transformation, this
chemical bond is usually broken and the daughter atom is
eliminated from the compound - there will be dissociation,
or establishes a new chemical bond.
*) With the exception of radioactivity g, in which the
charge of the nucleus does not change, so there is no
reconfiguration in the electron shell. However, there may be a
so-called internal conversion of g radiation (see the
"Gamma radioactivity" section below), which is
accompanied by the emission and skipping of electrons in the
envelope.
The newly formed
atoms just after the radioactive transformation of the original
parent nucleus are called nascent atoms (lat.nascendi = birth).
They have an initially deformed and excited
electron shell, they have a non-zero electric charge - they are
in the state of positive or negative ion, due to
the above-mentioned back reflection of nuclei they have high
kinetic energy ("hot atoms"). This leads to high
chemical reactivity of nascent atoms after nuclear
transformation.
Types of
radioactivity
Radioactivity is divided and classified not according to the
parent and daughter nuclei, but according to the type of
radiation emitted (particle C
in Fig.1.2.1). These types of radioactivity are indicated by the
first three letters of the Greek alphabet - a, b, g. This terminology has a random, purely historical
origin. Radioactive radiation was at that time labeled
in the order in which it was discovered, without knowing its true
physical nature. The only thing known at the time was that alpha
radiation in the electric field deflects toward the negative
electrode, beta radiation to the positive electrode, and gamma
radiation is not bent by the electric or magnetic field. If at
the time the "school-maniac pedants" they waited only a
few years with the establishment of mandatory terminology
"alpha-beta-gamma" in texbooks, now the radioactivity a
would be called helium, b- electron, b+ positron and g photon
radioactivity. These would be far more apt
names, expressing the true physical nature ...
Alpha
radioactivity
The basic scheme of radioactivity a is shown in Fig.1.2.2. When
this transformation is emitted nuclear particles a
which is a helium nucleus 4He2 - thus comprises two protons of p+ and 2 neutrons no :
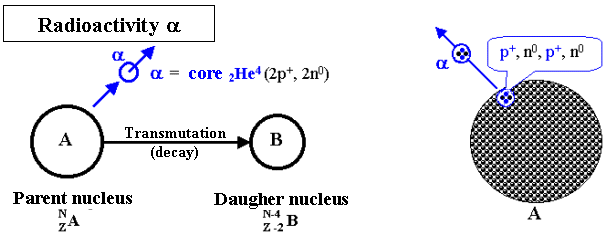
Fig.1.2.2. Basic scheme of radioactivity a .
From the parent nucleus with N nucleons
and Z protons, particles a carries out 2protons and
2neutrons, so the resulting daughter nucleus will have N-4
nucleons and Z-2 protons - in Mendeleev's periodic table of
elements will be shifted 2 places to the left
towards simpler elements. In order to radioactivity a may occur, must be
satisfied by weight ~ energy condition m(Z-2,
N-4) + m(a) < m(Z, N), where m(Z, N) is the mass of the nucleus
with atomic number Z and the nucleon number N, m(a) º m(2,4) is the
rest mass of the particle a.
For too large nuclei, the strong nuclear
interaction, due to its short range, is not enough to bind the
nucleus strong enough against repulsive electrical forces between
protons. Figuratively speaking, by alpha radioactivity
heavy nuclei "get rid of excess nucleons" to
make them lighter and more stable. These aspects
are discussed in more detail below in the section "Stability and instability of
atomic nuclei".
Example of alpha
radioactivity may be a remodeling of radium 226Ra88 ® 222R86 + 4He2 (sa) at radon 222. Daughter nuclei after a -decay is often
also radioactive (a or b), usually forming whole radioactive series
(see §1.4 "Radionuclides", passage "Decay
series"), until they reach a
stable configuration. In addition, after the a-decay the product
nucleus mostly in the excited state, so their dexcitation
accompanied by gamma rays (see "Radioactivity
gamma").
The spectrum of radiation a
Particles a carries the energy difference between the parent and
daughter nuclei DE = [m(Z,N)-m(Z-2,N-4)].c2, which is constant - all particles a during the transformations of a given type of nucleus,
they have the same kinetic energies Ea =
[m(Z,N)-m(Z-2,N-4)-m(a)].c2 - radiation spectrum a is
line, discrete. By spectrometric measurement of a number
of a -radionuklides
it was found that the shorter the half-life of a given
radionuclide, the higher the energy of the emitted radiation a. This dependence
between the half-life T1/2 , resp. the decay constant l = (ln2)/T1/2, and the energy Ea the
radiation a gives the approximate Geiger Nutall relationship
: ln l =
A . ln Ea + B,
where A and B are constants. These empirical
dependence corresponds well with the mechanism of disintegration a the tunnel phenomenon
of emission of particles a, mentioned below. For most a -radionuklides the energy
emitted alpha particles in the range of about 4 - 8 MeV, reaching a
rate of about 2-5% of the speed of light. The lowest
alpha energy 1,830MeV is observed in the long-term 144Nd (half-life 2.3x1015 years), the highest alpha
energy 11,650MeV was measured at 212mPo (half-life 45sec.).
Kinetic energy Ea
the emitted alpha particles are a
small percentage lower than the total decay
energy Q, because when the a-
particle is emitted, the nucleus is reflected
with low kinetic energy in the opposite direction due to the law
of conservation of momentum. For a parent nucleus with mass
number N , the resulting alpha-particle energy will be
related to the decay energy by Ea @ Q. (N-4) / N.
The mechanism of disintegration a
In the right part of Fig.1.2.2 is intellectually shows the
mechanism of radiate particles a. We can simply imagine that
a heavy nucleus with more than 210 nucleons is already so large
that the overall attractive field of strong interactions, due to
its short range, no longer acts strong enough in the peripheral
regions of the nucleus. It is not enough to sufficiently balance
the mutual repulsion of protons, which has a long range
(decreases with the square of the distance). This is used by some
nucleons, which "cluster" so that 2 protons and 2
neutrons form a local stronger bound "cell", which then
the so-called tunnel effect (described in §1.1, passage
"Quantum tunnel
phenomenon") overcomes
the potential barrier of binding nuclear energy and flies out as
particles a *). If a positively charged alpha particle (bound in the
nucleus by an attractive strong short-range interaction) crosses
the potential barrier, it is expelled from the nucleus by the
repulsive electrostatic force in the region beyond the reach of
nuclear forces, or rather ejected at high speed.
By analyzing the permeability of this potential barrier
through the tunnel effect, the mentioned Geiger-Nutall
dependence between energy and half-life can be derived .
*) The alpha particle in the heavy nucleus is
bound by a strong nuclear interaction with a potential wall
height of about 25 MeV. However, the energy of the particles
during decay is in the range of only about 4-9 MeV, depending on
the particular radionuclide, so that the particle itself does not
have enough energy to overcome this barrier. According to
classical physics, emission could not occur. According to quantum
physics, however, there is a small, but non-zero, probability
that a particle can pass through a higher potential dam (§1.1,
passage "Quantum tunneling").
Furthermore, the question may arise, why heavy nuclei are emitted
just particles aº 4 He 2 and perhaps no
individual protons, neutrons, deuterons, or heavier than helium
nuclei (e.g. carbon)? The cause is high binding energy particles
a (28.3MeV).
To escape from the nuclear field, a particle needs a certain
kinetic energy. Individual nucleons usually do not have
sufficient energy available, while the emission of a strongly
bound particle a (whose mass is less than the mass of the nucleons of
which it is composed) is more energetically advantageous.
However, the emission of individual nucleons occurs in strongly
excited nuclei, in some heavy nuclei radioactivity higher than
alpha was also demonstrated - with the emission of 14-C even in
heavier nuclear clusters (see below "Exotic types of radioactivity").
For the assessment of the binding energies of nucleons
in different nuclei, we recommend Fig.1.3.3 in §1.3., Section
"Nuclear energy".
Despite the fact that the letter a is
the first in the Greek alphabet, alpha radioactivity is the least
"important" of all types of
radioactivity. This is for two reasons :
1. Radioactivity a occurs only in the heaviest
nuclei from the very end of the Mendeleev table (N> 210) , mainly in the area
of uranium and transurans (light nuclei
simply "do not have the power" to radiate such a heavy
particle as the nucleus helium a).
Typical alpha emitters are, for example, radium 226Ra, plutonium 239Pu, americium 241Am.
It is rare in some moderate radionuclides
(see eg terbium 149Tb ). The lightest element in which alpha radioactivity
has been recorded is tellurium 107-109Te52. In connection with
alpha radioactivity, beryllium is sometimes
referred - its "exotic" isotope 8Be4 *). With an extremely short half-life of 6.7.10-17 s, it decays into
two helium nuclei (particles a): 8Be4®4He2+4He2. However, this is not
about alpha radioactivity in the true sense of
the word, but rather about fission highly
unstable core into two equal parts.
*) Despite its high instability, beryllium 8Be
is important as an intermediate in the thermonuclear synthesis of
helium to carbon inside stars (see §4.1 "Gravity and
evolution of stars", section
"Evolution of stars", passage "Helium combustion"
of the book "Gravity, black holes and the physics of
spacetime").
2. Radiation a, thanks to its double
positive charge, very effectively pulls electrons out of the
shell of atoms when it enters a substance, thus rapidly losing
energy and braking at about 0.1 mm in substances
of water or tissue density (however,
internally applied alpha-radionuclides are effective in radioisotope
therapy - §3.6, section "Radioisotope therapy"). Alpha-emitters are used
only sporadically in some detection instruments (e.g. gas density detectors, smoke detectors) or neutron generators (if we mix a-radiator with the target of a suitable material such as
beryllium, particles a penetrate into the nuclei of the target material and by
reaction (a,n) the neutrons are emitted from here), which are used in the laboratory, e.g. for neutron
activation analysis.
Note: In terms of natural
radioactivity, however, a-radioactivity is important. Most natural
radionuclides on earth (except e.g. potassium 40K) is formed of heavy
elements - thorium 232Th and uranium 238, 235U, which is a
-radioactive.
During the gradual decay of these radionuclides in decay series (§1.4, passage "Decay series"), many more nuclei are
formed, while the particles a
themselves after their braking add two
electrons, thus creating neutral atoms of gaseous helium 4He2. It is estimated that
about 3,000 tons of helium are produced in the interior of the
Earth in this way per year. It is assumed that practically all
helium occurring on Earth was formed during the radioactive a decay of natural
radionuclides thorium and uranium (the
story of helium is briefly mentioned in the conclusion of §1.1
"Atoms and atomic nuclei", part "Nucleogenesis"). Most of the helium formed
in this way remains absorbed in the crystal lattice inside the
rocks, part of which is released in the gas phase into the
cavities in the earth's crust, from where it is mined with
natural gas.
Radioactivity beta
On the contrary, the most common and most important type of
radioactivity is radioactivity b. There are three types of
radioactivity b, which we will gradually discuss :
Radioactivity b -
The basic scheme of radioactivity b- is in Fig.1.2.3. In this nuclear transformation, the particle
b- is emitted from the parent nucleus at high speed, which
is nothing more than an ordinary electron e- - the same as in the atomic shell.
Note: The names "radiation b",
"particles b" come from a time when they were not yet known to
be electrons.

Fig.1.2.3. Beta radioactivity.
Left: Basic scheme of radioactivity b-. Middle:
Continuous energy spectrum of radiation b. Right: Enlarged
detail of the end of the spectrum for zero and non-zero rest
masses of neutrinos.
If we remember the composition of the nucleus
(§1.1), we immediately see an obvious paradox: how can
(negative) electrons fly out of (positive) nuclei when there are
only positive protons and uncharged neutrons, but no electrons?
Note: For some
time, physicists believed that electrons b- came from the
atomic shell. However, it was found that in fully ionized
beta-radioactive atoms depleted of electron shells, electrons b-
continue to radiate unchanged. Thus, electrons b- really
fly out of the atomic nucleus.
When b- radioactivity
was found to occur in nuclei with an excess of neutrons,
an explanation for the formation of b- radiation was
found.: One of the "redundant" neutrons
"wants" to become a rarer proton *) - it will do so by
transforming: no ® p+ + e- (+ n) ( let's not notice the particle n yet).
The proton p+, as a legitimate nucleon, remains bound by a strong
interaction in the nucleus, while the electron e- flies
out at high speed as radiation b- (carries away
the energy difference between nuclei A and B).
*) That "neutron wants to become a proton" is, of
course, just a light allegorical expression; the actual
disintegration mechanism b
will be briefly discussed below in connection with
weak nuclear interactions , Fig.1.2.5.
However, a brief simplified explanation can be discussed here :
Cause of radioactivity
b- ; stability and instability
of the neutron in the nucleus
The primary cause of radioactivity b-
lies in the conversion of neutrons to protons,
electrons and antineutrinos - generally in the quark
structure of nucleons, where weak interaction can
cause mutual transformations of quarks "u" and
"d", and thus transformations neutrons (see below
"Mechanism of decay b ; weak
interactions", Fig.1.2.5).
After all, if a
neutron is free, it is unstable - with a
half-life of less than 15 minutes, it decays due
to a weak interaction by the mentioned b
-dissolution no ® p+ + e- + n to proton, electron and electron
(anti)neutrino. The neutron is slightly heavier than the proton,
the difference in mass is about 2.5 times the mass of the
electron (this difference comes from the
difference in the mass of "u" and "d" quarks
and the difference in binding energy). However, the
intermediate W boson, which mediates quark conversion, is about
80-times more massive than a proton or neutron, so there is a
high potential barrier. So, despite the small energy surplus, the
neutron does not immediately decay into a proton, but it takes 13
minutes on average to tunneling through this barrier.
In light of the
described mechanism of b-
radioactivity, consisting in the decay of a neutron inside a
nucleus, and the fact of instability of a (free) neutron, a paradoxical
question may arise: How can stable nuclei containing
neutrons exist at all? Why don't all the neutrons inside them
decay into protons, electrons and neutrinos? The answer is that
neutrons and protons in the nucleus cannot be seen as free - they
are part of a higher whole, bound by a strong
interaction. The stability of this whole, the nucleus, is then
determined not so much by the stability of the isolated
particles, but by the binding energy of the
nucleons. If in a given bounded configuration a nucleus coposed
of p protons and N
neutrons has a lower total mass (~energy)
than a core composed of the p +1
protons and n -1 neutrons, not
to b --decay
occur, neutrons will be "forced" to behave as stable.
Otherwise, when a nucleus composed of p
protons and n neutrons has a higher
total energy ~ mass than a
nucleus of p+1 protons and n -1 neutrons (at least by the rest mass of
the electron, ie by 511keV), a situation arises where b- decay may
occur.
Sometimes we can meet with the following argument :
If a neutron is strongly interacted in the nucleus
together with protons, there is a so-called parity
neutron-proton transformation: there is a continuous
change of n ® p ® n, etc., mediated by the exchange of virtual p- mesons (which
previously considered to mediate strong interactions between
nucleons). The neutron thus bond in the nucleus, before it
"manages" disintegrate by b -decay, changes (mutual
exchange of p-meson with the closest proton) into a proton, and the
newly born neutron "runs the decay time again from 0",
again transforms into a proton etc. As a result, the short
half-life of the neutron (13 sec.) by mutual conversion with
protons is constantly "renewed" - neutron is
stable in the core. Only when there is a
"surplus" of neutrons in the nucleus, does there arise
a certain probability that one of the neutrons will not
"find" a suitable partner for meson exchange in time
and will transfom by b-decay; this is then observed as the b --
radioactivity of such a nucleus.
However, the earlier opinion of exchanging virtual pions
is now abandoned. However, this view is still present in the
scientific literature and in nuclear physics textbooks...
The daughter nucleus after conversion of
beta-
During the conversion of b- the
nucleon number does not change, but since one neutron has changed
to a proton, the proton number increases by 1 -
the daughter nucleus shifts by one place to the right
in Mendeleev's periodic table. This remarkable fact that b- decay
produces a "more complex" nucleus than the original,
has played a crucial role in the cosmic nucleosynthesis of
elements heavier than iron inside stars and especially during
supernova explosions (see "Cosmic
Alchemy - We Are Descendants of Stars!"
§1.1, §4.1 "Gravity and evolution of stars"
of the book "Gravity, Black Holes and the Physics of
Spacetime", or the syllabus "Cosmic Alchemy"). The heavy elements were
created precisely due to the shift rule "to right"
in beta- radioactivity.
Typical example of radioactivity beta is
the b-conversion
of tritium 3H1 ® 3He2 + e- + n' to helium 3, or carbon 14C6 ® 14N7
+ e- + n' to nitrogen. Frequently used beta-emitters are cesium 137 Cs , cobalt 60 Co
, iodine 131 I , iridium 192 Ir and others. In most cases, however, beta electrons are
not used, but accompanying gamma radiation from the
deexcitation of excited daughter nuclei. An important exception
is biologically targeted radionuclide therapy, where
cells in the target tissue are killed by beta electrons and gamma
radiation only allows gammagraphic monitoring of the
uptake of the therapeutic radiopharmaceutical in tumor lesions
versus healthy tissues - Biologically targeted radioisotope therapy with
open beta and alpha radionuclides.
In order for radioactivity b- to occur, the mass-energy
condition must be met m(Z+1, N) + me < m(Z, N), where m(Z, N) is the mass of the nucleus
with proton number Z and nucleon number N, me is the rest mass of
the electron.
The energy balance of nuclei can be well
explained by the shell model of the atomic
nucleus structure discussed in the previous §1.1. If there is an
excess of neutrons over protons in the nucleus, neutrons will
fill slightly higher energy levels than protons.
The nucleus can then go into a lower energy state by converting
the neutron by b- decay
to a proton, which goes to a free lower energy
proton level.
In terms of the mass of quarks
"u" and "d", the stability and instability is
discussed in §1.3, passage "Stability and instability of quarks, hadrons,
nucleons".
Violation
of parity conservation and asymmetry of the angular distribution
of electrons b
For completeness, we mention one subtle property of radioactivity
b -
violation of the law of conservation of quantum parity
number (parity is defined in §1.5 "Elementary particles and accelerators", section "Physical parameters of
particles; quantum numbers").
This property leads to an asymmetry of the
angular distribution of the flying electrons b with respect to
the direction of the momentum vector (spin) of a given
radioactive nucleus. This phenomenon was experimentally
demonstrated on 60Co cores. Relevant experiments and theoretical analysis
are discussed in §1.5, passage "CPT
symmetry of interactions".
Violation of the conservation of parity
and other symmetries have some theoretical importance in particle
physics and interactions ("CPT
symmetry of interactions")
as well as in cosmology (§5.4 "Standard cosmological model.
The Big Bang. Shaping the structure of the universe." in book "Gravity, Black Holes and Physics of
spacetime"), but is insignificant
in practice for the beta radioactivity itself. It manifests
itself only in specially prepared experiments, at very low
temperatures and strong magnetic fields. It is never occurs in
nature or in physical practice, because the nuclei of radioactive
elements are chaotically oriented and the radiation is on average
isotropic in all directions.
Double
decay b
A rare type of beta radioactivity has been reported in some
nuclei - so-called double decay b.
It consists in the simultaneous conversion of two
neutrons in the nucleus into protons, emitting two
negative electrons: 2no ® 2p+ + 2e- + 2n´ and two electron
antineutrinos. This type of decay rarely occurs in some nuclei
with an even nucleon number (eg N = 48 or N = 116), in which
there three isotopes occurs NAZ,
NBZ+1, NCZ+2, whose weights gradually decrease in a specific way
(first by a smaller, then by a larger difference than 511keV).
Overall, the mass ~ energy condition m(Z, N) > m(Z+2, N) + 2me must be met and at
the same time the situation when normal beta decay cannot take
place - either m(Z, N) < m (Z+1, N) + me
, or some mechanism of its
"disadvantage" is applied. In this case, it is possible
to directly convert nucleus A to nucleus C
: NAZ ® NCZ+2 + 2e- + 2n´
by double beta decay. Denoted by (2n2b ), or (nnbb ) - two -
neutrino double beta decay. It has been observed, for
example, in nuclei 48Ca20, 116Cd48, 130Xe54, half-lives are very long, about 1020 years. Both double b-b- decay and double b+b+ decay are possible, as well as double electron capture.
For some nuclei (such as 76Ge) the possibility of neutrino-free
double decay b is considered, in which the neutrino would not be
emitted - (0nbb). We imagine the internal mechanism in two phases. In
the first step, in the nucleus b -radioactivity, one neutron
n1 is
converted into a proton: n1 ® p1 + e1 + n, after which in
the second step the resulting neutrino is absorbed by another
neutron: n + n2 ® p2 + e2. The emitted and
absorbed neutrino is only virtual, the result is the
transformation of (Z, N) ® (Z+n, N) + e1 + e2, in which two neutrons are converted into protons (the
proton number increases by 2) and only two electrons are emitted.
The neutrino-free double beta decay would violate the law of
conservation of the lepton number (0®1+1). Experimental
demonstration and analysis of this process could help to refine
the determination of the mass of the neutrino (reduce the current
upper limit of the mass) and would show that the neutrino is a
so-called Majoran particle, ie the neutrino and the
antineutrinos are identical.
b--decay into bound electron states
Another small interest is shown in the comparison of the
radioactivity of beta- in "bare" nuclei (in fully ionized atoms) and
nuclei surrounded by electrons in atoms. In classical
beta-radioactivity, an electron is emitted from the nucleus,
leaves the atom and flies into the environment. However, at low
energies, there may be a situation where the emitted
beta-electron does not leave the atom, but remains bound
to one of the lower orbitals of the daughter atom. This cannot
happen with neutral atoms whose internal electron orbits are
already occupied. However, for fully ionized b- radioactive atoms, emitted b-electrons can be bound to
the low orbitals of the daughter atom (which are all free here). Full
ionization of the atom thus can create an additional
"channel" of beta decay to bound electron state
(bound-state b-
decay).
This phenomenon is observed in 163Dy, which is a
stable isotope under normal conditions. However, when fully
ionized (163Dy66+), it undergoes a b-
decay to a K and L shell of 163Ho with a half-life
of 47 days. Another case is 187Re, which is in neutral atomic form b-radioactivity
converts with a very long half-life of 42.109 years to 163Os. At full ionization, however, this half-life is only
33 years - the b -decay channel to a bound electron
state has reduced the half-life by a billion times!
Under normal terrestrial conditions, the influence of
beta-radioactivity by complete ionization of the substance is not
commonly encountered, but it is assumed that it can be assert in astrophysical
processes of cosmic nucleosynthesis -
see §1.1, section "Cosmic alchemy".
Radiation
spectrum b . Neutrinos
What about the energy spectrum of emited
electrons of beta radiation? Electron b should carry away the
energy difference DE = EA - EB between the parent A and daugher B core
which is DE = [m(Z, N) - m(Z+1, N)].c2. This difference is always constant,
so all electrons b should fly with the same kinetic energy Eb = [m(Z,
N) - m(Z+1, N) -me].c2 - the spectrum should be line, as indicated by
the red dashed line in Fig.1.2.3 in the middle. However, if we
measure the actual spectrum of radiation b, we get a different result:
the spectrum will be continuous *) from zero and
with EA-EB energy will end - a
thick black curve in Fig.1.2.3 in the middle. The vast majority
of electrons b therefore fly out with energy much less
than would correspond to the law of conservation of energy!
*) The continuous spectrum of radiation b was first measured in
1914 by J.Chadwick using bending in a magnetic field (the first
prototype of a magnetic spectrometer) and detection by G.-M.
tube.
After some initial doubts about the
validity of the law of conservation of energy for radioactivity b (these doubts were
initially expressed also by N.Bohr) the
following solution was proposed: in addition to the electron b, at the same time another
(not yet observed) very light and electrically neutral particle n flies out
of the nucleus, which carries away the
appropriate kinetic energy, which it "shares" with the
flying electron, in accordance with the law of conservation of
energy. The Swiss physicist W.Pauli came up with the hypothesis
of this particle in 1930. The Italian physicist Enrico Fermi (a
pioneer in the research of radioactivity b and nuclear physics in
general) likened this strange particle to a "small
neutron" (tiny and neutral) - Italian neutrino
- and this name and the designation "n" it
has remained. Neutrino remained a hypothetical particle for more
than 20 years, experimentally was demonstrated in the 50s, see
below. The physical properties of
neutrinos and the possibilities of their detection are discussed
in more detail below in the section "Neutrinos".
If the neutrino "steals" almost
all the energy of decay, the electron b is "slipped out"
from the nucleus with the low energy (case I. marked in the
spectrum in Fig.1.2.3 in the middle). Conversely, if the electron
b
manages to capture most of the energy, it will fly out with high
kinetic energy (case II. in the middle part of Fig.1.2.3). And
case III. in the middle of the spectrum it occurs when an
electron and a neutrino "share" the energy roughly
equally. In most cases, the neutrino carries about 2/3 of the
total energy and about 1/3 of the maximum energy will remain on
the electron - this corresponds to the wide peak of the
continuous spectrum of radiation b in Fig.1.2.3 in the middle.
Beta radiation therefore has a continuous
energy spectrum, it contains electrons with energies
from zero to a certain maximum energy, which is
characteristic for a given radionuclide. Typical values of the
maximum energy of most beta emitters are tens of keV to MeV units
(the lowest energy of 2.5 keV is observed
for radionuclide 187Re, the highest energy of 16.6MeV was measured at 12N).
The
shape of the radiation spectrum b
The exact shape of the curve of the radiation spectrum b follows from the
analysis of the energy distribution of the emitted electrons
within the framework of Fermi's theory of weak interaction. It
follows from this theory that the intensity N(p) of radiation b of momentum p
and energy Eb is given by the relation N(p) = (Ebmax-Eb)2.p2.F(Z,p), where Ebmax is the maximum decay energy b and the constant F
(expressing the correction for the Coulomb field of the nucleus)
includes the relevant constants including the proton number Z.
From this relation follows for the spectrum b the equation Ebmax-Eb = Ö[N(p)/p2.F(Z,p)]. If we plot
the function Ö[N(p)/p2.F(Z,p)] on the vertical axis as a function of the
energy Eb on the horizontal axis, we get a linear
dependence called the Fermi-Kurie graph. It is a
descending line that intersects the horizontal (energy) axis at a
point indicating the maximum decay energy b. Fermi-Kurie graphs are
sometimes used in accurate spectrometric analysis of radiation b. The shape of the end
section of this spectrum (see Fig.1.2.3 on the right) -
deviation from the linear dependence in the Fermi-Kurie graph,
can also be used to determine the mass of neutrinos, see
"Resting
mass neutrino" below.
To determine the mean energy` Eb rays b from the shape of
the radiation spectrum b can come out in the first approximation of the laws of
the approximate` Eb ~ Ebmax/3. For higher energies, this value is relatively moves
slightly to the right, so that more accurate empirical formula
is: `Eb » (Ebmax/3).(1+1/4ÖEbmax); (in [MeV]). Certain impact on the final energy has a
Coulomb electric effect of flying particles b with a charge of the
nucleus of protons Z, which leads to a further correction
factor (1 - 1/50.ÖZ).
Inverse beta decay
The standard beta- radioactivity discussed above, also called beta
decay, consists in the conversion of the neutron no to the proton p+ with the emission of
the electron e- and (electron) neutrino n: no ® p+ + e- + n. However, there is
the opposite process, a nuclear reaction in
which a proton can combine with an electron to form a neutron and
emit a neutrino: p+ + e- ® no
+ n -
is called inverse beta decay (electron uptake by an proton is the opposite of
the emission of an electron from the nucleus during beta- -decay). It occurs either spontaneously in atoms
during radioactive electron capture (described below in the section "Electron capture"), or is forced by external
forces - either by the kinetic energy of accelerated
electrons, or by very strong gravity. In universe, this process
of neutronization takes place avalanche during the gravitational
collapse of massive stars - the supernova explosion
and the formation of a neutron star (it is discussed in detail in §4.2, passage "Supernova explosion. Neutron
star. Pulsars." in book
"Gravity, black holes and spacetime physics ").
Note.: For inverse beta decay
is sometimes considered the interaction
of neutrinos with protons to form neutrons and
positrons: n'e
+ p+ ® no + e+, or with neutrons
to form a proton and electron:
ne + no ® p+ + e-,
which are used to detection of neutrinos in
neutrino detectors (described below "Interactions and detection of
neutrinos").
Neutrinos
- "ghosts"
between particles
Although elementary particles will be systematically discussed
until later in §1.5 "Elementary particles", beta radioactivity is a good opportunity to
mention in more detail here very interesting and remarkable
particles of the microworld - neutrinos. We will
do so somewhat more generally, not only in direct connection with
radioactivity b *). However, the overall classification of neutrinos in
the systematics of other elementary particles will be discussed
in §1.5.
* ) The rationale for the existence of
neutrinos and the origin of their name was discussed above in the
section "Radioactivity b-", passage
"Radiation spectrum b .Neutrinos".
Neutrinos, once formed as an additional not very
convincing hypothesis trying to explain "something that was
missing", have become real and very interesting particles
not only for nuclear physics, but also for astrophysics and
cosmology.
A more detailed explanation of the origin, properties, meaning and detection of neutrinos is quite comprehensive, which is why we included it in a separate chapter :
Radioactivity
b +
Another type of beta radioactivity is radioactivity b+. Its
basic scheme is in the left part of Fig.1.2.4 :
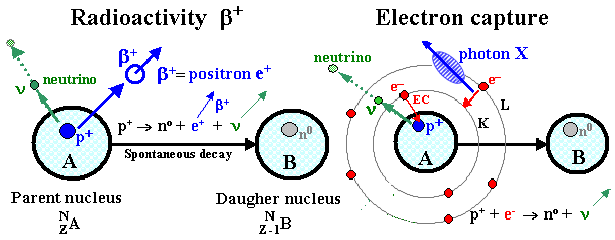
Fig.1.2.4. Basic scheme of b+
radioactivity and electron capture.
During this nuclear transformation, the nucleus
emits a particle b+, which is an antiparticle to the electron e- - positron
e+. From the point of view of electric charge, the
emission of b+ is not as paradoxical as b-, but there are
no positrons in the nucleus neither. Radioactivity b+ occurs
in radionuclides in which protons predominate over neutrons
(so-called neutron-deficient nuclei ). Thus, the
mechanism of the formation of b+ can be allegorically explained as follows: Some of the
"redundant" protons get "tired" of being a
proton and want to become a rarer neutron - it will do so by transforming
p+ ® no + e+ + n. The neutron no as a legitimate nucleon
remains bound by a strong interaction in the nucleus, while the
positron e+ flies out at high speed like a b+ particle. With
radioactivity b+, the nucleon number does not change (as with b-), but
the proton number decreases by 1 - the daughter
nucleus is shifted one place to the left in the
Mendeleev periodic table.
An example of beta+ radioactivity is the positron conversion of carbon 11C6 ® 11B5 + e+ + n for boron, or
fluorine 18F9 ® 18O8 + e+ + n for oxygen.
In order for b+ radioactivity to occur, the mass-energy
condition m(Z-1, N) + 2me < m(Z, N) must be met, where m(Z, N) is the mass of
the nucleus with proton number Z and nucleon the number N,
me is the
rest mass of the electron (which is identical with the rest mass
of the positron). Thus, the difference between the weights of the
mother and daughter nuclei must be greater than 1.022 MeV (=2.me).
Here again, the energy balance
can be well explained by the shell model of the
atomic nucleus structure discussed in the previous §1.1. If
there is an excess of protons over neutrons in
the nucleus, protons will fill slightly higher
energy levels than neutrons. The nucleus can then go into a lower
energy state by converting the proton by a b+ -conversion to a neutron, which goes to a free lower
energy neutron level .
Note: At first glance, it
may seem paradoxical that a lighter
particle - a proton, may spontaneously transform into a heavier
one particle - neutron, in violation of the law of
conservation of energy! Indeed, the free proton is never
disintegrate by b+ -decay on neutron (according to the classical theory the proton is stable,
although some hypotheses grandunific theories predict the
possibility of instability and decay of protons, but a different
mechanism in addition to the almost infinite life span greater
than about 1033 years). In nuclei, however, we cannot look at
protons and neutrons as free; they are part of a higher
whole (core) bound by a strong interaction. It is this
bond that will provide the energy needed to convert the proton.
The stability of the nucleus is then co-determined not only by
the sum of the masses of nucleons, but also by the binding
energy of nucleons. If in the coupled configuration, the
core consisting of p protons and N neutrons, has a higher total energy ~ weight than the nuclei of p -1 protons and n
+1 neutrons (at least by a rest mass of the electron, i.e. 511
keV), the situation arises, when b+
decay may occur. And it is completely in
accordance with the law of conservation of energy.
Positron
radiation b +
Everything about the continuous energy spectrum
and neutrino emission applies here analogously
to b- (only in the conversion of b- antineutrino is emitted, while in the case of b+ neutrino). As for the further
fate radiated by b+, it
would be the same as in b- only in
a vacuum - the positron e+ is as stable a particle as e-, so in
a vacuum it would "fly off to the other end of the
universe" (antiparticles, antiatoms,
antimatter, "antiuniverses" are discussed in §1.5.,
section "Antiparticles - antiatoms -
antimatter - antiworlds").
Note: Really to the end of the universe ?
Claim that the emitted particle in vacuum "flies
at the end of the universe" is here meant rather
theoretical and figuratively. Movement of particles in space is
actually influenced by three factors :
1.. Gravity that its universal action bends the
paths of all particles, including photons.
2. Magnetic field shaping paths of electrically
charged particles.
3 . The interaction of charged particles with
electromagnetic cosmic background radiation,
wherein the particles reverse Compton scattering lose energy.
These phenomena cause the actual range
of particles even in a free space is not
unlimited. Charged particles with lower energies remain
"trapped" in the space of the galaxy, where they will
be complicatedly to orbit in magnetic and gravitational fields.
Although high-energy particles can escape the galaxy's magnetic
field, they will be inhibited by inverted Compton scattering on
the ubiquitous relic electromagnet. radiation. And finally,
neither particles nor photons of electromagnetic radiation are
able to overcome the horizons of events arising
according to the general theory of relativity in the
gravitationally curved space-time of the universe ("Gravity,
black holes and space-time physics").
In matter, however, the
fate of b+ positrons is diametrically different (see Fig.1.6.1 in §1.6, section "Interaction of charged particles -
directly ionizing radiation". As long as the positron has a high velocity, it pulls
electrons out of the shell with its electric forces as it passes
around the atoms, and thus ionizes, similarly to
the beta- electron. However, after sufficient braking (in water
or tissue after about 1-4 mm), the positron e+ meets the electron e- (about the short episode just before the annihilation,
there is a small passage "Positronium"
below), and since they are
"antagonistic" antiparticles, they are mutually
destroyed ("eat each other"): they are annihilation
e+ + e- ® 2 g - transforms into two
quantum of hard radiation g with
energies of 511keV, which fly out of the annihilation site
exactly in opposite directions (at an angle of
180o in the center of gravity system). This fact is
used in the scintigraphic method of positron emission
tomography PET, as described in §4.3.
Intuitively - simplified,
approximately - we can imagine the emergence of gamma
radiation during e+ e- annihilation from the point of view of electromagnetism:
Electrons and positrons interact by their charges by
electromagnetic force. When these two identical opposite charges disappear
at once during annihilation, a disturbance in the
electromagnetic field is created, which spreads from the place of
annihilation as an electromagnetic wave. The
rest mass of the electron and the positron is also of
electromagnetic origin, so when they suddenly disappear, the
resulting electromagnetic wave also carries away their rest
mass of 2x511 keV. The detailed interaction mechanism (the law of conservation of momentum - in the center of
gravity system, the momentum is zero after complete braking) then leads to the emission of gamma radiation in
opposite directions.
Thus, if we have a
sample of the radioactive substance b+, positrons with
electrons annihilate already inside this sample, so that we do
not register practically any positrons in its vicinity, but such
a sample will be a source of intense hard radiation g with an energy of
511keV. And just as when a radiolabel labeled with b+
radionuclide is applied to the organism - each positron at a distance
of about 1-3 mm from the place of its origin annihilates with an
electron in the tissue and we can detect two quantums of g radiation in
coincidence about 511 keV energy flying in opposite directions -
this is the basis of PET scintigraphy (see
the passage "PET cameras" in Chapter 4 "Radioisotope
scintigraphy").
Positronium
Just before the actual annihilation, the electron e- and the positron e+ can orbit for a
around itself (they orbit the common center of gravity) - they
form a special bound system (similar to a
hydrogen atom) called positronium (Ps). The
dimension of the "atom" of the positron is twice the
hydrogen atom, the binding energy of the positron is 6.8 eV.
Depending on the mutual orientation of the electron and positron
spins, the positronium can be in either the singlet state 1S0 with
oppositely oriented spins - the so-called parapositon
p-Ps (1/4 cases), or in the triplet state 3S1 with consistently oriented spins -
the so-called orthopositonium o-Ps (3/4 cases).
However, this system of
positronium is unstable, the two particles
approaching each other in a spiral under the emission of
electromagnetic waves; in p-Ps in about 120ps they
"fall" on each other and there is annihilation on two
photons g, each with an
energy of 511keV. In the case of o-Ps, annihilation to two
photons is prohibited by quantum selection rules (related to the
law of conservation of the spin momentum - each of the photons
has spin 1), so o-Ps would decay in a vacuum with a relatively
long lifetime of about 140ns by emissions of 3 photons
with a continuous energy spectrum (the total energy of
1022keV is divided by the photons in a stochastic way). In the
substance, however, the positron bound in o-Ps much earlier is
enough to annihilate with some "foreign" electron from
the environment, which has the opposite spin orientation - again,
two photons g with
energies of 511 kV are formed.
The annihilation of a positron
with an electron produces 2 gamma photons in the vast majority of
cases, as mentioned above. Sometimes, however, there may arise
even more , but with a very small probability (the
likelihood that the e-e+
- anihilation in 2+n photons is proportional a-n, where a= 1/137 is the fine structure
constant). If a positron interacts with an electron bound in an
atomic shell, the extinction of such a pair may be accompanied by
the emission of only a single photon, and some of the
energy and momentum may be transferred to either the atomic
nucleus or one of the other electrons; however, the probability
of this process is very small and does not apply in practice.
The lifetime
of positrons in substances is in the order of hundreds
of picoseconds. However, the exact value depends on local
electron densities and configurations, which is used in the PLS
(Positron Lifetime Spectroscopy) spectroscopic method . The
investigated material is locally irradiated with a b+- g emitter (most often 22Na),
wherein the positron lifetime is determined by measuring the
delayed coincidence between the detection of photon radiation g of irradiating radionuclides (from Na22 on, it is g
1274 keV) annihilation photons, and detecting of g 511 keV.
The e+
positrons emitted by
beta+
radioactivity are actually a kind of "visitors from the
anti-world" - particles of antimatter.
The properties of antiparticles, antimatter, antworlds or
"antiuniverses" are discussed in §1.5 "Elementary
particles and accelerators", passage "Antiparticles
- antiatoms - antimatter - antworlds" (including the
possibilities of "production" and the use of
antimatter, with a somewhat light sci-fi story about the
encounter of a "human " with an "anti-human"...).
The
difference between the energy spectrum b- and b+
The spectrum of beta radiation drawn above in Fig.1.2.3 is
theoretical and ideological, it does not take into account the
electric forces between electrons or positrons and the atomic
nucleus that emits them. In fact, the continuous spectrum b- and b+ differs
somewhat in shape in the low energy region. In b- there is a higher proportion
of electrons of lower energies, because the electrons are
slowed down by electric attractive forces in the field
of a positively charged nucleus during the trip from the nucleus.
Positrons b+,
on the other hand, are accelerated by electrical
repulsion after leaving the nucleus, gaining additional kinetic
energy - there is a smaller share of low energies in the positron
spectrum. Thus, in the region of very low spectral energies, the
electric Coulomb interaction causes the enrichment of slow
electron emissions and the decrease of the slow positron emission
:
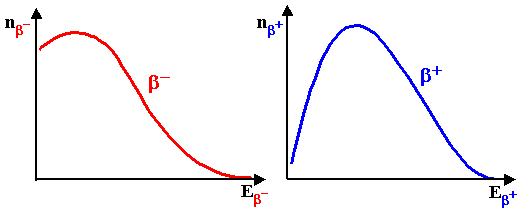
A
typical shape of the continuous spectrum of beta - and beta + radiation
Electron
capture
The last, and somewhat strange, type of beta
radioactivity is electron capture. It is an alternative process
to the decay of b+ in
nuclei with an excess of protons. An "excess" proton
can achieve its goal of "becoming a neutron" not only
by converting p+ ® no + e+ + n to b+ radioactivity, but also in another way. Around the
nucleus, electrons orbit in tha atom. A proton that "wants
to change into a neutron" can "to reach out" into
orbit, capture an electron *) and merge with it: p+ + e- ® no + n - Fig.1.2.4 right. This process is called electron
capture (EC - Electron Capture
); since the capture of an electron from the level of K ,
or L or M of the atomic shell can occur, this
process is sometimes also called K-capture,
or L or M capture. The most common is the
K-capture of an electron in the singlet state s, because
this orbital has a relatively significant overlap in the region
of the nucleus. Electron capture is also sometimes called inverse
beta decay (electron absorption is
the opposite of the process of electron emission from the nucleus
at beta- - decay). The shift rules between
the nucleon and proton numbers of the parent and daughter nuclei
are the same as for b+, i.e. (Z, N) ® (Z-1, N).
*) It's just a humorous-allegorical
formulation! According to the laws of quantum mechanics, part of
the wave function of the orbiting electron extends to the region
of the nucleus, so that the described process of electron capture
can occur directly and immediately...
During electron capture, no corpuscular
radiation is emitted from the nucleus (apart from elusive
neutrinos), the energy is divided into neutrino energy and
electron binding energy when absorbed by a proton in the nucleus.
So is it radioactivity at all in the sense of our initial
definition and scheme in Fig.1.2.1? The answer is yes!
First, there is transmutation of the nucleus. Second, the
electron from the higher shell (L) immediately jumps to
the vacant space after the electron on the shell K,
emitting characteristic X-rays; each electron
capture decaying radionuclide is a source of intense X-rays. And
third, as we will see below, the daughter nucleus B is
usually formed in an excited state and emits radiation g during
deexcitation. Electron capture is often accompanied by the emission
of so-called Auger electrons (see below in the section "Gamma
radioactivity", passage "Internal conversion of radiation g"), arising from the internal
conversion of characteristic X-rays.
Electron capture is an alternative
("competitive") way to decay those neutron-deficient
nuclei that have enough energy to emit a positron. Electron
capture occurs primarily when the mass of the parent nucleus m(Z,
N) is greater than the mass of the daughter nucleus m(Z-1, N),
but by a smaller difference than the rest mass of the electron
and positron 2me = 1.022 MeV. Positron emission b+ cannot occur in this case (not enough conversion energy
is available), so electron capture is the only possible way of
conversion. If the difference m(Z, N) - m(Z-1, N) is > 2me, it is possible to
convert the parent nucleus (Z, N) to the nucleus (Z-1, N) by both
emission b+ and
electron capture (usually the conversion of
b+ occurs
preferentially).
Electron capture converts eg
57-cobalt 57Co27 + e- ® 57 Fe 26 + n to iron, or
125-iodine 125I53 + e - ®
125Te52 + n to tellurium.
Two peculiarities of electron capture :
¨ 1. Electron capture EC
is the only type of radioactive transformation of the nucleus (in addition to the process of internal gamma
conversion during deexcitation of excited levels - isomeric
transition, is described below in the section "Internal conversion of g radiation"), in which electron
atomic envelope also participates. The rate,
probability, or half-life of a nucleus by electron capture can be
slightly affected by chemical bonding of a given atom. The rate of conversion is slightly
greater (i.e., the half-life is shorter) for the EC-radioactive
isotope in elemental form than if it were part of a compound. In
the chemical bond, the density of the orbital electrons of the
EC-radioactive atom is partially shifted to the adjacent bound
atom, which somewhat reduces the probability of electron capture
EC by the nucleus. This is observable for light EC-radioactive
atoms, whose valence electrons orbit relatively close to the
nucleus (especially s-electrons, whose
orbitals have a relatively significant overlap into the nucleus
region, are involved). For heavier atoms,
the chemical effect on the EC is negligible. Furthermore, the
conversion rate by electron capture can be increased
by applying external pressure to radioactive
atoms or molecules - higher pressure leads to an increase in
electron density and thus to an increase in the probability of
electron capture by the nucleus.
These effects have been demonstrated mainly in beryllium
7Be, as it is a small atom whose valence
electrons are close to the nucleus. Various compounds or 7Be implants in
different media (Au, Al 2 O 3 , LiO2 , graphite, fullerene
C60) were investigated. A difference of 0.9 % was observed
between the half-lives in metallic and dielectric media. When a
high pressure of 270 kilobars was applied to 7BeO, it was found that
the decay rate of 7Be increased by 0.59%, in 7Be(OH)2, at the same pressure, the EC conversion rate of 7Be increased by 0.88
%. External influencing on the decay rate of electron capture
have also been observed for 109In and 110Sn isotopes implanted in Au and Al foils (into the
respective crystal lattices).
The course of electron capture also
depends on the ionization of the respective
atom. The radioactivity of isotopes that decay by pure EC can be slowed
down (or theoretically even stopped ) if their
atoms are fully ionized (cf. for interest
with the opposite effect of acceleration of
low-energy b--conversions
by complete ionization in the rare so-called b - decay into bound electronic states, described above). Under normal
terrestrial conditions, we do not encounter such a situation, but
it is assumed that it can be able to affect astrophysical
processes of cosmic nucleosynthesis -
see §1.1, section "Cosmic alchemy".
During a supernova
explosion , elements are synthesized by the rapid fusion of
neutrons (the so-called r - process), launched into
space in a fully ionized state. Therefore, those that are
EC-radioactive cannot decay radioactively for a long time (until
they meet and connect to electrons in colder regions of space).
This could cause some anomalies in the distribution of elements.
The holmium 163Ho is considered, which under normal (atomic) conditions
is converted to 163Dy by electron capture. Fully ionized 163Dy with the
above-mentioned process b -decay to bound
electron states, decays to 163Ho.......
¨ 2. Since in EC there is no emission of
corpuscular radiation, the energy difference Q parent and
daughter nuclei is reflected in the excitation of the
daughter nuclei (with one or more excited
levels, followed by radiation g) and the rest of the energy is carried away by
the neutrino. If we could measure the spectrum of these
neutrinos, in the EC would be line (discrete),
as opposed to continuous spectrum of neutrinos from b-,+ decays.
Mixed
radioactivity beta - , beta + , electron capture
The possibilities of individual types of radioactive
transformations are mainly determined by the energy
balance between the respective "neighboring"
nuclei (discussed in more detail below in
the final part of this chapter "Stability and
instability of atomic nuclei"). If the mass-energy inequality m(Z, N)> m(Z+1, N) is
satisfied for the given initial nucleus (Z, N), the b- transformations will occur. Under the conditions m(Z,
m)> m(Z-1, N) <m(Z-1, N) + 2me , the nucleus (Z, N) will decay by electron capture. If
m(Z, N)> m(Z-1, N) + 2me , it is possible to convert the nucleus (Z, N) to the
nucleus (Z+1, N) by both beta+ decay and electron capture. If both the inequality m(Z,
N)> m(Z+1, N) and the inequality m(Z, m)> m (Z-1, N) + 2me are satisfied at the
same time, then all three types of beta conversion can occur simultaneously.
An example is the 64Cu
radioisotope, which decays from 39% of b- emissions, from 19% of b+ emissions and
42% of cases by electron capture.
Mechanism of beta conversion. Weak interactions.
When interpreting radioactivity b, we have clarified the
formation of radiation b- and b+
by the mutual transformation of
neutrons and protons in a situation where due to the increased
number of neutrons or protons, higher energy levels are occupied.
But what is the internal cause or mechanism
of these transformations? The first theory of decay b was presented by
E.Fermi in 1934, which introduced the so-called weak
interaction acting between elementary particles.
According to the laws of
quantum physics, Fermi described the emitted electron and
neutrino by wave functions depending on their momentum,
expressing the probability of electron and neutrino emission in a
certain range of momentum as the product of squares of these wave
functions and a special expression containing the wave function
integral of the original neutron and the resulting proton,
multiplied by the constant gF characterizing the strength of the interaction
leading to electron and neutrino emission - newly introduced weak
interactions. The radiation spectrum b corresponding to
this Fermi expression has a continuous shape according to
Fig.1.2.3 on the right in accordance with the experiment.
The original Fermi theory was
formulated in the spirit of quantum physics, but not quantum
field theory - the weak interaction was conceived as
"contact" or "point" - the decay products
arise at the same point and moment as the neutron disappears (no
intermediate particles here did not assume). However, in the
spirit of quantum field theory, each interaction should be caused
by the quantum of the field - the particle mediating the
interaction. This concept was developed in 1967-8 by
S.Weinberg, A.Salam and S.Glashow, who, due to the weak
interaction, introduced three mediating particles W+,
W-, Zo (with positive and negative charge and without charge)
and by adding photons created a unified theory of weak and
electromagnetic interactions - the so-called electroweak
interaction. This concept was experimentally verified in
1983: intermediate bosons W+, W-,
Zo with
masses mW
= 82GeV and mZ = 93GeV were discovered in interactions of upstream
proton-antiproton beams (270GeV versus 270GeV) of the collider of
the large proton synchrotron at CERN, whose modes of decay were
in good agreement with the predictions of the Weinberg-Salam
model.

Fig.1.2.5. Schematic
representation of the mechanism of b- -neutron decay
(top) and b+ -proton transformation (bottom) within the standard
model of elementary particles.
Now, within the standard model of elementary
particles (see §1.5), the beta decay mechanism is explained by
the quark transmutation scheme according to
Fig.1.2.5. The neutron no (with zero electric charge) consists of quarks u
- d -
d; quark u
has charge +2/3, quarks d charge -1/3.
One of the quarks d is transformed
into a quark u by the action of a field of
(electro)weak interactions by mediating a
virtual intermediate boson W-, which carries away the charge -1. From the
virtual boson W-
then the electron e- and the antineutrino n´ are formed, which fly out
in different directions. The result of the transformation is a
proton p+
consisting of quarks u - u - d.
The transitional stage between the initial and final state in the
middle of the image lasts only a small moment (approx. 10-27 sec.) and is not
directly observable. Analogous diagram can be drawn for the
conversion of b+ (bottom
of the image), wherein the proton p+ due to transmutation quark u to at
quark d for mediating intermediate boson W+ is converted to a
neutron no,
positron e+
and neutrino n. Feynman's diagram of the
transmutation of a quark inside a proton during beta conversion
is drawn in Fig.1.5.1.F in §1.5
"Elementary particles".
Complexity of beta
radioactivity
When we compare individual types of radioactivity according to
the complexity of their mechanism, we can state :
Alpha radioactivity is
basically simple (Fig.1.2.2). In a nucleus with a large number of
nucleons, where the nuclear forces of short-range at the
peripheral parts are not strong enough, small, more strongly
bound groups of two protons and two neutrons are formed, which
can (with the help of tunneling) leave the nucleus and fly off as
alpha particles - helium-4 nucleus.
Gamma conversion (Fig.1.2.6)
is also simple. In the energetically excited state, the nucleus
deexcites to the ground (or lower) state, while the energetic difference is emitted as a
gamma radiation photon by electromagnetic interaction.
However, beta radioactivity is
very complex ! Its mechanism is hidden not only inside
the nucleus, but even deeper - inside the nucleons themselves. It
consists in the transmutation of quarks "u" or
"d" through the intermedial meson W, which leads to the
mutual transformation of protons and neutrons (Fig.1.2.5).
Electromagnetic
radioactive transformations
These are radioactive processes of nuclear deexcitation caused by
electromagnetic interaction. We know two types
of these nuclear deexcitation: 1. Direct emission of gamma photons; 2. Internal
conversion with emission of orbital electrons from an
atom. Below we will discuss them mainly in connection with
radioactivity.
Note: In addition to the ground state,
atomic nuclei have a number of excited states (energy levels),
only a part of which is applies in radioactive transformations.
The other excited states arise only during the bombardment of
nuclei by energetic particles from accelerators.
Gamma radioactivity
So far, in interpreting radioactivity, we
have focused on our own mechanisms of radioactive transformation
and on the properties of emitted corpuscular radiation (a, b-, b+).
Therefore, we have deliberately drawn the basic schemes of
radioactive transformation in Figures 1.2.1 to 1.2.4 in a
somewhat simplistic way so that we can focus on the nature of
radioactive transformations. Now notice the behavior of
the daughter nucleus immediately after the radioactive
transformation. Fig.1.2.6 shows a complete scheme of radioactive
decay, including the behavior of the daughter nucleus :
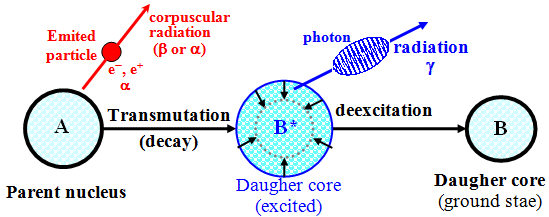
Fig.1.2.6. A typical diagram of radioactive decay of the parent
core A to the excited daugher nucleus B*
and its
subsequent deexcitation by photon radiation g into the
resulting daughter nucleus B .
After such a large "event", as
radioactive transformation means for the atomic nucleus, the
resulting daughter nucleus seldom remains in an unexcited basic
energy state. After changes in the number or type of nucleons in
the nucleus, the nucleons may not immediately occur in the lowest
energy states. The released energy results in the daughter
nucleus B, after radioactive transformation,
mostly being formed in the energetically excited state B*;
we can imagine that the nucleus is "inflated" 1) - nucleons are more
distant from each other, occupy higher energy levels - cf.
Fig.1.1.9. Such a "inflated" nucleus B* usually
"collapses" very quickly 2), nucleons rearrange to a lower energy state - deexcitation
occurs, in which the respective energy difference is emitted
in the form of one or more quantum - photons -
hard electromagnetic radiation - gamma radiation 3). The emission of
gamma quantum stabilizes the energy conditions in the nucleus.
The daughter core B then remains in the ground
state.
1 ) In the case of
non-spherical nuclei, which can perform a rotational motion, in
addition to the level excitation, we also encounter rotational
excitation. Here, too, deexcitation is
accompanied by the emission of the photon g.
2 ) In
some cases, the excited nuclear state can last for a very long
time - see below "Metastability and nuclear isomerism".
3 ) If
the core is part of an atom (which is almost always), alternative
way deexcitation of excited nuclear levels may be the emissions
of the envelope electron by the process of
internal conversion - see below "Internal conversion gamma and X". For very heavy nuclei in field
transurans highly excited states of these heavy
unsymmetrical nuclei, besides conventional gamma-deexcitation,
can succumb to spontaneous fission (§1.3, section "Fission of atomic nuclei" and "Transurans").
We can therefore
pronounce the following definition :
| Gamma
radiation is high-energy electromagnetic radiation
generated by deexcitation of excited levels of the atomic
nucleus *) . At radioactivity it is the deexcitation of excited levels of the daughter nucleus formed after radioactive transformation **) . |
| *) Gamma
radiation of non-nuclear origin In addition to deexcitation of excited energy levels in atomic nuclei, hard photon radiation - gamma - is generated even during annihilation of positrons with electrons and other particles and antiparticles, as well as in interactions of high energy particles (here can produce radiation g of energies GeV, TeV and higher). The category of radiation g also includes high-energy braking radiation generated by the impact of fast electrons on a target. **) Gamma radiation in nuclear reactions Excited nuclear states, giving rise to gamma radiation, also arise in most nuclear reactions (see §1.3 "Nuclear reactions", middle part of Fig.1.3.1) . |
Gamma-ray spectrum
The energy levels of the atomic nucleus are quantized
, so that all photons g emitted by a given type of deexcitation will have the same
energies - the spectrum of g- rays is line
*), discrete. If the B* nucleus has more excited levels, several
groups of monoenergetic photons g will be emitted,
so that the spectrum will be formed by several discrete
lines - peaks in the measured spectrum (measurement of gamma radiation spectra is discussed in
§2.4, section "Gamma ray scintillation spectrometry").
*) Width of gamma lines
Gamma-photons at radioactivity come from nuclear
transitions between discrete levels with
precisely given energies, so they are essentially monoenergetic,
their ideal physical spectrum represents a sharp line
on the energy Eg. Very small fluctuations in energy values are caused by
quantum uncertainty relations and backscatter of
nuclei during gamma-photon emission. Furthermore, since
these photons practically never come from free nuclei, but are
emitted from radioactive atoms contained in a substance (in a
certain material), some photons interact with the substance
before leaving the sample. It can also blur their energy
somewhat. The thermal motion of the atoms in the sample
causes by Doppler effect the small frequency - energy
shifts according to different velocities of emitting atoms
(nuclei), which is reflected in the Doppler extension of
the gamma line. However, the magnitude of all these extensions is
generally very small compared to the effects in
the actual detection of radiation. The real, physical, gamma-ray
spectrum can therefore be considered practically line -
discrete, monoenergetic.
Gamma-photons of annihilation radiation,
created by annihilation of positrons with electrons e+
e- ® 2 g, have an energy of 511 keV, are basically
monoenergetic. However, electrons and positrons annihilate
together at somewhat different residual braking rates, which the Doppler
effect leads to frequency-energy shifts. This results in a Doppler
broadening of the 511keV annihilation peak
from positron radionuclide samples. The 511 keV annihilation peak
is somewhat wider than other "nuclear"
near-energy gamma peaks in the spectrum. Under normal laboratory
conditions, this additional Doppler broadening of the
annihilation peak is about 1.2 keV and is observable only on high
energy resolution spectrometers (semiconductor
Ge detector or magnetic spectrometer).
In our spectrometric measurements of a number of radionuclides
(eg 18 F , 22 Na ., 68 Ga , 131 I ,
124 I ,
137 Cs ,
152 Eu ,
...) on a semiconductor HPGe detector, we observed FWHM
half-widths of about 1.4-1.5keV in "nuclear" gamma
peaks of medium energies between 400-700keV, in annihilation the
511keV peaks of the FWHM half-width were approximately 2.5-2.7keV
(Doppler broadeningwas observed).
The energy of radiation
g from radionuclides is usually in the range of about 5keV
to 5MeV. The lowest energy of photon radiation from nuclear
transitions is observed at 110mAg(1.1 keV) and 99mTc(2.17 keV; but the main peak here is 140keV); however, these low energies are almost completely
subject to internal conversion (see
"Internal conversion of gamma and
X-rays" below) and their intensity is immeasurably weak. So far, the
highest energy of 11.26 MeV gamma radiation from radioactivity
was recorded for the short-lived radionuclide 20Na. However, during
interactions of high-energy particles, gamma radiation of much
higher energies of the order GeV or TeV can also occur!
A typical example of the process according to Fig.1.2.6 may be
the b- radioactivity
of cobalt 60Co. In the actual b-
decay, the cobalt nucleus first emits an
electron e- (b- particle) and an electron antineutrino ne', thereby converting to the nickel core 60Ni in the excited
state: 60Co
® 60Ni* + e- + ne'. This newly formed excited nucleus is then freed of
excess energy by radiating a quantum of g : 60Ni* ® 60Ni + g. The daughter 60Ni* has two excited
levels, so that the emitted quantum g here has an energy of 1173
keV and 1332 keV (see §1.4, passage "Cobalt", Fig. "Co-60").
The spectrometry of
radiation g is discussed in §2.4, part "Scintillation spectrum of radionuclides". Gamma-spectrum (scintillation and semiconductor), a
number of important radionuclides are, together with the
description, displayed in §1.4, the "Most important radionuclides". Looking at the spectrum implies an interesting regularity:
if radioactive transformation occurs to a greater number excited
states of the daughter nucleus, then usually more likely to lower
energy levels than higher excited states - gamma spectra
are represented by higher intensity peaks of lower energies,
while high-energy peaks are much weaker, are often visible until
at high magnification and longer acquisition time.
The diagram in Fig.1.2.6 shows two
important facts for gamma radiation emitted by radionuclides :
1. Radiation g is temporally
following and concomitant after the
emission of corpuscular radiation during its own nuclear
transformation. This delay is usually quite slight (nanoseconds
and less), but can sometimes be very significant (see below "Nuclear isomerism and metastability") ..!..
2. Most radionuclides are mixted
emitters - either a+g or b+g. Only some emitters are pure a or pure b; radioactive
conversion sometimes occurs directly to the ground state of the
daughter nucleus (this is the case, for
example, with tritium 3H or carbon 14C). However, pure g emitters do
not exist in nature! Nevertheless, we can produce
pure gamma emitters artificially. This is made possible
by the remarkable property of some nuclear excited levels: their metastability
(see below "Nuclear isomerism and metastability").
Angular (directional) correlations
of gamma radiation
The quantum of ionizing radiation
generated during radioactivity are generally emitted completely
randomly and isotropically in all directions *). If, however, at one
and the same decay events are emitted simultaneously from the
core of two or more quanta, between the
directions of their trip may occur the angular
correlations. Let's show it in gamma radiation :
In most cases, when emitting independent
gamma photons from the nucleus, these photons fly completely
randomly, isotropically in all directions (angles). However, if cascade
deexcitation occurs with the formation of two
gamma photons emitted promptly in succession,
then after the emission of the first photon the nucleus is
polarized - its excited intermediate state is oriented
in a certain way, depending on the angular momentum carried by
the emitted photon. The second (subsequent) gamma photon will
then preferably be emitted in a certain direction, correlating
with the emission angle of the first photon. The increased
intensity of the second gamma radiation is then observed at a
certain angle (eg 90°, 180°) with respect to the direction of
the first radiation. The condition for the observation of these g-g angular
correlations at normal laboratory temperature of the
preparation is a sufficiently short lifetime of
the intermediate excited level in comparison with the average
frequency of thermal collisions of emitter atoms (to avoid angular momentum transmission and nuclear
orientation). Isotopes in which angular
correlations g-g occur are, for example, 60
Co , 111 In , 75Se, 169Yb, 81 Rb and many others. The perfect 100%
angular correlation is in the annihilation g-radiation,
which arises during the annihilation of electron-positron pairs
to two 511 keV photons, flying in exactly opposite directions at
an angle of 180°.
Furthermore, in some radionuclides that
are converted by electron capture to excited states of
the daughter nucleus, angular g- X
correlations occur between gamma radiation and
characteristic X-radiation accompanying electron capture (e.g. at
125 I , 198Hg). An angular
correlation b-g is also observed for combined beta-gamma emitters.
*) The random emission of radiation quanta
isotropically in all directions is related to the fact that under
normal conditions the atomic nuclei (their spins) are oriented
completely randomly and change chaotically due to
thermal movements. Only if the radioactive sample is placed in a strong
magnetic field (several Tesla), are the magnetic moments
and spins of the nuclei partially polarized and
then even single-photon radiation will show an increased emission
at a certain angle correlating direction of the
magnetic field (magnetic induction vector).
Coincidence tomographic scintigraphy
These angular correlations were once experimented with in coincidence
tomographic scintigraphy (§4.3 "Tomographic scintigraphy", passage "Technical development
of tomographic scintigraphy"), but this has
not been succesfull in practice. The perfect angular correlation
is in the annihilation g- radiation,
which arises during the annihilation of electron-positron pairs
to two 511keV photons, flying in exactly opposite directions at
an angle of 180° (in the center of gravity
reference system) - see §1.5, section
"Elementary particles and their
properties , passage "Positrons").
This 100% angular correlation is widely used in
gamma imaging by the method of coincidence positron
emission tomography in nuclear medicine (§4.3, part
"Positron emission tomography PET").
Rate of deexcitation and emission g. Nuclear isomerism
and metastability.
The vast majority of nuclear excited states are very
unstable and deexcite almost immediately (after the order of 10-12 s.) by gamma photon radiation. In
some cases, however, nuclear excited levels do not deexcite
immediately (the cause is discussed below), but only after a certain longer average time has
elapsed - we say that they are metastable. This
phenomenon is also called nuclear isomerism -
nuclei can exist in two isomeric states, called isomers.
Metastable isomers of a certain isotope are denoted by the index
"m" located after the mass (nucleon)
number of the nucleus - eg 99mTc, or Tc-99m. If a given isotope has more isomers, the
indices "m1, m2, ..."
are denoted, in order of higher energy of the respective excited
states - e.g. 152 m2Eu. Metastable isomers are
generally produced after the radioactive decay of the daughter
nuclei (as in the 99mTc), but
they may also exist separately without prior
radioactive decay, they can be prepared in nuclear reactions.
Isomerism metastable levels were first
observed at b-decay of thorium 234Th to 234mPa, in the case of an artificial radionuclide, then in
the case of bromine, 80mBr produced by irradiation 79Br with neutrons. More than 300 nuclear isomers are now
known, some of which are widely used - above all 99mTc.
Cause of metastability
and isomerism :
The main mechanism of suppression of gamma-deexcitation
of induced nuclear levels, to which metastable isomers owe their
long half-lives, is the relative "prohibition"
of gamma transition due to large difference in angular
momentums (spins) between the respective nuclear levels
- "spin mismatch". Photon
emission from the excited state of the nucleus leads to a change
in the spin of the nucleus. Because the photon has spin 1, transitions with DI =1are most
probable and fastest with a lifetime of excited states of about 10-16-10-10 seconds.
Transitions with DI = 2 are also very fast to lifetimes of the excited state in
the range of 10-11-10-4
s. In both of these cases,
therefore, the gamma-ray photons are emitted practically simultaneously
with the previous
transformation a or b (for the rate of deexcitation and
emission g we therefore observe the same half-life as for the
previous corpuscular
transformation). Transitions between levels with DI>
2 are much less likely, relatively "forbidden". Spin changes greater than 2,3,4, ... are
in principle possible, but each such unit of change causes a
significant inhibition of the transition probability (by about 5
orders of magnitude). Unless
there is another possibility of deexcitation *), it will be
reflected in a longer lifetime of the
excited level (10-3
s , seconds, minutes,
hours, years, occasionally even longer...). Deexcitation and photon emission are
then governed by its own half-life, independent of the half-life of the
previous transformation a or b. The nuclide in the excited nuclear state
with a longer half-life of the gamma transition is called the nuclear
isomer and is denoted by
the superscript "m" at the nucleon number - e.g. 99mTc , 81mKr.
*) However, if one or more other energy
levels lie between the excited and ground state of the formed
nucleus, deexcitation occurs in such a way that fast transitions
with DI
= 1 or DI
= 2 are preferentially applied and a metastable state does not
arise. Metastability
of excited levels occurs when there is an energy level near the
ground state of the nucleus, which differs
significantly from the ground state by its angular
momentum (at least 3 h , ie DI ³ 3). Then the
radiation g emitted at the transition from such a level to the
ground state must have a higher multipolarity (E3, M3 or higher)
- transitions between such levels are unlikely,
so that the corresponding lifetimes can take on large values.
Isomerism and metastable states do not occur in light nuclei
(where there are no excited levels with DI ³ 3), but only in nuclei
with a nucleon number from 24, from N> 40 they occur
relatively often. The shell model of nucleus explains the
details.
Transformation half -
lives of nuclear isomers
The deexcitation half-lives of metastable levels are
very different for various nuclides, depending on the quantum
nuclear configurations. They are usually very short,
on the order of nanoseconds or microseconds. Isomers with
half-lives of the order of seconds, minutes, hours and more are
possible for practical use. The shortest-lived radionuclide that
has practical use is the 81mKr krypton isomer with a half-life of
only 13 seconds (see §1.4, passage "Rubidium-Krypton").
However, long-term nuclear isomers
are particularly interesting from a physical point of view, even
for their numerous applications. Undoubtedly the most important
of these is technetium 99mTc with a half-life of 6 hours,
described below (see also references). The 99mTc core has spin +1/2 and is converted to the basic
state of 99Tc
with spin +9/2. An example of a truly long- lived isomer is
hafnium 187m2Hf with a high excitation energy of 2.45MeV and a
half-life of 31 years, or holmium 166m1Ho with a half-life of 1200 years.
The most stable known nuclear isomer is tantalum
180mTa (as a natural
primordial isotope contained in natural tantalum in a
concentration of 0.012%) with an extremely
long half-life >1015 years! - it is therefore almost stable;
while 180Ta
in the basic state is beta- and EC radioactive with a half-life of only 8.1 hours.
Remarkable stability of 180mTa is caused by a large spin mismatch: the
excited level of 180mTa (energy 75keV) with spin -9 should be photon deexcited to the base 180Ta with spin +1;
this large spin difference causes inhibition of photon
deexcitation by a factor of 1035 relative to the usual "permissible"
transition of 10-12 s, leading to a half-life of 1023 s, i.e. about 1015 years. Direct beta decay to
180Hf or
180W is also blocked here due to spin
mismatch...
Note: The
half-life of the g -deexcitation, which takes place by electromagnetic
interaction, is independent of the half-life of
the previous corpuscular radioactive transformation (alpha or
beta), but depends only on the specific configuration of the
excited level relative to the lower or basal level (see
mechanisms above).
Other (non-photon)
radioactivity of isomers
Metastable excited levels of isomers usually "decay" by
conventional electromagnetic deexcitation to emit photon g. As with other
excited states, an alternative method of deexcitation may be the emission
of the envelope electron by the process of internal
conversion - see "Internal conversion of gamma and X" below.
However, some nuclear isomers have such
different quantum properties from the ground state (especially
the spin value) that there is no isomeric transition to the
ground state of g- radiation photon emissions, but radioactive
conversion of beta- , beta+ or electron capture to another neighboring
nucleus. An example is the metastable 152mEu,
which does not pass at all to the basic 152Eu, but
from 73% is converted to 152Gd by b-
-radioactivity and by 27% by electron capture and b+
to 152Sm (half-life is 9.3 hours).
Note: However another metastable isomer
europium designated 152m2Eu pass regularly with a half
life of 96 minutes with isomeric transition to basic 152Eu
with photon emission g -radiation with energy 89.8keV ...
Another example is metastable lutetium 177mLu
with a half-life of 160.4 days, which in 22% of cases passes by
normal g -deexcitation to basic 177Lu
(which is then converted to 177Hf by
beta-radioactivity with a half-life of 6.68 days, but at the same
time in 78% is converted directly to 177Hf by direct
beta-decay. In the latter case, the baseline of 177Lu
is "bypassed" and, in addition, beta-conversion from
metastable lutetium goes to different (substantially higher)
excited hafnium levels than with the usual beta-radioactivity of 177Lu.
There are more similar cases of branched g-b
transformation of metastable states. After all, even in the known
technetium 99mTc, its metastable level of 140 keV, in
addition to the usual isomeric g-
transition to the ground state of 99Tc,
passes in a small percentage (0.003%) by beta-radioactivity
directly to excited states of ruthenium 99Ru (see §1.4, part "Molybdenum-Technetium", Fig.Tc99m) .
For very heavy transuranic
nuclei the highly excited metastable states of these heavy
asymmetric nuclei in addition to normal gamma-deexcitation may undergo
spontaneous fission (§1.3,
section "Fission of atomic
nuclei" and "Transurans"), mostly with a short half-life. These "fissile
isomers" are denoted by the index "f" (instead of
"m"), e.g. 240fPu.
Monopole E0 transitions 0+ ® 0+
A special case of strongly forbidden
deexcitation is the transition from an excited state with zero
spin and positive parity to a ground state, which also has zero
spin and positive parity - from an electrical point of view it is
a "monopole" transition, which does not occur in
electrodynamics. In such a case, the usual deexcitation does not
take place with the emission of one quantum gamma (the law of conservation of angular momentum would be
violated), but three alternative mechanisms
may come into play :
¨ Internal
conversion (discussed below in the
section "Internal conversion") - electrical transfer of
the transition energy to the electron in the atomic shell, which
is emitted and carries away the difference between the transition
energy E0 and the binding energy of the electron. It is the main
process here in the case of low energies E0 excitation;
¨ Emissions of electron-positron
pair (from Dirac's vacuum background) with oppositely
oriented spins can occur at high excitation energies - if the E0
transition has an energy greater than twice the rest mass of the
electron, i.e. > 1.022 MeV;
¨ Simultaneous emission of two
gamma photons with oppositely oriented spins. It
is a higher order process with a low probability of about 10-4 -10-3.
A practical example of this monopole E0 transition and its
manifestation in the gamma radiation spectrum is given in §1.4,
passage "Y-90".
Pure gamma-radionuclides; technetium 99mTc ;
radionuclide generators
The most important example of the formation of a metastable
nuclear isomer is the radionuclide molybdenum 99Mo, which with a
half-life T1/2 = 2.66
days b- -radioactivity
changes to 99Tc - to its excited level of 99Tc* with energy 140keV, which is metastable with a
half-life of T1/2 =
6.02 hours. The excited nucleus in the metastable state is
denoted by the index "m", so here the metastable
technetium has the designation 99mTc. If during this time separated daughter technetium from the
parent molybdenum, we get a pure preparation of technetium,
containing excited metastable nuclei 99mTc, which during gradual deexcitation emit g radiation with an
energy of 140keV - so we obtained a pure gamma emitter.
Laboratory equipment for obtaining
shorter-term radionuclides from the original parent radionuclides
with a longer half-life are called generators.
Molybdenum-technetium generator for the preparation of 99mTc consists of a
glass cylinder with a small "chromatographic" column,
in which it is on a suitable sorbent (eg Al2O3 , SiO3 , ZrO2) in the insoluble chemical form of the oxide the
longer-term parent isotope 99Mo is absorbed. Radioactive conversion produces a
short-lived radionuclide 99mTc, which is released from the insoluble bond and rinsed
with water (or saline) - so-called elution -
elutes from the column a solution of sodium pertechnetate Na 99mTcO4 containing atoms of
pure g- emitter
99mTc; b -radioactive 99Mo remains absorbed
in the column.
The continuous conversion of the parent 99Mo leads again after
the elution to the accumulation of 99mTc in the generator, so that the elution can be repeated
over time.
The principle and technical design of the 99Mo/99mTc generator is shown in Fig.4.8.1 in §4.8, which we
present here again for clarity :

Fig.4.8.1. Elution 99Mo - 99mTc generator.
Left: Principle functional diagram of
the elution generator. In the middle:
Technical design of a sterile generator with an evacuated elution
vial.
Right: Decomposition scheme of molybdenum 99Mo to technetium 99mTc, deexcitation to 99Tc and slow transformations to stable ruthenium 99Ru.
From above in the section "Exponential
law of radioactive decay", passage "Mixtures of radionuclides, decay
series, radioactive equilibrium"
the general equation of subsequent decay of radionuclides A(lA)®B(lB)®C(stable)
was derived. If we apply this equation (multiplied by the factor lTc to get the instantaneous activity in [Bq] from the
instantaneous number of nuclei) to our case of the Mo-Tc
generator 99Mo(lMo=0,0105hod-1)®99mTc(lTc=0,1155hod-1)®99Tc("stable") and taking into account that 87% 99Mo decays to a
metastable excited level of 99mTc, we get for the time dependence of the immediate
activity of the required technetium 99mTc relation: A99m-Tc(t) = 0,957.AMo(t=0) . (e-0,0105.t - e-0,1155.t ), where AMo(t=0) is the activity of 99Mo at time t = 0 of the previous elution, time t
is in hours. The activity of 99Mo changes with time T according to the decay law
AMo(T) = AMo(0).e-lMo.T = AMo(0).e-0,0105.T. Substituting
this basic decomposition of molybdenum we obtain the final
relation for the instantaneous activity of the eluted 99mTc
at time T from the delivery of the molybdenum generator
and at time t from the last elution :
A 99m-Tc (T, t) = 0.957.A Mo (0) .e - 0 , 0105.T . ( e - 0.0105.t
- e -
0.1155.t ) ,
where AMo(0)
is an activity of 99Mo at time T = 0 of the generator production, times t
and T are in hours. To determine the actually eluted 99mTc activity, we must
also take into account the elution efficiency,
which is usually approximately 75-85%. This time dynamics of 99mTc activity during
repeated elutions of the Mo-Tc generator is plotted in Fig.2.1.B
(d), which we present here again for clarity :

Fig.2.1.B. Time dynamics of radioactivity in a mixture of two
radionuclides.
a) In a mixture of two independent radionuclides
X, Y, each of them is
converted according to its own half-life and the total activity
of the preparation is given by the sum of both exponential
functions.
b) , c) In the decay series of two
generically related radionuclides X --> Y, the decay dynamics
depends on the ratio of the half-lives of the primary parent
radionuclide X and the daughter, further decaying radionuclide Y; depending on this
relation lX and lY a transient or secular equilibrium of both
radionuclides can then be established.
d) Specific radioactive dynamics of the
radionuclide molybdenum-technetium generator during repeated
elutions of the daughter 99mTc, resulting from the conversion of the parent 99Mo.
After elution, the 99mTc activity in the generator drops to almost zero, then
rises and reaches a (local) maximum 23 hours after the previous
elution, after which a radioactive equilibrium occurs and the 99mTc activity
decreases exponentially with a half-life of 67 hours of 99Mo. After 23 hours
from the last elution, the elution yield of 99mTc is the highest; the generator can of course be eluted
as needed in a shorter time, but with a lower yield of 99mTc.
These elution cycles can be repeated
many times until the activity of the parent radionuclide falls
below the applicable limit; for a Mo-Tc generator with an initial
activity of approx. 10-40 GBq it's about 7-15 days. The relatively long half-life
of the parent radionuclide allows for long-term use of the
generator, and the short half-life of the resulting daughter
radionuclide ensures a low radiation exposure to the patient.
Note: In the
past, were also rarely used generators of the extraction
type (by passing the methyl ethyl ketone through an aqueous
solution of 99Mo, extracting pertechnetate 99Tc and separating it from the aqueous phase from the
parent molybdenum) and sublimation type (using the
difference between the volatility of molybdenum oxide and the
resulting technetium oxide). Due to their excessive complexity
and operational difficulty, they are no longer used, they have
been pushed out by elution generators.
99mTc is the most
important radionuclide in nuclear medicine (see
Chapter 4 "Radionuclide scintigraphy",
§4.8 "Radionuclides
and radiopharmaceuticals for scintigraphy", where Fig.4.8.1 shows the principle of operation and technical design
of the 99Mo-
99mTc
generator). Pure gamma emitter with a short
half-life of 6 hours allows, without the risk of significantly
increased radiation exposure, to apply to patients a very high
activity of 99mTc (of the order of hundreds of MBq) needed to obtain
quality images in SPECT or dynamic scintigraphy. The radiation
exposure is relatively low because there is no cospuscular
radiation that would be absorbed into the tissue and give up its
energy; radiation g then, due to its penetration, usually flies out of the
organism, only a small part is absorbed.
Gaseous radioactive krypton 81mKr
is obtained from the generator 81Rb (T1/2 =
4.85 hours) (EC) ® 81mKr (T1/2 = 13s) -
§1.4, passage " 81mKr - scintigraphy of
pulmonary ventilation". The air stream, guided through a tube through a
container containing a layer of parent radionuclide 81Rb, carries away the
released daughter 81mKr, which the patient inhales, and a scintillation
camera uses external detection of g radiation showing the
distribution of this 81mKr in the pulmonary alveoli - ventilatory
scintigraphy of the lungs (§4.9.5
"Scintigraphy lung").
In terms of production and properties of
artificial radionuclides, generators are described in §1.4
"Radionuclides",
section "Production of artificial radionuclides", section "Radionuclide
generators".
Terminological
agreement: g and X radiation
The high-energy region of electromagnetic radiation consists of X
radiation (X-rays) and gamma radiation. In terms of spectral
classification, g -radiation lies energetically behind
the X-ray region, towards higher energies and
short wavelengths. Both of these radiations have the same
physical nature (photon radiation) and largely similar
properties, they may differ in the way they originate. In
connection with the above-described gamma radioactivity, the
following terminological agreement was made on
the distribution of g and X radiation according to their creation and origin
:
l Radiation gama is called photon radiation generated in atomic
nuclei (during deexcitation of excited nuclear levels) -
even in case if it has a low energy of several keV.
l Radiation X is called radiation caused by jumps of electrons
between internal levels in the atomic shell and braking
radiation by electrons - even if it has a relatively
higher energy of tens and hundreds of keV.
Thus, we can have, for example, radiation g with an energy of
only 14.4 keV (one of the energies emitted by the radionuclide 57Co) and at the same
time X-radiation with an energy of 75 kV (line Ka
characteristic X-rays of lead), or braking X-rays with a
continuous spectrum reaching energies of 120keV and higher
(depending on the X-ray tube voltage). However, photon radiation
with very high energies (of the order of MeV) is usually called gamma
radiation, regardless of the way it is generated.
Internal conversion of gamma and X-rays ; conversion and Auger electrons
If the nucleus is part of an atom (which is almost
always the case in our conditions), not all dexcitation in the
nucleus may radiate as photons of radiation g. Competitive processes
may occur, preventing the emission of part of the photons of g radiation during
deexcitation of excited nuclear levels - especially the process
of so-called internal electron conversion of
gamma radiation (abbreviated only internal gamma conversion
), abbreviation IC (Internal
Conversion). The energy of nuclear
deexcitation does not radiate, but is transferred to an electron
in the envelope, which then flies out as a so-called conversion
electron.
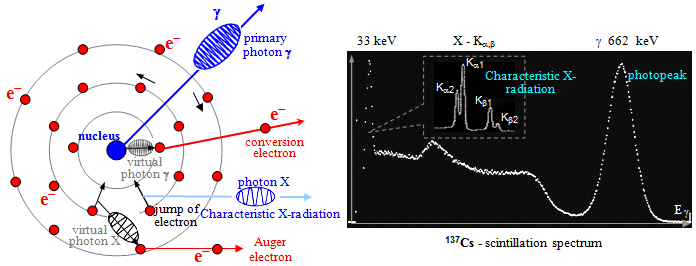
Fig.1.2.7. Schematic representation of the internal conversion of
radiation g to form conversion electrons and characteristic X-rays
and the internal conversion of X-rays to form Auger electrons.
The consequence of the internal conversion for the gamma
radiation spectrum is shown on the right - the presence of the
characteristic X-ray peak [the detailed structure of the Ka,b
characteristic X-ray peaks, measured by a semiconductor Ge(Li)
detector is shown in the box].
In the left part of Fig.1.2.7 all relevant
processes are schematically shown. In particular, the blue arrow
shows the basic case of "undisturbed" radiation of the
photon g from the excited nucleus. The process of internal
conversion can be simply imagined so that the gamma photon
emitted during deexcitation of the excited nuclear level can
"collide" with the envelope electron of its own atom,
which takes all its energy (a photo-effect occurs), the
gamma photon disappears and is replaced by an
electron flies out, released due to the energy received from the
bond in the atom (thicker red arrow). This phenomenon is commonly
observed, it is called the internal conversion
of gamma radiation (formerly also called
the "internal photo effect") and the corresponding electrons are called conversion
electrons.
Note: This older
explanation of the internal conversion mechanism should
now only be considered heuristic; the gamma radiation photon does
not actually fly out of the nucleus
at all (it is only virtual), but the
deexcitation energy of the excited level of the nucleus is
transmitted by the electromagnetic interaction to the nearest
envelope electron directly and it then flies out
of the atom with the kinetic energy given by the difference
between the deexcitation energy of the nucleus and the binding
energy of the electron in the envelope. Physical emission of the
gamma photon is not necessary here, because the wave function of
the envelope electrons partially penetrates the nucleus (there is
a non-zero probability of the electron occurring in the nucleus
region) and the interaction can occur immediately. Thus, despite
its name, internal conversion is not a "two-stage"
process (in which a gamma photon is first emitted and then
absorbed by an electron that ejected), but a direct
"one-stage" electromagnetic process.
Internal conversion is favored in cases where direct gamma photon
radiation deexcitation is prohibited due to "spin
mismatch" (discussed above in the
section "Nuclear Metastability and Isomerism").
The process of
internal conversion most often occurs with electrons on the
K shell (in the 1s state), which is closest to the nucleus, and the wave function
of whose electrons most likely penetrates to the nucleus.
However, it also occurs with less intensity on the L, M, ...
shells (electrons in the 2s, 3s, ... state). If the energy of a given transition is not sufficient
for the internal conversion on the K-shell, it cannot occur and
the internal conversion takes place only from higher atomic
orbits L, M .... An example is 241Am with an excited state energy of 59.6 keV, which not
enough for the binding energy of 118 keV on the K shell of
the daughter neptunium, so the internal conversion occurs mainly
on the L shell and the peaks of the characteristic X-ray
of neptunium in the range of about 12-20keV are clearly visible
in the spectrum- see spectrum in the "Americium" section §1.4. The process
of internal conversion is more efficient when the energy
difference of the levels of the excited nucleus is relatively
small (comparable to the binding energies of the envelope
electrons) and when the excited level does not have a large spin.
The kinetic energy of the conversion electrons is given
by the difference between the energy of the respective transition
of the excited state of the nucleus and the binding energy of the
envelope electron - see below "Discrete
spectrum of conversion electrons".
The probability of internal conversion is different for
different atoms and excited nuclear levels and is characterized
by the so-called coefficient of internal conversion,
which indicates the ratio of the mean number of conversion
electrons to the mean number of quanta g emitted
during a given nuclear transition.
The probability of
internal conversion depends somewhat on
the chemical composition of the radioactive preparation
by a similar mechanism to that described above for "Electron capture" radioactivity.
Characteristic X-rays
As a result of internal conversion, a space, vacancy, is
released on the inner shell (usually K) of the atomic shell after
the conversion electron, so that the electron immediately jumps
from a higher level (most often L) with a quantum of characteristic
X-rays emission (lighter blue arrow in Fig.1.2.7). Hence
the characteristic X-ray peaks, which often appear in the
gamma-ray spectra (eg the 33keV peak in the
radionuclide spectrum 137Cs with energy g 662keV, Fig.1.2.7 right). There is
a whole cascade of deexcitation in the atomic shell, in which
several photons of X-rays are emitted, the spectrum of which has
a fine structure with lines Ka,b, La,b, ...
Intense characteristic X-rays are emitted especially in
radionuclides converting with electron capture,
where, however, the free space in the electron envelope is not
caused by the emission of the conversion electron, but by the
absorption of the envelope electron by the nucleus (see above "Electron capture", Fig.1.2.4 on the right).
Auger electrons
The internal conversion may undergo also
X-rays emitted during electron jumps between the
internal levels of the atom (eg after electron capture,
photoeffect, internal conversion g). The conversion electrons
emitted in this way are then called Auger's electrons
(Pierre Auger first observed them in the
nebula chamber in 1923) - a thinner red
arrow in the left part of Fig.1.2.7. In one radioactive
transformation, several Auger electrons can be
emitted, corresponding to a cascade of deexcitation in the atomic
shell and a fine structure (Ka,b , La,b , ...), mostly low-energy electrons. Intensive sources
of Auger electrons are mainly radionuclides decaying by electron
capture (such as 125I); they are also emitted by some g- radionuclides (including metastable ones, eg 99mTc) - due to the internal
conversion of the nuclear g- transition and the subsequent series of deexcitation in
the atomic envelope.
A special case of the Auger effect is the
filling of a free vacancy by the jump of an electron from a
higher subsurface of the same electron shell (eg the transition LI ® LIII). This process is called the Coster-Kronig
transition in spectrometry (D.Coster
and R.L.Kronig observed it in the X-ray spectrum in 1935) and is accompanied by the emission of photons or Auger
(Coster-Kronig) electrons of very low energy.
Discrete
spectrum of conversion electrons
Conversion and Auger electrons have essentially the same
properties as b-, but
differ significantly in the shape of their energy spectrum. The
spectrum of radiation b is continuous (as explained in detail
above - "Radioactivity beta"),
while the spectrum of conversion and Auger detectors is discrete.
The energy of these electrons is given by the difference
between the primary energy of the transition (deexcitation) and
the binding energy of the electron on the respective shell of the
atomic shell; both of these energies have fixed quantum values.
For mixed b+g radionuclides, the conversion electrons appear as
discrete peaks on a continuous b-spectrum curve.
These discrete conversion electron peaks (of known energies) are
preferably used for the calibration of radiation
spectrometers b, in particular magnetic spectrometers.
Another difference compared to beta-
radioactivity is that during the internal conversion, of course, there
is no emission of neutrinos, only electrons fly out (and
subsequent characteristic X-rays + Auger electrons).
Mixed radioactivity - branched
transformations
In addition to the basic types of radioactivity (alpha, beta-,+,
EC, gamma), some radioactive nuclei have so-called branched
radioactive transformations of one parent nucleus by two
different types of radioactivity - with certain
probabilities - into two different daughter cores.
The ratio of the frequency of each alternative mode transitions
to the total number is called branching ratio. A
branched-converting radionuclide essentially has two
conversion constants and two partial half-lives. If
the imaginary experiment were able to block various alternative
types of transformation, we get for each line 1 and 2
different value for the decay constant l1, l2 and a half-life (T1/2)1 and (T1/2)2. The total value of ltot of the conversion constant by both branches will then be
given by the sum of the partial values of ltot = l1 + l2 and the resulting half-life of this radionuclide can be
considered as effective or total half-life both
branches: (T1/2)tot = (T1/2)1
. (T1/2)2 /[(T1/2)1
+ (T1/2)2] . The hypothetical
partial half-lives (T1/2)1
and (T1/2)2 are inversely
proportional to the relative proportion (branching
ratio [%]) of the individual branches.
The most common type of branched radioactive
transformation is [beta-] + [electron capture (EC) or beta+].
Of the natural radioisotopes, it occurs in potassium-40, which (with a half-life of T1/2 = 1.27.109 years) is converted by beta- radioactivity to argon 40Ar (89%) and by electron capture to calcium 40Ca (11%) - §1.4,
passage "40 K". It
occurs in a number of artificial radionuclides, the most
important of which are, for example, 152 Eu , 186 Re , 192 Ir and several others.
Branched [gamma (IT)]
+ [beta] transformation is observed for several
radionuclides conversion. This is the case when a certain excited
state of the nucleus is metastable (described above in the
passage "Nuclear isomerism and metastability") with a long half-life. Then, instead of
deexcitation of gamma photon emissions (or internal conversion),
there may be a certain probability of an alternative
beta-radioactive transformation of this excited nucleus to
another neighboring nucleus. An extreme example is europium 152mEu
(see the passage "Europium" in §1.3), on the contrary, it also occurs to a
small extent with the well-known technetium 99m
Tc . The preparation of lutetium-177 by the
branching IT-beta transformation is facing the reaction 176Lu (n, g )177Lu, when a
metastable contaminant 177mLu is formed, which in 22% dexcites by successive
isomeric transitions to the ground state 177Lu and in 88% is converted independently by b- -radioactivity to a relatively high excited state
1315keV of the daughter 177Hf - see 177 Lu .
Furthermore, it is a branched
transformation [alpha] + [beta-],
occurring in heavier nuclei. For natural radionuclides we are
occurring in the decay series of uranium and thorium (§1.4,
section "Decay series"), wherein the bismuth isotopes 211 212 213Bi
with both converted a radioactive isotopes of thallium on and radioactivity b to isotopes of
polonium. Furthermore, actinium 227Ac is converted by
alpha radioactivity to 223Fr and beta by conversion to
227Th. This leads to branching of the
decay chains.
Combined [alpha] + [spontaneous
fission] transformations occur in heavy uranium
and transuranium radionuclides. For uranium and
lighter transuranium, the proportion of spontaneous fission is
very small - the branching ratio of spontaneous fission is
approximately: 235U (7.10-9 %), 238U (5.5.10-5 %), 241Am
(0.36%). However, for heavier transurans, the proportion of
spontaneous cleavage is not negligible, sometimes even decisive.
E.g. californium 252Cf (T1/2 = 2.56 y.) is 97% converted by alpha-radioactivity to 248Cm
and in 3% spontaneous fission occurs into two lighter nuclei from
the middle of the periodic table and 2-3 neutrons. Californium 254Cf
with an effective half-life of 60.5 days is even converted in
only 0.3% by alpha-radioactivity to 250 Cm and in the
whole 99.7% spontaneous fission occurs ..!...
"Exotic" types of
radioactivity
In addition to the standard types
of radioactivity (a, b, g - described above), there are rarely occurs also less
common, "exotic" types of radioactivity (and some other types are only presumed and not yet
proven). So let's make a brief mention of
some less common (and sometimes debatable) types of radioactivity
:
Spontaneous
fission of heavy nuclei
Some heavy nuclei in the uranium and transuranic regions, in
addition to radioactivity a show another specific but less common type of
radioactive transformation: spontaneous fission of
heavy parent nucleus A into two lighter nuclei
F1 and F2 *) (located roughly in the
middle Mendeleev's periodic tables of elements), sometimes called
fragments or fission products : NAZ ® N1F1Z1 + N2F2Z2 + (2-3)no + Q(energy). In addition to these
resulting nuclei, neutrons are also emitted
during fission, in number usually 2-3. During the fission of
heavy nuclei into lighter nuclei, considerable energy
is released (derived from the difference of
binding energies, see §1.3), which is carried away in the form
of kinetic energy by the resulting nuclei and neutrons.
*) In addition to the usual binary fission,
there is also a relatively rare type - the so-called ternary
fission (0.2-0.3% of cases), in which the heavy nucleus
splits into three fragments. Two of these
fragments are medium-heavy nuclei from the middle of the periodic
table, the third can also be a very light nucleus - helium 4He, tritium 3H, 5He is also observed (which decomposes to 6Li with a half-life of about 0.8 s).
Interestingly, in spontaneous fission, a 25% higher proportion of
ternary fission is observed than in fission induced by neutron
absorption (this is probably related to the supply of some
additional energy during neutron absorption by the nucleus).
The cause of spontaneous fission of
heavy nuclei lies in their structure and in the properties of
nuclear forces. In §1.1, section "Atomic nuclei", it
was mentioned that nuclear forces are of short range and exhibit
a saturation state. Heavy nuclei therefore have a lower binding
energy per nucleon than lighter nuclei from the center of the
Mendeleev table of elements. The configuration of two lighter
cores is therefore more energetically favorable than the
configuration of one heavy core (see Fig.1.3.3 in §1.3, part
"Nuclear energy.
Fission and fusion of atomic nuclei"). The actual fission
process is hampered potential barrier strong interaction
holding the core together: in delaying one of the core portion
from each other, it is necessary initially to overcome the large
attractive force - increases potential energy that only after
reaching the height of the barrier (after
sufficient distance, where short-range nuclear forces begin to
decline sharply) begins to decline. In
order for fission to occur, it is necessary to overcome this
energy that holds the nucleus together. The fission process is
already energy efficient for cores with N> 80. However, the
energy gain in the division of these lighter nuclei is very small
and the height of the potential barrier is too high, so that
fission does not occur. Only in very heavy nuclei
do relatively weak nuclear forces (saturation state), so that the
height of the "potential wall" by which the individual
parts of the nucleus are held together is low *). Therefore,
there is a certain probability that the fragments pass through a
potential fission wall due to the "tunnel effect"
(similar to radioactivity a) and fly apart with high energy.
*) For the heaviest transurans, the height of the potential wall
for fission is already practically zero, so it is probably no
longer possible to form transuranic elements above a certain Z-
limit, which would not disintegrate immediately by spontaneous
fission. This is also one of the reasons why a kind of
"island of stability", expected by some experts for
superheavy nuclei in the area Z » 120-150, probably doesn't
exist.
Spontaneous fission occurs, for example,
with uranium 235,238U (demonstrated in 1940 by
G.N.Flerov and K.A.Petržak). It is a
process that proceeds with scant intensity and
compared with other kinds of radioactivity (in the case of heavy
nuclei mainly a) is practically negligible *). However, efficient
fission of heavy nuclei occurs upon neutron absorption,
as will be shown in the following §1.3; in this case, however,
this is not radioactivity, but a nuclear reaction. A
small amount of neutrons, originating from spontaneous fission,
can then initiate a chain fission reaction when
the so-called critical amount of fissile
material is reached (§1.3, part "Fission of atomic nuclei").
*) Exceptions are some heavy transurans
(described in detail in §1.3, part "Transurans"),
eg californium 252,254Cf, for which spontaneous fission is a common process
competing with alpha radioactivity. In practice, the isotope californium
252Cf
is mainly used as a source of neutrons (see §1.4
"Radionuclides", passage "Transurans") in some laboratory applications.
Radioactivity
"higher" than a-helium -
"cluster" radioactivity
Radioactivity alpha may be regarded as "split" parent
nucleus to a helium nucleus ( a
particles) and the remainder of the core: NAZ ® 4He2 + N-4BZ-2. From this point of
view, radioactivity a and a spontaneous fission can be understood as two
observed extreme cases of one and the same nuclear process. The
natural question arises as to whether (non-fissile) radioactive
transformation is possible with the emission of particles heavier
than particles a, for example, carbon, nitrogen nuclei or the like..?. (Or less massive nucleon particles? - see next
paragraph). This type of radioactivity was
first demonstrated in Oxford in 1984 for the radium isotope 223
Ra , where a small amount (1:10 billion a) of decays was
observed between the usual a -radioactivity with the emission of carbon
isotope nuclei 14C: 223Ra ® 209Pb + 14C (+12MeV). Later, a
similar type of decay was registered in other radium isotopes (222,224, 226 Ra ), as well as other heavy nuclei. Furthermore, eg for
isotopes 231Pa, 230Th, 233U, 237Np, 241
Am,... in addition to the dominant a radioactivity,
transformations with the emission of other heavier nuclei - neon 24Ne, magnesium 28Mg, silicon 32,34Si are rare
occur.
Since this is a nuclear transformation
with the emission of nuclear fragments - clusters or groupings of
nucleons (clusters), this rare type of nuclear
transformation is called cluster radioactivity (cluster
decay) or heavy ions radioactivity. It is a
kind of "transient type" between alpha-radioactivity
and spontaneous nuclear fission. Its mechanism is somewhat
similar to that of alpha radioactivity (see
above "Radioactivity alpha",
Fig.1.2.2 right) - a quantum
tunneling process in which a stronger bound group
(cluster) of nucleons within the nucleus overcomes and penetrates
the potential barrier of attractive short-range nuclear forces.
The probability of this tunneling is very small. The energy of
emitted clusters is substantially higher than in alpha
radiation - ranges from 20MeV (at 14C conversion) to 95MeV (at 34Si conversion).
Proton and
neutron radioactivity ?
In the vast majority of nuclei, strong interactions between
nucleons keep the nuclei in a relatively stable state - their
radioactive transformation can occur by mutual transmutation of
neutrons and protons (beta -, + radioactivity), deexcitation of excited levels
(isomeric transition - g emission ), or by radiation a. We do not observe
spontaneous emission of individual nucleons or light nuclei with
the exception of alpha particles and rare cluster radioactivity.
However, in nuclei with a high excess of protons
or neutrons, the balance is so disturbed that the emission of
individual nucleons or whole light nuclei is energetically
possible and advantageous.
Upon irradiation of some nuclei with
protons and accelerated heavier ions, it was observed that in
addition to the standard b+ radionuclides also
form nuclei with a large excess of protons, which emit
protons when they decay. This phenomenon has been
observed, for example, in 17Ne, 25Si or 41Ti. The proton can be emitted either directly from an
unstable nucleus with excited nucleons (tunneling similar to the
decay of a), or "in two stages" - following the previous
decay of b+; a case of emission
of 2 protons was also recorded. This process, in which the
neutron deficient nucleus NAZ of proton emissions is converted to the
nucleus N-1BZ-1, was called proton
radioactivity or proton decay.
Note: The proton
radioactivity presented here has nothing to do
with the hypothesis of decay or "radioactivity" of the
proton itself, discussed in §1.5 !
The question is whether the emission of
protons from short-lived excited neutron deficient nuclei can be
considered as a separate type of radioactivity. The specific
characteristics of this process (short half-life and very small
relative proportions) suggest that in many cases it is rather a
kind of retarded concomitant phenomenon in
nuclear reactions *). In some cases, however, the lifetime
(longer than the mere characteristic transit time of a nucleon
through the nucleus) suggests that there is some resemblance to
radioactivity. However, only proton radioactivity can be
considered as true a one-step process, in which a proton
is emitted from the ground state of the nucleus (or from the
isomeric state). Proton radioactivity was demonstrated in the
isomeric state of the cobalt core 53 Co. Proton radioactivity of nuclei in the ground state
was demonstrated in the 1980s in 151Lu: 151Lu ® 150Yb + p (+1,2MeV), then in 147Tm, as well as in lighter nuclei of isotopes cesium 113Cs and iodine 109I with a high
deficiency of neutrons. Such highly neutron-deficient nuclei are
prepared by special experimental methods of bombarding suitable
targets with accelerated heavy ions, with electromagnetic
separation of the required radionuclides. This process is not of
practical significance, the theoretical significance lies in the
illustration of the variety and diversity of phenomena
occurring in nuclear reactions and in strongly unbalanced nuclei.
*) A similar phenomenon, the emission
of delayed neutrons, is encountered in the fission of
heavy nuclei, where in addition to the "primary"
neutrons emitted immediately during the actual fission, other
neutrons with a relatively large time delay are emitted from the
fragments. However, this process is two-step: b occurs first-
decay of a chip with a longer half-life, after which only a rapid
neutron emission from the excited daughter nucleus occurs at a
time comparable to the kinematic nuclear time. Therefore,
"neutron radioactivity" is not mentioned. We can also
think about a free analogy with the so-called resonances
in high-energy interactions of elementary particles, discussed in
§1.5 "Elementary particles".
Another "exotic"
types of radioactivity ?? - muon, pion, hyperon radioactivity ??
Studies of the properties of heavy nuclei far from the region of
stability point to the possibilities of other, even more unusual
types of radioactivity. It could be pion
radioactivity, in which the heavy nucleus A
would split into two medium-heavy fragments B and C
(or several fragments) and simultaneously emit a p-
meson :
NAZ ® p±,0 + N1BZ1 + N2CZ2, whereas N = N1+N2, Z = Z1+Z2+Zp .
The muon radioactivity is discussed analogously
: NAZ ® m± + nm + N1BZ1 + N2CZ2 ; N = N1+N2, Z = Z1+Z2+Zm .
Or even hyperon radioactivity with lambda
hyperon emission: NAZ
® L0 + N1BZ1 + N2CZ2 ; N = N1+N2, Z = Z1+Z2 ,
or with hyperon emission S : NAZ
® S±,0
+ N1BZ1 + N2CZ2 ; N = N1+N2, Z = Z1+Z2+ZS .
Possibly, emission of nuclei with bound hyperons - so-called hypernuclei
or hyperfragments CL, eg: NAZ
® N1BZ1 + N2CLZ2 , followed by rapid
meson or nucleon decay of the hypernucleus...
Stability
and instability of atomic nuclei
The time stability or instability of an atomic nucleus is given
by a complex interplay of strong, electromagnetic and weak interactions,
determining particle processes and energy ratios in the
nucleus, related to the number of protons and neutrons,
their ratio and arrangement. Nuclei in which the energy level of
a given configuration of protons and neutrons is minimal are
stable over time. However, nuclei that are not in an
energetically stable state tend to go into a more energetically
stable state by a certain recombination of
proton and neutron states - by transforming protons and neutrons,
emitting particles or emitting quanta of "excess"
energy; there are radioactive transformations
of nuclei. In order for such a nucleus transformation to take
place, two basic conditions must be met :
1. Existence of a
nucleus with a lower energy level - usually
"adjacent" or close to its proton and nucleon number (except for spontaneous decay of heavy nuclei "Fission
of atomic nuclei").
2. A physical mechanism who
performs the transformation an energy-richer nucleus into a
lower-energy nucleus.
The energy
levels of proton and neutron configurations in nuclei
are determined primarily by strong ones nuclear
interaction, with minor corrections from the electromagnetic
interaction (proton and neutron levels are occupied
independently; it was discussed in §1.1, section "Nuclear
structure", passage "Strong
nuclear interaction"). The most
common physical mechanism of nuclear transformations is the weak
interaction, which through the transmutation of
quarks within nucleons can mutually transform protons
and neutrons - beta-,+ radioactivity.
However, this only happens when the energy condition
is met: the new configuration of protons and neutrons must have
less energy than the original configuration. For heavy uranium
and transuranic nuclei, another mechanism of transformation is short-range
strong nuclear interactions, causing relatively weak
binding of heavy nuclei, and conversely strong binding of helium 4He2
nuclei, which can "tunnel" from the peripheral parts of
heavy nuclei as alpha particles (again when the
energy condition is met). The short range of strong nuclear
interaction is also responsible for the spontaneous
fission of heavy nuclei. In gamma
isomeric transitions, the mechanism is the electromagnetic
interaction, thanks to which the energy difference of
the excited nucleus radiates as a high-energy quantum - a photon
of electromagnetic radiation.
According to the shell model of
nuclei due to the exclusion principle, a proton or neutron occurs
in the same energy state only 1 time (or 2
times, with opposite spins). Another proton
or neutron can only occupy a higher energy state. It is therefore
energetically advantageous to fill the same energy state with a
proton and then a neutron. From this it can be expected that
nuclei with the same number of protons and neutrons will
preferentially occur in nature. For lighter cores (N<»30) this rule is
actually confirmed. However, electrostatic repulsion increases
with large cores. Therefore, for heavier nuclei to ensure
stability, neutrons are beginning to predominate,
exhibiting only attractive nuclear forces and not electrical
repulsion.
In the above passages of this §1.2
"Radioactivity", we have discussed in detail the mechanisms
by which radioactive transformations of various types of nuclei
occur. Let us now look globally at the set of
all known atomic nuclei (nuclides) in terms of the laws of their stability,
or, conversely, instability - the
"tendency" to spontaneous radioactive
transformations.
For a detailed and clear capture of the properties of
nuclei, it is very useful to draw them in the so-called nuclide
map. It is a rectangular network of small squares in
which the nuclei are arranged in rows according to the increasing
number of protons p (= Z) and in columns according to the increasing number
of neutrons n (= N-Z). Each nuclide thus corresponds to one small
square with coordinates [p, n], in which we can then write the name and selected
characteristics of the nuclide *).
*) Such a table (map) of nuclides is ideologically somewhat
similar to Mendeleev's table of chemical elements. In addition to
the basic difference between the atomic nucleus and the envelope,
there are two differences in notation: 1.
Mendeleev's table is periodic, the table of nuclides is
sequential. 2. Mendeleev's table is
traditionally arranged according to the system of writing text in
lines below each other (from left to right + from top to bottom),
while our table of nuclides is arranged by the system of plotting
quantities in Cartesian coordinates (from left to right + from
bottom to top).
Note: Sometimes a special
system of hexagonal arrangement is used nuclide
tables ("trilinear arrangement"), in which, in
addition, the hexagons representing the nuclei are color-coded
depending on the half-life of the nucleus.
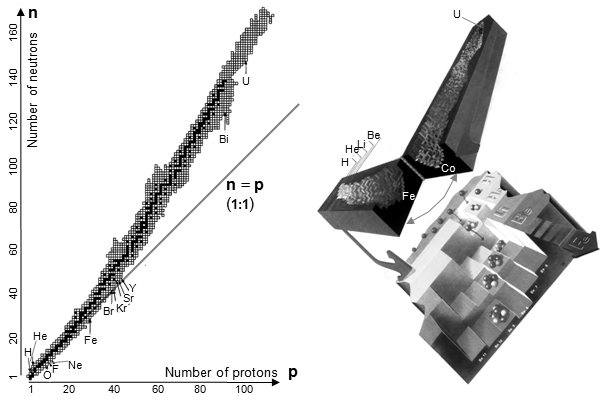
Fig.1.2.8. To clearly illustrate the properties of nuclei, their
drawing on the nuclide map is used.
Left: A simple two-dimensional map of
nuclides. Right: Three-dimensional map
including binding energies.
The three-dimensional model was made within the diploma thesis
under the guidance of Doc.Dr.J.Kleczek, DrSc.
A reduced schematic representation of the
nuclide map is in the left part of Fig.1.2.8. Details of the
characteristics of the nuclei are not marked here (they would not fit into a small picture), only stable nuclei are marked with
black squares, empty (white) squares correspond to unstable,
radioactive nuclides. From this diagram we see mainly three facts
:
¨ 1. All existing nuclei form in the map
of nuclides a band going to the right and up in
an approximately diagonal direction, which gradually expands
- with increasing number of protons increases the diversity of
existing nuclei (there are more different isotopes).
¨ 2. Stable cores form in
this general belt a kind of "stability line".
For lighter nuclei (N<»30) with stable nuclei centered around the line n = p , i.e. having
approximately the same number of protons and
neutrons, are symmetric. For heavy stable nuclei
gradually begins to dominate the number of neutrons
over protons. It due to the fact that with increasing Z (=
p)
increases the repulsive Coulomb force of protons, which is to
reduce the total energy of the core is advantageous to compensate
by the presence of more neutrons. The ratio of the number of
protons and neutrons decides on the stability and instability of
nuclei through weak interactions, causing radioactivity
beta (see note below "Weak
interactions influence on the stability of the cores").
¨ 3rd Stability line ends
with bismuth, 209Bi83, which is the last, most heavy (almost) stable nucleus
*). All the heavier nuclei (uranium and
transuranic region) are already radioactive (usually radioactivity a, possibly also spontaneous
fission).
*) Natural bismuth consists isotope
209Bi,
which until recently was considered stable. In
2003 it was found that this isotope is slightly
radioactive - with an extremely long half- 1.9.1019 years subject to
alpha-radioactivity. From a practical point of view, however,
natural bismuth appears to be non-radioactive (300 kg of bismuth would have an activity of 1Bq). Lead of 208 Pb is now considered to be the heaviest truly stable
nuclide.
Influence of weak interactions on the stability of nuclei
If there was only a strong interaction (and
electromagnetic) in the microworld, there
could be "mononucleon" nuclei composed only of protons
or only neutrons (mononeutron nuclei would
not have an electron shell). Nuclear
"monsters" composed of thousands of neutrons could also
form. However, we do not observe anything like this in nature,
there are no stable nuclei from either the two protons themselves
or the two neutrons; even the neutron itself is unstable. Namely,
there is another kind of force in nature - a weak
interaction, which ruthlessly transforms beta
(- or +) radioactivity each nucleus, in which a certain
ratio between the number of protons and neutrons is disturbed (if the energy condition in the potential well given by
a strong nuclear interaction is met). The
mechanisms of these processes have been discussed above in the
"Beta
Radioactivity" section.
When interpreting the mechanisms of individual
types of radioactivity, we have seen that the stability or
instability of nuclei is determined by two interrelated factors:
the number of protons and neutrons and the binding energy of the
nucleus. An even more illustrative picture of the properties of
nuclei is thus obtained by plotting the mean binding
energy of a nucleus per nucleon for each nucleus in the
third dimension (perpendicular to the drawing) of the nuclide
map. Since each nucleon in the nucleus is bound in a kind of
potential well, we carry this binding energy downwards.
This creates a three-dimensional table of nuclides,
having the shape of a "valley of nuclides" extending
diagonally through a coordinate network (Fig.1.2.8 on the right).
The most stable nuclei lie at the
"bottom" of this valley of radionuclides - the binding
energy of their nucleons is the largest. On the "left
slope" of the nuclide valley there are nuclei rich in
protons (sometimes referred to as the "proton slope"),
which decay by b+
-radioactivity, on the "right slope" there are nuclei
with a predominance of neutrons ("neutron slope"),
decaying with b-
-radioactivity. These facts are clearly visible in cross
sections of the valley of nuclides, where there are
nuclei with the same number of nucleons (isobars) - the left part
of Fig.1.2.9. The most stable cores are at the bottom of the
valley. Nuclei with an excess of protons (left) or with an excess
of neutrons (right) have excess energy *), which it tries to get
rid of b- or b+ decay. Therefore, the nuclei on the proton and neutron
"slope" are b- radioactive.
*) This energy balance can be well explained by the shell
model of the atomic nucleus structure discussed in the
previous §1.1. If there is an excess of protons over neutrons in
the nucleus, protons will fill slightly higher
energy levels than neutrons. The nucleus can then go into a lower
energy state by converting the proton by a b+ -conversion to a neutron, which goes to a free lower
energy neutron level. This is analogous to nuclei with an excess
of neutrons, where b- decay
converts a neutron into a proton, which occupies a free proton
level with lower energy.
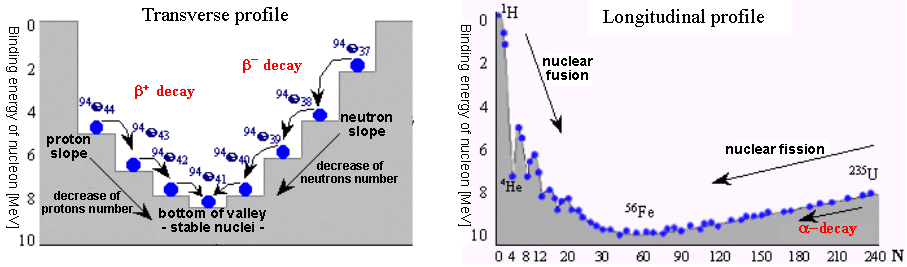
Fig.1.2.9. The "valley of nuclides" profiles in the
three-dimensional table give a clear idea of the energy balance
of the atomic nucleus bond.
Left: Example of a cross section
through a valley of nuclides. Right:
Longitudinal section through the valley of nuclides at the
deepest point (corresponding to the relatively most stable
cores).
The longitudinal section
through the valley of nuclides in the deepest places is also
interesting - Fig.1.2.9 on the right. This longitudinal section
gives a curve of the dependence of the binding energy (per
nucleon) on the nucleon number for the relatively most stable
nuclei, ie nuclei occurring in nature. From this curve, we see
that the most strongly bound nuclei have elements of the iron
group that are the most stable and form the deepest
"bottom" of the nuclide valley, while the light and
heavy nuclei have smaller binding energies. It is clear that
"falling to the bottom of the valley of radionuclides"
in the longitudinal direction is possible in two directions: By
merging light nuclei into heavier ones (nuclear fusion,
thermonuclear reactions), or decay (a) or fission of heavy nuclei
into lighter nuclei *); in both cases there is a release of
nuclear energy. We will deal with this curve in detail in the
following §3.3, part "Nuclear energy", in connection with nuclear energetics,
where we will redraw it in the inverted form (Fig.1.3.2).
*) Nuclear fusion cannot take place
spontaneously, but only at high kinetic energies of merging
nuclei at high temperatures (inside stars
or in a thermonuclear reactor, see §3.3, section "Fusion of
atomic nuclei"). Radioactivity a
it occurs spontaneously in heavy nuclei, whereby these nuclei
"fall" along the valley of nuclides towards lighter and
more stable nuclei. This process is often combined with b- radioactivity
in the transverse direction of the proton or neutron slope. The cleavage
of heavy nuclei can occur spontaneously, but usually only with
negligible intensity (with the exception of
heavy transurans) . Efficient fission of
heavy nuclei occurs during neutron absorption, these processes
will be discussed in the following §1.3 "Nuclear
reactions", section "Fission
of atomic nuclei".
The nuclide valley of a three-dimensional
table of nuclei thus gives us a clear energetic idea
about why some nuclei are stable and others decay radioactively.
Just as a stone released down a mountain slope rolls into a
valley due to gravity, so nucleons in nuclei on energetic
"slopes" try to get as low as possible to the bottom of
the valley, where they are "pulled" by nuclear forces.
Whether they "succeed" and nuclear transformation
occurs, is determined by the energy balance in relation to the
mechanism of radioactivity b, a, event. nuclear fusion or fission.
Unstable nuclei lying "low on the slope" of
the nuclide valley reach a stable configuration with only one
radioactive transition (b+, -, a). However, nuclei
with a large excess of protons or neutrons, as well as heavy
nuclei in the uranium and transuranic regions, lying high on the
"slope" of nuclides, must undergo a whole cascade
of individual radioactive transformations before resting on the
"valley floor" in a stable configuration. This creates
radioactive decay series (see
§1.4 "Radionuclides", part "Decay series", Fig.1.4.1).
| Back: Nuclear physics and physics of ionizing radiation | |||
| Nuclear and radiation physics | Radiation detection and spectrometry | Radiation applications | |
| With cintigraphy | Computer evaluation of scintigraphy | Radiation protection | |
| Gravity, black holes and space - time physics Anthropic principle or cosmic God | |||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | |||