Microworld particles, their origin, properties and
application in research and technology
1.
Nuclear and radiation physics
1.0. Physics - fundamental natural
science
1.1. Atoms and atomic nuclei
1.2. Radioactivity
1.3. Nuclear reactions, nuclear energy
1.4. Radionuclides
1.5. Elementary particles and accelerators
1.6. Ionizing radiation
1.5.
Elementary particles and accelerators
In interpreting the properties of atoms in
Chapter 1.1, we have learned that neither an atom, nor even its
nucleus, are elementary building blocks of matter, but are
composed of even smaller particles - electrons,
protons, neutrons. In the study of radioactivity, we also
recognized some other particles - positrons, neutrinos. Are these
subatomic particles really already internally
"monolitic" - elementary and fundamental? Or do they
have their internal structure, composed of "even
smaller" particles? (A more detailed
discussion is below in the section "Are elementary
particles really elementary?").
In this chapter we will try a brief but
systematic trip to the varied and wonderful world of elementary
particles. We will proceed inductively in the
interpretation. After introductory passages on the common
properties of particles, their classification and patterns of
interactions, we will move from basic, known and widespread
particles and their simple properties (straight from
experiments), through "more exotic" particles and more
complex mechanisms of interactions, to unitary symmetries and
attempts to clarify the internal structure of particles.
We will also mention hypothetical and model particles,
some of which have not yet been directly discovered, or their
role in nature is not yet fully understood.
We will first outline the systematics
of elementary particles and then analyze the properties
and interactions of individual specific types of
particles, including the formation of particles
in high-energy interactions. And also antiparticles
- their origin and annihilation, their role in nature,
possibilities of use. We will also think about what the
individual particles have in common and how we have progressed
towards a unified understanding of particle and field physics - unitary
field theory. Finally, we describe how we investigate
the interactions of particles at high energies on particle
accelerators.
Behind all this knowledge about elementary
particles is hidden the enormous effort and colossal
volume of work of thousands of physicists, technicians
and workers - designers of complex acceleration systems and
detection apparatus.
But before that, let's make a few general
remarks and discussions about particles as such :
Terminological note -
elementary ? :
The name "elementary" or "basic"
should mean that it is a further indivisible
object, without internal structure; it is thus the simplest
material object acting as a separate physical entity. However, in
the course of the scientific knowledge of the microworld, it has
been shown several times that particles previously considered to
be basic (elementary) have an internal structure and consist of
even "smaller", more basic or "more
elementary" particles. According to earlier opinions
"indivisible atom" (hence its name), has a complex
structure of the electron shell and the atomic nucleus. Protons
and neutrons in atomic nuclei have also been considered
indivisible, but next research (in a standard particle model) has
shown that they consist of quarks (as do other hadrons). Opinions
on the "elementality" of particles can thus vary
depending on the current state of physical knowledge (a more detailed discussion is in the passage below
"Are
elementary particles really elementary? ').
Therefore, since many particles are
"folded", the "elementary"
may be misleading. However, this is the established name, like
the name "atom", which has long been not
"indivisible". In recent years, often the word
"elementary"omits and speaks only of "particles".
Are
there any elementary particles at all? "Ball"
model.
Our idea of existence - that "something
exists" - is based on our daily experience of
observing the macroworld of the
surrounding nature. There are, for example, stones - we can see,
touch and weigh by hands, or throw them. There are different
species of plants and animals with specific looks and properties.
There are cells in organisms that can be observed under a
microscope, including their internal structure (see eg §5.2., Section "Cells - basic units of living organisms") and study their
biochemical manifestations. However, in a microworld
of subatomic or even subnuclear dimensions, it is more
complicated.
Particles of the
microworld we can't see even with the strongest
microscope - they are much smaller than the wavelength of visible
light. Even if we reduced ourselves in the imagined sci-fi
concept to "dwarfs" the size of a picometers and
observed with radiation of much shorter wavelengths, we would not
see any localized particles. Quantum uncertainty relations
"blur" the velocity determination with accurate
position measurement, and the particle velocity measurement in
turn blurs its position. We would perhaps only see blurred tufts
of fluctuating fields. From this usual point of view, we could
make a "heretical" claim that "elementary
particles do not exist "!
However, in more detailed physical
research, we come to the realization that there is a "something"
hidden that carries physical forces, such as an electric charge,
something that transmits energy trought space, that causes
mutually influences - interactions - of material
bodies. In classical physics it is a physical field, in quantum
physics the quantum of fields. We call this "something"
the elementary particles (the
word "elementary" discussed above).
We can not imagine it in any concrete way and that is why model
them as small spheres (small balls) - eg.
electrons draw a red protons as blue, neutrons as gray spheres,
neutrinos as perhaps green; it is a matter of convention. These
bullets, having a certain mass, charge and other physical
characteristics, are, according to the usual laws
of (relativistic) mechanics move through space
at a certain speed and the associated kinetic energy. With a
certain probability (see "Effective
cross-section" below), they can
"collide" - interact - with other
spheres (particles), while other spheres - particles of the same
or different properties - fly out of this place. However, during
the actual internal course of the interaction, the "ball
model" cannot be used, there are often quite complex quantum-field
processes (see "Feynman diagrams"
below).
The ball model is very successful
- in co-production with physical mechanisms of electromagnetic,
strong and weak interactions can explain or represent practically
all phenomena with particles of the microworld in atomic,
nuclear, radiation and particle physics. This "ball
illustration", possible supplemented by the wave nature,
therefore we draw in most of the pictures of our treatise "Nuclear
Physics and the Physics of Ionizing Radiation".
Who ordered the
"exotic" particles ?
To understand the structure of matter around us, we will suffice
with the few particles mentioned above (§1.1
and 1.2) - photons, electrons, protons, neutrons (in mor complex
phenomena also neutrinos, mesons, quarks u and d ).
Nevertheless, in the interactions of particles (whether
artificially induced or in cosmic rays) we encounter many
other particles, which - at is seem - they have no role
to play in building of matter. Nothing of them are composed, they
are not able to create bound structures, they usually
disintegrate immediately after their formation. The metaphorical
question arises "who ordered them?" -
what is the meaning and role in the functioning of our world? (This question was first raised by I.I.Rabi in
connection with the discovery of the muon).
The answer to this question is trying to find a unitary field
theories and particle physics in co-production with astrophysics
and cosmology.
Unitary field theories attempt to find
laws and mechanisms that allow or imply the existence of these
particles - as a quantum of excited fields or geometric
structures (§B.6 "Unification of fundamental
interactions. Supergravity. Superstrings."). Astrophysics and cosmology show, that all these
particles were probably once in the earliest
stages in the universe, they already played their role in
the "cooking" of
matter and then disappeared (see eg §5.5 "Microphysics
and cosmology. Inflationary universe."
of the mentioned books); without them the universe would not be
as it is, perhaps there would be no mass at all..?.. Some of
these particles perhaps still form a mysterious "dark
matter" in space (see eg § 5.6 "The Future of
the Universe. The Arrow of Time. Dart matter, Dark energy."). And we are now trying to re-create and
explore these particles in order to understand the early
universe and be able to answer the questions more surely, how
matter was formed and what is its internal properties ...
Indistinguishability of elementary
particles
Bodies and particles in classical mechanics do
not lose their "individuality" during
their motion, even if they are the same particles with the same
physical properties (from a macroscopic point of view). Such
particles forming a given physical system can be
"marked" or "numbered" at a certain initial
time and then, while monitoring their movement, we can, at least
in principle, identify each of the particles in
the system at any time - the particles are distinguishable
here.
In the analysis of motion and behavior of
particles in quantum mechanics the situation is
completely different in this respect. Due to corpuscular-wave
dualism and the uncertainty principle, particles, such as
electrons, have no trajectories in the sense of classical
kinematics. If we determine the position of a particle at a given
moment, its momentum becomes indeterminate; then in the following
moments it is not possible to determine any specific values of
the particle coordinates. Therefore, if we try to locate
electrons at a certain moment and imaginarily "number"
them, then at another point in time when locating an electron at
a certain point in space, we can no longer determine which of the
considered electrons got to this point. In quantum mechanics,
there is no possibility to continuously monitor the motion of
individual particles and thus distinguish them. Microparticles
are manifested only by their interactions with
other particles. Thus, in quantum mechanics, the same particles
completely lose their individuality - their
physical properties are identical, they are indistinguishable
from each other.
Spin, symetry of wave function and
statistical behavior of particles
The quantum-mechanical behavior of sets
consisting of the same type of particles is based on this
principle of indistinguishability of particles. Since the
particles are the same and indistinguishable, the physical states
of the system obtained by exchange (swapping, transposition) the
two particles "1" and "2" must be equivalent;
from a quantum point of view, the probability density ú yú 2 of this system must remain the same when the particles
are interchanged: úy ("1",
"2" y ("2",
"1") ú 2 , ie either y ("1",
"2") = y ("2", "1"), or y ("1",
"2") = - y ("2", "1") - the wave function of
the system can only change by a sign. Thus, there are two
possibilities: 1. The wave function is either symmetrical
and does not change with any permutation of particles; 2.
Or, the wave function of the system is antisymmetric
- it changes sign when each pair of particles is transposed.
Which of these options is realized depends on the type of
particles - it is related to their spin (§1.1,
passage "Spin").
Below, according to this criterion, we divide particles into bosons
with a symmetric wave function (integer spin) and fermions
with an antisymmetric wave function (half-number spin) - passage
"Fermions-Bosons". By analyzing the wave functions of a system of
the same particles, it can be shown that in a set of identical fermions,
two particles (or more particles) cannot be in the same
quantum state - the so-called Pauli exclusion principle applies.
While in a set of bosons there may be an unlimited number
of particles in the same quantum state.
The analysis of the
relationship between the spin of particles and their statistical
behavior in a set of particles decays into three sub-problems :
1. Relationship between the spin and symetry of
the wave function
Spin is an intrinsic angular momentum of
particles, analogous to the rotational angular
momentum of a particle during its rotation around its axis (but
it cannot be explained quantitatively in this way!), rather
related to symmetries with respect to spatial rotation (within quantum mechanics, spin is described in §1.1.,
passage "Spin").
From the point of view of quantum field theory (secondary quantization), a spin field is
interpreted as a measure of symmetry in the
plane wave of the field: a field has spin s (spin number s),
if its plane wave is invariant to rotation by an angle of
2p/s around the
propagation direction. Thus, the spin of a particle indicates the
rotational symmetry of the wave function
relative to the rotation in space. For particles with integer
spin, most often s=1, the wave functions are invariant to
rotation by an angle of 360o;
the wave functions are symmetric with respect to
the transposition. ..., the particles behave like bosons.
For particles with a half-numbered spin 1/2, the wave functions
are antisymmetric. ....... ......, the particles
behave like fermions.
Note:
This is just a brief heuristic outline of the
relationship between the particle's spin and the symmetry of the
wave function. In a more detailed derivation, analysis using
relativistic quantum field theory is used.
2. Relationship between symetry of wave function
and occupancy of quantum states
Consider two identical particles a, b with
the wave functions y(....... y(........ ......; the wave function for a system
composed of these two particles will then be Y(....... = ..... If
the functions y(.......
y(.....
are antisymmetric with respect to the transposition of
particles y(.......
= - y(....,
the resulting wave function Y(...... a pair of particles located in the same
quantum state will be equal to zero - the probability is
zero here. Two particles with an antisymmetric wave function cannot
be in the same quantum state, applies to them so-called Pauli's
exclusion principle. For particles with a symmetric
wave function with respect to transposition, all combinations of
state functions will have positive signs, so the resulting wave
function y will also be
positive and non-zero - any number of particles of this
kind can be in the same quantum state.
3. Own statistic behavior of particle sets
By statistical behavior (abbreviated as "statistics")
of particles we mean the average distribution of their
states - according to velocities, kinetic energies - in a large set
of these particles. This analysis is dealt with by a special
field of statistical physics, in practice mostly
in conjunction with thermodynamics. In the simplest case
of a sufficiently large set of non-interacting particles in
thermodynamic equilibrium, behaving according to the laws of classical
(non-quantum) physics, analysis by methods of statistical
mechanics shows that the average (expected) number of
particles <N (E)> with energy E is given by Maxwell-
Boltzmann distribution <N (E)> = 1 / e-E/kB.T, where T is the absolute
temperature [oK] and kB is the
Boltzmann constant (giving the conversion
coefficient between the average kinetic energy of the particles
in the gas and the thermodynamic temperature of the gas kB = 1.380649×10-23
J/oK).
In the case of the
above-mentioned quantum properties (point 2.),
the distribution function N(E) will depend on the occupation
rules of quantum states. In quantum statistical physics,
the distribution function according to the occupancy
possibilities of quantum states of particles is specified to the
form :
<
N(E) > = 1 / (e-E/kB.T ± 1)
,
where in the denominator the positive sign
"+" applies to fermions - Fermi-Dirac
statistical distribution and the negative sign "-" to bosons - Bose-Einstein
distribution.
Note: In the
thermodynamics of gases formed by atoms or molecules with a
certain chemical composition, the denominator of distribution
functions also has the so-called chemical potential m : e-(E-m)/kB.T, expressing
energetic changes in chemical reactions that may occur during
atomic collisions. For elementary particles, an analogy of this
situation could arise if the particles had sufficient kinetic
energy to interact with transmutations and the formation of new
particles.
In the Fermi-Dirac
distribution of particles that satisfy Pauli's exclusion
principle, there are also situations where the same energy
corresponds to some different states - the so-called degeneration
of energy levels occurs. In the numerator of the distribution
law, instead of "1", there is a degeneration factor
g, which indicates the number of different states corresponding
to a certain same energy level: <N(E)> = g / (e-E/kB.T + 1). Degeneration of energy levels
occurs mainly due to some kind of symmetry in
the system, such as motion in a centrally symmetric field.
An important
property of the Fermi-Dirac distribution of particles in a set of
fermions is the possibility of the formation of so-called degenerated
matter or degenerated gas. In a set of
non-interacting fermions - the ideal Fermi gas -
particles enclosed in a finite volume can acquire only discrete
energy values (quantum states). Pauli's exclusion principle
prevents identical fermions from occupying the same quantum
states. At high densities of matter, all energy levels of
fermions are occupied up to a certain maximum
energy, which corresponds to a certain maximum momentum; this
condition is called degeneration, it is a degenerate
fermion gas. Each additional fermion in a given volume must
occupy a new higher energy level and thus have a
higher momentum. The pressure here therefore increases
significantly faster than corresponds to the equation of state of
an ideal gas.
The statistical
behavior of electrons, protons and neutrons according to the
Fermi-Dirac distribution, with degeneration, is of great
importance in stellar astrophysics, where it co-determines the equilibrium
state of stars against gravity, disturbance of this
equilibrium and collapse of stars on white dwarf and
neutron star (§4.1 "The
role of gravity in the formation and evolution of stars" and §4.2 "The final stages of stellar
evolution. Gravitational collapse. The formation of a black hole." in the monography "Gravity, black holes
and space-time physics").
The outlined
analysis of the relationships between spin, symmetry of wave
functions and statistical behavior of sets of particles, can be
summarized in the resulting theorem :
| Spin => wave function
symetry => statistical behavior of particles |
| Particles with half-numbered spin (s =
1/2, 2/3, ....) have a wave function antisymmetric with
respect to the transposition of particles, in the same
quantum state there can be at most one of these particles
(Pauli exclusion principle) and in a set of particles is
controlled by Fermi-Dirac statistics - they are fermions. |
| Particles with integer spin (s = 0, 1,
2, ....) have a wave function symmetric with respect to
the transposition of particles, in the same quantum state
there can be an unlimited number of these particles and
in the set of particles they follow Bose-Einstein
statistics - they are bosons. |
Physical parameters of particles;
quantum numbers
The properties of elementary particles are characterized by
suitable physical parameters, some of which are also known from
classical physics, others are purely quantum and have no
classical analogy. These parameters of elementary particles,
which are mostly quantized, ie take on discrete values, are
called quantum numbers.
¨ Rest mass, lifetime
These are the basic unquantized characteristics of particles. Rest
mass of particles is rarely expressed in grams,
but most often in energy units electron volts eV, keV, MeV
*) - in connection with Einstein's relation E = m.c2 equivalence of mass
and energy. It is sometimes given in multiples of the electron
mass. Life time, resp. the half-life
of particles is expressed in seconds and their decimal
fractions (10 -xx sec.); for stable particles it is considered to be ¥ .
*) More precisely, the energy expression of
mass is in MeV/c2, but c2 is often omitted.
¨ Size,
dimensions and shape of elementary particles? - problematic!
In everyday life and in the physics of macroscopic phenomena, the
spatial size of bodies, their shape and
individual dimensions are of great importance. In the microworld,
however, this is problematic. In the case of
particles of the microworld, due to the wave nature and quantum
relations of uncertainty, the concept of spatial "size"
loses its meaning - it cannot be defined and
measured. These particles are not some tiny "material
bodies" with a solid surface, as we know from our usual
experience from the macroworld, but rather spatially distributed
"densities of fields" of a wave
nature. They have no specific boundaries. Only some of them can
be defined some "effective size" of particles
in interactions - using the range of
forces and the so-called effective cross section
(see below "Interactions of elementary particles", section "Effective
cross section of particle interactions"). From scattering experiments in particle bombardment -
in determining how "close to each other" particles
penetrated. However, such an "effective size" may be different
for the same particle in various types of interactions. These
problems with particle size are circumvented by a physical
agreement that elementary microworld particles will
in principle be considered to be zero-sized points,
while effective cross-sections being considered for
interactions...
Physical efforts
to determine the size of elementary particles
In the early days of the study of the microworld,
atomic and nuclear physicists worked hard to determine
the size ("radius") of newly discovered
particles - the electron and the proton. For an electron
with mass m e
and elementary charge e, three very different values were
reached in the analysis from different points of view :
- The
classical (non-quantum) or
Thomson radius of the
electron is based on the model that the electron is a sphere on
whose surface the electric charge of value e is uniformly
distributed. The radius of electron r e
is taken to be the radius of the sphere such that the
electrostatic potential energy of this charge corresponds to the
rest mass of the electron me according to the relativistic relation of the
equivalence of mass and energy E = me. c2. Comes out: re = e2/4peo me c2 = 2.818x10-13
cm. It's such a radius
that all resting electron mass me
had an electrical origin (was
formed by electrostatic potential energy; this approach is also
analyzed in §1.6, passage "Nonlinear Electrodynamics" monograph "The gravity, black holes and
spacetime physics").
- Bohr
radius of the electron comes from the fact that the
majority of electrons bound in atoms, so the size of the electron
would be natural to deduce from the dimensions of the atom.
According to Bohr's quantum model (§1.1 , part
"Bohr model of the atom") has the lowest (basic, unexcited) orbit
of an electron in a hydrogen atom radius r1 =4peo
h/m e e2 = 0.529
x10 -8 cm.
This value is considered here as the radius of the electron re .
- The Compton
wavelength of an electron is the smallest distance to
which an electron can be constrained ("compressed")
according to quantum uncertainty relations: lc ~ h / me c » 10-9 cm.
If we try to compress the electron to a smaller size, then
according to the uncertainty principle, its momentum
becomes so large that its kinetic energy exceeds the rest energy of the electron me
c2.
In this case, there will be enough energy to form a new
electron-positron pair. Compton length is therefore the smallest
distance, on which two electrons can penetrate without
the formation of new particles ...
From the current
point of view, these values are only of model and historical
significance and are not considered
"real" dimensions of the electron. For
electrons, in the end, no plausible value of
"size" could be determined, the higher
the kinetic energy, the deeper they approach each other during
the interaction - as if they were points with zero size
(<10-16 cm)..?..
Similar to that expected for other leptons *). From the point of
view of corpuscular-wave dualism, the effective size of an
electron, its "wavelength", would depend on its
velocity (§1.1, passage "Particle-wave dualism").
*) At neutrinos, which show only a weak
interaction, the effective "size" is assumed to be
significantly lower than for electrons, about 10-16
cm. No direct measurements are feasible here.
For protons
and neutrons, their effective "size" for strong
interactions was set at about 1.6x10-13
cm, according to
the measured range of these nuclear forces (see §1.1, passage "Strong nuclear interaction"), as a "residual"
manifestation of a strong interaction between quarks inside
protons and neutrons. Similarly for other hadrons
(pions, kaons, hyperons). For electromagnetic interactionthe
"size" of a proton is measured by the scattering of
accelerated electrons. Another method is hydrogen
spectrometry: accurate measurement of energy levels (difference in energies between 2S1/2 and 2S1/2 orbitals - hyperfine structure caused by Lamb shift due
to quantum fluctuations of virtual electron-positron pairs in the
electric field of a proton); this method resulted
in a value of 0.88x10-13
cm. These
measurements were modified in a new experiment where hydrogen
atoms were exposed to a beam of low-energy muons, whereas some of
the muons were captured, replacing electrons in the hydrogen
atom. Such a muon due to its higher weight (it
is about 200 times heavier than an electron) orbits significantly closer to a proton, so differences
in energy levels are "more sensitive" to the structure
of the proton. Here a slightly lower value of the proton radius
of 0.84x10-13
cm was reached.
Protons, like other hadrons, are not "elementary"
particles, but are composed of quarks, so the
so-called quantum chromodynamics
(see "Imprisoned quarks"
below) has something to say about their
structure and "size", at the fundamental level then
unitary field theory ("Unification
of fundamental interactions. Supergravity. Superstrings." in the monograph "Gravity, black holes and
space-time physics").
For photons, as quanta of
electromagnetic waves, their effective "magnitude"
depends on the wavelength of the radiation. Photons of
gamma radiation are effective only picometres dimensions, visible
light photons hundreds of nanometers, in the case of radio waves
we could absurdly imagine the many-meter dimensions of
"photons" - here, however, photons can not prove at all
...
¨ Electric charge
An extremely important parameter of particles is their electric
charge, which is quantized and therefore, instead of in
coulombs, is expressed in multiples of the magnitude of the elementary
charge of the electron |e| with the sign *) - the
electron then has a charge -1, proton +1, hyperon W charge -2, neutron
and other uncharged particles of course 0. Antiparticles to
charged particles have charges of opposite sign (and the same
absolute size). In all known interactions, the law of
conservation of electric charge is strictly fulfilled:
the sum of the charges of the particles before the interaction is
the same as the sum of the charges of the particles flying out
after the interaction.
*) Below we will also encouter the charge 1/3
e or 2/3 e in quarks.
¨ Spin, magnetic moment
Another important quantum characteristic of particles is their spin
or spin number s, expressing the own angular
momentum of a particle in multiples of the Planck constant h.
Except to the zero spin s=0 (occurring in the mesons p and K), the
smallest possible spin is the value s = 1/2 (electrons, protons,
neutrons, neutrinos, muons have such a spin). Spin s = 1 have
photons, s = 3/2 heavy hyperons W, spin s = 2 at gravitons.
Closely related to the spin of corpuscular particles is their magnetic
moment, given in multiples of the elementary Bohr
magneton e.h/4p me , resp. nuclear magneton e.h/4p mp (discussed in more detail in §1.1, passage
"Quantum momentum, spin,
magnetic moment"). The spin number of the particles further determines
the quantum-mechanical statistical behavior in
the sets of particles - see "Bosons -
Fermions" below.
Note: Spin - rotation ?
According to classical mechanics, the spin of particles is
usually interpreted as their rotational
momentum. However, this property of elementary particles has a
specific quantum nature and cannot be
satisfactorily explained by classical mechanical concepts (spin cannot be quantitatively explained, for example,
by the rotation of a particle around its own axis!) .
¨ Parity
is the quantum number, characterizing the behavior of the wave
function of quantum mechanical object - nuclei or elementary
particles - relative to a spatial mirror reflection, i.e. the
coordinate transformation x ®
-x, y ®
-y, z ®
-z, t ®
t. If the while doing so the wave function
describing the state of the particle does not change, the parity
is positive: P = 1, or "+". If the wave function of the
system changes sign during this transformation, the parity is
negative: P = -1, or "-". It can be shown that the parity of a system with
an orbital momentum l is (-1) l. Analysis of elementary particle interactions shows
that the parity of the proton and neutron is positive, while the
parity of photons and mesons p+, -, o is negative. The parity is sometimes given as the index
at the top right of the quantum momentum J of the system,
such as the nucleus, JP: either J+ or J-. For elementary particles then as an index for the spin
number: sP
- eg 0-, (1/2)+ and so on.
Overall, parity P is not a very
important quantum number. However, parity has its theoretical
significance in connection with symmetry properties and
conservation laws in particle interactions - see below the
section "CPT symmetry of interactions" in the section "Four types of interactions". Parity is maintained at a strong and
electromagnetic interactions, but with weak interactions are not
conserved (discussion and experimental verification see below
"CPT
symmetry interactions"; the hypothesis of the so-called mirror matter,
discussed below in the section "Hypothetical model particles",
passage "Shadow Mirror Matter - Cathoptrons?"
is based on the failure to preserve parity).
¨ Lepton and baryon number
In order to classify elementary particles, particles are
assigned a lepton number L, which for
leptons is L = ± 1 (depending on whether it is a particle or an
antiparticle), for other particles L = 0, and the baryon
number B, which for baryons is B = ± 1 (again
"+" for particles, "-" for antiparticles)
and for particles other than baryons is B = 0. The lepton and
baryon number is preserved for practically all
types of interactions *) - the sum of leptons and baryons
(respecting the signs) before and after the interaction is the
same.
*) The only exception is with the gravitational
interaction involving black holes: when
particles are absorbed below the horizon of a black hole, all
their individual characteristics are lost except mass, electric
charge and orbital momentum ("black hole has no hair");
the particle seems to "dissolve" in the total
gravitational field of the black hole - see §4.5 "Theorem
"black hole has no hair"", in "Gravity, black holes and spacetime
physics". Lepton and baryon number is not preserved even
during the quantum evaporation of black holes - §4.7
"Quantum radiation and the thermodynamics of
black holes" in the same
monograph.
¨ Another
quantum numbers isospin,
strangeness, and hypercharge will be
introduced below in connection with mesons K, hyperons, and
unitary symmetries of elementary particles - see the passage
"Unitary symmetries and multiplets of
particles".
Intermediate
and virtual particles
According to the ideas of quantum field theory,
the mutual force action of two particles takes place in such a
way that these particles exchange (transmit and
receive) so-called intermediate particles, which
are quantums of the respective field. Each particle subject to
interaction is surrounded by a "cloud" of respective
intermediate particles, which remain virtual, until there is an
act of interaction.
To explain the mechanisms of interactions
and mutual transformations of elementary particles, not only
observed "real" particles entering into interactions or
radiated as a result of the interaction are used, but often also
certain "auxiliary" particles mediating certain stages
of interaction, that are not directly observed. Such virtual
particles *) "exist" only for a very
short time, which is shorter than the time required to
measure their energy according to uncertainty relations. Commonly
known and proven particles, such as photons, can
serve as virtual particles, but often hitherto unknown and
unproven particles are often used - model and hypothetical
particles (they are mentioned below). Virtual particles
cannot be directly detected, but can manifest themselves in real
measurable phenomena because they interact with real particles
and fields; such latent interactions can cause, for example,
spontaneous emission of real particles or anomalies depending on
the effective cross sections of the interactions on energy.
Interactions using intermediate particles are represented by
so-called Feynman diagrams.
*) Virtual
= imaginary, apparent, unreal, potential, physically absent.
It originally comes from lat. virtus = man, masculinity,
virtue, but has undergone a significant etymological change.
The "temperature"
of the particles ?
In the science of heat - kinetic theory of heat,
thermals, thermodynamics - temperature is closely
related to the velocity or energy of particles. The temperature
of a normal substance environment is given by the speed of
oscillating or chaotic movement of particles of which a substance
is composed - atoms and molecules. Root-mean-square speed vk2 of the motion of particles is related to the
thermodynamic temperature T [oK] the relation
1/2 mo vk2 = 3/2 kB.T ,
where kB =
1.38.10-23 J . K-1 is Boltzmann's constant and mo is the rest mass of
particules of matter (in the simplest case
of an ideal monoatomic gas). Thus the
temperature is proportional to the mean kinetic energy of the
particles Ek = (1/2) . mo vk 2 .
This kinetic concept of temperature
is generalized from the material environment to
the environment composed of particles other than molecules and
atoms - to the physical sets of various microparticles and their
bound combinations *). The kinetic energy of the particles Ek is then measured here
in electron-volts [eV] and the Boltzmann constant has the value kB= 8.617.10-5 eV.K-1 (the carrier of kinetic energy in ionized
matter and sets of particles are mostly electrons). In principle, therefore, we can equivalently measure
the energy state of particle sets either by the mean kinetic
energy Ek of
the particles in [electron volts], or by the thermodynamic
temperature T in [degrees of Kelvin].
*) It would certainly be misleading to say that "the
particle has a temperature of xxx °K"; the particles have
no "temperature" quantity. More precise is the
formulation "a given set of particles has a thermodynamic
temperature of xxx °K". The temperature in such a
collection of particles has obviously not be measured by
conventional thermometer inserted into the system (with the
attainment of thermal equilibrium), but on the basis of the
radiation emission or directly by measuring the energy particles
by means of detectors.
Room temperature T = cca 300 oK corresponds to the
kinetic energy of the electrons Ek = about 26 millielectronvolts. The high-temperature
plasma required for efficient thermonuclear
fusion of deuterium and tritium must be heated to about
150 million degrees (regardless of Kelvin
or Celsius), which represents a kinetic
energy of particles of about 12 keV (see
§1.3, section "Atomic fusion"). nuclei "). And in quark-gluon
plasma a huge thermodynamic temperature higher than 1012 degrees is reached
for a short moment (see the passage "Quark-gluon plasma -"5th state
of matter" " below), the kinetic energy of the particles reaches the order
of TeV.
Classification
of elementary particles
Elementary particles are sorted and divided into groups according
to their significant properties, expressed by physical parameters
and quantum numbers. The most fundamental characteristic of each
subject *), and therefore also the elementary particle, is its weight
- more precisely the resting mass mo.
According to the special
theory of relativity, the actual mass m (inertial
mass, characterizing according to 2. Newton's law F = m.a the
resistance of the body to acceleration) depends on the speed
of motion of the body v : m = mo/Ö(1-v2/c2), where mo is the rest mass, determined in the inertial frame of
reference in which the body is at rest. The resulting mass m
is greater the faster the particle moves; for v ® c grows above all
limits. Therefore, no particle whose rest mass is non-zero can
move at the speed of light (or superlight speed). According to a
special theory of relativity, the total energy of a particle (the
sum of rest and kinetic energy) is equal to E = (mo/Ö(1-v2/c2)).c2 = m.c2 - Einstein's equation expressing the equivalence
of mass and energy.
*) Another basic characteristic of objects in the macroworld -
spatial size (dimensions, volume), has no
significance for elementary particles ! Due to
corpuscular-wave dualism and the uncertainty principle, no
certain size can be assigned to particles in the
microworld (discussed in more detail above
in the section "Size, dimensions and shape of elementary
particles? -
problematic!"). In the model ideas, however, we can consider some
"effective" particle sizes, given by
the interaction properties of these particles (eg the proton has
a dimension of » 1.6.10-13 cm in terms of strong interaction). On this ideas based
the so-called effective cross section
of particle interaction (see below).
According to the
rest mass, we divide the particles into four
groups :
- Particles with
zero rest mass
In atomic and nuclear physics they are mainly quantum of
electromagnetic radiation - photons, in
subnuclear physics also model particles gluons
mediating strong interaction. In the general theory of
relativity and quantum gravity, then possibly even a
quantum of gravitational waves - gravitons (gravitational waves are proven only indirectly
in astronomy, the first direct detection was achieved
only recently - see "The
first direct detection of a gravitational wave by LIGO"; there is no hope for experimental
detection of gravitons in the foreseeable future). From the point of view of quantum field
theory, particles with zero rest mass mediate - as exchangeable
intermediate particles - long (unlimited) range
interactions (electromagnetic
photons, gravitons of gravitational interaction, gluons
of strong interaction between quarks).
Note: It may seem
paradoxical to speak of "rest mass" for
particles that, in principle, can never be at rest.
However, in the special theory of relativity, the rest
mass of a particle is defined as the invariant size
(4-dimensional length, independent of the frame of
reference) of a 4-vector momentum of a particle - see
relation (1.101´) in §1.6 "Four- dimensional
spacetime and special theory of relativity" book " The
gravity, black holes and the physics of space-time". Photons have zero rest mass, but their
inertial (relativistic) mass depends on the frequency: m
= h.n/c2. When braked, the photon gives up all
its energy and disappears, unlike a particle with a
non-zero rest mass, which gives off only its kinetic
energy and after braking it still exists with its rest
mass.
- Leptons - light particles with low rest mass (Greek leptos = thin, fine, weak,
thin, thin *)
These include mainly electrons e-
and positrons e+ with rest mass me = 9.1.10-28
g = 511 keV ( in nuclear
physics, it is customary to express mass in connection
with the relation E = m.c2 in energy units electron volts). Then there are
neutrinos (electron ne , muon nm
, tauon nt)
and antineutrinos with a resting weight of about 2 eV.
Today, the muon m- (referred to as the "heavy
electron"), which has a mass of »206 me and even the tauon
t- with a mass of »3484 me , referred to
as the "superheavy electron", also belongs to
the category of leptons; and, of course, their
charge-coupled antiparticles.
*) Original designation leptons,
as light particles, is now losing its original literal
meaning, due to the inclusion of muons and tauons. The
role of leptons as the basic building blocks of matter,
along with quarks, will be outlined below in the section
"Standard Model of Elementary
Particles". According to
this standard model, leptons (together with their
antiparticles) form the so-called generations.
The first generation consists of an electron with an
electron neutrino. The second generation includes the
muon with its muon neutrino, the 3rd generation tauon
with the tauon neutrino. It is assumed that the next
generation, made up of even heavier electron analogues,
does not exist. Analogous 3 generations are distinguished
in quarks.
According to current
knowledge, leptons do not have an internal
structure, the standard model considers them as point
particles (another approach is
considered in superstring theory). All leptons are subject to a weak interaction,
charged leptons also to electromagnetic interactions.
- Baryons - heavy particles (Greek.
Baryos = heavy)
These include primarily proton p+ with a mass mp = 1836 me = 938 MeV/c2 and the neutron
n0
having slightly larger mass mn = 1838 me (and of course their antiparticle). Protons and
neutrons are collectively referred to as nucleons
- the building blocks of the atomic nucleus. The baryons
then include even heavier particles - hyperons.
These are formed by collisions of high-energy particles
and disintegrate very quickly - their
lifetime is of the order of »10-10 seconds.
Known hyperons Lo (mass 2183 me), S+, - , o
(mass » 2330 me), Xo, - (mass »2580 me), W-
(mass »3273 me).
The only stable baryons are protons
(so far we omit the hypothesis of
proton decay) , in suitable
connection with protons in atomic nuclei also neutrons.
Others are unstable, decaying into nucleons and pions.
Baryons are "equipped" with all kinds of
interactions - strong, weak, electromagnetic (if
electrically charged) - and of
course gravitational, which we do not consider here. In terms of interaction, they belong to hadrons.
- Mesons - medium-heavy particles (Greek
mesos = medium, between something -
their mass lies between an electron and a proton)
The lightest of them is a meson
m-,+, muon *) with mass mm
= 206 me, then a positive meson p+, pion, and a negative p- weighing 273 me, neutral pion po weighing 264 me. Finally, they are K-mesons K+, - (mass 966 me) and Ko (weight 974
me).
*) Note: The
muons m are here namely of weight included between
mesons, but by the characteristics of their interactions
and structures are now inserted between leptons! They are
formed in processes involving weak interactions, are
unstable and decay into electrons and neutrinos (see
below).
Mesons p and K
are formed in processes involving a strong interaction
and are unstable - they decay by weak
interaction into muons and neutrinos (K-mesons also by
strong interaction into pions); disintegration modes and
lifetimes are listed below. Like baryons, the mesons p and K
are hadrons, interacting generally with all 4
types of interactions.
The origin of particle
rest masses
The above-mentioned diametrically different rest masses of
different types of particles used to be a purely empirical matter
in the past. Now the standard particle model tries to explain
them by basically two mechanisms :
1. For basic, elementary
structureless particles - photons, leptons, neutrinos,
quarks, intermediate bosons - their mass depends on the values of
the coupling constants of the interaction of the
respective fields with the ubiquitous Higgs-Kibble scalar
field (whose quanta are Higgs
bosons). For fermions, this
interaction is also called the Yukawa coupling (it is modeled by the Yukawa potential with an
exponential dependence).We can imagine it
in a simplified way, that a particle "draggs" with it a
certain part of the energy-momentum of the Higgs field (according to the size of the coupling constant), which effectively makes it appear more massive
(according to Newton's 2nd law), puts up a greater resistance to
acceleration, and carries a higher kinetic energy at the same
speed.
Photons and gluons do not
interact with the Higgs field at all, so they have zero rest
mass. "Ordinary" electrons interact
with the Higgs field only relatively weakly (coupling constant g
~ 3.10-6),
they have a rest mass of 511keV. Their related leptons, muons
("heavy electrons") interact more strongly (coupling
constant ~ 6.10-4) and have a rest mass 200 times greater, 105.6 MeV. And
tauons ("super-heavy electrons")
interact with the Higgs field very strongly (coupling constant ~
1.10-2)
and therefore have a rest mass of 1777 MeV, more than 3000 times
greater than electrons! Quarks "d" with a coupling
constant ~ 2.6.10-5 have a mass of 4.6 MeV, "s" quarks with a
coupling constant ~ 5.10-4 have a mass of 94.6 MeV, "b" quarks with a
coupling constant ~ 5.10-2 have a mass of 4.3 GeV. The bosons W+,-, Z0, causing a weak interaction, have a particularly strong
interaction with the Higgs field (coupling constant g ~ 1), which
leads to their high masses of 80-90 GeV and a very short range of
the weak interaction.
Note: Even
this approach remains basically phenomenological: the
empirically measured masses of M particles are only
transformed into values of the coupling constant g with
the Higgs field according to the simple formula M = g .Vv/21/2, where Vv
is the "expected" value of the Higgs vacuum
potential Vv = (21/2. GF)-1/2
~ 246 GeV (GF is the reduced Fermi constant of the
weak interaction). The standard model cannot yet predict specific
values of masses or binding constants.
This mechanism is often associated with the rather
unintuitive concept of "spontaneous symmetry breaking"
- it is discussed in more detail in §B.6 "Unification
of fundamental interactions. Supergravity. Superstrings.", passage "Symmetry in physics
and their breaking" of the book "Black
hole gravity and the physics of spacetime".
2. For "composite"
particles, hadrons - protons, neutrons, hyperons, pions, kaons,
... - the rest mass of their structural components - quarks - is only
a small part of the total mass, around 1%. Most of a
hadron's mass comes from the kinetic energy of
the internal motion of its quark components. E.g. proton has a
mass of 938MeV, while the rest mass of the "u" quark is
2MeV and the "d" quark is 5MeV.
The spectrum of rest
masses of particles - is it limited or infinite ?
The rest masses of various types of particles are very
different, their values form a wide
"spectrum". From photons with zero or neutrinos with a
slight rest mass, through light electrons (about 0.5 MeV), mesons
(around 140-500 MeV), to heavy baryons with rest masses of 1-1.7
GeV. The heaviest known particles are bosons W+,-, Zo of weak interactions
weighing about 80-90 GeV and Higgs bosons with rest mass 120 GeV
approx. The question arises as to whether the mass spectrum is
already ending here, or are there even heavier particles? In
the 1960s and 1970s, the so-called Hagedorn hypothesis
was discussed of existence an infinite number of
particles of ever higher masses that could gradually
appear as ever more powerful accelerators were constructed. Current particle physics is rather skeptical
about this, it could possibly only be excited states of
quark-gluon combinations..?.. - only future experiments can
decide.
According to the way of interaction
between elementary particles, a special group is singled out :
- Hadrons - particles showing a strong nuclear
interaction (Greek hadros
= strong, heavy, thick, robust)
These include protons, neutrons, mesons p and K,
hyperons. The origin of the strong (nuclear) interaction
stems from model subnuclear particles of quarks
and gluons (see below). Hadrons are therefore particles
with a quark structure - baryons are composed of
three quarks, mesons of two. Hadrons are therefore not
"elementary" in the true sense
of the word, but their direct decomposition into quarks
is quite problematic - see the section "Quark structure of hadrons" below.
Note :
The name "hadron" was
first introduced L.B.Okun of the Physics Institute in
Moscow in 1962.
According to lifetime, we can
divide elementary particles into :
- Stable particles with an infinitely long lifetime.
These include the electron e-, the
positron e+, the photon, the proton p+ *), the neutrino n (apart from the
oscillation phenomenon of neutrinos, which cannot be
considered as decay).
*) According to some so-called grandunification
theories, the proton would not have to be a
completely stable particle, but should decay with a
half-life T1/2 > »1033 years. This
idea is largely speculative, because during the existence
of the universe, perhaps not a single proton has
decayed..?. Only in the case of an open universe with
infinite time evolution, the decay of protons could
perhaps in time scales »10100 years to
contribute to the so-called heat death of the
universe (see §5.6 "The future of the universe. The
arrow of time."
in "Gravity, Black Holes and space-time physics") ....
- Long-lived
particles .
This includes the neutron n0, which, if free (outside the atomic nucleus),
decays by the b- - transformation: no ® p+ + e-
+ ne´ with a
half-life T1/2 @ 13
minutes. With some reservations, we can also include the
muon m-
with a lifetime of 2.10-6 sec (decays into an electron and a neutrino: m- ® e-
+ ne´ + nm).
- Particles with a short
lifetime .
These are all other real particles, which are formed for
a short time by the interactions of high-energy particles
and then immediately disintegrate, their lifetime is in
the range of about 10-8 -10-20 sec. We can name some: mesons p+ and p-
with lifetime 2.6.10-8 sec, po (»10-16 sec), K+ (1.2.10-8 sec), K0 (»10-10 sec),
hyperons Lo (2.5.10-10 sec), S+
(8.10-11 sec), S- (1.5.10-10 sec), So (»10-20 sec), group
of hyperons Xo, - and W-
with lifetimes of the order of 10-10 sec.
- Ultra-short-lived
particles - so-called resonances
Form during some interactions of high-energy particles
(such as p+,- + p+ ® p+,- + p+, or the interaction of a proton with an
antiproton to form several p- mesons) and
immediately decay, their lifetime is about 10-23 to 10-20 seconds.
They are actually manifested only by a significant resonant
maximum in the energy dependence of the effective
cross-section of the given interaction, or by
densities and peaks on Dalitz diagram of the
energies of secondary particles (see the section "Analysis of the dynamics of particle
interactions" below). We
distinguish baryon resonances and meson
resonances (such as meson r or some types of
mesons K*). Resonances are often not even considered
special particles, they are called quasiparticles.
Rather, they are only temporarily excited states of two
or more baryons or mesons that decay as soon as they fly
beyond the boundaries of the region of strong nuclear
interaction in which they originated. Due to the
extremely short lifespan, they probably have no
significance for the structure and properties of matter.
However, their study is important for better penetration
into the subnuclear structure of hadrons, their quark
structure and understanding the properties of strong
interactions within quantum chromodynamics (QCD).
Fermions
- Bosons
In the passage "Indistinguishability
of particles" - "Spin, symmetry of the wave function and
statistical behavior of particles" we have shown how the spin of particles
determines the statistical behavior of sets of particles.
Thus, according to spin, and consequently also
according to quantum-mechanical statistical behavior
in sets of particles, elementary particles are divided into two
large groups :
- Fermions - particles with a "half- numbered"
spin s = ± (1/2) h, ±
( 3/2) h, ....
These are mainly all building blocks of
matter: proton, neutron,
electron. On the leptons, they are also muons
and all kinds of neutrinos. From other
baryons then also hyperons. All the
listed fermions have spin 1/2, except for the hyperon W which has
spin 3/2.
In quantum mechanics, it is shown
that sets of particles with a half-number spin follow the
so-called Fermi-Dirac statistics, which
is characterized by the fact that two or more particles
cannot be in the same quantum state (Pauli's exclusion
principle, they are "intolerant" particles) -
in a given quantum state it can be only one fermion.
Therefore, the individual electrons in the atomic shell
acquire and occupy different quantum states, and the
resulting electronic configurations of the atomic shell
levels are the cause of all the diversity of chemical
compounding of elements and their other properties *).
And in a similar way, in the atomic nucleus, nucleons
occupy different energy levels in a field of strong
interactions. It can be said that we owe the diversity
of nature to the fermions, which are able to
form diverse structures..!..
*) If all electrons could occupy
the same (lowest) quantum state, the atoms of all
elements would have the same properties and our world
would be very drab. Fortunately, however, due to their
"intolerance", electrons gradually occupy
different levels in the atomic shell, and different
elements thus have different properties and coupling
capabilities, given the number of electrons per outer
(valence) layer.
Fermion gas
Pauli's exclusion principle for fermions also has
important implications for the behavior of a set of free
fermions, the so-called "fermion gas".
When a such gas is strongly compressed, the fermions
occupy all the lower possible energy states, so that such
a gas is very strongly "prevented" from further
compression - the higher states are associated with high
momentum and thus high pressure. And every other fermion
that gets inside such a compressed mass, it cannot change
its state in collisions with other fermions, because all
the surrounding quantum states are already occupied and
no other fermion can get there; such a fermion then moves
as free, the environment cannot change its momentum. A
substance in such state with all occupied quantum states
is called degenerate fermion gas and
plays a major role in the final stages of stellar
evolution - white dwarf and neutron stars (discussed in
more detail in §4.2 "Final
Stages of Stellar Evolution. Gravitational Collapse" in monograph "Gravity,
Black Holes, and the Space Physics").
- Bosons - particles with "integer" spin s =
0, ± 1h, ± 2h, ....
This mainly includes a quantum of fields,
transmitting the forces by which particles act on each
other. They are also referred to as intermediate
particles mediating individual interactions.
Bosons with spin s = 0 are denoted as scalar,
with spin s = 1 as vector (the
designations "scalar" and "vector"
are related to the mathematical formalism of their
theoretical description in quantum physics).
The most important boson is the photon
(spin 1), then the p- mesons (spin 0), bosons W-, W+, Z0 (spin 0), gluons (spin 1),
hypothetical gravitons (spin 2).
Bosons do not follow Pauli's exclusionary
principle. From a quantum-mechanical point of view, sets
of particles with integer spin are governed by the
so-called Bose-Einstein statistic, in
which (unlike fermions) there can be an unlimited number
of particles ("compatible" particles) in each
quantum state.
The number of bosons is not
preserved in nature. For example, when we turn
on a light bulb, billions of newly formed photons flood
the surrounding space. Conversely, many existing photons
are absorbed in matter - they disappear upon interactions
with atoms and molecules of matter.
At low
system temperatures, each boson tends to occupy the
lowest energy state - a so-called boson
condensate is formed, which has superfluid and
possibly superconducting (in the case of
electrically charged particles) properties.
Fermions in the role of bosons;
Superconductivity
Under certain circumstances, even a set of fermions, such as
electrons, can effectively behave like bosons. If we reduce the
temperature of a conductive substance containing free electrons
in the form of an "electron gas", at temperatures
around 4 °K, electrons combine into pairs - so-called Cooper
pairs, in which the half-number spins of electrons in
the opposite direction add up to zero spins (singlet pairing), ie
integer. The bond between the electrons of a Cooper pair is
mediated by their interaction with an oscillating crystal
lattice. Such pairs then behave like bosons,
which at low temperature tend to occupy the lowest energy state
(Pauli's exclusion principle does not forbid them, because it
does not apply to bosons). The so-called boson condensate
is formedin the basic energy state, in which the paired electrons
move through the crystal lattice completely freely without
resistance - electrical superconductivity is
created.
Superconductivity
Superconductivity is thus a quantum-electric phenomenon in which
the material does not put any ohmic resistance to the passage of
an electric current and no heat is released in the material. It
was discovered in 1911 by the Dutch physicist H.K.Onnes, who
liquefied helium on a device of his own design and measured the
electrical resistance of metals at low temperatures
in further experiments. With decreasing temperature, the
resistivity of metals generally decreases (with
slower oscillating atoms of the crystal lattice, electrons
precipitate less often, they pass more easily). By extrapolating this slight almost linear decrease in
resistance with temperature to absolute zero, a certain small
residual value of resistance can be expected *).
*) From the classical point of view, the
opposite situation could be expected: when stopping their thermal
movements, electrons could combine with ions of the crystal
lattice, "freeze" and stop moving - the conductor would
become an insulator that does not transmit electric current.
When Onnes measured the temperature
dependence of the resistance on a sample of high-purity mercury,
he was surprised to find a sudden drop in the mercury resistance
to zero (unmeasurably small) at temperatures around 4.2 °K. Superconductivity was
then found for lead, tin and many other materials and alloys.
Microscopic theory of low-temperature superconductivity developed
in 1957 by J.Bardeen, L.Cooper and J.R.Schriffer (BCS theory)
- according to it, the bond between electrons and oscillations of
the crystal lattice (phonons) can effectively lead to an
attractive interaction between pairs of electrons: the electron
as it passes through the crystal lattice creates a positive
"hole" through which the second electron is attracted.
This dynamic bond creates effectively bound Cooper pairs
of two electrons, which form a boson condensate with a high
degree of correlated electron arrangement. The temperature
at which a substance transitions from a normal to a
superconducting state is called the critical temperature.
Intensive research on superconductivity has
revealed a number of materials with this property, which can be
divided into two groups :
-
Type I
superconductors are some metals that achieve
superconductivity at low temperatures (critical temperature lower
than 30 °K) and lose superconducting properties in stronger
magnetic fields (Meissner-Ochsenfeld
effect). This superconductivity is
explained by BCS theory.
-
Type II
superconductors are some alloys of metals (especially
copper) and non-metallic admixtures (ceramic oxides), which
achieve superconductivity even at higher critical temperatures
and retain this property even in strong magnetic fields.
Particularly interesting materials of this kind are composite
compounds of yttrium, barium, copper and oxygen Y1Ba2Cu3O7, or analogously lanthanum. This is where
superconductivity occurs at a critical temperature of 90-100 °K
- high - temperature superconductivity,
which allows the use of liquid nitrogen for cooling. A complete
microscopic theory of high-temperature superconductivity has not
yet been developed, but research to date has shown the mechanism
of electron binding to Cooper pairs by electron-spin interactions
of electrons with excitations of spin (anti) ferromagnetic
structures in a crystal lattice that has a "flake"
structure.
 |
Left: The
superconducting electromagnet consists of a coil wound
from a superconducting material, placed in a cryostat
with liquid helium (short-circuiting
bifilar line is used to turn on and off the current in
strong persistent electromagnets - see "Electromagnets
in accelerators")
.
Right: Temperature dependence
of the ohmic resistance of the Nb-Ti superconducting
material (for 1m of wire Ø 0.3 mm)
. |
Superconductivity is already finding
significant application in many areas of science, technology and
medicine. They are mainly superconducting electromagnets:
a coil wound into a large number of turns of suitable
superconducting material is placed in a Dewar vessel with a
cooling medium (so far mostly liquid helium), a strong current
(hundreds and thousands of amperes) is excited in it and both
ends are connected. The current then flows indefinitely without
consuming electricity and excites a strong magnetic
field - units up to tens of Tesla - see
below "Electromagnets in accelerators", section "Superconducting
electromagnets". The
condition of the function is, of course, continuous cooling to a
temperature lower than critical *). Such superconducting
electromagnets are preferably used in a number of areas - nuclear
magnetic resonance , circular accelerators
, thermonuclear tokamaks.
*) This continuous
cooling of the superconducting coil must be carefully monitored
! If, due to evaporation, the coolant level dropped so much that
part of the winding warmed above the critical temperature, the superconductivity
would suddenly disappear. At this point in the winding,
an ohmic resistance would arise, the current through the winding
would decrease rapidly, and the magnetic field would disappear.
This would result in an electromagnetic induction of a large
electromotive force in the winding. The considerable energy
stored in the magnetic field would be quickly converted into induced
current by the winding, which would be strongly
heated by the ohmic resistance, the rest of the cooling
medium would be brought to a boiling boil and the winding could
be burned!
The temperature transition from the
normal to the superconducting state in the vicinity of the
critical temperature Tc is very steep - there is an almost perpendicular transition
edge of the superconductivity at this point on the
resistance-temperature curve. This phenomenon is used in very
sensitive bolometers working on the edge of
superconductivityTES (Transition
Edge Sensor) - §2.5, section "Microcalorimetric
detectors".
If a really high-temperature
superconductivity could be achieved - to develop
materials that would be superconducting even at room temperature,
it would probably lead to a revolution in low-
and high-current electronics. Superconducting
wires could conduct electricity without losses, without the need
for high voltage transformation. It would be possible to
store-accumulate electrical energy in superconducting
electromagnets. Superconducting levitation is being used
in industrial applications, in which the interaction of induced
eddy currents leads to a force which allows the magnet to float
above the superconductor or "hang" in the magnetic
field. It is mainly considered for magnetic suspension instead of
bearings and for use in magnetically levitating high-speed
trains.
Superfluidity
Similarly, atoms composed of fermions can effectively behave like
bosons if their total spin is integer (or zero), resp. when there
is a singlet or triplet pairing of atoms with a half-digit spin
to the resulting integer spin (0 or 1). Here, too, boson
condensate can form at low temperatures, the particles of which
(or quasi-particles) can move freely in the environment without
frictional resistance. On this principle is founded superfluidity
some liquefied gases (especially helium) at low temperatures. It
is interesting that helium does not have a solid phase,
it remains liquid up to practically absolute zero. Below 2.17
°K, it becomes superfluid - flows without internal and
surface friction and has a very high thermal conductivity.
In relation to certain "strange"
asymmetries in the production and decay of certain particles (see
below), a special group is distinguished :
- Strange particles - this includes mesons
K and hyperons .
Within the quark model, the quark
"s" (strange) is the bearer of strangeness. The
properties of these particles will be discussed in the
relevant passages below.
Antiparticles,
antimatter, "anti-worlds"
In the world of elementary particles in general for each particle
there is its "opposite" or "associated"
partner - an antiparticle that has certain
physical characteristics identical to a given elementary
particle, but some other physical characteristics have the
opposite sign or direction. The antiparticle has the same
mass, spin number, lifetime and isospin as the particle,
but its charge and magnetic moment are opposite
(same in size but of opposite sign); the opposite sign is also
attributed to the lepton number, the baryon number, and the
isospin projection. In the case of neutral particles without
electromagnetic properties, they can either be associated either
to semselves (photon, po, graviton), so
actually they do not have antiparticles, or they
may have particles and antiparticles different from each
other (eg antineutron, antineutrino). In the case of
fermions, particles and antiparticles are formed in pairs
and also disappear in pairs.
In our nature (composed of matter),
antimatter, resp. antiparticles, occur where there is
interactions of the particles with high energies
- higher than twice the rest mass of an electron or positron 2 x 511 = 1.022 MeV;
then positrons are formed. Positrons are also
emitted during beta+ -radioactivity (see §1.2,
section "Radioactivity b+"), where they form during
the transmutation of quarks "u"-->"d"
inside protons due to weak interactions (Fig.1.2.5 below). Heavier antiparticles
(antiprotons, antineutrons, antihyperons) can then be formed only
at very high energies, 3 GeV and higher. This is the domain of
large accelerators (in very low intensity also cosmic radiation).
Note
1 - Antiworld
In many places in our treatise on nuclear and radiation physics,
we use the term "antiworld " - in an allegorical
sense. Antiparticles formed during interactions and radioactivity
in laboratories are, of course, part of "our"
world. "Anti-worlds" are sometimes
thought of in astronomy as those (hypothetical) formations or
parts of the universe that are composed of antimatter (cf. also
the passage "Antiatoms"
below). The difficult question is, why do we observe incomparably
fewer antiparticles than particles that are "normal and
ordinary" to us? It attempts to answer cosmological theories
in co-production with particle physics - see the link below in
the note to the passage "Antiatoms, Antiworlds".
Note 2 - Antiparticle =>
Negative energy? Time inversion? - No
!
In the early days of the development of quantum physics,
antiparticles (such as the positron) were considered to be
"negative energy" particles, or particles moving
"back in time" (formal coordinate
transformations in Dirac's equation allow this). At one time, these concepts played an important
heuristic role in the development of particle physics. Now these
misguided ideas are abandoned and particles and antiparticles
have an "equal" place in the standard model, in
applications, as well as in unitarization schemes.
Dirac
particles and Majoran particles
According to their antiparticles, elementary particles are
sometimes divided into two groups :
¨ Dirac particles have different
antiparticles. This includes in particular all
electrically charged particles, but also some neutral particles
such as neutrons or neutral K-mesons.
¨ Majorana particles have identical
particles and antiparticles. In addition to the photon, this
includes neutral p- mesons (pion po); some hypotheses
even consider neutrinos,
it has not been decided yet.
Some significant
antiparticles have their own name or designation
- antiparticle to electron e- is called positron e+, charge-associated antiparticles are denoted by opposite
signs of charges, eg muons m-, m+, analogously pions p-, p+ and other particles.
However, a number of antiparticles are simply denoted by the
prefix "anti" and the wavy line "~"
above the particle symbol *) - eg antiproton p´, antineutron
n´.
*) Unfortunately, in the fonts available in
the "html" format, characters with a wavy line at the
top are not available, so in our texts we denote antiparticles by
a comma ( ´ ) at the top right.
Annihilation of
antiparticles with particles
When antiparticles interact with their corresponding
"counterparts", particles, these pairs can disappear
from each other *) - annihilate - to form other
(lighter) particles or antiparticles. These are often photons (positrons annihilate with electrons to produce two
gamma photons flying out in opposite directions, at an angle of
180°, which is advantageously used in gammagraphic imaging by
the positron emission tomography method in nuclear medicine after
the application of a positron beta+-radionuclide, e.g. 18F - §4.3, part " Positron
Emission Tomography PET"). The laws of conservation of energy and quantum numbers
are met (opposite quantum numbers are "reset"). There
is a complete conversion of the rest mass (+
kinetic energy) into the rest mass and energies of other
particles and fields, while the original particles disappear.
Specific annihilation processes will be described below for each
particle type.
*) Annihilation of particles does not mean
their destruction, nor the transformation of matter into "pure
energy" !
There are still some almost mystical ideas about the process of
annihilation of antiparticles with particles. They come from a
time when these processes were just discovered and seemed so
unusual to physicists that they attributed special philosophical
significance to them. We now know two interrelated facts :
× During
the annihilation of particles, despite the name (Latin nihil
= nothing ; annihilation = destruction, disappearance
), they are not destroyed, extinct or disappear
from this world "without a trace", but their transformed
into other particles of the microworld, when all the usual
conservation laws (energy, momentum, charge and other quantum
characteristics). Nothing was lost or gained.
× Annihilation is not
the conversion of matter into energy, or matter into
"pure energy," as is sometimes stated. In annihilation
(as in any known natural process) the law of conservation
of energy is fulfilled - but the total, relativistically
understood energy, including the rest energy of particles .So
it's just about the transformation of one form
of matter into another.
After all, the conversion of "mass
particles" into a field (with zero rest mass quantities)
occurs in conventional particles only by annihilation of an
electron with a positron. Antiprotons or antineutrons
"annihilate" to form other massive particles (pions -
see below), so the "transformation of matter into pure
energy" cannot be spoken of at all ..!..
The largest
annihilation in the history of our universe
took place at the beginning of its evolution more than 13 billion
years, at a time of about 10-4 s. after the Big Bang, at the transition between the
hadron and lepton eras, when baryons and antibaryons
anihilated each other, and immediately after, at the end
of the lepton era (approx. 10 s.), when positrons with
electrons anihilated. The result was radiation
(now observed as relict) and remained a small excess of mass (1:109) from baryon asymmetry.
These grandiose events are discussed in
more detail in §5.4 "Standard cosmological model. Big Bang" passage "Baryon asymmetry of the Universe" in book "Gravity,
black holes and spacetime physics"
(see also below passage "Why is our world of matter and
not antimatter?").
"Antiatoms",
"antiworlds"
Antiparticles have exactly the same properties
*) of their interactions as particles, so that a positron can
orbit around the antiproton and thus form an "antihydrogen"
atom. Similarly, antiprotons and antineutrons can form atomic
"antinucleus-
", around which positrons+ in
shells of the same energies and according to the same selection
rules as we know from our atomic physics can orbit. Such "antiatoms"
will then have exactly the same chemical and
spectroscopic properties as the atoms of our matter -
they will create elements or compounds of antimatter
with the same properties as we know from our matter.
*) Is antimatter
exactly the same as matter ?
Matter and antimatter appear to us in practically all
experiments to be the same - except for the
opposite signs of el. charges and some other quantum numbers have
the same properties. Nevertheless, antimatter differs
slightly from matter in behavior - asymmetric production
and decay of some "exotic" particles and antiparticles (it was found experimentally mainly in K and B mesons). This hidden difference between matter and antimatter,
generated in the earliest stages of the separation of basic
interactions in the formation of the universe, may have
eventually cooperate in the hadron era to give rise to the baryonic
asymmetry (§5.4 "Standard
Cosmological Model. The Big Bang.",
passage "Baryon Asymmetry of the
Universe") in book
"Gravity, black holes and spacetime physics"). That's why there is
matter and we are here too..!..
Arises naturally
question whether somewhere in the universe is the antimatter? In
order to exist in the long term, it must find antimatter separated
from matter, otherwise there would be a massive annihilation. So
the question is: are there "anti-worlds"
somewhere? We do not know this remotely using
conventional spectrometric methods - light from
"anti-stars" or "anti-galaxies" would have
exactly the same spectra as we know from our stars and galaxies
due to the identical properties of "antiatoms".
However, there are two compelling indications that there
is no free antimatter in the available part of
the universe :
1. In primary cosmic rays from
outer space there are only protons, not antiprotons
(a small proportion of about 10-4 antiprotons observed
in cosmic rays are secondary antiprotons; they
form when high-energy protons interact with the interstellar
medium - with particles and photons of relic radiation; similarly
positrons). No more complex
"anti-nuclei" of helium or heavier elements
(which would be composed of antiprotons and antineutrons) have
been registered in cosmic rays so far *). Such
"anti-nucleus" would have to be emitted in large
quantities into space with each explosion of a possible
"anti-star" as a supernova, in an (anti)stellar wind,
as well as in jets from antimatter accretion disks around black
holes. If cosmic rays contained more antiprotons or more complex
"antinucleus", we could think of them as a kind of
"envoy" of anti-stars and antigalaxies. In reality,
however, we observe very few of antiprotons, just as many as are
created by the interactions of ordinary high-energy protons of
cosmic rays with ordinary matter.
*) A possible detection of more complex
"antinucleus" would be strong evidence of the existence
of a large amount of antimatter - "anti-stars",
"antigalaxies" - somewhere in space. Such more complex
"anti-cores" cannot be formed secondarily by any
high-energy particle interactions, but could only
originate in primary formation in a large amount of antimatter -
in the thermonuclear synthesis of antiparticles
in "anti-stars". Therefore, satellite "antimatter
detectors", such as the AMS (Alpha Magnetic Spectrometer),
are capable of detecting "antihelium" (anti-alpha
particles), are important.
2. If some stars, galaxies or clouds of gas
were made of antimatter, intense annihilation would occur at the
interface of matter and antimatter, producing hard radiation g of energy 511keV.
No measurements have yet recorded such annihilation radiation.
In the universe, therefore, there is
either no appreciable amount of antimatter, or the
"antiworlds" are so far away from us --> the
radiation is extremely weak that we are unable to register any of
its manifestations with our devices.
Why is our world made of matter and not antimatter ? (or
why isn't it just from radiation?)
The interesting question is, why
do we observe almost exclusively "ordinary" matter and
almost no antimatter in the universe today?
Or even why is there any matter at all and not just
radiation? To answer these questions, we would have to
go back to the very beginnings of the universe. According to
current physical ideas, the same amount of matter and
antimatter should initially be formed at the beginning
of the universe. All experiments in nuclear physics show that in
all particle interactions there is always a associeted -
equal production of particles and antiparticles, in a
ratio of 1:1.
Due to certain specific phenomena -
violation of the symmetry of interactions in the initial moments
of the evolution of the universe - the amount of matter slightly prevailed
over antimatter (ca. 1:109),
there was a slight baryon asymmetry of universe.
A more or less random quantum fluctuation caused the victory of
matter over antimatter in our very early universe. In
hypothetical other universes, the opposite could have been the
case, quantum fluctuation occurred at the appropriate moment
occured on the opposite direction, and such a universe would be
of antimatter ...
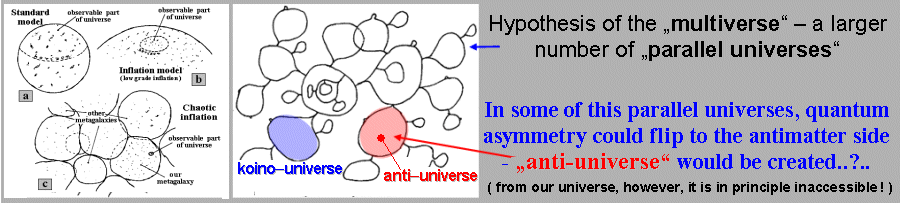
This slight excess of 1:109 caused this matter to remain for the further
development of the universe *), while all the other matter and
antimatter had already anihiladed each other
during the hadron and lepton eras and eventually transformed into
radiation (now observed as relic radiation). If there
were no baryon asymmetry at the beginning of the universe, all
particles would anihilate each other and the universe would
consist only of radiation (in
such dull univers could not have forme any stars, planets,
life...). The questions of antimatter and
baryon symmetry or asymmetry of the universe from astrophysical
aspects are discussed in §5.4 "Standard
cosmological model. Big Bang.",
passage "Baryon asymmetry of the
universe" and §5.5
"Microphysics and cosmology. Inflationary Universe." of book "Gravity,
Black Holes and the physics of spacetime".
*) The terminology of antimatter
is relative. What remains and what our surrounding world is, we
simply called matter -
"ordinary" matter, sometimes called koino-matter
(Greek koinos = usual, ordinary ). And a hypothetical
substance composed of opposite particles is antimatter
to us. In the imaginary universe, where baryon asymmetry would
prevail on the opposite side, the inhabitants there would have
the opposite terminology, for them ordinary matter would be what
we call antimatter.
Combined
particle-antiparticle systems
Interactions of antiparticles with particles result in
annihilation processes, but this annihilation may not
occur immediately. If the particles and antiparticles
have opposite signs of electric charge (+ and -), they can form a bound
particle-antiparticle system after sufficient
deceleration just before annihilation. The best known bound
system of this species is the positronium - a
bounded system of electron and positron, which according to the
model idea revolves around a common center of gravity to balance
the centrifugal force of circulation and the electric attractive
force (see below "Interactions of the most important
elementary particles", passage "Positronium").
Similarly, an antiproton can be trapped in orbit around an atomic
nucleus to load an electron - an antiproton atom is
formed. The simplest antiproton atom is protonium,
which is formed as a bound system of proton and antiproton
orbiting a common center of gravity. Both positronium and
protonium are unstable, in a short time (depending, among other
things, on spin orientations) the antiparticle with the particle
eventually annihilates. Thus, positronium and antiprotonium are
of no general importance (except in special cases and
applications).
However, bound combinations of positrons
and antiprotons (+ possibly also antineutrons), creating antiatoms,
are important. Only this it can be real antimatter...
From the point of view of nuclear physics, the properties of
these antiatoms are important. Primarily spectrometric
properties (briefly mentioned
in the passage "Artificial
production of antimatter. Antihydrogen.") and also gravitational
properties :
Antimatter:
gravity or
antigravity ?
The most difficult is the measurement of the gravitational
properties of antimatter. Although we know that particles and
antiparticles have the same (rest) mass, it remains to be
verified whether the anti-hydrogen "falls" in gravity
in exactly the same way as hydrogen? For ordinary matter
composed of atoms formed by electrons, protons and neutrons,
Newton's law of general gravitation ("Newton's law of gravitation") applies. In the general
theory of relativity - the physics of gravity and curved
spacetime - the very precisely proven principle of
equivalence ("Universality
- the basic property and the key to understanding the nature of
gravity") applies, with the result that gravity does not
depend on the composition and structure of matter. The
gravitational interaction between matter and antimatter should be
identical. An object made of antimatter will
thus fall in the gravitational field of the Earth with the same
acceleration as a body made of matter (here
on the surface of the Earth its fall will take place with a known
value of the gravitational acceleration of 9.81 m/s2) .
Logically, we conclude that this also
applies to individual elementary particles - common (electrons,
protons, neutrons), and probably also exotic (neutrinos, mesons,
hyperons, ...). However, direct experimental verification of the
gravitational properties of individual isolated particles is
practically impossible, because these particles move at high
speeds and show electromagnetic (and
possibly strong) interactions with the
environment, much stronger than gravitational - this completely
"overpowers" a slight gravitational force. In general,
however, it can be said that ordinary (koino) matter
gravitates, showing universal attractive forces.
However, as is the case with antiparticles
(positrons, antiprotons, antineutrons), "antiatoms"
composed of them, and antimatter in general? We
know from experiments on accelerators that particles and
antiparticles have the same inertial mass. But
will antimatter gravitate or antigravity
? - does attractive or repulsive gravity act between matter and
antimatter? However, some unsubstantiated hypotheses, as
well as laymen's opinions suggested by the name "anti-",
hold the opinion of antigravity of antimatter.
The analysis of the probabilities of
short-term existence of virtual electron-positron,
proton-antiproton and other particle pairs ("vacuum
polarization") shows that the results of Eötvös, Dicke and
Braginski measurements confirm the validity of the principle of
equivalence for common antiparticles (such as positron and
antiproton) with accuracy ~10-5 to 10-6. Therefore, "antigravity" can certenaily not
be expected with antimatter - no "falling
upward"! Antimatter will normally gravitate
(only the strength of this gravitational
interaction could theoretically be slightly different - a brief
discussion is in §2.2, section "Principle of equivalence" of the book "Gravity, black holes and
space-time physics").
How does an antiproton "fall" in
a gravitational field, compared to a normal proton? It is not
possible to measure the gravitational effects directly on the
basic particles of antimatter - positrons and antiprotons -
because they are charged and the electrical action with the
environment many times exceeds the investigated force of
gravitational (it is the same as discussed
above for particles of ordinary matter ). For
this purpose, it is necessary to prepare an electrically neutral
antimatter composed of antiatoms. It would be
optimal to create macroscopic bodies from antimatter-antiatoms.
We would then release them downwards in the earth's gravitational
field - as G. Galileo did historically (perhaps
from the Leaning Tower of Pisa...). These
bodies would be initially at rest and their instantaneous
velocity would be determined only by the acceleration due to
gravity. Alternatively, we would launch them horizontally with a
defined initial speed and track their movement along a parabola.
However, we cannot do anything like that
with individual atoms. We are only able to create a gas composed
of hydrogen antiatoms, in which the individual atoms move
chaotically at different speeds in different directions,
with a distribution of speeds according to the
"temperature" that we would try to minimize. These
atoms are not initially at rest, but have different initial
velocities in different directions. In the gravitational field,
they then fall along parabolic paths, whose instantaneous
velocities in the vertical and longitudinal directions would add
up to the initial velocities of the antihydrogen atoms.
However, experiments are being prepared that would be
able to eliminate or correct these effects and precisely measure
the gravitational effects directly on the antihydrogen atoms - as
discussed in the "Artificial Antimatter Production", section "Experimental Measurement of
Antihydrogen Atoms" - AEGIS :
Artificial
production of antimatter. Antihydrogen.
When antimatter does not exist in the available part of the
universe (we do not have any "mining
mines" for antimatter), would it be
possible to "make" it artificially? In accelerators, we
produce large amounts of positrons and amounts!), so it would seem that nothing stands in the way of
artificially (more difficultly) antiprotons and antineutrons (but
these are only submicroscopic "folding"
these particles into "antiatoms". In reality, however,
the artificial creation of antimatter is difficult
!
extremely The particles
produced in accelerators move at high velocities
close to the speed of light - they have high kinetic energies,
many orders of magnitude exceeding the binding energies of atoms.
If we aimed such fast antiprotons and positrons at each other,
they would fly past each other "without noticing" -
almost without interaction - and no antihydrogen atoms would
be formed. In order for the antiproton and positron to
electrically combine into an antihydrogen atom, they must be slowed
down a million times!
Therefore, in order for an anti-hydrogen
atom to form, positrons and antiprotons from the original
energies of the order of MeV must be slowed down
to a sufficiently low mutual speed, that the antiproton can
capture and hold the positron. This is not easy at all, so only
recently (1995) on the LEAR accelerator in the CERN laboratory
managed to create only 9 atoms of anti-hydrogen (now it has managed to produce many thousands of
antihyxdrogen atoms).
Antiprotons were
allowed to fly through the xenon, which slowed them down and the
interaction also created pairs of electrons and positrons. In
these several cases, the positron was subsequently captured by a
flying antiproton to form an anti-hydrogen atom. During the order
of 10-11
sec. then, during his flight through the environment, he
annihilated with normal matter, and a flash of annihilating
radiation proved its brief existence. With such a short period of
existence, no properties of antiatoms can be measured.
For more efficient "antimatter
production", resp. anti-hydrogen atoms, has now been
constructed at CERN electromagnetic antiproton
decelerator. In the electromagnetic field (generated by a high-frequency resonator), the antiprotons in the beam from the accelerator
decelerate from the original energy of about 100 MeV to MeV
units. This is still too high an energy for efficient production
of antihydrogen atoms and for further experiments. Antiprotons
are further slowed down by passing through thin aluminum
degradation foils to approx. 5 keV (the
yield here is very low, only approx. 0.1%).
However, the last effective deceleration stage ELENA
(Extra Low ENergy Antiproton ring), consisting of a 30 m
hexagonal ring with radio frequency cavities and electron
cooling, is in the preparation stage. Here, the antiprotons
received from the antiproton decelerator are further slowed down
from 5MeV to 100keV. Only a minor slowing down with degradation
foils to ~5 keV is then sufficient, with significantly lower
losses than with the use of only degradation foils; double the
number of antiprotons is achieved. This leads to significantly
more efficient production of a larger number of antihydrogen
atoms.
The slowed particles are then led to a cooled
magnetic trap, where a cloud of antiprotons is trapped
in a magnetic field and further "cooled" in it (the kinetic energy of their movement decreases). Positrons are simply obtained from
beta+ -radioactivity, most often the radioisotope 22 Na, or also by reactions
using a linear accelerator. After basic deceleration in a thin
film, they are led to a magnetic trap where they slow down
further ("cool" similar to
antiprotons) and then slow antiprotons and
positrons are simultaneously injected into a
reaction chamber with a magnetic trap, where positrons are
trapped by antiprotons to form antihydrogen
atoms. When decelerated and trapped in a magnetic trap, both
particles have enough time to bind to each other in anti-hydrogen
atoms. This method succeeded in detecting 80 antiatomic hydrogen
atoms in the first phase, but after further improvement - the ALPHA
device (Antihydrogen Laser PHysics
Apparatus) - it is possible to produce
tens of thousands of anti-hydrogen atoms for experiments, eg to
compare electromagnetic spectra of anti-hydrogen and hydrogen
atoms.
For the production
of anti-hydrogen atoms, it is advantageous to use positrons in
the form of positronium - the electrically bound
state of the electron and positron (see
"Electrons and
positrons"). Positrons from beta+-radioactivities are passed through a porous target of
siliceous material, in which they capture electrons and form
positronium e--e+. Using laser beams, the positronium is
then excited to a higher quantum state (up to n
= 25) and directed to the antiprotons. Highly excited positronium
can relatively easily transmit a positron to an
antiproton - there is a "charge
exchange" in which the antiproton assumes the
position of an electron in the positronium: (e--e+)*
+ p- -> H~* + e-, to form an
excited antihydrogen atom H~*. This
process has a relatively high effective cross section (depends on the 4th power of the quantum number n of positronium). Another advantage is the lower kinetic energy of the
formed anti-hydrogen atom. Antihydrogen atoms are created here in
a highly excited (Rydberg) state, so they are sensitive to
gradients of electric and magnetic fields, which makes it
possible to manipulate them in experiments.
In addition to the
production of the antiatoms themselves, another very difficult
problem is their isolation from the surrounding mass
in order to prevent immediate annihilation with the materials of
the reaction vessel. A magnetic field is commonly used to keep charged
particles (e.g. in tokamaks - see
§1.3, section "Tokamak", or in the above-mentioned magnetic traps). However, the hydrogen atoms are electrically neutral
on the outside. However, they have a magnetic moment,
so they react to the magnetic field (albeit weakly). With the
help of strong superconducting electromagnets, a "magnetic
trap" can be created, which is able to keep
anti-hydrogen atoms in the magnetic field inside the reaction
vessel for some time. The magnetic field is specially shaped so
that it is strongest at the edges and decreases towards the
center. The atoms are drawn into the "magnetic well" in
the middle, where they can remain trapped for some time. If this
time is long enough, antiatoms have time to return to a ground
state in which their physical properties can be measured, paving
the way for accurate testing of the presumed symmetry of
matter and antimatter (some minor
differences are discussed below in the passage "CPT symmetry of
interactions"). Revealing possibly small differences could help to
explain why our universe is made up only of matter (cf. "Baryon's asymmetry of the universe").
Experimental measurement of
anti-hydrogen atoms - AEGIS, GBAR
The AEGIS (Antihydrogen Experiment: Gravity,
Interferometry, Spectroscopy) project is being developed at
CERN for the precise measurement of the physical properties of
antihydrogen atoms. It consists of several basic follow-up steps
:
1. Production of antiprotons p- in the
proton synchrotron. A beam of protons p+ accelerated to
an energy of 25 GeV hits an iridium target, where, thanks to the
high energy, showers of many secondary particles, including
proton-antiproton pairs, are created. The antiprotons p- are
separated using a magnetic field. They have high energies,
velocities close to c, wide energy spectrum. They are not
directly applicable for the creation of antiatoms, they must be
slowed down :
2. The antiproton decelerator,
which applies a strong electric radio-frequency field of opposite
polarity, on a circular track in a magnetic field (created by
electromagnets), it works "oppositely" to a
synchrotron. It has an oval shape (diameter
60 m, in the diagram below it is drawn as a circle for
simplicity), along its perimeter there are
four short straight sections with radiofrequency electrodes,
where antiproton braking takes place. In AEGIS, there is
a slowdown to 5.3 MeV, which corresponds to about 10% of the
speed of light. Antiprotons are further slowed down by passing
through thin aluminum degradation foils to approx. 5 keV (the yield here is very low, only approx. 0.1%; not
drawn on the diagram).
3. Capture and accumulation of
antiprotons in an electromagnetic trap (the so-called
Penning-Malmberg trap), a chamber with a magnetic field and a set
of circular electrodes. Another slowing down of antiprotons by
collisions in the electron cloud is also carried out here.
4. Production of positrons e+ using
the beta+
radionuclide 22Na. ....
5. Creating positronium Ps
by passing positrons through a nanoporous
material. Ortho-positronium is used, which has a longer lifetime
of 142 ns (compared to para-positronium
which has a lifetime 1000 times shorter). Excitation
of positronium to the Rydberg state Ps* with n=~25 using UV and IR lasers.
6. Creation of antihydrogen atoms
H~ using the charge exchange reaction of an antiproton
with an excited positronium Ps*. The slow
antihydrogen atoms created in this way (with a speed of ~ 25-80
m/s, corresponding to a temperature of the order of 100 mK) are
then already led to experiments to measure their properties.
7. For AEGIS, the creation of a pulsed horizontal
beam of H*~
antihydrogen atoms with a constant speed
of around 400 m/s. The effect of the inhomogeneous electric field
on the highly Rydberg excited H*~ atoms is used here (it makes it possible to manipulate them using the Stark
effect). It is important for further
analysis of the parabolic motion of H~ atoms in the
gravitational field.

Framework simplified scheme of experimental study of physical
properties of anti-hydrogen atoms - AEGIS and GBAR.
In a gravitational experiment at
AEGIS, the horizontal stream of antihydrogen atoms is led from
there into a system of two separation slits (grids) *) with a
grid period of 80 mm, which create parallel bundles of
antihydrogens. Subsequently, at the end of the L- path,
these anti-hydrogens are annihilated by a silicon position-sensitive
detector with a spatial resolution of 10 mm. The structure of
the grating is analyzed, which is displayed on the
position-sensitive detector as a series of maxima and minima at
different heights when detecting a larger number of antiprotons.
Their vertical positions depend on the decrease (deflection) of
anti-hydrogen atoms in the Earth's gravitational field (approx.
20mm).
It correlates with the arrival times of anti-hydrogen atoms on
the detector (which correspond to their
horizontal velocities v ). It is
evaluated to what extent the height decrease h of antihydrogen at
distance L corresponds to the law of horizontal velocity
throw in the gravitational field of the Earth with gravitational
acceleration g~ : h = 1/2 .g~. (L/v)2. This is a direct laboratory test of the validity of
the weak principle of equivalence in the general
theory of relativity (see §1.2, passage
"Principle of equivalence" in the book "Gravity, black holes ...")
which says that the trajectory of motion
(here fall) of a material body depends only on its initial
position and velocity, not on its structure and other properties
- does it also apply exactly to antimatter..?...
The accuracy of the determination of g~ in the AEGIS experiment is expected to be approximately
Dg~/g~ ~1%.
*) This arrangement of two or
three grids equidistantly placed in a row is
called a moiré deflectometer in optics
(French moiré = fabric, fine structure, grid). The last
third grating is replaced by a position-sensitive detector. It is
not used here in the interferometric mode as in optics, but
serves to precisely define the horizontal parallel trajectories
of anti-hydrogen atoms. The annihilating anti-hydrogen atoms will
create bands on the detector - patterns of grid slits, by
analyzing which it is possible to determine how much H~
dropped when moving along the parabola from the second grid to
the impact on the detector.
In addition to AEGIS, the gravitational measurement of
antihydrogen is dealt with by the alternative experiment GBAR
(Gravitational Behavior of Antihydrogen at
Rest), operated at the same antiproton
decelerator at CERN. To measure the gravitational acceleration of
anti-hydrogen atoms, it does not use horizontal movement with
evaluation using a moiré-deflectometer, but the vertical
free fall of anti-hydrogen atoms in the measuring
chamber, with the evaluation of the exact time of annihilation
when the anti-atoms hit the bottom of the chamber from above. The
trajectory - the height h of freely falling H~ atoms - is related to
time by the relation h = 1/2.g~.(t2-t1)2,
where t1
is the time of entry of the atom into the upper detector of the
chamber and t2 is the time of impact and annihilation of the
antihydrogen atom on the bottom of the chamber. In the GBAR
experiment, additional stages of slowing down antiproons (ELENA)
and "cooling" of the p- beam will be
used, eventually down to an energy of 1 keV. Antihydrogen atoms
are prepared by further reaction with positronium in the form of
positive antihydrogen ions H~+- one antiproton and two positrons (this
requires a higher flux of positrons, which are generated here
using a 9MeV linear accelerator). These H~+ are then cooled
using Be+ ions to a temperature of around 10mK. Using a laser
pulse, the outermost positron is then removed just before the
measurement and a neutral antihydrogen atom H~ is created, whose
free fall time is measured in a vertical chamber with detectors.
Thanks to the measurement of the fall of very slowed down
antihydrogen atoms (with almost zero initial velocity, ~0.5m/s),
one can expect an improved accuracy of the determination of g~ about Dg~/g~ ~10-3.
In anti-hydrogen atomic spectrometry, a
slow beam of anti-hydrogen is led to another magnetic trap, where
it is excited and the radiation emitted or
absorbed during the jumps between the individual energy levels is
measured. The energy levels in an atom depend on the inertial
mass and the charge of an electron in a hydrogen atom or
a positron in an antihydrogen. By comparing the energy of the
electron transitions between the excited and ground levels of
hydrogen and antihydrogen, we can verify whether the inertial
masses and charges of the particles and antiparticles are exactly
the same, or there is a slight difference. If the inertia mass of
the particles and antiparticles differ, it could possibly be
measure a slight difference by this spectrometry.
Production of more and heavier
antimatter ?
Despite all the partial successes in the above-consuming
experiments is unfortunately necessary to admit, that the
creation of large quantities of antimatter, or more
complex antiatoms than hydrogen *), yet there is
no hope in the near future ...
*) The targeted "production" heavier
antinuclei really is not hope for the foreseeable future.
However, in small numbers (with negligible probability) they may
arise randomly in high-energy interactions.
Heavy nuclei collisions produce more antiprotons and
antineutrons. If several co-produced antiprotons and antineutrons
coincidentally fly in the same direction and at
approximately the same speed, they can "bind"
to the heavier antinucleus - nucleus anti-deuterium, anti-helium
- by nuclear forces. Because this process is very unlikely, many
billions of trillions of nuclear collisions to make any such
heavier anti-nuclear accidental to formation. In 2011, at the
RHIC heavy ion accelerator in Brookhaven, 18 nuclei of anti-helium-4
were identified in this way (during several
months of collisions), other successful
experiments of this kind are taking place at CERN. The formation
of even heavier antinuclides in this way, due to the almost zero
probability, will probably not be proven....
Antimatter - a possible source of
energy
?
In the popular science and sci-fi literature, it is often stated
that annihilation of matter with antimatter
results in a 100% conversion of matter into energy,
in accordance with Einstein's relation E = m.c2. Thus, in the distant
future, antimatter could be an inexhaustible source of
energy, or to power interstellar ships
(photon rockets - see below) at speeds close to the speed of
light? Unfortunately, this is not true, the
problem is much more complicated, there are obstacles
not only of a technical, but also of a fundamental
physical nature.
When annihilation an electron with a positron, in
fact all the rest mass of both particles changes into
electromagnetic radiation: e+ + e- ® 2 g. However, it is
not light, but hard gamma radiation, which would not be reflected
by the mirror of the photon rocket, but absorbed. However, the
annihilation of protons and neutrons with antiprotons and
antineutrons does not produce electromagnetic radiation (at least
not directly), but p- mesons, eg p~+ p ® 2 p+ +2 p- + po ; they
then decay into muons and neutrinos, eg: p- ® m- + n'm , p+ ® m+ + nm . This
is followed by the decay of muons, eg m- ® e- + n'e + nm , m+ ® e+ + ne + n'm , and only then could annihilation of electrons with
positrons e+ + e- ® 2 g ( all these
interactions are discussed in more detail below). Thus, in the
hypothetical "annihilation reactor" of
the future, would therefore need to achieve not only the
efficient energy utilization of hard radiation g, but also the
closure of proton, pion, muon and electron (+antiparticles)
high-energy "plasma" so that secondary particles can
effectively annihilate together. So far there is no known
physical mechanism that would alow this. And it is absolutely impossible
to use the energy carried away by neutrinos...
The energy utilization of
annihilation of matter with antimatter is also hindered by
technical difficulties. If, for example, we want to combine two
macroscopic bodies, one of matter and the other of antimatter,
with the aim of complete annihilation, it would not be very
successful in practice due to the emergence of the so - called Leidenfrost
insulating barrier*). When the surfaces of both bodies
touch, a powerful flow of energy (radiation and particles) is
created, which repels, delays and insulates the next mass of the
bodies from each other so that effective volume annihilation does
not occur; the reaction is planar rather than massive volumetric.
One possibility would perhaps be to collide the two bodies at
high speed so that the kinetic energy overcomes the pressure of
the generated radiation. Or even better, perform the annihilation
sequentially in a stream of particles of matter and antimatter
(the aforementioned "annihilation reactor"). None of
this is feasible in the foreseeable future ...
*) A similar phenomenon can be
observed in everyday life when we drip water on a hot stove.
Water droplets usually do not evaporate immediately
(explosively), but "jump" for a while on a hot plate:
when the droplet comes into contact with the plate, steam is
created, which for a while creates a gaseous "cushion"
isolating the droplet from the plate.
Photon
rocket
?
The collimated source of electromagnetic radiation shows the
effect of a "rocket thrust" (it is the inverse effect to the light pressure, which
Lebedev first observed with light). This is
a consequence of the law of conservation of momentum, or the law
of action and reaction: electromagnetic radiation has a flow
of momentum, which in clasical electrodynamics is
describes by the Poynting vector and from a quantum point of view
is given by the momentum of photons (each photon of the wave
frequency f has energy E = h.f and momentum p = h.f /c).
During radiation, this momentum is transmitted to the source in
the opposite direction, the transmitted momentum per unit time
indicating the applied "pull" force. In order for this
"rocket effect" to be noticeable, an extremely high
flux of radiation is required, which is not achievable
by existing technical means. The photon rocket
project envisages an annihilation reaction, or
with a thermonuclear reaction that would take
place in the focus of a large hemispherical or parabolic mirror
that would reflect the resulting photons and collimate
them "backwards". As already outlined above, the
radiation generated by an annihilation or thermonuclear reaction
is not light, but high-energy gamma and corpuscular radiation
for which the law of reflection does not apply; a mirror of any
known material would not reflect this radiation, but would mostly
absorb it, leading to its thermal destruction.
Note: Instead
of a "photon rocket", the name "quantum
rocket" can be used , as the desired effect is
created not only by the emission of photons, but also by other
quantum particles carrying momentum. However, for photons, the
most favorable ratio is [transmitted momentum ® thrust] / [required emitted mass and
energy].
Antimatter and
antiworlds in sci-fi
The mysterious impresion of the term
"antimatter" led in the science fiction literature to
the idea of "antiworlds", in which everything is
"opposite" and in which possibly our
"doubles" - "anti-people" may
live. This sci-fi
idea has no astronomical justification (as
discussed above in the section "Antiatoms,
Anti-Worlds") , it is rather a game for our imagination :
Consider,
therefore, the hypothetical situation that somewhere in the
distant universe there is indeed a large region of antimatter,
where (anti)galaxies and (anti)stars formed, including the
(anti)Sun with the planetary system orbiting and the (anti)Earth,
on which it evolved exactly the same life as here, including anti-people
:
 |
Imagine,
for example, in a sci-fi experiment, that would
"girl made of matter" here on Earth via
communications by electromagnetic signal,
colluded with "antimatter
boy"
somewhere from a distant galaxy, a meeting - "dating"
- at a certain point in space about halfway of path, without they would know they are composed mutually from
antimatter.
They would park in rockets near each other, get out into
the open, and go to greet each other -
"Hello!"; nothing special would happen yet.
However, the moment they shook hands, there would be a
massive annihilation of
matter and antimatter *) and both partners would be destroyed in a massive atomic-particle
explosion.
*) Due to the formation of the
above-mentioned Leidenfrost insulating barrier, there
will be no total annihilation of both bodies,
but only the surface parts of the palms of the hands.
Even that would be enough to doom and
destruction for both partners!
If they were far-sighted, they
could remotely test whether they were of the same nature.
The easiest way is to send a weak beam of electrons
against each other and measure whether annihilation gamma
radiation of 511 keV is produced after their impact. If
so, they should not approach each other (not a step!)
- they would have to run away from each other quickly so
that they do not perish ..!.. |
We do not deal here with the ideas of
antimatter and antiworlds based on errors and
misunderstandings, where the prefix "anti"
is mistakenly attributed to other meanings, such as
philosophical, reverse flow of time, etc. ..!..
Interaction
of elementary particles - general properties
Mutual actions - interaction - the various
objects are the basis of all events in nature. Interactions
transfer energy, momentum, angular momentum, and charges between
bodies. Physics has come to knowledge, that the essence of all
interactions and forces in nature is the interactions
between elementary particles of matter. In principle, we
describe the interaction of particles in three ways :
-> Mechanical force action
Bodies and particles when approaching and contacting each other
simply "act with a force" (the origin and microscopic
nature of which we are not interested here), and we investigate
the "mechanical" consequences of this force action
(basically according to Newton's 3 laws of mechanics). With this
immediate mechanical force action we have the greatest experience
of everyday life. This is how physics proceeds in classical
mechanics.
-> Physical field - acting at a
distance
One particle in the space around it creates a field that exerts a
force on another particle located in it. This very successful
description is the basis of classical electrodynamics and
gravitation.
We assign a
corresponding field to each type of interaction
- a space in which certain forces act on particles. The magnitude
of the field action at each point in space is expressed by the
field intensity (force acting on the "unit
test particle") or by its potential (work
associated with the transfer of particles to a given place). In
classical physics, it is an electric, magnetic, gravitational
field. The changes - "commotion" - in this field
propagate at a finite speed from place to place, which is
accompanied by the transfer of energy, momentum, and other
physical quantities.
From the point of view of classical
physics, quantities such as energy and momentum are transmitted continuously
during field changes. In quantum physics, it turns out that
during changes (disturbances) in the field, physical quantities
are transmitted discontinuously over certain
"portions" - by quantum. Quantum field
theory assigns certain particles to these quantums as
carriers of the interaction, which leads to the following process
:
-> Exchange of particles in quantum physics
Particles transmit and receive certain quantum of fields,
which causes their interaction. We imagine this exchange quantum
as a particle - a carrier of interactions. This
description is characteristic of quantum field theory (basic principles are outlined in §1.1, passage "Quantum
field theory").
In the standard particle model, interactions are
mediated by the exchange of intermediate bosons,
which are in a virtual state during this exchange - they
exist so short that we cannot directly observe them due to the
quantum principle of uncertainty. However, if the virtual
particle gains sufficient energy during the interaction, it can
be released and become a real particle; this is commonly
observed for photons, in accelerator experiments it is also
possible to indirectly observe heavy bosons W+, - and
Z0.
Spatial reach of
interactions
In everyday life and in the surrounding nature, we encounter two
types of interactions: electromagnetic and gravitational.
They have an infinite reach - the field
intensity E(r) at a distance r is given by the inverse
square law E(r) ~ k/r2 and the potential f(r) ~ k/r. The inverse square law has a geometric
origin: a spherical surface of radius r has a surface
S=4pr2. Coulomb's law of
electrostatics and Newton's law of classical gravity have this
dependence.
In the microworld, we encounter two other
types of forces, which, however, have a short reach:
the so-called strong nuclear interactions (§1.1, passage "Strong nuclear interaction") and weak interactions
(§1.2, passage "Mechanism beta. Weak interaction."). If the field-interaction
has a short range, the dependence of its
potential f(r) on the distance r is modeled by an additional
exponential factor e-m.m.r: f(r) ~ k.e-m.m.r/r, where m is the mass of the intermediate
particle, m is the scaling constant. Such dependence is called the Yukawa
potential (H.Yukawa introduced it
in 1935 for strong nuclear interactions; however, here it later
turned out differently...). The value r ~
1/(m.m)
is the effective reach of the interaction (the distance at which the interaction drops to a value
of 1/e).
The spatial reach of interactions
in the concept of particle exchange is closely related to the rest
mass mo (or rest energy Eo=mo.c2) of exchange intermediate particles. It can be shown
most simply using the quantum uncertainty relation DE.Dt » h, from which it
follows that for an mediated virtual particle that perturbs the
energy by the value DE (equal to its rest energy Eo=mo.c2), the maximum time of this perturbation can be Dt » h/DE = h/Eo. During that time,
this particle can travel the path áhu Ds= c.Dt » c.h/Eo at the speed of light, which represents the maximum or
effective range of the interaction mediated by this
mediated particle.
Electromagnetic interaction
has an infinite range, the mediating particle is a photon
with zero rest mass (photons can therefore
transmit almost zero energy in the limit, so according to the
uncertainty relations they can exist virtually for an almost
infinite time and reach an infinite distance also). Gravitational interaction also has an
infinite range, it is mediated by gravitons with zero
rest mass (so far hypothetical or model
particles that we cannot observe in any way).
On the other hand, weak
interactions are mediated by heavy intermediate bosons W+,- and Z0 with rest energies of
80 and 91 GeV/c2, so their reach is very small, on the order of
10-15cm (see the passage "Bosons W+,-, Z0" below). Therefore, even on
subnuclear scales, this interaction is very weak (on even smaller scales, however, it is not weaker than
the electromagnetic one).
The situation is more complicated for strong
interaction. In atomic nuclei (and in general between
hadrons) we observe a very short range of the strong
nuclear interaction of about 1,2×10-13 cm. This fact was
previously (provisionally, incorrectly...) explained using the exchange of intermediate p-mesons with a rest
mass of approx. 135 and 140 MeV/c2. However, after the clarification of the quark
structure of hadrons, this concept was abandoned. The strong
interaction is known to act primarily between quarks
inside hadrons and is mediated by gluons of zero rest
mass, so its range should be infinite. Now, the nuclear forces
between nucleons are understood as a residual
manifestation of the strong interaction between quarks
(discussed in more detail below in the
section "Quark structure of hadrons" and "Four
types of interactions in nature",
also in §1.1, section "Strong
nuclear interaction").
Scatering experiments
The basis of studying the structure of the microworld are the
so-called scattering experiments *). They
consist in firing the studied object with
suitable particles - electrons, protons, a -particles, etc., and we
study the products of collision (or close
convergence) of the arriving particle with the target object
(resp. with the second particle). These are either the original
particles dispersed (that is, at lower energies)
or other secondary particles, emitted during
interaction (this occurs at higher energies). By analyzing the
energies, momentum, charges, angles of flying away and other
parameters of secondary particles, we can obtain important
information about the structure of the investigated micro-objects
and the mechanisms of interactions of the respective particles.
Particle interactions are important in the study of the structure
of matter, and they play a key role in the formation of matter in
universe. All the matter that is here (and of which we are
composed ourselves) was formed during the interactions of
particles in the initial stages of the universe, or inside the
stars.
*) We simply do not have another option to
study microstructures so small that they are not directly
observable (after all, even ordinary visual observation is to
some extent a kind of "scattering experiment" with
visible light photons...). The first important scattering
experiment was carried out as early as 1911 by E.Rutheford
together with H.Geiger and E.Marsden - it led to the discovery of
the atomic nucleus (see §1.1, section
"Structure of atoms", Fig.1.1.4) .
By interactions of elementary
particles we understand the processes of mutual collisions
of two particles, or collisions of a particle with an atomic
nucleus (here the problem is partly
intertwined with the nuclear reactions discussed
in §1.3 "Nuclear reactions and nuclear energy"). The simplest two -
particle interaction of primary particles a and b
can be symbolically written as: a + b ® c + d - Fig.1.5.1.A. The
resulting secondary particles c and d
after the interaction can be either the same as a and b,
or different particles. However, the interaction often results in
different particles than the original and also a different number
of particles - especially at high energies, a higher
number of secondary particles is usually formed (see
below). Primary particles a and b, entering the
reaction, are already known "in advance" (they were
purposefully created in the "ion source" and
accelerated in the accelerator, or one of them prepared in the
target - see "Accelerators" below). Flying-out
particles c , d , or other new secondary particles,
we detect and measure their properties using detectors. The
processes of itself interaction (collisions) take place in a
spatial area with micro-dimensions of the order of 10-8 -10-15 cm, so they
are not available for direct observation. Based on
reconstructions of the interaction, we create certain model ideas
and theories about their mechanisms, which
explain the transition from the initial state (a + b) to the
final state (c + d + /or other particles).
During the interactions of particles
between them, there are three basic types of forces (physical
fields) *) :
- Strong interactions
between hadrons (mesons, baryons) can cause both
scattering and nuclear reactions, and at high energies
the processes of formation of new particles and
antiparticles, such as p- mesons, nucleons,
hyperons and their combinations.
- Weak interactions ,
manifested in leptons, mesons and baryons, are only
relatively marginally applied in collisions of most types
of particles. They are significantly manifest in neutrons
(due to their beta decay), neutrinos (interactions of
neutrinos with nucleons - see the description of neutrino
experiments in §1.2, section "Neutrinos") and at high-energy processes, where p and K
mesons , hyperons and other decaying particles are formed
due to weak interaction.
- Electromagnetic interactions
in charged particles cause Coulomb scattering, radiation
processes such as braking radiation, formation of
electron-positron pairs and their annihilation,
photonuclear reactions. It is characteristic of all these
types of processes that the interaction of electric
charges with the electromagnetic field in which the
charges are located produces a quantum of radiation - photons,
mostly gamma-ray photons. Electromagnetic interactions
are the most common processes occurring in the collisions
of most particles.
*) The gravitational interaction
of elementary particles is completely negligible and has never
been observed se far. It could perhaps only manifest itself at extremely
high energies (»1019 GeV), many
orders of magnitude higher than we can now achieve. However, this
would not be a commonly known gravitational attraction, but
gravity would be part of the unitary field (see
§B.6 "Unification of fundamental interactions. Supergravity.
Superstrings" in the book
"Gravity, Black Holes and the Physics of Spacetime").
In the interactions of particles,
the principle is generally applied: "what is allowed
is also realized" - all kinds of processes *)
occur, which are compatible with the laws of conservation
of energy, momentum, angular momentum, electric charge,
lepton number. If enough energy is available, a number of
processes take place during particle collisions, but with
different probabilities. This probability is given by the
internal mechanisms of interaction of the respective fields and
the relationship between the respective initial and final state
configurations. The probabilities of individual processes
("channels" of interaction) are determined by quantum
field theory using so-called matrix elements (elements of the scattering matrix S, see also
below "Feynman diagrams").
*) As if all quantum of all fields were potentially,
covertly and implicitly - virtually - present
everywhere in space, in a "vacuum". From this
"unitary" field, by supply of energy - excitation
of the field - then releases the relevant particles,
whether virtual or real.
The course and result of the interaction
of particles depends mainly on two circumstances :
¨ On the type of interacting particles.
¨ On the kinetic energy
with which the particles collide (determined
here by the energy in the center of gravity of
both particles).
Note: Even with collisions of the same particles and with the
same energy, however, the interaction usually takes place in a
slightly different way each time - through different
"channels" of the reaction. We can explain this by the
fact that on the one hand the collision can take place
"frontally" or "peripherally" (ie with
different impact factor and mutual angular momentum of both
particles), and on the other hand due to stochastic laws of
quantum physics the individual possible configuration states are
realized with different probabilities.
Feynman diagrams
The so-called Feynman diagrams are often used
for a clear graphical representation of the mechanisms of
particle interactions (R.Feynman first
introduced them in 1948). They come out from an exchange
description of particle interactions. The trajectories
of "matter" particles, fermions (electron, proton, ...)
are marked by straight solid lines with arrows -
particles have an arrow pointing to the right, antiparticles to
the left. Exchangeable intermediate particles (photons, W-bosons,
gluons ...) are marked with dashed lines or wavy
lines. In the horizontal direction there is a time
orientation (other conventions are
also used) - however, only symbolic, these
diagrams do not serve to concretely express the time course of
interactions, but only to "topologically" represent
their mechanisms; are a kind of analogy of spacetime diagrams
used in relativistic physics. The basic Feynman diagram of the
general unspecified interaction of two particles a + b ® c + d is shown in
Fig.1.5.1.A. The primary particles a and b arrive
into close proximity to each other - the interaction area,
the actual processes of interaction take place inside, after
which the resulting particles c and d fly out of
this area. The upper part of Figure 1.5.1.A shows the usual
spatial drawing of the collision of both particles, the lower
part of the figure shows Feynman's presentation of this
interaction.
Feynman's own diagrams then specify and illustrate possible
processes within the interaction region for specific
types of incoming and outgoing particles. Again, they consist of
outer lines with "free ends", showing the particles
entering and leaving the interaction. The actual interaction
processes are drawn by the so-called interaction vertices
- points at which wave or dashed lines connect to the initial
outer line of the particle, corresponding to exchangeable
intermediate particles mediating the interaction *). The laws
of conservation of energy, momentum, electric charge, lepton
number are fulfilled in the interaction vertices . The inner
lines between the interaction vertices of the outer lines
correspond to the virtual particles which do not
leave the interaction area and are not present between the
incoming or the resulting "physical" particles in the
initial or final state; however, in their own interaction, they
act and contribute to the result. Lines with a second free end
can also emerge from some interaction peaks: these correspond to real
particles (photons, W-bosons, fermions) emitted during
the process.
*) In quantum field
theory, these lines correspond to the so-called propagations
- functions indicating the amplitude of probability (amplitude of
"wave propagation") when moving a particle with a
certain energy and momentum. These are fermion (eg
electron) and boson(eg photon) propagator. Propagators
can be expressed using the so-called Green's functions ,
which are solutions of the wave equations of the respective
particles (either inhomogeneous Dirac equations with d -function of
coordinates and time, or d´Alembert's equation for
electromagnetic field potentials). The actual interaction peaks
correspond to the operators of creation and annihilation
of the respective particles.
We will give examples of Feynman diagrams for some
specific typical interactions of particles - Fig.1.5.1. From the
point of view of nuclear, radiation and particle physics, these
interactions are discussed in more detail in other relevant
places (§1.2, 1.3, 1.5, 1.6) of our treatise. Let's start with
low energy interactions. The simplest process with particles is
the interaction of two electrons under the
influence of electromagnetic force. According to the concept of
quantum electrodynamics, the basic mechanism operating in the
interaction region is the exchange of photons
between the two electrons - in the Feynman diagram, the electron
lines in their interaction vertices are connected by a photon
line (Fig.1.5.1.B) - one electron emits a virtual photon g*, the other
absorbs it, whereby both electrons scatter in
their orbits (elastic scattering). The resulting state is again
two electrons. However, this is only one of the possible
processes and, moreover, only in the first approximation. It is
already known from classical electrodynamics, that with each
accelerated movement of electric charges, electromagnetic waves
are emitted. Photon emission of braking radiation occurs even
when electrons are scattered. At higher energies, interaction
peaks with energetic particles can also be realized, which can
generate real particles - lines with free ends corresponding to
secondary leptons; at the highest energies also the production of
heavy particles (see below).
Another simple process of electromagnetic interaction is
the scattering of a photon on an electron - Compton
scattering (is described in §1.6 "Ionizing
radiation", part "Interaction of gamma and X-rays", Fig.1.6.3). In the Feynman diagram in the upper
part of Fig.1.5.1.C we see a solid electron line and a wavy
photon in the input region. In the interaction vertice, a virtual
electron e* (which seems to "absorb" the energy of the
photon) is formed, which in the second vertice changes again into
a flying away electron and a photon. The interaction of the positron
with the electron can take place again at low energies
either as a Coulomb elastic scattering (Feynman diagram is
completely analogous to Fig.1.5.1.B), or as a process of annihilation
with the formation of gamma photons - lower part fig.1.5.1.C. At
higher energies, there are again more possibilities in both of
these processes with the formation of additional secondary
particles.
At the highest energies, there are many possibilities
for the production of heavy particles, including Higgs bosons.
Two such possibilities of "electro-weak production"
of the Higgs boson are shown in Fig.1.5.1.D: direct interaction
of e+ + e- ® Z* ® Z + H ( H-emission
) and combined production of W or Z and their subsequent
fusion to H. Higgs bosons are highly unstable particles
and immediately decay into either two high-energy photons or four
leptons (via intermediate W or Z bosons), or other ways (the properties of Higgs bosons are described below in
the section "Hypothetical and model particles").

Fig.1.5.1. Examples of Feynman diagrams of some significant
particle interactions.
Note: Symbolic images of protons, neutrons and p- mesons are not
part of standard Feynman diagrams; they are drawn here for
illustration only.
Weak
interactions are mediated by exchangeable intermediate
bosons W (or Z). In Fig.1.5.1.F is a diagram of an important
process of transmutation of the d
to u quark in the b--radioactive conversion of a neutron to a proton, an
electron and an (anti)neutrino: no ® p+ + e- + n'e . This process, as
well as the analogous b+
process, corresponds to Figure 1.2.5 in §1.2 "Radioactivity", section "Radioactivity
beta". Other important processes,
taking place due to weak (or electroweak) interaction,
are decays of pions into muons and neutrinos, eg
p- ®
m- + n'm (the decay of p+ takes
place analogously) and muons into electrons and
neutrinos, eg m- ® e- + n'e + nm (analogously for m+) - this
is shown by the Feynman diagrams in Fig.1.5.1.G.
Strong interactions are mediated by
"exchange" gluons between quarks contained
inside hadrons - mesons (especially p and K) and
baryons (protons, neutrons, hyperons). The nonlinearity of quantum
chromodynamics of strong interaction together with the idea
of asymptotic freedom (see below
"Inprisoned Quarks", or "Unification
of Fundamental Interactions. Supergravity. Superstrings.") allows Feynman diagrams
(and the perturbation approach) to be used only in processes
where high momentum is passed to quarks. The
"quiescent" interactions of quarks in hadrons, the
strong interaction of nucleons in nuclei, and the
"hadronization" of quark-gluon plasma cannot be
analyzed in this way. However, high-energy interactions between
hadrons can be well described. Fig.1.5.1.E
shows a Feynman diagram of pion production in
the collison of twoo protons p+p®p+p+po; it is one of the possible processes, alternatively a
proton, a neutron and a p+ can be
formed , or two neutrons and a p-.
In high-energy interactions
(see below), when enough energy is available, a wide range of
different internal processes can be realized. In particular,
intermediate W-bosons or gluons attached at interaction vertices
can acquire such high energy that they can generate very
heavy particles - Higgs bosons H and
heavy t- quarks - in the associated production of
particle-antiparticle. These then disintegrate under the action
of intermediate bosons W to electrons, muons, tauons,
neutrinos and their antiparticles. Higgs bosons can also decay
into a pair of high-energy photons g. Furthermore, repeated
processes with intermediate particles can create multiple
particles in a single collision - including quarks,
which then hadronized. Fig.1.5.1.H shows an example of
high-energy collision of two protons at the energy of a hundred
GeV, where interactions with exchangeable gluons can also form
heavy t- quarks, b- quarks, then W-bosons and
finally leptons (electrons e±, muons
m±, tauons t, neutrinos n) that fly out of
the interaction area and can be detected. With an even higher
energy of tens of TeV (not yet achieved ...) one of the more
possibilities is the formation of the Higgs boson
("strong production" of H by the
exchange interaction of energy quarks with gluons or W-bosons)
and a series of subsequent decays into W-bosons and finally again
leptons or quarks - fig.1.5.1.I. And, of course, this is
accompanied by the hadronization of energy quarks. Fig.
1.5.1.I shows the formation of the Higgs boson by the so-called gluon
fusion; other possibilities are W or Z fusion
(analogous to Fig. D below, only instead of
electrons there are quarks), or combined
production with W or with t-t'-pair.
In these high-energy collisions, other
quarks of colliding protons also enter the interaction area - the
interaction with gluons can then create a so-called quark-gluon
plasma (see below the passage
"Quark-gluon
plasma -"5th state of matter"," and in §1.3
passage "High-energy
collisions of heavier nuclei. Quark-gluon plasma."), the hadronization of
which creates other secondary hadrons
(especially pions, nucleons), flying out of the interaction
region. In Fig.1.5.1.H,I two interaction areas are marked. The
first - "asymptotically free"-
corresponds to high-energy interactions in which even quarks
behave as free and their interaction can be described by Feynman
diagrams; it is analogous to the interaction areas in other
diagrams. The second interaction region corresponds to the hadronization
of quarks, which cannot fly out alone, but in the
gluon field generate further pairs quark-antiquark which combine
in pairs and triples - fly out as hardon - mesons p and K, protons,
neutrons, hyperons. These particles fly out often narrowly
directed sprays, called jets, at a small angle
around the direction of flight of the original energetic quarks.
In quantum field theory
(in the so-called perturbation access), Feynman diagrams
are used as a guide for counting contributions from different
kinds of possible processes with intermediate quantums into
so-called matrix elements ( S-elements of scattering),
indicating the probabilities of quantum transitions between
states of a given system - here between the state before
interaction and after particle interaction.
First, the
corresponding Feynman diagrams are constructed, the outer lines
of which correspond to the incoming particles of the initial
state and the outgoing particles of the final state. The 1st
approximation (diagram with 2 interaction vertices), 2nd
approximation (4 vertices), ..., N-approximation (number of 2N
vertices) are investigated. For each of these approximations, all
different ones are drawn ( topologically non - equivalent)
diagrams with the same outer lines and numbers of vertices. In
each such diagram, specific terms (coefficients) containing (4-)
momentum and the binding constant g of the respective interaction
are determined for its individual parts - outer lines, inner
lines, vertices. Then integration is performed across all
momentums. The contributions of all the diagrams are finally
added up.
.............. comes to add ?.................
Formation
of new particles during interactions
A specific phenomenon in high-energy interactions of particles is
the formation of new particles - the emission of
additional particles that were not previously present. They can
be either particles of the same species as entered into the
interaction, or particles of a different species. We explain this
phenomenon using Dirac's quantum concept of vacuum
*), which is not "empty space", but is filled with virtual
particles, resp. pairs of particles and antiparticles.
If a sufficiently large gradient of a certain field is created
during the interaction at a certain place - a sufficiently
large energy is transferred - these virtual particles
are transformed into real particles; we observe
it as the emission of new particles. Occur at the same time a associated
production of particle-antiparticle pairs. A necessary
condition for the formation of new particles is the achievement
of a sufficiently high energy of interaction - threshold
energy, higher than Smo.c2, where Smo is the total rest
mass of the resulting particles.
*) Quantum field theory
and unitary theory deal in detail with the mechanisms of particle
formation. The above-mentioned Feynman diagrams are also
used to represent them graphically.
Multiple
interactions - cascades of interactions and sprays of particles
When the interaction of high-energy particles in a sufficiently
voluminous medium environment, the effect of multiple
interaction occurs. The secondary particles, released
during the first interaction of the incident primary particle,
cause further interactions, producing additional
(tertiary) particles, which do the same. From one incident
particle, a whole spray of secondary particles
is formed in a cascade of interactions. As the evolving spray
penetrates to the depth of the material, the number of secondary
particles increases and their average energy decreases. Once this
energy falls below a certain threshold, the multiplication
process will stop and the energy of the particles will be
dissipated by ionization and excitation; the number of particles
in the spray will decrease until the spray finally disappears. In
practice, we distinguish two types of cascade interactions :
¨ Electromagnetic
sprays
arising from the interaction of high-energy photons or electrons
with atoms of matter. Secondary electrons and photons emitted
during the primary interaction, due to paired e- e+ production, Compton
scattering, photoeffect and braking radiation, produce additional
electrons (+ positrons) and photons; etc.
¨ Hadron
sprays
resulting from inelastic interactions of high-energy hadrons with
atomic nuclei of the material. Nuclear fragments are formed and
new secondary particles are produced - p, n, p, K. The number of
these secondary particles is approximately proportional to the
logarithm of the energy n ~ ln E.
In many cases in practice, this spray is
not purely hadron or electromagnetic, but mixed.
The hadron spray includes pions, which then decay: p+,
- ®m+, - + nm , po ®g + g; this leads to the
formation of an electromagnetic electron-photon-muon
spray that accompanies the hadron cascade. Thus, each
hadron spray also has an electromagnetic component. And with the
interaction of high-energy photons or electrons, photonuclear
reactions emit protons and neutrons, which can enrich the
electromagnetic spray with a hadron component.
Cascades of interactions and sprays of secondary particles are
observed in cosmic rays (see Figure 1.6.7 in §1.6, section "Cosmic rays") and in
particle interactions on accelerators (in bubble chambers,
trackers and calorimeters).
Effective
cross section of particle interactions. Impact parameter .
Similar to chemical and nuclear reactions, interactions of
elementary particles take place differently "willingly"
- with different efficiencies or probabilities, depending on the
type of interaction and energy of the particles. The probability
of particle interactions can be illustratively expressed in a
geometric way using the so-called effective cross section
of the interaction. The effective cross section
expresses the probability that the bombardment
particle will interact with the target particle in a given
specific way.
The concept of the effective cross-section is based
on the illustrative idea that the target particle (black disk in
the picture) behaves as an "absorbing body" with a
radius r with respect to the incident particle, which this
particle either hits and the desired interaction occurs, or it
does not hit (misses, flies around) and no interaction occurs.
The larger the radius of this body, resp. its effective area s = p .r2 - effective
cross section, the greater the probability of
interaction (probability that the particle "hits").
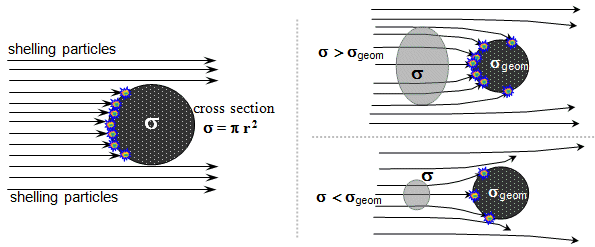
Expressing the probability of the interaction of a firing
particle with a target particle using an effective cross section
The cross section may, but need not be directly
related to the "geometric diameter" target particle rgeom or its
"geometric cross section" sgeom = p.r2geom . For "attracting" particles, is s > sgeom , for repellent particles, is s < sgeom . In addition, the same firing particle can cause different
interactions on the same target particle, the different
probabilities of which are described by different partial
effective cross sections. These effective cross sections no
longer have anything to do with the geometric dimensions of the
particles - they are the result of the internal mechanisms of
specific types of interactions
(the geometric dimensions of the particles
were discussed above in the section "Size of elementary particles ...").
The unit of effective cross section in the
SI system would be m2, which is, however, inadequately large and therefore
the unit barn (bn) is used in nuclear physics: 1
bn = 10-28
m2, which
has the order of magnitude of the proton geometric cross section
due to strong interaction (resp. heavy
nuclei - so this unit and its bizare name originated in the study
of uranium nuclear reactions...).
The effective cross section of
the interaction is very closely related to the absorption
coefficient, the so-called linear attenuation coefficient m, in the
exponential law of absorption of ionizing radiation in
substances. This connection will be clarified in the following
§1.6 "Ionizing radiation", passage "Absorption
of radiation in matter".
For specific course of the interaction is
important the impact parameter b: it is
the geometric distance of centers effective
"disks" interacting particles in which around fly
throughs or intersect. In the case of small impact parameter b
<< rgeom with it is a central collision, at
larger values of b it is a peripheral
collision. If the impact parameter is greater than rgeom , resp. greater
than the sum of the effective radii of the two particles (target
and flying), there is no longer a direct
interaction by the basic mechanism (strong short-range
interaction), but particles can interact through their electric
fields if they are charged (such a collision is sometimes called ultraperipheral).
Dependence
of the effective cross section on energy
For a given type of particles and interactions, the
effective cross section is a relatively complex function
of the energy of the incoming particle. The energy
dependence of the effective cross-section often has a resonant
character: if we change the energy of the interacting particle
continuously, significant maxima appear on the
curve of the effective cross-section around certain specific
energy values. By their shape, these dependences resemble the
dependence of current, voltage or impedance in RLC electrical
circuits (containing ohmic resistance R, inductance L and
capacitance C), on the frequency f of the AC electrical
signal around the frequency fres = 1 / [2pÖ(LC)]. For effective cross section of this kind of
interaction was already in 1936, derived important Breit-Wigner
relationship *)
s = (l/2p)2.g.G2. 1 / [(E-Er)2 + (G/2)2] ,
where Er is the resonant energy, G represents the width of the
excited level of the intermediate state during the interaction, l is the wavelength
of the particle, the factor g is a function of the spin ratio of
the initial and final states.
*) Breit and Wigner derived this
relationship for a special case of elastic scattering of
an incident particle in the potential field of a target
particle. However, with some modifications, this formula applies
to all types of interactions exhibiting resonant maxima of the
effective cross section.
The presence of resonant maxima in the
energy dependence of the effective cross section indicates the
existence of certain dynamic processes in the
interaction - the formation of bound systems, discrete excited
states or intermediate particles.
Interactions of high-energy
particles
In §1.3 and 1.6, interactions are discussed mainly at lower and
medium energies, which lead to characteristic phenomena of
excitation and ionization of atoms, or to nuclear reactions
associated with the transmutation of atomic nuclei and the
emission of nuclear particles. At low energies (less than about
1MeV), the total number of elementary particles before and after
the interaction does not change, arise event. only photons that
carry away energy during the deexcitation of excited states. If
the energies of interacting particles (including gamma photons)
exceed the threshold value 2.me.c2 = 1.022 MeV, new (secondary) particles can be formed
during the reaction - a pair of electron e- and positron e+.
Under the interaction of high
energy particles means the reaction induced by particles
with an energy which lies above the threshold for the production
of mesons p, which is above the energy »140 MeV in the center of
gravity system. With increasing energy, such interactions can
produce gradually more new secondary particles (mostly p- mesons) and also
particles with higher rest mass - mesons K, nucleons and
antinucleons, hyperons, bosons W and Z (at
the highest energies of many TeV and more are also expected the
production of Higgs bosons, supersymmetric particles, leptoquarks
and other "exotic" as yet unproven particles).
When atomic nuclei are bombarded by
high-energy particles (eg protons), several nucleons and
"splinters" are ejected - the "shatter"
or fragmentation of nuclei is occur.
At the highest energies (of the order of
100 GeV and higher), the interactions are already quite complex
and diverse, a large number of secondary particles
are produced. In a laboratory (target) system, a narrow beam of
secondary particles is formed, especially pions p, collimated
forward in the direction of movement of the primary particle - a
kind of nozzle or spray of particles.
Furthermore, a wider cone of heavier particles and also gamma
quanta is formed. In these reactions, the kinematic and dynamic
effects of the special theory of relativity are fully manifested
- sometimes referred to as ulrarelativistic.
During high-energy collisions of heavy particles (protons and
especially heavier atomic nuclei), a special mixture of locally
free quarks and gluons may form for a short time - the so-called quark-gluon
plasma (discussed in more detail
below in the section "Quark
structure of hadrons", passage
"Quark-gluon plasma - 5th state of matter").
The study of particle interactions
at high energies is of great importance for understanding the structure
of elementary particles and the nature of forces
that operate between them. During a high-energy collision,
particles penetrate each other "deep inside" and the
result of the interaction can tell something about their
structure. Due to quantum processes in the fields of strong, weak
and electromagnetic interactions, high-energy collisions create
new secondary particles, which are both interesting in themselves
and carry important information about the nature of fundamental
natural forces, including the possibility of their uniform
understanding within unitary field theory. Particle collisions at
high energies are a kind of "probe" into
the deepest interior of matter *) - and at the same time
into the processes of the formation of the universe
(see §5.5 "Microphysics
and cosmology. Inflationary universe." book "Gravity, black holes and space-time
physics"). Specific ways of particle
interactions will be described below for individual types of
elementary particles.
*) Let's also compare with the left part of
Fig.1.0.1 in
§1.0. "Physics - fundamental natural science".
Analysis of the dynamics of particle
interactions
High-energy interactions of elementary particles are
studied using large accelerators (see section
"Charged particle accelerators" below). The accelerator itself is followed by
very complicated and precise detection apparatus
and systems *) that analyze secondary particles and radiation
generated by the interaction of high-energy primary particles
with the target material or in mutually oppossite
collided beams. They contain a large number of individual
detectors of various types (scintillation, semiconductor,
ionization), located in strong and specially configured magnetic
fields (for the analysis of the momentum of charged particles).
By analyzing the type, charge and mass of these flying-out
particles, their energies, momentum and emission angles from the
site of interaction, a number of parameters of the interactions
that occur can be reconstructed. From this it is possible to
deduce the structure of elementary particles, the properties of
acting fields and interactions, the existence of new hitherto
unknown quanta and particles.
*) Large bubble chambers
were previously used for this purpose (see §2.2, part "Detectors trace particle"). Now
they are replaced by large and complex electronic
detection systems (§2.1, section" The arrangement and
configuration of the radiation detectors") containing, inter alia, so-called
trackers - electronic particle paths detectors. They
mainly use multidetector semiconductor systems (§2.5 "Semiconductor detectors"), or systems of special ionization chambers and
scintillation detectors.
Even when a particular intermediate
particle decays immediately at the site of interaction (and
therefore cannot be detected directly), the products of its decay
carry some information about its properties. From the measured
energies and momentum these secondry products, the mass of the
original particle can be determined. If we plot on the horizontal
axis the measured energy of the detected set of particles
corresponding to the respective "channel" of decay -
secondary particles on which the sought intermediate particle
should decay - and plot on the vertical axis the registered
number of cases (or normalized per unit energy of primary
collided particles, e.g. protons), a small "bump" may
appear on the otherwise smooth curve, indicating the existence of
a short - lived particle of appropriate rest mass corresponding
to the energy on the horizontal axis. Based on the quantum
uncertainty relation between the lifetime t of a particle and the
uncertainty of determining its rest energy E = m.c2 (t.DE » h), the lifetime t of the
intermediate particle can be estimate from the stastistic
"blur" of the rest mass values.
Dalitz
diagram
At the output of detection systems surrounding the site of
interaction, a large number of pulses of various
sizes, shapes, temporal and angular correlations appear, carrying
information about energies, momentums and other parameters of
secondary particles. It is by no means easy to find your way
around such a large amount of data. For clear display and kinematic
analysis products of particle interactions the so-called
Dalitz diagrams are sometimes used (diagrams of
this type were first compiled by R.H.Dalitz in 1953 during the
research of K-mesons and their decays). It follows from the laws
of conservation of energy and momentum, that the kinematics of
the interaction can be suitably parameterized by the square of
the energy of the particles. On the axes of the diagram, the
squares of the effective masses»energies of the pairs of
daughter particles (products of interaction *), mostly p- mesons, are
plotted (in GeV2 energy units).
*) If, for example, during the interaction of two primary
particles P1 and P2 : P1 + P2 ® A + B + C, three secondary
particles A, B, C are formed, we plot m2AB on the X axis and on the Y axis the values of m2BC
. These squares of masses are equal
to the squares of the sums of the 4-momentums of the particles: m2AB = (pA + pB)2, analogously to mBC .
If the studied type
of interaction takes place directly, without
being affected by dynamic processes of intermediate particles or
resonant states (which is the same from a
certain point of view...), the resulting
particles are randomly distributed and the distribution of
relevant measurement points on the Dalitz diagram is
approximately homogeneous, filling the
triangular area below the diagonal given the energy used.
However, if a short-lived intermediate particle
(or resonance process) is formed during the interaction, whose
decay products are detected secondary particles, the distribution
of measured points on the Dalitz diagram is inhomogeneous
- local densities appear (peaks in the profile -
slice of diagram) in the areas around the mass of the
intermediate particle.
Analyzes
of this kind were previously performed manually with dots drawn
on paper. They are now performed using powerful computer
technology, diagrams are digitized and displayed using computer
graphics, sometimes with color image modulation. Fourier
transforms are also introduced to analyze the relationship
between the time and energy spectra of the short-lived state of
an intermediate particle or resonance. All these methodological
approaches are useful not only in the analysis of particle
interactions, but wherever we need to distinguish
kinematic effects from dynamic ones, to prove the
existence of some short-lived bound state that is not directly
observable.
Energy
dependence of the effective cross-section
This procedure is suitably combined with the analysis of the
energy dependence of the effective cross-sections
an interaction, whose possible resonant character
is expressed by the above-mentioned Breit-Wigner relation.
If there are resonant peaks in the energy dependence of the
effective cross-section of the interaction and at the same time
local densities and peaks are visible on the Dalitz diagram of
the energy distribution of secondary particles, it is almost
certain that dynamic processes of excited states
or intermediate particles occur during the interaction.
Missing
energy
If the studied interaction is accompanied by the formation of
neutral weakly interacting particles, these cannot be detected in
the normal way. Here is a certain possibility an analysis of the energy
balance we determine the energies and momentums of other
particles and, based on the law of conservation of energy and
momentum, we determine the values of energy and momentum that an
unknown particle carries away. From them we can then determine
the rest mass of an unknown particle.
...? add-other types of diagrams +
pictures ..? ...
Properties
and interactions of the most important elementary particles
In this section we will briefly approach the individual most
significant particles of the microworld, their origin and
formation in the interactions of particles, their properties and
the main ways in which they interact with each other and with
other particles. In this brief description of the properties of
elementary particles, we will not stick to the systematics
outlined above, but will move from known, widespread and
practically used particles to "exotic", less known and
more hidden particles, whose significance for the structure and
properties of matter is sometimes unknown.
 Photons
Photons 
are a quantum of electromagnetic radiation. They have zero rest
mass, they move at the speed of light *), they carry energy E =
h.n,
where h is the Planck's constant and n is the frequency of the
electromagnetic wave of wavelength l = c/n. They are bosons with spin
number 1. According to the laws of electrodynamics,
photons are generally formed during all accelerated
movements of electrically charged particles (eg braking
radiation). They are emitted during deeexcitation
in atomic shells (visible and UV radiation,
characteristic X-rays - §1.1., passage "Radiation of atoms") and atomic nuclei (gamma radiation - §1.2, part "Gamma radiation")
, where they carry away the corresponding
energy difference of the excited states. Photons of gamma
radiation also arise during annihilation of
positrons with electrons e+ + e- ® 2g (§1.6, part
"Interaction of charged
particles - directly ionizing radiation", Fig.1.6.1 below, passage "Interaction of
positron (beta + ) radiation"), as well as in a number of
other elementary particle interactions. Here we will consider
mostly photons of higher energies - radiation g.
*) However, see the theoretical note on the
possible influence of quantum fluctuations of spacetime on the
speed of hard radiation g in §1.6: "Is
high-energy g-
radiation moving slower
than light?".
Interactions of medium energy photons with
matter are described in §1.6, part "Interaction of gamma and X - rays", it is mainly a photo effect, Compton scattering,
formation of e-e+ - pairs. High-energy photons (> 10MeV) can, through their
interactions, cause so-called photonuclear reactions,
in which neutrons, protons, or multiple nucleons, deuterons, a-particle, are
ejected from the nuclei. Above the threshold energy of gamma
radiation of about 140 MeV, other particles are formed during the
interaction, eg p -mesons: g + p ® n + p+ , g + p ® p + po, etc. At very high energies of gamma photons (> 300MeV) , a number of other
particles can be generated, including heavy ones (cf. above "Interactions of
high energy particles").
Photons, as a quantum of
electromagnetic waves, were actually introduced by A.Einstein in
1905 during the study of the photo effect (§1.1 "Atoms and
atomic nuclei", Fig.1.1.1); the proper name
"photon" was later proposed by the American
chemist G.N.Lewis.
 Electrons and positrons
Electrons and positrons 
 Electrons e -
Electrons e -
are basic, truly elementary, stable particles of matter that form
the electron shell of atoms. The electron carries a negative
elementary charge e = 1.60219.10-19 C, its rest mass is
me =
9.1095.10-31 kg (= 511keV/c2), it belongs to the leptons, it is a fermion with spin
(1/2) h. The magnetic moment of an electron is e.h/4p me - the so-called Bohr
magneton. According to the ideas of modern cosmology,
electrons were formed in the earliest stages of the evolution of
the universe after the Big Bang, during the separation of
electromagnetic and weak interactions. In addition, electrons are
formed in a number of processes and interactions of other
elementary particles, such as in b- -radioactivity no ® p+ + e- + ne´ and in many other processes, as can be seen from the
interactions of other particles described below. In addition to
atomic and nuclear physics, electrons play a key role in
electromagnetic phenomena, the vast majority of which are based
on the motion of electrons that generate electric current.

1895: J.J.Thomson - discovery of electrons =>
first model of atom
The electron was discovered, as the first
elementary particle of the structure of matter, in 1895 by
J.J.Thomson during the study of electric discharges in gases in a
cathode ray tube.
 Positron e +
Positron e +
is an antiparticle to the electron, so it has the same mass and
spin, the electric charge is the same size, but of the opposite
(positive) sign. In a vacuum, a positron is a stable
particle, just like an electron. However, as soon as it is in a
material environment filled with atoms and therefore also
electrons, it disappears in annihilation interaction
with electrons: e+ + e- ® 2 g (§1.6, section
"Interaction of charged
particles - directly ionizing radiation", Fig.1.6.1 below passage "Positron (beta +
) radiation interactions"), producing two quantums of
gamma radiation of 511 keV energies, flying out in opposite
directions (at an angle of 180°). This perfect angular
correlation is advantageously used in gamma imaging by positron
emission tomography imaging in nuclear medicine after
the application of a positron beta+-radionuclide, e.g. 18F (§4.3, section "Positron emission tomography PET").
Note
: These patterns
apply exactly only in the center of mass frame
of reference of the positron and an electron. The energy of
photons 2x511 keV is a consequence of the law
of conservation of energy (resting energy of the
electron and the positron is m0e .c2 = 511keV), the opposite direction of 180° is a
consequence of the law of conservation of momentum.
In the case of collisions of positrons and electrons of higher
energies, the angle of inclination of annihilation photons would
differ from 180°. In the material environment, however, the
positron and the electron have relatively low velocities at the
moment of annihilation, so that the emitted quantums actually fly
in almost opposite directions.
Positronium
Just before the actual annihilation, the electron e- and the positron e+ can orbit around
itself for a moment (they orbit the common center of gravity) -
they form a special bound system (similar to a
hydrogen atom) called positronium (Ps). The
dimension of the "atom" of the positronium is twice the
hydrogen atom, the binding energy of the positron is 6.8 eV.
Depending on the mutual orientation of the electron and positron
spins, the positronium can be either in the singlet state 1S0
with oppositely oriented spins - so-called parapozitronium
p-Ps (1/4 cases), or in the triplet state 3S1 with consistently oriented spins -
so-called orthopositonium o-Ps (3/4 cases).
However, this system of
positronium is unstable, the two particles
approaching each other in a spiral under the emission of
electromagnetic waves; in p-Ps in about 120ps they
"fall" on each other and there is a self-annihilation
on two photons g,
each with an energy of 511 keV. In the case of o-Ps, annihilation
to two photons is prohibited by quantum selection rules (related
to the law of conservation of the spin momentum - each of the
photons has spin 1), so o-Ps would decay in a vacuum with a
relatively long lifetime of about 140ns emission of 3
photons with a continuous energy spectrum (the total
energy of 1022 keV is divided by photons in a stochastic manner).
In the substance, however, the positron bound in o-Ps much
earlier is enough to annihilate with some "foreign"
electron from the environment, which has the opposite spin
orientation - again, two photons g with energies of 511 kV are formed.
The annihilation of a positron
with an electron produces 2 gamma photons in the vast majority of
cases, as mentioned above. Sometimes, however, there may arise more,
but with a very small probability (the probability that 2 + n
photons will be formed during e-e+
annihilation is proportional to a-n, where a
= 1/137 is the fine structure constant). If a positron interacts
with an electron bound in an atomic shell, the extinction of such
a pair may be accompanied by the emission of only a single
photon, and some of the energy and momentum may be transferred to
either the atomic nucleus or one of the other electrons; however,
the probability of this process is very small and does not apply
in practice.
The lifetime
of positrons in substances is in the order of hundreds
of picoseconds. However, the exact value depends on local
electron densities and configurations, which is used in the
spectroscopic method PLS (Positron Lifetime
Spectroscopy ....). Material tested locally irradiated b+- g emitter (usually 22Na),
the lifetime of positrons is determined by measuring the delayed
coincidence between the detection of photon radiation g of irradiating radionuclides (from 22Na, it is g
1274 keV) and the detection of the annihilation photons g 511 keV.
In terrestrial nature,
therefore, positrons do not normally occur permanently, they
occur only for a short time during certain interactions of
elementary particles and then (for about 10-10 -10-7 s) again annihilate with electrons. The most common
process in which positrons are formed is b+-radioactivity caused by the conversion
of the proton p+ in the nucleus into neutrons no, positron e+ and neutrino: p+ ® no + e+ + ne
(§1.2, part "Radioactivity b+"). Positrons are also
relatively common products in the interaction of particles at
high energies (will be shown several times
below) and in the decay of muons and pions (see below "Muons m and tauons t"); thus they occur in secondary
cosmic rays (see the passage "Cosmic rays"
in §1.6). Positrons can also be formed
with the aid of gamma radiation: if the higher energy gamma rays
than 1022 keV, one way of its interaction with matter is the
formation of an electron-positron pairs (§1.6, section "Interaction of gamma rays and X" passage "Formation of electron-
positron pairs").
For completeness, we will mention one
"exotic", not yet realized in practice, method of
positron formation :
Breit-Wheeler process of e+ e- pairs production
According to quantum electrodynamics the
electron-positron pair could theoretically be formed even when two
photons collide g1 + g2 ® e+ + e- ; it is
an inverse process to the above annihilation of a
positron with an electron: e+ + e- ® 2g (G.Breit and
J.A.Wheeler designed it in 1934). However,
this two-photon process has a very low probability (slight
effective cross-section), which would require extremely intense
collimated beams of gamma photons with an energy higher than
511keV; upon detection, the desired effect would be covered many
times by much stronger secondary radiation - so far it has not
been possible... Another possibility of photoproduction
could be the so-called multiphoton Breit-Wheeler process
(...), in which high-energy photons, when passing through a very
strong electromagnetic field, could decay into electron-positron
pairs. Here is a possibility of realization in the near future
using high-power laser systems ...
History: In 1932, the positron
first observed C.D.Anderson in cosmic rays detected by a Wilson
nebula camera placed in a magnetic field, where a trace of
particles with the same ionization properties as an electron
appeared, but with in the opposite direction of rotation in a
magnetic field, ie a "positive" electron.
 Protons and neutrons
Protons and neutrons 
Protons and neutrons, collectively called nucleons,
are the building blocks of atomic nuclei. These are heavy
particles from the group of baryons, they show a
strong interaction which ranks them among the hadrons
- they are composed of 3 quarks. They are of natural
origin - they originated in the "fiery furnace" of the
Big Bang at the beginning of the so-called hadron era,
in the first millionth of a second of the universe's existence.
In addition, they arise in a number of processes and interactions
of other elementary particles; during radioactive transformations
of b- , + there are mutual transformations of neutrons and
protons (§1.2, passage "Mechanism of decay b. Weak interactions.").
Protons, as nuclei of hydrogen,
were discovered in the study of electric discharges in gases at
about the same time as electrons (late 19th century). Neutrons
were discovered only in 1932 by J.Chadwick during the bombardment
of beryllium nuclei with alpha particles (§1.1 "Atoms and
atomic nuclei", part "Construction of the atomic nucleus").
 Proton p +
Proton p +
carries a positive elementary electric charge of the same
absolute magnitude e as the electron, its rest mass is mp = 1.6726.10-27 kg = 1836.151 me = 938.256 MeV/c2. The magnetic moment
of a proton is e.h/4p mp
- the so-called nuclear magneton, which is 1836 times
smaller than Bohr's magneton (simply put,
we can imagine that at the same spin and charge, a heavy proton
"rotates more slowly" than a light electron). A proton is a stable particle
(omitting here some speculation about the possible decay of a
proton *). The number of protons in the nucleus (proton number Z)
also determines the number of electrons and their energy levels
in the shell - and therefore the "size" of the atom and
its chemical properties when combined with other atoms. The
proton itself forms the core of the simplest element - hydrogen 1H1. Free protons are encountered in ionized hydrogen
plasma and in nuclear reactions in which accelerated protons
enter or are their products. Protons are the most common
particles that are accelerated in accelerators for the purposes
of nuclear physics (see the chapter "Charged
particle accelerators" below). The number of protons in the atomic nucleus indicates
the proton (atomic) number Z , which also determines the
number of electrons in the atomic shell and thus the chemical
properties of the atom - the position of the element in
Mendeleev's periodic table.
*) Instability of proton ?
The so-called grandunification theories admit the instability
of a proton,
which should decay into muons or positrons and into one neutral
or two charged pions [p+ ® (m+ or e+) + (po or p+ + p-)]
with a lifetime of the order of tp » 1030 -1033 years. This decay would be
caused by the conversion of a quark to a lepton via the X boson,
and due to the enormous mass of the X boson, its probability is
extremely small. Experiments so far give estimates of tp > 1030 years. These
attempts to observe proton decay are made deep underground (due
to cosmic ray shielding), where large water tanks are located,
equipped with many photomultipliers that could detect faint
flashes caused by the passage of fast particles formed as proton
decay products. The most perfect device of this kind is the Superkamioka-NDE
in Japan, which did not detect any proton decay, but was very
successful in the detection and spectrometry of neutrinos (see
the "Neutrinos" passage in
§1.2 "Radioactivity").
Note: Another
hypothetical and very curious mechanism could be the decay of a
proton through a virtual black hole (§4.8
"Astrophysical significance of black holes" in a monograph "Gravity, black holes and
spacetime physics"). Black mini-holes emitting by
quantum Hawking mechanism the particles that are generally
different from those that the black hole swallowed, violates the
law of conservation of baryon number (§4.7 "Quantum
radiation and the thermodynamics of black holes" in the same book). Therefore, if two quarks in a
proton fall into a virtual black mikro-hole, it is possible to
back emission of e.g. antiquark and leptons, thereby proton
converted into muon or electron and pion.
 Neutron n 0
Neutron n 0
is electrically neutral and its rest mass mn = 1.6748 .10-27 kg = 1838.65 me = 939.55 MeV/c2 is slightly higher than the proton. In stable atomic
nuclei, neutrons are stable, the free neutron (in vacuum) decays
with a half-life of about 13 minutes by b--radioactivity of no ® p+ + e- + n'e into proton, electron
and antineutrino. The difference in mass between a neutron and a
proton is about 2.5 times the mass of an electron (this difference comes from the difference in mass of
the "u" and "d" quarks and the difference in
binding energy). However, the intermediate
W boson, which mediates quark conversion, is about 80 times more
massive than a proton or neutron, so there is a high potential
barrier. So, despite the small energy surplus, the neutron does
not immediately decay into a proton, but it takes 13 minutes on
average to tunneling through this barrier.
Free neutrons are not commonly encountered
in terrestrial nature, in the upper layers of the atmosphere a
smaller number of them are formed during interactions of cosmic
radiation (§1.6, section "Cosmic radiation"). However, they are common products of nuclear
reactions and are also willing to enter into nuclear
reactions (§1.3, passage "Reactions
induced by neutrons"). Intensive
sources of neutrons are nuclear reactors, whether
fission or so far experimental fusion thermonuclear (§1.3, part "Fission
of atomic nuclei" and "Fusion
of atomic nuclei"). As laboratory neutron source are constructed as small
specific accelerators of charged particles (mostly deuterons with
tritium target) called neutron generators (see below "accelerators of charged
particles," passage "neutron generators"), or radioisotope source consisting of a
mixture a -radionuclide with light element (such as a mixture of
americium and beryllium, the reaction a, n), or a heavy transuranic
radionuclide (most often californium 252), during the spontaneous
fission of which neutrons are released (§1.3,
"Transurans").
Origin of the masses
of protons and neutrons
Protons and neutrons are much heavier than the sum of the masses
of their quarks. E.g. the proton has a mass of 938MeV, while the
mass of the "u" quark is 2MeV and the "d"
quark is 5MeV. Therefore, most of the mass of a proton comes from
the kinetic energy of the internal motion of its
quark components. This is explained on the basis of quantum
uncertainty relations, according to which the product of
uncertainty in the position and momentum of a particle is greater
than the Planck constant. Quarks are enclosed in a proton or
neutron ("imprisoned") in a spatial area with a
diameter of aprox. 10-13 cm; this forced very small uncertainty in position
quantum, implies considerable momentum and thus the kinetic
energy of each of the quarks, at least about 200MeV. The kinetic
energy balance of such three intensely oscillating quarks is
approximately equivalent to the mass of the proton.
If all quarks had the same mass, one would
expect the proton to be slightly more massive than the neutron,
because the electric charge of the proton (which the neutron does
not have) contributes to its internal energy. However, the
difference in the mass of the "u" and "d"
quarks (which is explained in unitary field
and particle theories by interaction with the Higgs field - see
below) causes the neutron (u, u, d) to be
somewhat "heavier" than the proton (u, d, d). This
difference in mass causes the instability of the free neutron,
its b--decay into
proton, electron and neutrino by weak interaction.
Antiparticles to protons and
neutrons
Antiproton p' - differs from a proton only in its negative charge and
the opposite direction of the magnetic moment, in a vacuum it is
also a stable particle. The antineutron n' 0 is a neutral particle like a neutron, from which it
differs only in the opposite orientation of the magnetic moment,
its half-life in vacuum is the same as that of a neutron, it
decays according to the scheme n'o ® p'- + e+ + ne to an antiproton, positron and neutrino.
Antiprotons and antineutrons are not
commonly found in terrestrial nature, they are formed by the
interaction of high-energy particles and then disappear by
interactions with nucleons. Due to the law of conservation of the
baryon number, antinucleons can only be produced in pairs
together with nucleons. The most common way of producing
antiprotons p' is in reactions p + p ® 2p + p + p' , resp. p + n ® 2p + n + p' ,
while the threshold kinetic energy of the firing proton (in the
laboratory target system) is about 5.6 GeV, resp. 3.6GeV;
however, if this interaction occurs during nuclear bombardment,
the threshold energy of antiproton production may be lower
(around 3GeV). Antineutrons are formed in similar reactions p + p
® 2p +
n + n' , resp. p + n ®p + 2n + n', furthemore in reactions antiprotons p' + p ® n + n' , p' + n ® n + n' + p-.
In antinucleon interactions, the most
important are the interactions (p', p) of antiprotons with
protons. At high energies, other heavy particles such as hyperons
can be formed here, which will be mentioned below. At low
energies of antiprotons or when they are stopped (see below),
leads to nucleon pairs annihilation with the
production of mesons, quantum gamma, or there is a reaction p' +
p ® n
+ n' occurs ("charge exchange"). The extinction of
pairs (p', p) is a strong interaction, in which mesons p *) are most often
formed (only in a small percentage of
mesons K); the smallest number of formed
mesons with respect to the law of conservation of momentum are 2
mesons p,
but most of them enter more, most often 5 mesons - a typical
interaction of this kind is: p' + p ® 2p+ + 2p- + po.
*) The formation of mesons p during the
annihilation of an antiproton with a proton is due to the quark
structure: antiquarks in the antiproton and quarks in
the proton combine into quark-antiquark pairs,
which are mesons.
When an antiproton enters a substance,
atoms are ionized by electromagnetic interaction, just like any
other charged particle, thereby the antiproton braking and
slowing down. During this deceleration may antiproton disappear
when interacting with the nucleus, but can be slow (or almost
stopped) so much, that it can be trapped by a proton (hydrogen
nucleus) - a new "exotic atom" is formed, called protonium,
consisting of a proton and antiproton orbiting a common center of
gravity. Similarly, it can be captured by another heavier nucleus
on some higher orbit (where eject the electron) and during its
orbit it then passes to lower orbits, which is accompanied by the
emission of either X-ray photons or Auger electrons. Finally, it
is absorbed by the nucleus and disappears by interaction with a
proton or neutron to produce pions.
Antimatter
Antiproton around which revolves positron constitute atom of
"antihydrogen", which has similar
properties as normal hydrogen. Antiprotons and antineutrons can
form "anti-atomic nuclei" around which positrons can
orbit in exactly the same configurations as the respective
ordinary atoms - they are "antiatoms",
that would have exactly the same chemical and spectroscopic
properties like our atoms, within the "anti-world"
- they would form antimatter - (discussed above, the passage "Antiparticles, antimatter, antisworlds").
History:
The antiproton was discovered in 1955 at an accelerator in
Berkeley while bombarding a copper target with protons
accelerated to 6.2 GeV. In 1956, an antineutron was discovered on
the same accelerator: a beryllium target was bombarded with
protons with the same energy and the resulting antiprotons were
led to a system of scintillators and a Cherenkov detector
connected in anticoincidence, where antineutrons were formed by
the reaction of p'+ p ® n + n' with hydrogen nuclei produced antineutrons, which
when interacting with nucleons in the Cherenkov detector were
registered as intense flashes.
 Neutrinos and antineutrinos
Neutrinos and antineutrinos
 (for more details, see the link "Neutrinos
- "ghosts" among
particles")
(for more details, see the link "Neutrinos
- "ghosts" among
particles")
These are ubiquitous but almost elusive particles. Neutrinos n and antineutrinos n' are the lightest
and weakest interacting of all known types of elementary
particles - they belong to the leptons. They are fermions with
spin number 1/2, they do not carry an electric charge, they do
not show a strong interaction, but only a weak
interaction (and a universal
gravitational interaction, which we are not interested in here
from the point of view of elementary particle physics, can have
certain Cosmological consequences). We recognize three types of
neutrinos: electron neutrino ne , muon nm and tauon nt neutrinos, which, however, can spontaneously transform
each other during the so-called neutrino oscillation.
Neutrino as such is a mixing of the proper states of electron,
muon and tauon neutrino and therefore there is a periodic
transformation of one neutrino to another.
Electron neutrinos are typically formed
during the mutual transformations of neutrons and protons by b-,+
-decay: no ® p+ + e- + n'e , p+ ® no
+ e+ + ne , muon and tauon
neutrinos then during the decay of muons and tauons: m- ® e- + n'e+
nm , t- ® nt + e- + n'e , t- ® nt + m- + n'e , ......
In addition, neutrinos arise in a number of interactions of
elementary particles in which weak interactions take place. Large
amounts of neutrinos are formed during thermonuclear reactions
inside the Sun and stars, from where, thanks to their very weak
interaction, they easily penetrate outside and are radiated into
the surrounding space. A extremely strong "flash" of
neutrino radiation occurs during a supernova explosion - see §4.2 "The Final Phases of Stellar
Evolution. The Gravitational Collapse" of the book "Gravity, Black Holes and the
Physics of Spacetime". There is also a huge amount of
so-called relict neutrinos in the universe, originating
from the lepton era of the universe just after the Big Bang.
Neutrinos, along with photons, are among the most
abundant particles in universe. Properties of neutrinos,
their origin, detection methods and possibly the cosmological
significance of neutrinos are described in more detail in §1.2
"Radioactivity", part "Neutrinos
- "ghosts" between
particles".
Neutrinos were introduced as
hypothetical particles by W.Pauli in 1930 in the study of the
energy balance of b- decay (see §1.2, part "Radioactivity
beta", Fig.1.2.3), their name and
specification of properties come from E.Fermi. Neutrino was
experimentally demonstrated only in 1956 by experiments outlined
in the mentioned reference "Neutrinos...".
 Muons m and tauons t
Muons m and tauons t 
 Muons m -
and m +
Muons m -
and m +
(they are antiparticles each other), also referred to as
"heavy electrons", are medium-heavy particles with mass
mm = 206 m e, carry a negative or positive electric charge of the
same size as the elementary electron charge; there are no neutral
muons without electric charge. Muons are unstable
particles that decay with a half-life of » 2.10-6 s. to an electron ,
resp. positron, and two neutrinos: m- ® e- + n'e + nm , m+ ® e+ + ne + n'm . This decay has the character of a weak interaction and
is similar to the radioactive decay of beta; also the energy
spectrum of electrons or positrons here is continuous, the
maximum energy is »53 MeV.
Muons occur in terrestrial
nature in secondary cosmic rays (see the passage "Cosmic rays" in §1.6). They are formed
in the upper layers of the atmosphere (above 10 km) during the
collisions of protons and other particles of primary cosmic
radiation with protons and neutrons in nitrogen and oxygen nuclei
in the atmosphere. In these primary collisions, p-mezons are formed
first, which decay into muons during about 2.510-8 s, which move with a
kinetic energy of about 4 MeV at a relativistic speed. Due to its
lifetime of »2.10-6 seconds, according to classical mechanics, the muon
would fly only about 500 meters and then disintegrate - so
virtually no muons should hit the Earth's surface. However, due
to the relativistic dilation of time , the muon
"lives longer" from the point of view of the observer
on Earth and has enough time to hit the Earth's surface. This
experimental fact that the muon flies a path 20 times longer than
would correspond to its lifetime in classical mechanics, is
convincing evidence of the effect of slowing the flow of
time according to a special theory of relativity.
The most common way of forming muons is during decay p -mesons: p- ® m- + n'm , p+ ® m+ + nm (see
the following passage "Mesons p and
K"). The interactions of
muons with nucleons proceed according to the scheme: m- + p ® n + nm , m+ + n ® p + nm , .....
If a negative muon m- enters into matter, it can (after its slowing down by
ionization) be captured by the Coulomb field of the nucleus and
form a peculiar bound system similar to an atom - the so-called muon
atom or mesoatom. A positive m+ mion passing through the medium can in turn capture the
electron and form an unstable bound system of the m+ mion and the orbiting electron e-, called the mionium;
it is a system analogous to positronium and has a
structure similar to a hydrogen atom.
The muon m was discovered in 1936 by
C.D.Anderson and S.H.Neddermeyer while studying cosmic rays in
the Wilson nebula chamber (similar to a positron).
 Tauons t-
and t+
Tauons t-
and t+
(they are antiparticles each other), also referred to as
"superheavy electrons", are very heavy particles with
mass mt » 3484 me » 1177 MeV/c2, carrying a negative or positive electric charge of the
same magnitude as the elementary charge of an electron. Tauons
are highly unstable particles that decay to an
electron or muon and two neutrinos with a half-life of »3.10-13 s: t- ® e- + n'e + nt , t- ® m- + n'm + nm .
However, due to their high rest mass, tauons are able to decay
even into hadrons, especially pions p-, p+, po and tauon neutrinos, eg. t- ® p- + nt , t- ® p- + po + nt , t- ® p- + p+ + p- +nt ,
etc.
Tauon t was discovered in
1974-77 by a team led by M.Perl during experiments with
high-energy collisions of positrons and electrons in the beams of
the accelerator at Stanford. During the collisions of electrons
with positrons, t+ and t- pairs were formed, which flew only a short distance
(about 1 mm) and then decayed into electrons, muons and
neutrinos. The formation of tauons was proved on the basis of the
detection of charged particles, analysis of their energies and
angular distribution (by the methodology mentioned above "Analysis of the dynamics of particle interactions").
 Mesons p and K
Mesons p and K 
 p -mesons
(also called pions)
p -mesons
(also called pions)
are the most common type of new secondary particles, formed by
particle interactions at high energies exceeding about 300MeV; at
even higher energies (above »1 GeV) K-mesons and hyperons are also formed.
The mesons p and K have the following
common properties: they are medium-heavy particles with spin 0
(thus belonging to the bosons), show strong interactions (they
are hadrons) and are very unstable. According to
the standard model of particles, they consist of a bound quark
and an antiquark.
Charged mesons p -
and p +, which are antiparticles to each other, carry a
negative or positive elementary charge of the same size as an
electron, have a rest mass »
2.4898.10-25 g »273 me » 140 MeV/c2 and with a half-life » 2.55.10-8 s disintegrate (by
weak interaction) to muons and neutrinos: p- ® m- + n'm , p+ ® m+ + nm (muons
then decompose further into electrons and neutrinos). During this decay, kinetic energy is released (mp -mm).c2 » 34 MeV, of which the muon m carries out a smaller part
of about 4.2 MeV and the rest of the kinetic energy of less than
30 MeV is obtained by the muon neutrino nm .
In addition to
particle interactions in accelerators, pions are formed for a
brief moment in the upper atmosphere during the interactions of
high-energy protons from primary cosmic radiation with nucleons
in the nuclei of nitrogen, oxygen and carbon; they immediately
decay into muons (see the "Cosmic Radiation" passage in §1.6).
The neutral meson p o
has a rest mass of »264 me » 135 MeV/c2 and with a very short
half-life »0.9.10-16 s decays (by electromagnetic interaction) into two
quantum gamma: po ® g + g.
Note
: In terms of
internal structure, mesons are a bound quark-antiquark
system. However, this system is unstable and its
disintegration can be simply understood as a process of "annihilation"
of a quark-antiquark pair; either by a weak interaction via the
intermediate boson W± , or electromagnetically directly on the quantum g (cf. the
corresponding Feynman diagram in Fig.1.5.1). It is a bit
analogous to the positronium mentioned above, which is
also an unstable bound state of a particle-antiparticle pair (e- - e+), which
annihilate to quantum g .
p- mesons
have played a varied and interesting role in the history
of nuclear physics. For a long time (40s-70s), they were
considered to be exchangeable particles,
mediating strong short-range nuclear interactions of protons and
neutrons in the nuclei of atoms (comes from H.Yukawa). The fact
that pions are often formed during high-energy collisions of
protons and neutrons also seemed to indicate this. Idea p -mezons
as carriers of strong interactions, however, did not work
in the end. It turned out that the essence of a strong
interaction lies deeper - it lies in the internal quark structure
of protons and neutrons. During the interactions of protons and
neutrons, pions are formed not as exchangeable
particles, but because p -mesons are lighter and simpler particles also composed
of quarks (and their antiparticles), just like nucleons.
Nevertheless, p- mesons are the most important of all
unstable "exotic" particles; they may have perhaps a practical
use, see eg §3.6, section "Hadron
radiotherapy".
 K mesons ,
K mesons ,
also called kaons, are more than 3 times heavier
than p- mesons.
Charged mesons K +
and K -
, which are mutually antiparticles, carry a positive or negative
electric charge of the same size as an electron, have a rest mass
» 966.6
me » 494 MeV/c2 and with a half-life » 1.24.10-8 s decay into p -mesons, muons and
neutrinos: K+®p++po, K+®m++n, K+®p++p++p-, K+®p++po+po, K+®po+m++n, K+®po+e++n; by analogy (associated) also K-.
The neutral meson K 0 has a mass of » 974.2 me » 498 MeV/c2 and decays very
rapidly into p -mesons and also into muons, electrons and neutrinos by
two types of decays :
two- particle decays : Ko ®
p+ + p- , Ko ® po + po, -
(half-time » 0.9.10-10 s) ;
three-particle decays: Ko®
po+po+po, Ko® p++p-+po, Ko® p+,-+m-,++n, Ko® p-,++e+,-+n, - (half-time » 5.7.10-8 s).
The fact that the
meson Ko decays with two different half-lives and different
processes, can be explained by the assumption that the meson Ko is a
quantum "mixture" of two neutral particles Ko L
("Long") and Ko S
("Short"), which have different
lifetimes and different decay patterns. These facts are
interpreted as the observed meson Ko being internally
a "mixture" or superposition of Ko and its
antiparticle K'o. Between these two states, the neutral kaon
spontaneously "oscillates".
Interactions of mesons p and
K
Mesons p- and p+ interact with nucleons at low energies mainly by
reactions: p- + p ® n + g , p+ + n ® p + g , at high energies pions there is also a combined
production of kaons, hyperons and antihyperons, eg p- + p ® K+ + K- + n , p- + p ® L + Ko, etc. -
for further reactions, see the section on hyperons below.
When interacting with the substance, p- mesons may be (after appropriate braking by ionization
energy losses) captured in orbit around the
nucleus (similar to electrons in an atom), so for a very short
time a mesoatom is formed with a pion p-, which is then absorbed by the nucleus and there it
combines with a proton (p- + p ® n + g).
Formation of mesons p and
K
p -mesons
are formed mainly as new secondary particles
during interactions of protons with nucleons, if the kinetic
energy in the laboratory (target) system is higher than 2.mp.c2 » 300 MeV. There can be several reactions of this type :
p+p ® p+n+p+, p+p ® p+p+po, p+n ® n+n+p+, p+n ® p+p+p-,
p+n ® p+n+po, n+n ® n+p+p-, n+n ® n+n+po , ....,
while these reactions can take place both on free nucleons and on
nucleons bound in the nucleus. Pions can also be produced by
photonuclear reactions of hard gamma radiation: g + p ® n + p+ , g + p ®p + po, whose
gamma radiation threshold energy is about mp.c2 » 140 MeV.
Mesons K are formed by the so-called associated
production in pairs either together or in pairs with
hyperons, either by mutual interactions of nucleons or p- mesons with
nucleons. Examples of such interactions are: p + p ® L + K+ + p , p- + p ® K+ + K- + n , p- + p ® L + Ko, etc.;
other combinations with hyperons are given in the following
section.
The strangeness of particles
These K-mesons, as well as the hyperons
mentioned below, have some special - "strange"
- properties that we do not encounter in other particles. These
are asymmetries in the production and decay of
these particles. These particles are formed in high-energy hadron
collisions with a high probability - pair production by strong
interaction. However, their decay is usually relatively
slower (on the order of 10-10 s) through weak interaction. To explain this
situation, a new quantity or (additive) quantum number called strangeness
S was introduced (for ordinary particles is S = 0,
strange particles have S = ±1, ± 2, hyperon W even S = -3), which is preserved in strong interactions,
but not in weak interactions. This explains that with strong
interactions of ordinary particles, strange particles are formed
in pairs, the sum of the strangeness of which is zero, but by a
weak interaction, the strange particles can decay into particles
without strangeness.
To explain the new quark model of hadrons,
a new quark "s"
(strange) has been introduced, which carries strangeness; quark s
has strangeness S = -1, antiquark s' has S = 1, other
quarks S = 0. The presence of the quark "s" in a
two-quark combination is characteristic of strange mesons
K, if "s" occurs in a three-quark combination,
there are hyperons - Fig.1.5.3.
 Hyperons
Hyperons 
The heaviest particles known to date (except
tauons), resulting from high-energy
particle interactions, are hyperons. All
hyperons are fermions, mostly with spin 1/2,
except W- which has spin
3/2. Furthermore, all hyperons are hadrons
showing a strong interaction and are highly unstable
particles with a very short lifetime. We know 7 types of hyperons
(+ their antiparticles), which we briefly list here :
Hyperon L
o is
electrically uncharged, has a mass of »2183 me » 1116 MeV/c2, lifetime » 2.5.10-5 s. and disintegrates
according to the schemes: L
® p + p- (66%), L ® n + po (34%).
Hyperon S + with a positive elementary charge has a mass of »2327 me » 1189 MeV and with half » 0.8.10-10 s. decays per
nucleon and pions: S+ ® p + p0 , S+ ® n + p+.
Hyperon S - with negative elementary charge has weight »2340 me » 1197 MeV and with half-life » 1.65.10-10 s. decays into
neutron and pion: S- ® n + p-.
Hyperon S 0 without electric charge has a mass of »2332 me » 1193 MeV and with a very short half-life close to 10-20 s it decays into a
hyperon lambda and a photon gamma: So ® L + g.
Hyperon X - with negative charge, weighs »2585 me » 1321 MeV and
with half-life » 1.7.10-10 s decays into hyperon lambda and pion: X- ® L + p-.
Hyperon X 0 - uncharged has weighs »2566 me » 1315 MeV and
half » 3.10-10 s decaying into
lambda hyperon and pion: X0 ® L + p0.
Hyperon W - with negative charge has a weight of »3405 me » 1675 MeV/c2 and with a half - life » 1.5.10-10 s decays into
hyperons and mesons: W- ® Xo, - + p-, o , W- ® L + K- .
Note: In a very small
percentage of cases, other possibilities of hyperon decay were
observed, eg L® p + e- + n , S+ ® p + g , Xo ® p + p-, and many others.
Hypernuclei
Hyperons show strong
interactions, so they can enter the nucleus and be bound there by
nuclear forces - a so-called hypernucleus or hyperfragment
is created. In a typical hypernucleus, one of the neutrons is
replaced by the hyperon Lo; such
hypernuclei then represents NAL. E.g. in nuclear emulsions irradiated with mesons K- from
the accelerator, hypernuclei 9BeL were observed. Hypernuclei are unstable
formations that decay in two ways: by meson
decay or by nucleon decay. In the meson method,
the hyperon L inside the nucleus decays according to the scheme L® p + p- , or L® n + po, so for
example the hypernucleus 9BeL decays into the meson p-, the proton p+ and the nucleus 8Be4 (which in this case then decays into two
alpha-particles 4He2). During nucleon decay, L + p ® p + n, or L + n ® n + n reactions
occur, so that, for example, the mentioned 9BeL hypernucleus would decay in the following way: 9BeL ® 4He + 3He + n.
Antihyperons
Similar to nucleons, there are antinucleons, so for each of these
hyperons there is a corresponding antihyperons
(all these hyperons are separate, they are not antiparticles, as
is the case with mesons p- and p+ or m- and m+). According to the principle of charge symmetry,
antihyperons have the same mass, spin and lifetime as hyperons,
but the opposite signs of el. charge, baryon number and magnetic
moment. The decay patterns of antihyperons are also
charge-associated with the decay patterns of hyperons, as well as
the reactions of particles in which antihyperons are formed are
analogous to hyperons (there is often "associated"
production of hyperons and antihyperons or mesons - see below).
It should be borne in mind that antihyperons to charged hyperons
have opposite signs of el. charges, eg antihyperon S'- has a
positive unit charge, so we could more accurately label it as ( S'-)+.
Hyperons formed by the interaction of
protons, antiprotons, p and K mesons with nucleons at high energies (> » 5 GeV), wherein the strong interactions of the type
(nucleon-nucleon) or (p + nucleon) two particles from the group of mesons and
hyperons (meson + meson, hyperon + meson, hyperon +antihyperon)
are formed simultaneously - there is a combined
or associated production of hyperons,
antihyperons and mesons, eg.:
p + p ®
2p + L
+ L' ,
p + p ®
p + L +
K+ ,
. ...........
.............
.............
K- + p ® W- + K-+ Ko .
Hyperon paths, resp.
of their decay products are observed in Wilson nebulae chamber,
nuclear photoemulsions and bubble chambers. Already in 1947
C.C.Butler and G.D.Rochester observed in the study of cosmic rays
in a cloud chamber tracks of two particles rising from one point
- further research showed that it was a Ko meson decaying into mesons p- and p+ and the
hyperon L crumbling on proton p+ and meson p-. When
accelerators with sufficiently high energy made it possible to
form beams of protons and mesons p, all other hyperons and
regularities of their associated production with mesons K
were discovered during the study of their interaction in bubble
chambers and photoemulsions.
 Resonances
Resonances
Form during some interactions of high-energy particles (such as p+, - + p+ ® p+, - + p+, or interactions of a
proton with an antiproton to form several p- mesons) and immediately
decay, their lifetime is about 10-23 to 10-20 seconds. They are manifested only by a significant resonant
maximum in the energy dependence of the effective cross
section of the given interaction, or by densities and peaks on
the Dalitz diagram of energies of secondary particles,
which indicate the formation of some temporarily bound state. We
recognize baryon resonances and meson resonances
(such as meson r or some types of mesons *K). Resonances are often not
even considered special particles, they are called quasiparticles.
Rather, they are only temporarily excited states created by the
interaction of two or more baryons or mesons, which decay as soon
as they fly beyond the region of the strong nuclear interaction
in which they originated. Due to the extremely short lifespan,
they probably have no significance for the structure and
properties of matter. However, their study is important for
better penetration into the subnuclear structure of hadrons,
their quark structure and understanding the properties of strong
interactions within quantum chromodynamics (QCD). Some meson and
baryon resonances are marked below on the quark diagram in
Fig.1.5.3.
 Bosons W - , W +, Z 0
Bosons W - , W +, Z 0 
These bosons are intermediate particles mediating weak
interaction (Weak int.) within the Weinberg-Salam model of
unification of electromagnetic and weak interaction.
W-
and W+ carry a negative and a positive elementary charge of
the same size as an electron, they have a mass of »82 GeV/c2, they are their
antiparticles to each other. W-bosons mediate mutual b -conversion of
neutrons and protons (according to the
scheme in Fig.1.2.5 in
§1.2 "Radioactivity", passage "Mechanism
of decay b. Weak interaction."). In this radioactivity b the W-bosons causes
conversion of "u" and "d" quark inside
nucleons, which themselves W remain virtual - it
immediately decays into the resulting quark, electron or positron
and neutrino.
The neutral Z0
boson has a mass of »
93 GeV and is its own antiparticle. Z0 is less important
than W, it does not show much in Earth nature or in the
present universe. However, it was apparently more significantly
used in high-energy processes in the extreme conditions of the
very early universe (possibly also during a
supernova explosion..?...) - it can mediate
mutual interactions between neutrinos (§1.2,
passage "Interaction of neutrinos with particles and matter").
When W or Z is formed by the
high-energy interaction of particles, they are highly unstable
(with a lifetime of approx. 3x10-25 sec.*) and then
break down into leptons and neutrinos; typically: W-® e- + n', W+® e+ + n, Zo® m+ + m- (or e+ + e-). Or
for quarks and antiquarks. At very high
energies, there are many other possibilities for their
interactions, including the production of heavy particles such as
Higgs bosons. Feynman diagrams of some important interactions
bosons W±, Z0 are illustrated in Figures 1.5.1.D, F, G, H, I . Particle interactions caused by the exchange of
charged intermediate bosons W± are sometimes referred to as "weak charged
currents", reactions caused by an uncharged Z0 boson as "weak
neutral currents".
*) Particles with such a short
lifetime cannot be directly detected
experimentally (they disintegrate before they have time to fly
out of the place of interaction, they will not reach any
detector...). Only their decay products can be
detected. Our detectors at accelerators are unable to detect
neutrinos at all (they have no electric
charge and hardly interact with anything),
they can only be proven indirectly by measuring a certain value
of the missing energy or momentum in the overall balance
of energy and momentum.
Intermediate bosons W-, W+, Z0 were indirectly
experimentally demonstrated in 1983 in interactions in opposite
proton-antiproton beams of the 270GeV « 270GeV Super Proton
Synchrotron at CERN.
 Hypothetical
and model particles
Hypothetical
and model particles 
For the sake of completeness, we will briefly mention some
"exotic" particles, which should exist according to
certain more or less verified theories and models,
but most have not yet been directly experimentally proven - they
remain hypothetical or model particles.
 Quarks
Quarks
are model "building" particles of hadrons (as outlined below - "Quark structure of hadrons"). Quarks are fermions with
spin 1/2 and carry a one-third electric charge -(1/3) e, +(2/3)
e. A total of 6 types of quarks have been introduced, each with
its own antiparticle - an antiquark. The individual
quarks and quark model of hadrons are briefly described below.
Quarks are the primary carriers of strong interaction,
mediated by gluons. At the same time,
however, they may be subject to mutual internal transmutations
under the influence of a weak interaction mediated by
intermediate bosons W-, W+, Z0 (the main
manifestation of this quark transmutation is radioactivity b , see Fig.1.2.5). Free quarks have never been
observed - see the following section "Gluons"
and below the section "Quark-gluon plasma".
 Gluons (glue - holding quarks "glued
together" in hadrons)
Gluons (glue - holding quarks "glued
together" in hadrons)
are particles that mediate strong
interactions between quarks (and with their
"residual manifestations" also nuclear interactions
between nucleons). They are bosons with spin 1, have zero rest
mass, have no electric charge, but carry the so-called
"color charge" *), which characterizes different types
of quarks. Like a photon, a gluon does not have an antiparticle
(it is its own antiparticle). The gluon interaction of quarks has
special properties. If the quarks have high energy and are close
to each other, the gluon interaction is negligible and the quarks
behave as free particles - so-called asymptotic freedom.
However, when the quarks move away from each other by about 10-13 cm, the gluon
interactions begin to act intensively and strongly bind the
quarks to each other - the quarks are "trapped" in
hadrons. Further discussion is below in the section "Quark-gluon plasma".
*) A photon that mediates an
electromagnetic interaction does not itself carry the charge of
that interaction (electric charge); photons do not interact with
each other. However, gluons carry a "color" - the
charge of a strong interaction, so they can interact with each
other. They could theoretically create bound systems - so-called gluonium.
Preons
- are hypothetical sub-quark particles that
could make up quarks (see the "Preon Hypothesis"
passage below).
 Gravitons
Gravitons
are the quantum of gravitational waves. Gravitational waves are
predicted by the general theory of relativity as a physics of
gravity and spacetime; they are solutions of Einstein's equations
of the gravitational field, similarly to Maxwell's equations of
electrodynamics implies the existence of electromagnetic waves.
Gravitational waves differ from electromagnetic waves in their
very slight effect on matter, and in their so-called quadrupole
character. The hypothetical graviton has zero rest mass,
moves at the speed of light, its spin number is 2.
Gravitational waves have alredy
been directly detected, although this is at the limits of current
experimental techniques. However there is no hope for
experimental demonstration of gravitons in the foreseeable
future. Gravitational waves are discussed in detail in §2.7 "Gravitational waves" in the book "Gravity,
black holes and space-time physics".
A skeptical note on the reality of the existence of gravitons is
there in the passage "Gravitons - a quantum of
gravitational waves? ".
 Higgs bosons
Higgs bosons
- they are quantum of the so-called Higgs-Kible *)
scalar field, that in the unitary calibration field theories is
introduced into the Lagrangian for purpose of so-called
spontaneous disruption of symmetry of the electroweak interaction
(see, e.g. §B.6 "Unification
of fundamental interactions"
in the book "Gravity, Black Holes and the Physics of
Spacetime"). This field also leads to
some intermediate bosons gaining mass (rest
mass) and the corresponding interactions becoming short-range
forces - they are mainly W and Z
bosons of (electro)weak interactions. In this Higgs mechanism
the rest mass of the particles is created by interaction
with the ubiquitous Higgs field, which permeates the entire
universe; the stronger the interaction of a given particle with
this field, the greater its mass. Some quantum, such as photons,
do not affect this field and therefore have no rest mass, other
particles attract the Higgs field and add mass to them. This
could explain why some intermediate bosons are so heavy, while
other particles, such as electrons, are very light. Simply put,
the Higgs bosons should be part of an invisible quantum field
that fills a vacuum in space and causes material particles in the
universe to form material structures; without them, there would
be no world as we know it. If some basic building blocks did not
gain mass, the universe would look completely different: Particles without a rest mass
would fly freely through space at the speed of light and would
never form atoms, from which stars, planets and life would then
form ...
*) This hypothesis was first introduced in 1964 by the
authors P.Higgs, F.Englert and R.Brout, G.Guralnik, C.Hagen and
T.Kibble. The Higgs field in 1967 was used by S.Weiberg, A.Salam
and S.Glasshow to build the theory of electroweak interaction
with heavy intermediate bosons W±, Z°.
The Higgs boson H
itself has a high rest mass, in the order of hundreds of GeV *).
Higgs bosons could be formed by a strong interaction in
high-energy proton collisions by the exchange
interaction of energy quarks with gluons or W-bosons (so-called gluon fusion, Fig.1.5.1.I, W
or Z fusion, or associated production with W
or with t-t ' pair), or an electro-weak
interaction at electron collisions eg by
interactions e+ + e- ® Z* ® Z + H (H-emission), or again by
W or Z fusions - see Fig.1.5.1.D. Higgs bosons are
highly unstable particles with a lifetime of
only about 10-22 seconds. Therefore, they cannot be detected directly,
but only on the basis of the analysis of secondary particles
formed during their decay - their decay products.
If the Higgs boson is formed during a high-energy interaction of
particles, it is assumed that it will decay very quickly into
other energetic particles. The simplest decay H® g + g per two
gamma photons could occur even at lower masses around 100GeV. If
the Higgs boson has a mass greater than 160 GeV, it can decay
into two W-bosons: H ® W + W, which then decay into two leptons and two
neutrinos (as mentioned above in the
passage "Bosons W-,
W+, Zo"). At a mass H higher
than about 180 GeV, the decay can lead to two Z-bosons: H ® Z + Z, which
decay into 4 leptons - by pairs of muons m+ + m- or electrons e+ + e-. In
case the Higgs boson is heavier than about 500 GeV, other ways of
its decay may occur, eg H ® b + b', or H ® t+ + t-, others may or may not go through intermediate
Z-bosons; finally, they can result in the production of quarks,
whose hadronization would create sprays (jets) of
particles. Feynman diagrams of some possibilities of formation of
Higgs bosons and their decay are given above in the section
"Feynman diagrams" (in Figure
1.5.1.D, I).
*) Collision experiments (on Tevatron and
LEP accelerators - see "Large accelerators" below)
previously provided only the lower limit for the mass of the
Higgs boson about 170 GeV/c2. After all, according to supersymmetric models, there
could be several species of Higgs bosons: light
scalar ho
, heavy scalar Ho, positively and negatively charged
H±.
Discovery of the Higgs
boson
At the ICHEP2012 conference in Melbourne, Australia, on July 4,
2012, the discovery of a new boson whose properties are
consistent with the Higgs boson was announced, based on data from
ATLAS and CMS experiments at CERN. Careful analysis of about
60,000 cases of photon pair detection (derived from high-energy
proton collisions) found a small (but
significant, about 160 photon pairs) peak
on the photon number -to-energy curve, in the energy range around
126 GeV. This peak should probably come from the 2-photon
decay of the Higgs bosons. The level of reliability of
detecting a new particle by detecting its decay products is 5s. Further
experiments are needed to make sure it is a Higgs boson and not
another unknown particle. For this discovery, the Nobel Prize was
awarded to P.Higgs and F.Englert in 2013.
 Source:
CERN-LHC
Source:
CERN-LHC
Discovery of the Higgs boson at the LHC great accelerator by
detecting its decay products - here two opposite photons of gamma
specific energies on the ATLAS detection system.
Higgs boson - a "divine"
particle ?
In the popularization literature, it is often stated in
the journalistic bonmot that the Higgs boson is a kind of "divine
particle" that gives the universe mass. That's not
quite true. More than 99% of the ordinary ("radiation")
matter that makes up the universe, ordinary matter, and our
bodies is made up of protons and neutrons. These consists of
quarks whose mass, associated with the Higgs mechanism,
represents only about 5% of the mass of protons and neutrons.
With the Higgs field substantialy related only the mass of the W
and Z bosons and the mass of leptons, but these represent only a
small part of the mass of the Universe. The importance
of the Higgs boson lies in the fact, that it was the
last undiscovered particle of the standard model, the discovery
of which confirms the (otherwise undetectable) Higgs field,
without which the standard model could not explain experimentally
measured masses of leptons, quarks and intermediate bosons -
force carriers. Without the Higgs mechanism,
quarks would be massless and would not create protons and
neutrons, atomic matter would not exist...
 Supersymmetric particles
Supersymmetric particles 
In supersymmetric unitary theories of elementary
particles, each basic particle is assigned its so-called superpartner
- each boson has its fermion superpartner and fermion, on the
other hand, has its boson counterpart. These "partner"
particles have not yet been observed. This is explained by the
fact that boson-fermion supersymmetry is disturbed; this means
that the mass of the superpartners is not the same, but the
supersymmetric partners to the known particles have a much higher
mass, so we cannot observe them at the energies available to us.
The names of these particles are formed by the suffix "ino"
(for interaction bosons) or by the prefix "s-"
(for fermions) to the name of the starting particle. The most
frequently discussed supersymmetric particles are gravitins,
photins, or neutralins :
Gravitins
are quantum of the calibration field in supergravity unitary
field theory (graviton superpartner), they have a 3/2 or 5/2
spin.
Photins
are weakly interacting particles with spin 1/2, introduced as a
supersymmetric partner of photon.
s - particles
Supersymmetric particles to other fermions are sometimes
discussed: s-leptons as superpatters to leptons, eg s-electron,
s-muon, s-neutrino (also called neutralino - should have a high mass of tens or hundreds of GeV);
or to the quarks - s-quarks.
Higgsino - a supersymmetric
fermion to the Higgs boson.
 Other hypothetical particles:
Other hypothetical particles: 
 Axions
Axions
are very light (rest mass approx. 10-5 -1 eV/c2) hypothetical particles with spin 0, which should
interact with the surroundings by weak and gravitational
interaction. They are considered possible particle candidates
for dark matter in the universe.
Within quantum chromodynamics, disturbances
of the combination of charge symmetry and parity in quark theory
are introduced in solving the CP-problem. CP symmetry, which is
disturbed by weak interactions, should theoretically be disturbed
even by strong interaction. Since this is not observed
experimentally, additional symmetry has been introduced into
quantum chromodynamics (which is spontaneously disturbed), the
quantum of the respective field being a new type of particles
called axions (their
supersymmetric partners are called axina).
Relict axions could
perhaps have been created in the very early universe shortly
after the big bang, in the lepton era or even earlier. It is
assumed that they could also be created in a small percentage by
the scattering of photons by electrons, so their intense source
could also be the interior of the Sun. A large number of axions
should be created in a supernova explosion (along with
neutrinos).
If axions have a very low mass, they will
be stable, because there are no lighter particles into
which they could decay (high-mass axions
would not have persisted in the universe for a long time until
the present). The universe could thus be
filled with a large number of primordial axions (their very cold Bose-Einstein condensate). Axions are therefore considered possible particle candidates
for dark matter in the universe.
A 2-photon interaction in a
strong magnetic field (Primakoff effect) has been proposed for axions: 1. An
axion interacts with the electromagnetic field to produce
photons. 2. The inverse process, in which a
photon in the presence of a strong magnetic field is converted
into an axion by a virtual photon. Some of the high-energy
photons can be converted into axions when scattered of electric
charges.
The curious passage of
light through walls with the help of axions
?
The process of converting photons into axions and vice versa,
axions into photons, could perhaps work in the following
experiment: We send an intense beam of photons from a powerful
laser through a chamber with a strong magnetic field against an
opaque obstacle (wall, metal plate, etc.). On the other side of
the plate, we also place a chamber with a strong magnetic field
and a photon detector behind it. If a small part of the photons
is converted into axions when passing through the magnetic field,
these axions will easily pass through the obstacle, since they
interact only weakly. On the other side of the plate, we also
place a chamber with a strong magnetic field and a photon
detector behind it. In the magnetic field, some of the axions
that have passed through could then be converted back into
photons and the laser beam slightly restored. So it would seem
that some of the light could pass through the opaque plate..?..
Some possibilities are being discussed as
to how axions could be detected. The interaction of an axion with
electrons or with a very strong magnetic field could lead to the
production of a quantum of electromagnetic radiation - a
microwave photon, which could be detected. Photons of this origin
could be registered during the explosion of a nearby supernova.
Experiments are also being tried with laboratory production
of axions using the interactions of intense photon beams
from powerful lasers with electrons in a strong magnetic field,
with subsequent detection during the reverse conversion
of axions into photons, again in a strong magnetic field. All
without success so far...
 WIMPs
WIMPs
The above (so far hypothetical) particles - gravitin, photin,
axions - are sometimes collectively referred to as "weakly
interacting material particles" - the abbreviation WIMP
(Weak Interacting Massive
Particles). They interact weakly and
gravitationally with the environment. They are predicted by the
supersymmetric extension of the standard model. They could form
an essential component of the so-called dark matter
in space (see eg §5.6 "The future of the universe. Time
arrow. Hidden matter." in the book
"Gravity, black holes, and physics of space-time").
They haven't been detected yet...
 Magnetic monopoles
Magnetic monopoles
- a hypothetical particle dual respect to electrical charge. The
magnetic monopole arises when exchanging the electric and
magnetic quantities in Maxwell's equations and subsequent
application of quantum field theory.
Classical electromagnetic theory does
nor allow magnetic monopoles: one of Maxwell's equations
div B = 0 says that the magnetic field is
non-source with closed lines of force, ie magnetic monopoles do
not exist (see eg §1.5 "Electromagnetic field. Maxwell's
equations" in the book
"Gravity, black holes and the physics of space-time").
Magnetic monopoles were introduced as an attempt (at least
hypothetical) formal equalization, or establish symmetry, with
electricity and magnetism. They have never been detected, they do
not exist in our nature, their hypothetical presence
just after the big bang was nullified by the inflationary
expansion of the early universe (§5.5
"Microphysics and cosmology. The inflationary
universe.").
 Leptoquarks X , Y
Leptoquarks X , Y
- hypothetical vector bosons X and Y
(called leptoquarks, they cause transitions between
quarks and leptons) introducing in the so-called grandunification
GUT theories (already mentioned §B.6
"Unification of fundamental inetractions" in "Gravity, black holes and spacetime
physics"). They should have a very
high weight on the
order of mX ,Y ~ 1015
GeV/c2,
so far beyond the possibilities of experimental proof in large
accelerators...
 Superstrings
Superstrings
are hypothetical (model) one-dimensional elementary structures of
the order of 10-33 cm (Planck's length), whose variously excited
vibrational states and interconnections should be the basis of
all particles and fields according to the so-called superstring
theory - the basis of unitary field theory
unifying all 4 interactions in nature. The strings can be open or
closed. Depending on the way the strings vibrate, different
weights, charges, spins, etc. are created. Such strings could
then form the basic particles (fermions - quarks, electrons, ...
and bosons - photons, gluons, ...) of a standard model.
The generalizations of superstrings are
the so-called p-branes, which can have more (p) spatial dimensions and evolve
in multidimensional (mostly 11-dimensional) spacetime. The theory of superstrings is
briefly discussed in the final part of §B.6 "Unification of
Fundamental Infections" of the
book "Gravity, Black Holes and the Physics of Spacetime".
 Tachyons (Greek: tachyos = fast)
Tachyons (Greek: tachyos = fast)
are purely speculative particles that can move only at
superluminal speeds and have (in connection with the
known relationship of mass versus velocity m = mo/Ö(1-v2/c2) in a special theory relativity) imaginary mass.
The motivation for the introduction of tachyons is only
speculation about a kind of symmetry with respect to the speed of
light, there is no physical arguments for them; rather, they
would raise serious problems with the principle of causality.
From the point of view of the theory of relativity, tachyons are
briefly discussed in the passage "Tachyons" §1.6 "Four- dimensional
space-time and special theory of relativity" of the mentioned book "Gravity,
black holes and space-time physics".
 "Shadow"
or mirror matter - Catoptrons ?
"Shadow"
or mirror matter - Catoptrons ?
At the end of our brief overview of the "zoology" of
hypothetical particles, we mention a somewhat vague idea of the
so-called mirror matter, which could perhaps
hiden coexisting with "our ordinary" matter. The
hypothesis is based on experimentaly measured non-preservation
of parity in weak particle interactions (discussed below -
"CPT symmetry of interactions"). The idea arose that mirror symmetry could be
restored if for every "our" observed fundamental
particle there was a hidden, "shadow" partner
("twin") - a mirror particle whose
interaction involves the opposite violation of parity. Our common
particles are "counterclockwise", mirror particles are
"clockwise", overall parity symmetry is maintained.
Parity can then be spontaneously disrupted by the Higs
mechanism; in the case of undisturbed parity symmetry, the
masses of the particles and their mirror partners are the same;
in the case of parity disturbance, the masses of the mirror
partners are different. Miror particles are somentimes
collectivery refered to as catoprons (Greek katoptro = mirror ).
Mirror matter, if it exists, interacts
only very weakly with ordinary matter. This is
because the forces between the mirror particles are mediated by mirror
bosons, which are generally different from the
intermediate bosons of "our" matter. The mirror mass is
therefore practically unobservable *), at least
not by direct methods, optically. The exception is gravitation,
so mirror matter should have gravitational effects
- it could therefore be a candidate for the still mysterious dark
matter in the Universe (discussed in more detail in
§5.6 "The Future of the Universe. Arrow of Time.
Hidden Matter.)"
monograph "Gravity, black holes and space - time
physics").
*) In superstring theories, mirror particles
are sometimes even placed not in "our" 3- dimensional
space, but in three other "extradimensions".
Unitary
symmetries and multiplets of particles
The large number of elementary particles discovered in
high-energy interactions naturally led nuclear physicists to try
to systematize them and introduce unitarization
schemes - to create a kind of periodic table
of particles, analogous to Mendeleev's periodic
table of elements (§1.1, part "Bohr's model of the atom" and "Interaction of atoms", passage "Periodic chemical
properties of atoms").
In particular, each baryon and lepton is assigned a baryon
number B and a lepton number L
(particle +1, antiparticle -1), which are preserved in all
interactions. Significant similarities and symmetries
between some elementary particles, especially hadrons, were
found.
If we look away from the electric charge, protons and
neutrons, for example, can be considered as two states (doublets)
of one particle - a nucleon. Similarly, the pions p+, po, p- form a triplet of similar particles. When studying the
strong interactions themselves, which are charge-independent, we
can disregard the charge. To describe these similarities and
symmetries, a new quantity isotopic spin or isospin
T was introduced *). Nucleons have an isospin T = 1/2,
with the projection of the isospin T = +1/2 corresponding to a
proton and a T = -1/2 neutron. The pions were assigned isospin T
= 1, with projections -1, 0, +1 for p-, po, p+. In the system of interacting nucleons and pions, the
law of conservation of isospin applies.
*) It was based on a formal analogy with
ordinary spin, where a particle with spin 1/2 occurs in two
states with spin projection -1/2, +1/2 and a particle with spin 1
in three states with spin projections -1, 0 , +1. Isospin T
is a vector in the imaginary (auxiliary) "isotopic
space". In general, a particle with isospin T can
occur in (2.T + 1)
states with isospin projections on the reference axis: -T, (-T +
1), (-T + 2), ..., -1, 0, 1, ..., (T-2), (T-1), T.
Another important step was the discovery of some
"strange" (unexpected) properties of the interactions
of mesons K and hyperons in their combined pair
production, which led to the introduction of the concept of strangeness
described by the quantum number S ("Strange").
Later we were introduced general quantum number called hypercharge
Y = B + S, the sum of baryon number B and strangeness S.
It turned out that both isospin T and hypercharging Y
are preserved during strong interactions. This extended symmetry
led to the construction of a baryon-decuplet multiplet (3/2+), which, however,
lacked one place at the time; was thus the prediction of the
hyperon W, which was soon actually discovered.
The individual hadrons were drawn in special
diagrams, where the horizontal axis showed the projection of
isospin Tz , the
vertical axis the hypercharge Y and the oblique axis the
electric charge Q. The connectors of the thus marked
multiplets of particles formed regular geometric shapes -
triangles, hexagons and their combinations, see below Fig.1.5.3. Such an analysis of unitary symmetry
(found in 1964 by M.Gell-Mann and Y.Ne'eman) showed that the
system of hadrons can be very well explained by the hypothesis
that hadrons are composed of subparticles called quarks
- baryons from a triplet of quarks, mesons from a pair of quarks,
as will be outlined in the following passage.
Are elementary particles really elementary ?
Let us now try to look at the "elementality"
and the internal structure of the basic building
blocks of matter. An important guide for assessing the
"elementality" ("fundamentality") of
particles can be whether the particle spontaneously disintegrates
(transforms) or does not disintegrate into other
types of particles. According to current knowledge, a photon
and an electron can be considered as truly
internally "uniform", compact elementary particles
without an internal structure, which always arise or disappear as
a whole and are not transformed into other types of particles.
The neutron and proton can transform with each other with the
participation of electrons, positrons and neutrinos; they cannot,
therefore, be "elementary" in the true sense of the
word. The same applies to p- mesons and hyperons. So generally hadrons ...
Note: Since many particles
are compound, the designation "elementary" is
misleading here. However, it is a common name, similar to the
name "atom", which no longer means
"indivisible". In recent years, however, the word
"elementary" has often been omits and speaks only of
"particles".
Bootstrap model of hadron interactions
The "predecessor" of the
quark model was the so-called bootstrap
hypothesis of hadron interactions developed by G.F.Chew in the
1960s. No more fundamental particles were found to be behind the
properties of the interactions, but it was assumed that they were
essentially the "same" hadrons (including hadron
resonances) acting in a kind of feedback (bootstrap,
self-booting). In particle physics,
this concept is now only marginal and is not generally accepted
...
Quark
structure of hadrons
The above described systematics of hadrons shows that significant
so-called unitary symmetries can be found in
their properties. Based on these symmetries, the so-called quark
model of hadrons was compiled in 1964 (authors M.Gell-Mann and Y.Ne'eman),
according to which all hadrons are composed of even more
"elementary particles" - quarks.
The word
"quark", which has no linguistic meaning, was taken
over by the authors of the quark model with a significant dose of
recession from the play by the writer James Joyse.
Quarks are fermions with
spin 1/2 and with a third electric charge:
-(1/3) e, +(2/3) e, each quark has its antiparticle - antiquark´.
To explain the system of hadrons using an additive quark model, a
total of 6 types of quarks were gradually introduced, the most
important of which are two: "u" (up), "d"
(down) - nucleons are composed of them. The third quark
"s" (strange) is the bearer of "strangeness".
The quark "b" (bottom) participates in the violation of
the CP symmetry. The characteristics of all quarks are given
below in a clear table in the section "Standard model - unified
understanding of elementary particles".
Mesons are composed of two
quarks - a quark-antiquark combination (q q´). In the
case of opposite orientation of the spins of both quarks, we get
the so-called scalar mesons with spin s = 0, eg p+ = (u d´), p- = (d u´), po = (u
u´) + (d d´). If one of the quarks is "s", these are strange
mesons K+, -, 0.... In the parallel orientation of the spins in the
quark-antiquark pair, so-called vector mesons with spin
s = 1 creates, which we observe only as meson resonances
with a very short lifetime (approx. 10-23 s) - meson r+, -
, 0
or *K+, -
, 0.
Baryons are composed of three
quarks, wherein the spins of these quarks can be
oriented so that the resulting spin baryon is s = 1/2, or s =
3/2. E.g. proton p = (u u d) and neutron n = (d d u) with spin
1/2, or hyperon L0 with spin 3/2.
Baryons containing the "s" quark are called hyperons (the properties of hyperons have been described above).
The system of mesons and baryons in terms
of quark structure is schematically grawn by the diagrams in the
following Fig.1.5.3 :

Fig.1.5.3. Schematic representation of unitary symmetry and quark
structure of hadrons.
Note 1: For
consistency with text where wavy fonts are not available,
antiparticles are marked with dashed lines (').
Note 2: The same quark combinations differing in
higher spin correspond either to a single particle (eg r, D), or are
denoted by the same symbol as a known particle with antiparallel
spins of the same quarks and the index "*" (eg *K, *S).
In addition to these basic multiplets, a number
of other combinations can be created from "exotic"
quarks c, b, t *),
whether (pseudo) scalar or vector; some of them have already been
experimentally proven. Eg :
D-mesons - contain c-quarks: D+ (c, d '), Do (c, u'), strange Ds (c, s'), charmonium
(c, c') ,
B- mesons - contain b-quarks: B+ (u, b'), Bo (d, b'), strange Bs (s, b'), Bc (c, b'), ypsilonium
(b, b') .
B-mesons (especially neutral Bo) are produced in particle-antiparticle pairs at the LHC
(LHCb experiment mentioned below) to investigate their asymmetric
production and decay with CP symmetry breaking.
All these combinations behave only as
resonant states with a very short lifetime (shorter than about 10-13 sec). They are
formed for a short time during high-energy interactions of
electrons, protons and other particles. They decay in a number of
different ways (lepton and hadron) into electrons e± ,
photons g, muons m± ,
neutrinos ne, m,
t , kaons K±,0, partly also
pions p± 0.
*) The top quark t, which is the
heaviest (approx. 170 MeV/c2), decays so quickly after its formation (typically into
a b-quark and W-boson) that it is not enough to form hadron bound
states, at him does not occur hadronization and formation of jets
.
Origin of the mass of
hadrons
Hadrons are much heavier than the sum of the masses of their
quarks. E.g. the proton has a mass of 938 MeV, while the mass of
the "u" quark is 2 MeV and the "d" quark is 5
MeV. Therefore, most of the mass of a proton comes from the kinetic
energy of the internal motion of its quark components.
This is explained on the basis of quantum uncertainty
relations, according to which the product of uncertainty in
the position and momentum of a particle is greater than the
Planck constant. Quarks are enclosed in a proton or neutron
("trapped") in area 10-13 cm; this forced very small uncertainty in position
quantum implies considerable momentum and thus the kinetic energy
of each of the quarks, at least about 200 MeV. The kinetic energy
balance of such three intensely oscillating quarks is
approximately equivalent to the mass of the proton.
The difference in the mass of quarks
"u", "d", "s" (which
is explained in unitary field and particle theories by
interaction with the Higgs field) then causes differences in the masses of
mesons p and K, as well as baryons - protons, neutrons and
different species of hyperons.
A virtual "sea of
quarks" ?
The basic idea explains hadrons as composed of two or three
"valence" quarks,
bound together by the strong interaction of the gluon field.
However, according to the concept of quantum field theory, it is
expected that in addition to "real, valence" quarks, virtual
quark-antiquark pairs should also be present in hadrons,
spontaneously arising and then annihilating. They could form a
kind of virtual "sea of quarks" inside
hadrons, which could "materialize" during high-energy
interactions and participate in the mechanisms of the formation
of emitted particles, quark-gluon plasma and its hadronization
..?..
Imprisoned quarks.
Jets. Hadronization of quarks.
The success of the quark model naturally led to intensive efforts
to find individual quarks experimentally.
However, no particles with a third electric charge could
be found in either the high-energy laboratories on the
accelerators or in the cosmic rays. If quarks exist at all, they
must be very strongly bound in the nucleons *),
they cannot be released. Quarks therefore remain hypothetical
particles, resp. model, which very elegantly
explain the properties of hadrons, but whose existence has not
been directly proven.
*) Impossibility
to obtain free quarks
Very strong bond makes it impossible to obtain
free quarks for the following reason: In an attempt to tear the
quarks apart in a hadron by supplying more and more energy (such
as by inelastic interactions of firing particles, Fig.1.5.4),
this energy will eventually be so high that it exceeds the
threshold energy for the formation of a new quark-antiquark pair.
These newly formed quarks then immediately combine
in pairs or triplets with the original quarks in the gluon field.
Although we "broke" the original hadron, we do not get
free quarks, but again only bound systems of two
or three quarks, ie hadrons.
An analogous situation is known from
classical magnetism when dividing a permanent bar magnet
having a north and a south magnetic pole. If we break the magnet
into two parts, in an effort to separate the south and north
poles, the magnetic domains will be reconfigured to form two
magnets, each with a north and south pole again. It is therefore
not possible to separate and produce a magnetic
"monopole" south or north, analogous to how it is not
possible to separate and release individual quarks from the
hadron ...
The asymptotic freedom of quarks
and their hadronization is mentioned even below.
Indirectly, however, the quark model was
supported by the results of experiments with electron
scattering on protons, in which the angles and energies
of scattered electrons and protons were measured. At lower
energies (up to about 1GeV) the proton behaves like a compact
"ball" with a radius of »1 fm (= 10-15 m). However, at
high energies, the behavior of protons is completely different;
for the first time, such an experiment with scattering of
high-energy electrons (with energies higher than 1010 eV) on nucleons was
performed on the SLAC accelerator in Stanford (1960-70 - J.I.Friedman, R.E.Taylor, H.W.Kendall et al.). In such a "hard bombardment", the nucleon
did not behave as a compact particle with a uniform charge
distribution, but as a system of three very small scattering
centers (about 10-16 cm) in which the electric charge
is concentrated. R.Feynman called these particles inside the
protons partons. However, the direct
identification of quarks and partons was hindered by a
contradiction - on the one hand, partons in nucleons behaved as
free in experiments, on the other hand, quarks are so strongly
bound that they cannot be released from nucleons.
To understand the specific properties of
the quark structure of hadrons, the so-called quantum
chromodynamics (QCD, Greek chromos
= color) was created in the 1970s,
which is a field theory of strong interaction. Within the QCD,
the concept of the so-called asymptotic freedom
of quarks was outlined (the binding potential of quarks is close
to zero at very small distances »1 fm) and the hypothesis of
a perfect trapped quarks in hadrons whereby
quark can not exist as free particles, but only bonded hadrons -
binding potential is growing rapidly with the distance, to
completely release quark would be required infinitely large
energy (compelling reason discussed above
in footnote "Inability to obtain free quarks"). The strong interaction between quarks in QCD is
mediated by a vector calibration field, whose zero rest mass
quantum, called gluons, play a similar role here
as photons in quantum electrodynamics, where they
mediate electromagnetic action between charged particles.
According to some
hypotheses, quarks could be composed of even "smaller"
particles, called preons- see below the section
"Standard model
- uniform
understanding of elementary particles", passage "Preon
hypothesis".
Fig.1.5.4. Schematic
representation of the mechanism of interaction of a high-energy
electron with a proton.
At very high energies, during hard and deeply
inelastic collisions of electrons with protons, a number of
secondary particles are formed, which fly out unisotropically
in some kind of directed "jets". A
detailed analysis of the angular distribution and energy of
particles in jets showed the following mechanism of interaction,
which can be divided into two stages (Fig.1.5.4): During the 1st
stage, a high-energy electron, in interaction with the proton,
transfers part of its kinetic energy to one of the quarks, which
after this scattering moves for a short
time practically freely (asymptotic freedom) inside the proton;
similarly, the remainder of the proton formed by the two
remaining quarks. However, the quarks will not be released from
the proton. Once the distance between the accelerated quark and
the rest of the proton exceeds about 1 fm (10-15 m), the 2nd stage
occurs: the forces between them begin to increase sharply and in
the quark-gluon field the quarks and antiquarks are produced,
which are formed into mesons and baryons - the so-called "hadronization"
of the quark-gluon plasma *). The result is the emission of two
angularly collimated sprays of particles - jets,
which fly out approximately in the directions of flight of the
incident quark and the rest of the proton in the first stage.
These jets are actually traces of quarks. The
quark structure of hadrons manifests itself in a number of
high-energy interactions.
*) We can simply imagine that the quarks in
hadrons are connected by a kind of "strings" (gluon
tubes) that hold them together as "rubber fibers". When
"trying to escape" quarks, ie when the distance between
quarks increases, this string "tears" into shorter
strings of about 1 fm in length, corresponding to mesons and
baryons (the free ends of the string lead to the formation of a
new pair of quark and antiquark). This older idea was often used
in the early 1970s. A more convincing reason was discussed above
in the note "Impossibility to obtain free quarks".
Quark-gluon plasma - "5th state of matter"
Under normal circumstances, quarks cannot
be free, they are always bound by a strong interaction into
hadrons. When the hadron mass is heated to an extremely
high temperature higher than 1012 °K, then the kinetic energy density is many times
higher than the energy density in the nucleus, the mean free path
of the quarks is smaller than the radius of the nucleus. At these
very high temperatures and densities, the hadrons are pressed so
close together that they "intertwine" with each other's
quark structure and lose their "identity". There is
such an amount of gluons in the space between the quarks, that
their force interaction "shields" the attraction
between the quarks. Mater in this state is for a short time
formed by an equilibrium mixture of (asymptotically) free
quarks and gluons. This highly "exotic" state of matter
is called quark-gluon plasma.
Quark-gluon plasma is sometimes considered
to be a kind of "fifth state" of
matter: the three commonly known states are solid, liquid, and
gaseous; at high temperatures, or by the action of strong
electric fields, discharges or radiation, an ionized gas is
formed - a plasma consisting of free electrons
and positive ions or atomic nuclei - referred to as the 4th
group; and nuclear quark-gluon plasma is Group 5. In connection
with this analogy and with the idea of the asymptotic freedom of
quarks in the gluon field, it could be expected that the
quark-gluon plasma will have the character of an ideal gas
of only weakly interacting quarks. However, complex experiments
on accelerators, combined with a thorough analysis of the data
from the particle detectors, have shown that it behaves rather
like a strongly interacting almost ideal quark-gluon
liquid, showing superfluidity properties. Residual
interactions , the relative strength of which is comparable
to the van der Waals forces observed in classical fluids
, appear to occur in this plasma .
Quark-gluon plasma is formed only for a
small moment during collisions of high-energy particles
- hadrons and especially heavier atomic nuclei - on accelerators (where complex sprays of secondary particles - baryons,
pions, kaons, are monitored using complex detector systems, see
"Large Accelerators"
below) , or in cosmic rays. In the context
of nuclear reactions, the quark-gluon plasma is discussed in
§1.3, passage "High-energy collisions of heavier atomic nuclei".
If no other forces act, in a short moment
approx. 10-22 sec. quarks and gluons are re-trapped from the
quark-gluon plasma into hadrons - the quarks begin to hadronize
in pairs (p and K mesons
are formed) and triplets (baryons are formed - mostly protons
and neutrons, in smaller amounts hyperons can also be formed, see
below a small passage "Strange quark matter?"). The quark-gluon plasma disappears, a
number of particles fly out of the place of extinction...
It is assumed that just such a quark-gluon
plasma formed the mass of the universe in its
initial stages - the so-called hadron era - a
few microseconds after the Big Bang (discussed
in more detail in §5.4 "Standard cosmological model.
The Big Bang. Shaping the structure of the universe." monograph "Gravity,
black holes and the physics of spacetime"). Formation quark-gluon plasma at high energy collisions
in accelerators are therefore sometimes referred to as a kind of
laboratory "small bang" or
"Little Big Bang". The only place in the
universe where a stabilized quark-gluon
plasma in large numbers could perhaps occur are the central
regions of neutron stars (§4.2,
passage "Internal structure of neutron stars" of the same book); however,
we cannot look at it there - we will be
permanently dependent on the study of its highly unstable state
during collisions in accelerators..!..
Strange quark matter ?
However, it has been hypothesized
(E.Witten, 1984) that if a quark-gluon plasma contained a
sufficient number of "strange" s -quarks (in
addition to the usual quarks u and d
forming nucleons), it could prevent hadronization and such "strange
quark mass"can be stable. In situation, when the
quarks are very "pushed" close to each other and all
lower fermion states are occupied, the quarks s
practically cannot be transformed into u quarks ,
because there is no longer a free quantum space for such
newly formed quarks. Opposite transformations can occur, so that
an equilibrium configuration of quarks u, d, s is established
in fermion gas, which is more energy advantageous than
hadronization. The resulting formation could then be stable, held
together by a strong interaction. The strange quark mass is able
to absorb neutrons, decompose them into quarks and form another
strange quark mass. It is thought that smaller fragments of
strange quark matter could survive from the hadron era at the
beginning of the evolution of the universe, or could form during
a supernova explosion. There is no experimental evidence for such
an exotic state of matter yet. Some astrophysical aspects are
mentioned in §4.2 "Final stages of stellar
evolution. Gravitational collapse" of the already mentioned book "Gravity,
black holes and space-time physics").
Stability and instability of
quarks, hadrons, nucleons
The temporal stability or instability
of particles is generally due to the complex interplay of strong,
electromagnetic and weak interactions,
determining the quantum processes of transformation
mechanisms and the energy ratios
between particles that are "at play". In hadrons, these
basic particles are quarks. In the nucleons that
make up atomic nuclei in our nature, they are the "u"
and "d" quarks. Their
stability, or mutual transformations, implies the stability or
instability of protons, neutrons and other hadrons. In neutrons
and protons, these transformations are caused weak
interaction :

Schematic representation of the
mechanism of b- neutron decay (top) and b+ -proton
transformation (bottom) by quark transmutation within the
standard model of elementary particles.
From an energetic point of
view, the differences in the mass of
the quark "u" and "d" determine the
possibilities of these transformations. If the mass differences
between the "u" and "d" quarks are too large,
the spontaneous transformation of protons or neutrons inside the
nuclei can occur.
But the decay of neutrons in the nucleus A,
leading to the radioactivity beta-, NAZ --> NBZ+1 + p + e- + n, cannot occur when the mass-energy inequality
md
< mu + me + EDem + EB ,
where md
and mu are
the masses of the quarks "u" and "d", EDem = 1.7 MeV is the electromagnetic contribution
to the mass difference between the proton and the neutron and E B is the binding energy
of the neutron inside the nucleus. Similarly, beta+
transformations of protons, NAZ
--> NBZ-1 + n + e+
+ n, cannot
occur in nuclei when the mass-energy inequality
mu
< md + me - EDem + EB .
At a given mass of md and mu quarks and protons and neutrons with beta- or beta+
radioactivity, the binding energy EB of a neutron or
proton in the nucleus according to the shell model is basically decisive.
The binding energy of protons and neutrons in nuclei differs in
detail for different nuclei, for medium and heavy nuclei the
average is EB = 8 MeV - see the graph in Fig.1.3.3 in §1.3., section
"Fission and
fusion of atomic nuclei. Nuclear energy". The properties of beta radioactive
transformations are analyzed in more detail in §1.2, section
"Beta radioactivity".
So that there could be a free separate stable
proton - the nucleus of hydrogen, to prevent its
spontaneous conversion p --> n + e+ + n to neutron and
positron, the inequality
md
> mu - me + EDem must be met .
And in order for there to be a stable hydrogen atom
that could not spontaneously convert to a neutron by the electron
capture reaction p + e- --> n + n, the condition
md
> mu + me + EDem must be met .
What
keeps the world together? - and/or: 4 types of
interactions in nature
All the results of previous
physical and scientific research show that all structures and
phenomena in nature are conditioned by the action of only four
basic types of interactions :
- 1. Gravitational
interaction
Gravitational interaction is the most common type of
interaction in nature. It acts between all
bodies, fields and particles - it has a universal
nature. It has a long range
(unlimited) and is always attractive *),
it has a "cumulative" character. It is a force
"holding the world together":
it binds terestrial bodies, water and atmosphere to
Earth, keeps the Earth and other planets in orbit around
the Sun, maintains the Sun and all stars in the function
of sensitively regulated thermonuclear reactor, binds
stars in galaxies, controls the evolution of the Universe
as a whole.
*) Only for some "exotic"
and hypothetical types of matter (or rather
configurations of physical fields, eg the so-called
"false vacuum") can gravity have a repulsive
character. This applies especially to
hypothetical phase transitions at the very beginning of
the evolution of the universe during the so-called inflationary
expansion of the universe. There is now
speculation about the presence of so-called dark
energy in the universe, which could accelerate
the expansion of the universe even today and future. Here
we can only refer, for example, to the relevant Chapter
5 in the book "Gravity,
Black Holes and the Physics of Spacetime"; see also
"Anthropic Principle or Cosmic God".
In classical level (for weak fields) gravity
is described by Newton's law of general
gravity, in general and exact form by Einstein's
equations of the gravitational field within the general
theory of relativity - gravity is expressed here
as curved spacetime. During the
accelerated motion of gravitational bodies, a
time-varying gravitational field is excited, and
according to Einstein's equations, gravitational
waves are created, which propagate into space
and carry away part of the energy (and momentum) of the
source (Gravitational Waves). The quanta of these gravitational waves are
hypothetical gravitons.
Although gravity is the weakest
force, due to its versatility, it is cumulative
in nature, and with a large accumulation of matter
in cosmic bodies, it can amplify enough
to overcome all other forces. It can then lead to catastrophic
phenomena such as gravitational collapse
and the formation of black holes (Final stages of
stellar evolution. Gravitational collapse. Formation of a
black hole.). On a
cosmological scale, gravity then decides the fate
of the entire universe - its origin, development
and possibly extinction (§5.4
"Standard cosmological
model. The Big Bang."
books "Gravity, black holes and
spacetime physics"). One possibility is even gravitational
collapse of the entire universe into a "fiery
furnace of the big crunch", although for our
universe, this probably does not apply, because under
current astronomical observation of the universe is
constantly accelerating expands (§5.6, passage "Accelerated
expansion space? Dark energy?").
In the ordinary study of the
interaction of elementary particles, gravity has no
effect due to its weakness, although we suspect
that at least mikroscales of the order of 10-33 cm (Planck length) it can
also play a decisive role in the geometric-topological
structure of spacetime..?..
- 2. Electromagnetic
interaction
This second most common interaction does not occur
between all types of particles, but only between those
particles that we say have an electric charge.
Electric forces are attractive and repulsive, which we
interpret using two types (signs) of electric charge - positive
and negative, while the charges of the
same sign are repelled and opposite charges are
attracted. The electric charge is quantized
- there is the smallest (elementary) possible amount of
charge e = 1.602.10-19 C. The basic carrier of the negative elementary
charge is the electron, the positive
elementary charge of a proton. The
attractive electric forces between the protons in the
nucleus and the electrons in the shell primarily keep the
structure of the atoms together (Chapter 1.1, Fig.1.1.3),
and subsequently bind the atoms in the molecules and in
the crystal lattices together. Electric forces are thus
responsible for all the diversity of
shapes and chemical composition of our
world.
Ordinary matter usually contains
on average the same number of protons and electrons, so
it is electrically neutral on the outside. Violation of
this equality in the representation of protons and
electrons is the basis of all electrical phenomena.
Electric charges around them excite the electric
field. An important feature of electromagnetism
is that the movement of electric charges creates a magnetic
field (acting on moving charges by the Lorentz
force) and the time variability of the magnetic field
creates (induces) an electric field. Electromagnetic
interaction is thus the basis of all phenomena of
electricity and magnetism, including their wide technical
applications.
The electromagnetic field is
physically described by the so-called Maxwell's
equations of electrodynamics, which in general
reflect all the laws of field excitation, mutual
inductive transformations between electric and magnetic
fields, as well as the dynamics of propagation of changes
in the field. The accelerated movement of electric
charges creates a time-varying electromagnetic field and
excites electromagnetic waves that
detach from their sources, propagate at the speed of
light and carry part of the energy (and momentum) of the
source system into space. The emission of electromagnetic
waves is quantized - it takes the form of photons.
Deexcitation of energetically excited states and levels
in atoms and atomic nuclei usually takes place by
emitting a quantum of electromagnetic radiation - photons
of light, X-rays, g -rays.
In addition to electrons and
protons, they show an electromagnetic interaction and
carry an electric charge in many other elementary
particles - eg mesons p-,
p+,
K, muons m-,
hyperons S-, S+, also hypothetical quarks or intermediate
bosons W-, W+ etc. The electromagnetic force thus plays an
important role in most mutual interactions (collisions)
of elementary particles.
- 3. Strong
interaction
As the name suggests, this is in practice the strongest
interaction, but it acts only between some types of
heavier particles, which we collectively call hadrons.
These are mainly protons and neutrons, then p -mesons,
K-mesons and hyperons. A significant feature of strong
interactions between hadrons is their short range
- they work effectively only up to a distance of the
order of 10-13 cm, at greater distances they weaken very
quickly and become negligible.
The greatest significance of
strong interactions is that they hold the nuclei
of atoms together against electrical repulsive
forces between protons. In addition, strong interactions
are involved in a number of processes with elementary
particles, especially at high energies.
In practice,
a strong interaction is usually
identified with a short-range nuclear interaction,
because its manifestations were first encountered by
physics in the atomic nucleus and they are the most
important in nature.. From today's theoretical point of
view, according to the model of the quark structure of
hadrons, however, the basic and primary
physical interaction is a strong interaction
between quarks, which is long-range
! The corresponding mediating quantums of the strong
interaction between quarks are called gluons.
The observed "strong interactions" between the
hadrons, and thus the nuclear forces, arise only
secondarily as a kind of "residual
manifestation" of this primary strong interaction
between the quarks within the hadrons. The differential
mechanism of "residual manifestation" causes
the short-range of observed interactions
between hadrons (§1.1, section
"Strong nuclear
interaction"). The situation here is somewhat analogous to
that of a chemical bond, where the short-range
binding forces in the molecules also arise as a
"residual manifestation" of a properly shielded
long-range electromagnetic interaction between atoms
(electrically neutral at a distance) in the molecule,
which is the essence of chemical bonding. The same is
true for the short-range Van der Waals force (see §1.1, section "Interaction of atoms") .
- 4. Weak
Interactions
The last type of "hidden", typically
short-range microscopic forces, are weak
interactions, which, however, act between a
wider class of elementary particles than strong
interactions; a weak interaction manifests itself in all
types of elementary particles except gravitons. Unlike
the other three types of interactions, weak interactions do
not form bound stable systems of
particles - this is due to the fact that they have a very
short range (on the order of 10-16
cm), so even at subnuclear
scales they only have a very weak intensity.
They are manifested only by the decay of
some elementary particles *). The main significance of
weak interactions for us is that they cause them beta
radioactivity - mutual conversion of neutrons
and protons, accompanied by emission of electron b-,
positron b+,
or absorption of electron from envelope (electron
capture). This is because the weak interaction is able to
transform the quarks d to u
and vice versa within the hadrons, under the action of
the intermediate intermediate bosons W-
and W+ (§1.2, part "Radioactivity
beta", Fig.1.2.5). A common side effect of all these
transformations is the emission of neutrino
n. Weak interaction is also manifested in other
processes in the microworld, especially in the
interactions and transformations of muons m, mesons p and K.
*) This does not mean, however,
that the weak interaction in nature and space plays only
a decaying role! He participates in the nucleosynthesis
of more complex elements from simpler ones inside stars
(conversion of a proton to a neutron in the p-p reaction
and the CNO cycle). And in the final stage of massive
stars, during a supernova explosion, radioactivity b-,
together with neutron fusion, is the driving force for
the synthesis of heavier elements up to
transurans (repeated neutron fusion + neutron conversion
to proton ® new nucleus with a higher proton number). See,
e.g., "Cosmic Alchemy", or "The role of gravity as the origin
and evolution of stars').
The influence
of weak interactions for building cores
Weak interaction plays an important role in the
construction of atomic nuclei in their stability. If
there was only strong interaction (and
electromagnetic) in the microworld, could
exist the "mononucleon" nuclei composed only of
protons or only neutrons
(mononeutron nuclei would not have an electron shell). Nuclear "monsters" composed of
thousands of neutrons could also form. However, we do not
observe anything like this in nature, there are no stable
nuclei of two protons alone or two neutrons, even the
neutron itself is unstable. There is another kind of
force in nature - a weak interaction that
ruthlessly transforms by beta (- or +) radioactivity
any nucleus, in which a certain ratio between the
number of protons and neutrons is disturbed. The
mechanisms of these processes are discussed in §1.2,
part " Radioactivity beta",
see also "Stability
and instability of nuclei".
An interesting rule of the hierarchy of
interactions turns out : a particle that is subject to
some of the 4 basic interactions is automatically subject also to
all weaker interactions.
Symmetry of interactions ( C
P T )
An important role in understanding the interaction of particles
is played by the properties of symmetry -
whether and how the behavior of the physical system changes
during a certain (imaginary or actual) transformation
of coordinates or other parameters of particles. By symmetry
we mean such transformations of quantities describing a given
physical system that leave the form of the laws of motion of this
system unchanged (for a general physical-mathematical analysis of
symmetries and conservation laws in field theory, see §B.6
"Unification of fundamental interactions. Supergravity.
Superstrings.", passage "Symmetry
in physics" book
"The gravity, black holes and the physics of
space-time"). Here we briefly mention three basic types of
symmetry in the interactions of particles, their combinations
and their disruption :
¨ C-symmetry , charge association ( Charge)
- is in the replacing all particles in the system with their antiparticle
with opposite charge. If such a system will behave as the
original particles, mark it as a C-invariant. The basic laws of
the world and antiword are actually the same. The existence of
only left-handed neutrinos and dextrotatory antineutrinos,
however suggests, that C-symmetry may be violated in weak
interactions.
¨ P-symmetry , mirror inversion
- parity symmetry
- consists in the mirror inversion of all positions and
orientations of particles in the system, including the exchange
of left - handed and right - handed angular momentum. In the
macroworld and for most processes in the microworld (strong and
electromagnetic interactions), P-symmetry is preserved. However,
in the decay of K-mesons due to weak interaction, as well as in
the b- decay of nuclei (eg
60Co),
certain asymmetries were observed, disrupting right-left symmetry
- violation of the law of conservation of parity *).
*) Until the mid-1950s, it was assumed that
parity was maintained in all particle interactions (similar to
the macro world) - that the law of conservation of parity
applied. In 1956, T.D.Lee and Ch.N.Yang began to investigate
the validity of parity conservation in weak interactions,
admitting its disruption, and designing appropriate experiments.
The decisive experiment was carried out in 1957 by the
Chinese-American physicist Ch.-S.Wu (with a
team of collaborators - E.Ambler, R.W.Hayward, D.D.Hoppes,
R.P.Hudson) on the b- decay
of cobalt cores 60Co. Sample 60Co, cooled to a very low temperature (0.01 °K by
adiabatic demagnetization - so that thermal movements do not
disturb the orientation of the nuclei) was placed in a strong
magnetic field that oriented the magnetic moments and spins of
the nuclei in a precisely defined direction. Using scintillation
detectors, the angular distribution of the flying beta electrons
with respect to the direction of orientation of the momentum
(spin) of the nucleus was measured. An anthracene scintillator
was used for the actual measurement of electrons b , the other two
scintillation detectors NaI (T1), placed perpendicular to each
other, registered the anisotropy of the accompanying radiation g to monitor the
achieved degree of orientation of the cobalt nuclei. Two series
of measurements were performed for two opposite directions of the
magnetic field vector B depending on the
temperature. Asymmetry in the angular distribution of radiation b was monitored by
the relative number of pulses in the anthracene scintillator as a
function of temperature: for low temperatures (high core
orientation) about 20% asymmetry was observed, at higher
temperatures (with decreasing degree of cobalt core orientation)
the degree of angular asymmetry in electron emission decreased;
with the disappearance of the nucleus orientation, the asymmetry
in the angular distribution of the emitted electrons also
disappeared. If P-symmetry is valid, the number of electrons
flying at a certain angle f should be the same as the number of electrons flying in
the opposite direction 180 ° - f . However, asymmetry
in the angular distribution of electrons b was reliably determined,
indicating violation of P-symmetry - failure to maintain
parity .
In addition to radioactivity b , non-preservation
of parity in weak interactions is also reflected in the decays
of mesons K (kaons) into mesons p (pions), which were
described above in the section "Properties
and interactions of the most important particles", passage "Mesons p and
K". Mesons K and p have negative parity. When
a charged K decays into three charged pions (eg K+ ®p+ + p+ + p-), the parity before and after decay is negative.
However, there is also a decay of a charged K (with
negative parity) into one charged and one neutral meson p , eg K+ ®p+ + po; this
resulting system of two mesons p has a positive positive
parity - the parity is not maintained. When these two
possibilities of 2- and 3-pion decays of a newly discovered meson
into states with different parities were discovered in 1953, it
was considered to be decays of two different particles, referred
to as J and
t particles.
However, further measurements have shown that these putative two
particles have the same mass, charge and lifetime - that
particles J and t are the only particle that have been named K
and that can decay in two (or several) ways, some of which do not
retain parity.
¨ T-symmetry - inversion of time
- consists in reversing the direction of time flow, in examining
whether all processes in the system can take place in the reverse
order. From a mechanical point of view, we swap the initial and
final states of the particles and reverse the vectors of their
motion velocities. The basic laws of electrodynamics and gravity
do not change when the direction of time is reversed. For large
statistical sets of particles, time-reversed processes at the
microscopic level are possible in principle, but their
probability is very small - in accordance with the 2nd Act of
Thermodynamics, the resulting macroscopic processes are
virtually irreversible (see for example "Determinism - chance - chaos?" §3.3 in the book "Gravity, black holes and
spacetime physics"). It turned out, moreover, that the
T-even symmetry entirely true on the level of colision of two
particles, is disturbed by the action of weak interactions.
Combined symmetry
Therefore, since the actual C, P and T symmetry may be impaired,
at least in processes involving weak interactions, it was
examined whether the symmetry not restored when combination
of respective transformations :
¨ CP - symmetry
is created by replacing the left and right simultaneously
exchange particle antiparticle. Even here it is shown that some
decay of K0-
mesons to pions *) in about 0.2% of cases they disrupt
CP-symmetry.
*) This is a quantum mixed state of meson K0 and anti-K0, in which two different states called KL (with a longer
lifetime of approx. 10-8 s) occur with a negative value of combined CP and KS (with a shorter
lifetime of approx. 5.10-10 s) with a positive value of CP. Both of these states
break down by weak interaction in two different ways. The
short-lived meson KS decays in two particles into two p- mesons, the longer-lived KL then usually into
three pions, or a pion and a muon or an electron and a neutrino.
In experiments at the accelerator Brookhaven in 1964, however, it
was the KL
observed insensitive "dopant" disintegration into two
mesons p,
representing a state with a positive CP value. The value of CP
thus changed from negative to positive - a violation of
CP symmetry was proved. Violation of CP symmetry also
occurs during decays of K0 into pions and leptons: KL ®p+ + e- + n ', KL ®p- + e+ + n , in which the decay to form positrons is about 0.2%
more common than electrons.
¨ CPT - symmetry
is created by: replacing particles with antiparticles + replacing
left with right + reversing the passage of time. Within the
relativistic quantum field theory in 1957, W.Pauli formulated the
CPT-theorem on maintaining combined CPT symmetry. Here
it is shown that no experiment yet contradicts this symmetry -
the validity of CPT-symmetry is assumed .
Disruption of symmetry
If there were always and everywhere absolute and perfect
symmetry, the world would be very dull and would not be
characterized by the observed diversity; there would not even be
matter in the usual sense, there would be no atoms, the universe
would consist of scattered particles and radiation. The disruption of C or CP symmetry in the microworld
probably had very important consequences in the earliest stages
after the creation of the universe: it led to a slight
predominance of matter over antimatter - to the baryon
asymmetry of the universe. In the period before the
great unification of interactions, X and Y particles, so-called leptoquarks,
caused transitions between quarks and leptons. Due to
the violation of CP symmetry, these processes took place slightly
asymmetrically - for about 108 mutual transformations, one transformation took place
more towards matter than towards antimatter. The subsequent
annihilation of matter and antimatter at the end of the hadron
era thus left a certain small predominance of the
particles forming the matter, of which the universe now
consists. For more details see §5.4 "Standard
cosmological model. Big Bang. Formation of the structure of the
universe." and §B.6
"Unification of fundamental interactions.
Supergravity. Superstrings."
in book "Gravity, black holes and spacetime physics".
The role
of interactions in the functioning of the world
The meaning and role of individual types of interactions in
nature can be illustrated (although perhaps
too popular and simplified, for which I apologize to
colleagues...) in the following thought
experiment. Imagine that there is a God who is absolutely
omnipotent and who decides to practically "test" the
importance of individual interactions for the construction and
functioning of the universe ("isn't some of them
useless?"). To this purpose, he will experimentall
"switch off" or "cancel" individual types of
interactions and observe what he will "do with the
world?" :
¨ God will say : "Well, from now on I am
canceling gravity !".
What would happen? There will be a weightless state immediately,
we will float, which we might like for a while. Apart from the
catastrophic events here on Earth (drop of atmospheric pressure
to zero, spillage of water from the oceans, escape of the
atmosphere into space, rupture of the earth's crust and volcanic
catastrophe), it immediately occurs to us that the Earth will
leave its orbit and fly away from the Sun into space. In reality,
however, he will not make it! In the meantime, the Sun would
explode like a gigantic thermonuclear bomb, and in about 20
minutes a huge wave of hot plasma would reach the Earth, in which
the whole Earth would evaporate. In this way, they would end all
stars, so that the universe would be filled with hot plasma and
then cooling gas, all structures would dissolve and eventually
disappear in the "thermal death" of the universe. So
not exactly a happy ending...
¨ If God said, "I cancel the electromagnetic
interaction ! ",
all atoms would immediately decay into nuclei and separate
electrons - all structures would disappear again and turn into
plasma.
¨ If God canceled the strong interaction
,
all atomic nuclei would immediately decay (electrically explode)
and thus all complex atoms; there would remain only hydrogen 1H1
.
¨ Cancellation weak interaction
should be somewhat more complicated and less straightforward
consequences, because the weak interaction produces no bound
system (type of atoms and their nuclei). In addition to stopping b-decayment would
probably be extinguished by thermonuclear reactions inside the
Sun *). Without a weak interaction, massive stars would not
collapse into a neutron star, but the star would probably remain
in the degenerate electron gas stage. However, if the abolition
of the weak interaction occurred already in the early stages of
the evolution of the universe, baryon asymmetry and the
predominance of matter over antimatter would not arise. There
would be no cosmic nucleosynthesis (neither primordial nor
stellar) and the whole universe would consist only of particles
and radiation. If the hypothetical abolition of the weak
interaction occurred in the Lepton era, the number of protons and
stable neutrons would be the same; in primordial and stellar
nucleosynthesis, not only would stable nuclei known today be
formed, but all isotopes would be stable - nuclear
"monsters" with a large number of neutrons or composed
only of neutrons would also be formed, light nuclei composed only
of protons and the like. The chemical composition of the universe
would be completely different from what we observe (and in any case unsuitable for the origin of life).
*) Thermonuclear synthesis in
stars begins with the fusion of two p+ protons, which
produces the 2H deuteron and emits a positron and a neutrino: p+ + p+ ® 2H1 + e+ + ne . The actual bonding
of a proton and a neutron in a deuteron is the result of a strong
interaction, but the necessary conversion of one of the
protons to a neutron (the bound state of two protons does not
exist) in the process p+ ® no + e+ + ne is the result of a weak interaction.
Without weak interactions, the fusion would not take place, the Sun
and the stars would not shine !
So we see that none
of the fundamental interactions are useless, they are all "vitally
important"! In order for the world to look and
function in its current way, it is even necessary that the force
ratios of individual interactions (coupling constants) have
exactly the values we observe - for a more detailed discussion
see §5.7 "Anthropic Principle and Existence of Multiple Universes" of the book "Gravity,
Black Holes and the physics of spacetime", or the work "Anthropic Principle or Cosmic God".
Standard
model - unified
understanding of elementary particles
A huge amount of experimental knowledge about the properties and
interactions of elementary particles, obtained in the 50s-80s,
processed and unified in the spirit of a number of
quantum-theoretical concepts, resulted in the so-called standard
model of elementary particles and their interactions,
which here can be briefly and simply summarized as follows :
The basic "building blocks" of
matter are fundamental fermions - quarks and
leptons :
¨ Quarks : u
, d , c , s , t
, b .
¨ Leptons : electron e,
mion m, tauon t; neutrinos - electron n
e , the muon n m , tauon n t .
These fundamental leptons and quarks are
divided into three generations (see 3 columns in
the table). Each generation is composed of two leptons and two
quarks, with the corresponding particles of different generations
differing significantly only in their masses;
other characteristics are the same.
Note: The reason why such a repetition of
structures occurs particles in large mass scales, we do
not know yet - this is one of the important questions of
contemporary particle physics and probably also unitary field
theory. A more detailed discussion is provided below in the
section "Preon Hypothesis".

A system of fundamental particles of matter and quantum fields,
forming the basis of the current standard model of particles.
The magnitude of the charge q is given in multiples of the charge
of the electron (e), the rest mass m of the particles in
MeV, unless otherwise stated.
Between these basics quarks and leptons acts fundamental
interactions - gravitational, electromagnetic, strong
and weak forces. Within the quantum field theory,
these forces can be described by the exchange of intermediate
particles - intermediate bosons. Leaving aside
gravity, which plays virtually no role in the microworld *),
these intermediate bosons have spin 1 (referred to as vectors, in connection with the
mathematical formalism of their theoretical description) :
¨ Photon - a quantum of electromagnetic
field, mediates electromagnetic interaction (usually mark it g).
¨ W+ , W- , Z - heavy bosons mediating weak
interaction, eg quark transformations inside hadrons (Fig.1.2.5).
¨ Gluons g - carriers of strong
interaction between quarks.
*) The role of gravity in the microworld
is a permanent topic of discussion for physicists, especially in
connection with the unitary field theory, see
§B.6 "Unification of fundamental interactions" of the book "Gravity, Black Holes ...".
Gravitons have spin 2.
Due to the electromagnetic
interaction, during the collisions of charged particles
in a variable electromagnetic field, photons of radiation g are generated,
electrons and positrons are born and annihilated.
Due to weak interaction
there is also the formation of electrons and positrons together
with neutrinos (from intermediate bosons W), the mutual transformation of individual types of
quarks inside hadrons - and thus the transformation of neutrons
and protons (radioactivity b), mesons and hyperons. The weak
interaction, due to its property of violating the invariance to
the combined spatial and charge inversion of CP, probably also
caused the baryon asymmetry of the universe -
the predominance of matter over antimatter.
The strong interaction
that perfectly binds the quarks inside the hadrons, binds the
nucleons in the atomic nuclei by its "residual
manifestation"; in addition, it causes a number of
interactions between elementary particles, in which new mesons
and baryons are formed in the quark-gluon field during the
"hadronization" process.
All
these processes among the few species of leptons and
quarks cause all the variety and diversity
of our world. The standard model, which
summarizes practically all our knowledge about elementary
particles, is on the one hand a great triumph of the
physics of the microworld, because it explains with
great accuracy the behavior of various phenomena between
particles. On the other hand, it is clear that the standard model
cannot be a complete and definitive theory of the microworld,
because it is incomplete. First, it does not
include gravitational action and the unification of gravity
(general theory of relativity) with quantum theory. Furthermore,
in some aspects it is too phenomenological in nature - it
contains many free parameters such as some
particle masses and binding constants of interactions that the
standard model cannot predict and must be determined
experimentally. A really complete theory should be able to
determine these parameters numerically - for example, what should
be the value of electric charge of an electron and its mass,
similarly proton and other particles, what is the force (or
ratios of forces - binding constant) of individual interactions,
etc.
Building particles
of quarks and leptons - Preons ?
According to the standard model of elementary particles, the
basic "building blocks" of matter are fundamental
fermions - quarks and leptons. The question arises as to
whether the hierarchy of the structure of matter is thus finite?
Or is each "elementary" particle made up of other, even
more "elementary" particles? The above table of the
division of quarks and leptons into 3 generations shows, among
other things, that the properties of particles are repeated
in large mass scales. This suggests (by analogy with the periodic
table of elements *) the possibility that differences between
generations stem from the arrangement of even smaller
building blocks of matter in leptons and quarks. These
hypothetical building "stones" of quarks and leptons
have been called of preons (Greek pre = before ).
*) D.I.Mendelev compiled a periodic
table of elements when he noticed that certain chemical
properties of the elements were repeated. Atomic physics later
explained this as a consequence of the structure of atoms. It
could be similar in particle physics. Even 12 known fundamental
particles have some recurring properties. This
may indicate that they are not in fact basic and elementary, but
that they are composed inside of even smaller
particles, the arrangement of which determines their special
properties..?..
Based on some (highly uncertain) results
of scattering experiments, it was hypothesized that quarks (and
perhaps leptons) could be composed of even "smaller"
particles, called preons. Each quark could be
made up of three preons. According to the Salam and Pati model,
these are somons determining generation (3 species, zero
charge), flavones determining "smell" (2
species, charge 1/2) and chromones determining
"color" (4 species, charge 1/6). An alternative model
proposed by Harrari, Shupe and Seidberg considers quarks and
leptons to be a combination of three preons (so-called rishons)
of two types, one with an electric charge of +1/3 and the other
with zero charge, each of which has its antiparticles with
opposite electric charge -1/3 and 0. The electron would be a
combination of the preons "---", the positron
"+++", the quark "u" would consist of
"++ 0", the electron neutrino of "000", etc. "Force-carrier"
mass bosons would consist of combinations of 6 preons, eg W+ = "+++ 000",
the photon would be a pair of preon and antipreon "+ -". The excited
states of the preon system could correspond to
individual generations of particles. At the next level of the
hypothesis could be pre-preons, pre-pre-preons,
etc., depending on how many undiscovered levels still exist in
matter..?..
Several preon models have emerged, trying to explain
different quarks and leptons by combining different numbers of
specific types of preons. So far, it's all just speculation and numerology
(after all, this was in the beginning also quark model of
protons, neutrons and other hadrons). Any experimental
confirmation of the preon hypothesis is still lacking.
It could be supported by experiments with particle collisions at
the highest energies, if they showed that quarks and leptons have
a non-zero size (previous experiments show rather the point
character of quarks and leptons). There are also some theoretical
problems related to very small dimensions (less than about 10-15 cm) of preons and
their localization, which according to the quantum principle of
uncertainty should imply unacceptably large effective momentum
and thus mass, many orders of magnitude higher than corresponds
to real weights - a mass paradox.
What we are composed
of
We humans, the surrounding nature and all the objects we come in
contact with are composed of quarks "u"
and "d" and electrons.
There are fields acting between them -
electromagnetic, strong and weak interactions. Other types of
quarks and leptons are used only in high-energy processes of
particle interactions in accelerators and cosmic rays, as well as
in some turbulent astrophysical processes.
Problems and possibilities
of extending the standard particle model ?
After the discovery of the Higgs boson, the standard model of
matter was practically closed, it had no missing elements,
basically explain all the observed experimental facts.
Nevertheless, there are many uncertainties. For the theoretical
ones, hopes are placed in future unitary field theories. However,
there is no explanation of the dark matter in the universe, which
is five times more massive than the mass known to us, described
by the standard model (§5.6 "The
future of the universe. Arrow of time. Dark matter. Dark energy." in the book "Gravity, black holes .... )...... .......
Are there new yet undiscovered particles
?
In common experiments, particle interactions manifest themselves
mostly directly, explicitly during collisions either by
scattering or reactions, with the disappearance and creation of
new particles. This is explored in detail. However, hidden -
virtual, vacuum - interactions also take place in quantum
physics. According to quantum field theory, the vacuum is filled
with virtual pairs of particles and antiparticles that are
constantly created and then disappear. If this happens in the
immediate vicinity of a "real" particle, even for that
brief moment of their virtual existence, they can interact
slightly with the real particle, which will somewhat change its
physical parameters. One such parameter that can be affected by
interactions with virtual particles in the vacuum is the
particle's magnetic moment (§1.1, passage
"Quantum angular momentum.
Spin. Magnetic moment.").
Anomalous
magnetic moment of the muon. Experiment g-2.
The magnetic moment of an electron is e.h/4pme - the so-called Bohr magneton (§1.1, passage
"Quantum angular momentum.
Spin. Magnetic moment.").
The so-called gyromagnetic ratio g is introduced for
the excitation of the magnetic field by the rotational movement
of particles, which is the ratio of the excited magnetic moment
and the mechanical moment of momentum of the rotating particle,
here spin. For an electron and muon with spin 1/2, this
coefficient should be g=2. But in the 1950s it was measured
that the g value of the electron is slightly greater than 2
(.........). It was attributed to the influence of interactions
with virtual particles of the vacuum - the slightly increased
value of g arises from contributions from interactions of virtual
pairs of all elementary particles that exist.
The actual measured value of the
gyromagnetic ratio g of fermions - electrons, muons - or its difference from
2, contains information about what all elementary particles exist
in nature and participate in vacuum virtual interactions. Muons
are 207 times more massive than electrons, so the vacuum virtual
particles act much more strongly on them, and the difference
between the actual g and the default value of 2 is larger here. Measuring
the g-2
difference for a muon can thus provide an independent idea of
whether only existing Standard Model particles contributed to it,
or whether the increased value is an indication of the existence
of other yet undiscovered particles..?.. Challenging measurements
of this kind are therefore called "muon experiments g-2"
(g minus two).
In vacuum virtual interactions, all
particles and quantum fields existing in nature should be used -
known and possibly even the others not yet discovered (the
vacuum "knows about them", virtually contains
them...). Experiments of the g-2 type can reveal them to us in advance, without the
need for their "physical production". However, they do
not give us any information about their properties, or whether
they are one new particle or several. To do this, we need to
physically create them for a moment in collision experiments and
deduce their properties from the detection of their decay
products. That will be the task of the new, larger
accelerators...
The experiment begins with a beam of a
large number of protons (approx. 1012 /s.) from the accelerator, which upon impact on the
target produce, among other particles, a large number of pions,
which quickly decay into muons. The muon+ beam is then
guided into the magnetic ring. The g-2 measurement itself is
carried out in a magnetic ring with a very homogeneous magnetic
field, in which a large number of muons circulate in the ring
under the influence of a strong magnetic field at a speed close
to the speed of light. During this circular flight, the spin and
magnetic moment of the muons precess around the magnetic field
vector. At the same time, muons constantly decay into positrons
and neutrinos. Neutrinos fly away without interaction. The
positrons, which travel in the same direction as the muons before
decaying, are detected by a series of detectors located on the
inside of the magnetic ring. They are, on the one hand, PbF2 scintillation
detectors and a series of trackers based on ionization chambers,
which register the trajectory of positrons from the decay of
muons. The energy, time and location of arrival of the decay
positrons are measured. The frequency of precession depends on
the value of the magnetic moment, i.e. on the gyromagnetic ratio g.
The first experiment of this arrangement
took place in the years 1997-2001 in Brookhaven, further
measurements under more modern and more precise conditions
continue from 2018 in Fermilab. The result of the experiment so
far is the value g = 2.00233184110(82). The calculated theoretical value
according to the standard model is g = 2.00233183620(86). Thus,
the experimental and theoretical values differ only slightly -
from the eighth decimal place. If the g-2 experiments confirmed an
anomaly indicating the existence of unknown elementary particles
- the existence of particle physics beyond the standard model, it
would be a great stimulus for the construction of new, larger
accelerators.
But there is another possibility: What if
the anomalous value of the muon's magnetic moment was
inaccurately calculated in the current version of the standard
model? The final objective results of these demanding studies
will hopefully be obtained in a number of years...
Unification of interactions - unitary field
theory and elementary particles
Although the reduction of the huge diversity of
phenomena and structures in nature to a mere 4 basic types of
interactions involved between a few types of elementary particles
(actually quarks and leptons), is the imposing contribution of
physics to a unified understanding of the world,
for physicists it still is not enough. They have even higher
ambitions: to create a definitive final theory
or a unified theory of everything (TOE - Theory Of
Everything) - to unify
the existing four types of interactions into a single
interaction, described by a unitary field,
whose quantum properties would then describe all kinds of
elementary particles.
Unitary field theory forms a very special
part of theoretical physics with links to nuclear and particle
physics, as well as to the theory of relativity, astrophysics and
cosmology. It thus lies outside the scope of our treatise on
nuclear and radiation physics. For further details, we can refer
to special literature, on these pages, for example, to Chapter B
"Unitary Field Theory and Quantum Gravity" in the book "Gravity,
Black Holes and the Physics of Spacetime".
Particle
accelerators
For the study of the properties, structure and
interactions of elementary particles, the production of
artificial radionuclides, as well as for applications in various
fields of science and technology (including medicine), it is
necessary to use particles accelerated to high kinetic
energies. Since the natural radioactive substances
provide limited intensity and especially energy of emitted
particles, it is necessary to turn to artificial
acceleration of particles. We can artificially accelerate only
stable *) electrically charged particles -
electrons e-, positrons e+, protons p+, deuterons d+, helium nuclei He++ = a-particles and the nuclei (ions) of heavier elements.
High-energy particles without charge (such as photons g, neutrons no, neutral pions, ...)
and short-lived particles (p- mesons, hyperons, ...) can then be obtained secondarily
- by interactions of accelerated charged particles with other
particles in a suitable target.
*) The only unstable particles that can basically be accelerated
are m± muons,
whose lifetime of 2.2 microseconds, in co-production with
relativistic time dilation, enables multiple movements along a
circular path in the accelerator for a period of approx. 0.1 s.
sufficient for effective acceleration . Muon accelerators
- colliders - can be promising for obtaining high energies due to
minimal synchrotron radiation and for realizing "clean"
collisions, in which all the energy is available for the creation
of new secondary particles (it is discussed
at the end of this chapter in the passage "Muon
accelerators?") .
Devices that accelerate charged particles
by strong electric and magnetic fields are called accelerators.
The actual acceleration of charged particles is
caused by an electric field (electric component
of the electromagnetic field of intensity E) by
its force acting on the charge Fe = q. E,
the magnetic field is used to change the
path of charged particles *). Or, the variable magnetic
field induces an electric field, which causes an accelerating
effect.
*) A magnetic field alone cannot accelerate,
because the Lorentz force Fm
= q. [v x B] acts in a magnetic
field of intensity B perpendicular to
the direction of motion of the charged particle at velocity v,
so that it does not perform any work. It only
appropriately changes direction, curves the path of the charged
particle, without changing the velocity or energy.
Note:
An X-ray tube
can already be considered the simplest particle accelerator
(§3.2 "X-ray diagnostics") - it is a linear electrostatic accelerator of
electrons, the source of which is a hot cathode, the (inner)
target is an anode, braking (+ characteristic) X-rays come out.
The first real accelerator was built in 1931 by R.J. van de Graff
using electro -mechanical high voltage generator
(called by its name), in 1932 J.D.Cockcroft and E.T.S.Walton
using a cascade voltage multiplier (a system of
rectifier diodes with suitably connected capacitors). An
accelerated proton energy of about 0.5 MeV was achieved, with
which the first nuclear transmutation caused by
artificially accelerated particles. The first circular
accelerator (cyclotron) was designed by E.O.Lawrenc also in 1932.
Thus began the era of the use of accelerators in nuclear physics.
Cosmic
accelerators
The processes of accelerating the building blocks of matter also
take place in nature, often on a much larger
scale and intensity than we can artificially. In stormy processes
in stars and galaxies, there are processes that
act as "cosmic accelerators" of particles. In
particular, three mechanisms of particle acceleration in space
are discussed :
¨ Fermi mechanism of
continuous diffusion acceleration during repeated interaction of
particles with moving large clouds of ionized gas, with the
interaction of magnetic and electric fields in space.
¨ Supernova explosion, in
which the outer parts of the star expand at a speed close to the
speed of light, while in the resulting shock wave, protons can be
accelerated to energies of up to hundreds of TeV in the rapidly
expanding ionized mass.
¨ Absorption of matter through a
black hole, when a large amount of matter attracted by a
black hole creates a so-called accretion disk around it,
in the lowest central area of which there is an extremely strong
heating of the absorbed substance descending in a spiral into the
black hole. Along the axis of symmetry of this thick rotating
disk, a "funnel" then escapes from the inner part a
stream of particles and radiation - the so-called jet ,
which contains particles accelerated to very high relativistic
energies.
These mechanisms (and possibly other
hitherto unknown ones) produce high-energy cosmic
radiation - for details from the point of view of
radiation physics, see §1.6 "Ionizing radiation",
section "Cosmic radiation", from the point of view of astrophysics and
cosmology, see chapter 4 "Black holes" in the book "Gravity,
Black Holes and the Physics of Spacetime".
Basic
division of accelerators
In terms of purpose and use, accelerators can be
divided into two groups :
¨ Small accelerators for
industrial and medical use ,
where extremely high energy is not required (usually units up to
tens of MeV), but it is often desirable to achieve relatively high
flow (fluence) particles so that the desired
technological, analytical or therapeutic effect is sufficiently
effective. These are relatively small devices with the dimensions
of the acceleration chamber in the order of tens of centimeters
to several meters. Such accelerators are the most common, they
are often also produced industrially and in series.
¨ Large
accelerators for research in nuclear and particle physics ,
where it is usually crucial to achieve the highest
possible energies of accelerated particles; high
effective energies of order TeV and higher for interactions can
be achieved only by using method collider, as
discussed below. To study interactions with a low effective cross
section, it is also necessary to achieve a high flow
of high-energy particles (often only one interaction out of
several billion is "the right one"!). These are unique
devices with large dimensions (tens and hundreds of meters, the
largest up to several kilometers!); they are part of complex
laboratory systems with complex detection apparatus. The
construction of such facilities takes many years and is very
costly - up to billions of dollars. The issue of large
accelerators will be briefly discussed below - passage "Large accelerators".
The
smaller structure we investigate, the larger instrument we need
When examining the microworld is manifested interesting at first
glance paradoxical regularity: the smaller the object investigate
or influence, the bigger - larger and more powerful - equipment
we need. This trend is not new, and there hass actually
manifested itself in the optical field. For the observation of
millimeter objects we can do with an ordinary magnifying glass,
for the study of cells we need a more complex and larger
microscope, for the study of processes in the cell nucleus we can
no longer do without a relatively large and complex electron
microscope. In general, to observe a given object, we need
radiation with a shorter wavelength than the effective dimensions
of the object.
Even more complicated is the situation in
the study of the smallest "elementary" particles of
matter, where specific properties of their interactions come into
play. Repulsive forces between particles can prevent the desired
interaction, different types of processes can take place under
the same conditions, new particles are often formed with a short
lifetime. To understand the structure of
elementary particles and the nature of forces,
which acts between them, it is necessary to realize particle
collisions at the greatest possible energies. In such collisions,
the particles penetrate each other "deep into their
interiors" and the result of the interaction can tell
something about their structure. Due to quantum processes in the
fields of strong, weak and electromagnetic interactions,
high-energy collisions create new secondary particles, which are
both interesting in themselves and carry important information
about the nature of fundamental natural forces, including the
possibility of their uniform understanding within unitary field
theory. Particle collisions at high energies are a kind of "probe"
into the deepest interior of matter - and at the
same time into the processes of the formation of the
universe (see §5.5 "Microphysics
and cosmology. Inflationary universe." books "Gravity, black holes and space-time
physics").
It can be said, that large accelerators
are the most powerful "microscopes" *)
into the interior of matter and with a bit of exaggeration also
the largest "telescopes",
which allow "oversight" to very early stages of
development of universe. This is not, of course, a direct
physical observation of the phenomena at the beginning of the
universe, but their experimental simulation, if
possible.
*) In the spectrum of "research
tools" in Fig.1.0.1 it lies on the left margin (§1.0., part
"Methods and tools
of nature study").
Regarding the type of accelerated
particles, some types of accelerators are
"universal" and can in principle work for different
types of particles if provided by an ion source; linear
accelerators or synchrotrons have this property. Other types are
able to accelerate only certain types of particles, eg betatron
only electrons. In practice, however, accelerators are mostly
"specialized" in their design and are divided into electron,
proton and heavier ion
accelerators.
Accelerator luminosity
The intensity (abundance) with which the accelerated particles
interact depends on their flux density. It is characterized by a
quantity called the luminosity of the
accelerator L [cm-2 s-1], which is the number of particles per cm2 per second (a kind of
"luminosity", "aperture"). On large
colliders, the luminosity reaches L » 1031-1033 cm-2 s-1, for accelerators working with a fixed target, it is up
to L » 1035 cm-2 s-1.
According to the method of
technical implementation and the shape of the path
on which the particle acceleration takes place, we divide the
accelerators into two basic types: linear (LINAC)
and circular (cyclic) - both types will be described in more detail
below. We will mention one more interesting and possibly
promising type of accelerators (belongs to
the category of linear, but its principle differs fundamentally), which is still in the stage of research and
development :
Laser
plasma accelerators LWFA
A new interesting and promising method of accelerating charged
particles (especially electrons) is the use of very intense
electromagnetic beams from high-power lasers.
When an intense light beam from a laser passes through a gaseous
medium, the gas is ionized and plasma
is formed. If we irradiate a gaseous medium with a very intense
short pulse of laser light, a plasma trace
is created in the medium, which entrains the released electrons.
While passing through the plasma laser pulse ponderomotive
force expels electrons out from areas of its HF. impulse, so
that a wave or a furrow of deflected
electrons is formed behind it in the plasma. The
electrons move in a positive ion environment and, under the
action of Coulomb's electric force, return to their equilibrium
positions (which "over-vibrates"), with a periodic deflection of the electron set
relative to the ion set (which in the high
frequency field due to its substantially greater mass almost not
enough to move) - to the oscillations
of electrons in the Coulomb field, accompanied by a periodically
variable electric field. This creates a kind of rippling trace
concentration of electrons and the electric field intensity - plasma
wave or "furrow field " (Wakefield),
similar to a rippling trail or furrow left behind by a ship
floating fast on the water surface. The frequency of electron
oscillations in a plasma wave (plasma frequency) is wp = Ö[rp.e2/(eome)],
where me is
the mass of the electron, e is the charge of the electron,
rp
is the density of the plasma (number
of particles per m3) eo permittivity of
vacuum. During the oscillations of electrons in a plasma wave, an
alternating electric field with an amplitude of intensity Emax = me. wp.c/e is created. Thus, the accelerating electric
gradient in a linear plasma wave can reach a maximum value of E =
c.Ö(me.rp/eo), proportional to the
square root of the plasma density. For density plasma rp »1018 particles/cm3 achieved by
accelerating gradient values E » 1GeV/cm, which is about
2-3 orders of magnitude higher than in linear accelerators.
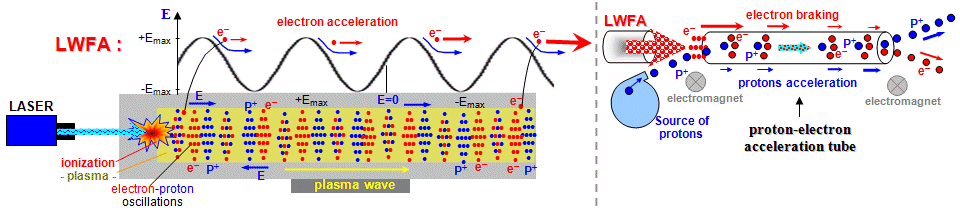
The longitudinal component of the oscillating electric
field in this plasma wave can accelerate electrons
under certain circumstances (synchronized energies and momentum),
which are carried on an electric field wave (similar to the high
frequency linear accelerators described below). When using a
laser with focused picosecond pulses of high intensity (approx.
1018 W/cm2) a very intense
longitudinal acceleration field is created, which can accelerate
electrons to energy of about 50 MeV (in top
laboratory experiments energy of the order of GeV was achieved,
but the electron yield is so far very small).
Experimental accelerators on this
principle given the name LWFA (Laser
Wakefield Accelerator - laser accelerators
trought the furrow field, here Wake =
track behind the boat, furrow), in
image on the left part. Their advantage is very small
dimensions *). The rapid progress of laser technology
promises the possibility of effective acceleration, controlled by
several sequential laser pulses (one pulse
excites a furrow field, the other a subsequent pulse releases
into it, "injects" electrons). If
this technology can be brought to the stage of practical
applicability, then such a tiny "table" LINAC,
accelerating electrons into energies of tens and hundreds of MeV
in a laser-excited plasma wave in a centimeter path, would find
wide application in research, industry and medicine.
*) In the case of plasma
accelerators, the acceleration field can have a much larger
gradient than with conventional electrostatic or
radiofrequency accelerators (linear and circular, described
below). In conventional electronic accelerators, the intensity of
the accelerating field is limited by the
electrical strength of the insulators and the corona discharges
in the accelerator tube. This limited value of the accelerating
gradient requires a long accelerating tube to
obtain high energies. The field gradients in the plasma are 2-3
orders of magnitude stronger than in conventional radiofrequency
accelerators, leading to much shorter
acceleration path lengths.
Laser acceleration of protons
Experiments are also performed with laser acceleration of
protons. Direct laser acceleration of protons does not
work, heavy protons are not enough to respond to a rapidly
changing field in a plasma furrow. It is necessary to use a two-stage
method, schematically shown in the right part of the figure
:
1. Short high-power laser pulses
first accelerate electrons to high energies of
the order of GeV using the LWFA method.
2. These high-energy electrons then pass through
a proton-electron accelerating tube, into which protons
are injected simultaneously (synchronously), pre- accelerated in a small accelerator to an energy
of about MeV (this is for better synchronization
and more efficient energy transfer between electrons and protons).
Attractive Coulomb forces act between groups of electrons and
protons, which slows down the electrons and accelerates the
protons (picture on the right). High-energy
electrons thus transfer energy to protons with their
electromagnetic field, "drag" them behind them and accelerate
protons to energies of the order of 100 MeV. At the
outlet of the tube, the electron and proton beams are then
separated by means of an electromagnet.
If this technology can be
brought into practical use, large cyclotrons and the complex
distribution of protons to irradiation facilities in proton
therapy (§3.6 "Radiotherapy",
part "Hadron radiotherapy") would be replaced by small compact
laser accelerators, which could be easily mounted in the gantry
of individual irradiation devices in existing radiotherapy rooms
...
Combining
multiple accelerators
For some special experimental and technical applications, two or
more linear or circular accelerators are combined
into one larger system. This is mainly to obtain very
high energies of particles, which are first
pre-accelerated in smaller accelerators and then injected into a
large accelerator for final acceleration (see "Large
accelerators" below). Some newly
developed systems for proton radiotherapy (§3.6 "Radiotherapy", part "Hadron
radiotherapy") they combine pre-acceleration of protons in a smaller
cyclotron with definitive acceleration in a linear accelerator
for better electronic regulation of proton energies to target the
Bragg maximum depth dose to the tumor area.
The
primary and secondary radiation from accelerators
Accelerated charged particles form so called primary beam
, which can be used in two ways :
¨ Direct use of the primary beam ,
which after incidence at the appropriate target
(or in interaction of opposite bundles - collider) evokes the
required interaction for the study elementary
particles, production radionuclides, radiotherapy or for another
radiation analytical or technological process. The target here
can be irradiated technological material, or even the patient's
body - tumor tissue ("Radiotherapy").
¨ The use of
secondary radiation ,
which arises from impact and interaction primary
accelerated particles with a target. The type
and properties of this secondary radiation depend mainly on the
type and energy of the primary particles and also on the material
and design of the target. For accelerated electrons, it
is mainly braking radiation (bremsstrahlung) g
(continuous spectrum similar to X-rays, but significantly higher
energy). Accelerated protons, when interacting with
target nuclei, can provide secondary neutrons, p- and
K-mesons, antiprotons, hyperons,
etc., depending on energy. Secondary radiation can be emitted in
so-called secondary beams for own use. In the medical
field, the most common use of braking g-radiation from an electron
accelerator in radiotherapy (see §3.6 "Radiotherapy", in the stage of experiments is the therapy of p--mesons or antiprotons).
The beam of high-energy particles, whether
primary or secondary, can be used for the respective interactions
either inside the accelerator where it is formed
(an internal target is installed), or it can be directed
and led out of the accelerator by means of
suitable electromagnetic fields. Using vacuum transport tubes, it
is then led to the laboratory space, to interact with the atoms
and nuclei of the outer target (see
also the "Target" passage below).
We will mention here three specific ways of using secondary
radiation produced by accelerators, which have practical use also
outside of nuclear physics :
Accelerators
as generators of braking g- radiation
If the accelerated particles are electrons, then
when they hit a target made of heavy material,
most often tungsten, braking electromagnetic radiation
with a continuous spectrum is generated. Its maximum energy is
almost equal to the kinetic energy of accelerated incident
electrons. This is a very common way of producing hard photon
radiation for use in nuclear physics, analytical methods (§3.4
" Radiation analytical methods of
materials") and especially in
radiotherapy (§3.6" Radiotherapy "). As electron accelerators previously used to be
a betatron, now mostly a linear accelerator (both
methods are described below, see also §3.6, section "Isocentric
radiotherapy", Fig.3.6.1).
Accelerators as neutron generators
Accelerators in a special arrangement can serve as electronic
sources of neutron radiation - so-called neutron
generators. Neutrons are formed or released in a number
of particle and nuclear reactions. From the point of view of easy
and efficient production of neutrons, the reactions of tritium
and deuterium nuclei are the most advantageous. It is enough to
accelerate the deuterons to an energy of about 100-200 keV and
let them fall on a target containing tritium to cause a nuclear
reaction 2D1 + 3T1 ® 1n0 + 4He2 (+17.6 MeV), at which
they release neutrons. A fairly small
"table" linear accelerator is enough for this. The
analogous reaction D + D ® 1n0 + 3He (+3.3 MeV) is less
advantageous because it has a lower effective cross section and
deuterons must be accelerated to a higher energy, about 1MeV. The
basic arrangement of such a neutron generator
consists of three main parts: an ion source, an acceleration and
focusing system, and a target. Diluted deuterium is filled into
the ion source, which is ionized by an electric discharge.
Ionized deuterium atoms - deuterons - are fed from this
plasma by an electric field between the electrodes of the
acceleration and focusing system. A tritium target is bombarded
with an accelerated beam of deuterons; tritium is bound in the
form of a hydride in a thin surface layer of the
absorber, most often titanium, zirconium or scandium, the base
material of the target is cooled, for high performances a
disc-shaped rotating target is used (the
beam then hits each of its places only for a very short time,
during which the exposed place does not overheat and the heat is
enough to dissipate - similarly to X-ray with a rotating anode). The nuclear reaction of deuterium with tritium is
exothermic and almost monoenergetic neutrons with an energy of
about 14 MeV *) fly out of it (they fly out of the target
practically isotropically to the whole spatial angle). With a
deuteron energy of 200 keV and a beam intensity of 1 mA, a yield of about
2.106
neutrons/second is achieved. In an effort to achieve high neutron
yields higher than about 2.1011 n/s., the tritium target is rapidly depleted.
Therefore, special closed acceleration systems were developed -
so-called neutron tubes, filled with a diluted
mixture of deuterium D and tritium T (regulated replenishment, with helium removal). Both of these types of ions, D+T generated by the
discharge in the ion source, are simultaneously accelerated and
bombarded with a target in the surface layer of which the same
concentration of D and T atoms stabilizes; the
required reaction then occurs in the impact of accelerated D
on T in the target, even in the impact of accelerated T
on target D. Recently, miniature neutron
generators have also been designed (laboratory,
"desktop"), using high frequency D and T
ion acceleration. The schematic drawing of the principle of
neutron generators will be supplemented ... (for now see the
indicative illustration at the end of §4.3, section
"Neutron- stimulated emission computed tomography NSECT").
*) The direct use of these high-energy neutrons is
suitable for neutron-stimulated nuclear
gamma-spectrometric analysis. For neutron
activation analysis, it is necessary to slow down these
neutrons in a moderator.
Neutron radiation finds application
in neutron activation analysis (§3.4, part
"Neutron
activation analysis"), in some radiation
technologies, is also tested in radiotherapy
(§3.6, part "Hadron
radiotherapy").
Accelerators as synchrotron
radiation generators
A very special way of using secondary radiation from the
accelerator is to use synchrotron radiation *).
It is electromagnetic radiation that is emitted by a charged
particle as it moves along a curved path. In terms of the
function of circular accelerators, it is a "parasitic"
and unfavorable phenomenon that "consumes" the kinetic
energy of the accelerated particles and prevents high energies,
especially electrons. However, the UV and X-ray components of
synchrotron radiation can be used in some applications in
materials analysis as well as in biology and medical diagnostics.
Therefore, special accelerators for synchrotron radiation
production are constructed, as briefly described below.
*) This name originated from the fact that
this radiation (in the visible part of the spectrum) was first
observed in 1947 at the GE synchrotron in New
York while accelerating electrons in a circular orbit. Intense
synchrotron radiation arises in universe during
the rapid movement of electrons in a strong magnetic field around
compact objects, especially neutron stars, which
are observed as pulsars - in more detail §4.2.
"Final phases of stellar evolution. Gravitational
collapse", part
"Pulsars", Fig.4.3, books "Gravity, black holes
and space - time physics". Here, however, we will deal with
the artificial production of synchrotron radiation on
accelerators.
Particle with rest mass mo and charge e,
moving with kinetic energy E along a path with radius of
curvature R, according to the laws of electrodynamics (see §1.5 "Electromagnetic
field. Maxwell's equations."
monograph "Gravity, black holes and space-time physics"; follows from Larmor's formula (1.61 ') ) emits the electromagnetic waves of
power P = (2/3).(e2.c/R2).[E/moc2]4. It can be seen from
this relationship, that radiation is relevant only for light
charged particles, electrons or positrons moving with
high energy, ie with a relativistic velocity, along a strongly
curved orbit. At slow motion (non-relativistic velocity), the
orbiting particle appears as an oscillating electric dipole,
emitting weak monochromatic radiation with a frequency given by
the period of circulation (similar to a transmitting antenna), in
practically all directions (with the
radiation diagram according to Fig.1.4 of said reference). However, as a particle moves at a relativistic
velocity, electromagnetic radiation is emitted in a narrow
cone whose axis is tangent to the orbit of the particle at a
given point. The opening angle of this cone is approximately
equal to mo.c2/E. The external
observer will see the radiation only during the time when this
cone intersects its position ("beacon effect"). As the
particle moves in a circular orbit, the fixed observer or
detector will register radiation pulses whose
frequency is given by the particle's orbital period T = L/c,
where L is the length of the orbit. The spectrum of the
synchrotron radiation S itself consists of a number of
harmonic components, which are so "blurred" due to the
continuous motion in orbit that the resulting spectrum appears continuous,
with a maximum energy around ESmax
[keV] » 2400.Ee3
[GeV] /R [m] » 0,6.B[T] .Ee2
[GeV] (motion of an electron with kinetic
energy Ee
along a path with a radius of curvature R , under the
influence of a magnetic field of intensity-induction B).
In the region of energies higher than ESmax
, the spectral intensity of radiation
decreases rapidly.
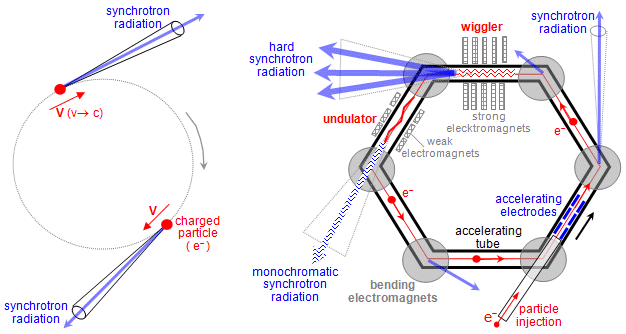
Experiments with synchrotron radiation have previously been
performed on synchrotrons designed to accelerate electrons ("parasitic" use).
Later, however, special single-purpose accelerators were
constructed, optimized for the production of
synchrotron radiation (2nd generation). They do not contain any
target, nor are any particles emitted from them. The electrons
are accelerated in the accumulation ring -
an evacuated polygon-shaped tube, in the rounded tops of which bending
magnets are placed. Electrons are injected into one of the
straight sections, while in the other there are accelerating
electrodes (high frequency resonator). The particles are
supplied with only as much energy as is electromagnetically
radiated, so that electrons can circulate in the tube for a long
time (electrons that fall out of
circulation due to collision with residual gas atoms in the tube
are replenished from the injector).
Synchrotron radiation is taken from curved paths in diffraction
peaks. For some types (3rd generation), special magnetic
devices are inserted into the beam path in straight sections of
the tube, consisting of a series of magnets with periodic
alternation of the direction. Their task is to wave the path of
electrons horizontally or vertically. They are called undulator
("crimping") with a weaker field, and wiglers
(Wiggle - flutter, tremble) a strong magnetic field (approximately 10T). In the
undulator, the electron path is wavy only weakly, which leads to
the emission of a harmonically modulated signal, an almost
monochromatic wave, the wavelength of which is given by the
so-called undulator equation : l = [lU/2(1-v2/c2) ]. (l + K2/2) with undulator parameter K =
e.Bo.lU/2pme.c.
In these equations, lU is undulator period
(spatial distance opposite polarity electromagnets undulator), e
is the electron charge and me its rest mass, Bo the maximum value of the magnetic field, c speed
of light. By changing the energy (velocity) of the electrons or
the intensity of the magnetic field, it is therefore possible to
change the wavelength of the output radiation in a wide range. In
the strong magnets of a wigler, the electron paths curve sharply
periodically, which leads to intense radiation of synchrotron
radiation of shorter wavelengths.
To produce synchrotron radiation are
starting to use also a linear electron accelerator
(4th generation sources), whose densified cloud (bunch)
when traversing the long undulator interacts with the
electromagnetic wave excited, by himself created. Electrons are
therein slightly accelerated or slowed down (depending on whether
they are in phase or antiphase) by so-called ponderomotive
force, which is formed inside the electron clouds of
redistribution of electron density with fine longitudinal
structure of the spatial period corresponding approximately to
the wavelength of the radiation - the so arises mikrobunching.
In this regular "micro-cloud" structure,
synchronization and coherent composition of electromagnetic
radiation from individual micro-clusters of electrons can be
achieved. If the electrons emit synchronously with the same
phase, the output radiation reaches many times higher intensity
and a considerable degree of coherence. This spontaneous
"self-amplification" of radiation from the periodically
"self" -modulated electron cloud in the undulator is
analogous to the formation of radiation in lasers - it is a kind
of "laser" with free electrons
(FEL - Free Electron Laser). The electrons leaving the
undulator are deflected by means of a magnetic field and led away
(to the absorber or for possible further use) so as not to
contaminate the photon radiation output beam. FEE systems are
currently being experimentally tested on large linear electron
accelerators (the highest electron energy
used so far was 14 GeV at the SLAC accelerator in Stanford, where
the undulator length was 112 m with 33 segments with a magnetic
field of 1.25 T; output coherent X-rays reached 8.25 keV and a
fluence of 1012 photons in a 0.07 ps pulse).
With the energies of accelerated electrons
Ee » 2-10 GeV, it is thus
possible to obtain a wide range of wavelengths even in the X-ray
region. The main advantage of these specialized sources
of synchrotron radiation, also sometimes referred to as "photon
factories", is the high intensity of
radiation, its narrow angular collimation, pulsed character, good
definability, stability and adjustable parameters.
Basic
parts of accelerators
Before we deal with individual types of accelerators, we will
mention four basic components that all accelerators have :
¨ The source
of accelerated particles (ion source)
emits the required type of particles, such as electrons, protons
or heavier ions, to the "starting" point of the
acceleration system. In the simplest case, it is an ionization
tube containing the appropriate dilute gas (eg hydrogen
H), where ions are formed (for hydrogen they are protons
p+) in a
smoldering discharge between the cathode and the anode (at a
voltage of about hundreds volts to tens of kV) and they are
guided by a thin capillary through a "suction"
electrode into the acceleration system. To obtain heavier
nuclei (ions), a discharge in dilute gas (containing the
relevant element) is used at a sufficiently high voltage to cause
ionization even on the K shell. This produces ions with
different degrees of ionization, from which the required nuclei
(ions with the highest degree of ionization) need to be separated
by means of an electric and magnetic field and introduced into
the acceleration system.
For electron
accelerators, the source is a simple heated cathode
(electron thermoemission) equipped with suitable accelerating and
focusing anodes - an "electron gun" - similar to a
screen. Event. the cathode can be provided with a grid
for electronic regulation of the electron flow.
Recently, laser sources
have also been developed, in which the emission of particles is
generated by a high concentration of energy from short and very
intense laser pulses impinging on a suitable target. This creates
primary clouds (bunch) of particles,
electrons or ions, which are then accelerated in a pulsed
high-frequency mode in accelerators or in a laser "furrow
wave" (the above-mentioned "Laser
Plasma Accelerators LWFA").
It is more difficult to obtain antiparticles
for acceleration. Positrons are obtained by
bombarding a target made of a material with a high proton number Z
(eg tungsten) with accelerated electrons, while the
electromagnetic interaction in the field of nuclei produces,
among other things, positrons e+. Similarly, antiprotons p' must be
obtained by bombarding a suitable target with protons accelerated
to energies higher than 3 GeV, where the reactions p + p ® 2p + p + p'
occur, among other things.
In large high-energy accelerators, injectors
are sometimes used as a source of particles for acceleration -
"pre-accelerated" particles are injected into the main
chamber by an auxiliary linear or circular accelerator (with
energy unit up to tens of MeV or GeV) and then accelerated to the
required high energy (GeV or TeV).
¨ Acceleration
chamber, tube
The space in which particles move and accelerate has different
shapes and sizes, depending on the type of accelerator. It can be
a narrower or wider, shorter or longer tube linear or
circular shape, flat cylindrical chamber. There must be a high
vacuum to prevent disturbing collisions of particles
with the gas atoms.
¨ Acceleration electrodes,
electromagnetic field
An acceleration system of electrodes or wave
resonators is located in the evacuated acceleration chamber or
tube, where an accelerating force is created by
the synchronized action of the electromagnetic field on the
passing charged particles. The accelerator system is powered by a
power supply - see the
section "Electrical supply of accelerators" below.
¨ The target ,
on which the beam of accelerated particles falls, is either internal
- is located inside the accelerator system, or external
- the particle beam is led out of the accelerator tube. Further,
the target may be material (usually solid), or
may be replaced by an interaction region, where
the particles collide in the colliding beams (see "Colliding beams" below). Also, secondary
particles produced on the inner target (such as p or K mesons) are
by to magnetic and electric fields sometimes they exported in the
form of a beam into the laboratory space, where measuring
apparatus (detection devices, bubble chambers, trackers, etc.)
are located. When accelerated particles hit an (solid) target,
most of the kinetic energy of the particles changes to heat - the
bombarded target heats up. In order to prevent
its thermal damage or evaporation of the target substance, it is
necessary to dissipate this heat loss (it
can be hundreds of watts) - the target is
fixed on a solid metal base with a cavity cooled
by flowing water (similar to anodes of
power X-ray tubes). Neither the target nor
the interaction region have the special accelerators for
synchrotron radiation production mentioned above.
A target, or generally a
place where accelerated particle interactions occur, is usually
equipped with a secondary particle detectors. In
simpler cases, it is used to monitor emerging
nuclear reactions. In large accelerators for the study of
particle interactions, it often consists of a whole complex detection
system, enabling a detailed analysis of paths, charge,
energies, momentums and other characteristics of secondary
particles arising from high - energy interactions - see §2.1,
section "Arrangement and configuration of radiation
detectors".
Colliding beams - colliders
When an accelerated particle hits a (fixed, immobile) target and
collides there with another particle or nucleus, only a small
part of the kinetic energy of the incident particle is actually
consumed for its own interaction, because according to the law of
action and reaction, part of the energy of the incident particle
is converted into kinetic energy of the reflected particle and
newly formed particles. The kinetic energy in the center
of gravity system (CMS) of both particles is important
for the result of the interaction - only this is actually
"consumed" for its own interaction *). A significant
increase in the effective energy of the interaction can be
achieved, by the incoming and target particles moving against
each other with comparably high kinetic energies (or
momentums). Both such particles then practically stop during the
collision and almost all of their kinetic energy can be used for
their own interaction and the formation of new particles. This is
the method of colliding beams without the use of
a classical target: the two particles whose interactions we want
to investigate, are accelerated to high energies and in opposite
beams they are directed against each other, so that they collide
head-on and interact of each other. Both beams are
accelerated either in one tube (eg electron-positron beams) or in
two different tubes. At a given location of the acceleration
ring, the two beams of accelerated particles, flying in opposite
directions to each other, are focused by the action of a magnetic
field and guided so as to collide head-on. Devices of this kind
are called colliders and make it possible to
study the interactions of particles at significantly higher
effective energies than in the case of classical accelerators
with fixed targets - currently up to TeV is achieved. The site
where the opposing beam interactions occur, the interaction
region, is surrounded by a complex detection system (as mentioned above, see also the "Large
Accelerators, LHC"
section) for a detailed study of secondary
particles. Colliders are used only for exploratory research
of particle interactions at very high energies, with the
formation of new "exotic" particles.
*) The relationship between the
energy of the interaction in the laboratory and the center of
gravity reference system is given by the dynamic analysis of the
collision using the law of conservation of energy and momentum.
When a particle of rest mass mo, moving with the kinetic energy E, hits the same
particle at rest, the effective energy of the interaction Eef = E1/2 (mo.c2)1/2. If, for example, a proton with a kinetic energy of 400
GeV collides with a target proton at rest, only the energy of 28
GeV remains for the interaction production of new particles. With
increasing energy, the energy efficiency of the interaction
decreases sharply. E.g. to achieve an effective energy Eef = 6TeV, we would
have to irradiate protons with a kinetic energy of about 2.104 TeV with a fixed
target (which, even with the use of powerful electromagnets with
B = 7T, would require a circular proton accelerator with a
circumference of about 105 km - larger than the Earth's circumference!). However,
in the case of a collision of the same particles, which move
against each other with the same kinetic energy E, the whole
energy Eef
= 2.E is available for the interaction - it is therefore the only
practically usable way to achieve very high effective energies of
interactions.
In order for the collisions to be
sufficiently frequent, it is necessary to ensure a very high
intensity of both beams (luminosity). Therefore, special
accumulator rings are used on some accelerators,
in which accelerated particles (eg protons and antiprotons)
accumulate from several doses in a strong magnetic field, and
only after reaching sufficient intensity does a collision take
place in the opposing beams.
Linear
accelerators
Linear accelerators accelerate charged particles by
applying an electric field during they linear movement
along a straight path. A linear accelerator is often
abbreviated Linac (Linear accelerator
). We can divide them into electrostatic (high
voltage) and high frequency.

Fig.1.5.5. Simplified scheme
of linear accelerator electrostatic (left) and high frequency
(right).
The basic scheme of the electrostatic
linear accelerator is on the left in Fig.1.5.5. From the ion
source, the required particles (electrons, protons, deuterons,
etc.) enter to the acceleration system, formed by several coaxial
metal cylindrical electrodes V1, V2, ..., Vn, between which a gradually
increasing high voltage is distributed U1, U2, U3, ...., Un . Through an electrostatic field, charged particles
with charge q in a linear path are accelerated to energy E = q.
(U1 + U2 + U3 + ... + Un)
given by the sum of the voltages at the individual electrodes.
The gap between two successive cylindrical electrodes acts on the
flying particles like an "electric lens" (similar to a screen), focusing a
stream of particles into a narrow beam that ultimatelly hits the
target. The accelerating electrodes are supplied with high
voltage either from an electronic cascade multiplier (a
system of suitably connected diodes and capacitors) or from an
electrostatic-mechanical Van de Graff generator.
Voltages from a few hundred kilovolts up to about 5 MV are used;
higher voltages are difficult to achieve for the formation of
corona and spark discharges *).
*) These problems with electric
shocks they are formed in material environments - in
air, dielectrics, insulators. For interest, we can have a small
discussion, how is it in a vacuum? :
What is the strongest
electric field can be ?
In classical (non-quantum) physics, the electric field in a
vacuum can be arbitrarily strong, almost to infinity (in the material environment, however, this is limited
by the electrical strength of the dielectric). From the point of view of quantum electrodynamics,
however, even in a vacuum there is a fundamental limitation
caused by the existence of mutual antiparticles
of electron and positron: it is not possible to create an
electric field with intensity stronger than Ee-e+ = me2 c3/e.h = 1.32 . 1016 V/cm, where me is the rest mass of
the electron or positron. When this intensity is exceeded, the
potential gradient is higher than the threshold energy 2me.c2 and a pair of
electrons and positrons is formed, which automatically
reduces the intensity of the electric field. Such a strong
electric field has not yet been created, with conventional
electronics this is not possible; one possibility in the future
could be strong pulses from extremely powerful lasers...
A more efficient way
to accelerate charged particles to a very high energy in a linear
path without the use of extremely high voltage is realized in
high-frequency linear accelerator, the simplest diagram
of which is shown in Fig.1.5.5 on the right. Charged particles
from the ion source Z enter the acceleration system of
cylindrical electrodes V1, V2, V3, ... ,Vn , which are connected to an alternating voltage
U(t) = Uo.cos(w.t) = Uo.cos(2pf.t) with amplitude Uo and frequency f. Odd
cylinders are connected to one pole, even cylinders to the other
pole of a high-frequency high-voltage source. If a positive
particle arrives with charge q and mass m from the source Z
in the phase when the first cylindrical electrode V1 has a negative potential -Uo, then it obtains the energy E1 = q.Uo and the velocity v1 = Ö(2q.Uo /m),
so that the length l1 inside
the cylinder V1 flies
through time t1 = l1/v1. If the frequency f of the AC voltage is chosen
so that the accelerated particle enters the gap between cylinders
V1 and V2 at the time when the polarity reverses and cylinder V1
has a positive and V2 negative potential, the particle is again
accelerated by energy q.Uo, ie it already has energy 2.q.Uo. If the synchronization between the
frequency f, the voltage Uo and the electrode lengths lk
*) is chosen so that the polarity of the
alternating voltage is always reversed during the passage between
the individual cylindrical electrodes Vk, these "synchronous" particles will reappear
as they pass through each electrode and again and again
accelerate.
*) As can be seen from Fig.1.5.5 on the right, to achieve
synchronization, the length of the cylindrical electrodes Vk must gradually increase as the
particle velocity increases. This is no longer the case when a
speed close to the speed of light is reached, when the speed of
the particle practically does not increase during acceleration;
with kinetic energy only the relativistic mass of the
particle increases.
It is also worth noting that the actual
electrical acceleration of the particle occurs in the gaps
between the electrodes, while inside the metal cylinder, where
the electric field gradient is close to zero (electric field is
shielded), particles fly through inertia (this also applies to
the electrostatic accelerator on the left side of the figure).
The
development of these accelerators proceeded by increasing
the frequency f, using cavity resonators
instead of cylindrical electrodes. Newer linear accelerators use
a waveguide to create an accelerating field,
divided by suitable disk protrusions into a series of resonant
cavities and fed at a frequency of several GHz (most often around
3 GHz) from a klystron or magnetron generator
(briefly described below). A high-frequency alternating
electromagnetic field is generated in the waveguide in the form
of a gradual or standing electromagnetic wave.
If the accelerated charged particle moves in synchronism
in the field of this carrier wave, a constant
accelerating force given by the electrical component E of
the electromagnetic wave acts on the particle. Particles for
acceleration are injected into the acceleration system of cavity
resonators or waveguides from an ion source, or electron nozzles
in the case of electrons, in the form of "clusters" (bunch)
in pulse mode, in precise electronic
synchronization *) with an accelerating high frequency field.
*) In order for a constant accelerating
electric force to act on a particle in a high-frequency field, it
must enter the waveguide acceleration system in a suitable phase
and at a speed close to the phase velocity of the wave - the synchronization
condition must be met. The pulse mode of the ion source
(or electron nozzle) and the high-frequency generator is
controlled by an electronic circuit equipped with special power
switching components - it is either a special thyratron
tube or a semiconductor thyristor. The accelerating
waveguide system consists of several specially shaped metal
(copper) resonant cavities, lined up in a row.
Electrons are injected in pulse doses into the acceleration
system from an electron nozzle ("cannon") with an
energy of about 30-50 keV, protons from an ion source with
significantly higher energy. The resonant cavities at the
beginning of the acceleration system have a shorter length and
distances from each other, the others lengthen so that the phase
velocity of the electric field coincides with the increasing
velocity of the particle. The whole system is a bit similar to
Fig.1.5.5 on the right, but instead of cylindrical electrodes
there are a number of resonant cavities and instead of conductors
supplying alternating voltage, a waveguide from a magnetron or
klystron leads to the initial part of the tube.
Small linear
electron accelerators (Linac) are now very often used in
radiotherapy - see §3.6 "Radiotherapy"
(where they gradually pushed out previously used betatrons),
mainly as a source of hard braking radiation (bremsstrahlung) gamma
with energies of about 6-18 MeV. Large high-frequency linear
accelerators with a carrier wave are used for energies up to tens
of GeV, they are also designed for several TeV. They are either
used as separate basic devices, or they can be used to
pre-accelerate particles - as injectors for large
synchrotrons (see below, Fig.1.5.6 top
right). Unlike circular accelerators, where
particles are repeatedly accelerated many times by one
acceleration system, in a linear accelerator there is a gradual
acceleration in many acceleration systems arranged in a straight
line. Even when using high gradients (up to 100 MV/m) and high
frequencies (up to 30 GHz) to achieve high energies (up to TeV),
the length of the largest linear accelerators is several
kilometers!
Circular
accelerators (cyclic)
A very effective way to accelerate charged particles to high
energies is to accelerate them many
times in an electric field, into which the particles are
repeatedly returned in a circular path
by the action of a magnetic field *). On a
particle with charge q is applied not only electrical
accelerating force Fe = q.E, but also the Lorentz force Fm = q.[v x B], acting in a
magnetic field of intensity B perpendicular to
the direction of motion of the charged particle at velocity v.
This magnetic force causes the charged particle to move in a circular
path with radius R = m.v.c/(q.B). If an electric
accelerating field (in the tangential direction) is applied
synchronously at suitable places in this circular path, the
particles will be periodically accelerated
during each its orbit.
*) This magnetic field is generated by electromagnets
- coils whose winding pass a strong electric current. Recently, superconducting
electromagnets have often been used, which significantly reduces
the consumption of electrical energy (the physical principles of
superconductivity are briefly discussed above in the section
"Fermions as bosons;
Superconductivity").
Cyclotron
The basic type of circular accelerator is a cyclotron (the first small cyclotron was constructed by
E.O.Lawrenc as early as 1932), the
principle of which is schematically shown in the left part of
Fig.1.5.6 :
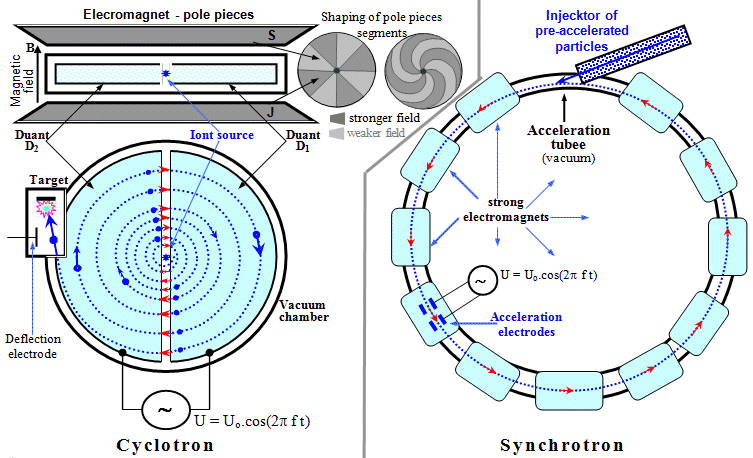
Fig.1.5.6. Left: Schematic
representation of a cyclotron. Right:
Schematic representation of a synchrotron.
Between the poles of a strong electromagnet, in
a flat circular vacuum chamber, two hollow metal half-cylinders
in the shape of the letter D, so-called duants of radius R,
are mounted, between which there is an acceleration gap.
The duants are made of a conductive non-ferromagnetic material
such as copper or brass. Duants D1 and D2 are connected to an AC voltage source U
= Uo.cos
(2p f.t)
with frequency f (depends on the
strength of the magnetic field and the mass of accelerated
particles - protons, deuterons or heavier nuclei; usually around
20MHz), so there is an alternating electric
field in the gap between the duants. The charged particles enter
the center of the acceleration gap from the ion source "]". As a result of the force exerted by the electric
field in the gap on a particle with charge q and mass m
, the particle is drawn into one of the duants (which has just
the opposite polarity) with a certain velocity v1. Inside the duant,
where the electric field is shielded, by the action of a strong
magnetic field B the particles describe a semicircle with
radius r1
= m.v1 /
(q.B) (this radius is given by the balance
between centrifugal force and Lorentz magnetic force: m.v12 / r1 = q.B.v1) . The time taken for a particle to pass through this
semicircle is T = p.r1/v1 = p.m/(q.B) - we see
that this time (half-period) of a particle's orbit does not
depend on its velocity v1 or its radius of travel r1 ; the frequency of the circular circulation of the
particle is thus f = q.B / (2p
m) and is constant *),
because m , q and B are constants in a given
arrangement. If the duants are supplied with alternating voltage
at this frequency f (the condition of resonance
or synchronization is met), then at the moment
when the particle describes the semicircle in the first duant and
finds itself again in the acceleration gap, the polarity of the
duants is already opposite and the particle will be accelerated
again by the electric field, so that it flies into the second
duant at a higher velocity v2 > v1 . In the second
duant, it will move again in a circle, but now with a radius r2 = m.v2 /(q.B), which is
larger than r1 , but with the same period and frequency of circular
motion. In the same way, the particle is then accelerated
again and again each time it passes
through the gap between the duants , moving in circles
with an increasing radius r , i.e. in a spiral (Fig.1.5.6
left). From the last path of its maximum radius (close to the radius of the duants R), the accelerated particle is deflected
electrostatically or magnetically and led into
the space of the target, which it encounters and
causes the appropriate nuclear processes there.
*) It is a so-called isochronous
cyclotron (Greek isos = same, chronos = time )
- uniform in time, regular, with a constant frequency.
The technical solution for maintaining the isochronous function
of the cyclotron even for the high - relativistic -
energies of accelerated particles will be outlined below in the
section "Isochronous cyclotron -
relivistic".
Movement and
acceleration of particles in a cyclotron
To clarify the laws of
cyclotron acceleration, we will analyze the motion of a particle
with charge q and mass m in the magnetic field of
intensity (induction) B in a cyclotron of radius R,
to whose duants an alternating voltage of amplitude Uo and frequency f
is applied. When a particle moves at velocity v in the
direction perpendicular to the magnetic field, it will be acted
upon by the Lorentz force F = q.B.v in the
direction perpendicular to the magnetic induction vector B
and the velocity v. Its path is thus curved into
a circle, creating a centrifugal force.
The motion of the particle will then be given by the equilibrium
between magnetic and centrifugal force: q.B.v = m.v2/r. The radius
r of the circle along which a particle moves,
that is r = m.v/q.B. The period T
circulating particles along the circle is equal to the
circumference 2pr, divided by the velocity of the particles: T = 2pr/v = 2p.m/q.B. Particle
circulation period T therefore does not depend on its
velocity (nor energy). The time between the individual passages
of the particle through the acceleration gap between the duants
is thus still the same during the acceleration. In order for a
cyclotron to accelerate a particle each time it passes through
the acceleration gap between duants, the frequency 1/T with which
the particle orbits in the magnetic field must be equal to the
frequency f of AC voltage sources: f = q.B/2p.m .
The particle enters from the ion
source to the center r=0 of the cyclotron with almost zero
kinetic energy. Each time it passes through the gap between the
duants, it gains the kinetic energy DE k = q.Uo when accelerated by the voltage Uo
. When flipping between duants
n-times, it gains the kinetic energy Ek and velocity v: Ek = n.q.Uo = 1/2
m.v2,
=> v = Ö(2 Ek/m). It will move along a circle of radius r = m.v/q.B =
[Ö(2m
Ek)]/q.B.
Therefore, if we have a cyclotron of radius R with
magnetic field B , the maximum energy of accelerated
particles Emax = R2.q.B /2m, while the number of cycles between duants will
be n = Emax / Uo .q.
Practical example: A
cyclotron with a radius of 38 cm with a magnetic
field of 1.5 T will accelerate protons at a frequency of 22 MHz
to a maximum energy of 15 MeV. At a supply voltage (amplitude)
between duants 50 kV , the protons orbit approximately 300 times
before reaching maximum energy.
Note: The maximum energy of accelerated
particles (of a given species with charge q
and mass m ) in a cyclotron depends
only on the radius R and the magnitude of the magnetic
field B, not on the supply voltage of the duants. This
could give the impression that to accelerate even to high
energies, it might be enough to supply the duants with a low
voltage of about 10 V and the particles would gain the required
energy of tens of MeV after several million cycles.. This would
perhaps be possible for individual particles in principle.
However, when accelerating a beam of many particles,
mutual repulsive forces are manifested, scattering the beam,
fluctuations and turbulence - if the path is too long, most
particles would not reach the maximum radius at all, they would
end up on the walls of the duants. For efficient acceleration, it
is therefore desirable to use as high a voltage
(amplitude) of tens of kV as possible to power the cyclotron
duants, so that the number of cycles is max. several hundred.
Synchrocyclotron
- relativistic
The principle of cyclotron operation outlined above will work at
a constant frequency only until the mass of the accelerated
particle can be considered constant, ie only in the non-relativistic
region. If we want to use a cyclotron to accelerate
particles to higher energies, when the speed of the particles is
already comparable to the speed of light, the inertial mass of
the particle m ceases to be constant, but increases with
increasing speed: m = mo/Ö(1-v2/c2). At the same rate, the radius R = mo.v/[q.B.Ö(1-v2/c2)] increases
and the frequency decreases - at circulation of
particles in a constant magnetic field: f = [q.B/(pmo)].Ö(1-v2/c2). In order for the
particle to continue to be accelerated even in this relativistic
region, it is necessary to modulate the
frequency of the accelerating voltage so that it is
still in resonance with the frequency of the particle's
circulation; or amplify the magnetic field. A
cyclotron modified in this way with "synchronization"
is called a synchrocyclotron or a relativistic
cyclotron (the name "phasotron"
also appears in the older literature).
These devices work in pulse mode, where the
frequency of the accelerating voltage on the duants is modulated
and changes about 50 times per second, from about 25 MHz at the
beginning of the cycle to about 12 MHz at the end of the cycle (depending on the strength of the magnetic field and the
mass of the accelerated particles).
Synchrocyclotrons are used to accelerate protons to energies up
to about 1 GeV.
Isochronous
cyclotron -
relativistic
An alternative to the synchrocyclotron is the so-called isochronous
cyclotron, which operates at a constant
frequency and time-constant magnetic field, but the
intensity of the magnetic field increases with radius;
this is achieved by special shaping solenoid
pole pieces *). This leads to greater curvature of the more
distant path of the accelerated particle, compensation
of the higher inertial mass of the particle and maintenance of
the cyclotron resonance at a constant frequency (and without the need for time modulation of the
magnetic field strength). Isochronous
cyclotrons are used for proton energies up to about 500 MeV,
while in the continuous mode they are able to
produce a significantly higher flux of
accelerated particles than synchrocyclotrons in the pulse mode.
*) However, this radial gradient of the
magnetic field has a diverging effect on the orbiting particle
beam in the transverse direction. This must be compensated by
so-called magnetic focusing: the pole pieces of
the electromagnet are divided into several segments
(mostly 8, is schematically shown in
Fig.1.5.6 above) in which the magnetic
gradients of stronger and weaker fields alternate in the
azimuthal direction (modeled protrusions -
segments - on the surface of the attachments), which have a focusing effect on the
beam of moving particles. For better focusing, the segments of
the pole pieces are often used they shape in spiral (Fig.1.5.6
above). The isochronous cyclotron is
therefore also sometimes called the AVF (Azimutal
Varying Field) cyclotron.
Acceleration of
negative ions
In a cyclotron, heavy positively charged particles
are accelerate as standard - protons, deuterons, alpha particles,
or heavier nuclei such as carbon 12C. In special applications, however, an interesting
modification is used to increase the "effective power"
of the cyclotron: the acceleration of negative ions.
Hydrogen or deuterium atoms are supplied with two electrons in an
ion source in an electric discharge, creating negative H- or D-
hydrogen
ions with two electrons. These are then accelerated in the
cyclotron. The technology of accelerating negative ions in the
cyclotron brings two advantages :
-> Possibility to produce more external radiation
beams with different energies
A thin film is inserted into the path of
accelerated negative ions in the appropriate path, which "strippes",
removes their two electrons - the desired p+ or d+ are created . This reverses the
direction of their curvature in the magnetic field, which causes
them to be rapidly brought out of the cyclotron
field into the external beam of the corresponding energy. This
technique thus allows the simultaneous production of several
external beams of different energies, which can be used
independently.
-> Possibility to increase the fluency power of
the external beam from the cyclotron
For small cyclotrons used for the production of
radioisotopes (§1.4, passage
"Production of artificial radioisotopes") is an important
requirement of high intensity - fluent power -
proton or deuteron beams. At energies around 40MeV thrive achieve
a relatively high current in the inner beam of about 2-5 mA. This
maximum output can be used fully only during the irradiation
of the internal target which is
installed inside the vacuum beam tube. For routine production of
radionuclides is however most advantegous bring out the
particle beam to irradiate the outer targets. In
conventional cyclotrons accelerating positive particles resulting
beam extracted electrostatic deflector. At the baffle of
the deflector is generated a considerable dissipative heat,
which is a limiting factor for achieving a high fluency
performance of the extracted beam.
These disadvantages are largely
eliminated by negative ion acceleration
technology. After the necessary acceleration of the negative
ions, efficient proton extraction takes place by stripping H- in a
thin carbon foil, which retains both electrons and releases a
heavy positive hydrogen nucleus p+ or D+, with minimal thermal dissipation. This achieves
significantly higher performance of radionuclide
production in the outer target. This is especially important for
the production of larger activities of short-term radioisotopes
for scintigraphic diagnostics (§4.8 "Radionuclides and
radiopharmaceuticals for scintigraphy") and
biologically targeted radionuclide therapy (§3.6
"Radioisotope therapy") in nuclear medicine.
S y n c h r o t r o n
To accelerate particles to very high energies,
the radius of their orbits comes out too
large in the circular accelerator, so that the cyclotron
method with spiral motion of particles in a flat vacuum chamber
is no longer practically applicable. In order for the perfect
vacuum space not to be enormously large, as well as for
electromagnets, it is necessary to use circular accelerators with
a fixed circular path. In order for the charged
particle to accelerate and stay on a solid circular path with
radius R, it is necessary that with incresing velocity
v(t) of the accelerated particles, both the frequency
f(t) of the accelerating voltage and the intensity of the
magnetic field B(t) increase synchronously
with time. Magnetic field can no longer be constant, but is also
a function of time B(t). Such a synchronously operating
accelerator with a fixed circular path is called a synchrotron
(in the older literature there was also the
name "synchrophasotron", "bevatron",
"cosmotron").
A schematic picture of its principle
is in the right part of Fig.1.5.6. The particles are accelerated
in a vacuum tube with a diameter of about 3-8 cm (mostly of
elliptical cross-section), twisted into a circle with a diameter
of hundreds of meters to several kilometers (!). The tube is
surrounded by a large number of segments of dipole
electromagnets (for large instruments even more than
1000 segments), which excites the magnetic field keeping the
particles in a circular orbit. The synchrotron accelerates the already
pre-accelerated particles, which are injected into the
acceleration chamber from a suitable injector,
which is usually a linear or circular accelerator with an energy
of about 20-100 MeV *). Accelerated electrodes
supplied with alternating high voltage are placed together with
the magnets in suitable places of the circular path, the
frequency f of which is synchronously modulated so that
the particle comes between the electrodes at a time when the
polarity ensures further and further acceleration of the
particle. Simultaneously with the frequency, the intensity B
(for historical reasons called magnetic
induction ) of the magnetic field also increases.
* ) Multi-stage
pre-acceleration is also needed for large devices- first
a linear accelerator, then a smaller synchrotron, which injects
particles into the main accelerator (synchrotron); for the
highest energies even a cascade of several synchrotrons in a row
- see below "Large Accelerators", LHC.
The synchrotron operates in a pulsed
mode, where protons entering in the accelerator tube at
regular doses from the injector at energies of the order of 100
MeV perform several million circulation during an acceleration
cycle lasting about 3-5 seconds, accelerating to the
order of 100 GeV to several TeV; the magnetic field increases
from a tenth of Tesla to a few Tesla during the acceleration
cycle. The acceleration cycle is periodically repeated about 5-10
times per minute.
At the end of the acceleration
cycle, the particles fall on either the inner target,
or are led out by an electromagnetic field to
the outer target, or are fed to an accumulation
ring to realize particle interactions in the opposing
beams. When a beam of protons, for example, hits a
target, a number of particles of various kinds are formed, from
which we can "separate" particles of the desired
species with a system of electric and magnetic fields, focus them
into a beam and aim them at another target. We obtain secondary
bundles of eg antiprotons, pions, muons, kaons,
hyperons. Variable electric and magnetic fields are used to separate
particles, and magnetic lenses are used to focus
the beams, mostly in a quadrupole arrangement,
where two magnetic fields intersect, the gradients of which
gradually focus the beam in the vertical and horizontal
directions.
At large values of radius
R, which must reach several kilometers to achieve high
energies of the order of hundreds of GeV, it is necessary that
the cross-section of the accelerating tube is as small as
possible - in order to achieve the required high vacuum (< 10-6 mm Hg) and that the
costs of manufacturing electromagnets, as well as the demands on
their electrical input, are not enormously high. After being
injected into the accelerating tube, the particles make radial
and vertical oscillations around their basic circular path. In
addition, the particles in the beam tend to diverge in all
directions because they are consistently charged and therefore repel
each other. If the particles are not to impinge on the walls of
the tube, the accelerated particles must be kept in orbit with
high accuracy, so that the amplitude of the radial and vertical
oscillations must be kept as low as possible, as well as the
scattering of the particles. In other words, there is a need for strong
focusing, in which the cluster of injected particles
concentrates during acceleration and forms into an intense narrow
beam rapidly flying particles. This strong magnetic
focusing is realized so that the synchrotron electromagnet is
composed of a large number of suitably shaped segments
which have alternating positive and negative magnetic field
strength gradients. These magnetic field gradients act
alternately in the radial and vertical directions as continuous
and scattering magnetic lenses, which ultimately
lead to a double focusing of the beam in both
directions. With newer large accelerators, the solenoid coils are
often superconducting .
Large
synchrotrons are very expensive unique devices,
built in major world research centers in the field of nuclear
physics and elementary particles, mostly in broad international
cooperation (construction costs amount to
several billion dollars). The accelerator
itself is followed by very complicated and precise detection
apparatures and systems *), which analyze secondary
particles and radiation generated during ultrarelativistic
interactions of high-energy primary particles with the target
material or with each other in opposing beams. By analyzing the
type, charge and mass of these particles, their energies,
momentum and emission angles from the site of interaction, a
number of parameters of the interactions that occur can be
reconstructed. From this it is possible to deduce the structure
of elementary particles, the properties of acting fields and
interactions, the existence of new hitherto unknown quanta and
particles- see above "Analysis
of the dynamics of particle interactions". The issue of large
accelerators will be briefly discussed below - the section "Large
accelerators".
*) For the methodology of
radiation detection, see Chapter 2 "Detection
and spectrometry of radiation",
detection systems of high-energy particle interactions are
generally outlined in §2.1, section "Arrangement and configuration of radiation
detectors".
Betatron
A circular induction electron accelerator is called a betatron
(it produces "artificial b-
radiation", which are fast electrons, otherwise known from
beta radioactivity). The principle of the betatron is
schematically shown in Fig.1.5.7 on the left.
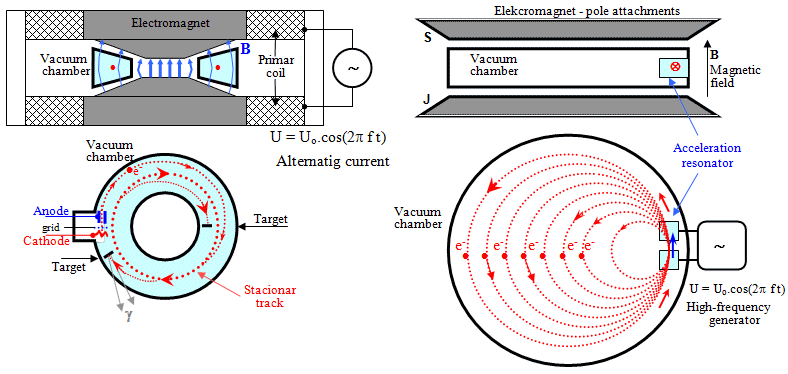
Fig.1.5.7. Left:
Schematic representation of the betatron. Right:
Schematic representation of a microtron.
The accelerating tube of the betatron has the
shape of a ring (toroid) made of electrically non-conductive
material (glass, porcelain) with a high vacuum inside. The tube
is located ("strung" as one thread) between the pole
pieces of the solenoid fed by alternating current.
Electrons are injected into the accelerating tube at an
appropriate time (the appropriate phase of the AC period) by an electron
nozzle consisting of a hot cathode, a
grid, and an accelerating and focusing anode - a similar
"electron gun" as a screen. The time-varying magnetic
field induces a swirling electric field
in the tube, the electromotive force of which,
directed along a circular path, accelerates
these electrons.
From an electronic point of view, a
betatron is actually a "transformer" whose primary
winding is supplied with alternating current and whose
"secondary winding" (of one "thread") is an
accelerating tube in which electrons, accelerated by induced
electromotive force, move in a vacuum (instead of winding wires).
In a circular orbit, electrons are maintained by a magnetic
field. The acceleration of electrons occurs only in the first
quarter sinusoidal course of alternating voltage in the
electromagnet. At the appropriate moment of the ascending part of
the sinusoid, electrons are injected, which are accelerated, the
magnetic field increases, the electrons spiral inwards and orbit
for some time along a stationary path in which they are
constantly accelerated. After reaching the peak of the
quarter-period, the vortex electric field weakens, reverses its
direction, and the electrons would eventually be inhibited. At
the same time, however, the magnetic field weakens and the
electrons begin to spiral along the outer edge of the tube, where
they hit the target or are brought out for external use.
Some types of betatrons have a radial magnetic field gradient and
an acceleration phase set so that the electrons move in a spiral
inward at the end of the acceleration cycle and the target is
located at the inner edge of the accelerator tube.
Electro-mechanical analysis of the trajectory
of an electron during acceleration induced by an electric field E
along a circular path of radius R (combining Faraday's law
of electromagnetic induction u = -dF/dt = 2p.R.c.E with an accelerating
electric force along a circular path q.E, perpendicular Lorentz
magnetic force q.[v x B] = q.v.B and centrifugal force m.v2/R) leads to the condition of equilibrium acceleration
of the electron in the path of radius R: 2pR2.B = F, or magnetic flux F through the surface p.R2
the paths of the electron must be twice the flux that would flow
through the path if there was a homogeneous magnetic field of
intensity B over the whole surface. This "betatron
condition" is ensured by a suitable shaping of the pole
pieces of the electromagnet.
The
electromagnet of smaller betatrons is often powered by
alternating current from a normal 220V electrical network with a
frequency of 50Hz, the power input is units up to tens of kW. The
radius of the circular path is tens of centimeters. During the
acceleration cycle, which lasts about 5 milliseconds, the
electrons perform about 2 million cycles, while the induced
electromotive force accelerates to about tens of MeV. Then they
hit either the inner target (while exciting the
gamma braking radiation), or they are brought out in a beam -
they are then used for electron irradiation, eg for technical or
medical purposes. Hard gamma braking radiation
has the same use.
Betatrons are used for electron
energies up to about 300 MeV. However, at high energies it is
necessary (similarly to the cyclotron) to perform synchronization
due to the increase in the mass of electrons with their energy.
By combining the betatron and synchrotron principles, a betasynchrotron
is formed which accelerates the electrons in a
circular orbit inside the vacuum ring first on the betatron
principle by means of alternating current electromagnets, after
which this pre-accelerated electrons are further accelerated
between the electrodes to which the synchronized frequency
high-frequency accelerating voltage is applied.
Smaller betatrons were widely used
in radiotherapy in the 1970s-1990s (see §3.6 "Radiotherapy"), mainly as a source of
hard braking gamma radiation with energies up to about 40MeV. In
recent years, however, betatrons have been virtually displaced by
linear electron accelerators, which have the advantage of smaller
dimensions, higher electron flux intensities, and easier beam
modulation options.
Microtron
A special, rarely used, type of circular electron accelerator is
the microtron, sometimes referred to as the
"electron cyclotron". Its activity is
schematically shown in the right part of Fig.1.5.7. A flat
cylindrical chamber with a high vacuum is placed in the
magnetic field between the pole pieces of a strong electromagnet,
similarly to a cyclotron, but instead of duants an electric
acceleration system is mounted at the edge of the chamber - a cavity
resonator, powered by high frequency voltage from a
magnetron or klystron generator (frequency f is a few
GHz). Electrons fly through this resonator many times, where they
are returned in a circular orbit by a magnetic field,
accelerating to higher and higher energy during each pass. Due to
the increased kinetic energy, the radius of the electron path
after each pass through the resonator is always larger and
larger. In order for the electron to come between the resonator
electrodes in the correct phase of the high-frequency voltage
period and be able to be accelerated again, the resonance
frequency condition 2p.f = k.e.B/(mo.c) must be met, according to which the circular
frequency of the accelerating voltage must be an integer
k-multiple of said fraction, where e is the charge of the
electron, B is the magnetic induction, m o is the rest mass of the electron.
The electrons for acceleration are injected
with an electron gun, or are obtained by emissions from the walls
of the resonator. Microtrons are sometimes used to accelerate
electrons to energies of several MeV, their advantage is the
achievement of high flux intensities of
accelerated electrons in the beam. Monoenergetic electron beams
can be extracted from individual paths, lower energy electrons
from smaller paths, of maximum energies from the largest path at
the edge of the acceleration chamber.
Electrical supply of accelerators
The particles in accelerators
obtain their high kinetic energy by the action of electromagnetic
fields, ie by converting part of the electrical energy with which
the accelerators must be supplied. Devices as complex, as
accelerators in general must be equipped with complex electronic
apparatus, containing several types and sources of electrical
supply :
n The supply of accelerating electrodes
is the basic electrical supply, that supplies its own electrical
energy to accelerate charged particles. X-rays tubes and
electrostatic linear accelerators have a high DC voltage
- tens of kilovolts, up to several megavolts. In high-frequency
linear accelerators and circular accelerators, the accelerating
electrodes are powered high-frequency alternating voltage
with a frequency of the order of MHz to several GHz (electronic circuits producing this RF voltage are
briefly described below in the section "High-frequency voltage generators").
n Power supply of the ion source
The accelerating particles themselves are also obtained
electrically in the ion source. It is simplest for electrons
obtained by thermoemission from a glow cathode,
which is powered by a glow current from a glow
transformer (220V is transformed to 6-24V,
glow current about 2A-20A). Protons and
heavier ions are obtained in an electric discharge
supplied with a direct voltage of hundreds to several thousand
volts.
n Power
supply of magnetic solenoid coils
Strong solenoids are used to shape the path of accelerated
charged particles, consisting of coils supplied with an electric
current of many tens to several thousand amperes. With
conventional electromagnets, it is energy-consuning, heat is
generated, the electromagnets must be cooled. The largest part of
the electrical energy for powering accelerators is mostly
consumed by electromagnets. In newer large accelerators, superconducting
coils are often used in electromagnets.
The issue of electromagnets in accelerators
is discussed in more detail below in the section "Electromagnets in accelerators".
n Vacuum and cooling system power supply
To provide high vacuum in the accelerator tubes
are used powerful vacuum pumps. Cooling the tube
(along with superconducting electromagnets) to low temperatures
can also help maintain a high vacuum, at which point any
remaining air will freeze on the tube walls. In many electrically
powered components, much of the electrical energy is converted
into heat, which needs to be dissipated by
ventilation system or other cooling systems.
Although superconducting electromagnets do not generate heat
directly, cooling helium must be recycled in liquefiers. All this
technical "background" of the accelerator contains a
number of electric motors, which are powered either directly from
the AC network (220V), or are controlled electronically.
n Power supply for control and regulation
electronics
The operation of accelerators is entirely conditioned by the exact
time and intensity interaction between electric and
magnetic fields in different parts of the accelerator system.
This must be ensured by complex electronic circuits,
currently controlled by digital computer technology.
Note:
For the simplest "accelerator", which is an X-ray
tube, the power supply diagram is drawn in Fig.3.2.2B in §3.2.2
"X-rays - X-ray diagnostics", part "Sources
of X-rays".
High-frequency
voltage generators
The acceleration electrodes of most types of accelerators are
powered by alternating high-frequency voltage or
RF electromagnetic waves. Frequencies of the unit up to hundreds
of MHz can be prepared in conventional oscillators with
inductive-capacitive LC circuits, equipped with tubes or, more
recently, semiconductor transistors. Very high frequencies
(needed, for example, for linear high-frequency accelerators,
microtrons, etc.) arise in high-frequency generators, which are
equipped with special tubes - magnetrons and klystrons,
which can work as high-frequency oscillators
with very high frequencies (HF) of the order of GHz. Gyrotrons
are used for the highest frequencies.
The magnetron
is a cylindrical vacuum diode, the center of
which is a heated cathode, around which is a coaxial anode. An
electrical voltage is applied between the cathode and the anode.
In addition, the diode is inserted into a longitudinal magnetic
field (between the pole pieces of the electromagnet, for
simpler applications a permanent magnet is sufficient), the
direction of which is parallel to the cathode - Fig.1.5.8 at the
bottom left. The electrons emitted from the cathode are thus
affected by a combined cross-field - the radial
electric field between the cathode and the anode and the
longitudinal magnetic field of the outer magnet. The electrons
emitted by the cathode are attracted to the cylindrical anode,
but the paths of the electrons are curved by the
Lorentz magnetic force, so that at a certain value of the anode
voltage and the intensity of the magnetic field, the electrons no
longer fall directly on the anode, but form a cloud
circling in the space between the cathode and the anode. The
anode of the magnetron is not a simple cylinder, but it consists
of a metal block containing several (mostly 8) peripheral cavity
resonators - Fig.1.5.8 at the top left.
Electrons, during their circular
motion as they pass around resonant cavities, release some of
their energy and cause electromagnetic oscillations
in the cavities. The most efficient transfer of energy to the
electromagnetic field in resonators occurs at such a speed of
electron movement that during its transition from one
circumferential slit to another, the polarity of the field in the
slit changes to the opposite; then the electron at each slit is
braked and transfers energy to the field in the resonator. This synchronization
(called p- mode) is achieved by a suitable choice of anode voltage.
Overall, the motion of electrons is quite complex. The
oscillating electromagnetic field density modulates the rotating
electron cloud - there is a clustering of electrons into
bent rays in the shape of a "wheel with spokes" (the
number of louvers is half that of the circumferential anode
resonators) which rotate about an axis; it is only symbolically
drawn in Fig.1.5.8 at the top left. It can be said that the whole
magnetron system is put into a state of intense
high-frequency oscillations (whose frequency is given by
the mechanical dimensions of the resonators), in which the
electrical energy of the flowing anode current is converted with high
efficiency into oscillating field energy. The generated
high-frequency signal is then output by antennas or waveguides
for external use.
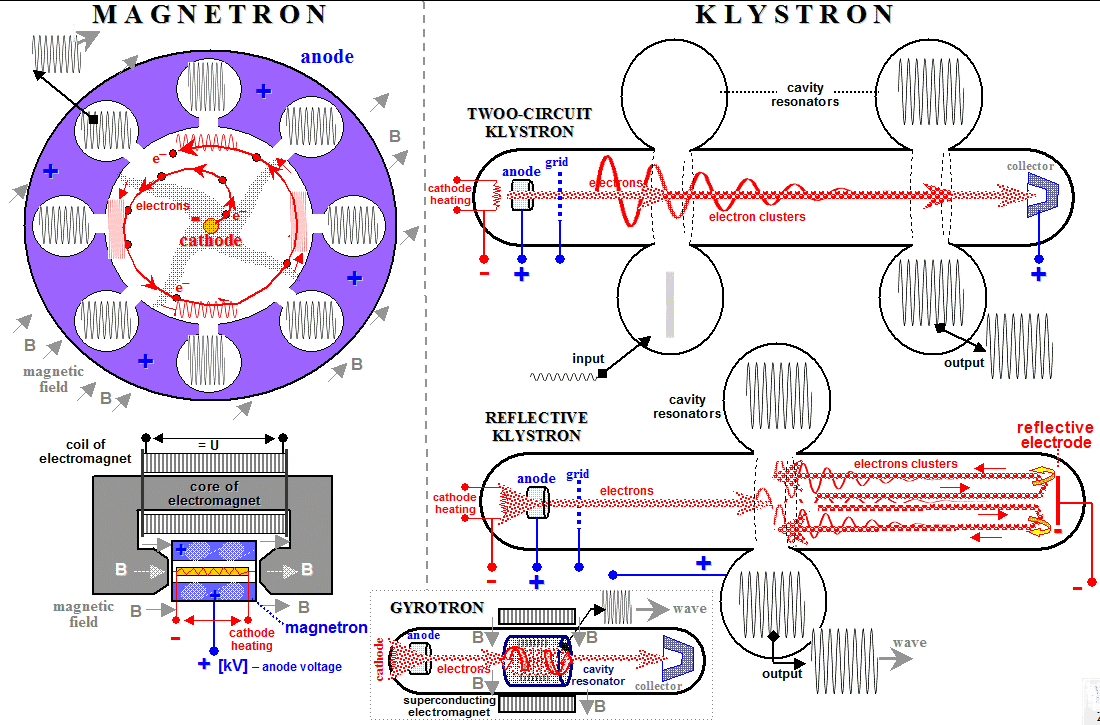
Fig.1.5.8. Physico-electronic principle of magnetron, klystron
and gyrotron operation.
Top left: Cross section of a magnetron
with the indicated movement of electrons between the cathode and
the anode in a crossed electric and magnetic field. Bottom
left: Connection and placement of the magnetron in
the magnetic field - longitudinal section. Top right:
A two- circuit klystron as an RF signal
amplifier. Bottom right: Reflective
single-circuit klystron as an oscillator and RF signal generator.
Bottom center: Gyrotron with an
indicated spiral motion of electrons in a strong magnetic field
and the formation of electromagnetic oscillations in a cavity
resonator.
Klystron (Greek klys = surf, waves crashing into the shore)
is also a vacuum tube in which electrons
emitted by a heated cathode are accelerated and focused into a
narrow linear beam by a hollow anode connected
to a positive voltage. The kinetic energy of an electron beam
(electron clusters) is converted into electromagnetic
oscillations in resonant cavities. Klystrons are divided into two
basic types :
¨ A two-circuit
klystron ,
where electrons from the cathode on their way to the anode first
pass through one resonator, which modulates their speed,
then the formed clusters of electrons pass
through a second cavity resonator, in which oscillations are
aroused when resonance is reached - Fig.1.5.8 top right. In the
area between the two resonators, a magnet is sometimes placed
around the tube to hold and focus the electron beam in the center
of the tube. Electrons that have already transferred their
kinetic energy are captured in the collector (the rest of their energy is converted into heat there;
in large devices, these electrons are returned to the space in
front of the resonators to increase efficiency). If we supply the first (input) resonator with an
external RF signal, then the oscillations excited in the second
(output) resonator have a larger amplitude than
the oscillations supplied to the input resonator - in Fig.1.5.8 on the right it is sybmolically indicated
by an amplifying wavy line. This type of
klystron serves as an amplifier of the RF
signal. By introducing feedback (by electrically
connecting the cavities of both resonators of a two-circuit
klystron) it is possible to construct a generator
of self-excited oscillations with high power, similarly to the
reflex klystron below. For special purposes of RF technology,
klystrons with a larger number of resonant cavities are also
constructed - this achieves greater amplification and the
possibility of tuning in a wider frequency range.
¨ Reflective klystron ,
in which after acceleration and focusing of electrons by the
anode into a linear beam, these electrons at the opposite end of
the tube are reflected by a negative reflective electrode
(repeller) and returned to the working space of the
tube. The speed of the electrons inside the klystron is modulated
by their interaction with a cavity resonator, in
which the passing electrons evoke electromagnetic oscillations.
Each electron passes through the resonator twice. In the forward
direction, the electron flow is velocity- modulated, the electron
clusters continue toward the reflecting electrode, where
they stop, reverse, and in the opposite field move rapidly back
to the resonator into which the electron clusters enter and
excite this resonator. With the correct setting of the voltage on
the reflecting electrode with respect to the geometric
dimensions, the electron clusters enter the resonator always at
the moment when the RF field has the maximum value of the
opposite polarity and give it energy - resonance
is achieved and, the oscillations are permanently maintained
(Fig.1.5.8 at the bottom right). The electromagnetic RF signal is
output from the cavity resonator by an antenna or a waveguide.
Comparison :
The magnetron achieves a relatively high efficiency of about
60-70% of the conversion of power supply to a high-frequency
signal. Klystron, whose efficiency is somewhat lower (about
30-40%), but generates RF oscillations with a more stable
frequency, with the possibility of its precise tuning and
modulation. Magnetrons and klystrons are widely used in high-frequency
technology - in UHF television broadcasting, satellite
communication, radar technology, microwave heating (eg in
microwave ovens, microwaves are excited by magnetrons); for us is
important here its application in particle accelerators.
They often work in pulse mode, achieving a
respectable performance of up to hundreds of megawatts! In the
area of lower powers, magnetrons and klystrons have recently been
replaced by semiconductor components.
Gyrotron
The so-called gyrotrons
(Greek gyros = turning, rotation, rolling, machining;
also a rotating grill ) were
constructed for the areas of the highest frequencies, Fig.1.5.8
in the middle at the bottom. They are vacuum tubes in which the
electrons emitted from the cathode are accelerated in an
"electron gun" by a voltage of tens to hundreds of kV
and concentrated in a linear beam. There is a cavity
resonator in the working space of the gyrotron and a
very strong magnetic field is applied (approx.
3-8 T), excited mostly by a superconducting electromagnet. When
moving in this strong magnetic field, the electrons
circle in a spiral with a Larmor frequency f =
e.B/(2p.me) depending on the
intensity B of the magnetic field. As this electron spiral
passes through the cavity resonator - if cyclotron resonance
occurs - intense electromagnetic oscillations of
high frequencies » 20-250 GHz are evoked in it (resonance can occur at the
fundamental frequency given by the dimensions of the resonator,
or at higher harmonics). After passing through the resonator, the
electrons that have already transferred most of their energy are
absorbed in the collector. Electromagnetic waves are at
the output by the waveguide for external use. In addition to
microwave RF electronics, gyrotrons are so far rarely used for RF
plasma heating in the most demanding applications, eg in the
field of thermonuclear fusion in tokamaks (§1.3, part "Fusion
of atomic nuclei"; more
than 20 powerful gyrotrons for deuterium-tritium plasma heating
in a working toroidal tube are planned in the ITER tokamak under
construction).
Note:
The formation of electromagnetic oscillations in the cavity
resonators of a magnetron and a klystron is sometimes explained
simplified from an electronic point of view as follows:
Individual chambers or cavity resonators can be imagined as small
oscillating circuits - LC connected in parallel.
The gap between the edges of the chambers acts as a small
"capacitor" C (capacitance of pF units), the conductive
inner sheath of the resonator represents a "coil" L.
The generated magnetic field induces the opposite current,
charging the "capacitor" to the opposite polarity ...
etc ... - in the chamber there is an alternating current of high
frequency f = 1/L.C, similarly as in the oscillating circuit LC.
Although this comparison is illustrative, it is not very suitable
for accurate analysis, it is necessary to use the methods of wave
behavior of the electromagnetic field.
Electromagnets in accelerators and other nuclear devices
An important part of most accelerators are electromagnets,
which are generally used to shape the path of
accelerated charged particles by applying a Lorentz force
perpendicular to the speed of motion. These are dipole
electromagnets for the basic curvature of the path, quadrupole
electromagnets for focusing individual particles into a defined
beam, sometimes even more complex shapes of pole pieces are used.
In the classic design, the electromagnets are formed by coils
wound with the required number of turns by insulated wire from a
good conductor, mostly copper, on a suitable ferromagnetic core
(forming a "pole pieces "). The strength of
the excited magnetic field (magnetic flux density) is
proportional to the electrical current through the coil. It is
supplied either by direct current - a permanent
electromagnets, or a variable or alternating current - gives
the time varying or alternating magnetic field.
The "auxiliary"coil for beam focusing, its corrections,
output or separation, have this classic design for all
accelerators. For smaller and older devices, this conventional
electromagnets are also used for basic curvature
of the particle beam in circular accelerators - cyclotrons and
synchrotrons.
In the case large high-energy
cyclotrons and synchrotrons, a very strong
magnetic field is required to keep the particles in
circular orbits, for the excitation of which an electric current
of many tens to several thousand amperes must flow through the
coils. When using conventional electromagnets, it
is energy-consuming, heat is generated, the electromagnets must
be cooled. For newer large accelerators, therefore, superconducting
coils are often used in strong electromagnets :
Superconducting
electromagnets
The physical principles of
superconductivity have been briefly discussed above in the
passage "Fermions as bosons.
Superconductivity.". Let
us recall only the basic fact that when some conductors cool
to a sufficiently low temperature - lower than the so-called critical
temperature Tc -
their specific electrical resistance drops to zero
( ohmic resistance for
direct current drops to practically zero; inductive component of
resistance, impedance, for alternating current remains unchanged). In this situation, even a strong electric current
flows through the superconductor with absolutely no heat
loss. The most used superconducting material
for electromagnets is the alloy niobium (53%) - titanium (47%)
working up to 9 Tesla, resp. Nb3Sn, usable even above 9 T. So-called high-temperature
superconductors have also been developed, which have a
critical temperature higher than -196 °C and can work instead of
liquid helium even when using liquid nitrogen. However, it is not
yet suitable for strong electromagnets, it is not possible to
create long thin wires from them.
Material note
:
It is interesting that copper, which is one of
the best electrical conductors at normal temperatures, can serve
as a suitable insulating material for
superconducting windings ! In the Kelvin units, however, copper
does not go into the superconducting state, it has a resistivity
many billions of times greater than the superconducting Nb-Ti, so
it acts as an insulator relative to the
superconductor. Superconducting wires are usually made up of a
large number (at least several tens, but sometimes several
thousand) of thin NbTi fibers embedded in a copper matrix (or
suitable alloys of copper, nickel).
Therefore, if we wind a coil made of
superconducting material, when an electric current passes through
its turns, a magnetic field is excited without heat loss in the
winding - a superconducting electromagnet is
created.. It can work in two modes :
l Continuous mode of power supply from an external current source -
constant or time-varying, analogous to conventional coils.
However, the advantage is the possibility of achieving a very
strong magnetic field with low electrical consumption. Strong
current is generated even at very low source voltage, without
heat loss. Continuous mode is used especially where it is
necessary to operatively change the intensity of
the magnetic field - for example in a synchrotron or tokamak.
l Persistent mode - in a closed superconducting winding,
the electric current is excited once and then spontaneously maintained
permanently, due to the absence of losses in the
winding in the form of heat production. The lossless current
circulating in the winding cannot decrease or increase unless
electromagnetic energy is supplied or consumed from the outside.
Of course, this also maintains a strong magnetic field - it is a persistent
superconducting electromagnet with a short-closed
winding in a very stable current and energy state. For
superconductivity, however, the winding must be kept permanently
at a low subcritical temperature of approx. 3 °K in a cryostat
using liquid helium *). Electricity is thus only needed to drive
the cooling system. To create a magnetic field of about 3 Tesla,
a superconducting coil with about 20,000 turns (with an
inductance of several tens of Henry) with a current of about 500
amperes is typically needed. Persistent mode is used where we
need it long-term stable magnetic field, eg in
MRI nuclear magnetic resonance imaging.
*) This continuous
cooling of the superconducting coil must be carefully monitored
! If, as a result of evaporation, the coolant level dropped so
much that part of the winding warmed above the critical
temperature, the superconductivity would suddenly
disappear - the so-called quench
(see below). At this point in the winding, an ohmic resistance
would arise, the current through the winding would decrease
rapidly, and the magnetic field would disappear. This would
result in an electromagnetic induction of a large electromotive
force in the winding. The considerable energy stored in the
magnetic field would be quickly converted into induced
current a winding that would heat up strongly
with ohmic resistance, the rest of the coolant would boil up and
the winding could burn out!
 |
Fig.1.5.9. Left:
The superconducting electromagnet consists of a coil
wound from a superconducting material, placed in a
cryostat with liquid helium. When exciting
and damping the superconducting current in strong
persistent electromagnets, a short-circuit with a
temperature-controlled superconducting key (bifilar
winding + heating wire) can be advantageously used.
Right: Temperature dependence
of ohmic resistance of Nb-Ti superconducting material (for 1 m of wire Ø 0.3 mm)
. |
"Switching on"
(excitation or charging) and "switching off" (damping or discharging)
of a strong electric current in the superconducting winding of a
large persistent electromagnet is a delicate
matter! Considerable energy is stored in a strong magnetic field,
so that due to electromagnetic induction in the winding, the
superconducting current appears to have considerable temporal inertia.
Therefore, switching on and off the superconducting current here
cannot be done at once by a simple switch, as we are used to in
conventional electrical circuits.(this
would lead to the induction of high voltage peaks and currents
acting against a sudden change which could lead to a violation of
the superconductivity), but it must be done
gradually - continuously. Superconducting
windings do not "tolerate" sudden current changes,
which can also induce strong eddy currents in the copper matrix
around the superconducting wires, or voltage spikes in other
components. The excitation of the current in the closed winding
of the superconducting coil requires a specific procedure.
Current excitation
is standardly maked by connecting an external source
with a low voltage of about 10 V (sufficient to "push" the current increase of
several amperes/min. against the inductive resistance of the
coil) which is capable of supplying the
required rated current (eg 500 A). The inductance of the
superconducting winding resists the increase in current, charging
takes about 50 minutes at controlled current rise approx.
10A/min. After reaching the required current (magnetic
induction), the coil terminals inside the cryostat must be superconductively
"short-circuited"; the external
current source can then be disconnected (in the specific way described below) and the current through the coil then flows
spontaneously "forever" *).
*) It is only approximately, the eternal
flow of constant superconducting current is an idealization! In
fact, even the superconducting current, and thus the magnetic
field B, will decrease over time very
slowly according to the usual exponential relation B(t) = B(0) .e- (R / L) .t,
with time constant R/L, where R is the residual
resistance caused by electrical connections and the
effects of the magnetic field on the electron flux in the
superconductor. In some devices, such as nuclear magnetic
resonance, an appropriate correction (eg a small
change in resonant frequency) is introduced for this gradual
decrease .
Disconnection
of the external source after superconducting short-circuiting of
the coil must also be performed continuously.
Immediately after short-circuiting, a relatively small current
will flow through the superconducting short-circuit, which will
also be in the opposite direction than it is necessary to create
a superconducting coil in a closed circuit. Abrupt disconnection
of the external source at this stage would lead to a jump in
current in the short-circuit line, which could impair its
superconducting properties. The current that has flowed into the
superconducting coil from the connected external source needs to
be "redirected" in a controlled and smooth manner so
that it begins to flow through the superconducting short circuit.
It is therefore necessary to reduce the current
flowing from an external source for a few minutes (which switches to the mode of a controlled current
source with a low internal resistance - there is no need for
a voltage acting against the inductive resistance of the coil) from face value to zero. The inductance of the main
winding maintains the current, so that the superconducting short
circuit gradually increases the current (which
had a smaller value and originally the opposite direction just
after the short-circuit!) up to the nominal
value; only then do we disconnect the external
source.
To switch off or discharge
the superconducting current, proceed in the opposite way: an
external source set to nominal current (eg 500A) is connected to
the external terminals, the superconducting short circuit of the
coil is interrupted and the current in the source is gradually
reduced with electronic control (approx. -50A/min.); after about
10min. is a superconducting electromagnet "discharged",
with intensive cooling of the source.
Superconducting short circuit or
disconnection - "keying"-
coil leads were previously made electro-mechanically. Now a temperature-controlled
superconducting key is used: a longer superconductor (bifilarly coiled to avoid an unwanted magnetic field) with a piece of resistance heating wire is connected in
parallel to the main coil terminals inside the cryostat. If -
when charging or discharging - the heating is turned on, the
short-circuiting superconductor is swithed to the normal
(resistive) state - short circuit is disabled
(off). After turning off the heater bifilar coil cooled, to restore
superconducting short-circuit and the superconducting
current can flow continuously through the closed circuit, without
an external source (Fig.1.5.9 on the left).
Quench of a superconducting magnet
An unplanned and uncontrolled sudden disappearance of a
superconductivity, called a quench,
is an unpleasant event for a superconducting magnet operating in
a high-intensity mode. It can basically occur due to 5 causes :
× Cooling fault
- the level of the cooling medium drops so much that part of the
winding warms above the critical temperature Tc and goes into the
normal resistive mode (already mentioned above)...
× Fault in the superconducting connection of an
electrical circuit - a defect in material or an
imperfectly made connection. At this place, a strong electric
discharge (arc) occurs with rapid heating and melting of the
components. The most serious accident of this type occurred in
2008 at a large accelerator LHC at CERN...
× Too strong electric current - the critical
current density Ic (approx.
1000-4000 A/mm2) will be
exceeded, above which the material used already loses
superconducting properties.
× Too strong magnetic
field - the critical value of magnetic induction
Bc is
exceeded, above which the used material already loses its
superconducting properties and goes into the normal resistive
mode.
× Too high rate of change of the magnetic field
- induced eddy currents in the supporting copper matrix can heat
part of the winding above the critical temperature at some point
by their thermal effects.
If superconductivity
were lost for any of these reasons, even in a
small area of the electromagnet, an ohmic resistance would arise
at this point in the winding, the current through the winding
would drop rapidly, and the magnetic field would disappear. This
would result in an electromagnetic induction of a large
electromotive force in the winding. The considerable energy
stored in the magnetic field would be quickly converted into an induced
current by the winding, which would it warmed
heavily with Joule's heat. The
loss of superconductivity within a few seconds and the strong
heating of the electromagnet has the irreversible nature of a chain
reaction in which most of the refrigerant evaporates by
boiling. It is very dangerous for workers near the electromagnet,
which can be permanently damaged..!..
Strong electromagnets, often
superconducting, are used in addition to accelerators in other
devices of atomic and nuclear physics, industry, medicine. The
most powerful electromagnets are used in tokamaks
to magnetically hold high-temperature plasma for thermonuclear
fusion (§1.3, part "Tokamak"). Medium - sized superconducting electromagnets (approx.
1-5 T) are routinely used in nuclear magnetic resonance
to achieve the basic orientation of the magnetic moments of
nuclei (§3.4, part "Nuclear magnetic resonance").
Large
accelerators
For research in the field of (elementary)
particle physics, large unique accelerators are being built in an
effort to achieve the highest possible energies
of accelerated particles. Their task is a detailed investigation
of the properties of particle interactions - specifying the
mechanisms of interactions of already known particles and finding
new particles. Large accelerators (especially
synchrotrons) were built, for example, in FermiLab near Chicago,
in Brookhaven near New York, at CERN, in Dubna or Serpukhov. New
discovery results have been or are expected on each of these
accelerators. Recently, interactions of accelerated particles in colliders
have mostly been used. Here are just a few of the biggest
accelerators from recent years in the table :
| Accelerator name |
Laboratory |
Particle |
Energy [GeV] |
Year |
| SLAC (Stanford Linear Accelerator
Center) |
Stanford |
e -
- e + |
50 |
1966 |
| Tevatron |
Fermilab |
p +
- p - |
980 |
1987 |
| LEP (Large Electron-Positron collider)
|
CERN |
e -
- e + |
100 |
1989 |
| RHIC (Relativistic Heavy Ion Collider) |
Brookhaven |
p - p, Au - Au, ... |
200 |
2000 |
| LHC (Large Hadron Collider) |
CERN |
p - p, Pb - Pb, ... |
7000 |
2008 |
| VLHC
(Very Large Hadron Collider) - the future ?? |
p - p, ..... |
? >> LHC? |
? > 2030? |
| CLIC (Compact LInear Collider) - the future ?? |
e - - e + |
3000 |
?? |
Large
Hadron Collider (LHC)
The largest accelerator so far has currently
been built at the Central European Nuclear Laboratory CERN
(Centre Europeen pour Recherche Nucleaire) *) on the Swiss-French border
under the name LHC - Large Hadron Collider
in 2008.
*) The name "nuclear research",
coined when the institute was founded in 1954, is no longer
entirely apt. The original field of nuclear research has long
been transformed. CERN's main focus has been research in the deep
subnuclear field and mainly in particle
physics for several decades, often without direct
connection to atomic nuclei. The name "European"
has also been extended, and experts from non-European countries
are also collaborating on many projects.
The LHC is a synchrotron
(the principle of operation was described above, Fig.6.6.5 on the
right), whose ring is located in the tunnel after the previous
electron accelerator LEP about 100m underground (50-150m below
ground), its circumference is 26.66 km long. The system of
magnets along the path of the accelerator is very complex. The
circular path of the accelerated particles with high accuracy is
ensured by more than 1200 superconducting dipole
electromagnets around the circumference of the tube.
Furthermore, there are almost 900 quadrupole
magnets even more complex shapes, for focusing the beam of
accelerated particles, correction and modification of the path
shape. The conductors of the superconducting electromagnets are
made of niob-titanium alloy and operate at a temperature of 1.9
°K. The actual acceleration of protons or heavier ions occurs in
one segment of the ring, where a system of radio frequency resonant
cavities is located, powered by an intense
high-frequency voltage of 400 MHz . The magnetic field curves the
paths of the charged particles exactly along the central
circumference of the tunnel and returns them periodically to the
acceleration cavities. In one cycle, the kinetic energy of the
proton increases by 480 keV.
The LHC, as a synchrotron, needs
particles already pre-accelerated for its operation (see
Fig.1.6.5 on the right). In the case of such high energies, the
protons are even 4-degree pre-accelerated, for
which the previously constructed accelerators at CERN are used,
arranged in series according to the size of the achieved
energies. The protons obtained by hydrogen ionization are first
accelerated in a linear accelerator (LINAC) to an energy of 50
MeV, from where they are fed to a circular accelerator PS
"booster", where they obtain an energy of 1.4 GeV. They
are then routed to the Proton Synchrotron Ring (PSR)
with an output energy of 25 GeV and finally to another Super
Proton Synchrotron (SPS synchrotron), which gives
them an output energy of 450 GeV. With this initial energy, they
are injected for final acceleration into the LHC ring, where they
will be accelerated to an output energy of 7 TeV during many
cycles, wherein the magnetic field in the electromagnet segments
changing from an initial value of 0.5 T (at 450GeV) to 8.3 T (at
7 TeV) during each cycle, the current in dipole electromagnets
reaches more than 10000 A. The increase in kinetic energy in the
LHC from the initial 450GeV to 7TeV takes about 30 minutes. Since
synchrotron operates in pulsed mode, the protons are accelerated
in groups or clusters (bunches). Protons accelerate in
two tubes (rings) in opposite directions for
interactions in the colliding beams. At speeds approaching the
speed of light (99.999995% c), the proton in the LHC will make
more than 11,000 circulations/second. In colliding beams, 1
collision per 10 billion particles is produced, at full power
there is more than 30 million collisions per second. The total
energy of the proton beam reach up to 350 MJ. In addition to
protons, the LHC can accelerate also heavier nuclei,
especially lead nuclei (for the ALICE experiment, mentioned
below).

There is four places around the perimeter of
the LHC, where the tubes connect and the opposing beams of
particles intercect - there are interactions in the
colliding beams. These places are surrounded by large
and complex detection systems (cf. §2.1,
passage "Arrangement and configuration of radiation
detectors"), by means of
which six main experiments are performed :
¨
ATLAS (A
Toroidal LHC ApparatuS
)
is the largest detection system (weighs about 7000 tons), the
main carrier program of the LHC. Comprehensively measure and
analyze particles arising from proton collisions with an energy
of 14TeV. The ATLAS detection system (and also the CMS below,
partly ALICE) has a cylindrical coaxial arrangement
similar to that in model figure 2.1.2 in §2.1, passage "Arrangement and configuration of radiation
detectors"), but much
more complex, it is the most complex and expensive detection
device in history !
The inner part of the detector, which records
the trajectories of charged particles flying out of the collision
site, consists of three coaxial layers ("shells") of trajectory
detectors (trackers): the lowest are pixel
semiconductor detectors, then strip detectors and transient
radiation detectors. The whole system is located in a strong
longitudinal magnetic field 2 Tesla of a superconducting solenoid
electromagnet; from the curvature of the particle paths in
the magnetic field, the charge and momentum of the particles can
be determined.
Another layer of the detection system is a spectrometer,
called a "calorimeter", whose
task is to absorb the energy of the flying particles and quantify
it (its "sample") using output electrical pulses. It
consists of two parts: electromagnetic calorimeter for
measuring the energy of photons and electrons and hadron
calorimeter ....
Last, the outer layer of the ATLAS detector
consists of a muon spectrometer, designed to
detect high-energy muons that are able to pass through the
calorimeter layer. By analyzing the orbits of muons curved by a
strong toroidal magnetic field, their momentums and
signs of electric charges can be determined. Drift tube and
multi-wire ionization chambers are used to detect muon
trajectories.
¨ CMS
(Compact Muon Solenoid) detector ,
optimized for detailed analysis of muons,
cooperates with the ATLAS system for comprehensive analysis of
high-energy interactions. Its structure is similar to ATLAS. For
the analysis of trajectories of fast muons, the detection system
includes a large cylindrical electromagnet (solenoid),
creating a magnetic field with a force of 4 Tesla.
The ATLAS and CMS
detection systems serve primarily for study of new particles,
especially the Higgs bosons (discussed
in more detail above in the section "Hypothetical and model particles"). If its decay went electromagnetically directly
to the high-energy pair g, or (via W-bosons) to electrons and positrons, these
secondary particles would be captured in an ATLAS or CMS
electromagnetic calorimeter. When decaying into muons (via
Z-bosons), the muon detection part of the CMS would come into
play. And all charged particles can leave their traces in the
intrinsic trajectory detectors (trackers) of both
systems.
¨ ALICE ( A Large Ion
Collider Experiment )
is another experimental system whose task is to study the collisions
of nuclei ("heavy ions"), especially lead, at
center of gravity energies up to 5 GeV/nucleon and to investigate
the properties of the resulting quark-gluon plasma (see above "Quark -gluon plasma"). Like ATLAS and CMS, ALICE
has a cylindrical coaxial arrangement of a large number of
detectors, designed to register and reconstruct the parameters of
mainly charged particles arising from nuclear collisions. It is
used to study extreme states of matter (nuclear, hadron) under
similar conditions as in the universe at the beginning of the hadron
era, in the first microseconds of the universe (see §5.4 "Standard Cosmological Model.
The Big Bang. Shaping the Structure of the Universe.", in "Black Holes and the Physics of
Spacetime", part "Stages of the evolution of the
universe - Hadron era").
¨ TOTEM
( Total Cross Section, Elastic Scattering and Diffraction
Dissociation )
serves to accurately measure the effective
dimensions of protons - effective cross sections - for different
types of interactions. Is also used for calibration measurements
of LHC properties (such as "luminosity" - the
efficiency of collision production in the accelerator). It is
consist of 8 detectors, located very close to the colliding beams
at the CMS detector.
¨ LHCb
( Large Hadron Collider beauty )
has a task to study the violation of CP symmetry in the decay of
B-mesons containing a heavy (second heaviest) b-quark. During
high-energy proton collisions in the LHC, a large number of pairs
of b-b' quarks-antiquarks are formed, and their hadronization
results in B-mesons and baryons. The mode of decomposition of
these particles is sensitive to the disruption of CP symmetries -
if matter behaves slightly differently than antimatter. The
particles are first localized by a VELO detector (VErtex
Locator), located near the collision site. Identification of
particles before and after passing through a dipole magnetic
field is performed using two ring imaging Cherenkov detectors
RICH (Ring Imaging Cherenkov detectors) - see §1.6, passage "Cherenkov radiation" and
§2.4, passage "Cherenkov detectors". The RICH1 chamber is located just behind the VELO
detector, behind the magnet is a particle traces detector,
followed by the RICH2 chamber for the identification of particles
with high momentum. Also included are electromagnetic and hadron
calorimeters for measuring particle energies. Finally, the muon
chambers are located. These results could be interesting in terms
of the imbalance of matter and antimatter (baryon asymmetries) in
the early stages of the evolution of the universe - why there was
an excess of matter over antimatter (§5.4
"Standard Cosmological Model. Big Bang.", passage "Baryon asymmetry of the universe" book "Gravity, black holes and space - time
physics").
¨ LHCf
( Large Hadron Collider forward )
study high-energy particles generated "forward" in the
direction of the proton beam. The LHCf spectrometer (calorimeter)
focuses mainly on neutral energy particles (g photons, neutral
pions, neutrons) emitted at small angles; charged particles can
be registered by trackers in ATLAS and CMS, particles emitted at
large angles in addition by calorimeters and muon spectrometers
of both systems. These complex measurements simulate
cosmic radiation and study the cascades of particles
arising from its interactions (cf. Fig.1.6.7 in the passage
"Cosmic radiation", §1.6).
Already
during the planning and construction, physicists promised, among
other things, this large accelerator that the
energy of collisions in in the LHC could be sufficient to
experimentally find the so-called Higgs bosons, so far hypothetical model
particles, generating the masses of some elementary particles -
quantum fields, especially bosons W and Z of electroweak
interaction (mentioned above in the passage
"Hypothetical and model
particles"; see also §B.6
"Unification of fundamental interactions.
Supergravity. Superstrings"
in book "Gravity, black holes and space-time physics",
part "Global and local symmetry; Calibration fields"). This is truly fulfilled !
Also the lightest supersymmetric
particle (LSP - Lightest supersymmetric particle),
when perhaps these interactions could be detected. The
possibility of obtaining circumstantial evidence for extra-dimensions
is also discussed assumed by some unitary field theories (see a
few lines above §B.6 ) - that has not
yet been fulfilled...
Discovery of the Higgs
boson
At the ICHEP2012 conference in Melbourne, Australia, on July 4,
2012, the discovery of a new boson whose properties are
consistent with the Higgs boson was announced based on data from
ATLAS and CMS experiments at CERN. Careful analysis of about
60,000 cases of photon pair detection (derived from high-energy
proton collisions) found a small (but
significant, about 160 photon pairs) peak
on the curve [number of photons -to-energy], in the energy range
around 126 GeV. This peak should probably come from the 2-photon
decay of the Higgs bosons. The level of reliability of
detecting a new particle by detecting its decay products is 5s. Further
experiments are needed to make sure it is a Higgs boson and not
another unknown particle. For this discovery, the Nobel Prize was
awarded to P.Higgs and F.Englert in 2013.
 Source:
CERN-LHC
Source:
CERN-LHC
Discovery of the Higgs boson at the LHC great accelerator by
detecting its decay products - here two opposite photons of gamma
specific energies on the ATLAS detection system.
The imposing system of the LHC accelerator and
detection apparatus is the most complex and sophisticated
work that humanity has created in its history! Details
of the design, construction progress and results of experiments
at the LHC are listed on the official CERN website: http://lhc.web.cern.ch/lhc/.
Dangers from large accelerators ?
In connection with the design and
operation of large accelerators, there are occasional
speculations and alarming reports in the mass media, that the
energy of colliding particles is so great that the interaction
may create a "black hole" or even a new "big
bang", which could allegedly endanger us,
or even devour and destroy the Earth and the whole
universe !! These speculations stem from a
misunderstanding of the issue, they are physically completely
unfounded and erroneous, for at least two
reasons :
1. Even if a high-energy interaction created a
black hole (which would be very interesting), due to the small
total energy, it would be a microscopic black hole
that would immediately quantum evaporate and
disappear - sending energy particles (less energy than had the
original particles). Such a black micro-hole therefore does
not absorb anything (it is not
capable of that, cf. §4.7 "Quantum
radiation and thermodynamics of black holes" of the above-mentioned book "Gravity
....."), can only be virtual;
it would be very difficult to prove it at all.
2. Particles with much higher energies (even 9
orders of magnitude higher!) commonly occur in cosmic
rays (see §1.6 "Ionizing
radiation", part "Cosmic rays"), interact and collide with
other particles in space and in the Earth's atmosphere for
billions of years already, without something
"catastrophic" happening.
Conceptual perspectives
of large accelerators
Circular
or linear accelerators ?
Although the principle of circular acceleration of charged
particles is very successful and effective, it seems that
circular accelerators have already approached the limits of their
possibilities in terrestrial conditions. If we wanted to
accelerate charged particles to even significantly higher
energies at realistically available circular orbital diameters
(ie accelerator tube diameters), the phenomenon of synchrotron
radiation *) would be increasingly applied, which would
carry away a significant part of the kinetic energy of particles
and ultimately prevent further acceleration. Thus, it seems that
future accelerators for the highest energies in terrestrial
conditions will have to be linear. The length of
linear accelerators to achieve high energies is many kilometers.
This is also a limiting factor in terrestrial conditions.
*) Synchrotron radiation arises
as braking radiation due to the uneven movement of electrically
charged particles in a circular orbiting. According to the
well-known Larmor formula of electrodynamics, the intensity of
this radiation is proportional to the electric charge and the
square of the acceleration of the particle motion, here it is a centripetal
acceleration of the circular motion. Thus, at a given
kinetic energy, the intensity of synchrotron radiation is
inversely proportional to the square of the particle mass. This
phenomenon therefore applies mainly during the circular
acceleration of light particles, electrons,
which move at high speeds and with high radial accelerations when
high kinetic energies are reached. Due to their high mass,
protons emit synchrotron radiation a million times smaller.
Linear colliders have another disadvantage:
while in circular colliders the accelerated particles
magnetically return repeatedly to the interaction site and their
paths intersect many times, in linear colliders the accelerated
cluster of particles meets its opposing cluster only once
and most particles flying through away - their energy is lost.
Therefore, a certain "recuperation" of the
energy carried by the beam of particles passing trought the
interaction areras is considered: these particles would, after
passing trought the interaction region, can successively transfer
their energy to the accelerating structure in opposed linear
accelerator. Another option is to use particles that have flown
through the interaction region without interaction, for the
experiments on fixed targets.
The
proton or electron accelerator ?
Protons and electrons (incl. positrons) in terms of its
characteristics and structure are very different particles, which
manifests itself by different mechanisms of interaction. Protons
have a complex internal structure quarks interacting via gluon
field. In their high-energy collision, they do not interact as a
whole, but the energy of interaction will be divided
to individual quarks, while in the gluon field a larger amount of
other particles is produced - two- and three-quark combinations,
mesons and baryons. Although these processes are important for
studying the strong interactions and properties of hadrons, the
energy of the interaction is "comminuted" into a large
number of secondary particles; energy concentration per small
number of particles cannot be achieved. About 1/2 of the proton's
momentum is carried by gluons, 3 quarks are bound in the proton.
For each quark, there is about 1/6 of the momentum of the proton,
so the effective energy of quark interactions is
Eef » E/6 (in an
electron-proton collision it is roughly Eef » E/Ö6). During proton
collisions, all quarks enter into interactions, which
"infest" the detection space around the interaction
site with a number of secondary particles (Fig.1.5.1G, H). In
this "ballast" it is very difficult to "find"
(separate) rare cases of the desired interaction of one of the
quark pairs.
An electron, on the other hand, is a
practically point particle without an internal structure (at least in the spatial scales known and available to
us). During a high-energy collision,
therefore, the electrons interact as a whole (Eef = E), significantly
fewer secondary particles are formed, on which it is concentrated
significantly more energy. Therefore, for the search for new
massive particles, the interactions of accelerated compact
electrons are more advantageous than intricately structured
protons. Simply put, at high energies, electron collisions are
"harder" than proton collisions. Electron collisions
are significantly "purer" than proton collisions, they
produce much fewer secondary particles (compare the corresponding
Feynman diagrams in Fig.1.5.1). The advantage is therefore the
lower radiation background of uninteresting particles, among
which it is easier to find the desired massive particles. Thus,
it appears that large electron accelerators -
opposite-electron-positron collisions - will be more
advantageous for achieving the highest actual energy
concentrations during interactions.
Note: The
designers from LHC accelerator at CERN to date are already
designing the construction of a large electron-positron
collider called the CLIC (Compact
LInear Collider) with 3 TeV energy.
Muon accelerators ?
In order to achieve the highest possible energy that would be
available for the creation of new particles during the collision,
proton and electron accelerators therefore have certain limitations.
Circular electron accelerators at a technically achievable
diameter have limitations due to synchrotron radiation. Linear
accelerators, in turn, have limitations in the technically
achievable length of the acceleration path. Synchrotron radiation
is weak for protons and antiprotons, so we can accelerate them to
significantly higher energies. However, protons and antiprotons
are not basic compact particles, but composite particles with a
quark-gluon structure. In a collision, "whole protons"
do not collide, but always only one elementary particle inside
each proton; others fly by without the direct desired
interaction. During the collision, only a fraction of the energy
of the accelerated proton is available for the creation of new
particles. A large number of particles fly out from the collision
site, most of which do not carry information about the direct
collision of two quarks.
A certain potential option to largely bypass these
limitations and obtain suitable elementary (structureless) particles accelerated to very high energy, which will
be entirely available for the creation of new particles upon
collision, is the acceleration of m±
muons. Muons (mentioned above in
the passage "Muons m and tauons t ") are particles very similar to electrons and positrons
e±. They have the same electric charge, are elementary and
behave like point particles. From the electron, the muon differs
in mass - it is 206 times heavier than the electron -
and it is unstable - with a lifetime of 2.2
microseconds, it decays into an electron and two neutrinos.
The instability of muons T1/2=2.2 ms is not so extreme (in contrast
to pions) that it completely precludes the
possibility of their acceleration. In co-production with the
relativistic time dilation of the special theory of relativity,
it enables multiple movement at speeds close to the speed of
light along a circular path in the accelerator for a period of
about 0.1 s., sufficient for effective acceleration. The great
advantage of muons is their relatively high rest mass,
206 times greater than that of electrons. This makes it possible
to accelerate muons in a ring accelerator to very high energies (similar to protons) with almost no
unwanted energy loss effect from synchrotron radiation.
Several steps are required to create a bunch of
accelerated muons :
=> Accelerate protons to high energies higher than about 300
MeV. => Let them hit the target (metal
or plastic). => This creates a shower of
particles containing fast charged pions. => The pions then
rapidly decay into muons and anti-muons. => These are led into
the counter-current acceleration rings of the synchrotron -
collider, where they are accelerated to high energies and then
allowed to collide.
The result would be net collisions at high
energies between point particles where 100% of their energy is
available for the creation of new particles. A relatively
"clean" signal would arrive at the detectors from the
collision site, without excessive contamination by parasitic
interactions. The expected disadvantage of this
technologically complex process of creating, collecting and
collimating muons and antimuons, will be a significantly
lower frequency of collisions (about
10-5-x compared to an
electron-positron or proton-proton collider),
so it will be difficult to accumulate the necessary statistics to
prove the discovery of new kinds of particles..?..
Muon accelerators - colliders - can be
promising for obtaining high energies due to minimal synchrotron
radiation and for the realization of "clean"
collisions, in which all the energy is available for the creation
of new secondary particles.
Space accelerators ?
These technical problems and
limitations are mostly due to the terrestrial conditions in which
the accelerators are constructed. Many of these problems would
automatically eliminated, if we installed accelerators outside
the space of our Earth. The design of accelerators
in universe has several principal advantages :
¨ Plenty of free space
for the installation of even the largest accelerator systems.
¨ Weightless condition
There is no need for robust constructions ensuring mechanical
strength. It is also possible, without structural interventions,
to make changes to the position and reconfiguration of individual
parts of the acceleration system in space.
¨ High vacuum ,
which is available everywhere, throughout the space,
"free". Thus, there is no need to design accelerating
tubes in which it is difficult to maintain the necessary vacuum
in terrestrial conditions. Accelerated particles can move in free
space along paths precisely determined and shaped by the magnetic
field.
¨ Low temperature (when shielding from sunlight, or in outer space) ,
which automatically ensures superconductivity
with suitable materials. Coils of electromagnets therefore
it is not necessary to cool, the once excited current
will be permanently maintained and excite a permanent magnetic
field for the necessary curvature of the paths of the accelerated
charged particles. Even electromagnets with a time-varying
magnetic field will work without energy losses by heat.
However, in the current state of our technology, the
real use of these fundamental advantages is hindered by technical
problems that are very difficult to solve. It is
primarily the transport of heavyweight construction material
(hundreds of thousands of tons) from the Earth's surface, against
gravity, into orbit around the Earth, or even into outer
universe. We do not yet have the technical means to do so, the
current rockets are too weak, slow and inefficient. Furthermore,
it is a question of remote power supply and also ensuring the
exact position of the individual parts of the acceleration system
with submillimeter accuracy. Only the area of transmission of
measured data from particle interactions would be solvable by
means of our current electronics (which in
recent decades - as the only technical discipline - has made
significant qualitative progress!).
In the future, experiments with particles accelerated to
the highest energies can be expected to move from Earth
to universe ...
Vojtech Ullmann







 Source:
CERN-LHC
Source:
CERN-LHC









