| (5.10) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 5
GRAVITATION
AND THE GLOBAL STRUCTURE OF THE UNIVERSE :
RELATIVISTIC COSMOLOGY
5.1. Basic
principles of cosmology
5.2. Einstein's and deSitter's universe. Cosmological constant.
5.3. Fridman's
dynamic models of the universe
5.4. Standard
cosmological model. Big
Bang.
5.5. Microphysics
and cosmology. Inflationary
universe.
5.6. The
future of the universe
5.7. Anthropic
principle and existence of multiple universes 5.8.
Cosmology and physics
5.2. Einstein's and deSitter's model of the universe. Cosmological constant.
Let's start with the simplest assumption about the static nature of the universe, which as we now know unrealistic, but has played an important heuristic role and still has a theoretical significance - Einstein and de Sitter cosmological models coming from it, are often used to compare and illustrate the properties of more complex and realistic models. In a homogeneous static universe, in which the conditions are the same everywhere at every point in time, it is natural to choose a coordinate system so that the space-time interval is spherically symmetrical with respect to any point. The space-time interval element will then have a general shape in spherical coordinates
| ds 2 = - A (r) c 2 dt 2 + B (r) dr 2 + r 2 (d J 2 + sin 2 J d j 2 ) , | (5.5) |
where A and B are functions only r ; for small r , this interval must take the form corresponding to the flat space-time of the special theory of relativity.
By directly calculating the components of the Ricci tensor Rik and substituting the energy-momentum tensor Tik of the form (5.3) corresponding to an ideal "liquid", the Einstein equations for the metric (5.5) can be converted to a system of ordinary differential equations (comma " ' " means derivative according to r)
| A'/A.B.r - (1 - 1/B)/r2 = 8p p , B'/B2.r - (1 - 1/B)/r2 = 8p r , p' = - A'.(r + p)/2A ; |
(5.6a, b, c) |
(the last equation can be most easily obtained from the law of conservation Tik; k = 0).
Since p' º dp/dr = 0 (homogeneity), equation (5.6c) gives the condition A'.(R + p) = 0. If ommit the case of empty space r = p = 0 , Einstein's equations have a static homogeneous solution only if A'(r) = 0. However, according to the field equations (5.6a, b), this leads to the condition r + 3p = 0, which again means r = p = 0 for real matter . Thus, Einstein's equations in the common form (2.50) do not allow any homogeneous static solution other than the empty flat Minkowski spacetime STR; they are therefore incompatible with the concept of a homogeneous static universe filled with matter with a constant positive density r.
In order for equations (5.6) to have a static homogeneous solution for the realistic case r > 0, p> 0, it is necessary to introduce a suitable constant L into them. In Einstein's equations, this can be ensured by introducing an additional cosmological term L .g ik , as suggested by Einstein in 1917 :
| Rik - 1/2 gik R - L.gik = 8p Tik , | (5.7) |
where L is a new (small enough) universal natural constant - the so-called cosmological constant, the value of which should result from a comparison of the relevant cosmological model with the results of astronomical observations.
For a static homogeneous metric (5.5), generalized Einstein's equations lead to a system of ordinary differential equations
| A'/A.B.r - (1 - 1/B)/r2 + L = 8p p , B'/B2.r - (1 - 1/B)/r2 - L = 8p r , p' º dp/dr = - A'.(r + p)/2A ; |
(5.8a) (5.8b) (5.8c) |
Due to the homogeneity requirement, dp/dr = 0, so equation (5.8c) can only be satisfied if (r+p).A' = 0. Equations (5.8) are therefore solvable in three cases, which correspond to the following solutions :
| A
' = 0 r + p = 0 A' = 0, r + p = 0 |
Þ Einstein's model; Þ de Sitter's model; Þ flat spacetime STR. |
Einstein's
model of the universe
In the case of
A' = 0, A(r) must be a constant, so that by
appropriate choice of the unit of time (time coordinates) A=1 can be
achieved; this ensures that for small r
the interval ds2
is the same as in STR. From equation (5.8a) by substituting A'= 0
we get a solution for function B
| B (r) = 1 / [ 1 - ( L - 8 p p) ] r 2 = 1 / (1 - r 2 / a 2 ) , |
where a new constant is introduced a using the relation
| 1 / a 2 = L - 8 p p . | (5.9) |
The metric (5.5) therefore for Einstein's cosmological model of a homogeneous static universe has a form
| (5.10) |
By comparing with (5.4) we see that the spatial part dl2 = dr2/(1- r2/a2 ) + r2 (dJ2 + sin2J dj2) of this spatiotemporal interval can be interpreted as a metric of in a fictitious three-dimensional hypersphere * ) of constant radius a, nested four-dimensional Euclidean space (Fig.5.1). If we introduce coordinates in this auxiliary space
w1 = a. Ö(1- a2/r2); w2 = r.sin J cos j = x; w3 = r.sin J sin j = y; w4 = r.cos J = z ,
we get the sphere
equation w1 2 + w2 2 + w3 2 + w4 2 = a 2, and the element of spatial
distance has the form dl2 = (dw1)2 + (dw2)2 + (dw3)2 + (dw4)2. If we consider not only the
spatial but also the temporal dimension, it is possible to
display the overall space-time geometry of the Einstein universe
as the geometry of a four-dimensional cylindrical surface nested
in a fictitious (auxiliary) five-dimensional space - Fig.5.1b.
*) Again, it should be noted
that the shape of the metric does not unequivocally determine the type of geometry, because
it is possible to assume different global topological properties,
as mentioned in §3.1. However, the choice of spherical geometry
is the simplest and most natural here .
The total volume of space in Einstein's universe is (assuming a spherical topology) equal to
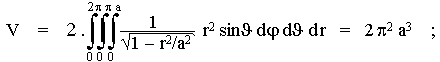 |
(5.11) |
the "perimeter" of the universe (the length of the principal circle of a three-dimensional sphere) is
| L = 0 ò 2p a dj = 2p a . |
Thus, Einstein's universe is finite, spatially closed; only a finite number of stars and galaxies "fit" into it.
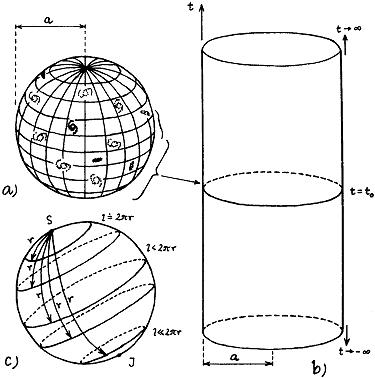
Fig.5.1. Einstein's cosmological model.
a ) The
geometry of three-dimensional space in Einstein's model of the
universe can be imagined as a three-dimensional hypersphere with
a constant radius, embedded in a fictitious 4-dimensional
Euclidean space.
b ) The
total space-time geometry of the Einstein universe can be
displayed as the geometry of a four-dimensional cylindrical
surface nested in a fictitious five-dimensional space.
c ) The specific peculiarities of the
spatial geometry and topology of a
closed universe can be clearly illustrated on a spherical
surface, eg on a globe - see the text.
The spatial closedness of
the universe has interesting consequences, which can be easily
imagined using a two-dimensional analogy on a spherical surface,
for example on the surface of the globe (Fig.5.1c). If
we stand on a pole (which from a geometric point of view we can
place anywhere on a spherical surface) and describe circles with
an ever larger radius, we find that the ratio of the length of
the circle to the radius will be less than 2p and
when crossing the "equator", the length of the circle
decreases with increasing radius. Similarly, when an observer
located anywhere in the closed universe demarcate spherical
surfaces around himself in a thought experiment, their surface
grows more slowly than the square of the radius, and after
exceeding a certain distance, the size of the surface begins to
decrease even as the distance (radius) increases. Another
characteristic of the geometry of the enclosed
space is the fact that the observer, still advancing straight in one
direction, for a period of time returns to the starting point (from the opposite side). The same is
true for rays of light: light sent from somewhere in a certain
direction "orbits the universe" and returns to the
starting point from the opposite direction. So if we look
ahead in a closed universe, we can see our own backs in the
distance after a certain time. Similar "ghosts" arise here when observing
each luminous object *), so we could see some stars or galaxies
twice in different places in the sky (however, the search for
identical duplicate objects in opposite places in the sky was not
successful).
*) By the way, this effect
would lead to Olbers' photometric paradox in Einstein's
cosmological model, similar to the earlier idea of an infinite
static universe. This is because each ray from each star will
constantly orbit the universe until it hits another star or
scatters on interstellar matter. In a closed static universe, in
which the average luminosity of the stars is the same for an
infinitely long time, it will not be dark at night, the sky will
be equally bright everywhere.
The relationships between the density, pressure, cosmological constant and radius of curvature of space in the Einstein cosmological model follow from equations (5.8) - (5.9) :
| 8p p = - 1/a2 + L , 8p r = 3/a2 - L , or L = 4p (r + 3p) , 1/a2 = 4p (r + p) . |
(5.12) |
Assuming that the matter of the universe consists of incoherent dust causing no pressure, it will
| L = 1 / a 2 = 4 p r , | (5.13) |
and the radius of curvature of space and its total volume is determined by the value of the cosmological constant :
| a = 1 / ÖL , V = 2 p 2 / Ö ( L 3 ) . | (5.14) |
The "total mass" of the universe is then equal to
| M = r . V = 1 / 2 p a = p / (2 ÖL ) ; | (5.15) |
however, the mass thus determined has only a formal significance from the point of view of non-gravitational physics as a measure of the amount of material particles filling the universe *). In the second extreme assumption that the universe is filled only with radiation for which p = r/3, we get
| L = 3 / 2a 2 , 4 p r = 3 / 4a 2 , 4 p p = 1 / 4a 2 . | (5.16) |
The effect of the total
gravitational field of the Einstein model on the test particle is
given by the equation of geodesy (2.5a). Substituting static
metrics (5.5) into the geodesic equation body which is at that
moment stationary relative to the surrounding mass, we obtain d2xi/dt2
= 0, so the total gravitational field
(space-time metric) in Einstein's universe cannot set a
motionless body in motion.
*) In fact, the total
gravitational mass, like the total electric charge of a closed
universe, has no real significance - it must be equal to zero. The electric charge and mass (4-momentum) contained in a spatial region are given
by the Gaussian integral fluxes (1.28) and (2.96) of the electric
and gravitational field over a closed surface bounding this
region. If we increase the spatial area in a closed space in
which we determine the amount of matter and electric charge, the
bounding box first increases, but then it begins to decrease
until it retracts to a point - see Fig.5.1c. The surface of the
closed area bounding
the whole universe is therefore
zero, so that the total 4-momentum (2.96) and the electric charge (1.28a)
are therefore equal to zero. The laws of conservation of total
energy, momentum and total electric charge of a closed universe
are thus reduced to physically meaningless identities 0 = 0. From a physical point of view, the
principal impossibility of determining the total mass or electric
charge of a closed universe is clear: there is no external
spacetime where the observer could stand and explore this
universe "from the outside" - eg "weigh it on a dish of some gigantic
scales" or to have a
test body run around it.
De
Sitter's cosmological model
Analogously to the previous Einstein case A'
= 0, equation (5.8)
is solved for the case r + p = 0. Using the requirement
that for small r the searched metric (3.45) changes to
Minkowski's form, we get
1 / A = B = 1 - r 2 ( L + 8 pr ) / 3 .
So the metric of de Sitter's model of the universe is
| (5.17) |
where the constant a is defined by the relation
| 1 / a 2 = ( L + 8 p r ) / 3 . | (5.18) |
For the motion of test particles and the propagation of light signals, which is generally given by the equation of geodesy (2.5a), for the deSitter metric after adjustments (thanks to spherical symmetry, it is enough to investigated the movement only in the plane J = p/2 without prejudice to generality) the equation is obtained
![]()
(H and L are integration constants); the speed of light in the de Sitter model is given by the relation dr/dt = ± (1 - r2/a2) for the case of purely radial propagation. From these equations it can be seen first of all, that at r = a the speed of motion of the particles and the coordinate speed of light become zero. By integrating from r=0 to r=a we find that from the point of view of the observer in the center r=0, every particle and light from the center r=0 to the place r=a arrives only in an infinitely long time. Thus, the observer in the deSitter model can never obtain any information about what happens at distances greater than a from it: in the de Sitter model there is a causal horizon of the universe at a distance r = a = Ö(3/(L +8pr) (= Ö(3/L) for r = 0).
It follows from the equations of motion that the originally stationary body will have a radial acceleration d2r/dt2 = r.(1 - r2/a2)/a, which increases with distance from the origin of local coordinates (which can be located at any point). If particles are homogeneously and isotropically distributed in the de Sitter universe, they will move away from each other at a speed proportional to their distance. The metric of the de Sitter universe is static (it does not depend on time in the given frame of reference), but in the interval (5.17) the coefficient at dt is no longer constant. Unlike Einstein's model, the total gravitational field (space-time metric) in de Sitter's universe causes the scattering of celestial bodies - as if each point were a repulsive center. The law of inertia does not apply here for large distances, the bodies will expand from each other with increasing speed. This variability in the own distances of the particles will cause a Doppler spectral shift of the light emitted by these particles; at not too large distances r, the Hubble's law dl/l » H.r will apply approximately for this frequency shift , where the " Hubble constant" H = a-1 = Ö[(L + 8pr)/3] (= Ö(L/3) for r = 0).
Thus, since de Sitter's
model captures the observed redshift of the spectrum of distant
sources in space, it could at first glance be considered a
realistic cosmological model. In reality, however, this model is
not physically consistent. The basic condition on which de
Sitter's universe is based is r
+ p = 0. The
intrinsic density of matter r
is (by its physical
nature) always non-negative. Although the pressure p
can in principle be negative, no form of matter creates such a
negative pressure, the absolute magnitude of which would approach
the density of matter r (in geometrodynamic units) - see
also §2.6 *). The condition r
+ p = 0 can
therefore be satisfied in practice only if r= 0
and p= 0. De Sitter's model thus corresponds to a completely empty universe , which does not contain any appreciable
amount of matter or radiation. Existing stars and galaxies should
be considered in this model as "test particles" that do
not contribute to the overall cosmological gravitational field.
And this is against the spirit of the general theory of
relativity, which puts gravity and the geometry of
space-time directly related to the distribution of matter.
*) However, current quantum unitary field
theories allow for the possibility of large negative pressures
leading to antigravity effects. According to this, the de Sitter
expansion could actually have taken place in a very early
universe (inflation expansion) - see §5.5 "Microphysics
and cosmology. Inflationary
universe.".
Government of cosmological
constant
De Sitter's model represents a cosmological solution of
Einstein's gravitational equations GTR for a universe in which
there is virtually no matter and radiation. The only thing that
determines the dynamics of the universe here - the behavior of
the scale factor a - is the cosmological constant L. From Fridman's
equations (5.23) (in the following §5.3
"Fridman's dynamic models of the universe") under conditions r = 0, p = 0, L> 0, follows for
time dependence of the scale factor a the exponential
dependence
| a (t) ~ e H . t = e Ö(L/3) . t , | (5.19) |
where H is the instantaneous value of
the "Hubble constant" (5.24) generated by the
cosmological constant L.
De Sitter's model is inadequate for the current universe
in the era of matter, in the evolution of which luminous
and dark matter play a significant role, as well as in the
earlier era of radiation. However, it could be adequate
in a very early period, in a time range aprox. 10-36 ÷ 10-32 sec., when a short
but powerful inflationary expansion is
theoretically assumed (§5.5 "Microphysics
and cosmology. Inflationary universe."). And also in the distant
future: if the currently observed
accelerated expansion of the universe is caused by a cosmological
constant generating dark energy, the universe
will continue to expand, all matter and radiation will dilute to
almost zero (§5.6, section "Dark
energy and accented expansion of the universe"). The vacuum energy
generated by the cosmological constant will then dominate and the
universe will expand exponentially (5.19) according to
de Sitter's model.
Cosmological
constant
Let us now
notice the general nature of the cosmological term. When Einstein
introduced the cosmological term, he placed it on the left side of the equation: Gik + L .gik = (8p G/c4) Tik , thus expressing that it is a geometric
property of space itself (spacetime).
However, the physical
significance
of the cosmological member becomes clearer after its
transfer to the right-hand side
of Einstein's equations
| Rik - 1/2 gik R = (8pG/c4) Tik + L.gik , | (5.7 ') |
ie from its inclusion in
the energy-momentum tensor Tik . If we consider the case of
vacuum Tik = 0, it can be seen that L.gik represents a kind of immanent
fundamentally irreversible curvature of empty space, which
is applied even without any matter,
radiation and
gravitational waves (for the ability of
gravitational waves to curve space-time and "imitate"
matter §2.8 and §B.3); in other words, the cosmological term
expresses the gravitational effects
of a vacuum.
If were L
¹ 0, it means that
the vacuum creates a gravitational field, as if it was (from the
point of view of the usual approach L=0)
filled with matter with effective density rcosm = c2 .L/8pG and effective pressure pcosm = -c4 L/8pG = - ecosm (ecosm is the effective energy density
of this fictitious mass), which corresponds to the equation of
state p = - r. c2 .
The cosmological term can be
considered as a manifestation of some "exotic" type of
matter - vacuum energy. It penetrates the entire space
and continuously fills it with a certain basic
energy density, even without the presence of
"normal" matter (in substance form). It does not dilute
with the expansion of the universe, nor does it cluster as a substance form of matter, but maintains a constant density *), contributing to the general energy
density, which gravitationally influences the dynamics of the
evolution of the universe.
*) Truth be told, this is how a standard
"geometrically induced" cosmological term behaves. In
principle, a physically conceived cosmological term could change
over time and also have a different value in different areas of
the universe..?..
According to current
astronomical measurements, the value of this vacuum energy is
very close to zero, less than about 10-9 J/m3, which corresponds to
a mass density of about 10-26 kg/m3.
The physical nature
and origin of the cosmological term ?
From the
point of view of the general theory of relativity, the
introduction of the cosmological constant as another independent
universal natural constant is purely phenomenological, although
the cosmological term may be an organic part of field equations
(§3.5) - the introduction of the cosmological member L.gik is the only permissible
modification of Einstein's equations in the sense that it does not
violate the law of conservation of energy Tik;
k = 0, because
the covariant 4-divergence of the tensor Rik - (1/2) gik R + L.gik is identically equal to zero as for
the tensor Gik º Rik - (1/2) gik R.
But what is the physical nature and origin of the cosmological term?
Attempts have been made to relate L to the "vacuum physics" of quantum field theory : the cosmological term should
be the result of polarization and quantum
fluctuations of the vacuum. Immediate calculation (resp. dimensional estimation), encompassing all vibrational modes of
energy with a wavelength greater than the Planck length (10-35 m), however gives
an unimaginably high vacuum energy density,
corresponding to a density rcosm ~ 1096 kg/m3..!.. In order for a vacuum to
look like an empty space, far-reaching compensations must be applied between the
vacuum fluctuations of the various fields, which cancel out the vast majority of the fluctuations.
No satisfactory explanation of
the cosmological constant based on microphysics yet exists;
perhaps some hopes are promised by calibration unitary field theories, where spontaneous disruption of
the symmetry of the Higgs scalar field could "generate"
a cosmological constant [113]..?.. - see also §5.5.
The history of the cosmological constant is quite varied, opinions on its significance have changed significantly during the development (from the beginning of the 1920s to the present). There have been periods when the cosmological member was completely rejected (eg after the creation of Fridman's model of the expanding universe and Hubble's discovery of the cosmological redshift), with periods of some "renaissance" when the cosmological member was to explain supposed or actual facts .
Most astronomical observations do not require L ¹ 0, but they do not strictly exclude this
possibility *) . The
study of extragalactic objects only increasingly limits the value
of the cosmological constant (now |L|
<~ 10-55 cm-2), so that the theory does not
contradict the results of observations of the available part of
the universe. It is obvious that laboratory determination of such a
small value of L is completely
hopeless. Even such a
small cosmological constant, however, could significantly affect the
structure and evolution of the universe as a whole. In the
interest of objectivity, it is therefore necessary to remember
the possibility of L ¹ 0 and to consider the
cosmolological term when studying the global properties of the
universe.
Inflationary
expansion, dark energy
?
In addition, it has recently been shouwn, that the cosmological term
could play a significant role in the earliest stages of the
universe's evolution, when the effects of quantum field theory
and uniformity of fundamental interactions manifested themselves
- the cosmological constant could be the "driving
force" of inflationary
expansion of the universe, as shown in §5.5 "Microphysics
and Cosmology. Inflationary Universe.".
According to current astronomical observations of
distant supernovae, there are strong indications that the expansion
of the universe is currently accelerating,
that in addition to ordinary matter and dark (non-radiant)
matter, there is also so-called dark energy in
space, which shows "antigravity ". So it seems that the
late evolution of the universe takes place under the influence of
the cosmological constant L>0 - it is discussed in
§5.6 "The Future of the Universe.The Arrow of Time.",
the passage "Dark Energy and the Accelerated
Expansion of the Universe".
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||