Four-dimensional spacetime and special theory of relativity

Spacetime and Relativity
We will assume that the reader is familiar with the basics of special theory of relativity (STR), or has at least some awareness of it *). For the coherence and compactness of the book, however, we include a chapter with a brief explanation of the special theory of relativity from a somewhat more general point of view, leading to the theory of space, time, electromagnetism and especially gravity.
*) The basics of STR are now included in the curriculum of high school physics. For a more detailed study of STR, we can recommend a great monograph by V.Votruba [263], then the relevant chapters in [183], [250], [271], [135], etc.
The aim of this chapter is not a detailed and comprehensive interpretation of the special theory of relativity, but rather recall and emphasize key elements of logical structures of relativistic physics and give an overview of the basic concepts, phenomena and relations of the special theory of relativity, to which we will refer in the following. We will also get acquainted with the geometric properties of 4-dimensional spacetime and give a 4-dimensional tensor formulation of the laws of mechanics and electrodynamics; this will often be used in subsequent chapters in terms of general theory of relativity, astrophysics, and cosmology .

Points and events in space and time
From a factual point of view, nature can be considered a world of events: every physical process can be divided into a sequence of individual elementary events. The event is, for example, the collision of two particles, the decay of the nucleus of an atom, the flashing of a lamp. The movement of the test particle is a sequence of events "the particle occurs at a certain place in a certain time moment". Experience teaches us that each event can be completely and unambiguously characterized by four numbers: the place "where" happened (3 spatial coordinates x, y, z *) and the time "when" happened (time instant of t ).
*) Numerical values and geometric meaning of these coordinates of individual points depend on the coordinate system used. The most used is the orthonormal so-called Cartesian coordinate system, which was introduced for the two-dimensional case of the plane by René Descartes (1596-1650); the name " Cartesian " is related to the Latin transcription of Descartes' name "Cartesius". This system consists of mutually perpendicular lines X, Y, Z - axes, intersecting at a common point called the origin of the coordinate system O (from Latin Origin ). The position (x, y, z) of any point P(x, y, z) is given here by the intersections of the perpendiculars running from this point to the individual axes X, Y, Z; we assign zero values of coordinates x = y = z = 0 to the origin O. Oriented line r from the beginning O to the point P we call the guide or the position vector (radius-vector) of the point P (for vectors see below).
In the next explanation we will meet even with more general coordinate systems - linear oblique coordinates (see below the section "Lorentz transformations and relativistic kinematics", Fig.1.5c) and especially with curvilinear coordinates (almost the rest of the book, starting with §2.1), where the position of points is determined by the intersections of precisely defined curves. The most common examples of curvilinear coordinates in a plane are polar coordinates (r, j), in space spherical coordinates (r, J , j) - see §3.2, §3.4.

Coordinate transformations. Scalars, vectors, tensors.
The choice of origin, orientation and scale of the coordinate axes is completely arbitrary; it is usually motivated only by the greatest possible simplicity of expressing the studied task. In general, however, we encounter coordinate systems whose origins are shifted relative to each other, the axes are rotated relative to each other, the scales on the axes are different. We then need to find the transfer - transformation - relationships between the coordinates of the points and other quantities, expressed in both systems S and S'.
The conversion of point coordinate values, expressed in different coordinate systems, is performed using algebraic-geometric relations, resulting from the analysis of positional relations between coordinate axes. In the case of a simple shift (translation) of the origins O, O' of the coordinate system O(x_o, y , z_o), the relations between the coordinates x, y, z and x', y', z' are given simply x' = x-x_o , y' = y-y_o , z' = z-z_o . When rotating the Cartesian reference system by a certain angle a around some axis, the transformation relations are given by the sinuses and cosines of the angle of rotation, eg around the Z axis: x '= x.cos a + y.sin a , y' = -x.sin a + y.cos a , z '= z. This is an example of linear coordinate transformations.
For a more compact notation of transformation relations, it is advantageous to denote the coordinates not by different letters (x, y, z), but by different indices: (x₁ , x₂ , x₃). The linear transformation can then be expressed by the equation x'_i = _{j = 1}S^³ a _ij .x _j , i = 1,2,3. We get an even more compact notation by introducing the so-called Einstein summation convention : if an index occurs twice in an expression, it means summation over this index, without listing the summation character "S" and the summation bounds (j = 1,2,3 in three-dimensional space) . Thus, we write the given transformation equation x'_i = a _ij.x ^j ; it is further customary to write summation indices one at the bottom and one at the top (here it is only formal, it has its significance for the so-called covariant and contravariant components of vectors and tensors, see below "Four-dimensional vectors and tensors"). The transformation equation x'_i = a_ij .x ^jalso describes general transformations between curvilinear coordinates, however, the coefficients a _ij are not constant, but are functions of place (coordinates) - see §2.4.
Mathematical and physical quantities can be classified according to their behavior in coordinate transformation :
¨ A scalar is a quantity that does not depend on the choice of the coordinate system - it is invariant (unchanged) during coordinate transformation. The numerical value of a scalar physical quantity can only depend on the choice of the units used (hence the name: lat. Scala = scale, ladder).
¨ Vectors in classical physics are called quantities which, in addition to their size, also have a certain direction in space (lat. Vector = rider, carrier). It is written in bold or an arrow above the character, it is represented with an arrow in space; the perpendicular projections of its length into the coordinate axes form the components of the vector. Typical examples are the position vector (guide, radius-vector) of a certain point r with components (x₁ , x₂ , x₃), velocity v with components v_i º dx_i /dt, momentum p with components p_i º m.v _i , acceleration a with components a _i º dv_i/dt, force F with components F_i º dp_i/dt. Since the direction is associated with the choice of the reference coordinate system, its components are transformed in the same way as the coordinates. From this point of view, we define the vector A as a trio of quantities A₁ , A₂ , A₃ (folder or components of vector), which is transformed in the same way as the coordinates when the coordinates x'_i = a_ij .x ^jaretransformed : A'_i = a _ij .A^j. The length, or absolute value or size of the vector, is the quantity A º |A| º (A _i .Aⁱ )^1/2 , which is a scalar.
¨ Tensors are called sets of quantities that are transformed as products of coordinates during coordinate transformations. The second-order tensor is called the set of quantities T_ij , which are transformed according to the law T'_ij = a _ik .a _jl .T^kl during the transformations of the coordinates x'_i = a_ik .x ^k (summed over k, l). Tensors are generalizations of vectors and describe quantities that are formed by products of vector components (such as angular momentum or quadrupole moment). The name "tensor " comes from the Latin word tensio = stress; they were first used to describe deformations of bodies by the action of a force vector on a vector-oriented planar element. Higher order tensors are defined analogously.

4-dimensional spacetime
From a mathematical point of view, each event can be displayed as a point in fictious four-dimensional space , the so-called spacetime (time-space), on the axes of which three spatial coordinates and time are plotted; points (events) in space-time are called worldpoints. The motion of a particle then corresponds to a certain line - the so-called world line - in this four-dimensional space-time, whose points determine the coordinates of the particle at individual time points (it can be said that over time, the world point corresponding to a given particle is continuously displace in space-time and describes a certain line - world line). A uniformly rectilinear moving particle corresponds to a straight line, the accelerated motion is expressed by a curved wordlline, the world line of a particle "standing" at rest with respect to a given frame of reference is a straight line parallel to the time axis. From the physical point of view, the worldline expresses the kinematic history of a particle, because each worldpoint expresses the position of the particle at a certain point in space and at a certain time. Because we cannot imagine spacetime in its four-dimensional form, one or two spatial dimensions are omitted for graphical drawing, thus creating a spatio-temporal diagram of the observed precess (Fig.1.6).
The introduction of four-dimensional spacetime in classical mechanics is so far only purely formal. It does not define metrics either, because the spatial dimension and the temporal dimension are not related in any way. It is the finding of deep connections between space and time and establishing metrics in four-dimensional space-time, that is the main succes of the special theory of relativity.

Classical Newtonian Mechanics
Classical mechanics is based on three of Newton's laws :

1. Law of inertia :
A body which is not acted upon by an external force remains at rest or in uniform rectilinear motion, ie v º d r / dt = const.
Note:This formulation refers to an idealized material particle without macroscopic dimensions and internal structure. For real macroscopic bodies, from a phenomenological point of view, the law of inertia for translational motion can be supplemented by the possibility of inertial rotation : " The body remains at rest or in uniform rectilinear or rotational motion until it is forced to change this state by force ". The adjective "external" in force may no longer apply here - see eg " pirouette effect"for a figure skater who reduces her moment of inertia by fitting her hands (by internal force action) , which leads to an increase in her rotational speed.
However, these external complex circumstances do not need to be taken into account in a fundamental physical analysis - in fact, they are summarized by the laws of mechanics for the individual particles of which the body is composed. The rotational inertial motion of a body is formed by a uniform circular motion of individual particles of the body around a rotational axis, in which the centrifugal force is compensated by the mechanical strength of the body material (essentially electrical bonding forces between atoms and molecules). Internally, it is an uneven motion of particles with centripetal acceleration caused by internal forces according to 2. Newton's law; it does not change size, but only the direction of speed. These movements, arising from the co-production of the law of inertia with the law of force and acceleration, fall into the field of solid mechanics , but are also applied in hydrodynamics . It is not necessary to introduce rotational motion into the basic formulation of the law of inertia - in the spirit of "Occam's razor". The real fundamental law of inertia thus lies in the above basic formulation 1 for translational motion.

2. Law of motion (force and acceleration) :
Acceleration of a body is directly proportional to the force acting on it, i.e. F = m. a , where F is the applied force, a º dv / dt º d²r / dt² is the acceleration, m is the (inertial) mass of the body.

3. Law of action and reaction :
In the interaction of two bodies, the force exerted by the second body on the first, of the same magnitude but in the opposite direction than the force exerted by the first body on the second: F_AB = - F_BA .

From a formal-mathematical point of view, the first law is a special case of the second law (for F = 0, a = 0, ie v = const.) . Nevertheless, the law of inertia has a fundamental and independent physical meaning, because the terms "velocity", "acceleration", "calm", "linear motion" appearing in Newton's laws, can be defined only when is pre-determined the frame of reference, with respect to which the motion of bodies is investigated. Newton's laws of 2nd and 3rd apply only in the inertial frame of reference, given by the law of inertia 1 .
These three basic laws of "terrestrial" mechanics are associated by Newton's law of gravitation (§1.2 "Newton's law of gravity") , which is the starting point of the so-called "celestial" mechanics of the motion of stars, planets and moons around them.

Reference system. Position and time measurement.
Whenever we talk about movement, we always mean movement in relation to the frame of reference. The reference system *) means a system of spatial coordinates indicating the position of bodies in space and a clock used to determine time intervals. The simplest way to measure the positional coordinates and distances of bodies in space is by applying sufficiently rigid and accurate - standard, ideal - measuring rods. The most common way to measure time is to use a periodic process (regularly recurring); the criterion of correctness is that the periodicity of one process agrees with the periodicity of others procesces. Factors that affect only some such processes (eg material temperature) are "non- universal", have a disruptive effect and must be removed or corrected during objective measurement. In the following, we will assume that all spatial and temporal measurements are performed using standard (ideal) clocks and measuring rods, ie such rods and clocks for which all non-universal disturbances are removed or corrected (discussed further in the section "Exact - ideal - measuring space and time"). In contrast, factors affecting all periodic processes in the same way (running of all clocks) and the lengths of all measuring rods - universal influences - cannot be corrected in any way and must be considered as influencing the course of time itself and the properties of space itself. In modern physics, we do not look at space and time as metaphysical categories, but as an expression of the relationship between objects and events.
*) The terms "reference system" and "coordinate system" are often merged. It can be said that :

Between the reference system and coordinate system is roughly the difference similar as between a landscape with real landmarks, and its map with cartographic coordinates. The reference system is based on certain real bodies forming "support points"; with their help, imaginary lines are drawn and individual places are provided with numbers - a system of coordinates is created. It should be noted that in general :

From a physical point of view, however, it is usually not necessary to distinguish the two concepts too much (an exception is, for example, the issue of gravitational energy - see §2.8).

Exact - ideal - measurement of space and time
For accurate measurement of physical quantities, it is generally necessary to use such methods, aids and devices that are sensitive enough to the measured quantity and are not affected by other interfering influences and circumstances of measurement. If this is not the case, at least an accurate correction for these disturbances and distortions must be possible. For the measurement of space and time in fundamental physics, especially in the theory of relativity, standard idealized clocks and measuring rods are introduced as models :
Ideal clocks
are calibrated clocks whose speed (frequency of used periodic events) is not affected by any non-universal influences such as temperature or applied forces. Thus, a pendulum or hourglass clock would be completely unusable here (whose running speed is directly determined by gravity, it stops in a weightless state); similarly, other mechanical clocks could be affected by mechanical deformations of their components. The most suitable in this respect are electronic oscillators, their most accurate variant is the atomic clock :
Atomic clock
The electronic basis of the atomic clock is a crystal-controlled oscillator - a small precision-cut piezoelectric quartz crystal tuned to a high Gigahertz frequency corresponding to the oscillations of the atoms used. The relative accuracy of this electro-mechanical oscillator alone reaches up to about 10^-7 (absolutely sufficient for most applications). Another substantial increase in accuracy is achieved here by sensitive electronic tuning of the oscillator by means of a feedback loop with a resonant frequency of the type of atoms used. The most common are cesium atoms with a resonant frequency of 9.192631770 GHz . The amplified signal from the crystal oscillator is connected to a radio wave transmitter to which cesium atoms are exposed in the chamber. If the frequency - resonance - of the oscillator coincides with the frequency of transition between the ground and excited levels of hyperfine splitting of energy levels in the cesium electron shell (caused by the interaction of nucleus spins and electrons), the cesium atoms go into the excited condition. By applying a magnetic field, these excited atoms are separated and detected. Using the number of excited cesium atoms, the frequency of the crystal oscillator is continuously tuned electronically in the feedback so that it constantly coincides with the resonant frequency of the transitions of the cesium atoms - 9 192 631 770 Hz *). The number of these oscillations then measures time very accurately. The source of the exact frequency here comes directly from the electron shell of the atoms, which is stable and is not affected by any common external influences. In the end, we get a "atomic shell-controlled oscillator " of cesium, which achieves a relative accuracy of 10^-13.
*) Based on the atomic clock, a new definition of the second was introduced in 1967 - as a time interval corresponding to 9,192,631,770 electromagnetic periods. radiation generated during the transition between two levels of the very fine structure of the ground state of the cesium 133-Cs atom.
Today's atomic clocks are quite complex and quite large laboratory equipment. However, with advances in technology, they can be expected to be at least partially miniaturized and compacted in the near future so that they can be used in "field" and space probes.
Ideal measuring rods
are length-calibrated scales whose length is not affected by any non-universal influences such as temperature or applied forces. Ideal measuring rods should therefore be made of a non-thermally expandable material, sufficiently strong and rigid.
If the influence of non-universal factors cannot be avoided (which is usually not 100% possible), a correction must be made for these non-universal influences. In physical practice, especially in the theory of relativity, "clocks" and "rods" are usually not used directly to measure times and lengths, but more complex methods using electromagnetic radiation - optical and radar methods . Rather, measuring rods and precision clocks are used to calibrate these methods.

In practice, the reference system is always realized by some material bodies. The reference system can be laboratory walls, the Earth's surface, the center of our Galaxy, the walls of the space rocket cabin, etc. In principle, any reference systems can be used, although in specific cases some of them may be more suitable for describing certain events than others. It is clear that for studying the motion of the planets is preferable reference system connection with the sun than the system with some of Jupiter months, or for monitoring the tennis ball is more suitable reference system consisting tennis court system than about associated with passing cars...
Newton's first law is then a statement that there are so-called inertial frames of reference, in which the law of inertia applies. It is clear that any reference system S', which moves uniformly in a straight line with respect to a given inertial system S , is also inertial; thus there are an infinite number of inertial systems. On the contrary, systems that move with respect to the inertial system with non-zero acceleration are not inertial - the law of inertia does not apply in them. The inertial frame of reference is idealization; in the general theory of relativity it is shown that global inertial systems do not exist, but it is always possible to find a local inertial system which in a sufficiently limited spatial area has all the properties of a real inertial frame of reference.

Galileo transformation and relativity
Consider two inertial frames of reference S and S' with parallel oriented Cartesian spatial coordinates x, y, z and x', y ', z' (Fig.1.5a) such that the system S' moves with respect to the system S in the direction of the X axis at speed V ; for the origin t = 0 = t' countdown of time in both systems we choose the moment when the origins O and O' of both systems coincided. If we measure position coordinates and time intervals in both systems with the same standard bars and clocks (which we will always assume in the next one), the relationship between coordinates and times measured in the non-dashed and dashed system will be the so-called Galileo transformation :

In the more general case, when the inertial system S' moves with respect to S at the velocity V in the general direction, the Galileo transformation has a vector form

Galileo's transformation (1.64) is an expression of common kinematic and geometric notions resulting from everyday experience. From Galileo's transformation follows the common additive law of velocity addition: if a body moves with velocity v' with respect to the system S', then in the system S its velocity is

that is, the velocity of the body in the non-dashed system is increased by the velocity V of the dashed system with respect to the non-dashed system (resp., both velocities are composed vectorially) .
Experience expressed in classical (Galileo and Newton) mechanics teaches, that there is no absolute rest or absolute velocity of uniform rectilinear motion. Galileo's principle of relativity argues that the laws of mechanics are the same for every inertial frame of reference - all inertial systems are equivalent in terms of classical mechanics; no internal mechanical experiment can determine how fast a given inertial system moves. Galileo came to this conclusion by observing that the mechanical processes on a ship floating at a constant speed on a calm surface proceed as if the ship were at rest, so that mechanical experiments cannot make find out, that the ship is at rest or moving in a straight line.
Indeed, the laws of classical mechanics are invariant with respect to Galileo's transformations (1.64). E.g. 2.Newton law F = m. a º m.d²x / dt ² = m.d² ( x + V .t) / dt² = m.d²x / dt² = F (if the external force does not depend on the velocity of motion of the body, ie F = F') retains its shape and the numerical value of the coefficient of proportionality m in Galileo transformations between by two inertial systems, similar to any displacements or rotations of the spatial coordinate axes. The laws of conservation of energy and momentum are also invariant to Galileo's transformation.
In formulating Newton's laws of classical mechanics, the fulfillment of two (seemingly) obvious assumptions is tacitly assumed :
a)Assumption of universal (absolute) time, according to which the time intervals between events are independent of the choice of the reference system.
b)The distances of the current positions of the points (and thus also the dimensions of the bodies) are absolute , ie independent of the choice of the reference system with respect to which the positions of these points are determined.
Both of these assumptions are contained in Galileo's transformation equations (1.64). Newton introduced the notion of "absolute space" and inertia was considered an attempt by material bodies to preserve the "state of motion" in this absolute space. However, the concept of absolute space is empty in classical mechanics, because due to the validity of Galileo's principle of relativity, nor the most careful examination of any mechanical phenomena can determine which body or reference system is in the "absolute rest". With no mechanical experiment by themselves can not distinguish two inertial system. If some physical laws differed for different relative moving observers, it would be possible based on these differences to determine, which objects are in the space in (absolute) stillness and which move.
It has long been thought that electromagnetic phenomena are such phenomena that make it possible to distinguish different inertial systems (and thus to distinguish absolute motion and rest). Galileo's principle of relativity proved to be incompatible with the classical Maxwell's electrodynamics. If we use Galileo's relations (1.64) to mutually transform equivalent quantities in the systems S and S' , Maxwell's equations will have a different form. Electromagnetic phenomena would therefore carried out differently in different inertial systems. Maxwell's equations are not invariant with respect to Galileo transformations. It follows from the law of velocity composition (1.65) that if the speed of light with respect to some "basic" inertial system S is equal to c , then with respect to another inertial system S', this velocity decreases or increases as the light beam moves in the direction or against the direction of movement of the dashed system with respect to the non-dashed system. The speed of light would therefore be different in different inertial systems.
According to this, Maxwell's theory could only apply in one of an infinite number of inertial systems; we could consider this significant system as an "absolute frame of reference" in accordance with Newton's conception. According to the ether hypothesis, such a system is represented by a stationary light-carrying ether, or it could be a system connected to the center of gravity of all the matter in the universe.
Accurate measurements by Michelson and Morley, who (with the intention of directly experimentally confirming the existence of the ether, determining the absolute frame of reference and determining the speed of absolute motion of the Earth relative to it) between 1881 and 1904 measured the speed of light in and against the direction of the Earth motion, showed that the speed of light in a vacuum it is the same in different inertial systems.

Einstein's special theory of relativity
Negative result of experiments Michelson and Morley, which was later repeatedly and accurately re-verified, physicists initially tried to explain (or rather to reconcile it with the classical physical opinions) introducing some artificial assumptions and additional hypotheses. However, these hypotheses do not stand in confrontation with the results of other experiments and observations. E.g. the simplest of them - the assumption that the ether is "entrained" around the Earth by its motion and is therefore locally at rest with it - is incompatible with the observed aberration of light of the stars. Lorentz on the basis of the study of the motion of electrons stated a contraction hypothesis, according to which the length of each body moving at velocity v shortens in the direction of movement in the ratio Ö(1 - v²/c²) compared to its rest length. However, the introduction of additional ad hoc hypotheses, which replace one mystery with another, cannot be a satisfactory explanation for any phenomenon.
The principle of relativity
A.Einstein took a new, completely principled position on the contradiction between mechanics and electromagnetism, unburdened by prejudices of mechanistic ideas. Einstein realized that measuring the speed of light in any inertial system gives the same result c @ 2,998 .10⁸ m/s, which is not at all contradictory, but on the contrary in full accordance with the principle of relativity valid in mechanics. In his epoch - making work "On the electrodynamics of moving bodies" [78] Einstein generalized Galileo's principle of relativity from mechanics to all physical phenomena :

Thus, all inertial systems are completely equivalent for the description of all physical processes; under the same physical conditions, physical phenomena take place in the same way in each inertial system, regardless of the speed of its movement. Every physical experiment turns out the same whether we perform it in any inertial system. Einstein's special principle of relativity is thus an expression of the undetectability and non-existence of a universal (absolute) reference system.
The special principle of relativity is also a reflection of the unity of physics, the common material essence of nature. No electromagnetic experiment can not be carried out without the use of physical bodies governed by the laws of mechanics and vice versa, every mechanical action involves an electromagnetic interaction between the particles of material of moving bodies. It follows from the validity of (Galileo's) principle of relativity in mechanics, that electromagnetic and other phenomena should also comply with the principle of relativity.
Why the name "special" and "general"?
Einstein's work from 1905 established the theory of relativity as such. It dealt with inertial frames of reference moving relative to each other. In principle, however, it could also work with accelerating frames of reference, but where "fictitious" forces arise (such as centrifugal force).
Einstein then tries to find a more general approach that would treat both inertial and accelerated systems equally, as if they were "equal". He arrived at the fundamental idea of the universality of gravity - the principle of equivalence of gravity and acceleration forces. In 1915, a newer generalized theory of relativity was created, which included inertia and gravity in mutual equivalence and in co-production with generalized Lorentz transformations even the geometry of curved spacetime.
In the absence of gravity, the new generalized theory reduces to the original relativity from 1905 - it is a special case in the absence of gravity. Therefore, the theory from 1905 began to be called "special theory of relativity" and the newer theory from 1915, including gravity, is called "general theory of relativity".
The principle of constant speed of light
In Newtonian mechanics, of course, the special principle of relativity is fulfilled. In order for the special principle of relativity to apply to electromagnetic phenomena described by Maxwell's equations, the quantity c (contained in Maxwell's equations either directly or through vacuum permittivity) indicating the speed of propagation of electromagnetic waves in vacuum, in all inertial systems must have the same value (from a general-physical point of view the speed of light is discussed in §1.1, passage "Speed of light"). The application of the special principle of relativity to electrodynamics thus naturally explains the result of Michelson's experiment.
However, in the axiomatic construction of a general theory, which should be the basis of all physics, the use of complex Maxwell's equations (describing a specific field of electromagnetic phenomena) as a starting axiom is disadvantageous. Einstein therefore took the knowledge of the constant of the speed of light as a primary independent postulate along with the special principle of relativity :

Classical Newtonian physics is based on the assumption of the instantaneous interaction of bodies: a change the position (or generally some characteristic) of one of the interacting bodies will be reflected on the other bodies at the same time, regardless of their distance. Formally, this is expressed by describing the interaction of particles using the potential energy U(x₁ , x₂ , ..., x_n ), which is a function of only the positional coordinates of the particles x_i. In reality, however, there is no direct, immediate action "in distance" in nature. If there is a change with one body, then on the other body that interacts with it, this change begins to manifest itself only after the certain final time interval. This time is needed for the interaction (the field that mediates it) to overcome the distance between the bodies. Thus, the interaction propagates at a finite rate, so that there is a certain maximum (limiting) rate of propagation of the interactions. From the first postulate of STR (special principle of relativity) it follows that this speed of propagation of interactions is the same in all inertial systems - it is therefore a universal constant. It follows from electrodynamics that this speed is equal to the speed of electromagnetic waves - the speed of light in vacuum c . The second basic postulate of STR can therefore also be formulated in the form :

There is a maximum velocity of interactions propagation in a vacuum, equal to the speed of light c , which is the same for all inertial reference frames .

Postulates 1.2 and 1.2' are not completely equivalent; formulation 1.2' excludes, for example, the possibility of the existence of tachyons (particles moving at super-light speed), because they could be used to interact at speeds in excess of the maximum rate of propagation of the interactions. However, tachyons can still be considered a figment of physicists' imagination, as there are no theoretical or experimental reasons for their existence (see below). The problems of relativistic astrophysics and cosmology are not affected by subtle differences in both formulations of the second basic postulate of STR.
The second postulate of the special theory of relativity - the existence of universal velocity, which does not add up in sizewith no other speed - it is in sharp contrast to the usual kinematic notions expressed by Galileo's transformations and based on the concept of absolute space and time. The usual rule of velocity addition does not apply here, simple Galileo transformations of coordinates between inertial systems must be replaced by more general transformations (Lorentz). Spatial distance and time interval cease to be objective absolute quantities *) , but depend on the reference frame of which measures - become relative. The principles of STR thus break down the usual intuitive concepts of space and time, based on experience with conventional movement of macroscopic bodies.
*) If the speed of light appears to be the same for observers moving at different speeds, this is only possible if their "watches" and "rulers" are different - time and space are different for different observers.
It can be said that when the speed of light c turned out to be absolute, the spatial scales and time intervals must be relative ...
Who is right? - or is wrong?
Within STR, observers moving at different speeds often differ on the size of the length proportions, the duration of time intervals, the time sequence (or present) of events. But it doesn't have to be that one of them was right and the other was wrong - everyone is right in its own frame of reference... But what all observers must legitimately agree on, is the objective existence and course of natural processes ! Whether two moving bodies collide or miss does, not depend on the observation frame; from the point of view of different systems, only the time indication may differ when and in what spatial coordinates this happens..?.. These questions are further discussed below in the passage "Paradoxes in the special theory of relativity".

Lorentz transformations and relativistic kinematics
Together with some other assumptions, such as the homogeneity and isotropy of space and time and their Euclidean geometric and topological properties, these two basic postulates 1.1 and 1.2 allow to establish new transformation relations, generalizing Galileo's transformation (1.64) for the transition from one inertial system to another, and to build a new kinematics and dynamics of the motion of material bodies - Einstein's special theory of relativity (STR).
Terminological note:
The name " special" because it is limited to inertial (evenly moving) systems, "relativity" because only relative motion is physically important. The word "relativity" further reflects the STR conclusions that some physical quantities - such as temporal and spatial intervals, present and same place of events, the weight of body - lose their former absolute importance and become relative magnitudes dependent moving reference frames ("observers"). However, one cannot agree with the oft-cited statement that "according to the theory of relativity, everything is relative"! Some important quantities, such as the speed of light or space-time intervals, on the other hand, are "absolute ", independent of the reference system (on the speed of motion of the observer).

Consider an inertial system S with the origin of O , coordinates x, y, z and time t , and further inertial system S' with the origin O', the coordinates x', y', z' and the time t' which moves relative to the S with velocity V. The physical measurements in the reference system S 'are carried out in the same way (using the same aids - standard measuring rods and synchronized clocks) as in the system S' . At time t = t' = 0, let a light flash be sent from the beginning of O , which at this moment coincides with O' (Fig.1.5b). In the S system, the propagation of this light signal is expressed by the equation

describing a spherical wavefront whose radius r = c.t increases with velocity c . In the reference system S' the light source moves at a speed -V, but due to the principle of constant speed of light (c' = c regardless of the speed and direction of movement of the source) the light signal propagation will look the same as in the system S :

In order to comply with the principle of constant speed of light, it is necessary to assume different times in both systems. From the simultaneous fulfillment of equations (1.66) and (1.66') will emerge the sought transformation relations between the coordinates (t, x, y, z) and (t', x', y', z').

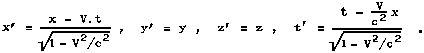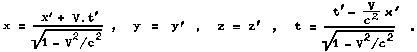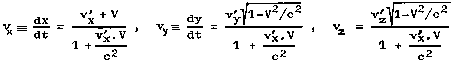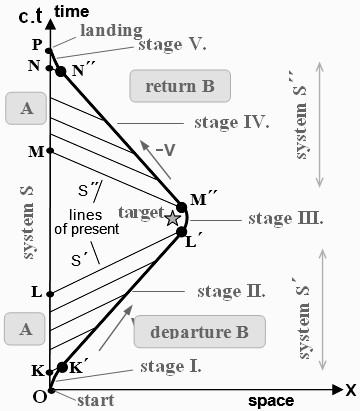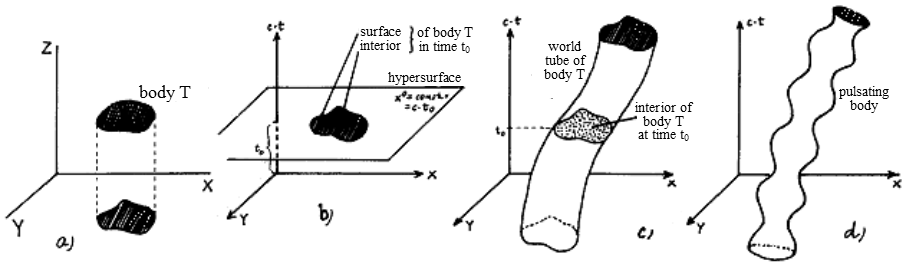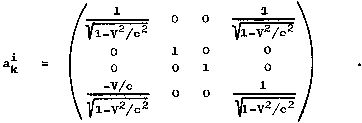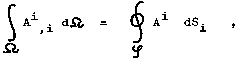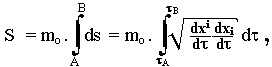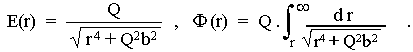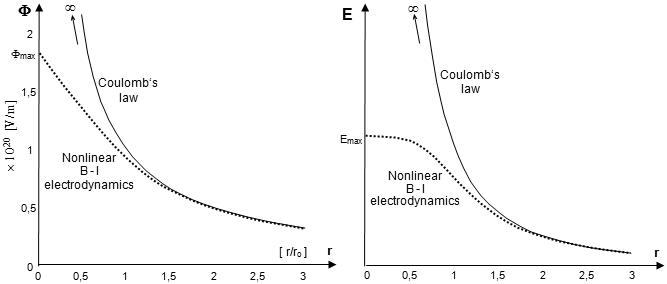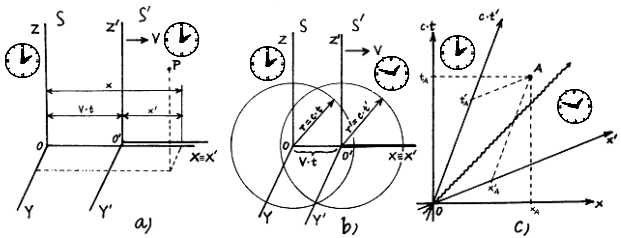
Fig.1.5. Coordinate transformations between inertial frames of reference.
a) Galileo transformation. b) Derivation of Lorentz transformation. The light flash emitted at time t = t' = 0 from the beginning O (which at that time coincided with O' ) propagates on all sides at the same speed c from the point of view of both systems S and S', so that at time t it fills the spherical wavefront o radius r = ct, resp. r' = c.t'.
c) Geometric representation of the Lorentz transformation. If the default reference frame is S in space-time ascribed (pseudo) Cartesian coordinate system ct, x, then the transition to the moving frame of reference S' geometrically means a deformation to oblique for the affine sharp-angled coordinates c.t', x'.
Note: The image of the clock symbolically shows the speed of time in the systems S and S' (see below - time dilation).

According to the principle of relativity, a body moving uniformly in a straight line from the point of view of the system S must also move uniformly in a straight line in the system S' . Therefore, the coordinates x', y', z', t' must be linear functions of the coordinates x, y, z, t. In order for equations (1.66) and (1.66') to be satisfied simultaneously, s'² = k.s² must hold , where k is a factor. This coefficient cannot depend on coordinates and time, because different points and moments of time would not be equivalent, which contradicts the homogeneity of space and time. The coefficient k cannot depend on the direction of velocity V either, because we assume the space in STR is isotropic; k could be a function of at most the magnitude of the velocity V = |V|, i.e. s' ² = k(V) .s² . However, the systems S and S' are equivalent. Therefore, the same consideration made from the point of view of the system S' with respect to which the non-dashed system moves at the speed -V shows that s ² = k (|-V|) .s'² = k(V) .s'², from which it follows k² = 1, so k = 1 (a positive sign applies in order to preserve the identity of the transformation of the system S to itself at V = 0). Quantity s , so-called space-time interval, defined in equations (1.66), thus remains invariant during the transformation between two inertial systems :

Consider, as with the Galileo transformation, the special case of Fig.1.5, where the axes of the two reference frames are parallel and in the same sense, the axes X and X' coincide and the system S' moves with respect to S at a constant speed V in the positive X axis. Then if y = 0, y'= 0 must be at any z and similarly if z = 0, z' = 0 must be at any y (areas XY and X'Y', as well as areas XZ and X'Z', transform themselves). Therefore, y' = k.y, z' = k.z where the coefficient k the same reasons as before, with an interval dependent on x, y, z, may be the only function of V . Coefficient k there is (again due to the indistinguishability of both systems) equal to one, so the coordinates perpendicular to the direction of motion do not change: y' = y, z' = z. The special transformation sought will therefore have (due to linearity) the form

This relationship must be fulfilled identically in all places of space and at all times, so that the coefficients at x and t on both sides must be equal to each other:

We obtain the fourth equation from it, of that system S' with respect to S moves along the axis X velocity V . The point O' at the moment t has the coordinates O' = (x = Vt, y = 0, z = 0) from the point of view of S , while from the point of view of S' there is still O' = (x' = 0, y' = 0, z' = 0). From the first equation (1.68) we get between A and B the relation x' = A.V.t + B.t = 0, ie A.V + B = 0. By solving this system of four equations we get the results for the transformation coefficients v (1.68),

A = 1/Ö(1-V²/c²) , B = -V/Ö(1-V²/c²) , P = (-V²/c²)/Ö(1-V²/c²) , Q = 1/Ö(1-V²/c²) ,

wherein the negative sign for B and P and the positive sign for A and Q is again due to the identity of the transformation at V ® 0.

This transformation, which generalizes the Galileo transformation (1.64) and guarantees the fulfillment of both basic postulates of STR, is called the Lorentz transformation. Even before the emergence of the special theory of relativity, Lorentz and Poincaré showed that Maxwell's equations of the electromagnetic field retain the same shape in two mutually moving inertial systems S and S' if between these systems not simple Galilei transformations but more complex transformations (1.69), called now Lorentz transformations. However, in his special theory of relativity, A.Einstein gave a general derivation of these transformations and showed that it is not just some peculiarity of a particular (electromagnetic) field, but they control all fields and all motion - they are an expression of the structural properties of space and time.
Spatio-temporal diagrams
For a clear graphical representation of spatial motions of bodies as a function of time - their worldline - the so-called spae-time diagrams in x, t coordinates are often drawn. Since STR deals with motions close to the speed of light, it is suitable in spacetime diagrams instead of the simple time t to plot its c-multiple - the time coordinate x ° = ct, so that the scale on the time axis is comparable to the scales on the spatial axes. Such a space-time diagram on which the horizontal axis x and the time axis perpendicular to it are marked (y and z coordinates are omitted for simplicity), corresponding to the initial reference system S , is shown in Fig.1.5c. On these coordinate axes, the space-time coordinates of any world point (event) in the reference system S can be read. In order to read these events spacetime are also in the reference frame S' moving relative to S in the direction of axis x with velocity V, the coordinate axes x' and x'° = c.t' corresponding to the system S' must be plotted on this diagram. The x' axis, which is given by the condition t' = 0, is according to (1.69) the line c.t = (V/c) .x; the axis t', given by the condition x' = 0, is the line x = (V/c) .ct. Thus, as can be seen from Fig.1.5c, the transition to another inertial system by means of Lorentz transformations geometrically means the transition to an oblique system of space-time coordinates, the axes of which are inclined with respect to the original axes by an angle a given by tg a = V/c. This angle of inclination a increases with the velocity of the system S' relative to S; at V ® c approaches 45°, where the x' and c.t' axes coincide. From such a geometric expression of the Lorentz transformation, the kinematic effects of STR, such as the contraction of lengths or the dilation of time, follow very clearly; the well-known paradox of the clock is also elegantly addressed here [232], [242] - it is analyzed in more detail below in the passage "Paradoxes STR" .
The inverted Lorentz transformations from the system S' to S are obtained due to the equivalence of both systems simply by exchanging the dashed and un dashed coordinates in the relations (1.69) and replacing the velocity V by -V :

The general Lorentz transformation, valid at any direction of the velocity V of the inertial system S' with respect to the system S , can be obtained from the special Lorentz transformation (1.69 ) by first using auxiliary coordinates such that movement occurs along the X axis, is applied (1.69) and then perform a backward transformation to the original coordinates. The general Lorentz transformation is usually written in vector form

where r º [O, (x, y, z)] is the position vector from the origin O to the event (t, x, y, z). Folding the two Lorentz transformations S ® S' and S ® S'' a proper Lorentz transformation between S and S'' only when the speed of system S'' to the system S' has the same direction as the velocity S' to the S . Physically, this is due to the fact that the magnitude of the speed of light c does not compose with any other speed, while the direction of the speed of light generally changes (aberrations of light, see below). Therefore, the general Lorentz transformation cannot be obtained by simply adding special Lorentz transformations in the individual X, Y, Z axes.

Kinematic effects of STR
From Lorentz transformations (1.69) follow the known kinematic effects of special theory of relativity - time dilation, length contraction and non-additive law of velocity addition :
If we have in the system S two same-place events x, y, z, t and x, y, z , t + Dt separated by the time interval Dt, then according to (1.69), since Dx = 0 (same-place), the time interval between these events measured from the system S' will be equal to

The time measured by an ideal clock moving with a given body is called the body's own time. This proper time t is related to the space-time interval by the relation (since dx = dy = dz = 0)

and is therefore also invariant. From relation (1.70), or equivalent by introducing velocity v² = (dx²+dy²+dz²)/dt² in relation dt = ds/c = (1/c)Ö(-c²dt²+dx²+dy²+dz²), we get

the interval of the proper time of the moving body is therefore always smaller than the corresponding interval of the coordinate time. An observer comparing the movement of the rest and moving clocks finds that the moving clocks go according to the relation (1.70) the slower the faster they move; this phenomenon is called time dilation.

Fig.1.5 - presented for clarity again
a) In classical mechanics (Galileo transform) the velocity of time is the same in all inertial systems, regardless of their velocity.
b), c) In the special theory of relativity, the effect of time dilation is applied - in a moving system S' time flows slower than in the initial rest system S .

In pre-relativistic physics, the simultaneity of two events taking place in different places could be convinced by means of a suitable signal, such as a light signal, for the speed of which the common law of speed composition applied. Two current events in terms of one frame of reference are then simultaneous in every other inertial system - the concept of the present has absolute meaning in classical physics and does not depend on the state of motion of the observer. From the Lorentz transformation (and actually has a simple consideration of the independence of the speed of light on moving reference frame) also suggests that the two events taking place in different locations, which in terms of a reference system appears to be present, runs in terms of other systems in different moments of time. So it is in STR the simultaneity concept of relative, depends on the state of motion of the observer. According to the STR, it is necessary to use light signals to define the simultaneity, for which the independence of their speed on the reference system is guaranteed.
Similarly, the dimensions of bodies and the distances between them in non-relativistic kinematics do not depend on whether they are observed by a resting or moving observer. To determine the length of a body (rod, scale) in STR, it is necessary to determine the current values of the coordinates x₁ , y₁ , z₁ and x₂ , y₂ , z₂of its ends at a given moment in the given reference system S. The length in the x direction is then Dx = x₂ - x ₁ , similarly in the y and z directions. If we do the same in terms of the reference system S' moving at velocity V , then from the Lorentz transformations (where Dt = 0 - present) it follows

The proper length of a given rod means its length l_o measured in the reference system with respect to which this rod is at rest. From relation (1.73) it follows that the length of the rod moving in the longitudinal direction at velocity v will be

This finding, called the Lorentz contraction of lengths, says that the dimension of each body appears to be shortened in the direction of motion in the ratio Ö(1 - v²/c²) compared to the rest dimension; the dimensions perpendicular to the direction of movement do not change, they are the same as the rest ones.

The Lorentz transformation formulas (1.69) also show the relationships between the particle velocities measured in different inertial systems. If in a system S' moving relative to a system S with velocity V in the direction of the X axis , the investigated particle will have velocity v º (v'_x = dx'/ dt', v'_y = dy' / dt ', v'_z = dz'/ dt'), then from the relations (1.69) rewritten in differential form, flow for the components of the velocity v in the system S transformation relations

representing Einstein's law of speed addition. In particular, if in S' a particle moves in the direction of the X- axis at velocity v , then the result of its composition with the velocity V (of the same direction) of the system S' relative to S will be

It can be seen that the sum of two speeds less than or equal to the speed of light always gives a speed not exceeding the speed of light. If in relation (1.74) we set | v'| = c (maybe a photon), we get |v| = Ö (v_x² + v_y² + v_z²) = c - the speed of light does not add up with any speed in size. Even if the system S' with respect to S moved at a speed V = c and a particle with speed V' = c in the direction of movement of the system S' passed through the system S', the resulting velocity of this particle with respect to S according to the relation (1.74 ') v = (c + c ) / (1 + cc / c ² ) = c would still be it was again equal only to the speed of light. This confirms the property of the speed of light c as the upper limit of the possible speeds of movement. If both velocities v i V are small compared to the speed of light c , the formula (1.74) turns into the common additive law of velocitycomposition (1.65), ie v = v '+ V.
An important special case of Einstein's law of velocity composition is the relation describing the change in the direction of light propagation when moving from one system to another inertial - so-called aberration of light. If the photon moves in the plane XY of the system S' so that the direction of its movement relative to an axis X (i.e. the direction of the velocity of motion V of the system S') makes an angle J, the components of its velocity in the system S' will be equal to v'_x = c.cos J', v'_y = c.sin J'. For the angle J of motion of this photon in the system S (v_x = c.cos J , v_y = c.sin J ) follows from the transformation relations (1.74)

sin J = [(1 - V²/c²)/(1 + (V/c)cosJ')] sin J' , cos J = (cosJ' + V/c)/(1 + (V/c)cosJ') .

In the case V « c (to the first order to the members of the V/c), hence the angle of the aberration of light DJ = J' - J classical relationship DJ = (V/c).sinJ .
Relativity of the kinematic effects STR
It should be noted that the above-mentioned kinematic effects, caused by the speed of movement of the body, are observable only relatively when the observed body and the observer move relative to each other. If the observer *) decided to "catch a moving object in the act" (what the hell is there conjuring with those scales and clocks..?!..), he would jump behind him, catch up with him and start moving with him the same speed, he would find nothing at all - scales and clocks would be fine, and all relativistic effects would disappear in such an observation..!.. There is no absolute point of view in the theory of relativity .
*) The very word "observer " must generally be taken with a "grain of salt" in physics: he must be free from any subjective influences, appearances and feelings! An objective "observer" can also be an instrument or the course of a natural event ...

Paradoxes of the Special Theory of Relativity
The unusual nature of kinematic regularities of the special theory of relativity, which seemingly contradict "common sense" *), have raised (and evokes in the lay public sometimes to this day) a number of objections, often formulated using "paradoxes". All these paradoxes are created by erroneous or inconsistent application of STR laws (most often forgetting the relativity of the present); part of the reasoning is done relativistically, part classically: Þ contradiction. Now apparent paradoxes of this kind are reliably solved [232], [242], they have only historical significance, but they have played an important role in formulating and refining STR thought processes.
*) STR is not a theory of "common sense", but - whether we like it or against our minds - it describes the properties of the real space-time in which we live. We can say that this theory is a real victory of an objective understanding over of the so-called "common sense", based on the limited experience of the everyday life of people in our terrestrial conditions ...
Paradox of time
Strangest outlet relativity seems the effect of time dilation - claims of different running speed time in different reference frames, for different observers. If we have the initial inertial frame of reference S and the second system S ', which moves at high speed V relative to S, the observer in S will see that the clock in S' is slower compared to its "rest" clock, according to the relativistic dilation of time. However, the observer in S 'can rightly claim that his system is "quiescent" and, conversely, the system S moves them at speed -V, so that the clock in S, on the other hand, goes slower. Who is right? This apparent discrepancy is often formulated as the clock paradox, also called the twin paradox :
In an imaginary ("sci-fi") experiment, imagine two observers, A and B , who are twins.of the same age (they may have an accurate, "ideal" watch on their hands). Observer A stays here on Earth (we will not consider here its gravity, rotation and circulation), while B gets on the rocket and flies off on an interstellar space travel at a speed close to the speed of light. If they are connected by radio signals, according to STR, Earth observer A will see a slower passage of time on rocket B .; astronaut B will in turn register the time dilation in terrestrial base A. After returning in a few years, the two brothers meet again and compare their age and watch. Will they have the same physical age *) and time on the watch? - or which of them will be "older" or "younger"?
*) When asked whether the traveler will age in accordance with the course of his standard "ideal" clock, biochemistry answers in the affirmative: aging is the result of biochemical processes at the molecular and atomic levels, the speed of which corresponds to the physical course of time measured by standardized clocks. From a philosophical point of view may be a slight exaggeration to say that "we are all kind of hours - and our faces are dials of years " ... (A.Eddington)
For the relativistic analysis of this imaginary experiment by STR we to primarily introduce a permanent inertial reference system S with the beginning of Oin the launch point, associated with the "rest" observer A ; it remains unchanged throughout the experiment. The motion of astronaut B can be divided into 5 stages:
I. Acceleration of motion after ignition of rocket engines at point O , at the end of which the rocket reaches speed V in the direction of the O-x axis, close to the speed of light c.
II. Steady motion of V speeds after shutting down rocket engines from Earth to the observation target (perhaps a distant star).
III. Accelerated motion - after reaching the observation target (distant stars) , the rocket engines are re-ignited to change the direction of the probe's movement to the opposite, to Earth.
IV. Steady motion again at a relativistic speed -V , after turning off the rocket engines, towards the Earth.
V. Decelerated motion after turning on rocket engines to brake from high speed V , to land on Earth.
In this idealized imaginary experiment, for simplicity, we will assume that the rocket engines are very powerful (and cosmonaut B very resistant to overload, as well as his standard watch) , so the acceleration phase (I.), reverse maneuver (III.) and braking (V.) will be very fast, with a negligibly short duration with respect to stages II. and IV. uniform motion relativistic velocity V . To move astronaut B then we can draw a space-time diagram :

Spacetime diagram of interstellar flight and return of cosmonaut B in the analysis of the "twin paradox". The motion of astronaut B is shown by the stronger line OK´-L´-M´´-N´´-P, which has short curved sections OK´, L´-M´´ and N´´-P, corresponding to the acceleration and braking of the rocket, and long straight sections corresponding to the inertial movement back and forth. Several lines of the present between the system S ´ of the departing rocket and the changed system S ´´ of the returning rocket are marked by oblique thinner lines - they have the opposite inclination!
Note:Own oblique coordinate axes of S ´ and S´´systemsthey are not drawn in the diagram, the picture would become confusing.

The world line of the rest observer A is the vertical line O-P along the time axis t in the rest inertial system S ; the countdown for observer A is on the vertical axis t (resp. c.t). The movement of the "twin" -cosmonaut B is shown by the line O-K´-L´-M´´-N´´-P, which is first inclined to the right after the start (section O-L´), then after the return maneuver it breaks to the left (section M''-L'') and finally lands on Earth in wordpoint P . In the temporal analysis between two mutually moving inertial systems, it is generally necessary to use coordinate lines of the present in the space-time diagram, which are inclined obliquely at an angle given by the ratio V/c (cf. Fig.1.5) . In our case, it is an important "trick" to read the time to realize that after the reverse direction of movement in stage III. already in stage IV. it is another inertial system that has the lines of the present inclined in the opposite way than in stage II. - in the "-V"! Detailed analysis yields the result that the sum of segments A-L + M-P displays a shorter time interval than the corresponding segment O-P observer A . Thus, astronaut B returns to the common point P in a shorter time - younger - than the time between the resting observer.A . In our simplified case, where astronaut B flew back and forth at speed V (and the sections of the accelerated motions are negligibly short), the difference of the time intervals Dt_A and Dt_B of both observers will correspond to the standard formula for time dilation (1.72) :
D t_B = D t_A. Ö (1 - V² / c² ) .
So if astronaut B went to the nearest star, Proxima Centauri, 4.2 light-years away, at a rate of, for example, 0.8c (approx. 240,000 km / s) there and back, then, according to Earth observer A, he would return in 14 years; by this time, Earth observer A would grow old. However, astronaut B would only age 8.2 years of his own time on this flight, so he would be 5.5 years younger than his Earth brother A when he returned .
In the general case of two standard clocks that fly apart at a learned moment and meet again later, the time difference will depend on the "histories" of their movements - the velocities and directions of inertial movements and the dynamics of non-inertial changes. Resp. on the symmetries of both movements. If both observers move symmetrically - the rockets will fly away in opposite directions at the same speeds and accelerations and then return again with the same movements, the relativistic dilatations are annulled at the meeting point. In the second extreme case - complete asymmetry, which corresponds to the case discussed here, the full value of the relativistic dilation of time is manifested.
Note:The popularization literature sometimes argues that the general theory of relativity (GTR) must be used to solve the twin paradox, because the traveler's frame of reference is non-inertial: that the time difference arises in the phase of braking and reversing the second observer's motion. This statement is misleading and unconvincing; the introduction of GTR is just another alternative solution, which is unnecessarily more complicated and does not bring new information unless there are "real" gravitational fields, excited by the mass-energy distribution. In fact, the twins' own paradox can be correctly solved within the special theory of relativity itself using three inertial frames of reference: one rest system S of the first observer and two different of the moving systems S ´ and S ´´ of the second observer as he moves back and forth, as outlined above.
The length paradox
The second strange conclusion of the special theory of relativity is the effect of the contraction of lengths in different frames of reference - different lengths for different observers. If we have the initial inertial reference frame S and the second system S', which moves relative to S at a large velocity V , the observer in S will see that the standard bars are in S' compared to its "rest" rods shorter, according to the relativistic contraction of lengths. However, the observer in S' can rightly claim that his system is "rest" and, conversely, the system S moves them at speed -V , so that the rods in S are truncated. Again, the question arises "who is right?". This apparent discrepancy is generally referred to as the paradox of lengths and is illustrated by various moving bodies - a bar and a barn, a car and a garage, a plane and a hangar, a train and a station or tunnel. The simplest formulation of the "rod and barn paradox" consists in the following :
Let's build a simple building (shelter, shed, barn) in an imaginary experiment of length L = 10 m, which has a door in the front and rear wall. This barn is managed (and front and rear door opens or closes) the observer A in the the rest default reference frame S. Furthermore, there is a distant observer B , which in the direction of the centers of these two doors throws at a relativistic speed eg V = 0.8c (approx. 240,000 km/s) a rod of length l = 12 m and will move with it as an observer B´ in inertial system S´. What happens when a bar enters and passes through a barn? - Does the rod "fit" inside or not? From the viewpoint of the observer A the bar appears to be shortened to a length l´ = 7.2 m by a relativistic contraction according to the formula (1.73') and therefore it should fit well into a 10 m barn. On the contrary, the length of the barn appears to the observer B´ shortened to L´ = 6 m, so he will expect problems when passing his 12 m bar through the barn. Moments of opening and closing the front and rear doors can be used to assess whether or not a flying bar can fit in a barn. If, from the point of view of system S, observer A closes both doors when the rod is completely inside (the end of the rod has passed through the rear door), the shortening of the rod will be demonstrated. From the perspective of the observer B but however, it looks different: the back door was closed when my bar had already hit the front door; my rod was longer than observer's A barn. Their disagreement lies in the timing of closing the door. In what is meant by the present of two distant events (although here only a few meters away, the time data differs by only picoseconds). From this point of view, the relationship of the present between the systems S and S´ needs to be analyzed using the lines of the present, parallel to the axis X´ on an oblique space-time diagram (somewhat similar to the above figure "Paradox of time"; relative to the total marginality of the problem we are not drawn special picture...) . According to the observer A (in the reference frame S ) are at some point the two ends of the rod inside the barn . From the perspective of an observer B' the ends of the rod were never simultaneously inside the barn, the rod is longer than the barn. From a formal point of view, both observers are right, it is in a way an “optical illusion”. From a physical point of view, only the situation where both observers meet in a “braked” state and from the point of view of a common frame of reference is easily will find out if the bar will fit in the barn or not. Everything else is just "STR folclore", which may be nice and interesting, but may no longer have anything to do with real natural reality..!..
Only the physical interactions of particles and bodies are important. If they run at high (relativistic) velocities, the effects of time dilation and length contraction can be realistically applied. - see eg "High - energy collisions of heavier nuclei. Quark-gluon plasma.", where it can be seen in the picture at the bottom left that at high energies the nuclei collide not as "balls" but as" flat disks", due to the contraction of length ...

Seemingly superluminal speeds of movement ?
Kinematic velocity, defined formally as the rate of change of coordinates of an object or phenomenon, can in some cases exceed the speed of light in a vacuum. A simple example can be a light trail - a spot of a beam from a rotating collimated source on a screen at a great distance (such as the movement of a light "piggy" in the distance when rotating a mirror reflecting the sun's rays, or the light trail of a lighthouse at a great distance) . However, such superluminal speed is not the speed of the photons that make up the light trail. The light trail in different places is formed each time by different photons (which come from the direction perpendicular to the apparent movement of the trail). There is no causal relationship between individual "pigs" in different places, no information is transferred between them. Therefore, the STR principles are not violated in any way.
In quantum physics , superluminal speeds can be virtually applied in connection with quantum fluctuations and relations of uncertainity (see, for example, part "Quantum Physics" in the monograph "Nuclear Physics and Physics of Ionizing Radiation"). Locally superluminal velocities are possible for virtual particles, which are created and destroyed in the course of interactions; their speeds fluctuate between moving slower and faster than light. However, for real particles , which exist in the initial and final states of the interaction, superluminal velocities do not arise. These initial and resulting particles do not interact with each other, and intermediate virtual particles are unable to transmit information.
A consequence of the principled non-locality of the quantum description of particles using wave functions is a phenomenon called quantum entanglement. It consists in the fact that two particles, whose quantum state is originally "linked" by a common wave function, remain connected in a certain sense - correlated, even over an arbitrarily large distance. If the state of one of the entangled particles changes, the state of the other particle will also change, "immediately" - a kind of " teleportation " of information occurs, transfer at infinite speed (passage "Quantum entanglement and teleportation" in the same chapter) . However, for a real measurement of the quantum state, information about the measurement in the initial system is required, which must be transmitted through a classical communication channel, i.e. at sublight speed. Quantum teleportation therefore does not allow the transfer of information at a speed greater than the speed of light.
Thus, there are no superluminal processes in quantum mechanics or quantum field theory that can be used to transfer matter or communicate information at superluminal speeds.
In relativistic cosmology , in the globally curved spacetime of an expanding universe, very distant objects can move away from each other at speeds exceeding the speed of light. In §5.3 and §5.4 "The Standard Cosmological Model. Big Bang. Formation of the Structure of the Universe." it will be shown that galaxies distant more than c/H (Hubble's constant H~ 70 km/s/Mpc) are moving away from each other at speeds greater than lights c . They will disappear beyond the event horizon and will no longer be able to interact with each other. In relativistic cosmology, space itself expands along with matter - or. expansion is a dynamic property of "free" spacetime itself. Particles of matter are only carried along by it. From this point of view, this is not a mechanical movement, so the relative velocities of particles during cosmological expansion can be superluminal (without violating the laws of the special theory of relativity) . ...
Observation of superluminal velocities of distant astronomical sources
If we observe a distant object (emitting light) at a distabce d, moving through space with a real speed v in a certain direction q, it will generally have some velocity component v.cos q towards us and also perpendicular to our line of sight v.sin q. The astronomically observed velocity v´ of shining objects is determined in a straightforward way by multiplying the distance d by the observed angular velocity w: v´ = d.w. The angular velocity is determined from the change in the observed angular position j₁, j₂ of the object at two different times t₁, t₂: w = ( j₂ - j₁)/(t₂ -t₁). However, this will not be the real speed v of the object, as we would measure at the source, but only the transverse apparent speed v´, created by the projection of the real speed in the direction of the observer. This apparent transverse speed is the only speed of astronomical objects that can be directly measured in the sky. At the same time, the final speed of light is not considered here, the instantaneous propagation is assumed. In reality, however, for the transverse movement the time interval t₂-t₁ between the two observations is shortened due to the approach of the object to the observer ...
From a relativistic point of view, this phenomenon has interesting consequences at high velocities close to the speed of light, which are often found in jets of high-energy particles from accretion disks in quasars and active galactic nuclei (in figure left).
If there is any astronomically observable distinct structure in the jet, we can determine the speed of movement of this structure in the sky by precisely observing its position A, B at two times t₁, t₂ (a few months apart) - in principle, we can measure the speed of the gas in the jet. Detailed measurements of the light (and electromagnetic radiation in general) of jets from quasars and active galactic nuclei have shown that in many cases the movement of the glowing gas structures in the jets appears to be faster than light. This deceptive effect occurs when the velocity of the jet is close to the speed of light (>0.9c) and there is a high component of the velocity towards the Earth (small jet angle q approx. 10°-40°). In such a case, as the observed structure in the jet moves towards the Earth, the distance d₂ is shortened compared to d₁ and thus the time delay of detection in both positions A, B by the value (v/c).cosq. As if the observed structure had managed to overcome the distance between the two places A-->B earlier. This means that the apparent observed velocity v´ appears larger than the actual velocity v, by the ratio 1/[1-(v/c).cosq]. The observed speed v' is not limited by the speed of light c because it is caused by retardation effects.

Actual and apparent velocity of quasar jets.
Left: Jet from the accretion disk of the central black hole, directed at an angle q with respect to the observer.
Right: Trigonometric analysis of the movement of investigated element in the jet and the observed light rays in two times t₁.and t₂

The figure on the right shows the geometrical situation during the emission of a certain monitored element in the jet from point A at time t₁ and its arrival at point B at time t₂. Light rays are sent from these places and at these times to the observer O - two astronomical observations of the position j₁, j₂ on Earth are made at times t₁' and t₂'.
From the trigonometric analysis according to the figure on the right, it follows that the actual cross-transverse speed of the observed object will be v_T = v.sin q. The observed apparent transverse velocity (angularly measured) of the monitoted object then, due to the shortened distance d₂ = d₁ - v.(t₂-t₁).cos q *), and thus the shorter detection time interval t₂´- t₁´ = (t₂-t₁)/[1-(v/c).cos q], will have value v´= v. sin q /[1 - (v/c). cos q].
*) Because the angle j, under which the details of jets near the quasar are observed from Earth, is very small (cosj~1), it does not need to be considered in the difference between the distances d₁ and d₂. For distant quasars, the velocity is corrected by a factor of d.(1+z), where d is the distance and z is the cosmological redshift, to give the value of the velocity that would be measured by an observer moving with the source (i.e. at rest relative to the source).
If the observed object is moving towards the observer, the observed velocity may be overestimated compared to the actual one. For certain combinations of true velocity v and beam angle q, the apparent transverse velocity can be greater than c. It is, for example, when v>0.9 and the angle q is in the range of around 5°-40°. With the opposite movement - in the direction apart of the observer (jet to the opposite side), on the contrary, the observed speed would be underestimated. And when the jet is headed straight for Earth (q=0), of course no motion is apparent...
This situation often occurs in jets from active galactic nuclei - from accretion disks around supermassive black holes - quasars - is discussed in §4.8, section "Thick accretion disks. Quasars." and "Mechanism of quasars and active galactic nuclei".

Relativistic dynamics
So far we have investigated only the purely kinematic laws of the special theory of relativity. By applying relativistic kinematics to the laws of dynamics, relativistic dynamics is created, providing other remarkable effects.
Newton's equation of motion of the mass point dp/dt = F , which is invariant with respect to the Galileo transformation, must be modified (generalized) so that it is invariant with respect to the Lorentz transformation, while at low speeds it passed into the original Newton's equation. To each material particle moving with respect to the inertial system S with velocity v is assigned a momentum vector p

proportional to speed v; the proportionality coefficient m represents the inertial mass of the particle.
In order for Newton's equation of motion and the law of conservation of momentum to be compatible with relativistic kinematics, the mass m will no longer be a motion-independent constant as in classical mechanics, but will be a universal function m = f(v) of the particle velocity v º |v| (the direction of velocity cannot depend, with respect on the isotropy of space). It follows from the principle of relativity that during the transition to another frame of reference S', against which the observed particle moves at velocity v', wil be p' = m'. v', where m' = (v') is the same function of argument v', as function m = f(v) of argument v (form-invariance). The form of this function f is unambiguously given by the requirement that the law of conservation of momentum applies in any inertial system. The easiest way to reach it by analyzing a collision of two identical particles is accomplished in terms of two different reference systems S and S' using a relativistic kinematics, i.e. Lorentz transformations (shape function f can also be obtained from the requirement that the p acted as a vector in the Lorentz transformation). Comes out the result f(v) = f(0)/Ö(1 - v²/c²), so that the mass of the particle moving at velocity v is equal to

where m_o is the proper or rest mass of the particle identical to mass in Newtonian mechanics. The moving body thus exhibits a higher inertial mass, gives greater resistance to further acceleration. In our daily lives, the velocities of bodies are small, so we do not observe any change in mass. In the microworld, however, particles often move at speeds close to the speed of light, and the change in mass is no longer negligible. In accelerators are prepared high-energy particles, which have a mass many times higher than their rest mass.
At v ® c the mass m increases above all limits, which is a dynamic obstacle preventing bodies with non-zero rest mass m_o can reach the speed of light v = c. However, there are also particles (quantum) with zero rest mass m_o = 0, such as photons or hypothetical gravitons. For these particles with m_o = 0, the momentum can remain finite even when the speed of light is reached (relation (1.75) gives an indefinite expression 0/0 at v = c). The velocity of particles with zero rest mass even must always be exactly equal to the speed of light c and their relativistic mass is given by the amount of energy they transmit (this energy is directly proportional to the frequency of the wave whose quantum is the given particle: E = h.f). The momentum of such a particle with zero rest mass must then be reported separately - independently of its velocity (which is identically equal to c).
The velocity, and thus the momentum of a free particle, is constant over time. When a particle interacts with its surroundings, the speed of its motion generally changes, whereby the measure of the force acting being the change in the momentum of the particle per unit time :

It is advantageous to keep this definition of force also in relativistic mechanics, because (unlike the product of mass and acceleration) it leads to the equivalence of the law of action and reaction with the law of conservation of momentum. If the force F, which is the cause of the change in the momentum of a particle, is given as a function of place and time, the relation (1.76) is the equation of motion of the particle. Unlike Newtonian mechanics, the variability of m means that the force and acceleration vectors may not have the same direction.
The work A performed by a force F with a given particle of mass m is, as in Newtonian mechanics, defined as the product of the applied force and the distance traveled by the particle during this action:

If the force F acts on an otherwise free particle, it can be assumed that the delivered work is converted into the kinetic energy of the particle:

If the particle of mass m moves with velocity v, after substituting z (1.76) and (1.75) we get

indicating the kinetic energy of a particle with rest mass m_o moving velocity v , i.e. with inertial mass m. At velocities v << c small in comparison with the speed of light, this relation takes on the approximate shape E_kin » (1/2) .m_o v² corresponding to the known formula for kinetic energy in classical mechanics.
Equation (1.78) indicates that the increase in the kinetic energy of a body is accompanied by a proportional increase in its (inertial) mass m. The analysis of mechanical processes, such as the perfectly inelastic collision of two mass bodies, using relativistic kinematics and the law of conservation of energy shows, that a similar relationship of direct proportionality applies between the supplied energy and the increase of rest mass of the body, while the conserved total energy

Between the changes of mass and energy applies the universal Einstein's relation "equivalence of mass and energy"

regardless of what causes the change in energy or mass. From (1.80) and the definition of momentum p = m.v follows (by excluding v ) an important general relationship between energy and momentum:

The relations (1.75) and (1.78) - (1.81), which are a dynamic consequence of relativistic kinematics, have been precisely verified by experiments in atomic physics, nuclear physics and elementary particle physics; they have already become an "engineering part" of nuclear technology.
In non-relativistic physics, two completely separate and isolated laws of conservation applied: matter and energy. There was no universal relationship between the (inertial) mass and energy of a body. In Einstein's theory of relativity, however, the general relation E = m.c² holds, according to which the mass m and energy E of each material object are mutually proportional to the universal coefficient c². Mass and energy, which in classical physics describe qualitatively different properties of matter, in relativity theory they show up to be equivalent characteristics of the amount of matter.

Spacetime geometry. 4-vectors, 4-tensors.
In pre-relativistic physics, space and time act as independent concepts for describing the motion of bodies. However, STR shows that in reality, space and time are inextricably intertwined. Lorentz transformations "mix" the time coordinate with the spatial coordinates as they move from one frame of reference to another. A physical quantity, for the measurement of which only ruler is enough for one observer, the other observer must measure using a ruler and a watch. The four-dimensional space-time, which we introduced at the beginning of this paragraph, thus ceases to be only a formal model, but acquires a deep geometric-physical meaning. To clarify this meaning, a metric needs to be introduced in space-time, ie to define the spacetime "distances" (remoteness) between events.

Spatio-temporal interval and metric
An important property of the distance l = Ö[(x₂-x₁)² +(y₂-y₁)² +(z₂-z₁)²] two points (x₁, y₁, z₁), (x₂, y₂ , z₂) in three-dimensional Euclidean space is its immutability (invariance) when transitioning to another system of spatial coordinates (for example, when shifting or rotating coordinate axes). We have shown above that the quantity s defined in (1.66) retains its value in any inertial system, with arbitrary Lorentz transformations of spacetime coordinates. Invariant quantity s defined relation

and called the space-time interval between events (t₁,x₁,y₁,z₁) and (t₂,x₂,y₂,z₂), thus plays the role of space-time distance - remoteness - of two events *).
*) The space-time interval s
and its differential element ds play a key role in the theory of relativity. It expresses how space-time events are "far" fron each other - in space and time. According to our conventional notions, two events can be "far apart" for two reasons :
1. Either they took place in different distant places in space;
2. Or they happened at different times, there was a long "time interval" between them.
The theory of relativity "mixes" space and time and combines them into a single space-time continuum. The spatio-temporal "distance" between the two events "1" and "2" is then expressed by a space-teme interval s_1,2 according to Equation (1.82). Something like a Pythagorean theorem, generalized to 4-dimensional (pseudo) Euclidean spacetime. This value of the space-time interval does not depend on the reference or coordinate system with which it is determined (it follows from the constant speed of light c; and from this then follows the Lorentz transformations (1.69) STR derived above) - it is completely objective.
In STR we ussualy suffice with a macroscopic expression of the interval s, resp. s². In the following section 2 (as well as in all other chapters of this book), we see that in the curved space of general relativity is necessary to use the differential element of interval ds (resp. its square ds²), which has a special function expressions characterizing curvature of spacetime - that in different places there are different spatial scales and different rates of flow of the (coordinate) time.
If we know the space-time interval, ie the dependence of the element ds² on the coordinates, we know "everything" about space-time and we can use it to study how bodies (particles) will move in it and light (photons) will propagate in it, as well as various physical fields. In other words, we know the metric tensor g_ik and the equations of geodetic lines - trajectories of free particles in the gravitational field (§2.4 "Physical laws in curved spacetime").
In this way we have the so-called Minkowski metric introduced in space-time, which we can write in differential form

if we introduce a new notation x° º ct, x¹ º x, x² º y, x³ º z, the Minkowski metric will have the form *)

It differs from the normal Euclidean metric by a negative sign at the time coordinate. Such a metric is called pseudoeuclide. While in Euclidean geometry the distance between two points is zero only when both points merge, the interval between two events in space-time can be zero even if the two events are very far apart (eg one such event can be the transmission of a radio signal here on Earth and the second event caused by it, the space rocket maneuver, perhaps somewhere near Jupiter).
*) In the special theory of relativity (especially in the older literature) the imaginary time coordinate x⁴ = i c.t is often used, which was introduced by Minkowski to make the geometry of spacetime formally similar to the geometry of Euclidean space: ds² = (dx⁴)² + (dx¹)² + (dx²)² + (dx³)². This formalism has at the geometric intetepretation of STR some advantages, e.g. Lorentz transformation can be represented as a rotation of the coordinate system. However, the use of an imaginary time coordinate also has disadvantages. It obscures some important structural properties resulting from the pseudo-euclidean character of spacetime, and operations with complex numbers are unnecessarily used to calculate some physical quantities that are real. Mainly, however, the use of an imaginary time coordinate loses any significance in the general theory of relativity, where the geometry of curved spacetime cannot be "make a similar" to Euclidean geometry. And since STR serves here as a basis for building a general theory of relativity and studying the general properties of spacetime, we will fundamentally use the real time coordinate x° = c.t .

Since the STR engaged movements at speeds close to the speed of light, it is useful in space-time diagrams on the time axis, instead of simply time t plot the time coordinate x° = c.t, so that the scale on the time axis is commensurable with the scales on the spatial axes. Such a space-time diagram, on which the x-axis is marked and the time axis perpendicular to it (the y and z coordinates are omitted for simplicity), corresponding to the initial reference system S, is shown in Fig.1.5c. On these coordinate axes it is possible to read the space-time coordinates of any world point (event) in the reference system S. In order to be able to read the space-time coordinates of these events in the reference system S', moving with respect to S in the direction of the axis x by the speed V, the coordinate axes x' and x'° = ct' corresponding to the system S' must be plotted in this diagram. The x' axis, which is given by the condition t' = 0, is according to (1.69) the line ct = (V/c).x; the axis t', given by the condition x' = 0, is the line x = (V/c).ct. Thus, as can be seen from Fig.1.5c, the transition to another inertial system by means of Lorentz transformations geometrically means the transition to an oblique system of space-time coordinates, the axes of which are inclined with respect to the original axes by an angle a given by tg a = V/c. This angle a increases with the velocity of the system S' relative to S, and at V ® c approaches 45°, when the axes x' and ct' coincide. From such a geometric expression of the Lorentz transformation, the kinematic effects of STR, such as the contraction of lengths or the dilation of time, follow very clearly; the well-known paradox of the clock is also elegantly solved here [232], [242] - it is analyzed in more detail above in the passage " Paradoxes STR " .

Causal relationships in spacetime
Spatial and temporal relationships between events and bodies are expressed by geometric relationships between the relevant formations in four-dimensional spacetime. The simplest geometric objects in space-time are the already mentioned worldpoints representing individual elementary events.
The basis of our cognition of objective reality are causal relationship between phenomena and events. Let us therefore look, what limitations on the causal relationships between events give the regularities of STR. Let us observe two events As(t_A,x_A,y_A,z_A) and Bs(t_B, x_B,y_B,z_B) in terms of the reference system S (Fig.1.6a). We denote the time interval between them t_AB = t_B - t_A and their spatial distance l_AB: l_AB² = (x_B-x_A)² +(y_B-y_A)² + (z_B-z_A)²; the space-time interval s_AB between them will be s_AB² = -c²t²_AB + l²_AB. Event B can have some causal connection with event A only if these events can be connected by a signal propagating more slowly than light, ie provided that l_AB < c.t_AB , or

The interval satisfying this inequality is called temporal (of the time type, "time-like"). Whether two events connected by a time-type interval are actually related depends on the specific circumstances - but in principle they always can.
If there is an interval between two events of a temporal nature, it is always possible to find such a reference system S' in which both events take place in the same place of the space (l'_AB = 0). The time interval between both events in this system is then t'_AB = Ö(-s²_AB/c²) > 0. If the interval between two events A and B is of a temporal nature and from the point of view of the reference system S event B occurred later than A , ie t _B > t _A , this time relation also applies in every other inertial system (there is no frame of reference, in which event B precedes event A ) - event B is therefore absolutely future with respect to A . If two events A and B take place with the same body, the interval between them is always of the time type, because the path l_AB, which the body runs between the two events, is always less than c.t_AB (the velocity of the body cannot be greater than c ), so s²_AB = l²_AB - c²t²_AB < 0.
If, on the other hand, two events A and C are separated by an interval satisfying the inequality

is l_AC > c.t_AC , so between these events can be no causal link (event A was not able to "let itself know" to the event C, because the event C occurred before they could overcome any signal the distance l_AC). For every two events A and C separated by a spatial type interval, it is always possible to find a reference system S' in which t'_AC = 0, i.e. in which both events take place simultaneously; the spatial distance of this two events is equal to l_AC = s_AC. In addition, if in system S, event C occurred later than A (t_C > t_A), there is a reference frame S', from whose point of view of both the time sequence of events opposite: t'_A > t''_C . At the same time, there is no frame of reference in which such events A and C are same-place coexistent - the events separated by the spatial type interval are therefore absolutely distant from each other.

Fig.1.6. Causal structure and motion of particles in Minkowski spacetime of special theory of relativity.
a ) Spatio-temporal diagram of three events A, B, C. Event B can be causally related to A (s²_AB <0), while event C cannot depend on event A in any way (s²_AC > 0).
b ) Mass bodies (particles) move in space-time along time-type world lines lying inside light cones, light propagates along isotropic light lines lying on the mantle of a light cone, hypothetical tachyons describe space-type world lines.
c) For each world point, the light cone divides spacetime into causally related areas of the absolute future and past and into absolutely distant areas without causation.

One-dimensional curves - world-lines - in 4-dimensional spacetime represent particle motions. Since the speed of each material body is limited by the speed of light, on the space-time diagram of the worldline of each particle it will form an angle of less than 45° with the time axis x°; the set of all worldlines of test particles passing through a given point O thus fills in spacetime the "cone" (4-cone)

with a vertex at this point O according to Fig.1.6b (where event O is taken as the origin of the coordinate system). Such worldlines are called of the time type, because the interval between their two arbitrary worldpoints (t, x, y, z) and (t+dt, x+dx, y+dy, z+dz) satisfies the relation ds² <0 - is of time character.
The photon moves along the world line dx² = (dx°) ², ie along a line inclined 45° to the time axis. The set of worldlines of all photons passing through point O (ie emitted from point O or coming to point O) forms a "surface" (hypersurface) in space-time

ie the mantle of said cone - the so-called space-time light cone diverging from point O on all sides at an angle of 45° to the time axis x°. This mantle of the light cone in space-time expresses the propagation of a spherical light wave emanating from the origin O (x = y = z = 0) at time t = 0. The world lines lying on the mantle of the light cone are called light, isotropic or zero word lines; the space-time interval between any of their worldpoints is equal to zero: ds = 0.
The light cone directed from a given event O to the future contains all events that can be an event O affected; light beam converging at a point O from the past includes all events that could have an event O influence. The set of all double light cones emanating from each point (event) of spacetime creates a branching causal structure in it The respective light cone for each event (world point) divides spacetime into three areas (Fig.1.6c): the area of absolute future and absolute past inside the light cone, and the area outside it containing "absolutely distant" events without causal connection.
In space-time, we can also imagine the spatial-type world lines, which lies outside the light cone and the interval between this world points ds² > 0 is spatial in nature. Spatial-type world lines represent motion at superlight speed and therefore cannot correspond to any real body. They could express the movement of hypothetical tachyons (see below). The movement of world lines of the spatial type is accompanied by "pathological" kinematic and causal behavior: on the space-time diagram it is easy to find a reference system in which such a particle will be in two different places, and systems in which the tachyon reaches its target before its source radiated - violates causality (although there is an intinterpretations in which the violation of causality does not occur, but there are also certain problems [102]). In the following, we will therefore not ascribe physical significance to spatial-type worldlines. But we will include here a brief passage about tachyons :

Tachyons - particles faster than light ?
It follows from the special theory of relativity, that no material body or particle can move faster than light, while only particles with zero rest mass move at the speed of light. However, some physicists did not want to accept this limitation and asymmetry in the region of velocities and expressed the speculative hypothesis that there could be exotic particles called tachyons (Greek: tachyos = fast ), which would move faster than light [80], [102] *).
*) Proponents of the tachyon hypothesis divide particles into three types: Particles with a (real) non-zero rest mass moving at sublight speed are called bradyons or tardyons. Particles with zero rest mass moving at the speed of light are called luxons. And particles that would move at super-light speeds are generally called tachyons.
From the basic relations (1.75) and (1.81) of relativistic dynamics between (inertial) mass, velocity, momentum and energy, some unusual "exotic" properties of tachyons follow. The relation m = m_o/Ö(1 - v²/c²) at v > c gives the imaginary mass of the tachyon; the same is true for its energy E. If we accelerate the tachyon, its energy decreases; a zero energy tachyon would move infinitely fast. From the point of view of quantum physics, the problem would be that in the formation of virtual pairs of tachyons, they would move farther apart from each other very quickly than Compton distance and could not annihilate - the vacuum would become completely unstable. If the tachyon were electrically charged, it would perhaps emit Cherenkov's electromagnetic radiation as it moved through the vacuum at superlight speed *) - this would reduce its energy and thus increase its speed, the electrically charged tachyons would spontaneously radiate all their energy. Even with electrically uncharged tachyon, according to the general theory of relativity, it can be expected that when moving through a vacuum at a speed greater than c the tachyon should emit gravitational Cherenkov radiation (creating a cone running behind it), which would carry away the energy of the tachyon, which would thus accelerate to an ever higher speed.
*) Cherenkov radiation is electromagnetic radiation generated when an electrically charged particle moves in an optical medium at a speed exceeding the speed of light in that medium (which is less than c ). This radiation is a kind of "shock wave" similar to an acoustic bang in the atmosphere of an aircraft moving at supersonic speed. The physical mechanism of Cherenkov radiation is described in the passage "Cherenkov radiation" §1.6 "Ionizing radiation" of the book "Nuclear physics and physics of ionizing radiation". "Classical" Cherenkov radiation is caused by interference of depolarizing electromagnetic waves of the material environment from individual parts of the particle path. However, in the case of tachyon in vacuum the material environment is missing, perhaps there could be electrical polarization of the vacuum, whose" virtuality " polarization would become real..?..
Because like electrodynamics accelerated movement of the electric charges generated electromagnetic waves, according to the general theory of relativity resulting accelerated movement of the mass gravitational wave propagating velocity also c , can be expected gravitational analogy of Cherenkov radiation (this is author of this book skeptical - by what mechanism would partial waves be aroused ..?..).
These "wild" dynamic properties of tachyons, as well as the kinematic and causal pathologies mentioned above, are difficult to accept from a physical point of view. Therefore, the real existence of tachyons in physics is generally rejected. No phenomena indicative of the participation of tachyons have been observed, these particles have no role in the logical structure of theoretical physics, they are not necessary to explain any phenomenon observed so far. According to the principle of Occam's razor (discussed in §1.1), it is therefore assumed that they do not exist.
Tachyons sometimes appear as some solutions in the formalism of unitary field theories, cf. §B.6 "Unification of fundamental interactions. Supergravity. Superstrings.". The classification of tachyons among other "exotic" and hypothetical particles in the systematics of elementary particles is mentioned in §1.5 "Elementary particles", passage "Hypothetical and model particles" of the book "Nuclear Physics and Physics of Ionizing Radiation".
___________________________________________

Due to the invariance of the interval, the classification of spacetime intervals between events and the particle line of particles into temporal, isotropic (zero) and spatial, as well as the division of spacetime regions according to a causal connection into absolutely future or past and absolutely distant, has absolute meaning, independent of the reference system. Although the specific spatial and temporal relations between events generally depend on the frame of reference from which they are observed, for causally related events, the terms "sooner" and "later" have absolute meaning. Only in this way can the concepts of cause and effect make sense. The theory of relativity thus physically concretizes the concept of causality based on the properties of the propagation of interactions. The connections between causality and the structure of spacetime will be elaborated in more detail in §3.2 and 3.3.

Fig.1.7. Expression of evolution and motion of bodies in four-dimensional spacetime.
a ) Solid body T in three-dimensional space and its projection into the XY plane.
b ) Hypersurface x° = const. = ct in four-dimensional space-time represents the whole infinite three-dimensional space at time t_o .
c ) Body T describes ("cuts out") a four-dimensional "world tube" as it moves in space-time.
d ) World tube of a pulsating body.

Other geometric shapes in space-time are two-dimensional surfaces and three-dimensional hyperareas ("supersurfaces"). Hyperplane x° = const., ie t = const. = t_o in space-time is actually the whole infinite three-dimensional space in time t = t_o. If we have some (three-dimensional) solid body T (Fig.1.7a) at time t_o, it will be expressed in space-time as the corresponding bounded shape in the hyper-plane x° = ct_o = const. (Fig.1.7b), whose (two-dimensional) boundary represents the surface of the body T at time t = t_o. Physical system of finite dimensions (eg interior of a body T ) in its movement and development, it describes ("cuts out") in space-time a kind of four - dimensional "tube" called space-time or world tube, which expresses the set of all points of the system (body) at all times t (Fig.1.7c). The three-dimensional "mantle" of this tube represents the surface of the body at all times - the evolution of the shape of the body. E.g. the surface of a spherical body of constant radius R with the center at the origin of the coordinates (ie spherical surface x² + y² + z² = R² = const.) at all times t will form a cylindrical hyperplot with x-axis in space-time.
An important special case of the 4-dimensional space-time (world) tube islight cone, analyzed above in the section "Causal relationships in space-time", Fig.1.6. Its three-dimensional mantle given by the equation x² + y² + z² - c² t² = 0 (light "hypercone") represents the surface of an ordinary sphere (light signal wavefront) with a center at the beginning, the radius of which first decreases with the speed of light from infinity to to zero, and then increases from time to speed c to infinity. Usually, however, only the half of the light cone that points to the future is taken.
Like worldlines, space-time hyperplanes are classified into spatial, isotropic (light), and temporal, depending on whether the square of the interval between their worldpoints is always positive, can be zero or negative. E.g. hyper-plane t = const. is a spatial type, the mantle of the light cone is an isotropic hyperplate.

Four-dimensional vectors and tensors
Spatio-temporal coordinates and components of quantities in spacetime will be denoted by Latin indices i, j, k, .., m, n, ..., which take the values 0,1,2,3; eg xⁱ º (x°, x¹, x², x³). We will provide purely spatial coordinates and components with Greek indices a, b, ...., m, n, ..., running values 1,2,3; eg x^a º (x¹, x², x³). When writing algebraic operations with these indexed variables, the advantage is very conveniently using so-caled Einstein's summation rule, according to which addition is performed over each index occurring twice in the product, whereas the summation symbol S being omitted. For example _i=0S^³AⁱA_i = A°A_o+A¹A₁+A²A₂+A³A₃ s AⁱA_i; simplification of writing formulas is evident.

The expression for the space-time interval (1.83) STR is a special case of the general quadratic form

whose coefficients, the so-called metric tensor g_ik (see §2.1) *), have a special simple shape

h_ik is sometimes called the Minkowski metric tensor.
*) Here in STR, the introduction of the metric tensor is only formal, when using common Cartesian coordinates it has trivial values of components. In Chapter 2 (and in all others) we will see that the metric tensor is of key importance in the general theory of relativity - it describes gravity as the geometry of curved spacetime.

Transition from inertial system S with coordinates xⁱ s (x°,x¹,x²,x³) to system S 'with coordinates x'ⁱ s (x'°,x'¹,x'²,x'³) it must be a linear transformation of spacetime coordinates

( aⁱ_k and bⁱ are constants independent of x ), because according to the principle of relativity a particle moving uniformly rectilinearly in the inertial system S must also move uniformly rectilinearly from the point of view of every other inertial system S'. In order to satisfy the principle of constant speed of light, this transformation must further satisfy the condition

of interval invariance. The transformations xⁱ ® x^'i (1.86) satisfying the condition (1.87) are a four-dimensional expression of the general Lorentz transformations between the inertial systems S and S' . If we measure coordinates and time in such a way that at t = t '= 0 the beginnings of Cartesian coordinates in both systems S and S' coincide, they are b ⁱ = 0 - these are the so-called homogeneous Lorentz transformations

In Fig.1.5c we have shown that the Lorentz transformation geometrically means a transition between oblique space-time coordinates.
The transformation relation (1.86) contains a total of 4 x 4 = 16 seemingly independent coefficients aⁱ_k. Substituting from the transformation relation (1.86') into (1.87) we get the condition h _ik = h _lm a ^l_i a ^m_k , which binds these coefficients by 10 equations (with respect to the symmetry in the indices i, k). Therefore, only 6 independent transformation coefficients remain in (1.86') - they correspond to the three parameters indicating the direction of the x', y', z' axes and to the three components of the velocity vector of the system S'against S . The set of all homogeneous Lorentz transformations (1.86') forms a group - a continuous 6-parameter Lorentz group ( ¥⁶ ).
Also, the set of all inhomogeneous Lorentz transformations (1.86), which arise from homogeneous transformations by adding four transformations of the shift of the beginning of space-time coordinates x^'i ® x^{' i} + bⁱ , forms a 6 + 4 = 10 -parameter group - the so-called Poincaré group.
In the case of a special Lorentz transformation, the relation (1.86 ') goes to (1.69), so the coefficients aⁱ_k have values

The main task of the special theory of relativity is the formulation of physical laws independently of the inertial frame of reference. In four-dimensional space-time, these physical laws translate into geometric relationships between objects in space-time that are independent of the choice of space-time coordinates. Like in the three-dimensional space of classical physics vector notation of physical laws guaranteeing their validity independent of the used spatial coordinates (permanence eg. in shifts or rotation appreciate the coordinate axes), fulfilling the principle of relativity in the STR can be best expressed by the fact that the physical laws are formulated as vector and tensor equations in four-dimensional spacetime. Such a vector or tensor equation valid in one coordinate system automatically applies in every other coordinate system. In addition, the laws of mechanics and electrodynamics take on a particularly simple and illustrative character when expressed by the relationships between vectors and tensors in four-dimensional spacetime - see below "Four-imensional mechanics" and "Four-imensional electrodynamics".
Coordinates (ct, x, y, z) = (x°, x¹ , x² , x³) º x ⁱthe given events can be considered as components of the four-dimensional "position vector" of the respective worldpoint in space-time. The "length" square of this position 4-vector can then be defined as the interval between the origin (0,0,0,0) and the given point (x°,x¹,x²,x³): (xⁱ)² = -(x°)² +(x¹)²+(x²)² +(x³)² = h_ik xⁱ x^k; it is an invariant quantity with respect to Lorentz transformations. In the context of the general definition of vectors in n-dimensional space, a four-dimensional vector (4-vector) Aⁱ means a set of four quantities A°, A¹, A², A³, which are transformed in the same way as the coordinates xⁱ during the transformations (1.69 ') of space-time coordinates :

In addition to the mentioned components of 4-vectors Aⁱ with indices at the top, called contravariant, the so-called covariant components A_i with indices at the bottom are also introduced using the relation

It can be easily shown that the transformation properties of the covariant components are

i.e., the covariant and contravariate components transform each other "contra-gradient".
The scalar product of two 4-vectors A and B means the algebraic expression AⁱB_i = A°Bo + A¹B₁ + A²B₂ + A³B₃ = h_ikAⁱB^k = -A°B°+A¹B¹+A²B²+A³B³ = A_iBⁱ; it is a scalar invariant with respect to coordinate transformations. The square of the size of a given 4-vector A is defined as its scalar product with himself: (A)² s AⁱA_i = -(A°)²+(A¹)² +(A²)²+ (A³)² . According to the sign of the square 4-vector space-time four-vector are divided into three groups: A ⁱ A _i <0 - vector of the time type; A ⁱ A _i = 0 - zero or isotropic vector; A ⁱ A _i > 0 - spatial type vector. The three spatial components A¹, A², A³ of the 4-vector Aⁱ form a three-dimensional vector A (due to transformations of purely spatial coordinates), so the set of 4-vector components can be symbolically written as A ⁱ º (A°, A). Such a distribution of the 4-vector into space and time can be done in any inertial system, but of course it changes with Lorentz transformations. The square of the 4-vector Aⁱ then is A ⁱ A _i = - (A°)²+ A². For vector Aⁱ of the time type, a system S' can always be found in which the spatial vector A' = 0 (it is a system S' whose time axis has the direction of the 4-vector Aⁱ); similarly, for each vector Bⁱ of spatial type, a system S' can be found in which its time component B'° = 0.

In space-time, more complex quantities - tensors - are also introduced by means of their transformation properties. The contravariant 4-tensor of the r-th order means the sum of 4^rof the quantities T ^ⁱ¹^{^{, i}}²^{^{, ..., i}}^r , which are transformed during the transformation of the coordinate system x ⁱ ® x' ⁱ = a ⁱ_k x ^k as a product of r -coordinates x ⁱ :

T'^ⁱ¹^{^,i}²^{^,...,i}^r = a^ⁱ¹_k_₁. a^ⁱ²_k_₂ ... a^ⁱ^r_k_{_r}. T^{^k}¹^{^,k}²^{^,...,k}^r .

Analogously covariant and mixed tensors - see general definition in §3.1. A scalar is a 0th order tensor, a vector a 1st order tensor.
The connection between covariant and contravariant components of tensors, ie "raising" and "lowering" indices, takes place via the metric tensor, in STR via the Minkowski tensor h_ik. E.g. T_ik =h_imT^m_k = h_il.h_km.T^lm. When used Minkowski metric is a simple rule: when lifting and lowering spatial indexes (1,2,3) the values of components do not change, when raising and lowering time index ("o") changes sign this component.
Arithmetic operations between tensors (components of tensors) are governed by simple and natural rules of tensor algebra [214], [163], [33]. With tensor product are created tensors of higher orders, e.g. 2nd order A^ijtensor product to B^k of the 1st order (i.e. four-vector) formed 3.order tensor T ^ijk = A ^ij .B ^k ; analogously for mixed tensors. Conversely, a "narrowing" operation, consisting of summation over a pair of indices in a given tensor, creates lower order tensors. E.g. from the tensor of the fourth order A^iklm by narrowing the tensor of the second order A^ik = A ^ikl_lis formed; by narrowing the tensor of the 2nd order A^ik we get the scalar A = Aⁱ_i = A°_o+A¹₁+A²₂+A³₃, which is called the trace of the tensor A^ik.
Among the 2nd order tensors, the Minkowski tensors h_ik and h^ik occupy a special position, as well as the so-called Kronecker delta-symbol dⁱ_k: d ⁱ_k = 1 for i = k, d ⁱ_k = 0 for i ¹ k - its trace dⁱ_i = 4; the components of these tensors are the same in all STR coordinate systems. Such tensors are called isotropic. Applies to h^im . h_mk = d ⁱ_k and for each vector Aⁱ is d ^k_i Aⁱ = A^k ; tensor d ^k_i thus has the character of a unit 4-tensor of the 2nd order. In the tensor calculus, a unit isotropic tensor of the 4th order - Levi-Civites tensor e ^iklm antisymmetric in all indices is also often used, whose component e ⁰¹²³= +1 and the other non-zero components (ie those for which all four indices are different) are equal to +1 or -1 depending on whether the given sequence of indices i, k, l, m is from the sequence 0,1,2, 3 formed by an even or odd number of permutations.

If we have scalar, vector or tensor quantities defined not only at one point, but at each point of a given area of space (here space-time), we speak of scalar, vector and tensor fields. The rules and operations of vector analysis, so useful in physics of field and continuum, are natural to transfer and generalize to four-dimensional spacetime.
The 4-gradient of a scalar field j = j(xⁱ) is defined as a four-vector whose covariant components are

The four divergence of the vector field Aⁱ = Aⁱ (x^k) means a scalar field

analogously, the 4-divergence of the tensor field T^ik is a four-vector (vector field) Tⁱ = T^ik_,
k º ¶ T ^ik / ¶ x ^k . It is advantageous to denote the differential operator ¶/¶x ⁱ simply by an index with a comma "_{, i} ", which considerably simplifies the notation of such relations. The operator ¶ / ¶xⁱ is a generalization of the Hamiltonian operator Ñ = i . ¶ / ¶x + j . ¶ / ¶y + k . ¶ / ¶z . The space-time generalization of the Laplace differential operator D = ¶²/¶x² + ¶²/¶y² + ¶²/¶z² is the d'Alembert operator

Thus žj = j^,i_,i = ¶²j/¶x² + ¶²j/¶y² + ¶²j/¶z² - (1/c²) ¶²j/¶t².
Gauss's theorem of vector analysis in three-dimensional Euclidean space

according to which the integral of the divergence of a vector A over some volume V is equal to the flow of this vector over a closed surface S = ¶V bounding this volume, is generalized to the shape in four-dimensional space-time

where dW = dx⁰ dx¹ dx² dx³ = c.t.dV is a 4-volume element in spacetime and dS_i are the 4-vector components of the hyperplanar element S = ¶W bounding the 4-volume W , through which it integrates on the left side; dS° = dx¹ dx² dx³ = dV, dS¹ = dx⁰ dx² dx³ = c.dt.dy.dz, similarly dS² and dS³ .
Relationship between the curve integral of a vector over a closed curve C and the area integral over the area S, bounded by the curve C, is given in the three-dimensional vector analysis by the Stokes theorem

The integral along the closed four-dimensional curve C is converted to the integral over the hyperplot S bounded by this curve C in general so that dxⁱ is replaced by dS^ik ¶/¶xⁱ. A direct generalization of the Stokes theorem for the curve integral of a 4-vector Aⁱ then reads :

where the components of the antisymmetric surface tensor dS^ik = dxⁱ dx'^k - dx^k dx'ⁱ give the projections of the planar element (taken as a parallelogram with the sides dxⁱ and dx'ⁱ ) into the coordinate planes. Analogously for higher order tensors.

Four-dimensional mechanics
In classical mechanics, the motion of a material particle is described by a trajectory in three-dimensional Euclidean space

In four-dimensional space-time, the motion of a particle is represented by its worldline, which can be described by a parametric equation

where l is a suitable parameter. As a parameter l it is possible to use either the coordinate time t , but better invariant quantities - the proper time t or directly the "length" of the worldline given by the space-time interval s .
The vectors of velocity v = dx/dt and acceleration a = dv/dt = d²x / dt ² play an important role in classical mechanics, so it is useful to introduce their four-dimensional analogies. The quantity dxⁱ/dt created by direct generalization is not suitable, because it is not a four-vector (dt is not an invariant). The invariant measure of time is the proper time t, so as a four-velocity it is natural to define a 4-vector with components *)

Given the relationship (1.72) between dt and dt, the four-velocity components can be expressed using the ordinary velocity v in the form

at low velocities v «c the spatial part of the 4-velocity changes to ordinary velocity v. From the relation dxⁱdx_i = c²dt²easily follows

From a geometric point of view, a four-vector c.uⁱ is a unit tangential vector to the world line of a given particle.
*) Often the 4-speed is defined as u ⁱ = dxⁱ/ds = c^-1 dxⁱ/dt; the four-speed defined in this way is a dimensionless quantity.
4-acceleration of particle is defined as

i.e., the four-vectors of velocity and acceleration vectors in space-time are perpendicular to each other. Movement of free particles, that runs uniformly and linearly (v = const., a = 0), is expessed in four-dimensional form by the equation

describing a straight line.
By four-dimensional generalization of momentum p = m_o .v of classical mechanics there is a 4-vector

By comparing relationships (1.75) and (1.80) for the momentum and energy in the STR is seen that the spatial portion 4-momentum is equal to the relativistic momentum p = m. v = m_o . v / Ö(1-v²/c²) and the time component is p° = E/c. The 4-moment components can therefore be written as

From the space-time point of view, therefore, the energy E and the momentum p of the particle are components of a single four-vector - 4-momentum, which can therefore be described as a kind of "energy-momentum vector" unambiguously characterizing the state of motion of the particle. According to (1.101), the square of 4-momentum p ⁱ p _i = (m_o u ⁱ ). (m_o u _i ) = m_o .c² is equal to p ⁱ p _i = E² / c² - p.c², which leads to the relation (1.81).

4-vector of force or 4-force is defined as the time change of the 4-momentum of a particle

This 4-force components are related to the ordinary three-dimensional force vector F = dp / dt by relation

Between the 4-force and the 4-momentum, the relation f ⁱ .u _i = 0 holds, ie the 4-force is "perpendicular" to the 4-velocity in space-time.
Newton equation of d p / dt = F has a four-dimensional generalization shape

the spatial part of this equation describes the change in momentum, the time component the change in energy of a particle under the influence of the applied force.
In theoretical physics, the laws of motion are often derived using the variational principle of least action [165]. A free (relativistic) particle of rest mass m_o, moving in spacetime from point A or point B , is described by the integral of the action

where s is the space-time interval and t is the particle's own time. This action S is proportional to the length of the particle world-line, ie the relativistic interval s . The variational principle of the smallest action dS = 0 then leads to Lagrange's equations, from which the equations of motion of relativistic mechanics (1.100 ) follow.

Energy-momentum tensor
The quantities of energy and momentum are used either as characteristics of individual discrete particles and bodies, or as aggregate quantities characterizing the system as a whole. However, if the particles in the investigated system are distributed densely enough that we can consider them as a continuum, or even a field (in §1.5 we have shown that the field is a certain "spread" form of matter), it is necessary to investigate the density with which basic physical characteristics such as mass, energy, momentum, angular momentum, electric charge, etc. are distributed in space. In addition, it is useful to describe how these quantities flow from one place to another in the system.
If we denote the energy density e= dE / dt, the local law of energy conservation is expressed by the continuity equation

Due to the universal relationship (1.81) between energy, mass and momentum , the density of momentum distribution P = dp / dV is given by the energy current density v.e : P = v . e / c (= v . r for incoherent dust). The local law of conservation of momentum can be written in the form

(preserves each component P^a of momentum).
We know that energy and momentum are components of the 4-vector of energy-momentum (4-momentum) in space-time. Likewise, equations (1.104) and (1.105) of conservation of energy and momentum can be combined into one tensor equation

T^ik = e .	/	1	v_x/c	v_y/c	v_z/c	\	(1.107')
	\|	v_x/c	v_xv_x/c²	v_yv_x/c²	v_zv_x/c²	\|
	\|	v_y/c	v_xv_y/c²	v_yv_y/c²	v_zv_y/c²	\|
	\	v_z/c	v_xv_z/c²	v_yv_z/c²	v_zv_z/c²	/

is the energy-momentum tensor .
The energy-momentum tensor, which completely describes the distribution and motion of energy and momentum in a given physical system, generally has the structure :

T ^ik =	/	energy density	energy current density, ie (momentum density) / c	\	(1,107)
	\|			\|
	\|	energy current density, ie (momentum density) / c	momentum current density, ie pressures and stresses (stress tensor)	\|
	\			/

The physical significance of the individual components of the energy-momentum tensor T^ik is thus as follows :

By breaking down the tensor law of conservation (1.106) into the component and separating the spatial and temporal derivatives we get the equations

(1/c) (¶T°°/¶t) + ¶T°^a/¶x^a = 0 , (1/c) (¶T^a°/¶t) + ¶T^ab/¶x^b = 0 .

(1/c) ¶/¶t _VnT°° dV+ _Vn(¶T°^a/¶x^a) dV = 0 , (1/c) ¶/¶t _VnT^a° dV+ _Vn(¶T^ab/¶x^b) dV = 0

and after adjusting with a Gaussian theorem (three-dimensional), two equations are created

wherein the integral on the right side they are taken across the closed surface S = ¶V surrounding volume V. According to the first of these equations, the rate of change of the energy contained in the volume V is equal to the flow of energy through the closed area S bounding this volume. Similarly, the second equation says that the momentum contained in volume V per unit time is equal to the flow momentum through the boundary surface S . Equations (1.106'') express the law of conservation of energy and momentum in integral form. In general, the total 4-momentum pⁱ is expressed by an integral using the energy-momentum tensor

across a hypersurface covering the entire three-dimensional space. Equation (1.106) is then equivalent to the assertion that this 4-momentum is preserved.
The ordinary (three-dimensional ) angular momentum vector J of classical mechanics, defined as J = r ´ p (vector product), is replaced in STR by a more general 4-angular momentum tensor

It antisymmetric tensor whose components are equal to the spatial components of a three-dimensional vector J. For the continuum, J^ik = n(xⁱdp^k -x^kdpⁱ) = (1/c) n(xⁱT^km - x^kT^im)dS_m. For the law of conservation of the angular momentum J^ik_,
k = 0 to apply, it must be (x ⁱ T ^km - x ^k T ^im ) _{, m}= 0; in addition to the law (1,106), it is necessary for the energy-momentum tensor to be symmetric (T^ik = T^ki).

The simplest type of substance - of the continuum - is a set of non-interacting particles called incoherent dust. The density of 4-momentum of particles in such a system is then r .u ⁱ , so T°^a = r .c² u ^a ( a = 1,2,3). The energy density is T°° = r .c² and density the momentum current T^ab = r .c.dx ^a / dt dx ^b / dt . Thus the energy-momentum tensor for incoherent dust is

If we use a reference system in which the considered volume element is at rest when monitoring the ideal fluid, Pascal's law will apply according to which the pressure p is the same in all directions. In such a reference frame the stress tensor will be equal s ^ab = p. d ^ab = T ^ab; the momentum density is equal to zero here, so T°^a = 0, and the energy density T°° = e = r .c ² .
The energy-momentum tensor of an ideal fluid in the rest frame is therefore

After the transformation into a general frame of reference in which a given volume element moves with a four -velocity u ⁱ , the energy-momentum tensor of an ideal fluid will be given by

It is advantageous to maintain the concept of the energy-momentum tensor even if it is not a real continuum. If the investigated system consists of N "point" parts of masses m_a (a = 1,2, ... , N), which move at 4-velocities u ⁱ_a , then the energy-momentum tensor can be defined as

Four-dimensional electrodynamics
Maxwell's equations of electrodynamics, although originally based on classical non-relativistic ideas, are invariant with respect to the Lorentz transformation. Electrodynamics is therefore fundamentally relativistic - electromagnetic phenomena are actually the only case where we encounter relativistic effects in everyday life (but it is not easy to notice!). Electrodynamics therefore does not need any relativistic reformulation, the theory of relativity does not lead to any new and unexpected electromagnetic phenomena. However, the application of the laws of the special theory of relativity introduces a clearer and more uniform order in electrodynamics and points to the deep internal context of phenomena, which are classically understood as independent empirical facts. This unity of electromagnetic laws stands out especially clearly in a four-dimensional space-time formulation. The basic quantity of electrodynamics is the electric charge, for which the law of conservation applies (1.31). The electric charge is defined as an invariant scalar quantity, so the magnitude of the charge of a body is the same in all inertial frames of reference :

Since the volume is transformed according to the relation dV' = Ö(1 - V²/c²) dV during the transition to another inertial system, the transformation law for r is the same as for dx°: r' = r /Ö(1 -V²/c²). Thus, the density of an electric charge is transformed as a time component of a four-vector. Current density vector components j = r . v , which are j^a = r .v^a = r .dx^a/dt (a= 1,2,3), due to the behavior r are transformed as dx^a, ie as spatial components of the four-vector. It is therefore natural to unify the quantities r and j into one 4-vector j ⁱ º (c. r, j), the so-called four-current, the components of which are

Since the component j° = c. r can be expressed by x° = ct as j° = r .dx°/dt, the 4-stream components can be defined as follows :

The continuity equation (1.31b) ¶r/¶t + div j = 0, expressing the law of conservation of electric charge, can then be written in four-dimensional form

(4-divergence of four-currents is equal to zero).
Similarly, for the potentials from equations (1.46a, b) it follows that in terms of transformation properties the quantity j behaves as time and the quantities A^a = ( A ) as spatial components of the 4-vector, so the electric scalar potential j and the magnetic vector potential A can be unified into a single 4-vector

which is called the four-potential. Equations (1.46a) and (1.46b) can then be combined into one space-time equation

indicates that the 4-potential is chosen so that its four-divergence is equal to zero. The development of the relations E = -gradj - (1/c)¶A/¶t , B = rot A between the potentials and intensities of the electric and magnetic field shows, that the components of the vectors E and B can be interpreted as components of the antisymmetric 4-tensor F^ik

which is called the electromagnetic field tensor. This electromagnetic field tensor, expressed by the components of the vectors E and B , has the structure :

It is a unifying "conglomerate" of electric and magnetic field components, that completely describes the electromagnetic field in four-dimensional spacetime.
Note:The electromagnetic field tensor F^ik is sometimes called the Faraday tensor, although no tensors (and not 4-dimensional at all!) were not known in Faraday's time. It reflects the unification of the electric and magnetic fields in the spirit of Faraday's law of electromagnetic induction.
Lorentz equations of motion (1.30) of a charged mass particle in an electromagnetic field

can be interpreted as spatial components of the four-dimensional equation of motion of a charged particle

the time component of this equation describes the changes in the energy of the particle as a result of the work performed by the electromagnetic forces.
The first pair of Maxwell's equations (1.40) - (1.41) can be written as one equation for the components of the electromagnetic field tensor :

The second pair of Maxwell's equations (1.38) - (1.39) can then be unified into a single four-dimensional equation using F^ik

describing the excitation of the electromagnetic field by four-currents j ⁱ .
To formulate electrodynamics using Hamilton's least action principle, the Lagrangian of the electromagnetic field is in a 4-dimensional form:

from the variational principle d S = d ò L d W = 0 (with variation of the 4-potential components at the given distribution and motion of charges) we can then obtain Maxwell's equations of the electromagnetic field (116a, b).
The relations (1.52) - (1.56), expressing the density and current of energy and momentum in an electromagnetic field, can be summarized using the energy-momentum tensor of the electromagnetic field, which is equal to

After substituting the values F^ik from (1.114') it can be seen, that T°°_elmag.is equal to the energy density (1.52) and the components T°^a_elmag.are equal to the components of the Poynting vector (1.55). Spatial components

Thus, for mechanical and electrodynamic phenomena, the special theory of relativity is perfectly elaborated and experimentally verified. However, it must be admitted that for other than electromagnetic phenomena, the special theory of relativity is not directly verified... However, indirect indications are very convincig..!..

Nonlinear electrodynamics
At all intensities we observe in nature and in the laboratory, the electric and magnetic fields in vacuum appear to us to be linear - for the values of intensities E and B , as well as for potentials, the principle of superposition applies exactly. The question is, what about extremely strong electromagnetic fields? Variants of generalized nonlinear electrodynamics NED were constructed for this situation, in which the principle of superposition does not apply (the resulting electromagnetic field of two charges is not equal to the sum of the fields of individual charges). There is self-interaction field - there is, for example, the scattering of "light on light". It is expected that these phenomena of nonlinear electrodynamics *) could manifest themselves in the field of very strong electromagnet. fields and high-intensity beams of electromagnetic radiation (not yet achieved in our experiments).
*) We mean the behavior of fields in vacuum, not the phenomena of nonlinear optics caused by nonlinear polarization or magnetization in material environments.
Motivation for the generalization of classical electrodynamics began to appear at the beginning of the 20th century in connection with a not entirely satisfactory model of a charged particle (a point charged particle in the center showed infinite values of the Coulomb field, with infinite energy - singularity ). In 1912, G.Mie suggested that the electromagnetic field could be composed of the sum of the classical Maxwell field and a second nonlinear additional term (composed of potentials A ), which would be significant only in the area of atomic dimensions (this variant did not penetrate into the wider physical consciousness public).
Some other modifications of Coulomb's law for intensity E and potential F were also tried :
- Small correction "e" in the law of inverted squares: E(r) = Q / r ²⁺^e ;
- To the standard Coulomb potential F(r) = Q / r include componentr wit Yukawa potential F'(r) = Qc ^-^m^.r / R (used in nuclear physics - is mentioned e.g. in the passage "Strong nuclear interactions" §1.1 monograph "Nuclear Physics and ionizing radiation"). This would be equivalent to the introduction of a non-zero photon mass m_f with a Compton length m = m_f .c / h ......
None of these initial attempts at nonlinear extensions of electrodynamics led to satisfactory results...
Basic consistent variant of nonlinear generalization of classical Maxwell's electrodynamics NED was designed in 1934 by M.Born and L.Infeld [23] - Born-Infeld electrodynamics (BI). The motivation was to remove the singularity in the point charge - in order to determine the final value of the electron's own electric energy. For this purpose, they introduced the hypothesis of the maximum possible value of the electric field intensity E_max and the potential F_max , analogously to the relativistic mechanics STR there is a maximum possible (limit) speed c of motion of material bodies. They realized this by introducing a special parameter of nonlinearity "b" in the modified field equations so that the intensity of the electric field of the point charge Q (instead of the standard Coulomb's law E = Q / r² ) depended on the distance r according to the law :

(dotted curve in Fig.1.8 on the right), at which the intensity of the electric field at the beginning r = 0 is finite and also the total energy of the electric field is finite (relations (1.122-123)).
Note:Sometimes the parameter "b" is denoted by the Greek "b" and its inverse value 1/b or 1/b .
In classical Maxwell's electrodynamics, the Lagrangian in a 4-dimensional formulation is given by the above relation (1.117) :
L = (1/16p c) F ^ik F _ik + (1 / c ² ) A _i j ⁱ .
Lagrangian of the electromag. field in BI is modeled in a generalized form containing the nonlinearity parameter "b" (which then characterizes the maximum possible electric field intensity in the equations - see relations below (1.123) ) :

where F_ik is the tensor of the electromagnetic field (1.114) (F = F .. ... e Iklm. .. his ..associated multiplied unit ... Levi-Civitùv tensor e ^Iklm antisymmetric. .. add, modify , in Lagrangians, we are omitting c (convention c = 1) ............ ).
For a pure electric field E, i.e. when B = 0, is L = b^-2 [1 - Ö(1 - b².E²)].
In 3-dimensional vector symbolism of electric intensity E and magnetic induction B is the standard Maxwell's lagrangian (1.42): L = 1/8p (E² - B²) + j . A - r . j , while in B-I NED the Lagrangian has the form :

In the limit b -> 0 we get the standard Maxwell electrodynamics, for b> 0 we are in the variant of nonlinearity.
The equations of the electromagnetic field in the BI model follow from the principle of the smallest action with the Lagrangian L_BI (1.119´) :

which are formally the same as standard linear Maxwell's equations (1.38-41). Nonlinearity is "hidden" in quantities D ("electrical induction") and H ("magnetic intensity") :

D = ¶L/¶E = [E + b²(B.E) B]/Ö[1 + b²(B²-E²) - b⁴.(B.E)²]] ,
H = ¶L/¶B = [B - b²(B.E) E]/Ö[1 + b²(B²-E²) - b⁴.(B.E)²]] ,

(1.121)

which contain factor "b". This is analogous to the electrodynamics of the continuum, where the relationships between E and D = E e , B and H = B/m contain the material coefficients of electrical permittivity e and magnetic permeability m (including possibly inhomogeneities and nonlinearities of polarization and magnetization).
The solution of the field equations (1.120-121) for a spherical symmetric electrostatic field leads to a functional dependence of the potential F and the intensity E of the electric field on the radial distance r from point charge Q :

The integral contained in the function F(r) for the potential can be explicitly expressed using two types of special functions :

where "F(...)" is the Legender elliptic function of the 1st kind and " ₂ F₁ (...)" is the so-called hypergeometric function (more complex power series from Q² b² / r⁴ ). Specific values of these complex functions can be found for physical calculations in special tables, recently there are also computer programs for them.
You can also write:

E(r) = q/Ö[r_o⁴ + r⁴] ; E_max = 1/b ,
where r_o = Ö (q.b/4p) is the " effective radius of the point charge " .
F(r) = F(r/r_o) .q/r_o ( F is a combined elliptic function) , a value is based numerically F(0) = 1.854 E_max .

(1.122b)

These dependences of electric potential and intensity in the B-I NED model (dashed curves in Fig.1.8) are at greater distances r similar to the standard Coulomb's law (solid curves in Fig.1.8). However, they differ significantly at small distances: while according to Coulomb's law, with the approximation r -> 0, the potential and intensity increase to infinity, in the BI model, the final values reach F(r = 0) = F_max , E (r = 0) = E_max ~ 1 / b.

Fig.1.8. Dependence of potential F (left) and intensity E (right) of electric field on distance r from point charge (electron) according to standard Coulomb's law ( ^_____ ) and according to nonlinear B-I electrodynamics ( ........ ).

The specific value of the basic parameter "b" in nonlinear BI electrodynamics can be determined from the physical analysis of the electric field of an electron - the electron is a fundamental elementary particle without internal structure - is not "composed" of anything, from classical physics it can be considered a "field object". It can therefore be physically require all the rest mass of the electron m_e was of electrical origin. The rest energy of an electron m _e .c ² with charge q = e should therefore be given in classical physics by the total energy of its electric field : m_e.c² = e . ₀n^{^A}dr/Ö[r_o⁴ + r⁴]. For the electron we get values :

The value of E_max applies not only to the electron, but in B-I electrodynamics it is the fundamental maximum possible value of the electric field intensity, given by the parameter "b".
In classical physics, BI electrodynamics is considered primarily as an electron model .
From a physical point of view - atomic, nuclear and particle physics - the questions of "size" or particle dimensions of the microworld are discussed in §1.5 "Elementary particles and accelerators", passage "Size, dimensions and shape of particles? -Problematic! " in monograph "Nuclear physics and physics ionizing radiation".
Recently, modified variants have sometimes been introduced nonlinear electrodynamics of NED with Lagrangian in exponential or logarithmic form :
L_NED = b^-2[exp(-F_ikF^ik/b²) - 1] or L_NED = -8 b^-2 ln[(1 + F_ikF^ik/(8b²)], for the purpose of wider possibilities of gravitational-electrodynamic solutions...
Nonlinear electrodynamics, although so far only theoretical and hypothetical, provides interesting possibilities of solutions in theoryelectrically charged black holes, where under certain circumstances it allows to get rid of singularities (!) - §3.5, passage "Reissner-Nordstrom solution with nonlinear electrodynamics", §3.6, passage "Kerr-Newman geometry with nonlinear electrodynamics" and mention in §4. .. .... . It is some hope that the nonlinearity of electrodynamics could "disturb" the nonlinearity of gravity in OTR to give a more realistic regular physical solution..?.. - will certainly be the subject of future theoretical research. .. .
Whether this is somewhere in nature "is realized" is not known yet - there is no hope for experimental verification in the foreseeable future...

Classical, quantum and gravitational nonlinear electrodynamics
In classical NED, the maximum possible value of the electric field intensity E_max near the point charge was "artificially" hypothetically postulated by introducing the parameter "b" of nonlinearity in the field equations. In quantum electrodynamics, the limit electric intensity is based physically - dynamically as a consequence of the increased production of electron-positron pairs from a polarized vacuum in a strong field near the point charge.
The nonlinearity of electrodynamics, geometrically induced by the gravitational curvature of space-time in GTR, is another matter - it will be analyzed in §2.4 , part "Gravitational electrodynamics and optics". The "exotic" effect is the curvature of spacetime by the energies of the electromagnetic field - massive electromagnetic waves within geometrodynamics (§B3 "Classical geometrodynamics. Gravity and topology.", Geons , Fig.B2) .

F ^ik =	/	0	E _x	E _y	E _z	\	.	(1.114 ')
	\|	-E _x	0	0	0	\|
	\|	-E _y	B _z	0	-B _x	\|
	\	-E _z	-B _y	B _x	0	/

Gravity, black holes and space-time physics :
Gravity in physics	General theory of relativity	Geometry and topology
Black holes	Relativistic cosmology	Unitary field theory
Anthropic principle or cosmic God
Nuclear physics and physics of ionizing radiation
AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy


1.5. Electromagnetic field. Maxwell's equations		2. General theory of relativity - physics of gravity

Space - time - relativity