Final stages of evolution - supernova, neutron star, black
hole .
Chapter 4
BLACK HOLES
4.1. The
role of gravity in the formation and evolution of stars
4.2. The
final stages of stellar evolution. Gravitational collapse
4.3. Schwarzschild
static black holes
4.4. Rotating
and electrically charged Kerr-Newman black holes
4.5. The
"black hole has no hair" theorem
4.6. Laws
of black hole dynamics
4.7. Quantum
radiation and thermodynamics of black holes
4.8. Astrophysical
significance of black holes
4.9. Total
gravitational collapse - the biggest catastrophe in nature
4.2. The final stages
of stellar evolution. Gravitational collapse. Formation of a
black hole.
Thus, most
of the active life of stars is a quasi-static
phase (1010 years long
for ordinary stars, but may be less than 106 years for
giant stars), during
which fusion nuclear reactions take place and heat and
radiation pressures balance the gravitational force. In the previous chapter, "Thermonuclear reactions inside stars", we discussed the whole sequence of
thermonuclear reactions - from hydrogen fusion to helium,
fusion of helium to carbon, subsequent synthesis of oxygen,
magnesium, silicon, ...., to the last iron in sufficiently
massive stars. However,
each star contains only a finite amount of
available "nuclear
fuel", so time must come, when all the energy-releasing
nuclear reactions stop, and the star's active life ends.
The extinction of
all energy-releasing nuclear reactions can occur for two reasons.
Either because the star is not massive enough to be able to
develop the necessary high temperature in its interior to
continue the fusion of heavier nuclei. Or because it has already
exhausted all its available nuclear fuel (its
interior is composed mainly of heavier elements like iron and
surrounding elements that are no longer capable of exothermic
nuclear fusion). After the end of thermonuclear reactions,
the stars are definitely seized by gravity, which squeezes the star
"as far as possible" - to high
densities; the greater
the mass of the star, the higher the
densities. These stage
star evoution and subsequent
phenomena are
referred to as the final stages of
stellar evolution.
What happens next?
The ultimate fate of a star is determined by its remaining
mass M' *) at the end of evolution (ie,
the initial mass, minus the mass of all matter, particles, and
radiation ejected and radiated by the star during its evolution) after depletion of thermonuclear reactions.
*) During their evolution, stars lose
a large amount of their mass - they eject it during instabilities
in eruptions and in a stable stellar wind, they emit a lot of
energy by radiation. The more massive a star is, the more weight
it loses over the course of its life. It is estimated that stars
born with a mass of 6-8 M¤ at the end of their evolution will have a residual mass
M' of only about 1-1.5 M¤, so they will probably end up as a white dwarf.
Most stars formed with an initial mass of about 10-15 M¤
will have a final residual mass M' of about 1.5-2 M¤,
will explode as supernovae, and their evolution will end at the neutron
star stage. Only highly massive stars with an initial mass
greater than about 20 M¤ will have a residual mass M' >2 M¤ and
will succumb to complete gravitational collapse with the
formation of a black hole.
For simplicity, we will first consider
a spherical star, around which it will be
according to Schwarzschild-Birkhoff's
theorem 3.3 the Schwarzschild
geometry of outer spacetime (3.13); inside the star, it will be
seamlessly followed by the metric of Schwarschild's inner
solution. First, we outline the final stages of stellar evolution
globally according to Fig.4.2.
White Dwarf
After consuming all available nuclear fuel - depending on the
mass of the star - all nuclear fusion reactions releasing energy
are extinguished and the star reaches its lowest energy state (if we do not consider gravitational energy). In the case of less massive
stars (M<1.5 M¤), the resulting star consists
mainly of light elements - residual hydrogen and helium, further
formed carbon and oxygen (it is not able to
develop the necessary high temperature in its interior to
continue the fusion of heavier nuclei). These lighter elements are still
potential thermonuclear fuel that can be used in a thermonuclear
explosion, see below. In more massive stars, the light elements
are already thermonuclearly burned, and further collapse can
continue into a neutron star or black hole.
After the thermonuclear reactions
are extinguished, the thermal pressure and thus the radiation
disappear, and due to gravitational forces the star is compressed
*) from the original few hundred thousand
kilometers in diameter to several thousand kilometers, and the
density of the order of thousand kilograms per cm3.
The substance of the star is fully
ionized and
the gravitational forces are balanced mainly by the Fermi pressure of the degenerate electron gas.
*) In the late stages of evolution, the inner part of
the star contracts and heats up, but the outer parts expand and
cool - the star temporarily becomes a red
giant. The more weakly bound surface layers eventually
disperse into the surrounding space under radiation pressure and
form the so-called "planetary" nebula (see the passage "Late stages of stellar evolution" in §4.1), in the middle of
which is the hot inner part of the star, most often a white
dwarf, in the case of massive stars here a supernova explosion
may then occur, forming a neutron star or black hole.
Fermi pressure of degenerate gas
Particles with spin 1/2, such as electrons, protons and neutrons,
are classified as fermions - their sets are
governed by the so-called Fermi-Dirac statistics. The
basis here is Pauli's exclusion principle, according to
which only one fermion can occupy a single energy state (or at
most two particles with oppositely oriented spin). At high
densities of matter, all electron energy levels are occupied
up to a certain maximum energy, which corresponds to a certain
maximum momentum; this condition is called degeneration
*), it is a degenerate electron gas. Every other
electron in a given volume must occupy a new higher energy level
and thus have a higher momentum. The pressure here therefore
increases significantly faster than corresponds to the equation
of state of an ideal gas. The pressure of the degenerate electron
gas is applied in white dwarfs, at even higher densities the
degenerate neutron gas is applied in neutron stars. The behavior
of a substance at high pressures and densities is discussed in
more detail below in the section "Behavior of a substance at high pressures;
neutronization".
*) Lat. degeneratus = different
from its species, perverted, declining, with loss of diversity.
The way in which the
spin of particles determines the statistical
behavior of sets of particles is shown in the passage
"Indistinguishability of particles" - "Spin,
symmetry of the wave function and statistical behavior of
particles" in the monograph "Nuclear physics and
physics of ionizing radiation".
In
the end, therefore, all the matter inside the star is
gravitationally compressed into a compact structure with
a diameter of only a few thousand kilometers with a very high
density and temperature. If the remaining mass M' is not too
large (less than the so-called Chandrasekhar
limit of approx. 1.4 M¤, see below),
this compact body will be stable. A star in this state is called a white dwarf. It typically has a mass
roughly like the Sun, but a size similar to the Earth's; the
density here is higher than about 104 -106 g/cm3. A large supply of thermal energy is accumulated inside
it, coming from earlier thermonuclear reactions (and from
gravitational contraction), which radiates only very slowly due
to the small surface. Therefore, the white dwarf can shine even
without the ongoing nuclear reactions, by the remaining heat, for
many billions of years. Only after this very long time does it
gradually cool; after emitting thermal energy, it becomes an
infrared and finally a black dwarf *). The best-known
white dwarf is binary star guide of the Sirius, a Sirius
B.
*) The Fermi pressure
of the degenerate electron gas has a non-thermal origin
and acts even after the white dwarf has cooled down - it then
maintains the gravitational balance of the black dwarf. However,
due to the small surface area and the insulating plasma layer,
the white dwarf has a very low luminosity (one hundred to a
thousand times smaller than the Sun), so its cooling time is in
the order of billions of years.
As the white dwarf cools inside, under
high pressures, carbon atoms may gradually coalesce into a
crystalline form known as diamond. After cooling down, a
black dwarf remains, inside which are single diamond crystals,
which in certain circumstances may reach perhaps even planetary
dimensions ..?!..
In connection with the cooling of the
white dwarf, a rather bizarre hypothesis of "neutrino
cooling" of the hot plasma appeared - is critically
discussed below "The role of neutrinos in energy leakage from collapsing
stars - "Urca" processes".
If the white dwarf
is part of a close binary with a giant star, the substance may
overflow from the giant to the white dwarf. The gradual
accumulation of matter on the white dwarf then leads to instabilities
and cataclysmic processes. A thicker layer of hydrogen can form
on the surface of the white dwarf, in which, due to high
temperature and pressure, a thermonuclear reaction of an
explosive nature can be ignited, accompanied by a sudden release
of energy and a flash of radiation - a nova explosion
(discussed in the previous §4.1). This process can be repeated several times. The
accumulation of mass on a white dwarf can eventually lead to
exceeding the Chandrasekhar stability limit (1.4 M¤ - see below) and the collapse of
the star, which results in a supernova explosion
(type Ia - thermonuclear explosion,
or collapse into a neutron star - type II and other
subtypes ). These events are discussed in
more detail below in the section "Supernova
explosion. Neutron star. Pulsars." and in the passage "Types
of Supernovae and Their Astronomical Classification".
Stability of the white
dwarf. Chandrasekhar limit.
As S.Chandrasekhar showed already in 1930, the white dwarf is
stable only when its weight is not too great. The limit
of stability for a spherical body of mass M and
radius R, containing the total number N of fermions
of mass mf,
can be roughly determined by the following model consideration:
Since the concentration of fermions is rf ~ N /R3, in the context of Pauli's principle the volume
occupying per one fermion is ~ 1/rf = R3/N. According to the quantum uncertainty relation, the
momentum of a fermion is ~ h.rf1/3. The
relativistic energy of fermions is then Ef ~ h.rf 1/3/c ~
h.c.N1/3/R.
The gravitational energy per fermion is Eg ~ -G.M.mf/R. The total energy is
E
= E f + E g ~ h.c.N1/3 / R - G.M.m f / R .
Equilibrium configuration is achieved at the minimum value of
total energy E. The analysis of the equation for total
energy shows that at low mass M the energy E is
positive, with increasing radius R decreases to negative
values, reaches minimum and at R ® ¥ approaches zero - at a certain final value of R
there is a configuration of stable equilibrium
between the gravitational force and the Fermi pressure of the
degenerate particles. For high masses, the total energy E
is negative and as R decreases, the value of E
decreases indefinitely - the equilibrium state does not
exist and gravitational collapse
occurs.
Thus, the maximum mass at which an equilibrium
can still occur is given by the condition E = 0 in relation to
the total energy, ie h.c.N1/3 = G.M.mf .
We can now distinguish two boundary cases of the composition of
the star's matter :
¨ 1.
If the mass of the star is formed only by those N
fermions, which at the same time create Fermi pressure, then the
total mass of the star is M = N.mf . In practice, this situation may occur in
degenerate neutron gas, so mf = mn , where mn is the mass of the nucleon (it doesn't matter if we use
the mass of the proton or neutron). The solution of the equation
E = 0 then for the maximum number of nucleons Nmax and for the maximum
mass Mmax
of the degenerate star gives the relation :
Nmax ~ [h.c/G.mn2]3/2 » 2.1057 , Mmax= Nmax.mn ~ [h.c/G ]3/2.1/mn2 » 1,5M¤
.
In this basic approximation, not considering numerical
corrections depending on the chemical composition of the
substance, the maximum mass of a degenerate star is given only by
the basic physical constants.
¨ 2.
The Fermi pressure is caused by electrons,
so mf = me, while the
gravitational mass of a star is made up mainly of nucleons
(protons and neutrons in the nuclei of the star's mass); so it is
with the white dwarf . The total mass of a star
is M = Nn
.mn, where
Nn is the
total number of nucleons, related to the number of electrons N
by the relation Nn = N.Z/A, where Z is the proton number and A
is the mass (nucleon) number of atoms of a stellar substance. The
solution of the equation E = 0 then for the maximum number of
nucleons and the maximum mass of the white dwarf gives :
Nmax ~
[h.c/G.(Z/A).mn.me]3/2 , Mmax s MCh ~ [h.c/G ]3/2.(A/Z)3/2.(1/me)3/2.(1/mn)1/2 .
This maximum possible mass of the white dwarf MCh is called the Chandrasekhar
limit. In addition to the basic physical constants, it
also depends on the chemical composition
substances of the white dwarf, on the ratio of the number of
protons and neutrons.
The above calculations are only model and have the
character of rather dimensional estimates. More accurate values
of the limit masses of compact stars can be obtained by solving
the Oppenheimer-Volkov-Landau equation (4.3) using an appropriate
equation of state, eg the Harrison-Wheeler equation of state (see
below).
The Chandrasekhar limit for a hypothetical star from hydrogen
itself (proton star), ie Z/A = 1, is 2.74 M¤, for the
realistic case Z/A = 0.5 (helium, carbon, .. calcium, ... iron )
is MCh = 1.44 M¤ .
White dwarfs, which occur very abundantly in space, are
therefore the final stages in the evolution of small and
medium-sized stars (masses
similar to our Sun), in the interior of
which only lighter elements such as carbon,
oxygen and magnesium were created by thermonuclear fusion. When
thermonuclear reactions cease, the pressure of electron
degeneracy stops the star's gravitational contraction and its
composition no longer changes.
In terms of their composition, there are 3
types of white dwarfs :
-> Helium white
dwarfs are the end stage of low mass (tenths of M¤)
main sequence stars. These small stars, if alone, evolve very
slowly, over tens of billions of years, longer than the duration
of the universe. So the helium white dwarfs of this origin have
not yet formed. Helium white dwarfs can also arise from binaries
of medium masses, which, after the transformation of hydrogen
into helium in their core, lose their hydrogen envelopes, reduce
their mass, and further fusion no longer continues. This
mechanism may work, but it probably only happens rarely, so
helium white dwarfs are rare..
-> Carbon-oxygen
white dwarfs develop from stars of approximately solar mass
(approx. 0.8-6 M¤), which reach this stage in approx. 10 billion years.
They are the most common white dwarfs.
-> Oxygen-neon-magnesium
white dwarfs arise from somewhat heavier stars (approx. 8 M¤);
are less common than carbon-oxygen.
More massive stars (>10 M¤) no
longer end up as white dwarfs, but undergo gravitational collapse
to form a neutron star or black hole.
Generally, stars with an initial mass of 2-6 M¤ do
not reach a sufficient temperature in their cores to
thermonuclearly burn elements heavier than carbon, oxygen,
magnesium and then collapse and explode as type II supernovae
into a neutron star or black hole. Thus, the white dwarf was
formed before all the thermonuclear fuel in the star was used up.
When such a white dwarf gravitationally collapses, this leftover
fuel (mainly carbon and oxygen) ignites thermonuclearly, suddenly releasing a large
amount of energy that greatly exceeds the gravitational binding
energy, so that the star is blown apart in a supernova
explosion (type Ia).
Metaphorically, one
can say that white dwarfs in their collapse are the most powerful
"thermonuclear bombs" in the universe..!. However, we
will see below that an even more powerful "explosive
charge" is the gravitational collapse into a
neutron star... And a more permanent source of enormous
energy is accretion disks and jets from massive rotating black
holes.
Supernova
explosion. Thermonuclear explosion. Core collapse - Neutron
stars. Pulsars.
Exceeding the Chandrasekhar mass limit for the stability in the
final stage of stellar evolution basically occurs in two
situations :
1. A
white dwarf is part of a close binary
star with a
standard ordinary star, from whose surface layers it
"sucks" gases, thereby increasing its mass, until
exceeding the Chandrasekhar limit.
2. The
massive star, after the fuel is exhausted and all thermonuclear
reactions have ended, has a residual mass M' exceeding that of Chandrasekhar,
so the white dwarf does not even stabilize - the contraction and
gravitational collapse of the star's core continues, during the
supernova explosion (type II).
So if the
mass of the white dwarf greater than the afore mentioned Chandrasekhar limit (which is about 1.4 solar mass M¤ *), the presure of degenerate electron gass is no longer able
to balance such large gravitational forces.
*)
Chandrasekhar's limit
of 1.4 M¤
applies to non-rotating (or slowly rotating) white dwarfs. With
rapid rotation, this limit can be up to ~3
M¤
[73].
When the Chandrasekhar limit is
exceeded, further contraction occurs - the collapse of the star,
during which two diametrically different phenomena can occur,
depending on the composition of the white dwarf or the core of a heavier star :
--> Thermonuclear
explosion
If the white dwarf is composed of light
elements (carbon, oxygen), the increase in pressure and temperature
during contraction will trigger a rapid thermonuclear
reaction (such as the fusion of carbon and oxygen into heavier
nuclei up to nickel)
throughout the white dwarf's volume. The large released energy
leads to a thermonuclear explosion and the scattering of the white dwarf, which
manifests itself as a supernova
explosion,
according to the astronomical classification of type Ia (the spectral
lines of hydrogen are not represented in the radiation spectrum:
at the end of its evolution, the star has already consumed
hydrogen in its core and blown off the outer hydroen layers in
the red giant stage).
In the place where the star once was, after the Ia supernova,
only an expanding cloud of gases will remain, no compact object will be formed.
Why the explosion ?
The question may arise why the usual regulatory
mechanism
[temperature->pressure] of the stability of
stars is not applied during this contraction, when during
contraction and growth of thermonuclear reactions the thermal
pressure (caused by the kinetic energy of the heated substance)
will increase due to the increase in temperature and the star will expand, which is resulting in a drop in
temperature and pressure and a slowdown in nuclear reactions.
However, in the case of a white dwarf, this does not work: the
pressure that maintains it against gravity is non-thermal in origin - it is due to the Fermi
pressure of degenerate electrons, which is independent
of temperature.
At the same time, the intensity of thermonuclear reactions increases rapidly with increasing temperature.
The white dwarf is
therefore unable to regulate the fusion
process in the
usual stellar way, so fusion reactions
can run wild.
The increased energy-heat production without expansion cooling
sharply increases the internal temperature, further increasing
the rate of fusion very rapidly. This is a significantly unstable
supercritical situation with "positive
feedback".
Within a few seconds, all fusion-capable "fuel" (mainly carbon and oxygen in common white dwarfs) is fused thermonuclearly. If the
released energy exceeds the white dwarf's gravitational binding
energy, the individual gas-plasma particles gain enough kinetic
energy to overcome the gravitational binding, fly away from each
other, and escapes into space. Its complete
destruction
will occur into a cloud of rapidly expanding gas.
Alternative options for launching
explosive fusion ?
The mechanism of thermonuclear fusion outlined above in a type Ia
supernova quite convincingly explains the observed properties and
is well justified astrophysically. Nevertheless, there are some
ambiguities and questions in connection with a more detailed
analysis of the model and with astronomical observations :
Most white dwarfs have masses
significantly less than Chandrasekhar's. In such a case, it would
take an excruciatingly long time before a white dwarf would be
able to acquire the necessary material in a binary system.
Therefore, alternative mechanisms for triggering explosive fusion
are also being investigated. One is the participation of helium
that the white dwarf could siphon from a neighboring star
containing a helium outer envelope. A relatively thick layer of
helium could thus accumulate. Helium has a lower fusion
temperature than carbon or oxygen, so the helium layer could
undergo a rapid fusion reaction and send a shock wave inside the
white dwarf that would initiate thermonuclear fusion of carbon
and oxygen. However, the helium layer around the supernova cloud
has not been observed spectrometrically...
The possibility of a close binary system
of white dwarfs has also been discussed, which would come closer
by emitting gravitational waves or viscous friction until the two
white dwarfs merge into a star with a mass greater than that of
Chandrasekhar, thus there was a meltdown and a thermonuclear
explosion was ignited. However, in the fusion process,
thermonuclear reactions would first occur, in which carbon and
oxygen would be converted into neon and magnesium, so then there
would be nothing to explode, but it collapse into a neutron
star...
Released energy
As shown in §4.1, "Thermonuclear reactions in stellar interiors", the fusion of hydrogen to helium in stars
releases 0.7% of the rest mass of burned hydrogen. This energy is
released slowly, over a long period of time. The amount of
thermonuclear energy released during the conversion of carbon to
iron-56 is 0.12% of the rest energy of the mass of carbon, the
conversion of oxygen-16 to Fe-56 releases somewhat less, 0.086%
of the rest energy of the mass of oxygen. For medium-mass stars,
the energy released by the thermonuclear combustion of carbon and
oxygen into iron is about (1-2)x1044 J.
In a thermonuclear supernova, this energy is released suddenly,
explosively, within a few seconds. All of the thermonuclear
energy from the explosion is instantly converted into heat
energy, which exerts a pressure substantially in excess of the
white dwarf's gravitational pressure. The white dwarf material is
therefore rapidly expanding with an initial velocity of 0.3-0.4%
of the speed of light.
Thus, the released thermonuclear energy is
converted into kinetic energy (after subtracting the
gravitational binding energy of the white dwarf). Relatively
little energy is emitted as light in the initial stages of the
explosion, and the dense material of the cloud is also opaque to
light. After a few days of expansion, the cloud can
thermodynamically glow more prominently, but another phenomenon
shows itself the most: a huge amount of thermal
energy is provided by the radioactivity of
nickel 56Ni, which is produced
in a colossal amount in a thermonuclear supernova (as shown below
in the analysis of nuclear reactions) :
Nuclear reactions in a
thermonuclear supernova
A number of very diverse nuclear reactions can occur during the
violent gravitational contraction of a white dwarf. These are
primarily fusion reactions of carbon 12C and oxygen 16O. As shown in §4.1 (section
"Thermonuclear reactions in the
interior of stars", passages
"Carbon combustion" and "Oxygen
combustion"), these fusions proceed smoothly in more
massive stars, with iron 56Fe nuclei as the final product.
Stable isotopes of iron have more neutrons than protons, while
the stable isotopes of carbon and oxygen have equal numbers of
protons and neutrons. Obtaining stable iron nuclei by fusion from
carbon and oxygen therefore requires that some protons be
converted to neutrons in the fusion reaction sequence. This is
done through beta+- transformations, which they are
relatively slow, but it doesn't matter in the stars, they take
place smoothly and for a long time.
Due to the high speed of the thermonuclear explosion, the usual
accompanying beta radioactivity (which is slower) does not apply
here; these reactions are bypassed. Lighter elements based on
carbon and oxygen can combine here only into heavier elements
with the same number of protons and neutrons. They are elements
that are multiples of helium - 2 protons and 2 neutrons. Therefore, 56Fe nuclei cannot be formed directly, but initially only
"similar" nuclei of this group - 56Ni. Nuclear
physics, which studies various types of nuclear reactions in
detail using accelerator experiments, basically offers a series
of :
12C->16O->20Ne->24Mg->28Si->32S->36Ar->40Ca->44Ti->48Cr->52Fe->56Ni ,
involving protons p, neutrons n and helium nuclei 4He, in both forward and reverse
directions. The first reactions that occur during the explosion
are between the carbon nuclei: 12C + 12C
-> 20Ne + 4He,
12C + 12C -> 23Na
+ p, 12C + 12C ->
23Mg + n.
Reactions involving oxygen follow, for example 16O
+ 16O -> 31P
+ p, 16O + 16O ->
28Si + 4He, 16O + 16O
->31S + n, 16O
+ 16O -> 30P
+ 2H. After
several more nuclear fusion reactions with helium, eg.
28Si + 4He ® 32S , 32S6 + 4He ® 36Ar , 36Ar + 4He ® 40Ca , 40Ca + 4He ® 44Ti , 44Ti + 4He® 48Cr , 48Cr + 4He ® 52Fe , 52Fe + 4He ® 56Ni ,
eventually the white
dwarf material consists mostly of nickel 56Ni and 4He.
Nickel-56 is radioactive and
undergoes beta decay (by electron capture) to cobalt-56 with a half-life of
six days. Cobalt-56 is also unstable, decays (by beta+ and electron capture) with a half-life of 77 days to 56Fe, which is already stable. The decay diagrams and gamma spectra of both
nickel+cobalt-56 radionuclides are analyzed in treatise 4.1
"Radionuclides", passage
"Ni-56->Co-56" of the monograph "Nuclear Physics and
Physics of Ionizing Radiation".
This means that the radiation we
see two weeks after the supernova explosion is mainly from the
decay of 56-Ni, and the radiation seen in the following months is
from the decay of 56Co. But many other elements and
isotopes are also represented. These elements are dispersed into
the interstellar medium and, together with nuclides created in
core-collapse supernovae (and in "planetary" nebulae
from red giant stars), form the diverse mix of chemical elements
found in space and on Earth, including the biogenic elements from
which we are composed even we...
As the hot cloud expands after
the explosion, its surface area grows,
while continuing the heating by the radioactive decay of nickel into
cobalt and then into iron. The increasing surface area of the
photosphere and increasing temperature causes the brightness to
increase. A Type Ia supernova reaches its maximum brightness
about 20 days after the explosion, at a luminosity nearly 10
billion times that of the Sun. When the cloud expands
significantly, most of the energy already escapes from the center
of the explosion, the cloud cools and also ceases to be heated by
radioactivity. Luminosity first decreases with a half-life of 6
days, then the decrease slows down to a half-life of 77 days. A
distant supernova then ceases to be visible after a few months.
--> Core collapse,
neutron star
If the rest of the masive star's interior (with
a mass exceeding Chandrasekhar's) does not contain sufficiently
large concentrations of light elements, a massive thermonuclear
reaction will not ignite and the gravitational
contraction will initially continue undisturbed. Soon, the density and temperature increase so much, that high-energy electrons are
"pushed" into the nuclei and absorbed by them; they
combine there with protons to form neutrons and flying neutrinos: e- + p+ ® no + n 'e - so-called inverse beta-decay (see
§1.2, section "Radioactivity beta" , passage "Inverse beta decay") - lower part Fig.4.2. As aresult, the
electron content in
the star decreases and the Fermi pressure therefore decreases. Substance stars is becoming more easily
compressible, there is therefore a further contraction, thereby
electrons become even faster and easier are absorbed by nuclei.
This is considerably unstable
situation ("positive feedback") and the process will continue
with avalanche increasing speed. Due to
gravity, so there is a sharp
shrinkage
(a "implode") of a star, in which almost all the
protons and electrons combine to neutrons; at this stage,
equilibrium can be occur again. This created
a neutron star, which has a diameter of only a few tens
of kilometers and its density is of the order of density in
atomic nuclei ~1014 g/cm3
(a teaspoon of such a mass would weigh billions of tons!). The gravitational forces are
balanced by the Fermi pressure of the degenerate
neutron
"gas". A neutron star is a kind
of gigantic "nucleus" *) composed mostly of neutrons
and held together by its own gravity
of total
matter (the
structure of a neutron star is discussed below "Internal structure of neutron
stars"). However,
at too much large masses M' (greater than
about two masses of our Sun - the Oppenheimer-Landau limit), the gravitational forces overcome even the Fermi
forces between neutrons, the equilibrium of the neutron star does
not occur, and the collapse continues further, into the black
hole (below in the section "Full
Gravitational Collapse. Black hole.").
*) The word "core"
is used in stellar astrophysics in two completely different
meanings: 1. |Atomic nucleus; 2. The dense interior of a star.
The balance of neutrons, electrons
and protons
On the part of nuclear physics, the question may arise about the stability
of neutrons forming a neutron star. Free neutrons,
without strong interaction with protons, are unstable
and have a half-life of less than 15 minutes decays by b- decay into protons, electrons and (anti) neutrinos.
This is also common in atomic nuclei with an excess of neutrons
(radioactivity b-, see
§1.2, passage "Radioactivity beta" of the book "Nuclear Physics and Physics of Ionizing Radiation"). So how can the absolute excess of neutrons in a
neutron star be maintained?
The force that prevents the massive
neutron decay in a neutron star is gravity. Though not directly,
but indirectly, by inducing such a density and pressure that the
Fermi energy of the electrons is higher than the maximum energy
of the beta-electron during the decay of the neutron (which is
780keV). In such a case, the electrons created by the decay of
neutrons acquire such an energy as their number increases (Pauli's exclusion principle) that
they are pushed back into the protons to form neutrons. In the
neutron - proton - electron plasma, the formation of a neutron
star creates an equilibrium between b-
neutron decay and electron capture of
protons, ie between direct and inverse beta decay. Then the
electrons contained in the plasma are occupied by all energies
(including high energies), so event. electrons from neutron decay
"have nowhere to emit" energetically (in terms of phase
space) and therefore do not fly out - no further b- decay of neutrons
occurs.
Thus, in a neutron star, there is a
certain amount of high-energy electrons in the
mixture with neutrons, sufficient to prevent the decay of
neutrons (and, of course, the same number of protons to
maintain electrical neutrality). In the simplest approximation,
it can be shown that this ratio will be 1: 8
(see below).
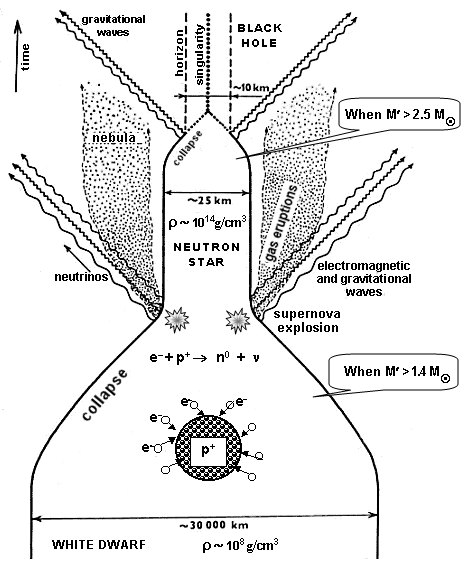
Fig.4.2. A general simplified scheme of the final stages of
stellar evolution and gravitational collapse: a white dwarf, a
neutron star and a black hole in a cross-sectional space-time
diagram (on the horizontal axis, the radial dimension is spatial,
on the vertical axis is time).
In this way, ie through all three stages, however, the collapse
could only take place in very special cases - if a
collapsing star would draw a significant amount of mass from its
surroundings by gravitational accretion (perhaps
from a neighboring star in a close binary system..?..). At remain masses M' lower than the respective limit, the
collapse actually stops in the stage of a white dwarf or neutron
star, at high masses M' these
stages do not stabilize and the collapse continues up to
the black hole stage.
During the implosion
leading to the formation of a neutron star, a large amount of
energy is released rapidly - both gravitational energy during
collapse and energy during specific nuclear reactions inside.
This energy radiates in the form of electromagnetic (in the non-spherical case also gravitational) waves, and is carried away by neutrinos (the largest part!) and the upper layers of the star,
which expand rapidly into space to form a glowing
nebula: the
neutron star is accompanied by a massive explosion
supernovae (middle
part of Fig.4.2) - according to the
astronomical classification of type II. Such a supernova glows with the intensity of hundreds of millions of Suns
for several days to weeks.
The category of supernovae with core collapse also
includes types Ib and Ic (according to the astronomical classification). They arise from very massive stars, which in the final
stage got rid of their gaseous envelopes of hydrogen (type Ib) or
also helium (type Ic). Either they were "blown away" by
radiation pressure, the stellar wind, or they were "sucked
out" by a stellar companion in a close binary system. The
remaining core, with an iron interior and carbon and nitrogen in
the outer layer, collapses into a neutron star or black hole.
During the collapse, due to the law of conservation of
angular momentum, a sharp acceleration of rotation
occurs and a rotating accretion disk is formed
around the resulting neutron star - and even more significant in
the case of a black hole - and intense jets of gases and
radiation are formed in the direction of the rotation axis (detailed in §4.8, part "Accretion
disks around black holes").
Note: This scenario outlined
above is just one of four of the possible mechanisms of a
supernova explosion (these other mechanisms
are briefly discussed below "Supernova
Types and Their Astronomical Classification"). Although, according to
astronomic observations, it may be a minority, from our point of
view of gravitational physics and the formation of compact
gravitationally collapsed objects, we will deal with it here
the most.
Energy transport from the
collapsing core and neutron star to outer space
When the core of a massive star collapses to form a neutron star,
about 15% of the rest mass of that core is converted to kinetic
energy, and when it stops suddenly due to nucleon degeneration,
it is converted to heat. This energy substantially exceeds the
gravitational binding energy of the nascent neutron star. If the
material of the star absorbed this thermal energy (a few percent would be enough),
it would be destroyed. However, this energy is carried away from
the emerging neutron star into the surrounding space by neutrinos.
These particles interact weakly with matter, so they freely
penetrate most materials, with the exception of their own
collapsed core, with which they can reach thermodynamic
equilibrium. They then escape and fly almost freely through the
mass surrounding the core. Although only a very small percentage
of neutrinos impart energy to the surrounding matter, this is
enough to "blow" it away from the nucleus to form a
rapidly expanding, glowing nebula of gases (plasma) and
electromagnetic radiation. However, most neutrinos fly away
without interacting. So we can only observe part of the released
energy and the rapidly expanding nebula. Only later can be
observable even the resulting neutron star (mostly
in the radio field, see below "Pulsars - rapidly rotating
neutron stars").
The
role of neutrinos in energy leakage from collapsing stars
- "Urca" processes
It can be said that the evolution of the inner parts of stars is
actually a gradual long-lasting gravitational contraction,
with occasional episodes of rapid contraction - collapse.
Gravitational contraction basically takes place at such a rate as
the energy radiated into the surrounding space is lost. The
interior of the star initially shrinks very slowly, as the energy
output of thermonuclear reactions is able to replace the radiated
energy. In the early stages of development, during the burning of
hydrogen and helium, energy from the star is emitted mainly by
electromagnetic radiation of various wavelengths (depending on
the temperature of the photosphere) and by the movement of
stellar wind particles. Only a small part is carried away by
neutrinos arising during partial thermonuclear reactions (described in §4.1, section "Thermonuclear reactions in the interior of stars"). However, in the case of
core collapse leading to a supernova explosion, this situation
changes, neutrinos can become dominant.
Although neutrinos are minute
electrically neutral weakly interacting particles (the properties of neutrinos are detailed in the
section "Neutrino - ghosts
among particles" in §1.2
of the book "Nuclear Physics and Physics of Ionizing
Radiation"), they have an
important role in nature - in nuclear physics (beta radioactivity
) and astrophysics (early phases of the evolution of the
universe, neutrinos from stars, from supernova explosions).
Neutrinos can participate in several processes of particle
interactions :
--> Beta processes of mutual
conversion of protons and neutrons, caused by the transmutation
of quarks "u" and "d" in nucleons due to the weak
interaction - Fig.1.2.5 in the passage "Mechanism of beta conversion. Weak interactions." in the monograph mentioned above. This is a well
theoretically justified and reliably experimentally verified
process, on which the widely used beta radioactivity is based in
practice.
Particle physics admits several
other processes based on electroweak interactions, e.g. :
--> Neutrino annihilation of
electron-positron pairs e- +e+ -> n + n´ .....
--> Plasmon decay: plasmon -> n + n´. A free
electron cannot emit a neutrino pair (energy
and momentum conservation cannot be fulfilled), but an electron interacting with the plasma
environment - a plasmon - in principle can.
--> And several other processes with neutrino
emission, e.g. synchrotron neutrino radiation of
electrons, photoneutrino emission e +g -> e +n + n´, neutrino
bremsstrahlung radiation, ........
All these processes are only hypothetical,
they could perhaps work at very high plasma densities and/or very
high temperatures. There is no hope for their direct
experimental verification in the near future. However, it may be
interesting to model them with actual observed processes during
the collapse of the cores of stars and their possibly to infer
validity indirectly from the agreement of the measured values.
Neutrino removal of energy
from collapsing stars at nucleon beta processes is almost certain
in the formation of neutron stars, as discussed above in the
passage "Core Collapse. Neutron Star.".
However, there have also been hypothetical opinions about the
cooling of the interior of white dwarfs by Urca-plasmon decay, or
the interior of stars during the burning of carbon or silicon in
the late stages of the evolution of stars ..?..
In the community of astrophysicists
studying supernovae, the collective name "Urca"
*) has been adopted for neutrino energy removal processes.
*) The name "URCA" is
not an abbreviation, but a humorous-recession naming after the
name Urca of one casino in Rio de Janeiro, where
astrophysicist Georgij Gamov and his Brazilian colleague Mario
Schenberg first discussed the role of neutrino emission in
supernovae. The escape of thermal energy from a supernova was
compared to the disappearance of gamblers' money from the
roulette table....
Supernova radiation. Light curve. Spectrum of supernovae radiation.
In addition to the primary energy of corpuscular particles and
photons during the explosion itself, other downstream processes
can also contribute to the observed bright radiation of a
supernova :
- Shock
wave, which is formed when the very rapidly expanding
gases from the inner regions of the star "catch up"
with the more distant and slower layers and the "stellar
wind" that the star emitted before the explosion. The
kinetic energy of this collision strongly heats the expanding
cloud.
-
Radioactivity of
elements that were synthesized in the star (and especially formed
during the supernova explosion) mostly in the form of radioactive
isotopes *). These then gradually decay into other
(more stable) isotopes, emitting high-energy radiation
(especially electrons b - and
photons g and X). As a result of the energy released in this way,
the expanding cloud glows for some time thermal and fluorescent
radiation. In addition to short-term radionuclides, there is
undoubtedly a large number of longer- lived isotopes
(T1/2 > 102 years), thanks to
whose radioactivity the expanding supernova cloud still glows
intensely in the X and gamma range for hundreds or thousands of years (but
it is still difficult for current detectors to measure and
view...). The radioactivity of some
long-lived radioisotopes, as is iodine 129I, aluminum 26Al and iron 60Fe, which may have been used in the formation of the
protoplanetary disk, planets and asteroids at the beginning of
the solar system. And extremely long - term
radionuclides (T1/2 >
109 years),
especially 40K potassium , thorium 232Th and uranium 238,235U, persist for billions of years; moreover with us on
earth is still preserved (§1.4 "Radionuclides" passage "Natural radionuclides"
in the monograph "Nuclear physics and ionizing radiation")
...
*) When massive nuclei absorb
electrons in a supernova explosion, releases huge amounts of neutrons
from part of which is absorbed by the cores of light and medium
heavy elements. These nuclear reactions produce a large number of
radioactive isotopes (eg Al-26, Ni-56, Fe-60,
I-129, ...) - see §1.3 "Nuclear reactions", passage "Neutron-induced reactions", monograph "Nuclear physics and ionizing
radiation physics".
Light curve
An important characteristic of a supernova is its light
curve - time course of radiation intensity (magnitude)
of the supernova. At the very beginning, at the moment of
supernova explosion, the light curve starts at the value "0",
respective on the luminosity value of the original star - the
evolutionary predecessor (progenitor) of the supernova.. The
surrounding dense gas envelope is impermeable to light radiation.
The enormous energy of the supernova explosion is initially
transformed into the kinetic energy of the expansion of this
cloud. Only then, when it has sufficiently expanded, thinned out
and the inside has warmed up, will it begin to shine intensely
into the surrounding space. ...
The light curves of supernovae
depend on explosion mechanisms and properties of ejected material
(its transparency and content). After a very sharp
initial increase in brightness, a maximum is reached
within a few days, after which the radiation intensity begins
to decrease gradually, over tens to
hundreds of days. The fastest decrease is observed in type
Ia supernovae, whose visible light is excited by the
radioactivity of nickel 56Ni, created by the thermonuclear fusion of carbon and
oxygen in the inner part of the white dwarf. Just after the
explosion, this beta and gamma radiation is absorbed by the dense
outer layers, heating it up and glowing in visible wavelengths.
In about a month, as the outer layers expand and thin, gamma rays
can escape. The brightness of the supernova here depends on how
much gamma radiation is absorbed and converted into heating and
visible light.
After reaching the maximum, the
decrease first begins with a half-life of about 6 days, which is
attributed to the radioactive decay of nickel 56Ni beta-
radioactivity with a half-life of T1/2 = 6 days for cobalt 56Co. It is also radioactive, by beta+ -radioactivity
and by electron capture is converted by a half-life of 77 days to
stable iron 56Fe; roughly with this half-life, the slower phase of the
supernova brightness decrease continues. The decay diagrams and
gamma spectra of both nickel+cobalt-56 radionuclides are analyzed
in treatise 4.1 "Radionuclides",
passage "Ni-56->Co-56" of the monograph "Nuclear Physics and
Physics of Ionizing Radiation".
A further decrease in the brightness
of the supernova is already very slow, in
addition to adiabatic expansion, it is involved in the
radioactive decay of long-lived radioisotopes (some of which have been mentioned above) . The intensity and width of the supernova Ia light
curve is determined by the amount of nickel-56 produced in the
given supernova, as well as the amount and composition of other
ejected matter. Comparing the shape of the light curves (a narrow
or wide graph that maps how quickly the supernova reaches maximum
brightness, how intense it is, and how quickly or slowly it
fades) with their spectra makes it possible to analyze the
dynamics of Ia supernovae and standardize them for more accurate
measurements of cosmic distances.
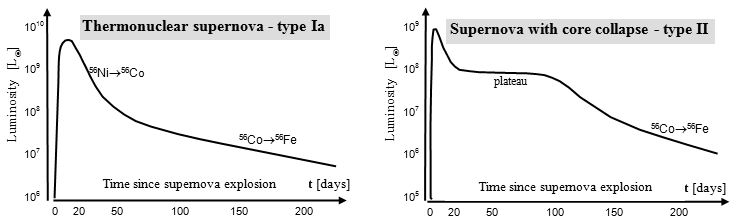
Typical shapes of light curves of type Ia and type II supernovae.
During the absorption of
electrons and the neutronization of matter inside the supernova II
type, huge amounts of neutrinos are
emitted, which carry away energy and effectively cool
the collapsing central portion of the star's burnt matter. Due to
their weak interaction, neutrinos practically do not create
pressure *) and fly into the surrounding universe without
resistance. Effective cooling by neutrino radiation aids in the rapid
gravitational collapse of the central part of the
supernova, which can stop even the Fermi pressure of the
degenerate neutron "gas" (see
below "Behavior of the substance
at high pressures; neutronization") .
*) During the formation of a neutron star, however, a
tiny percentage of the huge number of neutrinos is captured in
the dense layers of the star's envelope, transfers energy, and
the resulting pressure, together with the
pressure of electromagnetic radiation, causes the rapid expansion
of these ionized gases into a glowing nebula, observed as a
supernova explosion.
The initial increase in the light curve is caused by the
increase in the surface area of the star, in the interior of
which a type II supernova explosion took place. The peak of the
light curve occurs when the temperature of the outer layers
begins to drop more significantly. The subsequent rate of
decrease in brightness is somewhat different and probably depends
on the size of the star's hydrogen envelope. The shock wave
during the explosion heats this outer layer to a high temperature
(about 100,000 degrees), so that all the hydrogen in it is
ionized. Ionized hydrogen has a high opacity for light, so it
does not transmit light from deeper layers. As the supernova
cools, the ionized hydrogen recombines (at 3,000 degrees) into a
neutral form that is transparent to light. We can also see
photons from deeper, warmer layers. The recombination energy of
hydrogen atoms is also emitted. The combination of these opposing
tendencies - reducing radiation due to cooling, versus reducing
the opacity of the hydrogen shell and releasing recombination
energy - leads to a slowing down the decline of the light
curve, which has a certain temporary plateau, the
length of which depends on the depth of the hydrogen shell. As
recombination takes place throughout the hydrogen shell, the
plateau phase ends and the light curve transitions to the
standard shape with a dip given by the adiabatic expansion of the
nebula and radioactive conversion of 56Co to 56Fe. If the star's hydrogen envelope is absent or
negligible, the light curve (instead of plata) shows a temporary
rather rapid almost linear descent after the maximum. According
to the shape of the light curve after the maximum, in the
astronomical literature, the light curves of type II supernovae
are categorized into type SNII-L with linear echo and type SNII-P
with plateau after the maximum.
In supernovae of type Ib and Ic, due
to the absence of a hydrogen envelope layer, there is no plateau
in the decline, their light curves have a similar shape to that
of supernovae Ia.
Spectrum of supernovae radiation
Spectrometric analysis of radiation emitted by objects in space
generally provides essential information about temperature,
chemical composition and speed of movement (Doppler
spectrometry). It is extremely important especially in stellar
astronomy, including the final stages of stellar evolution.
Similar to the radiation from stars, the electromagnetic
radiation from supernovae is emitted only from the uppermost
layers - from the photosphere, where the gas is mostly
already cold enough, recombined from the ionized plasmatic state
to the atomic state, and therefore permeable to light.
Unfortunately, it is not possible to spectrometrically examine
the inner regions of supernovae...
The spectra of supernovae are measured against a background of
continuous thermal radiation, so the spectral lines of the
elements present are both emission and absorption.
The emission spectrum is emitted by hot gases expanding from the
inner layers of the supernova. The absorption spectrum is caused
by the selective absorption of light by atoms in the outer gas
envelope around the supernova. In this "mixture" of
measured radiation, some spectral lines interfere with others or
are "overpowered" by background radiation - they are
difficult to see. Next to the spectral lines of neutral atoms,
e.g. hydrogen Ha,b,g , sodium Na I, calcium Ca I, oxygen O I, spectral lines
of ionized atoms are most often visible:
1-times, e.g. Ca II, Si II, Fe II, Co II; or 2-times, e.g. Fe
III, Co III.
For supernovae, their astronomical classification was
based on spectrometry (below in the passage
"Types
of supernovae and their astronomical classification"). A supernova is
practically never observed and measured from the very beginning
of the explosion, but only somewhere around the maximum
brightness and then in various phases of decline.
In the case of thermonuclear supernovae (type
Ia), spectral lines of hydrogen or helium are not observed in the
early phase, because the white dwarf from which the supernova
arose does not have an envelope of these gases, which the star
"blown away" already in the red giant stage. However,
there are lines of silicon Si II 6347, 6371 Å. At a later stage,
in the expanding nebula, spectral lines of iron Fe II, III and
cobalt Co II, III dominate, originating from cobalt and iron
resulting from radioactive transformations of nickel 56Ni.
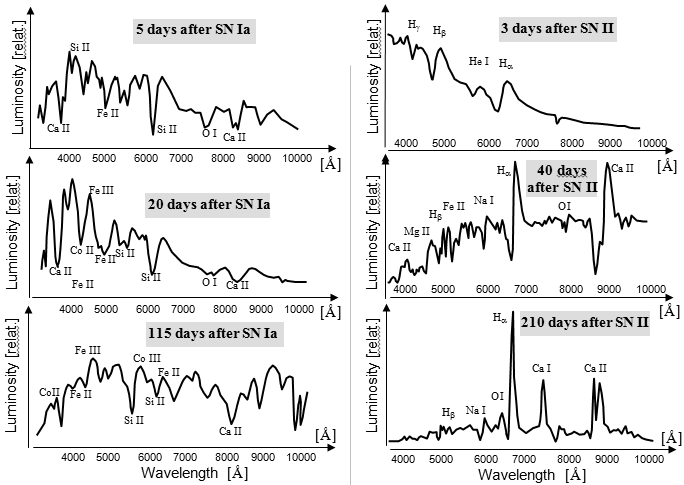
Examples of the approximate shape of the optical spectra of type
Ia and type II supernovae at different time periods after the
explosion.
Note:
These are only illustrative shapes of the spectra created by
averaging several measured spectra of specific supernovae using a
graphic editor.
In the spectra of type II core-collapse
supernovae, in the peak period and in the later phase of
descent, spectral lines of hydrogen (Balmer lines Ha,b,g),
originating from the recombination of the hydrogen shell around
the star, are strongly represented. Fe II, Na I, Ca II lines are
also observed. If it is possible to measure the early period of
the explosion, the He I spectral line is also observed.
Supernovae with core collapse are
also types Ib and Ic, where hydrogen (and silicon) spectra are
missing. In the spectra of type Ib supernovae, the spectral lines
of helium are visible, in the case of type Ic, the spectral lines
of helium are weak or absent.
Neutron
star
In a type II supernova, after radiating enormous
energy for several months, its core remains in place of its
original star, collapsed into a compact structure with only a few
kilometers in diameter and an unimaginable density of the order
of 1014 g/cm3 (nuclear density), composed mainly of neutrons
- a neutron star. Further shrinkage is then
prevented by the Fermi pressure of the
degenerate neutron gas, caused by Pauli 's fermion exclusion
principle.
Note: However,
a very massive star can overcome Pauli's
exclusion principle by its gravitational shrinkage. The neutrons
approach each other at such a small distance that the asymptotic
freedom of strong interaction between quarks is exerted. The
neutron substance "melts" into a mixture of free quarks
and gluons - the quark-gluon plasma - see "Internal structure of neutron
stars" below. And with an
even heavier weight, no more force can stop the
gravitational shrinkage, complete gravitational collapse occurs
(described in more detail below in the section "Complete gravitational collapse.
Black hole.").
The
site of the supernova's explosion is surrounded by a rapidly expanding
nebula from
the ejected outer parts of the star. Very well known is the Crab Nebula, which is the remnant of a supernova
explosion observed in 1054 by Chinese astronomers :
 |
 |
| Supernova explosion
observed in 1054 in China. Today, a Crab Nebula
containing a pulsar inside - a rapidly rotating neutron
star - is observed at that place. |
Destruction of the
planetary system
If the original star had a planetary system, it
will probably be destroyed in a supernova
explosion. The nearby inner planets usually evaporate
with a huge flow of energy, and their gas is blown into
interstellar space by the pressure of radiation. The orbits of
more distant planets will become unstable due to the loss of much
of the star's mass during a supernova explosion. However,
protoplanets can condense again from the gas disk around the
neutron star, and later new (exo)planets
perhaps may also form..?..
Supernovae - space
killers and also creators of new life-giving worlds !
A supernova explosion is the biggest disaster
what can hit heavy stars. Not only is its own star destroyed, but
it is scattered and evaporated possible orbiting planets, even
nearby partner stars (in a binary or
multiple system) can be ejected. From the
point of view of nuclear physics, it can be said that the
supernova explosion is, among other things, the biggest
radiation accident in the universe! If one of the
surrounding stars (tens of light-years
away) exploded like a supernova, our Earth
would be hit by such intense radiation that it would exceed the lethal
radiation dose to humans more than 100 times (see §5.6, passage "Astrophysics and cosmology: - human
hopelessness?")..!.. A supernova explosion "sterilizes" the
vast surroundings of many light-years in space, where life
will not be possible for a long time.
On the other hand, these destructive
and murderous supernovae "positively" contribute to the
further evolution of matter in the universe. The
supernova-ejected cloud contains a large number of heavy
elements - including biogenic ones -
which will enrich the surrounding interstellar matter. The
explosion also creates a massive shock wave that can compress gas
clouds in the surrounding space. This can initiate the gravitational
contraction of these gas-dust clouds, which can result
in the formation of new young stars, enriched
with heavier elements. In planetary systems around such stars, life
can then develop in principle (discussed in more detail in the section "Origin and
Evolution of Life") of the work "Anthropic Principle or
Cosmic God"). Without a
cataclysmic supernova explosions, we probably wouldn't be
here..!.. General importance of supernovae for the
universe is discussed below in the passage of "Astrophysical importance of
supernovae".
Types of supernovae and their astronomical
classification
In astronomy,
supernovae are
extremely bright stellar objects of an explosive nature that
suddenly appear in the sky and whose brightness then decreases
again by many orders of magnitude over the course of weeks to
months. The name is derived from Latin. words nova, ie new,
because visually it seemed that a "new star" was born (stella
nova). But now we know that this is really the opposite
- a manifestation of the demise of the old star,
which has reached the final stages of its life and irreversibly
transforms into an object substantially different from ordinary
stars. In the previous §4.1, in the passage on the basic
evolution of stars, the instabilities, pulsations, and
"smaller" explosions of a star were mentioned, which
lead to a sudden brightening of a weaker star; this phenomenon is
astronomically observed as a nova - the original
star is usually not visible in smaller telescopes, it looks like
the birth of a "new star". The name super
nova expresses that this is a much more grandiose cosmic
phenomenon.
The oldest surviving records of
supernova sightings come from 1006 in Egypt and Mesopotamia, the
most famous is the above-mentioned supernova from 1054 observed
in China (gave rise to the Crab Nebula), then from 1181 in China and Japan. Significant was the
supernova in 1522, which Tycho Brahe observed and called it the
"nova stella", and the supernova from 1604,
which was observed by J.Keppler and which Galilei mentioned as an
argument against the then dogma of the immutability of heaven,
traditionally from the Aristotle period *). The current
observation of the SN1987A supernova in the Large Magellanic
Cloud, is very significant, including the capture of neutrinos in
the SuperKamiokaNDE device (see the "Neutrinos"
passage in §1.2 "Radioactivity" of the
monograph "Nuclear Physics and Ionizing Radiation
Physics"), allowing to be tested
current theories of formation and dynamics of supernova
explosions.
*) The supernova explosion is an
astronomically very short, fast and transient event
that is not easy to observe and analyze in detail. The
above-mentioned historical observations of supernovae took place
visually either directly or on small simple telescopes, without
the possibility of quantification and spectral analysis. The
observation data are therefore only very rough and incomplete.
Even current observations are often not enough to capture the
initial period of an explosion, before reaching maximum
brightness.
However, astronomy offers a certain possibility
of "retrospective" observation
of supernova explosion. The explosion, accompanied by extremely
intense radiation, takes place not only towards us, but also in
the opposite direction, to more distant areas. In these more
distant regions, the radiation may strike a cloud of interstellar
dust, which will then emit secondary (much weaker) radiation of
the same time course and spectrum as the primary radiation of the
supernova. In principle, this radiation can then be analyzed
additionally and later, according to the
distance of the respective cloud. Another promising possibility
is the observation of images of a supernova split by a gravitational
lens (§4.3, passage "Gravitational
lenses in space"), coming with
different time shifts.
Astronomical
naming of supernovae consists of the
abbreviation "SN", the year of discovery and finally
possibly letters of the alphabet denoting the order of multiple
supernovae discovered in the same year - eg the afore mentioned
SN1054, or the current SN1987A. Now, with the help of large
telescopes, several supernovae in more distant galaxies are
observed every year.
How often do
supernovae explode? - continuous fireworks lasting billions of
years !
Until recently, supernovae were
considered a rare event, observed in the deep
stillness of the night sky about once a century. However, it is
only an optical illusion caused by three
circumstances :
× The enormous vastness
of the universe, in which the stars are very sparsely
distributed; the vast majority of stars are extremely far
from us.
× Long lifespan of stars - millions and
billions of years.
× Very short duration
of a supernova explosion - hours, days, months.
The vast majority of supernova explosions take place very
far from us (billions of light
years). So even though, at the peak of
their activity, supernovae can shine brighter than a billion of
our Suns, we can't either see them at all, or they appear to us
as tiny light powders that we can easily overlook in the vast
starry sky. Only those supernovae that explode in our Galaxy can
be observed directly through the eyes (that is, at intervals of
hundreds of years); in the surrounding galaxies by astronomical
telescopes (several supernovae per year). Extrapolation of
astronomical observations *), as well as astrophysical analysis
of the life of massive stars - in relation to their number in the
universe - leads to an estimate that roughly every few
seconds (and perhaps an average of
once per second) somewhere in our
observable universe explodes some supernova. It
is a bit of an exaggeration to say, that this amount of
supernovae is a continuous, billion years running "cosmic
firework show" - but extremely diluted in the vast
space of universe...
*) Special telescopes equipped with robotic
systems for searching large bands of the sky are being prepared
any new resources that appear. This will allow the registration
of many distant supernovae that would escape the attention of
large telescopes with a narrow field of view.
Four different mechanisms of a supernova explosion
Contemporary nuclear astrophysics presents four
possible, diametrically opposed, supernova explosion scenarios :
1. The classical Chandrasekhar scenario
explained in more detail above: after crossing the limit of
instability, electrons are absorbed by atomic nuclei to form
neutrons during the rapid shrinkage of the star's interior. The
decreasing Fermi pressure of the disappearing electrons leads to
the implosion of the star, creating a neutron star.
2. Thermonuclear
explosion of the star: by an enormous increase in
pressure and temperature during shrinkage, a rapid thermonuclear
reaction of carbon and oxygen in the whole volume of the shrunken
star occurs, while the released energy leads to
"scattering" of the star. This will manifest as a type
Ia supernova explosion. No neutron star is present inside the
rapidly expanding cloud formed by this mechanism.
3. Thermonuclear
explosion of a star due to e- e+-pair instabilities (the process is discussed in more detail bellow, passage
"Electron-positron pair formation").
4. Gravitational
collapse of the central part of the star into a
black hole, if the residual mass M' is greater than the
so-called Oppenheimer-Landau limit of 2.5 M¤ (discussed in detail below "Complete
Gravitational Collapse. Black Hole.").
The various mechanisms of supernova formation will be
briefly discussed below in connection with the astronomical
distribution of supernovae :
The astronomical
classification of supernovae
originated at a time when the events taking place there were not
yet known, so it has no clear and logical connection with the
mechanisms of supernova formation. Supernovae are astronomically
classified according to the presence of spectral lines
of various elements in the spectrum of their radiation and
according to the shape of the light curve (time
curves of supernova magnitude, especially the dynamics of
brightness decrease). If the spectrum of a supernova does
not contain hydrogen lines, it is classified as type I;
if it contains Balmer lines of hydrogen, it is referred to as a type
II supernova. Each of these two
categories is further subdivided into subgroups according
to the presence of other spectral lines or the shape of the light
curve. Type Ia supernovae do not
contain helium lines in their spectrum either, but a silicon
absorption line ( Si II at 615 nm) is
present, especially in the region of the brightness peak.
Type Ib supernovae contain a helium line (He I
at 587.6 nm). Type II supernovae are divided into type II-P
with flat light curve and type II-L with linear
decrease of the light curve.
From an
astrophysical point of view, this classification is essentially
irrelevant. A more accurate division is into two types:
"thermonuclear supernovae" for type Ia
and "core collapse supernovae" for
types Ib, Ic and II, which distinguishes the internal mechanism,
not what they look like from a distant observation... It was
distinguished right in the opening passage of this of "Supernova
explosion. Neutron star. Pulsars." .
Supernova
formation processes
In terms of the dynamics of formation and mechanism, we
can divide supernovae into three (or 4) basic types :
- Gradual
accretion of matter to a white dwarf
This situation occurs in binary (or
multiple) stellar systems. A type Ia supernova is
formed in a tight binary star formed by a giant star and
a white dwarf, where matter flows from the giant to the
white dwarf. This leads to a gradual accumulation of
matter, until the white dwarf eventually exceeds the
Chandrasekhar limit of stability (1.4 M¤) and
collapses into a neutron star *), which manifests itself
as a supernova explosion. Astronomically,
these supernovae are classified as type Ia.
*) An alternative mechanism is also
discussed, that increasing the pressure and temperature
during shrinkage will result in a rapid thermonuclear
reaction (such as combining carbon and oxygen to nickel)
in the entire volume of the white dwarf; the released
energy leads to its scattering (thermonuclear explosion)
and this manifests itself as a supernova explosion.
A
similar but slower and less dramatic mechanism is
explained in the above-mentioned nova:
overflow of gas, a certain amount of hydrogen accumulates
on the surface of the white dwarf over a period of time,
which is compressed and heated to a high temperature due
to strong gravity. Upon accumulation of a sufficient
amount of strongly compressed and heated hydrogen, this
layer undergoes an explosive thermonuclear fusion , which also releases
large amounts of radiant energy, including X-ray and
gamma radiation. However, it is many orders of magnitude
less than a supernova, and the process takes place at the
surface and does not cause the entire star to collapse or
explode. The nova explosion process can be repeated
(quasi) several times, for the entire duration of the
second partner in the red giant stage.If the
binary system is tight enough and the accretion is fast
enough, it is enough (accompanied by a series of nova
explosions) to accumulate enough mass on the white dwarf to exceed Chandrasekhar's limit - the last,
definitive and many times more powerful supernova
explosion will occur. However, in most novae, the
accretion to the white dwarf is slower and
Chandrasekhar's limit is not reached (for as long as the
second binary partner is in the red giant phase).
The
whole process takes place in roughly the following six
stages :
¨ The initial
situation is a binary system of two less massive stars
(units M¤)
of the main sequence.
¨The more massive
star enters the final stages of its life and becomes a
red giant. After "blowing" the upper layers and
terminating thermonuclear reactions, its remaining core
becomes a white dwarf (a blown gaseous
envelope in which the two stars move for a long time can
reduce the orbital distance of the two stars by its
viscous braking) .
¨ Even the second
star of the binary system eventually reaches the final
stage of its evolution and becomes a red giant.
¨ If the binary
system is sufficiently tight, the dimensions of the red giant
approach the so-called Roche between , which is the first common
equipotential of a binary system (see §1.2, Fig.1)..1d,
passage "Binary system"). From the red giant, a stream of gas can then
flow to the white dwarf
around the so-called Lagrange liberation point
(which is the
intersection of the equipotentials) ; this gas enters
almost circular orbits around the white dwarf , forms an accretion disk, loses energy due to viscous
friction, and gradually descends to the white dwarf.
¨ By
accreting this mass, the mass of the white dwarf
gradually increases until it reaches Chandrasekhar's
critical limit and explodes as a supernova (Ia).
¨The massive
outpouring of particles and radiation during the
explosion will cause a shock wave in the envelope of the
red giant, the pressure of the radiation will disrupt and
blow away the outer layers of the red giant and expose
the heart of the star, a bluish smaller glowing star
shining in the UV region. It is possible that the force
of an explosion, according to the law of action and
reaction, may even throw mutually the supernova and its
binary star away from each other - the binary system may
disappear.
Type
Ia supernovae are of great importance for astronomical
observations. Their explosion always occurs
according to the same scenario and with the same
parameters *). As the mass to the Chandrasekhar between
increases gradually, the initial mass of the collapse and
therefore the amount of energy released is always practically
the same, so that the distance
of such a type Ia supernova can be determined from the
relative observed brightness. Supernovae Ia can therefore
serve as a kind of "standard candle",
replacing Cepheids in extragalactic astronomy; they allow
the measurement of large intergalactic and cosmological
distances of the order of billions of light-years (see
§5.6 "The Future of the Universe. The Arrow of Time.
Hidden Matter.").
*) However, rotation can
be a variable parameter. First, the speed of rotation,
which affects (reduces) the value of the Chandrasekhar
limit. Furthermore, it is the angle of inclination of
the axis of rotation relative to the observer; in
fact, during rapid rotation, significantly more
electromagnetic energy is emitted in the direction of the
axis of rotation than in other directions.
- Direct
collapse into a neutron star
With the remaining mass M' of the star greater than the
Chandrasekhar limit, the phase of the white dwarf does
not stabilize and collapse onto the neutron star occurs,
as described above. The accompanying supernova explosion
is referred to as a type II supernova .
- Complete
collapse to black hole
At high star mass (>
~ 20 M¤), neither the white dwarf nor the neutron star
configuration stabilizes, but the collapse of the central
part of the star's continues directly to the black
hole stage (as discussed
below - "Complete gravitational collapse. Black
hole.") - to the collapsar. The
accompanying supernova phenomenon here may be weaker or
stronger, depending on the rotation of the collapsing
star. With a slower rotation, most of
the ejected mass will fall back to the nucleus, with
which it will collapse into a black hole - only a weaker
supernova effect will be created .
If the star rotates fast
enough, the falling mass will form a massive, rapidly rotating
disk with high-energy jets, in
the direction of which the explosion will be seen much brighter
than in conventional supernovae. Such a "more
powerful" supernova is sometimes referred to as a hypernova.
During this catastrophic event, high-energy particles are
emitted in the form of jets along the axis of rotation of
the collapsing star, which generate a massive flash
of gamma radiation. The possibility of producing
heavy elements by the r-nucleosynthesis process is also
likely in a dense accretion disk and neutron-containing
jets.
Direct
collapse into a black hole without a supernova explosion ?
For the most
massive stars (> ~250 M¤),
gravity is so strong that after the burning of lighter
elements and loss of stability, most of the star's mass
could collapse directly into a black hole,
without significant energy and matter eruptions (energy
processes would take place below the horizon, from where
nothing gets). Only the outer gas envelope can
subsequently be heated during accretion and possibly
thermonuclear explode. However, the effect would probably
be much weaker than in supernovae -
paradoxically, the most massive stars probably end up
relatively "inconspicuously"..?..
- Thermonuclear
explosion of a star can
occur by two mechanisms :
¨ Enormous increase in pressure
and temperature during shrinkage will cause a rapid
thermonuclear reaction of carbon and oxygen in the entire
volume of the shrunken star, while the released energy
leads to "scattering" of the star - type Ia
supernova.
¨ Due to the collapse of the e- e+ -pair instability, the star may be
completely "scattered" and dispersed in the
form of a rapidly expanding cloud of gases (the mechanism was discussed in more detail in
passage "Electron-positron pair
formation" below). This scenario could perhaps apply to very
massive 1st generation stars (~ 150÷250 M¤), formed in the early universe from dense
clouds of hydrogen and helium. An explosion of this kind
(not yet observed astronomically) can be called a type
IV supernova ..?..
The thermonuclear explosion
of a star does not produce a neutron
star or a black hole.
Electron-positron pair formation; Thermonuclear
explosion of a star
The pressure of electromagnetic radiation
generated by hot gases (plasma) is an important force in
maintaining the star's balance against its own gravity. Photons
of this radiation transfer energy to electrons by Compton
scattering, they increase their momentum - pressure is created.
The higher the temperature, the more intense the radiation and
the greater its pressure. In very massive stars ( > ~150 M¤) in the
final stages (burning carbon, oxygen, silicon) the temperature
inside them reaches ~1010 °K, which causes the hot gas to generate
radiation not only of great intensity but also high
energy; a significant portion of photons will have
energies much higher than 1 MeV. In this case, a new phenomenon
begins to apply: the formation of electron-positron pairs.
High-energy photons g are transformed into electron-positron pairs during
electromagnetic interaction with atomic nuclei: g ® e- + e+ (from
the point of view of nuclear and radiation physics, this
mechanism is described in more detail in §1.6, section "Interaction
of gamma and X-rays",
Fig.1.6.3, monograph "Nuclear physics and physics of
ionizing radiation"). The photons
disappear gradually and their
energy is "trapped" in the rest masses of electrons and
positrons, which have relatively low kinetic energies and exhibit
significantly lower pressure than the photons from which they
were formed. Thus, a large part of the photons, whose pressure
protected the star from collapse by its own gravity, disappears.
This leads to shrinkage of the star's core, which further
increases the energy of photons with temperature and increases
the efficiency of their extinction by the formation of e- e+ -pairs.
This is a highly unstable situation, the star's
core begins to collapse rapidly, density and temperature rise
sharply and intense thermonuclear reactions ignite - fusion of
oxygen, silicon, ... etc. In the collapsing star's core, colossal
nuclear energy is explosively released within minutes, which may
exceed the total gravitational binding energy of the star. It
will happen a thermonuclear supernova explosion
in which the star is completely "scattered", leaving
only a rapidly expanding cloud of gases, formed
(in addition to the parent hydrogen and helium) by a number of
elements synthesized during the "quiet" and explosive
phases of the star.
With this e-e+
-instability and subsequent rapid fusion leading to a
thermonuclear explosion, some very massive stars could avoid
the compactification and expected inevitable fate of a
neutron star or black hole. We can consider this scenario only as
a hypothetical possibility, not yet
substantiated by astronomical observations. Nuclear astrophysics
proposes it for stars with a mass of approx. 150-250 M¤. It could perhaps apply to very massive 1st
generation stars, formed about 100-200 million years after
the Big Bang from dense clouds of hydrogen and helium. The
thermonuclear explosion caused by e- e+ -pair
instability would differ from a
"normal" supernova explosion (type
I or II - see next §4.2, passage "Types of supernovae
and their astronomical classification") in four consequences :
-> The explosion would be overall
more powerful, with a somewhat slower onset and significantly
longer fading of the light curve.
-> There would
be no instantaneous emission of a colossal amount of neutrinos.
-> In an expanding cloud, there would
be a smaller proportion of very heavy elements (heavier than
iron), but a large number of medium-heavy elements formed in the
star. Unlike a conventional supernova, where most of the
synthesized elements are destroyed and trapped in a neutron star,
here all "boiled" elements are ejected; there is a more
efficient enrichment of the universe with heavier elements in
cosmic nucleogenesis.
-> There would be no
neutron star (pulxar) or black hole inside the expanding nebula.
Astrophysical importance of supernovae
Supernova explosion, which belongs to the
most massive and the most dramatic phenomena which universe we
observe has several important astrophysical implications :
×
Chemical
evolution of the universe
Above all, supernovae contribute to the chemical
evolution of the universe - thrown substance enriches the
surrounding outer space of the heavier
elements
that were synthesized inside the star in thermonuclear reactions (as discussed in more detail in §4.1, section "Thermonuclear reactions inside the star").
These ejected heavier elements in space may become part of future generations of stars and planets. Figuratively speaking, in
cosmic nucleogenesis, stellar generations "pass the baton" of elements created during the
demise of the old generation to the formation of other heavier
elements by the stars of the new generation. Thanks to this
nucleosynthesis, there is also living nature and we humans -
without carbon from inside the stars and the explosion of
supernovae, we could not exist as a carbon form of life! We are
all made of stellar ash ...
Type Ia supernovae, which arise
from white dwarfs with a mass of 1.4 M¤, enrich the surrounding space mainly with
carbon, oxygen and other lighter elements (in
less massive stars, the end product of thermonuclear fusion is
mainly carbon and oxygen). Type II supernovae, formed from massive
stars with heavier elements synthesized down to iron, enrich the
surrounding universe with these heavy
elements -
and even more heavily: this is because a supernova
explosion releases a large amount of neutrons, which are
effectively trapped in the nuclei of the expanding layers within
a few seconds, where heavy neutron-rich nuclei are formed. Their
repeated b- transformations create heavy and very heavy nuclei (including uranium and
transuranium) in the expanding envelope. This rapid capture of neutrons, called the r-process, has created about half of all elements
heavier than iron in the universe (see
syllabus "Cosmic alchemy"
or passage "Cosmic alchemy - we are the
descendants of the stars!"
in monograph "Nuclear Physics, ionizing radiation").
The other half of them is formed with
s- process -
slow neutron fusion inside heavy stars in the late stages of this thermonuclear development (as
shown in §4.1, 'The thermonuclear reaction in stars" passage "Neutron capture and generate
heavy elements").
Particularly
efficient nucleogenesis can be expected in the
explosion of rapidly rotating supernovae with a
strong magnetic field, where a large amount of neutron-rich
plasma is ejected and intense neutron r-capture
occurs. This significantly enriches the ejected substance with
heavy nuclei up to uranium. Due to magneto-hydrodynamic
processes, this enriched substance is ejected into the
surrounding space at high speed in the narrow cones of the poles
of the axis of rotation.
× Cosmic
radiation
Huge number of energetic particles and
radiation emitted in the supernova take off into the space and is
probably important source of
cosmic rays propagating through space - see the discussion "Cosmic radiation" in the above monograph; in §4.8 "Astrophysical
significance of black holes"
we will see that another possible source of cosmic radiation can
be massive jets from the interior of rotating accretion disks
around massive black holes.
× Stimulation
of star formation
The shock wave created by a supernova explosion can stimulate the gravitational contraction of gas dust
clouds in the surrounding interstellar mass and thus the formation of other stars.
Neutron stars - permanent destruction and
trapping of heavy elements ?
As discussed above, the supernova explosion "liberates"
the heavier elements thermonuclear synthesized by the star and
ejects them into the surrounding universe. If a star's core,
which contains most of the nuclei of heavy elements
from stellar nucleosynthesis, collapses into a neutron
star during a supernova explosion, these nuclei are destroyed
and their neutronized "remains" are forever imprisoned
by massive gravity inside the neutron star - so for
cosmic nucleogenesis are "lost". However, this only
applies to solitary neutron stars. If neutron
stars are part of a binary (or multiple) system, then during
their mutual circulation, gravitational waves
are generated, which gradually carry away the kinetic energy of
the orbital motion, whereby the orbiting bodies gradually approach
each other until they finally merge. During this
fusion of neutron stars, a large amount of neutron matter can be ejected,
which immediately explodes (rapid
decompression from nuclear density) and
"nucleonizes" to form the nuclei of heavy
elements.
In §4.8, the passage "Collisions and fusions of neutron stars", is discussed this possibility of the formation
of heavy elements in collisions
and fusions of "already finished" neutron stars (after many millions of years) in
the binary systems of two neutron stars (or neutron star + black hole) by
the mechanism of "nucleonization" of
the ejected neutron substance. This is an "additional"
formation of heavier elements from matter that would otherwise be
lost to the chemical evolution of the universe..!..
When can we expect an
observable supernova explosion ?
In the above discussion, "How Often Do Supernovae
Explode? - A Continuous Billion-Year Space Fireworks!" we put a relatively high astronomical observation
frequency of supernova explosions in the observable universe. The
vast majority of these events, however, occur in billions of
light years distant universe. Relatively early supernova
explosion, the time horizon of a million years, expected
for a very massive stars observed in the phase of the red
giant *). Such "old" stars at the end of their
lives already in his heart burn all hydrogen, the envelope
strongly "inflated" and cooled, and in the shrinking
cores occurs thermonuclear "burning" of helium and
other heavier elements (as was explained in
more detail in the previous §4.1, section "Thermonuclear reactions inside stars"). This less
energy-intensive "fuel" is only enough for a few
million years. Once everything burns, the star will rapidly
collapse into a neutron star or black hole, with a huge explosion
of a type II supernova.
*) One such "endangered" relatively close
massive star is Betelgeuse in the
constellation Orion, about 600 light-years from Earth. It is a
red giant the size of about 1000 solar radii, the luminosity is
about 100,000 times greater than our Sun, the mass is about 15-20
M¤. The spectral class of radiation M1-2 IAB shows that
the star is already in a very advanced stage of its development.
This period of the red giant is highly unstable, it is a
precursor to extinction by a supernova explosion; this is also
indicated by the observed variability of the star (with a semi-regular period of about 6 years). The explosion of Betelgeuse as a type II-P supernova
can be expected in about 1 million years! When this happens, this
supernova will be the brightest object in the night sky (perhaps brighter than the Moon) and
for 2-3 months it will be seen as a bright shining point even in
the daytime sky. Fortunately, the Betelgeuse's axis of rotation
is not rotated toward Earth, so we are unlikely to be threatened
by an intense flash of ionizing radiation (cf.
the following paragraph "Danger from supernovae")
.
Furthermore, a supernova explosion - type Ia - can occur in one
of the many binary systems of a white dwarf and a normal (or
giant) star by mass overflow, the mechanism described above (in the section "Types
of supernovae and their classification").
Danger from supernovae
A supernova explosion releases
such a huge amount of radiant energy, that if one of the nearby
or "neighboring" stars in our Galaxy explodes like a
supernova, intense ionizing radiation could seriously endanger
the existence of life here on Earth! - issues of threat
to life by cosmic radiation are discussed at the end of the
already mentioned treatise "Cosmic radiation",
passage "Biological significance of cosmic radiation".
Strong magnetic field of
neutron stars
Thanks to the law of conservation of the star's rotational angular momentum
during shrinkage, white dwarfs, and especially neutron stars,
will rotate very quickly - one to several hundred
revolutions per second (possible
explanation of such high speeds see below "Pulsars").
Neutron stars can also have a very strong
magnetic field. As already mentioned in the previous
§4.1, passage "Compact objects", due to the shrinkage of
the star in the final stages, the magnetic field lines of the
original field are compressed and the intensity (induction) of
the magnetic field near this object increases sharply. Even a
relatively weak magnetic field of a normal star, which is of the
order of B » 10-4 T, so due to the "compaction
of the lines of force" (assuming that 4p.R2
B » const.) during contraction, it will
increase at the surface to a huge value of B » 108 Tesla and higher.
Magnetar
If a neutron star rotates at high speed (frequency), the
intensity (induction) of the magnetic field of the neutron star
can reach extreme values in some cases with the
magnetohydrodynamic effect »
1010 - 1012 Tesla. A neutron star with such an extremely strong
magnetic field is called a magnetar. The rotating strongly magnetized neutron
star acts as a massive "alternator" that converts some
of the mechanical rotational energy into the energy of a variable
electromagnetic field. This weakens the magnetic field and the
magnetar gradually becomes a normal neutron star. Mechanical changes or defects in the crust of such a
neutron star (similar to an earthquake - "star quake")
can lead to a sudden rearrangement of magnetic field lines
("magneto shake"), which induces massive
magnetohydrodynamic currents in the surrounding plasma leading to
strong heating and energy release - this is accompanied by short
, but with a very intense flash of
electromagnetic radiation, radio waves including X
and g- radiation .
P u l s a r s - fast-rotating neutron stars
In 1968, at the Radio Astronomical Observatory in Cambridge,
experts led by A.Hewish (pulses were
measured mainly by J.Bell) when examining
the radio signals from space, registered very regular
pulses, coming with nanosecond accuracy. Their source
objects were called pulsars (short for "pulsating radio source", or
"source emitting radio pulses").
It seemed so strange that some astronomers even initially thought
it might be the signals of other civilizations that were often
discussed at the time. Eventually, however, Hevish and other
astronomers tended to believe that they were very fast-rotating
compact stars -neutron stars. The periods of
most pulsars range from 0.03 sec. *) to 4 seconds. No normal star
is able to rotate so fast without being torn apart by centrifugal
forces. It must be a highly compact object with
a high mass, the inertia of which ensures such a
high stability of the rotational frequency, resistant to
environmental influences; no other mechanism (perhaps pulsation)
could do this. And only a neutron star, thanks to strong gravity,
"can withstand" very fast rotation (up to about 600
rpm), without tearing by centrifugal forces.
*) The formation of such a rapid rotation
is difficult to explain by the rotational angular momentum of the
original star. A possible mechanism for the "additional
spin" of a neutron star could be accretiongas
flowing, for example, from a co-rotating companion in a binary
system. This gas would form an accretion disk around the
neutron star and, when absorbed by the neutron star, would impart
additional angular momentum (cf. the analogous mechanism of
"spinning" a black hole by an accretion disk discussed
in §4.8, section "Accretion
disks around black holes"). Lone
neutron stars rotate more slowly, with longer periods of the
order of tenths to units of seconds.
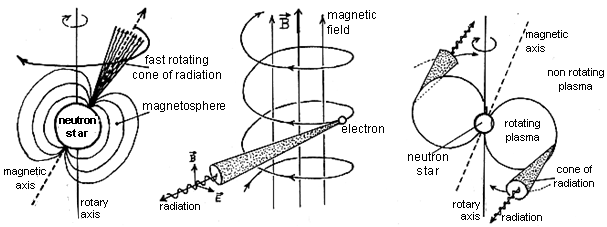
Fig.4.3. Pulsar like a fast rotating neutron star.
a) Global beacon model of a neutron star as an inclined magnetic
rotator.
b) Formation of synchrotron radiation during the motion of a
relativistic electron in a magnetic field. The electron acts as a
glowing "reflector" orbiting in a spiral path.
c) A somewhat more detailed model of the pulsar shows that the
radiation does not arise at the surface of a neutron star, but in
its magnetosphere at the interface between a stationary plasma
and a rotating plasma entrained by a neutron star.
As fast-rotating neutron stars, pulsars therefore, they are now being
considered. The mechanism of why we observe very regular rapid flashes of radiation in pulsars is not yet known in
all details. The so-called the beacon
model (Fig.4.3)
explains the pulsar as a neutron star with
a strong "frozen" magnetic field, that rotates around
an axis making a
small angle with the axis of the magnetic field. The interaction
of a rapidly rotating magnetic field with electrically charged
particles in the plasma surrounding a neutron star accelerates
electrons to relativistic velocities. These accelerated electrons
moving in a strong magnetic field are then a source of strong synchrotron radiation *) emitted
anisotropically in a narrow cone in the direction of the
magnetic axis. The electromagnetic radiation emitted in this way
then "hits" the distant observer at regular intervals
(equal to the period of rotation of the neutron star), similar to
the cone of light of a rotating beacon reflector. However, the
acceleration of charged particles is at the expense of the
rotational energy of the neutron star, which contributes to the
period of the pulsar slowly lengthening (see
below the passage "Smooth and sudden changes in
the rotational speed of pulsars").
*) The radiation arising from
the movement of a relativistic charged particle along a curved
path in a magnetic field is called synchrotron because it was first observed in 1947 at a
70 MeV synchrotron.The mechanism of
synchrotron radiation is outlined in §1.6, passage "Cyclotron and synchrotron radiation" of the book "Nuclear physics and physics
of ionizing radiation".
Neutron stars are also likely
to be very intense sources of long-wave electromagnetic
radiation magneto-dipole character,
generated at a frequency given by rotation. From an electrical
point of view, a rotating magnetized neutron star acts as a
massive "alternator" that converts some of the
mechanical rotational energy into energy of a variable
electromagnetic field carried away by long-wave electromagnetic
waves. Here on Earth, however, this radiation cannot be detected
due to the opacity of the interstellar plasma; although this
plasma is very sparse, due to the large distance of the source,
long-wave electromagnetic radiation is practically completely
absorbed.
Radio pulsars
Due to the very weak light emission
of neutron stars, they are not optically observable, we can only
register their radiation as radio pulsars.
"Lone" neutron stars can only be observed in this way
if they are relatively young. The intensity of this pulsar
radiation gradually decreases (as the ionized
plasma disappears around the neutron star),
so older neutron stars are difficult to observe. However, if
neutron stars are part of tight binary stars with gas overflow,
then when this substance falls on a neutron star, a large amount
of gravitational energy is released, which is converted into
thermal motion of particles - the gas is heated to temperatures
of millions of degrees, so it shines even in the X-ray spectrum :
X-ray
pulsars
In addition to the usual radio pulsars, X-ray
pulsars, which emit regular short bursts of
X-rays, are also observed in much smaller quantities.
The period of flashes is on average somewhat longer than that of
radio pulsars - from about 0.1 second, usually several seconds to
about 10 minutes. It also tends to be somewhat more variable,
on the one hand regularly as a result of the Doppler effect
during mutual orbit in a binary star system, and a decrease in
frequency is also manifested by the transfer of momentum from the
slower accreting gas to the faster neutron star. The first X-ray
pulsar Centaurus X-3 was observed in 1967, with more
precision using the X-ray satellite Uhuru in 1971.
X-ray
pulsars are neutron stars with a strong magnetic
field that are part of a binary star with an
active star. This active star supplies the neutron star with
ionized gas, which is directed towards the
magnetic poles by the strong magnetic field and intensively accelerated
by gravity. On the surface of the neutron star, where it falls at
a high speed (up to c/2), a large amount of energy is released -
"hot spots" are formed here, in which the temperature
reaches millions of degrees, radiation in the X-ray range
of the spectrum is emitted. If the magnetic axis is
tilted relative to the axis of rotation, periodic pulses
of X-radiation are observed during the rotation of the
neutron star according to the "beacon model", which
"reaches" distant observers.
The method of "supplying" a neutron star with gas from
a binary partner can be twofold :
--> In
weaker X-ray pulsars, it is a radiation-driven stellar
wind from an active star (mostly a young giant star), in
whose "flood" the neutron star orbits and constantly
gravitationally absorbs particles of this ionized gas. The strong
magnetic field directs them to the polar regions, where a lot of
energy is released, with the emission of X-rays.
--> In
strong X-ray pulsars, it is a close binary
system where the neutron star intensively
"sucks" a large amount of mass from the neighboring
star by gravity. It passes through the inner Lagrangian point L1, forms an accretion disk that spirals inward on
the neutron star, and the strong magnetic field directs it to the
polar regions of the neutron star, where it falls at high speed.
Upon impact on the surface of a neutron star, a large amount of
energy is released, the temperature reaches millions of degrees,
and radiation is emitted in the X-ray range of the spectrum. With
sufficiently massive accretion, a very high luminosity
of the X-ray pulsar can occur (possibly even
amplified by the directional geometric effect of the narrow
radiation cone). Such an extremely bright X-ray pulsar is M82
X-2 with a luminosity of about 107
L¤ !
Internal structure
of neutron stars
It is in principle impossible for any observer
composed of known forms of matter to directly examine (visually
or experimentally) the interior of neutron star. No
electromagnetic signal gets out from inside the neutron star, no
neutron sample can be taken (neutrinos
and gravitational waves that could theoretically get out
of the neutron star, due to the absence of nuclear reactions and
axially symmetric rotation in the neutron star do not arise). Therefore, we can try to reconstruct the internal
structure of neutron stars only theoretically, on the basis of an
analysis of the properties of the substance of which neutron
stars are composed - its equations of state, gravitational,
nuclear, mechanical and hydrodynamic behavior. Based on current
knowledge in these areas (see also below
"The behavior
of materials under high pressures; neutronization") was created by the current
model of the internal structure of neutron stars
:
Around the neutron star is probably
only a very thin gaseous atmosphere of dense hydrogen and helium,
the thickness of only a few meters . The surface of a neutron
star is formed by a rigid outer crust (several
hundred meters thick) composed of a crystal lattice of iron
nuclei and heavier nuclei, along with electron gas. The density
here ranges from »106 g/cm3 in the upper layers to »1011 g/cm3 in the lower layers,
while in the depths there are nuclei with an increasing
proportion of neutrons (it is more
energetically advantageous to combine electrons with protons in
the nuclei to form neutrons).
When, in depth, in the inner
crust, the density exceeds about 1011 g/cm3, neutrons are released from the nuclei and form a
neutron liquid penetrating the nuclear crystal lattice (Area 4 in the section "Behavior of a substance at high
pressures; neutronisation"). With the increasing density in the depth increases the
proportion of free neutrons, when it would exceed the density of » 2.1011 g/ cm3 nuclei completely dissolve and the substance is in the
form of neutron liquid in admixture with about
10% of protons and electrons (region
5 in "Behavior of the substance at high
pressures; neutronization"). This area is called the outer core of
neutron stars. Free neutrons inside a neutron star are due to
extremely high pressure in a highly degenerate state, where
nuclear forces can cause neutron pairings of opposite spins,
analogous to Cooper's electron pairs in
superconductivity; these paired neutrons can form a so-called Bose-Einstein
condensate (§1.5 "Elementary
particles and accelerators", passage "Fermions as bosons; Superconductivity" in the book "Nuclear Physics and Physics
of Ionizing Radiation"), causing
a partial superfluidity of the neutron fluid. This
effect can also cause better compressibility than the
Fermi pressure of degenerate neutron gas.
The innermost region, the inner
nucleus, of mass neutron stars can reach a density 2 to
10 times higher than the nuclear density. Here, specific
properties of interactions
of elementary particles at high energies with the participation
of quarks can come into play :
Quark matter,
quark-gluon plasma ?
It is possible that a hyperon or quark mass could form inside a massive neutron star.
Fast-rotating neutron stars lose some of their energy and
rotational angular momentum
from the emission of radio waves, electrons and other charged
particles from their magnetosphere. This shrinks the star and
increases the pressure inside it, which can lead to the merging
of nucleons into hyperons, or even the destruction and decay of
baryons into quark mass - quark-gluon plasma (see §1.5 "Elementary particles", section
"Quark structure hadrons" in the book "Nuclear physics, ionizing
radiation"). Under
normal circumstances, quark-gluon plasma is highly
unstable, for a brief moment, about 10-22 sec. experiencing its hadronisation,
conversion into baryons and mesons. However, extremely high pressures
act in the neutron star, so that the hadrons are
pressed so close to each other that they "intertwine"
with each other's quark structure, lose their
"identity" and "dissolve" into a mixture of
almost free quarks and gluons. Hadronisation no
longer occur, there is "no place" for hadrons.
Extreme gravitational pressure can thus stabilize the
quark-gluon plasma inside the neutron star. Here,
too, quarks, pushed very close to each other by massive gravity,
could form Cooper's pairs, behaving like bosons, and
form superfluid condensate..?.. It could also lead to better
compressibility than the Fermi pressure allows; massive
neutron stars could thus shrink to a smaller size than would be
expected for a composition of neutrons alone.
These possible processes in neutron stars
can therefore be summarized in a remarkable statement from the
point of view of (sub)nuclear astrophysics :
| The
neutron star is the only object in the universe, that can
produce and "tame" an
otherwise highly unstable quark-gluon plasma in
large quantities, stabilize it inside with powerful
gravitational forces and hold it for billions of years ! |
Strange quark mass ?
A hypothesized was
made (E.Witten,
1984) that if a sufficient number of "strange" s
-quarks (in addition to the usual quarks u and d forming nucleons) are present in
a quark-gluon plasma , it can prevent hadronization and such
"strange quark mass" may be stable, even under normal conditions;
strong interaction holds it together. In a situation where the
quarks are "pushed" close to each other and all the
lower fermion quantum states are occupied, the quarks s are practically unable to transform into u quarks, because there is no more free space for the
new u quarks thus formed .
Opposite transformations can occur, so that
an equilibrium configuration of the quarks u, d, s in
the fermion gas is established, which is more energetically
advantageous than hadronization. The resulting formation could
then be stable, held together by a strong interaction. The
strange quark mass is able to absorb neutrons, decompose them
into quarks and form another strange quark mass.
A suitable quark
mass has very unusual properties. These unusual properties would
also have hypothetical "strange stars" composed of
strange quark matter. In particular, the stability of such a star
would not be determined by the above gravitational criteria.
Unlike a neutron star, a strange star has no minimum mass, it is stable for any small mass : not held together by gravity, but by
strong interaction. The maximum mass here is » 2M¤, at higher mass it would
collapse into a black hole similar to a neutron star. The radial
course of the density of a strange star is quite different from
that of a neutron star: the density of the strange quark mass
changes very little from center to edge (from the outside, the
density on the surface changes almost abruptly from zero to ~ 1014 g/cm3; however, a quark star may be
surrounded by a thin "crust" of normal material such as
electrons).
The question is, how could such
strange quark stars form? Conventional baryon mass does not
contain any strange s-quarks, randomly formed strange particles
(K-mesons, hyperons) containing s-quarks are highly unstable and
decay rapidly. It has been hypothesized that small macroscopic
islands of strange quark matter could form during the high-energy
processes of a supernova explosion, or could persist in space
from the hadron era just after the Big Bang. Ordinary
proton-containing matter hardly interacts with this strange quark
mass due to its repulsive electrical force. However, the neutron
can be absorbed by this quark mass and decomposed into quarks. So
if a macroscopic "piece" of strange quark matter enters
a neutron star, it will absorb
neutrons rapidly, thereby it growing and absorbing neutrons even more efficiently.
Thus, such a strange quark mass can initiate an avalanche-like
process of transforming a neutron
star into a strange quark star , in which a huge amount of energy is
suddenly released. This energy does not destroy a strongly bound
quark star, but it probably radiates in the form of a massive flash
g .
There is no experimental evidence for such an exotic state of
"strange quark matter", as well as observational
indications for "strange quark stars".
So the strange quark mass probably
isn't
...
Pulsars
- precision "clockworks" in space
The neutron star, as a very
massive compact structure,
rotates at a constant speed for a long
time, so that the pulsar emits very regular
pulses of electromagnetic
radiation. As if "accurate watches were ticking" there.
The registration of these regular electromagnetic pulses of
pulsars and their small changes can be used to analyze some
subtle astrophysical phenomena in outer space :
- The accretion of matter to a neutron star changes its rotational angular
momentum, which also changes the
frequency of pulses. Accretion disks around neutron stars are
mostly co-rotating, so
accretion increases the frequency (for
neutron stars without accretion disks, the rotation slows
down due to the entrainment of the angular momentum of the
"stellar wind" particle emissions and the acceleration
of the charged pulsar particles) .
- The
circulation dynamics of compact binary systems can be accurately analyzed on the basis of
periodic changes in the pulse frequency of the pulsar, caused by
the Doppler effect during its orbital motion. A typical example
is the binary pulsar PSR 1913 + 16, for
which the decrease of orbital energy by gravitational
wave radiation has been measured (it
is described in more detail in §2.7, section "Detection of gravitational waves", passage "Binary pulsar)
.
- Detection of gravitational waves using
pulsars.When regular
electromagnetic pulses from pulsars pass through space containing
low-frequency gravitational waves, there is a certain (albeit
very weak) effect on their propagation - there may be a long-period
modulation of short-period
electromagnetic signals from pulsars due to gravitational waves (see again § 2.7., part "Detection of gravitational waves", pasage "Time modulaion of the period of
signals from pulsars"). Microsecond pulsars are particularly suitable
for this purpose, in which the effects of
"star-shaking" and accretion, which may affect the
period of the pulsars, are less pronounced. This phenomenon will hopefully be used in
principle in the future to detect
long-period gravitational waves in space - systems of a larger
number of radio telescopes are being built for this detection
using the Pulsar timing array method.
Smooth and sudden changes in the
rotational speed of pulsars Although the neutron star rotates at a
highly constant frequency due to the law of conservation of angular
momentum, there are very small changes
in rotational speed, which are twofold :
¨ Smooth changes in rotational frequency - very slow long-term
deceleration due
to three phenomena :
a) Emissions
of "stellar wind"
particles from the surface of a neutron star slowly carry away
the rotational angular momentum.
b) Electromagnetic
dipole radiation of a neutron star (mentioned in the previous
passage).
c) The
acceleration of charged particles in the pulsar magnetosphere is at the expense of the rotational
energy of a neutron star.
¨ Sudden
step changes of rotational
frequency - small short-term irregularities (disturbances -
sudden shortening) in the period of pulses with relative
amplitude dT/T »
10-10 - 10-5. Even though the cause is unknown with
complete certainty, assume the two possible mechanisms
related to the effects caused by the internal structure of
neutron stars (as outlined above in the passage
"Internal structure of neutron stars")
:
1.
Disorders and fractures the crystalline crust neutron stars (a "starquake") during the gradual reduction of
its flattening during decelerating rotation. The neutron star has
a high rotational speed after its formation and is flattened due
to centrifugal force. During the gradual deceleration of the
rotational speed this leads
to a gradual increase in stress in the crust, after exceeding the
"limit of strength" the crust bursts ("star shake") and takes on a
less eccentric shape. This suddenly reduces the moment of
inertia of the neutron star and, according to the law of
conservation of angular momentum, suddenly increases the
rotational frequency, or shortens the period T.
2.
Changes in neutron fluid flow - turbulence and vortices in neutron
"fluid" flow (which
is possibly partially superfluid) with a gradual slowing down of the
rotation of a neutron star. The fluid inside a neutron star
probably rotates somewhat faster than the crust, which is
inhibited by electromagnetic radiation and particle emissions
("stellar wind"). When larger differences in the
rotational speed of the crust and the neutron fluid are achieved,
turbulences in the flow and vortices can occur at their contact,
which can transfer part of the higher rotational energy from the
inside to the crust and accelerate its rotation. Furthermore, the
shear stress at a larger difference between the rotational speed
of the inner fluid and the outer crust can lead to deformation
and cracking of the crust, similar to point 1.
These step
changes are accompanied by strong electromagnetic emission - a flash
of radio waves, for magnetars it can also be X and gamma
radiation. After a sudden abrupt
acceleration of the rotational speed again results in a slow
frequency "relaxation" to the original rotational
speed; the relaxation time is several tens or hundreds of days.
This is followed by the usual long-term slowing down of the
neutron star's rotation. During the long life of a neutron star,
accompanied by a gradual deceleration of rotation, many sudden
abrupt changes in rotational frequency are likely to occur, which
will be repeated with increasing intervals of occurrence.
Neutron
star stability. Oppenheimer-Landau limit.
In the section on white dwarfs, it was shown above that the Fermi
pressure of a degenerate electron gas has a limited ability to
balance (self) gravitational forces - there is a Chandrasekhar
limit for the mass of a white dwarf. Even the Fermi pressure of
the degenerate neutron "gas" is not unlimited.
Analogous considerations as outlined above for white dwarfs can
be applied to neutron stars, with that this is the case 1. of the passage
"Stability of the white dwarf. Chandrasekhar's limit.".
The corresponding maximum possible mass of the degenerate neutron
configuration, allowing further stability, is called the Oppenheimer-Landau
limit. The above dimensional estimates resulted in a
value of »1.5 M¤, more accurate calculations based on the solution of
the Oppenheimer-Volkov-Landau equation (4.3) using the "Harrison-Wheeler
equation of state" (see below, Fig.4.5), give higher
values, around 2-3 M¤.
Complete
gravitational collapse. Black hole.
Thus, like the white dwarf, even
the neutron star has
a limited mass from above. At too large masses, greater than
about two masses of our Sun *) - Oppenheimer-Landau
limit, the
gravitational forces are already so great that they overcome both
Fermi and nuclear forces between neutrons (nuclear
forces have a short range - state of saturation); the star's substance no longer
has any sources or mechanisms of sufficiently large internal
repulsive forces to be able to balance such strong gravity (it is discussed in more detail below in the section
"Behavior of matter at high pressures"). In this situation, the
catastrophic gravitational collapse continues, Fig.4.2 above (we will not consider here the
possible stages of the hyperon or even quark stars mentioned
above) until the
star falls below its gravitational (Schwarzschild's) radius rg
= 2G.M/c2 (see §3.4), crosses the horizon and a black
hole, also called a collapsar, is
formed. The
properties of black holes will be discussed in more detail in the
remaining paragraphs of this chapter (§4.3 - 4.9). Here we will
only outline some characteristics of the gravitational collapse
and the formation of a black hole.
*) Here, too, rotation
matters and, moreover,
uncertainties in the theory of nuclear substance. The mass of a neutron star should
probably be limited by [227] Mn» (5M¤).(rnuc/r')1/2
, where rnuc
» 2 . 1014
g/cm3 is the ordinary nuclear density and r' »
(0.5 - 5).rnuc is the density at which there are
significant deviations from the current theory of nuclear matter
on a larger scale. The maximum mass of neutron stars is most
often estimated in the range of 1.5 - 2.5 M¤.
The direct formation of a black
hole without a supernova explosion ?
When collapsing very massive stars, there is a theoretical possibility that
after depletion of nuclear fuel, the interior star will reach the gravitational radius
(horizon) before a supernova explodes. The formation of a black
hole would then be "silent and inconspicuous" - the
star simply "disappears", without the accompaniment of
a more pronounced light phenomenon (it was
mentioned above in the passage "Processes
of supernova formation") .
Gravitational
radius, event horizon
Gravitational forces are by far the weakest of all known types of
interactions. However, with a sufficiently large accumulation of
matter, these weakest gravitational forces, due to their universatility, can become dominant and can even be so powerful that
nothing can withstand them, not even light.
Let us have some (non-rotating) spherical star or planet with total mass M
and radius r . In order to have a body from surface
of such planet or star to completely overcome its gravitation attraction, and freely to move away from it into space infinitelly,
it must be given a radial velocity at least equal to (according to Newton's theory)
v 2 = Ö (2 G M /
r) ;
such velocity v2 is called escape
velocity or also 2. cosmic velocity (it was derived in §1.2, passage "Gravitational
bodies" and "Movement of bodies in the gravitational field"). The escape velocity does
not depend on the mass
or the composition of the escaping body (universality
of gravity), it
depends only on the mass M of the gravitational body and the
radius r from which the escaping body starts. For
a body starting from the Earth's surface, the escape velocity is
about 11.2 km/s - the second cosmic
velocity. With
increasing mass M or with decreasing radius r
the escape velocity increases from the surface of the body *). Already in 1783
J.Mitchell and independently in 1795 P.Laplace, based, of course,
on Newton's non-relativistic law of gravity and the corpuscular
theory of light, pointed out that very massive and dense stars
may not be visible at all because the escape velocity from their surface may be
greater than the speed of light - they would be "dark stars". An emitting particle of
light (the concept of a photon or
electromagnetic waves was not known at the time) like an upwardly thrown stone, slowed down by the
star's strong gravitational pull, stops, and then falls back onto
the star. Thus, although "black hole physics", as a
subdiscipline of astrophysics and the general theory of
relativity, is one of the youngest disciplines, its ideological
roots go far back.
*) If we take the for illustration as a basis the mass of the Sun
M¤ = 1.989 . 1030 kg, the radius of which is R¤
» 696 000 km, then according to the above
formula the escape velocity v2 from the gravitational field of a body of mass M
with radius R can be expressed as v2 = 617.7 . ( M / R
)1/2 [km/s], where the mass M
º M/M¤ and
the radius R º
R/R¤ are expressed in "solar units". The
coefficient of 617.7 km/s is equal to the escape velocity from
the surface of the Sun. If we demand that the escape velocity v2 be equal to the speed
of light c = 299,792 km/s, we obtain for the body mass M
critical radius rg = 2.95 . M/M¤, ie about 3
kilometers/s. for each "Solar mass".
The radius rg
, at which the
escape velocity is just equal to the speed of light (for a spherically symetric body M), is called the gravitational or Schwarzschild
radius :
2 G M
r g =
--------- .
c 2
This formula, which can
be easily obtained within Newtonian theory by
placing escapes velocity v2 equal to the speed of light c ,
coincidentally applies exactly also in GTR; here, however, this
Schwarzschild sphere has a profound significance of the event horizon causally separating the area inside and
outside, as shown in §3.4 "Schwarzschild
geometry"
and as we will see in the following.
The first relativistic analysis
of the gravitational collapse (for the simplest case of a
spherical homogeneous cloud of free-falling dust particles) was
performed in 1939 by Oppenheimer and Snyder [195], who came to the conclusion that
in the final stages of collapse, a horizon of events emerges, ie
according to today's terminology "black hole". However,
the intensive development of black holes physics begin
until about the
1960s.
The research of the
English physicists S.Hawking and R.Penrose has the greatest
credit for it; also made significant contribution to it B.Carter,
J.A.Wheeler (who is the author of the name "black
hole"), R.Kerr, D.Christodolau, R.Ruffini,
W.Israel, J.Bekenstein, J.Zeldovic, I.Novikov, K.Thorne,
J.Bardeen and many others.
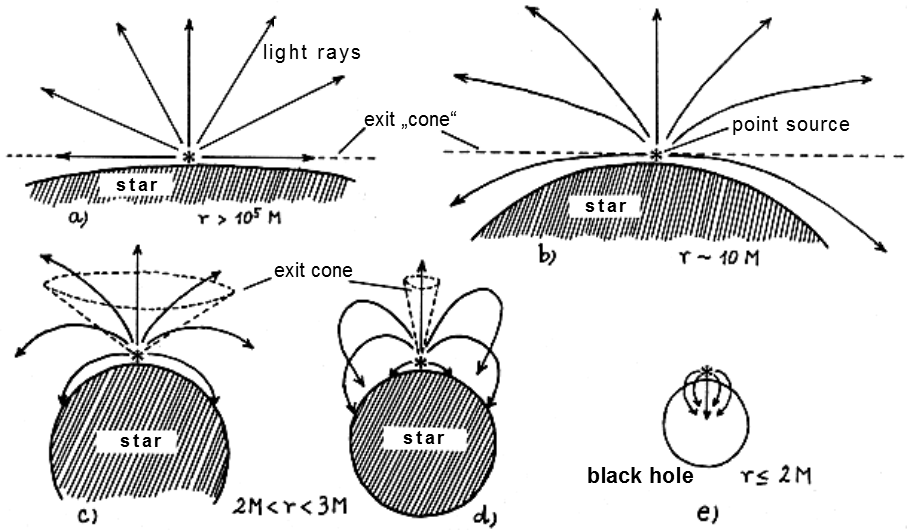
Fig.4.4. Gradual closing of the exit cone of light rays from a
point source located on the surface of the star during its
collapse.
a) For
bodies with a very large diameter in comparison with rg = 2M,
the gravitational field is relatively weak and the light rays
from a point source located on the surface propagate practically
in a straight line.
b) With the
continuing collapse the gravitational field increase, the rays are curved, but if r > 3M, the exit cone still remains 180°
.
c, d) In the late stages of collapse, the output
light cone begins to narrow: more and more of the light emitted
by the source is pulled back to the surface of the body by
gravity; only rays in a narrow cone vertically upwards can be
radiated into the space.
e) After
exceeding the gravitational radius, no more emitted photon can
get into the surrounding space, all the light is drawn by gravity
towards the center - a black hole is formed.
Fig.4.4 shows one of the
most interesting phenomena accompanying the gravitational
collapse: the gradual narrowing and closing of the exit cone of
light rays. An output cone (not to be confused with a space-time light cone
!) means a space cone with a vertex at a given
point, that only rays emitted in the direction
inside this cone from a given point can enter the outer space,
while rays in directions outside the output cone are absorbed by the gravitating
body. If the body (planet, star) has a weak
gravitational field, the rays propagate from each point on the
surface practically in a straight line, so that the output
"cone" is the entire half-space above the surface of
the body (angle 180°) - Fig.4.4a. During the collapse, the
gravitational field strengthens and the rays are curved
(Fig.4.4b). In the late stages of collapse (after crossing the photon sphere - see §3.4) the gravitational field
intensifies to such an extent that the rays emitted too
"obliquely" are bent by gravity so that they strike the
surface; only rays radiated in a narrow cone almost vertically upwards, can escape
- Fig.4.4c,d. After exceeding the gravitational radius, the output cone
is completely closed - all light is pulled
back by gravity (Fig.4.4e)
*), a black hole is formed. The spacetime around a black
hole curves so much (an extremely strong gravitational field)
that it "closes in on itself " and is
interrupted in terms
of the causality the connection with the outside world.
*) The difference between classical Newtonian
and general-relativistic behavior of a black hole
The described scenario of the
formation of a black hole qualitatively resembles the
above-mentioned situation of the "dark star",
which was speculated at the end of the 18th century Laplace and
Mitchell. However, there are two significant differences between
the Newtonian and relativistic versions of the "dark
star" compressed below the gravitational radius :
1. From the usual Newtonian point of
view (but it stops working here!) photons emitted from the star's
surface will first fly out towards larger radii (they may even
rise a little outside the critical gravitational radius) and then
be turned by gravity and pulled back inwards - rays or photons
the lights would fall back onto the star, much like the stones
thrown upward hit the Earth.
However, according to the general theory of
relativity, every photon emitted in any direction within the
critical sphere (below the gravitational radius) will always move
only inwards, to smaller and smaller radii. Not even for a moment
the photon can flying up !
2. According to the laws of classical
Newtonian mechanics, a star compressed below the gravitational
radius can remain permanently in a static non-collapsing state,
if the gravitational compression is balanced by its internal
pressure. The light won't get out, but a brave astronaut in a
powerful enough rocket could land on the surface, take a sample,
and then take off and fly out into outer space.
According to the general theory of relativity, any
star that compresses below the sphere of the gravitational radius
will have such a strong gravitational compression that no
internal counterpressure can equal it, and the star must
inevitably collapse. No observer, even if equipped with a
extremely powerful rocket, can reverse the direction of its
motion and return to outer space after entering space below the
gravitational radius; will inevitably fall inwards.
Time interpretation of the horizon of a
black hole
In §3.4, part "Motion
of light in the Schwarzchild field"
we showed that below the event horizon of a black hole, the
components of the metric tensor grr and gtt change signs, which means that within the horizon, the role
of the flow of time into the future is taken over by the
constant reduction of the radius r of each
object's movement. The space-time light cones here are completely
turned inward, so every real body here must move in such
a way that r is constantly decreasing - so it must fall
towards the center of r=0.
If we emphasize this spatiotemporal
phenomenon of the exchange task of space and time
below the horizon, we can interpret the impossibility of
returning from below the horizon to outer space in terms of the
causal flow of time. For observers outside the
black hole, the event horizon is forever in the future
(cf. the passage "Are there "complete" black
holes in the universe?"). For the
observer who crosses the horizon, this event horizon becomes part
of his past. Once inside the event horizon, the event horizon is no
longer a place in space to which we can return, but a past
moment in time. So we can't go back, because we would have
to travel through time (we don't
have a "time machine" to the past...). Such a time interpretation, however, can be somewhat
misleading or at least less intuitive for those interested, not
dealing with the theory of relativity..?..
Where and how can black
holes form ?
The basic rectilinear mode of formation of black hole with star
mass was given above "Complete gravitational
collapse. Black hole." :
A sufficiently massive star (M> »10-20 M¤)
after consuming all the thermonuclear fuel will have a residual
mass M' higher than the Oppenheimer-Landau limit. The
substance of the star no longer has any sources or mechanisms of
sufficiently large internal repulsive forces that would be able
to balance such strong gravity. In this situation, a complete gravitational
collapse occurs, the star shrinks below its
gravitational radius (rg = 2GM/c2 for a non-rotating
star), crosses the horizon,
and a black hole or collapsar is
formed.
In a close binary system,
a black hole can be formed by an indirect mechanism, so that from
one component (which is a giant star) it flows a considerable
amount of matter through the inner Lagrange point (see §1.2, Fig.1.1d, passage "Binary system") to the other component, which is white dwarf or neutron
star. After a certain time, the Oppenheimer-Landau limit
is reached by accretion, a complete collapse occurs and a black
hole is formed. The flowing mass is then still absorbed by this
black hole, around which an accretion disk is formed -
§4.8, part "Accretion disks around black
holes", Fig.4.26.
In large regions with a dense accumulation
of gases and tight star formations, especially in the center
of galaxies, giant - supermassive black holes
can also form (it is discussed in §4.8,
passage "How did central supermassive black holes form?").
It is possible to see
a black hole ?
Thus, since no radiation emanates from the black hole (we do not consider the astronomically irrelevant
Hawking radiation of quantum evaporation),
it cannot be "seen"
directly in the sense of the usual astronomical observation. At a
sufficiently close or large (supermassive) black hole, we could at most observe its shadow
image - "silhouette"
- against the background of a diffuse light source - a galaxy,
nebula (cf. discussion in §4.3, section
"Gravitational lenses. Optics of black holes."); however, our telescopes
are not enough for that yet (they were only succeeded by
connecting several telescopes *))... In §4.8 "Astrophysical
significance of black holes"
it will be discussed how the black holes can be indirectly
"observed" on the basis of radiation generated during
the absorption of the surrounding mater. During this accretion, an otherwise
non-radiant black hole becomes a
brightly shining object ! More precisely,
the glowing object
is the absorbed gas in its immediate vicinity - §4.8, part "Accretion
disks around black holes".
And also huge jets of gases and radiation from the accretion
disks of quasars and radio galaxies - §4.8, passage "Mechanism of quasars and active nuclei of
galaxies".
*) Note: However, by combining
with the precise synchronization and interferometry of large
radio telescopes on several continents in the Event
Horizon project, in the years 2019 - 2022 it was
possible to take images of the silhouettes of two large
black holes: in the center of the galaxy Messier 87 and
in the center of the Milky Way (Sagittarius A* ).
Planets around black holes ?
At greater distances from the black hole's gravitational field is
exactly the same as around a normal star, so there after
Keplerian circular or elliptical orbits in principle, orbiting
the planet. If we were in a hypothetical (astrophysically unreal) the
scenarios presented that the central star immediately collapsed
into a black hole without the above-mentioned accompanying
explosive phenomena, orbiting planets would not feel it at all (except for the light going out in a few minutes or
hours, depending on the orbital distance).
The gravitational field would not change at all, and the planets
would continue to orbit in their original orbits.
However, previous dramatic phenomena in the final stages of
stellar evolution, especially the supernova explosion, can destroy
and destabilize the planetary system (discussed above) , so less
orbiting planets can be expected around black
holes..?..
Black holes - extremely exotic objects !
When astrophysicists learned in the 1940s
of the unusual and incomprehensible phenomena that gravitational
collapse could lead to, they sought "a law of
physics that would prevent stars from making such nonsense"
(as the prominent British astrophysicist
A.Eddington put it). It turned out that
such a law did not seem to exist, and now the consequences of the
gravitational collapse are almost universally accepted. If the Sun collapsed into a black
hole (but this cannot happen), its gravitational radius would
be about 3 km; the gravitational radius of the Earth would be
only 0.9 cm - you can already see how exotic
objects
black hole are! In general, as mentioned above, the
gravitational radius of a black hole (non-rotating) we can simply determine by
dividing its mass by the mass of the Sun and multiplying the
result by a factor of 2.95 km - ie about 3
kilometers for each "Solar mass".
Lower mass - stronger
gravity ..?..
The following comparison may seem paradoxical: The star already has all that huge
gravitational mass in it during its "active" life - and
initially even greater (during its
evolution, the star loses much of its initial mass stellar
"wind" emissions and gas eruptions during
instabilities), and yet light escapes uninterruptedly. And after the gravitational
collapse of the remaining object, with less mass, does gravity no
longer let light out ? The simplified explanation is
as follows :
During the equilibrium evolution in the main
sequence, the star has a diameter of hundreds of thousands to
millions of kilometers, so the surface gravity in the photosphere, from
which light is emitted, is relatively faint and light
can escape almost undisturbed (only with a
slight gravitational redshift) into space. And inward gravity even
decreases (it's more complicated, depending
on the density distribution of the substance).
During the gravitational collapse,
the diameter of a star decreases sharply and the gravity on its
surface increases dramatically. Finally, to the level where the
escape velocity reaches the speed of light - an optical
horizon is created , which according to the general
theory of relativity is the horizon of events.
The light will no longer come out. At greater
distances, the intensity of gravity remains as low
as before the collapse (or rather smaller -
in proportion to how the total mass of the star decreased in the
final stages of its evolution). Following
the usual Kepler orbits around the star - now black
holes - planets can continue to orbit here as before.
So globally - at
greater distances - gravity decreases , while locally
(near the center) gravity increases enormously !
A similar pattern applies to gravity in the immediate
vicinity of the horizons "large" and
"small" black holes. The gravitational
field of giant black holes is, of course, more powerful, but it
is more "spread" into space - there are only small
gradients of gravitational forces around their horizon (we could
temporarily survive here). But with smaller black holes of
stellar masses, the tidal forces near the horizon are so great,
that they ruptures each macroscopic body into a stream of atoms
and particles..!.
"Pit"
or "hole" in
space-time
The name "black
hole" (first used by J.A.Wheeler) describes very well the basic properties
of a collapsar, creating a deep defect in space-time that does not emit any
light. However, it is a very strange "hole", some of the
properties of which are completely different from the usual
"pit in the ground". We can measure its width
(diameter), but we cannot measure
its depth; it
is "infinite" or indefinite - the question arises here
"what is depth?". Every ordinary hole, pit,
shaft, well, can be backfilled or filled when we no
longer need it (or it would be dangerous) - if we try to do so, the black
hole will increase even more, each mass we throw into it will
increase the radius of its horizon (see
also §4.6 "Laws of dynamics of black holes"); the bottomless pit will remain. Even with the
"blackness" of a black hole, it's more complicated. It
is black in the sense that it does not emit any radiation *),
from an optical point of view it is an absolutely
black absorbing body. Against a light background, it appears
as a dark disk, but it does not overshadow anything, it has the
properties of a gravitational lens, around which interesting light
effects arise (for a more detailed
discussion, see §4.3, section "Gravitational
lenses. Optics of black holes.").
*) This is so from a classic point of view.
In §4.7 "Quantum radiation and the thermodynamics of black holes" however, will show the possibility of radiation
emission from a black hole under the influence of quantum
effects. However, this possibility is probably only theoretical
and does not occur with astronomical black holes
.
Two different views of
gravitational collapse - outer and inner
The collapse in the late stages, when
approaching the gravitational radius, is already completely relativistic and appears completely different for
an observer on a star than for a distant outer observer.
From a physical point of view, this is due
to the principle of equivalence, according to which acceleration
can compensate for the effect of the gravitational field. For
observers falling near the Schwarzschild sphere with the
acceleration of free fall, the strongly curved spacetime here
seems to be "leveling out" locally and the horizon
disappears (for this observer, on the
contrary, due to the acceleration, a kinematic - Rindler
- type horizon arises in the outer distant region, as if there
were a strong gravitational field). The different external and
internal manifestations of gravitational collapse are caused by
the effect of gravitational dilation of time in
the general theory of relativity (we derived it in
§2.4 "Physical laws in curved spacetime",
passage "Space and time in the
gravitational field").
In
§3.4 "Schwarzschild geometry", the passage
"Radial motion of particles", we found that particle falling radially towards
the center exceed the gravitational radius r=2M for a finite
proper time interval (and will
continue to move to singularity). While
from the point of view of the external observer, due to
the gravitational dilation of time near the radius r=2M, the
particle's motion begins to slow down and stops
completely at the gravitational radius - the particle would need
an infinitely long coordinate time from the view-point
of external observer to cross the horizon. And in the same way
will behave the surface of the star, which
gravitationally collapsing into a black hole :
¨ Exterior view
For the outside observer the collapse from the time t0
when it gets into the relativistic area, starts gradually slowing down due to deceleration the
passage of time by the
gravitational field and never in the final time reaches gravitational radius - in horizon
time stops, collapse "freezes" due to extreme gravitational time dilation. However, the decrease in the
brightness of the star L and the increase in the gravitational redshift is exponential [285] :
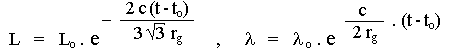
(Lo is the luminosity and lo wavelength
of the star's light at time to) with a half-life roughly equal
to the time of light passing through the distance rg (on the order of units to tens of
kilometers for black holes of stellar origin), so that the star practically
"goes out" in a fraction of a second from the onset of
relativistic influences in time to. If we take into account the
quantum nature of light, then in a finite (and very short) time,
the surface of the collapsing star really leaves the last photon
and the collapsar becomes "absolutely
black".
As light laboriously
"climbs" out of the pit of the collapsing star's strong
gravitational field, losing energy and lengthening its
wavelength, shifting to red. The flow of time on the surface of a
collapsing star is gradually infinitely prolonged (it is
"frozen"). Each light (regardless of its original
color, wavelength or photon energy during its emission) will move
very far beyond the red border, beyond the infrared and then the
radio field as it moves away from the stellar surface. When light
(and all electromagnetic radiation) is overcome by gravity, all
of its energy is removed, making it cease to exist. The
collapsing star, with its gravity, "visually cuts off"
from the surrounding universe. What's more, it also cuts off in
terms of causality ...
¨ Interior view
For observers on a collapsing star (if
he could stay alive)
the horizon is no obstacle and can, after a finite (and very
short!) interval of his own time, in principle
overcome it without difficulty - there is no real space-time
singularity on the horizon (§3.4 "Schwarzschild
geometry"). However, below the gravitational radius,
this observer can no longer send any information out; gravity "will not let out" nor light. No
phenomena taking place below the horizon can in any way affect
the outside world and cannot be observed from it in any way. The horizon is a kind of
"membrane" permeable only in the inward direction. Once an object crosses the event horizon, it loses all
hope of escaping or returning. If the falling body emits light or
other radiation, it is also absorbed, so that the outside
observer will never see it again. Whatever happens below the
horizon (in a black hole), will stay there as well.
The deep connections between space, time
and gravity in the general theory of relativity show (see §3.4
and §4.3), that after reaching the horizon, all
bodies will move towards the center
r = 0 with
the same fatality with which time runs from the past to the
future (spacetime light cones are completely turned inwards).
Even if the observer was in the rocket, for example, even the
greatest force of the engines could not prevent him from falling
to the center. Once the gravitational radius is reached, no known
(and perhaps none at all!) force can stop the gravitational
collapse, because no force can turn back time. The collapse
continues and after the final own time the star collapses to the
point r = 0, to the so-called singularity *) with zero volume, infinite density and curvature
of spacetime, with infinite pressures and gradients of
gravity forces (this is at least according
to the classical GTR).
*) Spacetime singularity (lat. singularis = unique, exceptional,
extraordinary ) in the general theory
of relativity is a terrible place where the curvature of
spacetime becomes infinitely large and spacetime analytically
ceases to exist (from a
geometrical-topological point of view, singularities are analyzed
in §3.7 "Spacetime singularities"). Infinite curvature of
spacetime means infinite gradients of gravitational forces -
infinitely large tidal forces acting on any object of non-zero
size. Everything is destroyed here!
After the creation of the horizon of
the black hole, the mass of the spherical star from the inner
point of view will continue to collapse unstoppably
and compress to zero volume and infinite densities - it will
create a space-time singularity, into which it he
plunges and "disappear" in it (limit
prediction according to classical GTR; some alternative
possibilities will be discussed in §4.7 "Quantum
radiation and thermodynamics of black holes").
For a black hole, we can paraphrase
a familiar proverb about hell : "What a
black hole catches, it will never return!".
Nothing, not even light, can overcome the gigantic gravitational
force of this ghostly object...
Gravitational oscillation during collapse
inside a black hole
During spontaneous shrinkage of mechanical systems (elastic
bodies, tension springs, gas cloud), reflection and temporary
opposite movement occur when the smallest volume is reached,
replaced again by shrinkage, etc. - oscillations
occur, which are gradually attenuated by dissipative processes.
An analysis of the course of gravitational collapse, carried out
in 1970 by V.Bìlinský, I.Chalatnikov and E.Lifšic, as well
as independently by Ch.Misner, shows that a similar phenomenon
occurs during gravitational collapse inside a black hole,
although by a slightly different mechanism (collapsing
the mass cannot "bounce" off the center with increased
pressure and move upwards, because the space-time light cones are
uncompromisingly turned inwards within the horizon). As matter falls toward singularity, tidal forces
deform it into an ellipsoid - stretching in the direction of the
fall and compressing in both perpendicular directions. This very
fast dynamic shear curvature excites another
dynamic gravitational field due to self -gravity (this nonlinear property of gravity in GTR was
mentioned in §2.5 "Einstein's gravitational field equation"). This causes compression
in the vertical direction of the fall materials and expansion in
the horizontal direction. And the resulting self-gravity field
again has the opposite effect, etc.... The result is an
alternating stretching and compressing the collapsing matter -
chaotic oscillations tidal forces as they
approach singularity, leading to dynamic "kneading" and
mixing of collapsing matter (Ch.Misner called it "
mixmaster dynamics"). The oscillations of tidal forces
around the singularity are very strong during gravitational
collapse and the formation of a black hole. Then gradually dampen
and weaken exponentially due to the intense
radiation of gravitational waves (absorbed by the singularity),
until they finally disappear. Again, however temporarily excites
during accretion and absorb some mass by black hole. In the case
of stellar mass black holes, tidal oscillations disappear in
fractions of a second, but in giant black holes they can persist
for several months.
Tidal gravitational forces
at black holes. "Spaghettification".
Every gravitational field excited by material objects (planets,
stars) is inhomogeneous - it has different
intensity in different places. This creates gradients of
gravitational force, often called tidal forces (here on
Earth, the tides of the sea are caused by the action of the
Moon's gravity). Within the framework of Newtonian gravity, we
discussed them in more detail in §1.2, passage "Gravitational
gradients - tidal forces".
In the case of common astronomical bodies such as planets and
stars, tidal forces are weak and only become noticeable
at distances of the order of kilometers. An ordinary observer of
human dimensions does not feel them. Tidal forces are
significantly stronger in gravitationally collapsed objects -
partly white dwarfs, more pronounced in neutron stars and strongest
in black holes.
The gravity near stellar-mass black holes is so strong
and inhomogeneous, that even a relatively small spatial
distance means a significant difference in gravitational force.
If we were to fall into such a black hole by feet first, the feet
would be attracted by a significantly greater force than the
head, and our body would be gradually stretched by this.
On the contrary, compressive tidal forces would act in
the perpendicular direction. Near the horizon of a stellar black
hole, the massive gradient tidal forces would shape each body
into a thin long cylinder resembling Italian spaghetti.
The metaphorical name "spaghettiization"
has therefore been adopted for this effect. Towards the interior
of the black hole, the spaghettiization gradually becomes so
extreme that the falling body becomes a "string of atoms"..!..
For large black holes, such as those found at the center
of galaxies, the tidal forces would be weak at the horizon so
far, an observer would freely fly through, however the
spaghettiization effect would still end up affecting it deeper,
near the singularity.
Observer falling on a collapsing
star
Let's imagine that we decided to observe the gravitational
collapse of a star into a black hole up close. So, with a
very powerful space rocket, we would fly to the selected star at
the time when its collapse begins (which
results in a black hole) and we would fly
towards the center at a certain small constant distance from the
surface. Initially, we will observe the spherical surface of the
star below us. But soon this spherical surface begins to appear
"bent up" on the sides. It is due to the gravitational
bending of light (see the schematic
drawing above in Fig. 4.4 c, d), when many
light rays, emitted obliquely upwards from different parts of the
surface, will be bent downwards, so that it will appear as if
they fall on us from above. As the collapse continues, the
originally spherical surface below us begins to form a sort of cylindrical
surface around us, as if we were in a vertical tunnel
whose opening is rapidly closing above us. Soon there will be a
moment when this tunnel - the output light cone - will
be completely closed (Fig. 4.4 e), its walls will also disappear, we will find ourselves
inside the horizon with the inexorable collapse of all matter
towards the center, in a black hole. Before closing the exit
cone, we could, in principle, turn the high-performance rocket
around and fly out, but after closing never again...!..
An
observer falling into a black hole
Let's further imagine that as an observer we falling down
into a black hole - already "done", long after
the end of the collapse - and we are watched from a distance by a
second, external observer. For the outside observer, the time of
the falling observer seems to stop near the horizon due to
extreme gravitational time dilation. For the inner observer,
everything happens in his frame of reference as if there had not
been a fall into a black hole (we assume here that
it is a supermassive black hole, on the horizon of which only
weak tidal forces act). However, when looking at the outer
universe, he will observe that events flow faster
and faster there, he will see a number of supernova explosions,
as he will observe the slow and long evolution of stars very
accelerated in time. At the moment of falling over the horizon of
events, the whole future of the universe is projected to him very
quickly.
An outside observer records a
completely different course of our fall into a black hole. He
will see how the fall into the black hole is constantly slowing
down near the horizon due to gravitational time dilation,
and in the immediate vicinity of the horizon the movement seems
to freeze and the fall into the black hole will never occur.
So far, we were only interested
in the issues of movement and passage of time for observers. At
the end of the next paragraph (in the passage
"A Man Falling into a Black Hole"),
we will look at what the observer would physically feel
and what would happen to him if he fell into a black hole.
What
happens to matter, its atoms and molecules when it is absorbed by
a black hole ?
Above all, this question can only be solved theoretically, but
experimentally it is in principle untestable! Even if we had a
black hole somewhere nearby. In §4.8 we will see that the
substance creates a glowing accretion disk around the black hole,
along the axis of which jets are formed, through which up to 25%
of the absorbed mass can escape - in the form of ionized
substance and radiation. And never
in a finite time we could see a mass fall below the event
horizon, or what is going on inside. If we jumped into a black hole behind a falling mass (see below "Man falling into a black
hole"), we
would go below the horizon of events, but thus we would seal the
fate of our demise; nor could we send our information to our
colleagues, the event horizon will not let out any signal. The course of this
"suicide" case would depend on how big the black hole
is. With "small" black
holes of stellar masses, with a horizon diameter of several
kilometers, we would not get alive into a black hole - huge
gravitational field gradients (tidal forces - §1.2, passage "Gravitational
gradients - tidal forces")
would tear us far ahead of the horizon , we would fall into a
black hole as wellas a
"string of atoms". In the case of a large black hole,
such as those in the cores of galaxies, we would not even notice
that we have penetrated below the horizon, tidal forces would not
be large yet. However, they would soon grow strongly and we would
eventually be torn and crushed at the same time... The final fate of matter inside a black
hole can be assessed from two points of view :
1. According to the
"classical" general theory of relativity, all matter
collapses into a point singularity
with zero volume and
infinite density. The paradox of such a state suggests that here
the theory reaches the limits of its possibilities...
2. According to the quantum
approach, this matter "dissolves" in the "topological
space-time foam"
quantum fluctuations geometry of
space in the scales Planck order of 10-33
cm (cf. §B.4 "Quantum geometrodynamics") .
In both cases it is the irreversible
termination of the substance,
including particles of which it is composed. According to the
theorem "Black
Hole has no hair" (§4.5 "The "black hole has no
hair theorem") no
individual characteristics of absorbed matter are preserved for
the outer universe, except mass, charge and angular momentum. Hypotheses about the possibility
of penetrating other universes through black holes are not
confirmed (shown in §4.4 "Rotating
and electrically charged Kerr-Newman black holes"). In
§4.7 "Quantum radiation and the
thermodynamics of black holes"
is critically assessed the "return" of the substance
from the black hole by effect Hawking quantum evaporation.
People falling into the black hole
Imagine in an imaginary experiment astronaut - a suicide
man, who jumps out of the rocket at a certain greater
distance and falls feet forwards in direction towards the
spherical black hole. We will briefly describe his feelings and
destiny. As mentioned above, where a living person can enter or
around a black hole depends on the size (weight) of the black
hole. The larger the black hole, the closer to or deeper below
the horizon an astronaut can penetrate and the longer it can
survive. In the case of black holes in stellar masses, the tidal
forces of an astronaut would immediately kill ("spaghetti") at a
distance of tens of gravitational radii.
In order to give the falling astronaut at least
a little longer life, we choose a resting *) large black
hole with a mass of the order of 109
M¤; such giant
black holes are found in the centers of galaxies and are often
observed as quasars (§4.8. "Astrophysical
significance of black holes"). In this case, the falling astronaut can, alive and
well, cross the horizon and enter a black hole. At this moment
(of his own time) he practically does not feel anything
extraordinary **), he is still moving freely in a weightless
state. However, his fate is inevitably sealed, he has only a few
tens of hours left to live. As his fall gradually accelerates and
gets closer to singularity, tidal gravitational forces begin to
apply: he begins to feel a pull on his legs
toward the black hole and on his neck and head in the opposite
direction (and at the same time pressure from
side). In the spherical case of tidal forces, all bodies expand
radially and compress transversely. These forces will grow
rapidly, so that his muscles and bones will no longer be able to
withstand them, the body will rupture and the astronaut will perish (he
will be "spaghetti"). And near
the singularity, the remnants of the body are immensely deformed,
tidal gravitational gradients ripping and crushing cells, then
individual atoms, even electrons, protons, and quarks inside
them. All these fragments eventually nest into the singularity
and become part of it, they disappear in it ...
*) If an astronaut jumped into a
black hole during a collapse, or just after the collapse or after
a larger mass was absorbed by a black hole, he would still be far
from the singularity torn and "kneaded" by the chaotic
oscillations of tidal forces (mentioned above in the passage
"Gravitational oscillations during a collapse inside a
black hole"). Here we consider the situation after the
complete suppression of gravitational oscillations inside a black
hole (which can take several months for a giant black hole).
**) The hypothesis has emerged, that just below the
horizon of a black hole there could be a kind of "fire
wall" made of high-energy quanta and radiation
(A.Almheiri, D.Marolf, J.Polchinski, J.Sully, 2012), which would
burn a falling astronaut. It could allegedly arise from Hawking's
quantum radiation, whose pairs of quanta below and above the
horizon could remain "quantum entangled" even after
emission. Such quantum effects could perhaps occur with black
mini-holes, not with black holes in stellar masses (or even
larger ones).
The presence of a "fire wall" contradicts
Einstein's principle of equivalence, on which the general theory
of relativity is based. Therefore, the "fire wall"
hypothesis is erroneous probably, so we will not
consider it in the further analysis of the properties of black
holes (except for a brief mention in §4.7, the passage "Paradox of information loss ?").
The fall
of a body into a black hole - a brief recapitulation
If we were to watch an object fall into a black hole from a
distance, we would see the following progression :
Initially, away from the black hole, the
fall would accelerate. But as the object approaches the horizon,
the fall would begin to slow down from our perspective due to
gravitational time dilation. Any signals coming from it would be
increasingly delayed in time, subject to an exponentially
increasing redshift, and would soon be practically invisible. If
we were to continue to track the movement of the object using
sophisticated methods of detecting long-wave electromagnetic
radiation, we would find that it never actually reaches the
horizon. From our perspective, its motion will appear frozen
at the moment it reaches the horizon.
If the object were ourselves and we were
observing from the perspective of a falling observer, we would
see a constantly accelerating fall, we would feel no
acceleration. We could experience tidal forces because
different parts of our body would try to follow slightly
different trajectories. For black holes of stellar and
intermediate masses, tidal forces would tear us apart and
"spaghettiize" us far before the horizon. If it were a
giant black hole, we could survive reaching and crossing the
horizon. At no point would we feel any acceleration, we would be
in a state of free fall the entire time. Only deeper, towards the
center (theoretically towards the singularity), would we be
irreversible completely destroyed by tidal forces...
The paradox of the
external and internal view of the gravitational collapse
The collapse of a star stops - it "freezes" forever
when it reaches the horizon when it is observed in an external
static frame of reference. But it does not freeze and,
conversely, continues rapidly beyond the "freezing
point" when viewed from the point of view of an object
collapsing with the star's surface. Who is right? External
or internal observer? In terms of the theory of relativity, both
! The collapsing star - as such - actually shrinks below the
critical gravitational radius. The fact that this seems like a
"freeze" when viewed from a distance can be considered
a gravitational-optical-time "illusion". Or can it be
reflected "pragmatically" in the spirit of the
following passage "Are there 'complete' black holes in
the universe? " :
Are
there 'complete' black holes in the universe ?
As mentioned above, to an outside observer at first the rapidly
accelerating gravitational collapse gradually slows
down as it approaches the
causal horizon due to relativistic phenomena, and immediately
above the horizon it comes to a complete stop (all movement completely
"freezes"). The horizon is reached only in infinite
(external) time - so never! From the point of view of the outer
universe, the horizon of events can never be crossed and a real
black hole cannot be created.
The exact Schwarzschild or Kerr solution to the spacetime
geometry describing a black hole is just the asymptotic
final state of the
gravitational collapse process. To an outside observer, it takes
forever to fully reach this end state and form the horizon. In
reality, however, long before, if the collapse reaches the
relativistic stage, the gravitational time dilation leading to
the redshift becomes so large that the collapsing object
"goes out" in a fraction of a second and ceases to be
detectable by any means other than its gravity (we are not considering the tiny Hawking radiation). We can effectively consider this
collapsed object as a black hole - "almost done",
nothing more will happen (except accretion). From an
astrophysical point of view, it will have all the properties of a
"ready-made" black hole.
For the outside observer, the worldlines
of all particles end on the horizon of events (Schwarzschild's
sphere in the spherical case); whatever happens below the
gravitational radius with the falling observer (in terms of his
own time), as if it did not exist for the outside observer. From
the point of view of events in the universe, only the outer
part of the "black hole", which behaves like
a compact gravitationally collapsed object, actually applies and manifests itself -
see §4.8. "Astrophysical significance of black
holes".
From a purely theoretical point of view, we could therefore claim
that "finished" or
"complete" black holes (including the
"inside" below the horizon) do not exist in the
universe, but from a "pragmatic" point of view, compact
collapsed objects are astrophysically indistinguishable from
them. And they are thus observable.
However, physics, as a universal and
objective natural science, is obliged to deal with natural
phenomena from all possible points of view. That is, also
from the point of view of collapsing matter - an observer who
"falls" in the gravitational field of a collapsed body
together with matter. From this point of view, the collapsed
object - the black hole - continues to live
an intense "inner
life" (invisible by distant observers), in which a
relentless collapse dominates and some very unusual phenomena may
occur there. We also analyze these phenomena from a theoretical
point of view in a number of places in this chapter, as well as
in the previous chapter 3 "Geometry and topology of spacetime", although they are probably not
directly relevant for
"practical" events in outer universe. However, they certainly have their
gnoseological interest ...
The absolute nature of
the black hole horizon raises an interesting paradoxical
question: "How can the
gravitational force get out from under the black hole horizon and
act on external bodies when the horizon does not let anything
out?". This issue will be discussed in §4.5
"Black hole has no hair",
in the section "Preservation of interaction with
matter absorbed by a black hole".
Behavior
of the substance at high pressures; neutronization
To better understand why a star in which all nuclear fuel has
burned, with a mass M' higher than a certain limit, can no longer withstand its own gravity, it is useful to study the lowest energy state of a system of a given number of
atoms containing N nucleons [115].
In the "cold" substance *), in which neither the
pressure caused by the thermal motion of the particles nor the
radiation pressure is substantially applied, the main role is
played by the Fermi pressure related to the Pauli principle. If we have a set of N
fermions of mass m concentrated in a unit volume, it will be according to Pauli's principle, each fermion
occupies an effective volume of 1/N, and thus according to
Heisenberg's uncertainty relation, its momentum will be of the
order of ~ h.N1/3. The velocity of the fermion
will be on average ~ h.N1/3/m in the non-relativistic case (ie
when h.N1/3 <<m), and of course
practically equal to one (units c=1) in the relativistic case
(for h.N1/3 > m). The pressure, which is
the product of the momentum, velocity and density of particles,
is then of the order of P ~ h2 N5/3 /m in the non-relativistic case
and P ~ h.N4/3 for the
relativistic Fermi gas.
*) A cold substance is
considered to be a situation where the temperature is so low that
it does not have a significant effect on the physical properties
of the substance. This can be achieved even at temperatures of
tens of thousands of degrees (eg with white dwarfs).
If the number of
nucleons N is not too high (less than about ~1052, i.e. total mass less than ~1025 kg - so that the
total gravitational force does not deform the atoms), the lowest energy state of
such a system will be the crystal lattice of iron atoms Fe56. The strongest here are nuclear
forces, the minimum of which corresponds to the Fe56 nuclei with the highest binding energy
per nucleon *). In second place are the electromagnetic forces
that determine the dimensions and shape of the crystal lattice.
It can be said that the Fermi pressure is compensated by electric attractive forces
between particles in the crystal lattice. The forces of
self-gravity are practically negligible here and cannot prevail
over the valent forces in the crystal lattice, much less over the
nuclear forces.
*) See Fig.1.3.3 in
§1.3 "Nuclear reactions
and nuclear energy" in
the book "Nuclear physics and physics of ionizing
radiation".
For large
weights (greater
than about ~1026 kg), self-
gravity
already becomes substantial, the gravitational forces inside
the system exceed the valent forces, and the crystal lattice disintegrates. The electrons then behave as free
particles forming a degenerate electron
gas. If the density is
not very high, and these electrons are non-relativistic, the
Fermi pressure is capable of balancing the gravitational force
(in the nonrelativistic case the bulk of the pressure caused by
the Fermi electrons because the value of 1/m for them is much
higher than for nucleons and nuclei). The relationship between
pressure and density in specific situations is described by the equation of state of matter. The relatively complex
and realistic multicompartment equation of state of "cold
matter" was constructed by Harrison
and Wheeler
[115] (Fig.4.5). In this equation of state, several significant areas
differ according to which physical processes dominate here and
how the pressure is balanced. We would gradually find all these
regions on the way from the surface to the interior of the
neutron star :
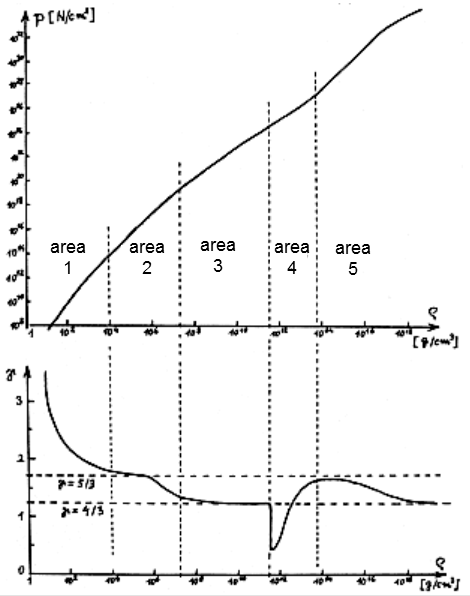 |
Fig.4.5. Relationship between pressure and
density for high pressure values occurring in stars.
Top:
Diagram of course
Harrison-Wheeler equation
of state (depending of the
pressure p on
the density r)
of "cold material".
|
Bottom:
Diagram shows the
dependence of exponent
g = [ (p + r ) / p ] . dp
/ d r
- a compressibility
factor - on the
density of the mass-energy equation of state for the
transcribed shaped adiabat (polytropey): P = C . r g . |
Area 1: r <10 4 g / cm 3
This first area of low densities is sometimes divided into two sub-areas :
a) The
lowest with r < ~ 50
g/cm3, where the usual laws of solid state
physics apply and the properties of individual substances
strongly depend on their chemical composition according to
Mendeleev's periodic table. The pressure here is caused by
electrons in the outer (valence) orbitals.
b) ~ 50 g/cm3 < r <~
104 g/cm3, where the elastic properties
already depend only on the average Z
(continuously), but
not on a specific chemical composition. The electron orbitals are
strongly compressed and the electrons in the lower orbits also
contribute to the pressure.
Area 1 is not interesting for the
analysis of the end stages of stellar evolution, but it plays an
important role, for example, for the structure
of planets
.
Area 2: ~10 4 g / cm 3 < r < ~10 7 g / cm 3
At densities above ~104
g/cm3 the Fermi energy of electrons
already exceeds their binding energy in the atom, these electrons are released and the substance takes the form
"gas" mixtures of nuclei and electrons. The
pressure here is caused practically exclusively by degenerate electron gas. As the density increases to a
value of about ~107
g/cm3, these electrons become relativistic.
Area 3: ~ 10 7 g / cm 3 < r <~ 10 11 g / cm 3
If the density
exceeds a value of about r »
1.5.107 g/cm3, electrons begin to enter the nucleus and combine there with protons *) to form
neutrons and flying-out
neutrinos. In this
situation, the iron core with A=56 is no longer the core with the
greatest stability. With increasing electron pressure, the range
of mass numbers of the most stable nuclei, in b- equilibrium
with such an electron gas, shifts to higher
values.
*) This nuclear process is sometimes called
inverse b-decay - see §1.2
"Radioactivity", part
"Radioactivity b+ " in the monograph "Nuclear physics and
physics of ionizing radiation".
Area 4: ~ 10 11 g / cm 3 < r <~ 10 14 g / cm 3
As the density
increases further, around the value of r ~ 1011 g/cm3 the nuclei
become so heavy and enriched in neutrons, that they become unstable with
respect to emission neutrons. As the density increases, more and
more neutrons leave the nucleus, so that the substance consists
of a mixture of neutrons, heavy nuclei and electrons. At
densities close to 1014
g/cm3, the individual nuclei disappear
and the substance consists of a mixture of neutrons (mostly),
protons and electrons. We say that the substance
is neutronized.
Area 5: r ³ ~ 10 14 g / cm 3
At these densities, the Fermi momentum of the baryons reach
relativistic values. The neutron, electron and proton
"gas" is in equilibrium with respect to the direct and
inverse b- decay, so that the total energies
of protons Ep , electrons Ee and neutrons En are related by the relation Ep + Ee = En and the
Fermi momentum of the neutron is twice that of an electron or
proton. The relative representation of individual types of
particles will then be given by the ratios ne= np, nn= 8.np= 8.ne, ie nn : np : ne = 8 : 1 : 1. In this
last area, however, there is great uncertainty in the equation of
state, because in addition to the Fermi pressure of relativistic
baryons, nuclear interactions between them and the formation of
other particles. The precise nature of nucleon-nucleon
interactions under such extreme conditions is not
exactly known. Also, nothing definite is known about the nature
of particle formation (eg whether to
consider particles also from grandunification theories?). In the Harrison-Wheeler
equation of state, at densities close to nuclear and densities
higher, no nucleon-nucleon interactions or effects of new
particle formation are considered, the substance is considered to
be a mixture of non-interacting neutrons, protons and electrons, forming
Fermi gas. It is assumed here that with increasing densification,
the momentum of nucleons increases and thus the influence of
nuclear forces on their motion decreases.
In fact, at very high densities
of 2-10 . 1014 g/cm3, which could be in the center of massive
neutron stars, however, extremely high pressures thicken
baryons so close to each other that their quark structure
connects to each other and "dissolves"
into a mixture of almost free quarks and gluons - the so called quark-gluon
plasma is formed, which can be stabilized
by massive gravity. Quarks, pushed by strong gravity very close
to each other, could form Cooper pairs, acting like bosons, and
form superfluid condensate. These effects could lead to better
compressibility than the Fermi pressure allows; massive
neutron stars could thus shrink to a smaller size than would be
expected for a composition of neutrons alone. It was discussed
above in the passage "Internal structure of neutron
stars".
In general, the equation
of state of a "cold" substance is relatively reliably
known for densities much lower than nuclear ones, while at high
densities there are considerable uncertainties stemming from
ignorance of the exact nature of elementary particle interactions
at very high energies. Unfortunately, we know very little about
the behavior of matter under very extreme conditions, rather we
make certain more or less substantiated assumptions about how
matter could behave under such conditions...
In connection with this, there is
often an objection to complete gravitational collapse: "What if, after reaching a certain (albeit very high)
density, the substance of the star is no longer compressible
?". The answer
is: "If the accumulation of matter
is such that the gravitational radius is reached, then in
principle no matter can be incompressible
!". In §3.4 "Schwarzschild
geometry" we saw, that
the Schwarzschild spacetime geometry that places such
configuration will (if spherically symmetric), dictates each object below the horizon, to move
towards the center r = 0. A each object must
"listen" - the universal laws of space are superior to all
other laws, because all physical phenomena are ultimately
governed by the laws between quantities in space and time. Even
the laws of special relativity prohibits
absolute rigidity and incompressibility for bodies of
non-zero dimensions, because "sound" (mechanical vibration)
would have to propagate in them at infinite speed. In reality,
however, the speed of sound vacus.~ Ö(dP/dr) must
in any case be less than the speed of light, ie dP/dr < c2. This fundamental limit is
however still unrealistically high, because
for an isotropic
medium (alone it may be well to define the
pressure in the normal sense) satisfying the strong
energy conditions (see §2.6, the
relation (2.60) ),
according to which a trace of the tensor of energy-momentum it
must be positive definite, we get three times the lower limit
for the ratio of pressure and mass density: dP/dr £ c2/3.
Even if we accept an unrealistic case of
incompressibility, there will be a certain limit mass above which
there can no longer be any equilibrium configuration. This is
because pressure also appears in the energy-momentum tensor of a
given substance and thus contributes to the excitation of the
gravitational field; it also appears in the numerator of the
relation (4.3). At high pressures can occur somewhat paradoxical
situation, where the pressure does not prevent, but rather helps
to further gravitational collapse ...
In practice, i.e. in
gravitational kolaps with a sufficiently massive stars, no
uncertainty in the equation of state super-dense substance at r l 1014 g/cm3
have no influence, because the interactions responsible for them
can come into play only below the event horizon; therefore, they
cannot prevent a black hole from forming.
What's inside the black
holes ?
The inquisitive question "What's
inside something?" is completely legitimate, and one we
commonly ask it for all macroscopic and even
most microscopic
objects. Exploring what is inside
cells
("Cells - the basic units of living
organisms") has fundamentally shifted our
understanding of the nature of life and made biology and medicine
a powerful and exact science. Examination of what is inside atoms has revealed the physical and chemical
structure of matter and the nature of radiation ("Atom Structure"), has yielded a vast
number of applications. In each area, the answer to the question
"what is inside?" of some object, has substantially improved the
level of our knowledge of the truth.
Black holes
are somewhat resist this trend. And not just because there
are no black holes within the distances available to us, and
there is no hope of exploring them directly in the foreseeable
future. There are mainly fundamental
obstacles.
How can we observe "what's inside" by observation, when no
signal can ever get out of a black hole and give us an answer?!
Whatever is inside the black hole, due to the event horizon, it
cannot manifest itself outside the hole to affect the surrounding
world. Even if a brave researcher set out to investigate the
interior of a black hole, he would never be able to return and
tell us his discoveries; nor could he send any message about them
before his inevitable death. The only way to answer the
inquisitive question is "what's
inside the black holes?", is a theoretical study of what
the laws of physics predict - their analysis and
extrapolation. In the above passage "What happens to
matter, its atoms and molecules when it is absorbed by a black
hole?" we have already partially outlined what is
going on there according to the general theory of relativity.
Basically, three possibilities are discussed, what could be
hidden inside a black hole :
¨ Singularity with infinite gravitational
forces. This is predicted by the "classical " general
theory of relativity and concretizes it in
more details the Penrose's
and Hawking's theorems about
singulatities (§3.7
"Spatio-temporal singularities ", §3.8 " Hawking's and Penrose's
theorems about singularities
"). However,
singularity is not a very acceptable solution...
¨ Quantum
foam in
which the geometric properties of space and the causal properties
of time end. The singularity "dissolves" in the quantum
foam. This is, yet indeterminate, a view of quantum
gravity and
quantum geometrodynamics (§B.4 "Quantum
Geodynamics") .
¨ A tunnel to another universe or other parts of space. This is
suggested by the analysis of the complex geometric and
topological structure of spacetime of rotating or electrically charged black
holes (§4.4, part "Black
holes - bridges to other universes?").
However, the real existence of such "tunnels" or
"wormholes" is physically questionable (it is critically discussed in the mentioned §4.4) .
We do not yet know the definitive
and irreversible answer. Perhaps the expected advances in unitary field theories will shed new light on these questions
(§B.6 "Unification
of fundamental interactions. Supergravity. Superstrings.") ...
The
reality of the existence of black holes
If we recapitulate the results of the outlined analysis of the
properties of the final stages of stellar evolution and
gravitational collapse and compare it with the situation observed
in space, we can draw the following conclusions :
- a) The end product of
stellar evolution can be either a white (or black) dwarf, a neutron star or a black
hole, depending on the remaining mass M' of
the star after completion of all
nuclear reactions.
- b) There are limit values
for the masses that white dwarfs (Chandrasekhar
limit)
and neutron stars (Oppenheimer-Landau
limit)
can have. For masses M' greater than this
Oppenheimer-Landau limit, there is no stable equilibrium
configuration, the system will collapse indefinitely.
- c) A large number of stars (even in our Galaxy) have a mass significantly greater
than needed to reach a residual mass M' exceeding these
cut-off masses, and the time it takes for these stars to
deplete all their "nuclear fuel" is short
compared to the age of the galaxy.
- d) If such stars do not
expel most of their mass (in very
massive stars almost all of their mass), they will succumb to
complete gravitational collapse and end their existence
as compact gravitationally completely collapsed objects -
black holes.
- e) Black holes can
participate in a number of significant astrophysical
phenomena in universe (it is described
in §4.8 "Astrophysical significance
of black holes"; at the end in
the passage "Holes in space" the
hypothetical objects of white hole, gray
hole and wormhole are also
discussed).
This gives us a real basis and
sufficient motivation to study the specific properties of
different kinds of black holes in the remaining paragraphs of
this chapter. Here we can expect that in the analysis of
black holes (which will be perhaps the most
interesting part of the book for many readers) we can look forward to very
unusual and fascinating phenomena
!
Brief recapitulation :
The formation and evolution of stars
Before we begin to analyze in more detail the astrophysical
properties of individual types of black holes, for clarity, we
briefly recapitulate the processes of star formation and
evolution (described in more detail in
§4.1 and 4.2) according to a simplified
picture (special and borderline cases are
not discussed here) :
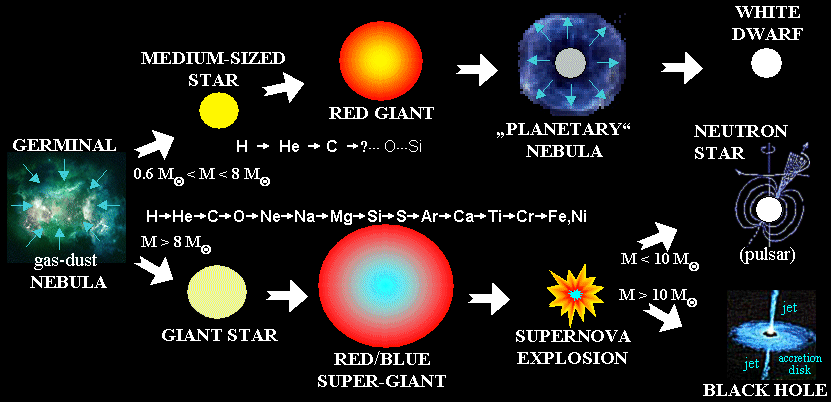
-> At the beginning is a nebula - a cloud
of gas and dust, originating from the cosmological primary era of
matter, or as a remnant after the demise of other previous stars.
-> Under the influence of its own gravity (or with the contribution of radiation pressure from
surrounding stars and supernovae), the
cloud begins to contract, the gas condenses and
heats up, and a protostar is formed.
-> During contraction, the gas in the center heats up
to several million degrees, until the ignition of thermonuclear
reactions, mainly the synthesis of hydrogen into helium.
A star is formed, shining steadily for millions
to billions of years thanks to the energy of thermonuclear
reactions. Most stars of average size (similar
to the Sun, often smaller) are formed, less
often giant stars.
-> After the consumption of hydrogen in the star's
interior, its core shrinks, heats up enormously, and further
thermonuclear reactions of fusion of helium into carbon,
even higher ones, can occur. The outer parts of the star, on the
other hand, expand - a red giant or supergiant is
created.
-> These outer envelopes are eventually thrown away and a
so-called "planetary nebula" is formed (it has nothing to do with planets...), in the middle of which, in the case of less massive
stars, there is a white dwarf; it then becomes
independent (the possibility of a white
dwarf thermonuclear explosion - a type Ia supernova - is
discussed in §4.2, passage "Supernova
explosion. Thermonuclear explosion. Core collapse.").
-> In the interior of larger, more massive stars, a whole
sequence of thermonuclear reactions will take place up
to iron.
-> The core of heavy stars then collapses in a supernova
explosion, ejecting a large amount of material enriched
with heavier elements. The end result can be either a neutron
star (observed as a
"pulsar") or, in the case of very
massive giants, collapse to form a black hole.
Vojtech Ullmann








