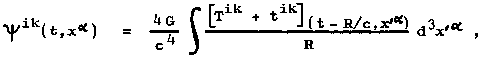 |
(2.65) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 2
GENERAL THEORY OF
RELATIVITY
- PHYSICS OF GRAVITY
2.1. Acceleration and gravity from the point
of view of special theory of relativity
2.2. Versatility
- a basic property and the key to understanding the nature of
gravity
2.3. The
local principle of equivalence and its consequences
2.4. Physical
laws in curved spacetime
2.5. Einstein's
equations of the gravitational field
2.6. Deviation
and focus of geodesics
2.7. Gravitational waves
2.8. Specific
properties of gravitational energy
2.9.Geometrodynamic system of units
2.10. Experimental
verification of the theory of relativity and gravity
2.7. Gravitational waves
Wave
propagation - a general natural phenomenon
An important natural phenomenon of waves in material environments and
physical fields lies in the propagation
of certain changes (commotions,
vibrations, oscillations)
through space. Wave propagation is generally
conditioned by two basic aspects :
1. The mechanism of changes - excitations, oscillating motion - in a given
environment or field. Without the dynamic emergence of change,
"there would be
nothing to spread"...
At the water surface, the
commotion may be caused by the impact of a stone, after which the
deflected water particles periodically oscillate up and down
under the influence of the Earth's gravitational field. In the environment of elastic
materials, under the action
of the force the mechanical
deformations can occur, which then periodically oscillate around
the equilibrium position due to elastic forces. In the
electromagnetic field, changes in the intensity of the electric
and magnetic fields occur during uneven movements of electric
charges and are mutually generated due to the Faraday-Ampere law
of electromagnetic induction. In the gravitational field,
temporal changes in its intensity, or changes in the curvature of
spacetime, are caused by the uneven motion of material bodies; periodic oscillations of the gravitational field
(curvature of spacetime) arise mainly during the mutual orbit of
massive bodies around a common center of gravity under the
influence of gravitational attraction (according
to the general theory of relativity, it is again the motion of
bodies in curved spacetime) .
2. The final rate of propagation of changes
(disturbances) in this environment or field. At an infinite rate
of propagation of the interaction, the change would not
propagate, but would take effect immediately on
all bodies, even very distant; the ripple would not occur...
In material
environments, the commotion and oscillating motion spread to the
environment due to the elastic interaction with neighboring and
with more and more distant atoms and molecules of the
environment, which are gradually set in motion. The rate of this
propagation depends on the strength of the elastic interaction
(expressed as Young's modulus of elasticity) and on the density
of the environment. In air, where there is a relatively weak
elastic interaction between adjacent molecules, the speed of
propagation - the speed of sound - about 330 m/s., In water about
1500 m/s., in hard solids is significantly higher (eg in steel
about 5000 m/s.). However, it is always finite
and substantially lower than the speed of light c .
In an electromagnetic field, the commotion
propagates into space at the speed of light c (in vacuum)
in the form of electromagnetic waves, where the electric and
magnetic fields excite each other by their variability (law
of electromagnetic induction - Maxwell's equations, §1.5 "Electromagnetic
field. Maxwell's equations."). As we will see below, even in the gravitational field,
the commotion propagates at the speed of light in the form of gravitational
waves - the oscillating curvature of space-time.
Wave function, wave equation
The propagation of a wave is mathematically expressed by means of
a special differential equation between the rate of time
change (time derivative) of deflection f and the gradient
of spatial change (derivative by
coordinates) of this quantity f - using the wave
equation. In the simplified one-dimensional case
of a plane wave propagating in the direction of the X axis
at a phase velocity c *), the wave equation has the form :
d2 f /
dt2 = c. d2 f / dx2 .
*) The speed of wave propagation is denoted by c
here, but it does not have to be the speed of
light in general.
The solution of the wave equation is a special function f(x,
t) of spatial coordinates and time - a wave function
that has the general form :
f (x, t) = f
(x, t- x/c) .
If we start from some initial point with the coordinate xo in time to , then the same value
of the deviation f as in the point with the coordinate xo at time instant to , will be in all
places whose coordinates and time satisfy the equation x - xo = c. (t - to). It thus describes
the ripple of the deflection f ,
gradually propagating through space in the direction of the
X-axis at the phase velocity c
. The most commonly considered is the harmonic
(sine or cosine) time dependence:
f (x, t) = f
.cos [ w . (t - x/c)] ,
where w =
2p f is
the circular frequency; waves are often caused by periodic
oscillating movements of electric charges (eg in antennas supplied with a high-frequency signal of
frequency f) or circular orbiting
of gravitational bodies. Even in cases where this is not the
case, the resulting wave can be Fourier- decomposed into
harmonic components of different frequencies and
amplitudes. When using complex (imaginary "i") numbers,
harmonic wave functions are often written in the form
f (x, t) = Re
(f. e -i w (t- x/c) ) .
In the three - dimensional analysis in the coordinates
x, y, z, the wave equation has the general form :
(1/c2) .¶2f/¶t2 = ¶2f/¶x2 + ¶2f/¶y2 + ¶2f/¶z2 ,
which is often equivalently written using the Laplace
operator D : (1/c2) .¶2f/¶t2 = D f . In a
4-dimensional relativistic formulation, then using d'Alembert's operator o s - (1/c2) .¶2/¶t2 + ¶2/¶x2 + ¶2/¶y2 + ¶2/¶z2 as o f = 0 .
The wave equations are derived from the equations
of motion of the elements of matter in continuum
mechanics, and from the field equations - Maxwell's
equations of electrodynamics
(§1.5 " Electromagnetic field. Maxwell's equations ", part" Electromagnetic waves ") and from the Einstein's
equations of the gravitational field (shown below in the section "Origin and properties of gravitational
waves"). If
from these fundamental equations of substances or fields results
the wave equations, it means that in the given substance
environment or a physical field can propagate waves.
From a somewhat different perspective, the wave function
is widely used in quantum physics. In quantum
mechanics, the state of the particle (or a
collection of particles, and generally any physical system) is
described by so-called wave function y(x, y, z). The
physical meaning of the wave function is that the square of the
modulus of the wave function ú
yú 2 determines the probability dW that the
particle at a given time t is in the element of volume dV
= dx.dy.dz around the point (x, y, z): dW = ú yú 2 .dx.dy.dz. Schrodinger's equation and another
apparatus of quantum mechanics and quantum field
theory then operate with the quantum wave function conceived
in this way in order to determine quantum states and transition
probabilities between different quantum states. However,
this concept of the wave function is already outside the scope of
our treatise on physical waves (it is
discussed in §1.1, part "Corpuscular-wave dualism" and "Quantum nature of the microworld" in monograph "Nuclear
physics and ionizing radiation physics")
.
Graphically, the
wave propagation is represented by wavefronts. A
wavefront is a geometric location of points in space
that oscillate with the same phase when
rippling. Waves from a point or spherically symmetric source in a
homogeneous and isotropic medium are a spherical
(round) wavefront, the points of which lie on a spherical
surface. The wavefront that a wave reaches in a given time is
called the front wavefront. The perpendicular to the
wavefront indicates the direction of wave propagation.
Huygens principle
The propagation of waves using wavefronts is analyzed in an
illustrative way by means the so-called Huygens-Fresnel
principle : At any moment, each point where the front of the
propagating wavefront has reached, can be considered a new
source of secondary elementary waves, from which
secondary waves propagate again in all directions, while they interfering
with the original waves, as well as with all other elementary
waves. The total wavefront in the next moment of time then arises
as the outer envelope of all elementary wavefronts. We
can thus construct a wavefront at a certain moment, if the
wavefront is known at a previous point in time. It can be deduced
from the shape of the resulting wavefronts the laws of
reflection, diffraction and refraction of waves.
A common general
feature of wave propagation - radiation
- is the fact that the relevant waves gradually detach
from the source and carry some a
part of his energy,
momentum and angular momentum into space, even without the
presence of any distant "receiver" of
these waves. In fact, the waves themselves (their fields) actually have energy.
Inductive and wave
zone
From the point of view of mutual energy connection
between the source and the receiver, the space around the
oscillating wave source of frequency f can be divided into
two areas :
¨ The inductive zone is a close range of distances r from the source,
smaller than the radiation wavelength: r < c/f = l. Here, in the
first approximation, the action of the source on the test bodies
can be explained by the direct action "at a distance"
under the influence of Coulomb's law of electricity or Newton's
law of gravity. The loss of energy of the source here
significantly depends on the presence of other bodies or systems
that "receive" energy from the source - in which
movements in the source "induce" by their force action
certain movements of charges or gravitational bodies, while
performing work. And this induction, in turn, manifests itself in
the loss of energy in the source.
¨ The wave zone is the more distant region of several wavelengths r >> c/f = l; often they are places hundreds, thousands, millions of
l. If
we place a "receiving" system here (electric charges in a coil or antenna for
electromagnetic waves, or test bodies for gravitational waves), no amount of energy received by this system will
affect the energy ratios in the source. We can say that
the waves have already irrevocably took away from this energy
source to a remote space, without any feedback, what will hapen
there with this energy...
The time course of field and the shape of the wavefront
Time course of oscillation in a wave field generally depends on
the dynamics of power, it may not have a regular
sinusoidal shape. As we will see below ("
Sources of gravitational waves
in universe"), the waves from the final phases of the binary
system are not exactly sinusoidal, they consist of harmonic
waveforms of different frequencies and amplitudes. And when the
bodies merge with each other, they even have the aperiodic
character of a powerful pulse! On the other hand, using Fourier
analysis, each waveform can be expressed as a superposition
of harmonic functions (sine or cosine) with
different amplitudes, phases and frequencies. In general
analysis, therefore, waves are usually drawn as sine waves.
Also, the shape of
the wave propagation can be more complicated. In principle, the
waves propagate isotropically over a spherical wavefront. However, near the source, in the inductive or near-wave
zone, the field in the wave may have a complex irregular course
and also the wavefront may be deformed and time-varying, not
necessarily regular in spherical shape (heterogeneity
in structure and motions in the source system). However, at greater distances from the source, these
irregularities are usually gradually smoothed out and the waves converge
to a regular spherical waveform with isotropic
propagation and a harmonic (sine - cosine) time
course of the field in the wave. And at great distances, the
spherical wavefront has such a large radius that its curvature is
almost zero, we observe a plane wave.
Longitudinal and
transverse waves, polarization of waves
According to the direction in which the wave
oscillates with respect to the direction of wave propagation, we
distinguish two types of waves :
l Longitudinal
wave , in which the amplitude of oscillations in the
wave occurs in the same direction in which the
wave propagates. Longitudinal waves most often arise in elastic
media environments, where due to the binding forces between
particles (atoms, molecules) of matter, the deflection of a given
particle is transmitted to adjacent and then to more and more
particles. The wave is formed by alternating areas of dilution
and compaction.
l
Transverse wave ,
where the amplitude of the oscillation in the wave is perpendicular
to the direction of wave propagation. The simplest example is
waves on the water surface... However, physically important
transverse waves arise in fundamental physical fields -
electromagnetic and gravitational. Electromagnetic waves
are formed by oscillating vectors of electric intensity E
and magnetic induction B, which are
perpendicular to each other and oscillate in a plane
perpendicular to the direction of propagation; thus
cause the oscillations of electric charges in directions
perpendicular to the direction of wave propagation. In a gravitational
wave, the components of the metric tensor of the curved
space also oscillate in such a way as to cause the test particles
to oscillate in directions perpendicular to the direction
of propagation of the wave (although
in a more complex way - see below "Plane gravitational waves in linearized gravity").
For transverse waves, the oscillation
vector can be oriented - within a plane perpendicular to the
direction of propagation - in different directions. If this
oscillation direction randomly and chaotically changing, we are
talking about non-polarized waves. In many
cases, however, the direction of oscillation along the wave is
constant or changes regularly - it is a polarized wave.
If the oscillation takes place during the propagation of
the wave at the same angle at all times in a
plane perpendicular to the direction of propagation, it is
referred to as linear polarization. The
direction of oscillation while doing so may be inclined in any
constant direction - the angle of polarization. In some cases, the direction of oscillation in a plane
perpendicular to the propagation of the wave can change
regularly and continuously, orbiting along a circle - it is
a circular polarization (clockwise
or counterclockwise). More generally, elliptical
polarization may occur.
Waves emitted by rotating sources - spiral
polarization of waves
A very special polarization can be imparted to the waves by
rotation. When waves are emitted by a rotating source,
this rotation leaves specific traces on the structure of the
emitted waves. At the emission of the wave, the maximum and the
minimum during the rotation of the source periodically shift
in time relative to each other, so the phases of the wave -
the alternation of maximum and minimum - will shift as the wave
propagates at speed c. The wavefront takes on the helix
shape of a spiral. A kind of "rotating,
twisting or spiral radiation" with specific
polarization properties is created. If it hits interacting
particles, it causes, among other things, their rotation around
the direction of propagation of the beam, which can be considered
as a manifestation of the angular momentum of this
radiation. It therefore behaves like a wave with orbital
angular momentum (for electromagnetic waves it is discussed
in §1.5, passage "Intrinsic and orbital angular momentum of waves").
Note: In laboratory optical
experiments, this light with helically rotating polarization is
generated by special rotating sources, cylindrical lenses,
lasers, holograms, and measured using spatial light modulators.
For radio waves, helical polarization can be achieved by a
special spatial configuration of antennas powered by
phase-shifted alternating signals, for sound waves analogously by
speaker systems. Gravitational waves arising in rotating systems
of black holes or neutron stars should also have a component of
helical rotating polarization (however, their measurement is
complicated, so far it has not been possible).
Bodies - particles that get into the wave field, oscillate
in different ways, depending on the intensity
and polarization of the waves. They can also spin around their
axis (spin) or rotate around the axis of the wave beam (orbital
momentum of waves).
We will now examine how these general physical-wave laws apply to a specific region of the gravitational field - gravitational waves :
Time-varying
gravitational field
The gravitational field is excited by matter
localized or distributed in space, according to the GTR the
distribution of matter curves space-time. If the distribution of
matter changes with time (the shape or position of material objects changes), the excited gravitational field
also reacts to this: we will observe a time-varying gravitational field, according
to GTR the changing curvature of space-time. If the source body moves periodically or the distribution of matter changes
periodically, it is reflected in the surrounding space by an
oscillating state of gravitational action - oscillating
deformations of the curvature of spacetime. How will such a
time-varying or oscillating gravitational action and the
curvature of space-time behave?
The gravitational field has many
features in common with the electromagnetic field (see §1.4),
Einstein's equations of the gravitational field are to some
extent constructed "according to the pattern" of
Maxwell's equations of electrodynamics. While watching the
analogy between electrodynamics and gravity, emerges most important questions
:
¨ What is the
speed at which gravitational interaction propagate
- the gravitational response to changes in the
distribution of matter ?
¨ Is there a
gravitational analogy of electromagnetic waves - gravitational waves ?
¨ How does gravity mediate energy transfer ?
We will try to answer the first
two questions in this chapter, we will discuss the issue of
gravitational energy and its transfer in the following §2.8
"Specific properties of gravitational energy".
Origin and properties of gravitational waves
In
principle, gravitational waves should arise wherever the position
or shape of a material object changes unevenly, with accelerated
motion and non-spherical changes in the distribution of matter.
Similarities
and differences of electromagnetic and gravitational waves
Gravitational waves are very similar in
nature to electromagnetic waves: both types of
waves have a transverse character and propagate at the maximum
possible speed of interactions - the speed of light c .
Einstein's equations of the gravitational field are analogous in
structure to Maxwell's equations of the electromagnetic field.
However, there are certain structural differences
between gravitational and electromagnetic waves :
× In universality
of action -
an electromagnetic wave vibrate only electrically charged
particles (such as electrons), while a gravitational wave,
representing changes in the geometry of space-time, can oscillate any mass.
× In polarization properties - electromagnetic waves have
mainly dipole character, while gravitational waves have quadrupole character * ), they represent periodic
changes of tidal effects.
*) "Monopole moment" represents the total
mass-energy of the system, which is maintained and therefore does
not cause radiation. A certain argument why even dipole
gravitational waves cannot arise is the basic one itself
the principle of equivalence, according to which gravity
is a universal interaction and mass always has the same
sign. Thus, unlike an electric dipole, it is not possible to
create a real gravitational dipole with different signs. The mass
dipole corresponds to the center of gravity of the mass of
the system, the first derivative of which corresponds to the
momentum, which is also a conserving quantity, so that the mass
dipole also does not emit any gravitational radiation. Only oscillations
of quadrupole and higher mass distribution moments can
emit gravitational radiation, just as oscillating electric and
magnetic dipoles and higher multipoles in electrodynamics emit.
× In intensity of radiation
Penetrating the gravitational and electromagnetic waves varies in intensity - "force".
Electromagnetic waves of relatively high intensity are generated
by electromagnetic interaction during normal natural processes
and can be efficiently generated in electronic sources
(transmitters). We can also easily receive them and transform
their energy. The intensity of electromagnetic wave radiation is
determined at the basic level by the Larmor
formula (1.61)
in §1.5 "Electromagnetic field. Maxwell's equations.". However, gravity is by
far the weakest interaction in nature - the bond between the
gravitational field and matter is very small compared to
electromagnetic or nuclear action. As will be shown below in the
section "Sources of
gravitational waves", the intensity of gravitational
wave radiation is given by the so-called quadrupole
formula (2.77), in which there is an extremely
small coefficient G/c5 ;
for the amplitude of the waves, according to formula (2.77b), the
coefficient G/c4 is. The
efficiency of gravitational wave generation and detection is
therefore extremely low - under normal circumstances, gravitational waves are very weak, almost unmeasurable. Stronger
gravitational waves can only occur with extreme
mass accumulation, under the action of very strong
gravitational fields on some compact
objects in universe (will be discussed below in the section "Sources of gravitational waves").
Basic different structural property of gravitational waves (according
to the general theory of relativity) can be expressed by the following comparison: Wave usually means the ripples of
"something" in space. In gravitational waves, space
itself is rippling.
General properties of
gravitational propagation in GTR
Consider an isolated material system described by the
energy-momentum tensor Tik in asymptotically planar
spacetime. We choose the coordinate system such that at large
distances from the material source it continuously changes into
an asymptotic inertial (Lorentz) system. The components of the
metric tensor can be examined in the form
| g ik = h ik + h ik , | (2.63) |
| where h ik = | / | -1 | 0 | 0 | 0 | \ | is a Minkowski metric |
| | | 0 | 1 | 0 | 0 | | | ||
| | | 0 | 0 | 1 | 0 | | | ||
| \ | 0 | 0 | 0 | 1 | / |
and hik = def gik - hik are deviations from this metric; so far we do not have to assume that the hik are small everywhere. We can agree that the indices will be "raised" and "lowered" using hik (even if it is not a tensor in the given geometry). If we define modified metric quantities
h =def hii = hik hik , yik =def hik - 1/2 hik h
and we choose the coordinates so that yik satisfies the four conditions yk i, k = 0 everywhere , we can express Einstein's equations of the gravitational field using yik :
| y ik , lm h lm = - 16 p (T ik + t ik ) , | (2.64) |
where tik are the quantities of the second and higher order in yik (t ik are the components of the so-called pseudotensor of energy-momentum of the gravitational field, as will be shown in the next §2.8). The solution of these "forcibly linearized" (or "seemingly linearized") Einstein equations can be expressed in the form of retarded integrals similar to electrodynamics
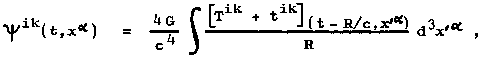 |
(2.65) |
where R = ÖS(xa -x'a)2 is the distance between the individual points x'a of the source system and the reference point xa, in which we determine the field (Fig.2.8). If t ik ¹ 0, this relation is actually an integral equation, because tik is a function of yik. However, for weak fields in the approximation of the linearized theory, the pseudotenzor tik is not present , and the relationship (2.65) passes in the relationship (2.55) in §2.5.
How fast is gravity?
According to the relation (2.55), resp. (2.65), the resulting
gravitational field at each location is given not by the
instantaneous distribution of matter ~ energy, but by the delayed distribution - retarded, shifted to the past - always by
the time the field needs to overcome the distance R
from individual locations x'a
of the source system to the investigated point xa by speed c (Fig.2.8). Thus, changes in the
gravitational field propagate at a finite
speed equal
to the speed of light. In other words (in the terminology of gravitational waves, see below), gravitational waves move at the
same speed as electromagnetic waves - at the speed of
light c .
At first glance, it may seem
strange that the gravitational field propagates at the same
velocity as an electromagnetic field, as light. However,
this is not a
miraculous coincidence, because the general theory of relativity,
as the physics of gravity, is built on the basis of the special
theory of relativity, in which the speed of
light plays a
decisive role in the structure of spacetime *). Rather than specifically the
speed of light, this is the maximum
speed of propagation of interactions, which has the value c .
The answer to the question about the speed of gravitational waves
can be formulated in reverse: Light
propagates at the speed of gravitational waves
! Gravity
determines the structure of spacetime, and it determines how
objects can move - including ligh ...
*) Compare relevant discussions in §1.6
"Four-imensional spacetime and special theory of
relativity" and §2.2 "Universality -
a basic property and the key to understanding the nature of
gravity".
Direct experimental confirmation of the
speed of propagation of the gravitational interaction is still lacking
*), we cannot produce detectable disturbances in the
gravitational field, so far it has been difficult to capture
gravitational waves from distant space objects (see below "Sources of gravitational waves"
and "Detection of gravitational waves"). However, since all
other experiments and astronomical observations so far support
the general theory of relativity as the correct theory of
gravity, the light velocity of gravitational
propagation is highly probable.
*) So far we have only indirect
astronomical methods . The most convincing of these is
the observation of tight binary pulsars, showing
the effect of accelerating their circulation due to the emission
of gravitational waves, as described below in the section "Indirect Evidence
of Gravitational Waves".
The extent of this effect is very sensitive to the value of the
velocity of gravitational waves; the measurement of the binary
pulsar PSR1913 + 16 gives the speed of gravity equal to the speed
of light with an accuracy of about 1%.
In
principle, astronomical methods for comparing the speed of
gravity with the speed of light are applicable. It consists in
observing the optical eclipse of a distant
strong cosmic source of electromagnetic radiation (such as a
quasar) by a near massive moving body (such as a planet or the
sun during a total eclipse), analyzing the dynamics of
gravitational bending of electromagnetic beams and gravitational
lensing (see §4.3, part "Gravitational lenses. Optics of black holes").
This depends on the identity or difference in the speed of the
observed electromagnets. waves from a distant source and the
speed of gravitational interaction from a "lensing"
moving body. Either a slight shift in the image position of the
remote source can be observed due to the movement of the test
("lens") body, or a slight time delay in the arrival of
electromagnetic waves. These position and time shifts depend on
the speed at which the gravitational field propagates from the
test body, compared to the speed of the measured electromagnetic
waves coming from the remote source object. However, our (radio)
telescopic technology has not yet sufficiently to observe these
subtle effects...
Versatility - the basic
physical property of gravitational radiation
The basic physical property that distinguishes
gravitational waves from all other types of radiation in nature
is its completely universal action - it interacts in
exactly the same way with all kinds of particles and
antiparticles, with all forms of matter. It
causes periodic changes in the geometric properties (curvature)
of spacetime, which affect the movements of all
particles and the behavior of all fields in the same way.
Planar gravitational waves in
linearized gravity
At sufficiently large distances from the source masses, the
gravitational field will be very weak, so that in the relation gik = hik + hik there will be |hik| << 1. We will first
assume that spacetime is practically planar with the Minkowski
metric, only slightly altered by the gravitational field
expressed by the quantities hik . In this case, all the nonlinear
effects of the field feedback on the metric will be negligibly
small, and such a gravitational field can then be investigated
(as an independent field) against the background
of Minkowski spacetime, much like an electromagnetic field. Linearized theory of the gravitational field
we have already
outlined in §2.5 as the simplest possibility of solving
Einstein's equations. Under suitable gauge conditions (2.53), the
linearized Einstein equation (2.54) applies to weak fields. For a
vacuum, oyik = 0, which is the wave equation
(same as in electrodynamics - cf. equation (1.46-47) in §1.5), the solution of which are waves propagating at the speed of light, in this case gravitational
waves *).
*) The existence of gravitational
waves is not a specific consequence of only the general theory of
relativity. Gravitational waves must exist within each relativistic
theories of gravity (as a consequence of the finite velocity of
disturbance propagation in the gravitational field); only some of
their properties may be different.
The simplest solution of
linearized gravitational equations in vacuum
| y lm = Re (A lm . e i. k r x r ) | (2.66) |
describes a monochromatic plane wave
with amplitude Alm and wave vector kr . From equations (2.54) and 2.53) the relations kr kr = 0, Alm km = 0 follow, according to which k is an isotropic vector perpendicular to A; gravitational waves are therefore transverse waves (oscillating
bodies only in a plane perpendicular to the direction of
propagation) with
frequency w = k° = Ö(kx2 + ky2 + kz2) propagating at the speed of light in the direction k. Harmonic solutions (2.66) form
a complete system (basis) of y
functions and any
solution of wave equations can be composed as superpositions of
these solutions.
Lorentz condition (2.53) reduce
the number of variables yik from 10 to 6 independent components.
Lorentz conditions do not change during the transformation yik ® yik + fi,
k + fk, i , where fi are four arbitrary functions
satisfying the condition fi, l l = 0 (and small enough not to violate the
condition |yik| < <1) . The quantities y can
be a suitable choice of fi also reduced to only two independent
components corresponding to the two
polarization states.
As shown below, the
component hxx oscillates the test particles in ellipses with x, y
axes, while the component hyx oscillates them in a transverse plane rotated by 45°
relative to x, y. The polarization of a gravitational wave is
called the "+" and " -
" polarizations .
For a monochromatic plane wave (2.66) the
gauge function fi can be selected so that yio = 0, yaa = 0. Then hik = yik and hio = 0, haa = 0. Such a gauge, which is very advantageous, is called TT-gauge (Transversal Traceless
calibration) *). In this TT-gauge, the components of the
curvature tensor have a very simple connection with the
components hik :
| Raobo = Roboa = - Raoob = - Roabo = - (1/2) hab,oo = - (1/2c2).¶2hab/¶t2 . | (2.67) |
*) The procedure of gauge
transformation in field theory is generally discussed in
§B.6, passage "Calibration - gauge
- transformation; calibration - gauge - field".
If a plane wave propagates in the direction of the X
axis, it is described by a tensor
| h ik = | | | 0 | 0 | 0 | 0 | | | . |
| | | 0 | 0 | 0 | 0 | | | ||
| | | 0 | 0 | h yy | h zz | | | ||
| | | 0 | 0 | h yz | -h yy | | |
Nonzero are therefore only two components hik :
hyy = - hzz = Re ( A+ .e-iw(t-x)) , hyz = - hzy = Re ( A´ . e-iw(t-x)) .
Note the symmetry properties of the plane gravitational wave when
rotated around the propagation axis. During the transition to the
new coordinate system S', twisted around the axis of propagation
of gravitational waves Z by the angle J, ie during the transformation t' = t, x' = x.cos J + y.sin J , y'
= y.cos J -x.sin J , z' = z, the
unit vectors of the gravitational wave polarization are transformed according to the
relation e + = e+ cos 2J + e´ .cos 2J , e'´ = -e+ sin 2J + e´ cos 2J.
The definition of classical spin is as follows: A plane wave y has spin s if, when rotated by an angle J around the propagation direction, it
transforms according to the law y' = e i s.J.y
- in other words it
remains invariant when rotated by an angle of 2p/s around the propagation axis. This
symmetry is closely related to the spin
of the quanta, of which, from the point of view of
quantum field theory, the respective wave consists. For
gravitational waves, therefore, this invariance angle is equal to 180°,
so that the gravitational waves have spin
s = 2 *).
This spin s = 2 should therefore have a quantum of gravitational
waves, so far hypothetical gravitons (see
below) .
*) The polarization vectors
of the electromagnetic wave transform when rotated by an angle J around
the direction of propagation: ex = excosJ + eysinJ, ey = eycosJ - exsinJ - electromagnetic waves have spin
s = 1 , are symmetrical
about a 360° rotation around the propagation direction.
Gravitons
- a quantum of gravitational waves?
According to the
concept of quantum physics, each energy should radiate not
continuously, but in quantums. The well-known and experimentally proven
quantum of electromagnetic waves are photons (see "Particle-wave dualism").
Although a complete quantum theory of gravity has not yet been
developed, the analogous application of the quantum model to
gravitational waves has led to the idea of the graviton: a hypothetical quantum of
gravitational radiation -
elementary particles mediating gravitational force in quantum
field theory. The graviton is expected to be a particle with zero
rest mass (the gravitational interaction has an unlimited range)
and will be a boson with spin s = 2 (related to the quadrupole
character of gravitational radiation discussed above); the
electric charge of the graviton is,
of course, zero (or irelevant).
How the graviton arises in the quantum theory of gravity is
discussed in §B.5 "Quantization of the Gravitational
Field".
From the point of view of the physical
analysis of gravitational waves in universe (perhaps with the
exception of the cosmology of the very early universe and unitary
field theories), gravitons
are pointless. They would only occur at very
high frequencies of
gravitational waves of the order of
gigahertz and higher (a kind of "gravitational
gamma radiation").
Such gravitational waves do not arise anywhere in the universe known to us.
Gravitons will perhaps remain permanently only hypothetical
or model
particles, the direct or
indirect demonstration and detection of which is unlikely
in the foreseeable future (for hypothetical and model particles in
elementary particle physics, see the passage "Hypothetical and model particles")... In our treatise on gravitational waves
we will therefore not consider them.
"
Gravitationally charged " gravitational
waves
Within the linearized theory of gravity, gravitational waves are
completely analogous to electromagnetic waves in classical
electrodynamics. In reality, however, there must be the important
difference between electricity and gravity, which was already
mentioned at the beginning of §2.5 "Einstein's
equation of the gravitational field". If an electromagnetic
wave passes through an area of space in which an electric field
acts, there is no effect on the wave through that field; similarly,
when the two electromagnetic waves meet,
they pass "one
over the other" without interfering
with each other and will continue
to move, as if the second wave was not. In
other words, electromagnetic waves are electrically
neutral (uncharged).
Gravitational waves, however, are
not gravitationally neutral: they transfer energy (~ mass), and are
therefore both influenced
by the gravitational field through which they pass, on the other hand, they (co-) acts as a another
source of gravity. This is due to the versatility
of gravity. It
can be said that gravitational waves are "gravitationally
charged", they themselves cause
gravity! Below it will be quantified by the so-called Isaacson
tensor of energy-momentum of gravitational waves. A hypothetical extreme consequence of this is the model
of the gravitational geone (§B.3
"Wheeler's geometrodynamics. Gravity and
topology."), or even"gravitational-wave" black hole
created by the collapse of massive gravitational waves (mentioned in §4.5 "Black hole has
no hair", passage "Uniformity
of black holes") .
Locally (in not very large areas) we can
consider gravitational waves as a commotion caused by some uneven motion of
matter (eg orbiting, binary supernova, non-spherical
gravitational collapse, etc. - see the
section "Sources of gravitational waves" below),
propagating in plane space-time and it is not necessary to take
into account the interaction with the total curvature space-time
growth and nonlinear interactions of waves with each other.
Globally, however, the curvature of spacetime caused by the
distribution of other matter (such as stars and galaxies) will
affect the propagation of gravitational waves - it will cause a
frequency shift and change the direction of propagation. For this global
curvature while also contributing the energy carried by waves
themselves (see below). Thus, when propagating gravitational
waves, characteristic nonlinear
effects
will arise [58], eg two gravitational waves will scatter each
other.
So let's investigate gravitational waves in general curved spacetime. In order to be able to talk about gravitational waves at all, we must be able to distinguish the rippling part of the curvature caused by gravitational waves from the global curvature of the "background" caused by other influences (the distribution of material bodies). This separation of the global curvature of spacetime from the local fluctuations of the waves is possible in cases where the mean wavelength l is much smaller than the characteristic radius of curvature R of the spacetime against which the waves propagate :
| l << R . | (2.69) |
Similarly, we can
distinguish the global shape of the Earth from the local
unevenness of the terrain, or the shape of an orange from
the small local unevenness of its surface. The local curvature of
the wave can thereby be significantly larger than the global
curvature of spacetime (distinguishing the background from the waves
is made possible not by the difference in the value
of the curvature,
but by the differences in the scales at which the
curvature changes) *).
*) But as we will see below,
the gravitational waves themselves cause, according to Einstein's
equations, a global curvature of space-time proportional to A/l.
Therefore, in order to satisfy the basic condition of the
shortwave approximation (2.69), the amplitude A of
the gravitational waves must also be
small enough.
Spacetime satisfying condition (2.69) can then be analyzed both in terms of small scales ("local approach") and in terms of global properties of spacetime. This approximation is called the shortwave approximation and the corresponding method of gravitational wave analysis Isaacson's formalism [140]. The metric tensor (field potentials) can then be re-writen in form
| g ik = g ikglob + h ik , | (2.70) |
where gikglob is a global space-time metric of background against which the waves hik propagate. Similarly, the curvature tensor Rik can be decomposed in series according to the small dimensionless parameter l/R << 1 :
| R ik = R ik glob + R(1) ik + R(2) ik ) + F [ l/R)3 ] , | (2.71) |
where Rglob is the global curvature of the background (monotonic over a range of multiple wavelengths).
| Rik(1) = 1/2 (-h;ik - hik;ll +hlk;il+ hli;kl) | (2.72) |
is the undulating part of the curvature linear in l/R and
| Rik(2) = (1/2) [1/2 hlm;i hlm;k + hlm(hlm;ik + hik;lm - hli;km - hlk;im) + hkl;m(hli;m - hmi;l) - (hlm;m - ...... no longer fit on line - will come to add... | (2.73) |
is the part of the curvature tensor quadratic in l/R. Triggering and raising indices, as well as covariant derivation ";" is performed everywhere according to the metric gikglob.
The general equations of the field in vacuum Rik = 0 can then be divided into parts and analyzed from two points of view :
a) Local
access
At small scales (in areas comparable to the
wavelength l), where the global curvature of
space is not directly applied, the linear part R(1)ik induced by
the waves must be equal to zero
| R (1) ik = 0 . | (2.74) |
With the help of the quantities yik = def hik - (1/2) h gik glob, by choosing a suitable gauge in which yk i; k = 0 and by omitting members of higher orders, this equation can be rewritten in the form
| y ik; l l + 2.R glob likm y lm = 0 . | (2.74 ') |
Equation (2.74) is therefore the equation of the propagation of gravitational waves - the generalization of the wave equation (2.54) to curved spacetime.
From equation (2.74) follows the basic laws of propagation of gravitational waves in curved spacetime, analogous to the "geometric optics" of electromagnetic waves [271], [181 ] :
Thus, optical effects in GTR, such as redshift or curvature of rays in a gravitational field, also apply to gravitational waves.

Fig.2.9. In the Isaacson shortwave approximation, the global
curvature of spacetime ("background") can be
distinguished from the local fluctuations of gravitational waves
if the wavelength is much smaller than the characteristic radius
of curvature of spacetime. This separation is performed by
averaging over a region of several wavelengths using a suitable
standard weighting function W(z) converging to zero with
increasing distance.
b) Global
approach
In the global approach, we perform an averaging
of "< >" all quantities over an area of
dimensions of several wavelengths, to separate the global curvature
of spacetime from local fluctuations in waves. All the structure
of the fluctuating curvature caused by gravitational waves is
smoothed during this averaging - <R(1)
ik>
= 0 - while the global curvature of spacetime is practically
unchanged: <Rikglob > @ Rikglob. Appropriate standard weight functions
converging to zero with increasing distance (with
number of wavelengths)
can be used for averaging for number of wavelengths, and
parallel transmission to the investigated site along the
appropriate geodesy in the metric gikglob [140] - see Fig.2.9. The field
equations will then sound Rikglob + <Rik(2) )> = 0, which can be adjusted
to the form of Einstein's equations
| Gikglob
º Rikglob - 1/2 Rglob
gikglob = |
(2.75) |
where the source on the right side
| Tikwaves = - (c4/8pG) [<Rik(2)> - 1/2 gikglob. <R(2)>] | (2.76) |
is the so-called Isaacson's tensor of "effective
spread" energy-momentum of gravitational waves *).
*) How the source of the
global gravitational field appears on the right side (2.75) of
the global gravitational field even in "empty" space
without material sources, is
somewhat analogous to how the Maxwell shear
current appears even in a vacuum
without currents for a non-stationary electromagnetic field, exciting the magnetic field as well as the
current of real electric charges (compare with §1.5,
equation (1.34)).
Equation (2.75) describes how gravitational waves curve space-time globally as they propagate. Thus, Tikwave we can
interpreted as a tensor
of energy-momentum of gravitational waves in global surrounding space-time
(it is a tensor only in global geometry gikglob, not
in complete metric gik = gikglob + hik !), for
which equations (2.75) follow common the laws of conservation of Twavesik;
k = 0. The
Isaacson tensor plays an important role in the correct
understanding of the specific nature of gravitational
energy, to
which we return in the following §2.8 "Specific
properties of gravitational energy".
Note: The remaining members of higher orders in
equation Rik = 0 describes the above-mentioned nonlinear
"corrections" and effects, such as distortion of the
waveform and the interaction of the waves with each other (wave
scattering on the wave, etc.).
The fundamental issues of gravitational
wave energy transfer will also be discussed in more
detail in the §2.8, in the context of general aspects of
gravitational energy. In this §2.7, we focus on the method of origin (generation) of gravitational waves and
on the possibilities of their detection.
Gravitational waves
propagation
In the vacuum of cosmic space, gravitational waves propagate in a
completely analogous way to electromagnetic waves in a vacuum. In
plane spacetime with the Minkowski metric, it propagates
rectilinearly at the speed of light in a vacuum, according to the
universal wave equation. Graphically, wave propagation
is represented using a wavefront, which is a geometric location
of points in space that oscillate with the same phase during the
wave. For waves from a point or spherically symmetric source,
this is a spherical wavefront, the points of which
lie on the spherical surface. The perpendicular to the wavefront
indicates the direction of wave propagation.
In curved
spacetime,
gravitational waves propagate along zero (isotropic) geodesics (2.5b), again analogous to
electromagnetic waves: gravity bends - curves the direction of propagation of
gravitational waves. Various "optical" effects arise
here, including the possibility of gravitational
lensing (for light described in §4.3, passage "Gravitational
lensing. Black hole optics.") and the spectral
shift of the
frequency of gravitational waves. Due to the weakness of
gravitational waves and the difficulty of their detection,
however, these interesting effects will probably not be observed
in the foreseeable future.
During the
propagation of gravitational waves through a material-substance
medium there is a mechanical oscillation of the particles of
this environment, which in general can lead to the absorption
of gravitational waves. However, due to the very weak
gravitational interaction with matter, this absorption of
gravitational waves is normally very
small. By
analogy with light, we could also think about the slowing down of the speed of gravitational waves in a material
medium, which could cause the "refraction" of
gravitational waves - hypothetically about the
"gravitational index of refraction" in the material
environment. However, this has nothing to do with the common
optical index of refraction and is practically exactly equal to 1
for all common environments (the difference
compared to vacuum is not measurable). Only in an environment with enormous
density, such as in neutron stars, would there be a more
pronounced interaction between gravitational waves and matter,
which could slow down the propagation speed of gravitational
waves and generate a non-negligible index of refraction..?..
A common general property of wave propagation -
radiation - is the fact that the corresponding waves detach
from the source and carry with them part of its energy,
momentum and angular momentum into space, even without the
presence of any distant "receiver" of these waves. The
waves themselves (their fields) have energy. This is the
energy of the gravitational field (whose special
features are discussed in §2.8 "Specific
properties of gravitational energy").
Gravitational
waves emission and sources
Under what circumstances do gravitational waves arise? By analogy
with electrodynamics, it can be expected that gravitational waves
will be emitted during accelerated (uneven) motions of
bodies, when the
excited gravitational field changes over time - when the position
or shape of material objects changes unevenly.
The most common type of radiation
in electrodynamics is the radiation of an electric
dipole, the
intensity of which is given by the second derivative of the
dipole moment d = n =
1S
N q n . r n systems of N electric charges qn , located in positions rn , according to time (§1.5,
relation (1.61)). In gravity, the role of the electric dipole
moment is played by the dipole moment d = Smn
. rn mass distribution in a system of
N particles mn . The first time derivative of
this dipole moment d .
= S m n . r
n.
º p is equal to the total momentum p system, so its second derivative
will be equal to zero due to the law of conservation of momentum.
It turns out that dipole gravitational radiation cannot exist,
gravitational radiation must have at least
a quadrupole character *).
*) This is related to the
theorem of classical radiation theory [166], according to which the lowest
"multipolarity" of radiation that can be emitted is
greater than or equal to the classical spin of a given field. This spin is given by the
degree of symmetry in the plane wave: spin s = 360°/(angle
of rotation around the axis of propagation maintaining symmetry),
so that for electromagnetic field with spin s = 1 the radiation
is at least dipole, for gravitational field with spin s = 2 is at
least quadrupole.
Thus, we can generally consider as a
source of gravitational waves any physical system with a time-varying mass distribution r(t, xa), in which the quadrupole moment of the spatial distribution of matter also
changes over time - when matter-energy moves in an accelerated non-spherical manner. Temporal changes in the
distribution of matter cause corresponding temporal changes in
the geometry of the surrounding spacetime - they "vibrate"
the curvature of spacetime. These waves spacetime curvature -
i.e. gravitational waves - detach
from the source system and propagate into the surrounding space,
wherein carrying away part of the kinetic energy of the moving
matter in the source system.
To determine the strength -
intensity - amplitude of
gravitational waves radiated by a certain physical system, we
use the general solution of linearized gravitational equations in
Lorentz gauge in the form of retarded potentials
| formula (2.55) is presented here again for clarity |
similarly in
electrodynamics, where R = Ö[a = 1S3 (xa - x'a)2] is the distance from individual places x'a the source system to the investigated
point xa (according to Fig.2.8). If the mass-energy distribution
(components of the energy-impulse tensor Tik ) is time-varying, it will excite the time-varying
potentials yik of the gravitational field, which can describe
the radiated gravitational waves.
If the speed of movements in the investigated source system will
be small in comparison with c and the gravitational contribution to the
total mass-energy will be small, we can express the
energy-momentum tensor as using the mass density r and the four-velocity ui
: Tik = r . ui uk and using the conservation laws (2.90) of
energy-momentum in the source introduce a tensor of quadrupole mass distribution in
the source Kab = Vn Too(t,x) xa xb dV = c2 Vn r(t,x) xa xb dV.
In the limit of a weak field (and in the so-called
TT-gauge-calibration) then the general relation (2.55) can be
expressed using the important quadrupole
formula :
| hab(t,R) = [(2G/c4). ..Kab(t-R/c)] / R , | (2.77a) |
expressing the "amplitude" of a gravitational wave - fluctuation of the metric hab(t, r) at time t and at a distance R from the source with a time-varying quadrupole moment tensor Kab mass distribution in the source :
| K ab (t) = ò r (t, x) · (3 x a x b - d ab x g x g ) dV . | (2.78) |
The amplitude of the waves thus decreases with
the distance from the source as 1/r and is given by the second
time derivative ..Kab
quadrupole moment of mass-energy distribution in the source
system, with retardation R/c (according to
Fig.2.8).
The quadrupole formula (2.77b) is derived
within linearized field equations with source T ik , into whose
solution (2.55) or (2.65) in the form of retarded potentials the
quadrupole moment (2.78) of mass distribution in the source
system is implemented in the above TT-gauge (see
the passage "Gravitational radiation of the
island system" in §2.8 "Specific
properties of gravitational energy") . The quadrupole formula
was first derived by A.Einstein in 1916-18.
To calculate the energy radiated by such a system in the form of
gravitational waves (ie the intensity of gravitational waves),
the methods outlined in the following §2.8 are used. If the
motion of matter in a source is slow compared to the speed of
light, the source is small compared to the length of the emitted
waves and the field in it is weak enough, the instantaneous
amount of energy gravitationally emitted by the system per unit
time - "gravitational wave
power" - is given again by quadrupole
formula (derived in the following
§2.8 "Specific properties of gravitational energy", passage "Gravitational radiation of the
island system") :
| d E / dt = - (G / 45.c 5 ) ... K ab 2 , | (2.77b) |
where the dots mean derivatives according to time t - this is the 3rd derivative; Kab2 = Kab Kab , adds over a, b = 1,2,3. In astronomical terminology, the quadrupole formula (2.77b) expresses a kind of "gravitational-wave luminosity" of the source system. The intensity of radiation in the direction of the (unit) vector n to the element of the spatial angle dW is given by the relation
| (2.79) |
Equations (2.77) and
(2.79), in agreement with the above arguments, show that only the quadrupole
moment of the source is essential for the emission of
gravitational waves, which must change with time, while the
monopole and dipole moment do not contribute to the radiation.
The coefficient
G/(45.c5)
shows that the radiation of energy by gravitational waves is a 5th-order
effect with respect to 1/c, which, together with the small
value of the gravitational constant G, leads to a very
small intensity of this effect under all common
conditions, except for tight orbit and merging black holes or
neutron stars (discussed below in "Sources of gravitational waves in space").
Clasificattion of gravitational wave
sources
Sources of gravitational wave can be classified from different
points of view. According to the dimensions and location, we can
distinguish between laboratory
(terrestrial) and astrophysical (space) sources . In terms of the time course of
the motion of matter in the source (and thus the frequency
spectrum of the emitted waves), we can divide the sources of
gravitational waves into two types :
However, some
astrophysical sources that were originally periodic may become
aperiodic over time. E.g. a body orbiting in an almost circular
distant path around a black hole will be for a long time
practically a periodic source of (weak) gravitational waves until
it falls to a limit stable orbit ( §4.3 passage
"Emission of gravitational waves when moving in a
black hole field"). Then it is quickly absorbed by the black
hole, emitting an intense flash of gravitational radiation - it
becomes an aperiodic source. However, these phenomena most often
occur in close binary stars (see below "Sources of
gravitational waves in space", Fig.4.13-GW) .
The simplest laboratory source of gravitational waves is a rod rotating
around the perpendicular axis at an angular velocity w (Fig.2.10a). According to Equation (2.77),
such a rotating rod will gravitationally radiate energy
| d E / dt = - (32.G / 5.c 5 ) I 2 w 6 , | (2.80) |
where I is the moment of inertia with respect to the respective axis of rotation. How little energy is radiated in this way can be illustrated by the example of a steel rod 1 m in diameter and 20 m long (total weight almost 500 tons!) rotating at a maximum speed of about 4 revolutions per second (limited material strength), when gravitationally radiating energy dE/dt @ 2.2.10-29 W; such a neglibigle value is well below the current possibilities to register it in any way. It can be seen from this that laboratory gravitational wave generators (at least in terms of mechanical-based sources) are not yet applicable to gravitational wave experiments.
Sources of gravitational waves in
space
A more favorable situation can be expected in some space objects, where incomparably heavier masses come
into play than in laboratory generators. An isolated star is able
to emit gravitational waves either when it pulsates non-radially, or when
it rotates without being axially symmetrical. In the case of a
rotating star at an angular velocity w , the formula for the gravitational
radiation energy is based on the formula ( 2.77)
| d E / dt = - (288.G / 45.c 5 ) I 2 e 2 w 6 , | (2.81) |
where I is the moment of inertia and e = (a-b)/Öab expresses the deviation from axial
symmetry (a, b are the principal axes in the
equatorial plane). According to the relevant model, the
gravitational radiation generated by this mechanism could cause
the deceleration of the PSR 0532 pulsar in the Crab Nebula (pulsar has a period of about 33 ms, deceleration rate
1.3.10-5 s./year, radiated gravitational wave power should be
about 1031
W [ 89]) .
Note: Supernova is only a weak source of
gravitational waves.
In §4.2, the section "Supernova
explosion. Neutron star. Pulsars." it is shown that the supernova
explosion is the most catastrophic
phenomenon in the universe, emitting enormous electromagnetic and
corpuscular energy. However, in terms of gravitational wave
emission, a supernova is usually only a relatively weak
source of gravitational wave pulse. The reason is that the
collapse of the nucleus and the subsequent explosion of the
supernova usually takes place almost symmetrically,
without significant gravitational radiation. However, if this
process were to proceed asymmetrically (perhaps
due to a previous collision of the original stars in the binary
system..?..) , possible detection and
analysis of generated gravitational waves could yield valuable
information (otherwise unattainable) about the processes in the infernal hearth of the
"heart" of the supernova ...
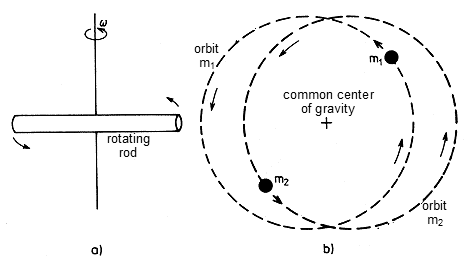 |
Fig.2.10. a) Rotating rod as a (laboratory)
source of gravitational waves. |
Binary
stellar systems -
cardinal sources of gravitational waves
The most important sources of gravitational waves are, however,
tight binary systems of compact
astronomical objects - neutron stars and
black holes. A
significant portion (more than half) of stars are part of binary or multiple systems. Individual stars in
these binary systems will sooner or later deplete their
thermonuclear fuel and reach the final
stages of
their evolution (§4.2 "Final
Stages of Stellar Evolution. Gravitational Collapse. Black Hole
Formation.") - and
according to their remainig mass, they become white dwarfs, or collapse into
neutron stars or black holes. These compact
objects
will then continue to orbit each other, creating
gravitational waves.
If we have two bodies with masses
m1 and m2, which are gravitationally
attracted (according to Newton's law) and orbit in circular orbits of
radius r around a common center of gravity at
angular velocity w (Fig.2.10b), this system will be
according to quadrupole relation (2.77) radiate energy
| d E / dt = - (32.G / 5.c 5 ) [ m 1 . m 2 / (m 1 + m 2 ) ] 2 r -4 w 6 , | (2.82a) |
in the form of almost
monochromatic gravitational waves with frequency f = 2p/w (so far we will
not consider the acceleration of rotation due to the approach of
both bodies, see below).
When orbiting along an elliptical orbit with a major
half-axis a and an eccentricity e , the
gravitationally radiated energy is given by a more complex
relation [285]
| d E / dt = - (32.G / 5.c 5 ) [m 1 2 .m 2 2 / (m 1 + m 2 )] a -5 . f (e) , |
where the function f(e) = (1 + (73/24) e2 + (37/96) e4 ). (1 - e2 )-7/2 captures the
growing influence of eccentricity on radiation intensity. In
elliptical motion, the emitted gravitational waves contain not
only the second harmonic frequency of the orbital motion (as in
circular orbital motion), but also higher harmonics. The
intensity of the radiation is highest in the
"perihelion" where the two bodies are closest and the
acceleration is greatest. This effect leads to a gradual decrease
in eccentricity - the elliptical motion slowly changes
to circular; overall, the orbital period is shortened.
Taking away of the
energy of the orbital motion by gravitational waves leads to
mutual approaching orbiting bodies, shortening
the orbital period, increasing the speed of circulation and increasing
the frequency and intensity of gravitational waves. This
is captured in Fig.4.13-GW (it is a
modification of Fig.4.13 from §4.3 passage "Emission
of gravitational waves when moving in the field of a black hole") :
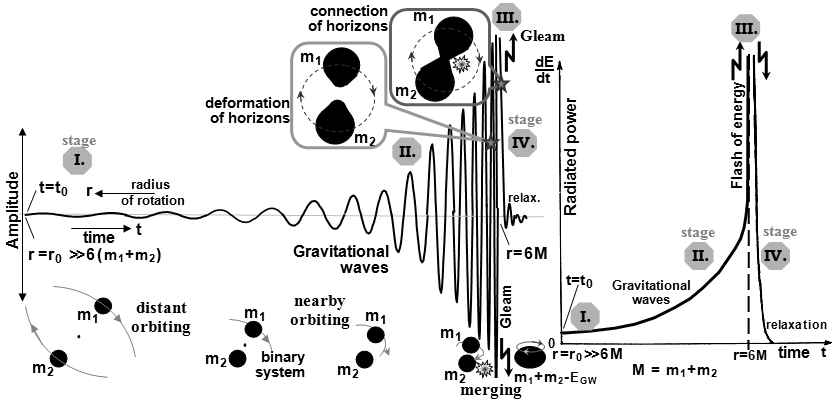 |
| Fig.4.13-GW.
Time course of amplitude, frequency and intensity of
gravitational radiation of a binary system of two compact
bodies m1 and m2 orbiting a
common center of gravity. Bodies that begin their orbit at time t = t0 on some large radius r0 descend very slowly in a spiral and continuously emit gravitational waves, initially weak (stage I). Even with tight binary systems, it is a process that lasts hundreds of thousands and millions of years. As they approach, the intensity and frequency of the radiation continues to increase. After reaching the circulation distance of several tens of gravitational radii, there is an avalanche-like increase in the intensity and frequency of gravitational waves (stage II). After reaching the limit of innermost stable orbit, the bodies fuse rapidly, sending a short intense flash of gravitational waves ( stage III ). In the upper part of the figure, enlarged sections from the last few cycles are symbolically drawn, during which both horizons are deformed and finally they are connected to the deformed horizon of the resulting black hole. The resulting black hole m1 + m2 is rotating and rapidly relaxes to the stationary axially symmetrical configuration of the Kerr black hole (stage IV) by radiating damped gravitational waves. |
The reduction of the radius of circulation r of a binary system of bodies m1 and m2 with time t due to gravitational radiation is (in a linearized approximation) given by the relation
| dr / dt = - (64.G 3 /5.c 5 ) [ m 1 . m 2 . (m 1 + m 2 ) ] / r 3 . | (2.82b) |
The time t r®0 until the fusion of the two bodies of the binary system *), currently circulating at a distance R , is then comes out :
| t r ® 0 @ ( 5.c 5 /256.G 3 ) . R 4 / [ m 1 . m 2 . (m 1 + m 2 ) ] . | (2.82c) |
Using the current orbital period T of the binary system, this can be expressed by the relation :
| t r®0 @ (5.c5/256) . (T/2p)8/3/[G5/3.(m1.m2)/(m1+m2)3] » 107[year]. T[hour.]8/3.{[(m1.m2)3/5/(m1+m2)1/5]/M¤}-5/3 . | (2.82d) |
For conventional binary systems, this fusion
time is very long (on the order of billions
of years or more), but for tight binary
systems of compact objects, it can be relatively short from an
astronomical point of view (discussed
below).
*) Note: This
would be the expected fusion time of idealized material
points m1 and m2 when the distance r = 0 is reached; for real bodies of
finite dimensions, this fusion time is somewhat shorter.
For the time increase of the
frequency df/dt of emitted gravitational waves in the
mutual circulation of two bodies with masses m1 and m2 in circular orbits (around the
common center of gravity) in the
post-Newtonian approximation (to the order
O[(G.m/r.c2)]) of the quadrupole formula [...] the relation can be derived :
| df/dt @
(m1.m2)/(m1+m2)2/5.G-3/5.c-12/5.(96/5)p8/3.f11/3 , which
can be adjusted to the form : (m1.m2)3/5/(m1+m2)1/5 @ (c3/G). [(5/96)p-8/3. f -11/3.(df/dt)]3/5 . |
(2.82e) |
The advantage of relations (2.82d, e) is that
they do not explicitly contain parameters of the orbit (radii r),
which are astronomically mostly unknown. By analyzing the
relationship between the frequency f of the received
gravitational waves and its time increase df/dt, it is possible
to determine the parameter of the proportion of masses M = (m1 .m2 )3/5 / (m1 + m2)1/5 *) of radiating bodies. From it,
in principle, the total weight m1 + m2 of the system can be determined and
further detailed computer analysis (modeling
according to "nonlinearized" general theory of
relativity and fitting with the measured course of the signal
from the gravitational wave) it is possible to determine in principle
the masses of individual components, the radiated power of
gravitational waves, or even the rotational
angular momentum.
.....
*) This mass parameter M = (m1 . m2)3/5 / (m1 + m2)1/5 in gravity-wave slang, it is sometimes called the chirp
mass - "chirping matter" because
the rapid increase in frequency just before the fusion of the two
compact bodies resembles a bird chirp. The value of this mass
parameter M is approximately equal to the geometric mean of the
masses of the orbiting bodies m1 and m2.
In general, the most
important permanent (periodic or
quasi-periodic) sources of gravitational
waves in the universe are massive bodies that orbit
each other (orbit around a common
center of gravity). The orbing planets,
such as the Earth around the Sun, emit only faint gravitational
waves (in the order of fractions or units of Watts). It is
different when compact gravitationally collapsed objects
orbit each other - neutron stars and especially black holes. Each
such body creates a deep gravitational potential pit around
itself - a large curvature of spacetime. As these objects revolve
around each other, the periodic motion of potential pits causes
strong periodic changes in curvature - a kind of
"furrow" in space-time, which, as the gravitational
waves, detaches from the source binary system
and propagates into the surrounding space.
Gravitational waves carry the kinetic energy of rotation
- as they fly into outer space, according to the law of action
and reaction, they "push" back (in the opposite
direction) on orbiting bodies, braking them and forcing them to
move closer together, with a higher orbital speed. They are
slowly approaching each other in a spiral (phases I
and II in Fig.4.13-GW). Half of the released
gravitational energy is carried away by the waves, the other half
increases the orbital velocity (according
to the Virial Act ).
Massive sources and
flashes of gravitational waves
As long as the bodies
orbit the common center of gravity at great distances (due to
their gravitational radius), and thus with a long period, the
gravitational radiation according to Equation (2.82) is very
weak. E.g. in the solar system during rotation of Jupiter
generate gravitational wave carrying scant about 5.10-2 W, during its orbiting the Earth
gravity emits only about 20 W. For distant (visual) binary stars, the flux of gravitational radiation is also relatively
low (~103 -107 W); in the case of tight
(eclipsing) binary stars, however, the gravitationally radiated
power is already ~1020 -1025 W (even
that is quite small for astronomical conditions...).
However, truly massive
sources of gravitational waves may be a binary
system of compact gravitationally collapsed objects such as
neutron stars or black holes, orbiting close
to each other, only a few dozen gravitational radii away *), - the possibility of their occurrence see §4.8 passage
"Binary
gravitationally bound black hole systems - collisions and fusion
of black holes" - phase II in Fig.4.13-GW. A
hypothetical binary system of two neutron stars or black holes
with masses of the Sun orbiting at a distance of 104
km would gravitationally emit about 3.1036 W, with an orbital radius of 100
km the radiated power would even be about 3.1046 W! Such objects would have been only quasiperiodic with a lifetime (the time of falling along the spiral of one body to
another - by
relation 2.82c) from several years to fractions of a second.
During the actual extinction of the binary
system (phase III in Fig.4.13-GW), a gigantic flash of
gravitational waves with a frequency of tens to hundreds
of Hz releases energy reaching a power of up to 1047 W; for a few
milliseconds, the two collapsing components "shine by
gravity" as intensely as the entire observed universe in the
electromagnetic field! Gravitational waves will carry about 5% of
the total weight of both merging compact objects !
*) Mutual
convergence of compact bodies circulation
The problem, however, is how do these circulating compact bodies get
so close to each other ? In conventional binary systems,
the orbital distance is at least 106 km (close "spectrometric" binary stars),
which is more than 100,000 gravitational radii. Should such a
massive star collapsed into neutron stars or black holes at their
circulation would radiate a relatively weak gravitational waves
about 1025 W.
They would reach the stage of close circulation by gravitational
radiation in a few million years (see formula above (2.82c)).
However, most binary stars are much more distant (...-...) - due
to gravitational radiation, they would not reach the stage of
close orbit and fusion even during the entire existence of the
universe! There are two possible mechanisms that compact objects
could "converge" in the foreseeable
future :
¨ Friction
in a large and sufficiently dense cloud of gas
surrounding a binary system. If more gas from the envelope
of collapsing stars remains inside the binary system, dissipative
convergence can occur over several million years. However, the tight binary systems created by the
collapse of the oldest stars of the 1st generation, during the
more than 10 billion years of the universe, could converge to a
phase of intense gravitational radiation and fusion, even when
there was almost no gas environment left.
¨ Gravitational
interactions with surrounding stars, unless the binary
system is isolated, but is located in an environment with a
denser concentration of stars, such as globular clusters. To a
nearby star approaching, the binary system can transmit
kinetic energy through the dynamics of its orbit ,
bringing the two components closer together.
This could also happen in the case of a multiple system.
In the final stages due
to the close approach of both black holes, due to strong mutual
gravity, both horizons deform strongly, "they
go agains each other" *) and vibrate
wildly during rapid orbit, with unusually strong
emissions of gravitational waves. Then the two horizons
are interconnected into one horizon of the resulting
black hole - stage III, during which there is a massive
"explosion of gravitational waves". This
resulting horizon is rotating and initially
strongly deformed. As it rotates, it emits
damped, rapidly fading gravitational waves, thereby
"relaxing" to the stationary configuration of Kerr's
axially symmetric rotating black hole (phase IV in
Fig.4.13-GW) - "hair loss",
gravitational waves carry away "hair asymmetry" - §4.5
"Theorem" black hole has no hair".
*) In the direction of the junction of the circulating black
holes, "bumps" initially appear indistinct and round on
their horizons, but when approached more closely, they are
already sharp protrusions. These protrusions then connect the two
horizons, momentarily in the shape of a rotating "8 -
eight". However, due to the massive emission of
gravitational waves, this shape merges into the ellipsoidal
horizon of the resulting Kerr axially symmetrically rotating
black hole in a few tenths of a second (at
unit weights or tens of M ¤ ). Gravitational radiation then
stops forever...
To summarize, the
dynamics of the orbit of a binary system of compact objects and
the emission of gravitational waves can be divided into 4 stages
according to Fig.4.13-GW :
I. Distant
circulating along almost Kepler orbits, with weak
gravitational radiation and very slow spiral
approach. The duration of this stage I depends (according to formulas (2.82)) on
the initial distance of orbit, it can last several billion years.
II. After approaching
a distance of several tens of gravitational radii, the intensity
of gravitational radiation increases greatly, which leads to a rapid
spiral approach of both bodies, with the emission of
increasingly massive gravitational waves with rapidly
rising frequencies, from units to several hundred Hz.
The final part of this stage II for compact stellar mass
objects lasts only on the order of seconds.
In the jargon of hunters gravitational
waves, this phase is sometimes called a "chirp",
because the rapid increase in frequency just before the fusion of
the two compact objects resembles a bird chirp. The dynamics of
growth of the amplitude and frequency of gravitational waves is
characteristic here for the masses of converging black holes.
III. The
merging (fusion, collision) of both compact
objects into one resulting rotating black hole, emitting a
gigantic flash of gravitational waves, lasting
only milliseconds.
IV. Relaxation
the resulting black hole, initially strongly deformed,
to a stationary axially symmetrical configuration of the Kerr
rotating black hole, with a rapid attenuated reverberation
of gravitational radiation in fractions of a second. Then already
no more gravitational waves are emitted.
The dynamics of this reverberation of gravitational waves
(reminiscent of a kind of "bell reverberation")
is characteristic for the mass and speed of rotation (angular
momentum) of the resulting black hole.
If the collision and
fusion of black holes takes place in a
"clean" environment without gases and other bodies, only
gravitational waves are emitted. However, when merging
in the binary system of neutron stars, in
addition to strong gravitational waves, intense emission
of electromagnetic waves - gamma, X-rays, visible light,
radio waves (it is discussed in §4.8,
passage "Collisions
and fusion of neutron stars") .
Other compact objects serving as potential
sources of gravitational waves could be binary
supermassive black holes in the center of galaxies (see §4.8, section "Quasars"). According to galactic astrophysics, they could form
during galaxy collisions in situations where
galaxies penetrate each other with a small impact parameter and
at a lower mutual speed. Black holes in the center of both
galaxies can then form a bound binary system as
they "pass". As they circulate, gradually approach, and
eventually fuse these giant black holes, massive
gravitational waves of low frequencies, milliHertz and
lower, would be created... This whole final process would be far slower
than the binary black holes of stellar masses. Due to the
slowness and long term of these processes, it can be expected
that space will be filled with a flood of low-frequency
gravitational waves of various intensities and frequencies,
from many sources - the stochastic gravitational-wave
background.
The expected frequencies of gravitational
waves from tight binary astrophysical sources
are given by the mass of the components :
- Units up to hundreds of M¤ :
frequency 10Hz - 10kHz, possibility of detection by terrestrial
interferometers.
- Thousands to
millions of M¤ : frequency 0.0001Hz - 0.1Hz, detectable by space
interferometers.
- 108 to 1010 M¤ :
period of the month up to decades, possibility of detection by
monitoring changes in pulsar frequency.
An medium power source of gravitational waves can
also be the gravitational collapse of a star, if it occurs asymmetrically
(in the case of a spherical collapse, gravitational waves do not
emit - see §4.3 "Schwarzschild static black
holes"). An extreme example of such a
process is shown in Fig.4.14 in §4.4 "Rotating
and electrically charged Kerr-Newman black holes", where during the collapse
of a rotating star may occur its fragmentation and re-absorption
of individual parts, accompanied (and caused) by very
intense emission of gravitational waves. In any case strongly
nonspherical collapse stars under the gravity radius is
accompanied by a strong flash
gravitational waves to carry away a considerable part of the
total rest mass [289].
An already "finished" black
hole, when alone, does not emit gravitational waves, but if it
forms a binary or multiple system (as mentioned above) or
interacts with the surrounding matter, it can become a powerful
source of gravitational waves. If a small body of mass m
falls directly on a (non-rotating) black hole of mass M ,
the total amount of energy radiates
| D E » 0.0025 m 2 c 2 / M | (2.83) |
in the form of a "flash" of gravitational radiation with a continuous spectrum. When a body orbits a black hole in a circular path, it emits periodic gravitational waves with the total intensity given by (4.19). As a result, it constantly decreases in a spiral, the intensity and frequency of the gravitational waves increasing until the body is finally absorbed. In §4.3 (passage "Emission of gravitational waves while moving in a black hole field") and §4.4 will be shown, that the total amount of energy that can be emitted during this process by gravitational waves, makes for the non-rotating Schwarzschild black hole about 6% od rest mass falling body, while for a rotating black hole can represent up to 40% of its rest weight ! Thus we see that the unfavorable situation of excitation of gravitational waves in laboratory conditions can completely reverse for us in astrophysical scales: not only that there may be the sources of massive gravitational waves with high powers, but also the efficiency of converting rest mass to gravitational radiation can be incomporably higher than the efficiency, with which we can "benefit" from matter here on Earth, eg electricity (the efficiency of thermonuclear power plants will be only about 0.7%).
Primordial gravitational
waves
The most powerful source of "all time" gravitational
waves was undoubtedly the stormy creation
of the universe - the "big bang". Thus, in
addition to the gravitational waves of the above-mentioned
astrophysical origin, the universe can also be filled with "cosmological" or "primordial" gravitational waves
generated by inhomogeneities and turbulences of the super-dense
substance in the period around the Big Bang [288]. These gravitational waves emitted in Planck's
time, in the inflation phase (§5.5 "Microphysics and Cosmology. Inflation
Universe ") ,
or in the event of inhomogeneities, turbulence and topological
defects during symmetry breaking, would probably
have the stochastic character of some "gravitational
noise".
The primordial gravitational waves have weakened
so much during billions of years of universe expansions, that
there is probably no hope of their direct detection in the
foreseeable future; in contrast to the detection of gravitational
waves from relatively close astrophysical sources. An interesting
possibility of indirect demonstration of primordial gravitational
waves by measuring the polarization of relic microwave
radiation will be discussed below in the section "Detection of gravitational waves" (passage "Measurement of polarization of relic microwave
radiation").
Also in all high-energy microscopic
processes (with elementary particles), in principle,
gravitational waves should be emitted, but of very slight
intensity, with no hope of measurement...
Detection
of gravitational waves
So much therefore for the origin and properties of
gravitational waves. This brings us to the last point of this treatise -
the issue of gravitational wave
detection.
If we compare the situation with electrodynamics, then we have at
our disposal very strong sources of electromagnetic waves of
natural and artificial origin, which we can sensitively detect
and receive. In the field of radio waves, these are, in the
simplest case, ordinary radio antennas, in which the received signal is
generated by electromagnetic induction. Electromagnetic waves
from space are very sensitively received by radio telescopic
antennas. Visible light is effectively emitted by all heated
bodies (eg a filament of a light bulb), discharge
lamps, in the universe of a star; and our eyes are a sensitive
detector. We also have sensitive radiometers and spectrometers (Detection and spectrometry of ionizing radiation) for
shortwave X and gamma radiation. However, for gravitational
waves, we only have resources available in a very distant
universe, whose waves are naturally very
weak here
on Earth. The detection of gravitational waves - the construction
of a sufficiently sensitive "gravitational
receiver"
- is therefore an extremely delicate matter !
To better understand this issue, let us
first notice the effect of gravitational waves on the motion of
test particles. According to the principle of equivalence (and in context with what was said in §2.6) the local action of
gravitational waves on a single isolated particle does not exist.
A gravitational wave cannot be detected by a given observer who
"vibrates with her". Therefore, we must take two close or more distant test bodies A and B (Fig.2.11a) and observe the
periodic changes in the distance between them, caused by the
oscillating curvature of the space metric in the gravitational
wave. The gravitational wave causes transverse
deformations of space.
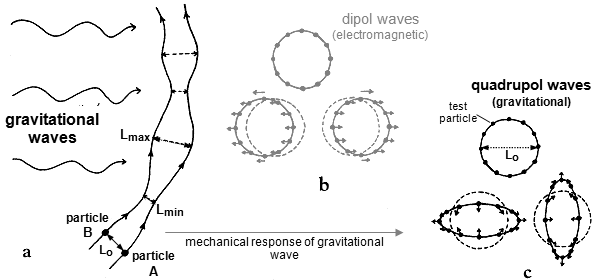
Fig.2.11. Effect of gravitational waves on test particles.
a) The world lines of two free-falling particles A
and B periodically diverge and approach due to gravitational waves.
b) For
comparison - the action of a (linearly
polarized) plane
electromagnetic wave incident perpendicular to the drawing on a
set of test charged particles placed on a circle leads to
periodic shifts of the whole circle of test particles in the
direction dependent on the polarization of the wave.
c) The
action of a plane gravitational wave incident perpendicular to a
circular arrangement of mass test particles causes periodic
deformations of this arrangement into an ellipse alternately in
two perpendicular directions given by the polarization of the
wave.
With the particles A, which we take as the reference, we connect the reference system, which will be locally inertial along the whole worldline of the particle A. The vector ei in the equation of deviation of geodesics (2.57) will then be equal to the coordinate xiB of the particle B, so
![]()
Because we work in a locally inertial Cartesian system connected to the particle A, the absolute derivatives will change into ordinary derivatives and with the accuracy of the 1st order the coordinate time t coincides with the proper time t. With respect to relation (2.67), the deviation equation takes on a simpler form
![]()
If at time t = 0 was ha b = 0 and the particles were at rest with each other, by integrating this equation we can obtain the relation
xaB(t) » xb(0) [ dab + 1/2 hab(t, xgA=0) ] ,
expressing the oscillations of the position of the particle B
with respect to A caused by the gravitational
wave. The oscillations while doing so show only those components xaB(t) which are perpendicular to
the propagation vector of the plane wave ka (gravitational waves are transverse).
Fig.2.11c shows the periodic deformation action of a plane
gravitational wave on a system of regularly (in a circle)
arranged test particles.
If the monitored test particles A
and B are not free, but interact with
non-gravitational forces, the deviation equation (2.57) must be
replaced by the equation
![]()
where Fi is nongravitational 4-force describing the interaction of particles A and B . Such a case is shown in Fig.2.12a. In practice, the force Fi always electromagnetic origin (all the powers of strength and flexibility in the body are caused by electromagnetic forces). As in the previous case, the oscillations of particles A and B can be used to detect gravitational waves. If we also include dissipative processes (viscous friction), we can imagine real bodies as composed of a series of such non-gravitational interacting material parts.
Gravitational
wave amplitude
The force of a gravitational wave can be simply
and concisely expressed by its amplitude h = DL/Lo , where DL = Lmax - Lmin is the maximum
change in the distance of two test particles, whose original
(initial) distance was Lo (Fig.2.11a). It is a dimensionless number expressing
how large a relative change in the distance of
the two test particles will be caused by the wave passing through
it. This number is then also used to characterize the sensitivity
of gravitational wave detectors.
Very roughly we can estimate the expected amplitude of the
gravitational wave from the above quadrupole formula (2.77b)...
Strength
- weakness of gravitational waves from space
To assess the chances, possibilities and methodology of detecting
gravitational waves, it is useful to estimate how strong (or unfortunately weak...) gravitational
waves can be expected to come from universe? In the passage
"Origin and properties of gravitational
waves", it was discussed above
that gravitational waves are generally very weak.
According to the calculations mentioned above in the section
"Sources of gravitational waves", as well as in §4.3, passage "Emission of gravitational waves when moving
in the field of a black hole"
and in §4.4, passage "Movement of particles in the field of a
rotating black hole", however,
with relativistic mass movements in very strong gravitational
fields of compact objects, 5% of the total mass can
radiate in the form of gravitational waves in a short
time interval (for a rotating black hole it
can hypothetically be up to 40%!). In the
astronomical vicinity of such objects, we could observe quite
strong gravitational waves!
Unfortunately, nowhere in the around *) do
we have any such strong source of gravitational waves...
The basic obstacle to successful detection is therefore the extreme
weakness of gravitational waves coming to us from space.
This is due to the vast distance of probable
strong sources of gravitational waves - thousands and millions of
light-years.
*) It is perhaps fortunate
for us ! If there were such a binary system of closely
circulating black holes near a few light-years away,
gravitational waves strong enough to come to us, that they could destabilize
the solar system !
The expected amplitudes of the gravitational
waves coming to us from the presumed sources in space are
therefore very small. The main factor
influencing a particular wave strength is the distance of
the source r in relation to its
gravitational-wave power Pgw
, ie to the amount of energy that is
transferred to the gravitational waves in a given process. The
amplitude of the wave then approximately comes out h » 3.10-22 ..? .. .P gw/r , where the source
distance r is measured in light years. If, for example, a
supernova exploded near the center of our Galaxy in such a way as
to transmit about 1% of the Sun's energy M¤.c2 to gravitational
waves, the amplitude of the gravitational waves measured here on
Earth could be estimated at h »
10-19. For gravitational waves from supernovae in nearby
galaxies, their amplitudes are estimated to be 10-19 -10-21 ; gravitational
waves from a non-spherical supernova explosion would have the
character of a pulse. During the collision and fusion of two
neutron stars or black holes in distant galaxies, we could
capture a flash of gravitational waves with increasing frequency
with an amplitude of about 10-20 -10-22. The sensitivity of current gravitational wave
detectors makes it possible to detect only these "catastrophic"
events, accompanied by a powerful
"flash" of gravitational waves; previous
"quieter" phases with "moderate"
gravitational radiation are still well below the detection
threshold.
The intensity of gravitational waves in our
environment is therefore estimated at a maximum h » 10-21, so that a rod with
a length of units of meters could vibrate to an amplitude of
about one hundred millionths of the diameter of the atomic
nucleus. With such small response values, a major obstacle to
detection can occur - quantum uncertainty relations
(see eg "Quantum Physics") *). As we will see below,
the only way to detect weak waves is to increase the
distance of the test specimens and use highly sensitive
methods of measuring position changes, especially interferometric
ones.
*) Below in the section "Interferometric
detectors of gravitational waves", Note 2: "Limitation
by quantum uncertainty relations? - can they be bypassed!", it is discussed how in interferometric detection
of gravitational waves it is possible to "overcome" the
usual quantum relations of uncertainty, or more precisely to
bypass them...
Disturbing background
As little regular signals as can be expected from gravitational
waves from outer space will usually be lost in
terrestrial detectors in the ubiquitous chaotic
"cacophony" of interfering signals -
in the background of the noise. The disturbing background in our
terrestrial conditions is formed mainly by seismic waves.
It is also noise and vibration from trucks,
trains or aircraft flights. Electronic instrument noise
and quantum noise caused by statistical
fluctuations due to quantum laws of the microworld are
also manifests in signal measurement (cf.
eg "Quantum Physics" and "Statistical Scattering
and Measurement Errors"
in the monograph "Nuclear Physics
and Ionizing Radiation Physics ). It
is the background of interfering signals, which are usually much
stronger than the useful signal, that is the basic limiting
factor in the detection of gravitational waves...
Gravitational wave detectors - direct detection
Like sources, also gravitational wave detectors can be
divided into individual types according to various aspects. As
for the basic principle of their operation, we distinguish
between mechanical detectors (measuring
the movements of bodies caused by gravitational waves) and non-
mechanical
detectors (analysis of the influence of
gravitational waves on electromagnetic fields - not yet
practically implemented). Depending on their size and location, they can also
be laboratory (terrestrial) and astronomical (space) detectors. Mechanical
gravitational wave detectors can be divided into two groups :
Gravitational wave detectors, especially terrestrial waves, should operate at least in pairs at a sufficiently large distance from each other (at least hundreds of kilometers) in coincidence mode This makes it possible to distinguish local disturbances (eg seismic or technical), manifested in only one of the detectors, from the signal of cosmic origin, which is detected simultaneously by both detectors.
Gravitational
wave resonant detectors
Let's first notice the resonant detectors. The simplest (model)
type of such a gravitational wave detector is drawn in Fig.2.12a,
where two mass bodies A and B
are connected by a
spring. In practice, however, the resonant gravitational wave
detector consists of three basic parts (Fig.2.12b) :
1. A flexible
body of
suitable shape and properties, which responds by mechanical
movements - oscillations, vibrations, deformations - to the
incoming gravitational waves.
2. A sensor that registers these mechanical
oscillations and converts them into electrical signals.
3. Electronic evaluation device which amplifies, processes and
records these electrical signals.
The physics and technique of these
detectors is quite complicated (we can
refer in detail to the literature [270], [29], [30], [6]) and it is quite similar to the
theory of antenns for radiowave reception; for this reason,
resonant bodies used in mechanical detectors are also called
"gravitational antennas". The basic requirements
for these gravitational antennas are sufficient weight and the
highest possible parameter of mechanical
quality (ie the smallest possible
damping of mechanical vibrations by dissipative processes).
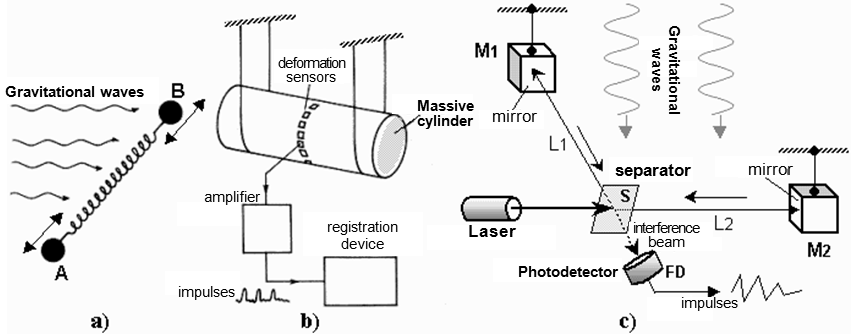
Fig.2.12. Detection of gravitational waves.
a) A harmonic
oscillator formed by two bodies A and B connected by a spring is the simplest
resonant detector of gravitational waves.
b) Resonant
detector of gravitational waves formed by a massive (flexible)
cylinder in which gravitational waves cause oscillations. Using
suitable deformation sensors, these mechanical oscillations are
converted into electrical signals and further processed. A
detector of this type was designed by J.Weber in 1968.
c) Interferometric gravitational wave detector (for description see "Interferometric detectors" below).
The pioneer in the field
of gravitational wave detectors was Joseph
Weber [269],
[270], who in the 60s-70s designed the first gravitational wave
detectors, consisting of aluminum cylinders with a diameter of 66
cm and a length of 153 cm (weight about 1.4
tons , fundamental resonant frequency 1660Hz), suspended in a vacuum and
mechanically isolated from the surroundings. The oscillations of
the cylinder were registered by piezoelectric deformation sensors. To eliminate local interference during
measurement Weber installed two such detectors, one of which was
located in the University of Maryland and the
second in Aragon
Laboratory near Chicago (distance between the two locations about
1000 km). Pulses that occurred simultaneously were considered positive cases
of gravitational wave detectionin both detectors. In 1979, Weber
actually registered several such coincidences, which he considered to be
caused by gravitational waves. However, this optimism was not
confirmed in further developments. Subsequent experiments
performed with improved detection of higher sensitivity no waves
being registered ...
Furthermore, a
sensitivity analysis
of Weber cylinders showed that supposedly received
gravitational radiation would have to have an intensity of about
1 W/cm2; if the source of this radiation were in
the center of the Galaxy (as Weber estimated), then assuming
isotropic radiation, the source would gravitationally emit a
power of about 1043 W, which corresponds to a mass
loss of about 103 M¤ per year. Such a large
gravitational power could hardly be explained by possible
physical processes in the center of the Galaxy. The origin of the pulses detected by Weber is therefore
unclear (the vibration of both cylinders may have been caused by
disturbances in the Earth's magnetosphere caused by magnetic
eruptions on the Sun..?..). However, if we look from above in the
passage "Sources of gravitational waves in space", Fig.4.13, hypothetically, a rare event of fusion
of two black holes (their fusion or collision) in the
binary system in our galaxy could be recorded, during which it
radiates in a fraction of a second. colossal energy - a
"flash" of gravitational waves..?.. But it would be a
big coincidence ...
Laboratory mechanical
gravitational wave detectors were further improved, with the
trend being to increase detector quality parameters and noise
suppression (instead of aluminum eg
sapphire resonators, cooling to fraction of °K, electronic
sensing apparatus improvements) rather than increasing detector weight
[29], [6]. However, mechanical gravitational wave detectors have
two major disadvantages :
¨ Principle
limitations of sensitivity resulting from the laws of quantum
mechanics: the accuracy of rod vibration measurements is limited
by the quantum uncertainty
principle *).
The vibrations of the cylinder caused by the weak gravitational
waves will be very small, of subatomic dimensions, so
that quantum phenomena will be significantly applied in their
measurement.
*) Below in the section "Interferometric
detectors of gravitational waves", Note 2: "Limitation
by quantum uncertainty relations? - can they be bypassed!", it is discussed how in interferometric detection
of gravitational waves it is possible to "overcome" the
usual quantum relations of uncertainty, or more precisely said bypass...
According to the
original estimates, these vibrations are less than a tenth of the
atomic nucleus diameter (later estimates even gave amplitude
amplitudes of only »10-20 m, ie ten millionths of the
atomic nucleus diameter! - was discussed
above in the section "Amplitude of gravitational
waves"). The quantum uncertainty principle shows
that the more accurately the sensor measures the position of the
ends or circumference of a vibrating cylinder, the stronger and
more randomly it influences its vibrations. No sensor can monitor
vibrations more accurately than quantum uncertainty relations
allow. For Weber-sized cylinders, the smallest detectable
vibration amplitude is about 10-18 cm (100,000 times smaller than
the size of an atomic nucleus). This seems fantastic at first
glance, but for the detection of gravitational waves from distant
space objects (assumed amplitudes 10-21) probably no technically feasible resonant cylinders,
using the best known types of sensors, will not be enough
...
¨ Narrow bandwidth frequency
sensitivity - are tuned to a fixed resonant frequency,
given the mechanical dimensions and elastic properties of the
material used (usually hundreds of Hz or
several kHz) and are
not capable of efficiently registering signals of other
frequencies. This significantly reduces their overall effective
sensitivity and potential chance of successful gravitational wave
detection.
To detectively cover the expected
variable frequency spectrum of gravitational waves, we would need
a kind of "gamelan" composed of many cylinders
tuned to different frequencies. However, we would not cover the
low frequencies of the Hz unit in this way, and certainly not
frequencies less than 1 Hz.
Effect of gravitational
waves on electromagnetic waves ?
Since gravitational waves interact not only with material bodies
but also with the electromagnetic field, the respective effects
can be in principle used to detect gravitational waves in a
non-mechanical way. One of the designs of such a detector [30]
uses the resonant action of gravitational waves on
electromagnetic waves orbiting in a circular (toroidal)
waveguide, if the period of circulation of electromagnetic waves
through the waveguide is equal to twice the period of incident
gravitational waves. Then one part of the electromagnetic wave
will still be in the "accelerating" field of the
gravitational wave causing the "blue shift", while the
other area will be permanently in the "decelerating"
gravitational field leading to the "red" frequency
shift. This resonant gravitational-electromagnetic interaction
will lead to an ever-increasing phase difference and frequency of
electromagnetic waves, which with a sufficiently long duration of
action could in principle be measured (the waveguide would have
to be superconducting). All research proposals are still only in
the stage of theoretical projects. The disadvantage of this
solution would be the narrow spectral sensitivity, similar to
that discussed above for mechanical resonance detectors. .....
Earth and Moon ?
Another type of mechanical detector could be the Earth
itself, in which gravitational waves would cause
mechanical deformations and oscillations. However, the
considerably high seismic background is a
problem here. The connection between some earthquakes and intense
flashes of gravitational waves is theoretically possible [74],
although unproven. As for aperiodic gravitational wave detectors,
such a gravitational "antenna" could be used by the Earth-Moon
system, the distances of which would be continuously
measured, for example, by means of lasers. To do so, however, the
accuracy of these measuring methods should be significantly
improved ..... ....
Interferometric gravitational wave
detectors
In aperiodic gravitational wave detectors, subtle changes in distances between test specimens caused by
a gravitational wave are monitored. The most sensitive method we
have available for measuring changes in distances between bodies
is laser interferometry. The great advantage of these
detectors is their broad-spectrum
sensitivity
- they are able to register gravitational waves of different
frequencies, especially low
frequencies;
such waves should most often come from real space sources.
 Fig.2.12
Fig.2.12
The basic arrangement of the interferometric gravitational wave
detector is shown in Fig.2.12c (which we
have presented here again for clarity). It consists of two free-hanging massive
test specimens M1 and M2, on which light-reflecting
mirrors are mounted. These test specimens gently "sway"
on the gravitational wave - as the gravitational wave passes, the
distance between the mirrors increases periodically as the space
expands and contracts.
The geometrically perpendicular arrangement of the test mirrors (measuring arms) is
advantageous in terms of better sensitivity, due to the quadrupole nature of gravitational waves, that
oscillate space alternately in two perpendicular directions - the
incoming gravitational wave slightly stretches one arm and
compresses the other in the perpendicular direction. The beam of
light emitted by the laser is a semi - transmissive plate S,
serving as the separator, divided into two beams which
are reflected from the mirrors located on the bodies M1 and M2 and
returned to the plate S; here they interfere and the resulting light signal
is recorded by a photoelectric detector FD. The passage of the
gravitational wave in the direction perpendicular to the plane of
the laser beams causes mechanical
displacements of the bodies M1 and M2 such that in one half period the
distance L1 increases and L2 decreases, while in the other
half period L1 decreases and L2 increases. This change in the
length of the paths of the interfering rays causes the two light
waves to meet at different phases, which is reflected in a change in the intensity of the resulting interference signal
measured by a photometer.
For a measurable effect, a change
of only a fraction of the wavelength of the laser light is
sufficient. Interference detectors are therefore characterized by
high sensitivity and appear to be very promising,
especially after the expected improvement of the measuring
technique and the achievement of a large length L1 , L2 of the measuring
arms. The sensitivity can be further significantly improved by
the optical realization of multiple
light reflections between pairs of parallel mirrors - Fabry-Perot interferometer.
The described interferometric detector
with two perpendicular arms is basically sensitive to
gravitational waves coming from different directions, but with
different directional sensitivity. The best
sensitivity is for waves coming perpendicularly from above (or
below), while waves from the direction of the shoulder plane
would be virtually undetected.
In two notes below,
we will try to mention some debatable aspects in the detection of
gravitational waves :
Note 1: Elimination of the gravitational
frequency shift of light in the interferometer
The passing gravitational wave
periodically changes not only the distance of mirrors but also changes
the geometry of spacetime, which naturally affects the
movement of photons and laser light between the mirrors of the
interferometric system. Above all, it causes
gravitational frequency shift of light, alternately to
lower and higher frequencies, which could be interfering in
interferometric measurements. However, the measuring laser beam
travels back and forth between the interference
plate and the test specimen mirrors in a very fast
sequence (even many times using
the Fabry-Perot interferometer method), and
the transit time and reflection of the beams in the
interferometer is incomparably shorter than the detected
gravitational wave period. The gravitational red and blue
spectral shifts thus cancel each other out
immediately and continuously. Thus, in the end,
only the avtual change in distance, caused by
the oscillation of the gravitational wave, is manifested in the
event of interference.
Note 2: Constraints on quantum uncertainty
relations? - they can be bypassed !
The need to measure extremely small (subnuclear)
shifts the test bodies, caused by weak
gravitational waves, naturally raises the question whether it
ever allow Heisenberg quantum
uncertainty relations..?.. Basic quantum uncertainty
relations between the change in position of the Dx particle and its
momentum change Dp is given by the product Dx. D p ³ h . If we needed to determine both the change in position
and the momentum of the test mirrors at the same time in the
interferometric measurement of the gravitational wave, we would
have no chance. However, we only need here to
measure the longitudinal change in position of
mirrors that are free, not their momentum (which becomes
unlearned, but we do not need it here). Thus, in this
circumstance, it is possible not to violate, but to "bypass"
the quantum uncertainty relations ..!..
Despite all the
technical improvements (see below "New
experiments for the detection of gravitational waves"), gravitational waves could not be detected
directly for many years. The gravitational waves coming
from space were apparently weaker than the sensitivity of the
existing detectors. In gravitational physics, then, we were in a
similar situation as electrodynamics after Maxwell, but before
Hertz. In the end, however, it succeed - see the passage
bellow "The good news - the direct
detection of a gravitational wave by the LIGO device".
Indirect
evidence of gravitational waves , indirect
detection
However, despite the difficulty of direct
detection, we
already have some indirect evidence
for the existence of
gravitational waves. Namely, if a system emits intense gravitationally, considerable energy is carried away from it, which leads to changes in the physical parameters of such a system. E.g. in a tight
binary system, the intensity of the gravitational radiation is so great
that the two bodies will approach each other
in a spiral and the
orbital period will be noticeably shortened; this
will further increase the radiated power, so that this
effect will take place with increasing speed. However, the
finding of such a reduction in the period (ie an increase in the
orbital frequency) in a binary star does not in
inself prove that this is an effect caused by gravitational radiation. Changes in
the orbital period can also be caused by the loss of mass of one
of the stars, viscous braking in a gas cloud, or the overflow of
mass from one component to another due to the close proximity of
the two stars. In the case of tight binary systems of ordinary
stars, the latter possibilities probably play a dominant role.
However, if the components of the binary system are sufficiently compact (eg neutron stars or black holes), then
the mutual flow of matter and viscous friction is negligible -
the system is "clean" - and the reduction of the
orbital period will be caused exclusively by the
emission of energy
by gravitational waves.
Binary pulsar
Indeed, in 1974, J.Taylor, H.Russel, J.Weisberg and other
collaborators on the large radio telescope of the Arecibo
Observatory discovered the binary system PSR
1913+16
containing a pulsar (§4.2,
part "Pulsars"),
which proved to be very suitable not only for the given purpose, but also
for testing of relativistic effects in general - it is therefore
often referred to as the "astrophysical
relativistic laboratory PSR 1913+16". Careful measurements have shown
that the second component is also a compact object and no gas or plasma is present in the orbit of
the pulsar, so that subtle
relativistic effects are not overlapped by
phenomena caused by
mass transfer, the viscous braking, tidal forces and the like
[243], []. From the point of view of GTR, it is therefore an
almost ideal clock (§4.2,
passage "Pulsars - precision 'clockworks' in
universe") moving in strong gravitational
field at a high speed
along a considerably eccentric path. In addition to a number
of other relativistic effects, at this
object was succeeded to measure the rate of change of the period (T = 7.75
hours) of the pulsar circulation, which is about DT @ -6.7.10-8 s/circulation. This observed rate of change of the pulsar's orbital
period agrees very well with the value predicted for a given system
by the general theory of relativity due to losses of orbital energy by gravitational
radiation.
According to the relation (2.82), the kinetic energy of the
orbital motion is carried away from the binary system by the
emission of gravitational waves, whereby the two components spirally approach each other (in this
case by about 3 mm with each cycle, which is about 3 m/year) and according to Kepler's law,
the period of their circulation
decreases.
Other alternative explanations of the observed changes in the
pulsar circulation period - e.g. a third body of appropriate mass
orbiting at a suitable distance - in the light of the observation
data seems considerably unlikely.
The binary pulsar PSR 1913+16 has the following basic
characteristics [243]: the mass of each of the components is
about 1.4 M¤, the elliptical orbit around the common
center of gravity has a major half-axis a » 1.9.106 km and an eccentricity e @ 0.62,
the circulation time is 7.75 hours, the basic pulse period of the
pulsar is 59 milliseconds. The twisting of the periastra here is about 4.2° per
year, which is about 107-times faster than Mercury. By analysing of various variables components of periods of the pulses arrival from the pulsar was also able to measure the
effect of time dilation (transverse
Doppler effect), gravitational red shift and delay of the
signal in the gravitational field.
A number of binary pulsars have been
discovered in recent decades, some of which are interesting for
studying the dynamic gravitational effects of GTR, including the
emission of gravitational waves. We can name eg PSR 1534+12, PSR
033+1715, especially interesting is PSR 0737-3039 (contains 2
pulsars).
The measured data from the PSR
1913+16 pulsar and others have become very convincing (albeit
indirect) evidence for the
existence of gravitational waves.
Time
modulation of the period of signals from pulsars by gravitational
waves
In addition to the above-mentioned dynamic effects in
binary systems of compact objects, pulsars can potentially serve
also to study "already finished" gravitational waves in
another way. Pulsars - fast-rotating, strongly magnetized
neutron stars are sources of highly regular pulses of
electromagnetic waves in outer space (§4.2,
passage "Pulsars - precision 'clockworks' in universe"). As these
pulses pass through space containing low-frequency gravitational
waves, there is some (albeit very weak) effect on their
propagation - long-period modulation of
short-period
electromagnetic signals from pulsars may occur due to
gravitational waves. A gravitational wave of amplitude h
would lead to a relative change
in the repetition frequency of the pulses no by the order of Dn/no » h. By sensitive analysis of these radio
signals using large radio telescopes or their systems in the
future, it will be possible to measure these subtle deviations.
A correlation of times would be
performed detection of pulses from several pulsars according to
their angular distance.
Microsecond pulsars are particularly
suitable for this purpose, in which the effects of "star
shaking" and accretion, which may affect the pulse period,
are less pronounced. In the future, this phenomenon will
hopefully be used in principle to detect long-period
gravitational waves in space - systems of a larger number of
radio telescopes are being built for this detection using the Pulsar
timing array method.
This method is sensitive even to
very low frequencies of 10-9-10-6 Hz gravitational waves, which predominate
in space. They occur during the orbit of massive objects (such as large black holes in the centers of colliding
galaxies) with an orbital
period of several months to years. Low-frequency gravitational
waves could also come from space-forming processes (reduced frequency due to cosmological expansion of the
universe). Such measurements
could be complementary to interferometric methods that are unable
to detect low frequency gravitational waves.
In 2008, the virtual project NANOGrav
(North American
Nanohertz Observatory for Gravitational Waves) was founded as a
consortium of about 190 astronomers who, through regular
observations of a set of 68 millisecond pulsars, try to detect
low-frequency gravitational waves by means of fine monitoring of
changes in the observed frequencies of pulsars. By sophisticated
stochastic analysis of large amounts of data, it tries to
distinguish the signal from certain localized sources from the
stochastic background of random gravity waves from many distant
sources. An analysis of the angular correlation of measured pulse deviations between
pairs of pulsars in different parts of the sky may be a certain
possibility. Other random variances would not show the same
correlation.
Measuring
the polarization of relict microwave radiation
As mentioned above at the end of the "Sources
of Gravitational Waves"
section, the most powerful
source of gravitational waves was probably the turbulent formation
of the universe - the
phenomena around the "big bang". Especially with the
gigantic and rapid inflationary expansion
of the very early
universe (§5.5 "Microphysics
and cosmology. Inflationary universe.")
there should be an
intense ripple in the curvature of space-time - massive primordial gravitational waves should emerge, which will then
propagate through space. However, with the expansion of the
universe, they have become so weak and enormously lengthened
their wavelengths at the present time, that there is no hope for the direct detection of these primordial gravitational waves by the methods described above. However, there is
an interesting indirect method of finding
"traces" *) of
primordial gravitational waves, which they may have left in the
ubiquitous relict microwave cosmic background at a time when these waves were still relatively strong, at the end of the radiation era. This "trace" could be a
partial polarization of the relic microwave
radiation that was being
created at that time (separated from the substance).
*) We can symbolically compare
this to how we observe trilobite prints on some
stones. From such imprints, we can relatively realistically
reconstruct the sizes and shapes of these ancient animals, even
though their organic bodies have decomposed irreversibly and have
long since disappeared. Similarly, primordial gravitational waves
have now weakened and almost disappeared. However, in earlier
times of space, when they were still strong, these
"inflationary" gravitational waves left characteristic
traces - "imprints" - on microwave
relic radiation. And we can now find and measure them in
principle, although it is much more difficult and complex than
with those trilobite prints..!..
The origin and properties of the relict
microwave cosmic background are discussed in §5.4, passage
"Microwave relic
radiation - the messenger of early news space" (see also §1.1, part
"Methods of nature
research").
Most of the relic microwave radiation generated by the chaotic
interactions of particles in a hot plasma does not show any
regular polarization, their electrical and magnetic vectors E
and B oscillate randomly in different planes. At
the end of the radiation era, the so-called Thomson
scattering occurs during the last scattering of photons on
the rest of the free electrons. If photons of different
frequencies from different directions collectively interact with
electrons in a heterogeneous plasma, the resulting waves with a
preferred plane of electric field oscillations can be generated:
this is called the E-mode of polarization. However, if
there is an interaction of photons that have a changed frequency
due to the passage of gravitational waves (with
a tensor quadrupole character), the so-called B-mode of
polarization arises, which in space shows a certain
"arc" or "twist" around the center of
fluctuation.
Strong gravitational waves traveling
through space at the time of the formation (separation) of relic
radiation should somewhat affect its properties - causing a very
weak but characteristic polarization
of relic microwave
radiation. With sufficient accuracy and sensitivity in measuring
this polarization (especially its vortex mode
B),
hypothetical inflationary primordial gravitational waves could
thus be indirectly demonstrated.
This will require a significant increase in sensitivity
and the resolution of the receiving "antennas" of
microwave radiation. A different problem could also be to distinguish
the gravitational-wave polarization of relic radiation from the
polarization on interstellar dust *). All astronomical observations outside
our galaxy necessarily take place through radiation passing
through interstellar dust in our galaxy.
*) The polarization of electromagnetic
radiation by interstellar dust is caused by the predominant
ellipsoidal shape of the dust grains, which are slightly oriented
in the galactic magnetic field. The degree of this
polarization is about 3%. Another source of polarization may be synchrotron
radiation of electrons circling in a magnetic field (due to
a very weak magnetic field, it manifests itself only in long-wave
regions).
The astrophysical significance of gravitational
waves
The
prediction of Einstein's general theory of relativity, that at an accelerated moving matter must lose energy by emitting
gravitational waves has been confirmed. It was another stimulus for the
designers of sophisticated gravitational wave detectors, who could be
sure of the ultimate success of their endeavor, because gravitational waves probably exist ! The astrophysical significance
of gravitational waves is basically twofold :
¨ Dynamic-evolutionary
effects
The
emission of gravitational waves affects or is responsible for
important astrophysical processes in space, leading to the
evolution of many space systems. We will briefly discuss this
below in the passage "Gravitational waves and dynamics of
space systems ".
¨ Observational -
epistemological importance
Gravitational
waves are the "messengers" carrying valuable information
about their sources. And if these resources are at
great distances (cosmological) can carry also information that
they "imprinted" on
them by the intermediate interacting matter *). The cognitive significance
of gravitational
waves will be discussed in the following passage.
*) It is similar to the cosmic microwave radiation, in which in
passing through the large space structures there is a slight
modulation of temperature anisotropy (cf.
§5.4, section "Microwave relict radiation - a unique messenger
of early space news"
passage "The
influence of gravitational fluctuations of metrics in the
universe to the relic radiation - Sachs-Wolf effect ").
From the observational point of
view, the successful detection of gravitational waves and their
practical applications in astronomy is
important - to gain
a new perspective on the processes in the universe :
Gravity-wave astronomy
The observation and analysis of gravitational
wave is of great potential to deepening our understanding of the
universe. To reflect on how extremely important a
"window"
into space is gravitational wave detection and imaging, let's first briefly summarize the
important stages of observing the universe with electromagnetic
waves (it is also discussed in §1.1,
section "Electromagnetic radiation - the basic source of
information about space").
Until the middle of the 20th century all our knowledge
of the universe came from the observation of visible light
- the narrow spectral range of wavelengths of electromagnetic
radiation to which our eye and photographic materials are
sensitive. In this optical field, the universe
appears to us as a relatively calm system of
stars associated in galaxies and planets orbiting smoothly (we observe the planets of our solar system directly; we
would probably get a similar picture if we could observe planets
around other stars). The properties of
stars and planets change significantly in the optical field only
over time scales of millions or billions of years (except for rare phenomena such as novae or supernova
explosions). The brightest objects observed
in the optical field (eyes or optical telescopes) are the Sun,
planets and nearby stars, and in the more distant universe
nebulae and galaxies. Light with a wavelength of about 0.5 mm is emitted mainly
by excited atoms found in the hot atmospheres of
stars and planets, or in large gas nebulae. Optical photometry
and spectrometry therefore bring us information about
temperatures and chemical composition, through Doppler
spectrometry as well as the velocities of objects and gas flow.
Since the 60's we have been observing
using radio waves showed another, far more
dynamic side of the universe - massive jets of gas from
the nuclei of galaxies, quasars with extremely high but
fluctuating brightness, pulsars rotating at high speed and
emitting narrow cones of radiation. The brightest objects
observed by radio telescopes are gigantic intergalactic clouds
("lobes") and jets from galactic nuclei, probably
propelled by giant black holes. Radio waves (with a wavelength 10
million times longer than light) are emitted mainly by fast
electrons moving at almost the speed of light in
spirals in magnetic fields.
Astronomical observations in the field of
X-rays using X-ray telescopes installed
on satellites began in the 1970s. Here again, a different picture
of the universe appears, showing local turbulent processes around
neutron stars and black holes in stellar masses, with the
accretion of hot gas in binary systems. X-rays with a wavelength
of the order of 1000 times shorter than light are emitted mainly
by high-energy electrons in an extremely hot gas,
such as those formed in accretion disks around
black holes or neutron stars. Due to turbulence and shock
waves in the accretion disks, this X-ray radiation has an
irregular, rapidly changing intensity. It can be synchrotron
radiation emitted by relativistic electrons moving in a strong
magnetic field, braking radiation, radiant recombination of atoms
in an ionized gas. Flashes of X-rays can occur when thermonuclear
ignites hydrogen accumulated by accretion from a red giant to a
white dwarf in a tight binary system. During the
gravitational collapse and the birth of a black hole
in the surrounding shock wave, intense flashes of gamma
radiation also occur.
Thus, astronomical observations in
different spectral domains of the wavelengths of electromagnetic
radiation provide significantly different images of the
universe, which, however, do not contradict each other,
but complement each other and compose a "mosaic"
of an objective picture of the structure and
dynamics of space systems. However, a number of important
"stones" are still missing in this
mosaic. From some places (such as the interiors of stars or
regions of dense gas and dust in the central parts of galaxies),
light and no other electromagnetic radiation can penetrate
outside. Neutrinos can get out of here, or high energy particles.
Therefore, certain hopes are placed in the detection of
neutrinos and primary cosmic radiation
which, however, is very difficult and is still in its infancy.
Some compact objects, such as black holes, do not emit
electromagnetic waves at all if they do not have accretion disks;
however, if they are part of a tight binary object, they will
emit gravitational waves.
An important missing "mosaic
stones" of knowledge of the universe could therefore bring
the most difficult "window" into space - gravitational
radiation, which - as discussed above in the section
"Detection of gravitational waves" - is just beginning to "open"! ... see below "The first direct detection of a gravitational
wave by the LIGO device"
...
Analogy with music
- "see" and hear the music ?
The basic force, that
controls the construction and evolution of the universe, is gravity.
So far, we have only observed these gravity-controlled objects in
space by analyzing electromagnetic radiation. In this way we
learn a lot about the positions and movements of bodies and the
behavior of matter in the universe, but we learn only indirectly,
vicariously, incompletely about the goverging force of it all -
gravity. With considerable exaggeration (but
with some concise features) we can compare
this situation with an imaginary example of orchestral music :
Imagine that a concert of classical music
for a large orchestra takes place in the exterior, which we
observe with a powerful telescope from a hill about 4 km away. By
observing the movements of the conductor's baton, violin strings,
drumsticks, etc., it would be very difficult even for a good
expert to know what musical composition is being played. Only the
capture of sound waves by a sensitive directional microphone
would help to know whether the P.I.Tchaikovsky !Concerto for
Violin and Orchestra in D major" or the L.v. Bethoven's
"9th Symphony" are being played. Similarly, capturing
the dynamics of gravitational forces in distant cosmic objects by
detecting emitted gravitational waves can help to concretize the
local dynamic situation...
However, the very sound of music does not
give us complete information about its specific origin in the
orchestra, for that we need visual information. Similarly,
gravitational waves, due to their long-wavelength, cannot give us
a detailed sharp image of astronomical objects. Only future multimodal
astronomy, which studies astrophysical objects and events
simultaneously using electromagnetic radiation, gravitational
waves, and various emitted particles, can provide us with
comprehensive knowledge.
In addition to the astronomy of
electromagnetic waves (radio, optical, X-ray and g - astronomy
- §1.1, part "Electromagnetic radiation - the
basic source of information about the universe"), the detection of neutrinos and cosmic
ray particles, the future "gravitational-wave
astronomy"
is beginning to emerge, which would probably significantly expand
our knowledge of the phenomena taking place in space. Detecting gravitational waves,
measuring their frequency and intensity, along
with showing the direction they come from, will
reveal important dynamic processes with compact objects, often invisible
in other ways *), including the most tumultuous processes of
gravitational collapse and collisions of neutron stars and black
holes.
*) They are mainly binary compact objects,
which are mostly astromically and optically "silent".
During their long-term close orbit, they probably lost their
accretion disks (they were "torn down" or black holes
had already "consumed" them before), so their fusion is
not accompanied by a more powerful electromagnetic flash (radio,
optical or gamma). The only way to detect these dramatic
astrophysical events is to detect gravitational waves
!
Some possibilities of more complex
scenarios of fusion of a binary system of compact objects, in
which photon radiation could also be emitted, are discussed in
§4.8, section "Binary gravitationally coupled
black hole systems. Collisions and fusion of black holes".
Observations
in the electromagnetic spectrum and in gravitational waves complement
each other : photon radiation, including X and gamma-ray
bursts, informs about the material nature of
objects and the environment (such as
accretion disks), gravitational waves can
show dynamics leading to observed turbulent
astrophysical phenomena - "make the invisible
visible".
New information from gravitational waves
Gravitational waves bring us very different information
from that of electromagnetic radiation. This is given by the
mechanism of their origin and the properties of their interaction
with matter :
l The mechanism of origin
Electromagnetic waves from cosmic sources are emitted (during
deexcitation of atoms and electron interactions) individually
and independently by a huge number of separate atoms and
electrons. These individual electromagnetic waves, each of which
oscillates somewhat differently, then fold together in the
resulting radiation we observe (this is the
case for radio waves and light, for X and g radiation we register
individual photons that were emitted by atoms and electrons with
a certain probability). Using spectrometric
analysis, they carry information about temperature, composition,
magnetic fields and density, which act on radiating atoms or
electrons (due to the Doppler effect also
the speeds of motion) .
Gravitational waves are excited collectively, by synchronous large-scale motions of a
large amount of matter - the collapse of the star's core, the
mutual orbit of massive objects (stars, neutron stars, black
holes). Therefore, gravitational waves bring us information about
the motions of large masses and the dynamics of large curvatures
of space.
l Interaction
with matter
Although electromagnetic waves pass freely through the almost
empty vacuum of interstellar space, but as they pass trough
matter, they interact significantly with atoms and
electrons, causing them to be absorbed.
The areas where the supernova exploded, the gravitational
collapse, the collision of black holes, or the big bang at the
beginning of the universe, are surrounded by a thick
layer of matter which absorbs all electromagnetic waves;
neither light nor other electromagnetic waves, potentially
carrying information about stormy events at this place, will
simply "get out". Astronomically, we
can only observe electromagnetic waves coming from weakly
gravitational regions (star surfaces, glowing nebulae), which are
not overshadowed by clouds of interstellar dust or ionized gas.
Gravitational waves, which arise
most intensively in such places of large mass accumulation,
strong gravity and stormy phenomena, on the other hand, easily pass through clouds of gases and dust. Within
these areas, they bring information about the dynamics of relativistic processes taking place there.
Thus, in the direction, amplitude
and frequency of gravitational waves (and in temporal changes of
amplitude and frequency), information about turbulent processes taking
place in the vicinity and inside of massive objects is encoded in some way; this information can be
"bring out" only by gravitational waves, as these
are areas that do not emit light and are opaque to light and
other electromagnetic waves. Monitoring gravitational waves could
reveal a lot about dynamic phenomena around compact
gravitationally collapsed objects. In the quite characteristic time course of the amplitude and
frequency
of the strong gravitational waves produced in the final
stages of the close orbit and collision (merger) of two
neutron stars or black holes, significant
information
about the course of this dramatic event, involving large masses and
extremely strong gravitational fields is encoded - see above the sharp increase
in amplitude and frequency in Figure 4.13-GW
in the section
"Sources
of gravitational waves in space".
Gravitational waves can
potentially also provide information about the dynamics of the earliest stages of the universe, when the universe was impermeable to all other forms of
radiation *), but the "primordial" gravitational
waves derived from that period can in principle be detected.
With the help of large-scale space gravitational wave detectors,
in the distant future, it would theoretically be possible to even
take a "snapshot of the universe" during Planck's time
and thus bring "light" into the mechanism of space
formation..?..
*) We will never see the "Big
Bang" in light or other electromagnetic radiation, because
it is hidden behind its own powerful flash. However, with the
help of gravitational waves, we could be able (at least in principle or theoretically) to "look" into the events of the very
beginning of the universe.
In principle, gravitational waves arise
with each accelerated motion of matter, ie also in the
orbit of planets around stars or the orbital motions of distant
stars around a common center of gravity in binary or multiple
stellar systems. However, the gravitational waves generated in
this way are extremely weak and also very "slow" (low
frequency) - their frequency is given by the period of
circulation, it is one cycle in several hours, days or even
years. There is no hope for the detection or even astronomical
use of these gravitational waves in the foreseeable future (and
probably never!)...
What would a gravitational-wave universe
look like ?
If, in a hypothetical (or rather sci-fi
) concept, we had "gravitational eyes"
sensitive only to gravitational radiation, or were equipped with
a gravitational-wave telescope, we would see a
completely different image of the universe than
looking at the sky (whether night or day) than we know from
previous astronomical observations. We would not see the Sun or
known bright stars, constellations, nebulae. Instead, we would
see numerous objects in places where we do not observe any
brighter stars in the optical field. These are tight binary
systems of orbiting compact objects - neutron
stars and black holes, emitting gravitational waves of high
power. These objects would be more numerous in those parts of the
galaxy where there is a greater accumulation of older stars (there is a greater probability that many of them have
already reached the final stages of their evolution and collapsed
into compact objects). When we are patient,
from time to time we see dazzlingly bright flashes
of gravitational waves. These can be four types of dramatic
events :
- The collapse of the star's core, which "detonates"
a supernova explosion. If this collapse or
explosion is asymmetrical, produces a strong
flash of gravitational waves. Here there is a correlation between
a short impulse of gravitational waves and a visual astronomical
observation of a massive light brightening, which fades for weeks
and months.
- Gravitational collapse of a rotating star
into a black hole with fragmentation and subsequent fusion of
some ejected parts (see Fig.4.14 in §4.4 "Rotating
and electrically charged Kerr-Newman black holes").
- The "collision" of two neutron stars or black
holes - such a direct collision is probably a very rare
phenomenon.
- However, tight rotation and merging of compact
objects in the above-mentioned binary system
is common, in which gravitational waves have already carried away
almost all the kinetic energy of the orbit. These should be the
most common and strongest sources of
gravitational wave flashes - see above "Sources of gravitational waves in
space", Fig.4.13, passage
"Massive sources and flashes of gravitational
waves".
If we had a very powerful "sci-fi"
gravitational wave telescope, we would see a large number of
gravitational flashes from the fusion extinctions of binary
systems of compact objects (these events
fill the universe with a faint spreading gravitational wave
background) in distant space. If this
telescope were able to detect even very low frequencies, we
could see even more distant orbiting binary sytems and a faint
continuous background of relict gravitational waves from the
first moments of the origin of universe..?..
Gravitational waves and dynamics of
space systems
In addition to observational significance (gravitational-wave
astronomy), gravitational waves are also of fundamental
astrophysical importance for the dynamics and evolution
of many systems in space. Above all, it is the development of
massive compact objects and their binary or multiple systems. As
an example we can mention the process of fragmentation and
reconnection during the collapse of a rotating star
in Fig.4.14 in §4.4 "Rotating and electrically
charged Kerr-Newman black holes".
Without the gravitational waves, there would be no connection of
fragments and "completion" of the gravitational
collapse, the theorem "Black hole has no hair"
would not apply (§4.5 "Theorem "black hole has
no hair""). At tight binary systems of
orbiting compact objects, it causes gravitational radiation,
carrying away orbital kinetic energy, approaching rotating
objects and shortening the orbital period until they eventually
merge (as discussed above in the "Binary
Pulsar" section). However, in distant binary star
systems and planets orbiting stars, gravitational radiation is
irrelevant: it is so weak that it is completely
outweighed by dissipative tidal forces in the orbiting materials
and friction when moving in sparse interstellar or interplanetary
gas.
The emission of gravitational waves is
probably also important for the evolution of rotating galaxies in
the long term.
New experiments for gravitational wave detection
- LIGO, VIRGO, GEO, TAMA, LISA -
Despite improving and increasing the sensitivity of Weber-type
resonant detectors (eg the detector at
Stanford University reaches a sensitivity of 10-18), interferometric detectors appear to
be the most promising gravitational wave detectors.
The physical principle and basic arrangement of the
interferometric gravitational wave detector was described above
in the basic text, section "Gravitational wave detectors" and schematically sketched in Fig.2.12c. The
first such detectors, designed in the 70s, with a sensitivity of
10-15 did
not exceed Weber's original detector. Over the years, however,
they constantly improved, especially through the development work
of physicists and engineers in a group led by R.Weiss, K.Thorne
and R.Dever. At the end of the 1980s, a laboratory interferometer
MARK2 with an arm length of 40 meters was built at the California
Institute of Technology, reaching a peak sensitivity of 10-18 at that time.
LIGO -
large gravitational wave detector
Under the leadership of the above mentioned group was started in
2001 in the USA the construction of the largest and the most
sensitive devices for detecting gravitational waves - of LIGO
( Laser Interferometer Gravitational
wave Observatory). This major project, built in
collaboration with the California Institute of Technology and the
Massechussets University of Technology, consists of two
remote observatories. One is located in Livingstone
(Louisiana), the other of the same type is located in Hanford,
near Washington. Sensitivity should be in the order of h @ 10-21 and after
reconstruction even 10-23 ! Coincidence analysis of signals from
remote interferometers makes it possible to eliminate spurious
signals originating in local disturbances.
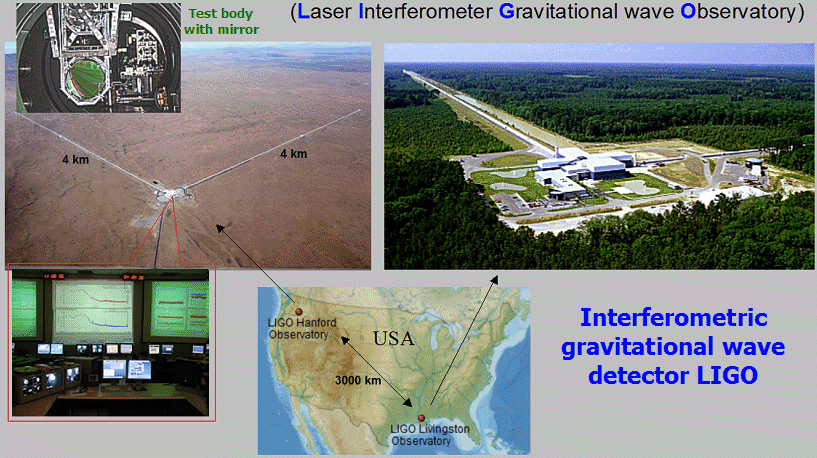
A significant increase in sensitivity by
several orders of magnitude compared to previous detectors has
been achieved through a combination of a number of top
technical innovations. On the one hand, they are huge
dimensions - the length of the arms of the interferometer is 4
kilometers (which is more than 100 times greater than
with previous interferometers). The optical system of both arms
is placed in two tubes 4 km long and 120 cm in diameter, in which
a high vacuum is maintained. Instead of the
usual two test bodies, the LIGO system uses 4 free-hanging bodies
with precise mirrors with high reflectivity, two on each arm. The
special geometric configuration of the pair of mirrors (and the
inlet and outlet openings of the interior mirror) ensures that
the laser beam is reflected many times between
these parallel mirrors in each arm and only then passes through
the opening in the interior mirror to the beam splitter,
interfering with its partner from the other arm and hits the
photodetector. This multiple reflection on the principle of the
so-called Fabry-Perot interferometer allows to effectively
extend the optical length of the device by a coefficient
equal to the number of reflections. With 100 reflections, the
optical length of the arms will be 100 times greater than the
physical dimensions, ie as if the arm were 400 km long!
In the default (idle) state, the
interferometer is set so that both output interfering beams meet
in antiphase and cancel out - the photodetector window is
"dark". Changing the distances of the test specimens
changes this phase shift, the photodetector window brightens and
the photoelectric sensor sends an electrical signal proportional
to the intensity of the interference beam.
The LIGO system is
equipped with a number of other advanced electronic, optical and
mechanical conveniences, contributing to the improvement of
sensitivity and isolation of disturbing influences - vibrations,
tidal forces, thermal noise, pressure changes. The laser beam is
"cleaned" into a perfectly coherent shape. Part of the
beam is diverted to a frequency modulator, which creates two reference
beams with a slightly higher and lower frequency than
the main beam; these reference rays pass through part of the
optical system, but are not subject to multiple reflections in
the arms, but are reflected from the first two mirrors and fall
into the photodetector, where they are compared with the
interference rays from both arms. Test specimens with mirrors are
suspended as pendulums on special suspensions; the hinges are
fixed to the frames anchored to the columns in several
mechanically insulating layers. The position of the mirrors is
finely corrected by magnetic coils.
Improved aLIGO
detector
In 2013-2015, a general reconstruction of the
instrumentation of both LIGO detectors was carried out in order
to significantly increase the sensitivity.
Several significant technical innovations have been implemented :
- Increase of
laser power from the original 10W to 200W. This significantly
reduced quantum photon noise.
- Larger and heavier
quartz test optical mirrors, which reduced the effect of thermal
noise and radiation pressure of the laser radiation (and thus reduced small random movements of the mirror).
- Magnetic neutral
silica fibers were used instead of the original steel wires to
hang the mirrors.
- Use of electronic
active seismic isolation.
This advanced detection system, called aLIGO
(advanced LIGO), has about 10-times better
sensitivity than the original LIGO (sensitivity
increase by a factor of 10 leads to an increase
in the detectable volume of the universe by a factor of 1000
!). This significantly increased the
"radius of action" of detection from many more distant
sources, which increased the probability of incidence of
gravitational waves; this was actually done by the first
successful detection of a gravitational wave shortly after
starting aLIGO (see "FirstDetection of Gravity Waves" below).
Is built (or is under construction) several
other somewhat smaller terrestrial interferometric gravitational
wave detectors are being , eg :
VIRGO (Italian-French project) :
Arm length 3 km, sensitivity 10-22 at a frequency of 500Hz. The name was chosen from a
cluster of about 1,500 galaxies in the constellation Virgo,
about 50 million light-years from Earth; there one can expect an
increased probability of occurrence of sufficiently strong
sources of gravitational waves. The Virgo device has a very well
solved active seismic correction. This observatory, the
second largest after LIGO, is located in Cascina near the Italian
city of Pisa.
GEO 600 (British-German project) :
Arm length 600 m, declared sensitivity 10-22 at a frequency of 600Hz. Located near Hanover.
TAMA 300 (Japan) :
Arm length 300 m, sensitivity 5.10-21 at a frequency of 700-1000Hz. This device serves as a
precursor to a larger system: KAGRA ( KAmioka
GRAvitational wave detector) :
(Large-scale Cryogenic Gravitational wave detector)
with an arm length of 3 km (located
in close proximity to the famous underground neutrino
detector SuperKamiokaNde - see "Neutrino
detection", passage "Neutrino
detector Kamioka NDE"). It will be part of a worldwide system of gravitational
wave detectors.
The construction of a detector of
type LIGO in India is in the
project stage.
Furthermore, the gradual improvement
of large detection systems LIGO (-> aLIGO) and VIRGO
is planned, where by increasing the laser power, improved active
seismic isolation + correction, using more precise mirrors and
other state-of-the-art technologies, sensitivity up to h @ 10-23 should be achieved.
The
worldwide network of gravitational wave detectors
Experts have high hopes for the cooperation and electronic
interconnection of several gravitational wave detectors
located in different parts of the Earth. On the one hand, the simultaneous
detection of pulses by independent remote detectors
makes it possible to eliminate accidental false
vibrations of local origin. Furthermore, as the
gravitational wave travels across the earth's surface (at the
speed of light), various of these detectors strike at slightly
different times (in the order of a few
milliseconds). The evaluation of the delayed
coincidences of the signals between the individual
remote detectors, it will thus allow by triangulation to
determine the direction from which the gravitational
wave is coming and thus to make an astronomical assignment of a
place in the sky.
The interconnection of six large gravitational wave detectors is
being prepared: in Hanford (LIGO) and Livigston (LIGO), in
Hanover (GEO), in Pisa (VIRGO) and in Japan (TAMA-KAGRA); all are
of the interferometric type. It is planned to build another LIGO
detector in India.
Cosmic
detectors of gravitational waves
One of the main problems limiting the sensitivity of the most
advanced terrestrial gravitational wave detectors, especially in
the low frequency range, is the "turbulent Earth"
- a seismic background of natural origin
(geological, atmospheric, tidal) as well as man-made disturbances
( crossings of heavy cars, earthworks and mining work,
overflights of aircrafts). The ubiquitous seismic background
makes it impossible for terrestrial instruments to detect mainly
gravitational waves with frequencies less than 1Hz. For technical
and geological reasons, it is also no longer possible to increase
the arm length of terrestrial interferometers. Future large
gravitational wave detectors will therefore have to be built
in space - a network of satellites connected by laser
interferometers.
LISA - cosmic
gravitational wave observatory
NASA and the European Space Agency is preparing the project of
detection of gravitational waves located in the universe,
called LISA (Laser Interferometer
Space Antenna). Three space
probes equipped with lasers are to be launched into orbit around
the Sun, creating a triangular interferometric system with an arm
spacing of 5 million kilometers (about 10
times the Earth-Moon distance). The system
of these three probes is to be launched around 2011 and will
orbit the Sun at a distance of 1 astronomer units (such as
Earth). As they orbit the Sun, these three probes will maintain a
constant distance between them with an accuracy of one
micrometer. To avoid non-gravitational effects on the movement of
the probes, these probes will be maintained in an ideal geodetic
path using active correction so that the position of the
free-moving test specimen floating in the cavity inside the probe
remains constant. The probes will emit and use special mirrors to
reflect laser beams, the interference of which will be detected
by detectors and transmitted to Earth.
The LISA system will achieve much higher
sensitivity and will also be able to detect gravitational waves
at a much lower frequency (and therefore long
wavelengths) than terrestrial detectors - frequencies from 1Hz to
10-4 Hz.
Such (and even longer) gravitational waves should predominate in
the gravitational-wave spectrum from space. It will make it
possible to record, among other things, the movement of neutron
stars or black holes in compact binary systems (even longer before they merge) and
massive black holes (weighing millions to
billions of M¤), which probably orbit around the center of galaxies
and generate slow gravitational wave frequencies. In this way, it
may be possible to capture primordial gravitational waves..?..
The LISA project has not yet been launched, NASA has withdrawn
from it.. .... Was designed a reduced eLISA project.
....
DECIGO ( Deci-hertz
Interferometer Gravitational
wave Observatory)
- Japanese Project Space gravitational wave detector. Length of
the arms 1000 km, max. sensitivity range 0.1 - 10 Hz. ......
The first direct detections of gravitational
waves
Large and highly sensitive systems for the detection of
gravitational waves have been "silent" for many years,
except for noise and accidental fluctuations, no signal was
recorded that would correspond to the detection of a
gravitational wave.
The turnaround occurred on September
14, 2015, when at 9:50:45 UTC both detectors in the Laser
Interferometric Gravity-Wave Observatory
LIGO simultaneously recorded a short but
significant signal
from passing through the gravitational waves whose frequency during 0.45 sec. increased from
35 to 250 Hz; then the signal dropped quickly and
virtually disappeared. At the top of the peak, the amplitude
reached h @
1.10 -21,
the signal-to-noise ratio was 24. It was shortly
after the equipment was improved to increase sensitivity (advanced LIGO). The
aLIGO staff called this newly detected gravitational-wave source
(event, signal) GW150914 (according
to the date of discovery). A detailed
article on this first successful detection, signed by a team of
almost 1,000 researchers and technicians, was published in
February 2016 in the leading physics journal Physical
Review Letters 116, 061102 (2016) .
 |
Signal processing GW1504914
from the first successful detection of a gravitational
wave by the LIGO system. The signal was detected
simultaneously by an interferometric detector in Hanford
(left) and Livingston (right) in coincidence with a time
difference of 7 milliseconds, corresponding to a distance
of 3000 km from both detectors. At the top of the figure is the primary captured signal in both interferometers (only with a 35-350Hz baseband frequency filter) . In the middle, this signal is fitted by a computer-modeled waveform for binary systems of two black holes. The narrow graph below it shows the differences between the actual and best suited modeled signal. At the bottom of the figure is a two-dimensional time-frequency spectrogram (diagram) of the signal, color and brightness modulated by its amplitude. On the horizontal axis is time, on the vertical axis is frequency, color and brightness express the amplitude of the signal. It clearly shows the increase in frequency ("chirp") during the detection time. < - Phys.Rev.Lett. 116, 061102 (2016) |
Interpretation
The detected signal has a similar shape as the theoretical course
of radiated waves in the mutual circulation of two massive
compact bodies m1 and m2 just before and during their fusion in
the above figure 4.13-GW in the basic text, passage "Sources of gravitational waves in
space" (only the increase in the amplitude of the gravitational
wave before fusion is not as sharp as it appears in Fig.4.13-GW -
it is because the measured signal captures only a very narrow
spatial and temporal region of only a few (about 8) cycles just
before fusion; to capture previous slower cycles, detection
sensitivity is not sufficient) . We will
present this picture again for clarity :
 |
| Fig.4.13-GW.
Time course of amplitude, frequency and intensity of
gravitational radiation of a binary system of two compact
bodies m1 and m2 orbiting a
common center of gravity. Bodies that begin their orbit at time t = t0 on some large radius r0 descend very slowly in a spiral and continuously emit gravitational waves, initially weak (stage I). Even with tight binary systems, it is a process that lasts hundreds of thousands and millions of years. As they approach, the intensity and frequency of the radiation continues to increase. After reaching the circulation distance of several tens of gravitational radii, there is an avalanche-like increase in the intensity and frequency of gravitational waves (stage II). After reaching the limit of innermost stable orbit, the bodies fuse rapidly, sending a short intense flash of gravitational waves ( stage III ). In the upper part of the figure, enlarged sections from the last few cycles are symbolically drawn, during which both horizons are deformed and finally they are connected to the deformed horizon of the resulting black hole. The resulting black hole m1 + m2 is rotating and rapidly relaxes to the stationary axially symmetrical configuration of the Kerr black hole (stage IV) by radiating damped gravitational waves. |
The character of the captured signal thus
corresponds to the gravitational waves emitted
in a binary system during a close
approach and connection ("collision", fusion)
of two orbiting massive compact objects. It can be said that this
detected signal carried a true "signature" or
"imprint" of its origin, visible even at from a visual
viewing: it is a rapid increase in frequency and amplitude (after conversion into an acoustic signal resembling a
bird "beep" - chirp ) and
after reaching the maximum, then a sudden drop and rapid decay of
the amplitude.
The detected signals were subjected to a very
careful highly sophisticated computer analysis.
Using the above formula (2.82e) (in the
passage "Gravitational wave sources in space") based on the frequency and
dynamics of the frequency increase, a basic estimate of the total
mass of the source M = m1 + m2 > @ 70 M¤. Of course, the binary system cannot be smaller than
corresponds to the sum of the Schwarzschild radii of the two
binary components, which here it gives 2GM/c2
> @ 210 km.
In order to achieve an orbital frequency of 75 Hz (half the
measured frequency of the gravitational wave max. 150Hz), objects
m1 and m2 had to orbit very close to each other (which is only possible when they are very compact), at a distance of about 350 km from each other. In the
final stage, the orbital speeds reached up to 2/3 of the speed of
light!
These parameters, derived from signal analysis,
place significant limitations on the nature of the binary source.
Pairs of neutron stars, which are compact, would not have the
required mass. For a pair of black holes and a neutron star with
the required total mass, a neutron star (@ 2 M¤)
with a large black hole (@ 60 M¤) would combine at a significantly lower frequency.
Thus, black holes are here the only known
compact objects that, when circulating with
each other, can reach an orbital frequency of 75 Hz without being
in contact before their connection. After a sudden drop in the
signal behind the peak corresponding to the connection of the two
black holes, smaller waves appear with rapidly decreasing
amplitude, corresponding to damped oscillations of the resulting
deformed black hole as it transitions to a stationary axially
symmetric Kerr configuration (gravitational waves carry away "asymmetry
hair" - §4.5 "The theorem "black hole
has no hair"").
This was followed by a complex computer search
of the parameters of the source from which the detected
gravitational waves came. In the range of weights of individual
components 1-99 M¤ and total weight up to 99 M¤ binary
systems with different circulation parameters were modeled using
post-Newtonian approximations, perturbation analysis of black
holes and other methods of numerical theory of relativity.
An entire "atlas" of many thousands of theoretical
binary sources with various parameters was created. The results
of this modeling were fitted with the measured
signal curves and the deviations were assessed by statistical chi-
square methods and Bayesian
coherence analysis. This detailed analysis of the
detected signals led to the following conclusions :
The detected signal GW1504914
came from gravitational waves emitted by a binary
object of two black holes in the last phase of their
close mutual circulation and merging - fusion (collision).
Specified parameters of the source system :
| Weight of black hole m 1 | -4 36 +5 M ¤ |
| Weight of black hole m 2 | -4 29 +4 M ¤ |
| Weight of the resulting black hole M | -4 62 +4 M ¤ |
| Rotational angular momentum (spin) J / M of the resulting black hole | -0.07 0.67 +0.05 |
| Total energy radiated by gravitational waves | -0.5 3.0 +0.5 M¤ c 2 |
| Peak power radiated by gravitational waves during fusion | -20 200 +30 M¤ c 2 / s |
| Luminosity distance of a binary source | -180 410 +160 Mpc |
The total value of energy
carried away by gravitational waves is remarkable - three
masses of our Sun have radiated! And absolutely colossal
is the instantaneous gravitational-wave power -
the gravitational "luminosity" of the
source in the final phase at fusion - 200 M¤ c2 per second, which is 10 times more than the radiant
power of all stars in all galaxies in the universe!
From the coincidence analysis of the
time difference of the 6.9 ms signal between the
detectors in Hanford and Livingston, it was possible to determine
by triangulation only a very rough approximate position
(direction, angle) of a source in the sky that does not allow
accurate astronomical assignment; it is an area of about 600
square angular degrees in the southern sky, approximately in the
direction of the Magellanic Clouds (but the
source was much further than these smaller neighboring galaxies). More detectors would be needed to more accurately
locate a place in the sky (Virgo detector
in Italy, preparated KAGRA in Japan and LIGO India) . But even then we would probably not see
anything at this place *), because the black holes
probably lost their accretion disks during their long-term close
orbit (they were discarded, or the black
holes had already "consumed" them before), so their fusion is not accompanied by a more powerful
electromagnetic flash. However, a significant optical effect can
be expected for the fusion of white dwarfs and neutron stars.
*) Although there was a report that at the
same time a faint flash of gamma rays from about
the same place in the sky was registered; however, due to the
uncertainty of the position, it was probably a coincidence.
However, if this side effect of photon
emission were confirmed in further observations, it would be
interesting to speculate what the X or gamma-ray burst might
cause, when the original accretion disks were probably ejected at
high angular velocities during long-term orbits (and may have
been long before consumed "by black holes). Perhaps a "common
accretion disk" could have formed there around a
tight binary system ..?.. Or it is a multiple system of two black
holes and a white dwarf or neutron star
, which in they destruction could supply a binary black hole
system with a substance (gas) that interacted with hard photon
radiation during a collision...?.. Some possibilities of fusion
scenarios of a binary system of compact objects are discussed in
§4.8, passage "Binary gravitationally coupled
black hole systems. Collisions and Mergers of Black Holes".
A
breathtaking story from the distant universe
So we can tell a fascinating story that took place in ancient
times in a very distant place in the Universe; however, the
gnoseological denouement had "here and now" on our
Earth..!.. Somewhere in the immense depths of space, at a vast
distance (about 1 billion light-years), there is an unnamed galaxy in space, which would appear
even in the largest astronomical telescopes only like a tiny
speck (although it contains hundreds of
billions of stars). About 10 billion years
ago (when neither the Sun nor our solar
system yet existed) two 1st-generation
stars with masses of about 30-50 solar masses formed near each
other from a dense gas-dust cloud, which orbited
each other in a tight binary star system. These
stars consumed hydrogen, helium, carbon and heavier elements very
quickly in intense thermonuclear reactions (cf.
§4.1, section "Thermonuclear reactions inside stars") and in about 1 million
years exploded as supernovae and subsequently collapsed
into black holes. The resulting black holes around each
other (around the common center of gravity)
continued to orbit several million
kilometers away - as a binary system of compact objects.
At first, they had accretion disks from the remaining gases from
the cloud around them (there is a section
on them in §4.8 "Accretion
disks around black holes"), but gradually they "consumed" them (or discarded them in the final stages). These black holes orbited each other for billions of
years, emitting relatively weak gravitational waves at
first. This caused a gradual decrease in the radius of
circulation, initially very slow (only
about millimeters per year). Over time -
billions of years, with a gradual approach, however, the
gravitational radiation intensified and the
approach accelerated. As the two black holes orbited several
hundred thousand kilometers in their orbits, the intensity of the
gravitational waves began to increase avalanche,
along with an increase in the frequency of the
orbit, leading to an increasingly rapid helical decrease
in orbit. This "death spiral"
then very quickly resulted in a "collision"
- merger, fusion - of both black holes. In this
final phase of the last few orbits and mergers, a colossal
amount of gravitational wave energy was radiated. It was
a lucky coincidence, that these gravitational
waves had arrived to our Earth right now, when
the immense efforts of many hundreds of physicists, engineers and
workers managed to construct such a sensitive detector of
gravitational waves (LIGO), that could detect these
gravitational waves even over a hughe distance..!.. So that was
the signal GW1504914 .
Significance of direct
detection of gravitational waves
The gnoseological significance of the first
direct detection of gravitational waves GW1504914 can be
summarized in 5 points :
¨ 1.
Direct proof of the "physical" existence of
gravitational waves and the properties of their
interaction with bodies.
¨ 2. The measurement shows the existence of binary
systems of black holes of stellar mass, confirming the
correctness of the ideas of stellar relativistic
astrophysics about the evolution of massive stars and
their binary systems (more frequent
occurrence of such massive double black hole systems, however,
was not expected ..!..).
¨ 3.
It is the first observation of a "catastrophic process"
of close circulation and the fusion of two black holes
to emit a colossal flash of gravitational energy.
¨ 4.
Further confirmation of the correctness of the general
theory of relativity, under very "exotic"
conditions of very strong time-dynamic gravity
and highly relativistic velocities (all
previous tests were based on sensitive analysis of subtle
relativistic effects in weak gravitational fields).
¨ 5. This success is likely to stimulate the upgrading of
existing detectors and the construction of new ones - building a
denser global network of gravitational wave detectors,
enabling accurate coincidence-triangulation determination of the
position of detected sources in the sky and thus their
astronomical assignment. And perhaps even the construction of
large space gravitational wave detectors with
many times higher sensitivity and spectral range. This will open
a new "window into space" - gravitational-wave
astronomy (outlined above in the
section "Astrophysical Significance of Gravitational Waves").
Pitfalls and doubts in
the detection of gravitational waves
When measuring such subtle effects (at the limit of
detectability) as gravitational waves provide, there are
naturally many pitfalls and technical difficulties. And even
after overcoming them, some problems with interpretation and
doubts about the validity of the obtained results remain ...
A certain "disadvantage" of the first direct detection
of gravitational waves GW1504914 is loneliness -
the fact that it could not be verified by other independent
measurements or correlated with any particular astronomically
observed object. Old binary compact objects are astromically and
optically silent. During their long-term close
orbit, they have already lost their accretion disks (discarded
them or "consumed" them before), so their fusion is not
accompanied by a more powerful electromagnetic flash (radio,
optical or gamma). The only way to detect these dramatic
astrophysical events is to detect gravitational waves. Their
direct astronomical assignment is usually not possible ...
This is a rare astrophysical event
*), which has been secretly "prepared" for millions or
billions of years (according to the above
formula (2.82c) in the section "Space sources of gravitational waves") during the orbiting of
compact stars in a binary system under weak gravitational
radiation, which was well below the sensitivity of our detectors.
It is only possible to capture it completely the last
phase of this process - a close approach, several dozen
last orbits and the interconnection of the two black holes,
emitting a huge "flash" of gravitational waves.
*) A rarity event ?
The " rarity " is only relative
from a global perspective . With a huge number of stars in the
astromically observed universe, estimated at @ 1022
(our galaxy has about 2.1011 stars, in the field of
view of large astronomical telescopes there are about 1011
galaxies), the gravitational collapse of more massive stars,
which are mostly part of a binary or multiple system, very often
occurs, creating black holes (mass greater than @ 5
M¤). It can be expected that for billions of years, fusion
in the binary systems of orbiting compact objects probably occurs
several times a day, emitting massive gravitational waves (space
is as if "flooded" with a weak background of
gravitational-wave "noise" from these sources) - see
"Gravitational-wave universe". Usually, however, it is too far away for us to
detect them with today's detectors. In the 1Megaparsek circuit,
the frequency of fusion of binary compact objects is estimated at
about 2-400/year. Only the strongest ones have a chance to
detect; if it were to succeed again repeatedly in the near
future, it would make it possible to specify this hitherto very
indeterminate range of incidence of mergers of compact objects.
This has already succeeded, below are listed
other successful detections of gravitational waves.
The fact that the aLIGO system detected a significant
gravitational-wave signal GW1504914 so soon after its improvement
is certainly a big coincidence on the one hand... The
original LIGO detector would not detect it either at all or with
such a large disturbing background that a more detailed analysis
would not be possible. The original LIGO would perhaps in a few
decades significantly capture another, much stronger, fusion
signal in a much closer binary system of compact objects..?..
Reconstruction and improvement of the LIGO system significantly
increased the "radius of action" - the probability of
detecting gravitational waves from much more distant binary
resources, or from closer weaker sources. The incidence of
gravitational wave capture on aLIGO could thus be significantly
increased. .......
Thus, even if GW1504914 is very well
physically and technically substantiated, the
possibility of some unknown interfering effect
*) cannot yet be ruled out with absolute certainty..!.. Eg. a
weak but extensive variable magnetic field from disturbances in
the Earth's magnetosphere caused by eruptions on the Sun might
also be able to slightly vibrate the metal components in the arms
of the interferometric detector..?.. However, such fields are
monitored around LIGO.
*) How was it probably in 1979 with Weber's
cylinders..?.., see "Gravitational wave detectors".
However, astronomers hoped, that in the near future a similar stormy astrophysical
events will occur in our or some nearby galaxy, whose
gravitational waves will be detected independently by
several systems - and hopefully can be assigned
astronomically..?.. It has already succeeded
- see below "Further direct detection of gravitational
waves".
Further direct
detections of gravitational waves
Following the signal GW1504914, another weaker signal was
detected at aLIGO on 12.10.2015, which could also probably come
from gravitational waves emitted during close circulation and
fusion of two compact objects, LVT151012 (a more
pronounced signal was recorded in Livigston).
However, the amplitude was more than 10 times weaker than that of
GW1504914 and it could not be reliably evaluated against the
background of the noise signal.
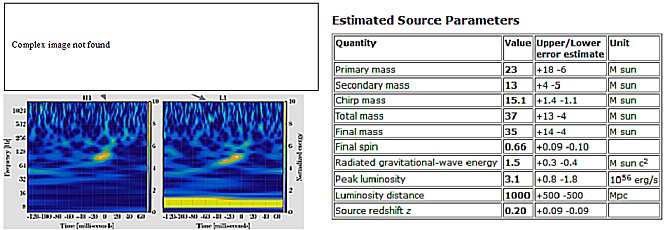 |
Computer evaluation of gravitational-wave signal LVT151012 |
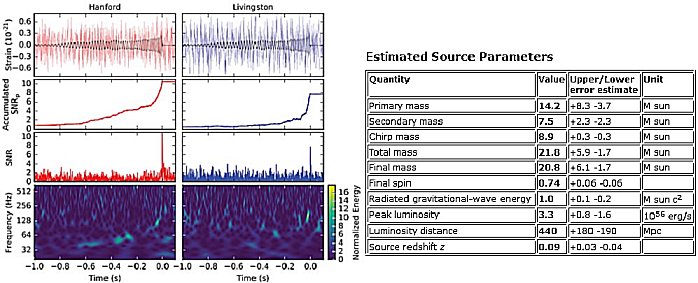 |
Computer evaluation of
gravitational-wave signal GW151226 PhysRevLett.116.241103 |
On December 26, 2015, another
gravitational-wave signal GW151226 was detected. Although
this signal was more pronounced than LVT151012, but in comparison
with the first signal GW1504914 it was also not very good - with
the naked eye we would not find a gravitational wave on the graph
of the measured signal; only very careful computer analysis was
able to "extract" useful data from it.
The third direct detection of gravitational
waves occurred on January 4, 2017, the signal was named GW170104.
This was again a typical signal from the fusion of a binary black
hole system :
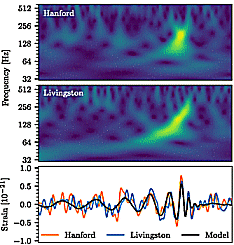 |
Source: LIGO |
|||||||||||||||||||||
The fourth direct detection of gravitational waves from the fusion of black holes was successful on August 14, 2017, the signal was named GW170814 . It is remarkable that for the first time a gravitational wave signal was detected simultaneously by three instruments: first LIGO Livingstone, 8 milliseconds apart LIGO Hanford and finally Virgo in Italy after 14 ms. (from Livingstone). This allows to more accurately locate the place in the sky where the gravitational waves are coming from. For GW170814, this stereotactic analysis showed an area of the sky as small as 60 degrees2 in the constellation Eridanus in the southern sky. The localization here is about 10 times better than just two LIGO detectors; however, no astronomical (optical, radio) side effect was observed here, which is not to be expected with the fusion of black holes. The different orientations of the arms of these three detectors further make it possible to analyze the polarization of the gravitational wave (the measured data corresponded to the above-mentioned polarization alternating in two perpendicular directions according to Fig.2.11) .
| LIGO Hanford | LIGO Livingstone | Virgo (Italy) | ||||||||||||||||||||||
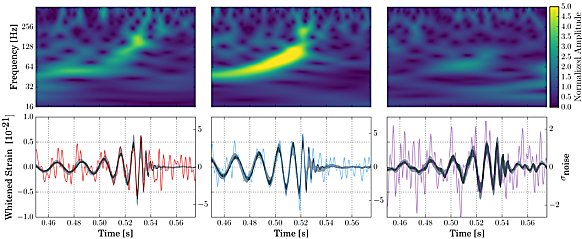 |
Source: LIGO |
|||||||||||||||||||||||
GW170817
- Merging neutron stars
Three days later, on August 17, 2017, another gravitational-wave
signal GW170817 was detected by LIGO and Virgo
detectors , which was interpreted as the last phase of the orbit
and merging of two neutron stars. Two observed
facts led to this remarkable conclusion :
1. Analysis of the course of the gravitational-wave
signal .
The gravitational wave signal was observable for about 100
seconds, with a low amplitude starting at 30Hz, and during about
3000 cycles, the amplitude and frequency increased to about
400Hz; then the signal stopped. This course corresponded to the
collision and merging of both compact objects with a smaller
weight and a diameter larger than a black hole. A
detailed analysis of the course of this gravitational-wave signal
determined the masses of orbiting and converging compact bodies
in the range of about 1.2-1.6 M¤ and the
total weight of the binary system 2.75 M¤ . This corresponds to the masses of astronomically
observed neutron stars.
The signal first came to the Virgo detector in Italy, then about
22ms. later to the LIGO-Livingstone detector and for another 3ms.
to the LIGO-Hanford detector. These three detections made it
possible to triangulate the source to an area of 30
degrees2
in the southern sky in the region of the constellation Hydra.
2. Emissions of electromagnetic radiation
.
For the first time when capturing gravitational waves, the optical-electromagnetic
counterpart in the form of a gamma-ray burst
GRB170817A (1.7 s. after merging) was astronomically registered here and after about 10
hours also in the optical and infrared field - object SSS17a
in galaxy NGC4993, in the region localized by gravitational wave
detection. After a few days, the object was observed with X-ray
cameras Chandra, then in the area of radio waves at the VLA. The
spectral maximum of electromagnetic radiation quickly shifted
from the gamma, X-ray and UV regions to the optical and infrared
regions. These observations in the electromagnetic region
correspond to the situation at the fusion of two neutron
stars, when the ejected material, rich in neutrons,
explosively "nucleonizes" and transforms
radioactively into the nuclei of heavy elements and glows
intensely (§4.8, passage "Collisions and fusion of neutron stars"), which observationally
manifested itself similarly to the nova explosion *).
*) Such an astronomically
observed event is sometimes called a "kilonova"
- it can be up to 1000 times stronger than a normal nova,
especially if viewed from the direction of the rotational axis of
the binary system. However, this was not the case, the optical
flash was relatively weak despite the relative proximity of the
source. This can be explained by the fact that the axis of
rotation was inclined at least 30 ° from the viewing direction.
However, the fusion of neutron stars is a
completely different process that has nothing to do with
the explosion of a nova. Therefore, we do not use the
misleading name kilonova in our treatises ...
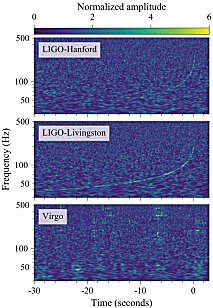 |
Source: PhysRevLett.119.161101 (2017) |
Upper:
Time-frequency diagram of detected GW170817 signals from
individual detectors. Unfortunately, a graph of the primary detected gravitational-wave signals has not yet been published (perhaps due to the disturbing short-term electronic fluctuation that occurred at LIGO-Livingstone about 1 second before the maximum ...). |
||||||||||||||||||||||||
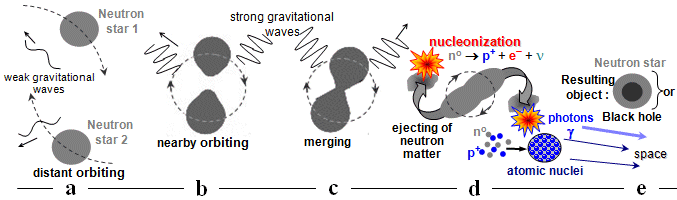 |
||||||||||||||||||||||||||
| Bottom:
Fusion of neutron stars. a) Two neutron stars orbiting in a binary system at a great distance descend very slowly in a spiral and continuously emit gravitational waves, initially faint. b) As you approach, the intensity and frequency of gravitational radiation continue to increase. c) Upon close approach, deformation occurs and eventually a collision and fusion of the two neutron stars occurs. d) During rapid rotation during fusion, a large amount of neutron substance can be ejected, which immediately nucleonizes to form predominantly heavy nuclei, followed by radioactive decay. e) The resulting object, after the instabilities disappear, is either a neutron star or a black hole (depending on the remaining mass). This resulting object will have only a small accretion disk around it (since most of the substance has been ejected away by the enormous energy released during explosive nucleonization). (Source: AstroNuclPhysic §4.8, passage "Collisions and fusion of neutron stars") |
||||||||||||||||||||||||||
Neutron stars emit weaker
gravitational waves than black holes as they orbit and merge.
However, compared to previous gravitational wave detections, the
GW170817 event was much closer - at 130 million
instead of billions of light-years, so it could be detected. The
final product of the observed fusion neutron stars is probably a
black hole, but it could be even larger neutron star..?..
The case of detection of neutron stars fusion
detection is a harbinger of multimodal - multimessenger
astronomy - here dual-modality [gravitational-wave +
electromagnetic]. It will also be a new way to study the
relationships between matter, gravity and electromagnetism.
The third modality is also perspective - detection
of neutrinos, if the merging of neutron stars occurs at a
closer distance (cf. §1.2, part "Detection of neutrinos"; promising here is mainly the Antarctic glacier
detection system IceCube, see passage "Detection of
neutrinos in glaciers").
GW170817 has
important astrophysical significance. This is
the first direct observation of neutron star fusion,
in which a large amount of neutron material is ejected followed
by explosive nucleonization to form a large number of heavy
elements - see the figure in §4.8 above, passage "Collisions
and fusion of neutron stars". These heavy elements (including gold, platinum, uranium, ...) have
enriched outer space. Other such observations will help refine
estimates of how common these events are in
space and the extent to which neutron star fusions are involved
in the cosmic nucleogenesis of heavier elements;
together with stellar synthesis and supernova
explosions (cf. §4.1, part 4 "Evolution
of stars" and §4.2,
part "Astrophysical significance of supernovae").
Note: Overestimated share of
nucleogenesis from neutron star fusion
When the first multimodality detection of gravitational waves
from the fusion of neutron stars was achieved, in the first
enthusiasm, opinions began to emerge that most (or even all?) of the heavy
elements in the universe came from fusions of neutron stars.
However, more sober analyzes have shown that these estimates are
strongly overestimated. The fusion of neutron stars is
not so frequent as to explain the observed number of heavy
elements in space. It is an important part, but the main source
of heavy elements is probably stellar nucleosynthesis and
supernova explosions...
Gravitational
"Standard Siren"
The detection of gravitational waves from the fusion of
neutron stars, together with the simultaneous detection of
electromagnetic radiation from their optical counterparts, also
has astrophysical-cosmological significance for the independent
determination of the distance of the respective objects.
This measurement makes it possible to combine the determination
of the distance to the source derived from the gravitational wave
analysis with the receding velocity derived from the redshift
measurement using electromagnetic signal spectrometry. This
approach not requires the use of a cosmic distance
"ladder" (discussed in §4.1, passage "Determining
the distance of cosmic objects - a fundamental condition of
astrophysics"). The
analysis of gravitational + electromagnetic waves can thus be a
measurement of the direct determination of the relationship
distance <--> luminosity in cosmological scales,
without the use of intermediate distances, with sometimes
problematic continuity. This independently determined value of
the Hubble constant is here 70.0+12.-8 km/s/Mpc, in good agreement with existing measurements
by other methods. The uncertainty of about 10% here is mainly
caused by the uncertainty of the orientation of the axis of
rotation of the binary system with respect to the Earth.
Gravitational wave detection is therefore sometimes
metaphorically referred to as a "standard siren"
- a gravitational-wave analogue of the electromagnetic "standard
candle" (cepheids, Ia supernovae) used to determine
large cosmological distances...
GW190425 - another neutron star
merger ?
The next detection of gravitational waves from the merger of
neutron stars occurred on April 25, 2019. Unfortunately, they
were full-fledged detected only by the LIGO Livingstone detector (the second detector at Handford was currently shut
down, the Virgo detector had a low signal-to-noise ratio). Therefore, localization of the source in the sky could
not be done. Analysis of the signal showed that it was probably
the collision of two atypically massive neutron stars of 1.6-2 M¤ and
1.4-1.7 M¤, total mass 3.4 M¤ (it is also considered that they
could be even small black holes..?..),
luminosity distance 160 Mpc. No emission of electromagnetic
radiation was found to correlate with the detection of
gravitational waves. It could therefore be the situation
mentioned in §4.8 (passage "Collisions and mergers of neutron stars"), when during the collision
of more massive neutron stars, the resulting object can almost
immediately collapse into a black hole, which quickly eats up
almost all the mass of both neutron stars. No radiation will then
escape from the collision site - the kilonova is not observed...
GW190521
Another interesting gravitational wave detection event was
recorded on May 21, 2019 from the direction of constellation Coma
Berenices. A detailed analysis of the results showed that it was
a merger of the two largest black holes so far, weighing 85 and
66 M¤,
which took place 17 billion light-years away :
 |
Source: LIGO |
|||||||||||||||||||||||
From an astrophysical point of view, this event is interesting
due to the relatively large masses of black
holes involved and the resulting black hole. Black holes with
masses greater than about 60-70 M¤ should be rare
according to current astronomical knowledge, a kind of
"gap" is observed in masses between 60 and 100,000 M¤.
Nuclear-astrophysical analyzes show that massive stars with a
residual mass greater than about 65 M¤ in the final stage
of evolution during contraction, they probably do not collapse
into a black hole, but before reaching the horizon they succumab
to the so-called electron-positron pair instability (see
§4.1, passage "Electron-positron
pair instability"). In this process, the star is smashed
- scattered when the supernova explodes, leaving no
black hole behind. If this is indeed the case, medium-weight
black holes should be rare. Measurements of GW190521 show that
the final stages of massive stars may produce black holes of
higher masses, and even more massive black holes form when merging
between pairs of smaller black holes. This process of multiple
merging can then continue hierarchically ...
Another
point of interest here is the capture of a flash of light (at the
Palomar Observatory), which could be related to this event. Since
no light is emitted during the actual merging of the black holes
(discussed above), it has been hypothesized that the resulting
black hole could have entered the path through the accretion disk
of a nearby supermassive black hole, in the material of which a
light effect could occur..?. .
In the 10 years since the first detection of
gravitational waves GW151226 in 2015, more than 300 signals have
been recorded by the LIGO, Virgo and KAGRA instruments, mostly
corresponding to black hole mergers, several neutron star mergers
or transient phenomena. The cleanest and strongest gravitational
wave signal so far (with a signal-to-noise
ratio of ~77-80) was detected on January
14, 2025 and named GW250114 :
It was evaluated as originating from the merger of two black holes of masses 33 M¤ at a distance of about 1.1 billion light years. Both had a relatively slower rotation of about 0.25 of the maximum possible rotational angular momentum Jmax (=....), the resulting black hole of course has a faster rotation, here 0.68 Jmax was measured. The high quality of the signal made it possible to analyze some other phenomena and parameters than just masses and radiated energy. First of all, it is rotation. The inspiration phase before the merger provides us with information about how massive both black holes are, how fast they rotate and how they orbit each other. At the end of the merger, the resulting black hole "vibrates" in spacetime during its rotation, and the dynamics of these vibrations depends precisely on its resulting mass and rotation. From these parameters, the surface area of the final event horizon can then be determined. Analysis of GW250114 shows that the final horizon area of the resulting black hole (about 400,000 m2) is significantly larger than the sum of the horizons of the two original black holes (about 240,000 m2), in agreement with Hawking's theorem that the total horizon area can never decrease under any process ("Laws of Black Hole Dynamics"). The obtained data also show that the merged black hole corresponds to a rotating Kerr black hole ("Rotating Kerr Black Hole") with a rotational angular momentum of 0.68 Jmax, which can be fully described by its mass and rotational angular momentum.
Gravitational-wave
astronomy
The ever-increasing number of other detected signals - despite
their rather weak signal-to-noise ratio - show that the first
successful detection of the GW151226 gravitational wave was
not a coincidence, but that the possibility of "gravitational-wave
astronomy" is beginning to develop promisingly..!..
And also multimodal - "multi-messengers"
- astronomy.
So far, existing ground-based gravitational
wave detectors are only able to detect powerful one-time
gravitational waves from catastrophic events such as collisions -
mergers - of black holes or neutron stars. And that only from the
last stages of these fusions, lasting around one minute,
with relatively high frequencies. Future detection
systems (such as the planned LISA), in addition to higher
sensitivity, will also be able to detect low-frequency
gravitational waves - from many hundreds or even thousands of
close binary star systems.
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||