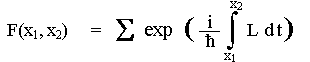 ,
,| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Appendix B
UNITARY FIELD THEORY
AND QUANTUM GRAVITY
B.1. The process of unification in physics
B.2. Einstein's
visions of geometric unitary field theory
B.3. Wheeler's
geometrodynamics. Gravity and
topology.
B.4. Quantum
geometrodynamics
B.5. Gravitational field quantization
B.6. Unification
of fundamental interactions. Supergravity.
Superstrings.
B.7. General
principles and perspectives of unitary field theory
B.5. Gravitational field quantization
In the previous
paragraph on quantum geometrodynamics, we have already partially
"bitten" the issue of quantum gravity, but from a very
specific and unusual point of view. Here we will mention in a few
words the general aspects and basic approaches to the
quantization of gravity (for further
details see eg [279], [280], [177], [258]) .
The vast majority of phenomena in nature
are caused by either gravity or quantum phenomena, but not both
at the same time. Quantum phenomena are crucial in the microworld
of molecules, atoms and elementary particles, but gravity is
negligible. In astronomical scales, on the other hand, planets,
stars, and galaxies are firmly dominated by gravity, while
quantum fluctuations are unobservable. Therefore, the connection
between gravity and quantum physics is not important for almost
all natural sciences. We do not know how gravity works at the
level of atomic and subatomic particles. We are not yet able to
combine general theory of relativity and quantum mechanics into
"one formula" ...
In short: Gravity is so weak
that its local effect on small objects such as quantum systems is
immeasurably small. Conversely, quantum effects are immeasurably
small for objects large enough to exhibit more significant
gravity.
At the very beginning (see §5.4 - 5.5),
however, the universe could be so "small" that quantum
fluctuations could "shake" the entire universe. And the
concentration of matter and gravity so great that gravity could
play an important role in the formation of quantum fields and
their further behavior. The quantum concept of gravity can thus
become key to understanding the earliest stages of the evolution
of the universe. In general, it would be highly desirable to combine the general theory of relativity and quantum
physics into one theory that would describe the universe at all
levels.
Quantum gravity can manifest
itself significantly in basically three (astro) physical
situations :
-> The
initial "singularity" in the formation of the universe
by the big bang (§5.5 "Microphysics
and cosmology. Inflationary universe.") .
-> "Singularity"
inside a black hole (§4.2 "Final
stages of stellar evolution. Gravitational collapse. Formation of
a black hole.") .
-> Spacetime quantum foam in
microscales of quantum geometrodynamics (§B.4
"Quantum geometrodynamics") .
Although the gravitational field in
Einstein's general theory of relativity differs considerably in
its geometric character from the fields with which other parts of
physics work, it also has some significant properties in common
with them. Since all these other fields are governed by the laws
of quantum physics, it is necessary to investigate the
consequences of the application of quantum
laws to gravity. The quantum approach to gravity basically
has two stages :
a)
Semi-quantum
approach - semiclassical gravitation ,
which applies quantum laws only to a non-gravitational field,
serving either as a source of a gravitational field or responding
to a given gravitational field.
Here includes quantum field theory in curved
space that studies the behavior of the quantized
non-gravitational fields at a given (fixed and not quantized)
gravitational field, i.e. against the background of curved
spacetime. This method has celebrated great success in the Hawking effect of the evaporation of black holes (see §4.7 "Quantum radiation and
thermodynamics of black holes"). According to Einstein's
equations Rik - 1/2 gik R = 8p Tik , the quantum behavior of the mass
exciting the gravitational field causes that even the excited
gravitational field will carry significant traces of this quantum
behavior. Here, however, these are
exclusively "induced" quantum properties, have nothing to
do with the nature of the gravitational field itself.
Such an approach can not be considered
entirely consistent, because the question arises of quantizing
those "degrees of freedom" of the gravitational field,
that are not directly related to the excitation matter. In fact,
there are independent excitations (gravitational waves)
transmitting positive energy in the gravitational field. It is
unlikely that the gravitational field has any property that
avoids the quantization of quantities, which in all other physics
are subject to universal quantum laws (discussed below in the passage
"Quantum or non-quantum nature
of gravity?").
There is also a mathematical reason for quantizing
gravity: in Einstein's GTR equations, one side characterizes the
gravitational field, the other side the mass. If matter is
quantized, the energy-momentum tensor Tik would be expressed in terms of quantum-mechanical
operators. And classical gravity is described by ordinary numbers
(the values of the components of the metric
tensor and the curvature tensor). There is
no known way to consistently relate the non-quantized
gravitational field on the left side of the equation to the
source of quantized matter on the other side (like if we wanted to figure out how many pears it takes
to make a watermelon...).
If we did not require gravity to be an
intrinsically quantum theory, we would use the average-expected
values of energy, momentum, mass density in the energy-momentum
tensor. There would then be the usual numbers on both sides of
the equation, the equation is consistent and solvable.
At the same time, this semiclassical
(or semiquantum) theory of gravity is capable of very precisely
describing all gravitational phenomena observed
in nature, in the laboratory, in space - now and in the
foreseeable future. Apart from hypothetical singularities. From
the side of quantum physics, the semiquantum approach is
criticized for its inconsistent approach and incompatibility with
interpretations that consider the superposition of states and the
collapse of the wave function as a real physical process.
However, we do not share this interpretation (it is discussed in the passage "Interpretation of quantum physics" and "Disinterpretation").
In §3.4-3.9, §4.9 and §5.3, we saw that
some (otherwise realistic) solutions of GTR equations have
singularities indicating that the general theory of relativity
ceases to function in their vicinity. GTR alone is no longer
enough to describe the enormous mass densities that occur here,
but a new theory involving the laws of the microworld is needed.
It is hoped that it is the quantum theory of gravity that could
shed light on these difficulties of standard GTR, especially the
elimination of spacetime singularities. Quantum theory of
gravity, as a theory of the microstructure of space and time,
could perhaps also help to overcome the basic problems of
contemporary quantum field theory with "ultraviolet"
divergences *). We see that the quantum theory of gravity
promises the possibility of better penetration into the structure
of elementary particles and their interactions, the possibility
of revealing new important laws of nature.
*) According to some research
[65], for example, elementary black micro-holes could play an important role in the
physics of elementary particles: Contributions of intermediate
states of arbitrarily large energy are included in the
calculation of the particle's own energy, which usually leads to
divergences. Inclusion of gravitational interaction respective
virtual particles and the possibility of virtual
black micro-holes in
intermedial statecould
perhaps potentially lead to the elimination of these
divergences..?..
The basic principles of contemporary physics therefore require a more consistent approach :
b) Quantization
of the gravitational field itself ,
in which
gravitational energy would be transmitted in quantums, as well as
all other forms of energy.
We will first mention very briefly some
basic methods of quantization in general and then the
gravitational field :
Canonical
quantization
The most common
and straightforward way to move from classical theory to quantum
theory is the method of canonical quantization. Applying this
method to the mechanics of mass particles creates quantum
mechanics. In such quantization (sometimes
called "primary"), field-forming probability waves are
assigned to the mass particles.
When using the canonical method on the
physical field (or continuum mechanics), particles appear as quantum
excitations of these systems - whether they are quasiparticles
(phonons) existing only against the background of the mechanical
continuum, or especially real particles (such as photons,
fermions etc.) existing against the background of the
"vacuum" of the respective fields. This method is
called secondary quantization [164],
[177].
The first step in canonical quantization is to convert
the equations of the investigated system into Hamilton's
(canonical) form. Normal level approach to the theory of dynamic
variables qA (generalized coordinates, A =
1,2,3, ...) and a Lagrangian L(q, q.) can be converted to canonical
form, it consists in introducing s canonical momenta pA
= ¶L/¶q
.A, expressions of (generalized)
velocities q.A
using the momentums pA and in the construction of the
Hamiltonian function H(p,q) = ASqApA - L(q,p) expressing the total
energy of the system using the quantities q and p. The equations
of motion of the system in the variables paq then have a simple
and symmetrical form q.A
=¶H/¶p.A
, pA = - ¶H/¶q.A - Hamilton's canonical
equations.
For the functions of generalized
coordinates and momentums f(p, q, t), g(p, q, t) the so-called Poisson brackets {f,g} = AS ((¶f/¶qA)(¶g/¶pA)- (¶f/¶pA)(¶g/¶qA)) are introduced, satisfying
simple algebraic relations: {f,g} =-{g,f},
{f1 +f2,g} = {f1,g} + {f2,g}, {f,{g,h}} + {g,{h,f}} + {h,{f,g}]
=0, etc. Eg. Poisson
brackets formed from coordinates and momentum have the form {pA,
qB} = dAB ·
During
the actual transition to quantum theory, the state of the system
is described by a certain (generally complex) function y(q) of generalized coordinates - a wave function, and the quantities appearing in
classical theory are replaced by the appropriate operators. The
wave function gives the probability distributions of the
different system configurations: |y|2.dq
is the probability that the value of the generalized system
coordinates will fall into the dq element of the configuration
space during the measurement. The mean value of the observable
quantity f, characterizing the state of the systems
, is then equal to <f> = <y|F^|y> º òy(F^y) dq, where F^ is the Hermitian operator
assigned to f .
The behavior of the quantized physical
system is then determined by a simple one the
wave equation ih ¶y/¶ t =
H^y,
where H^ is the Hamiltonian (operator assigned to
the Hamiltonian function H). Operators assigned to classical
physical quantities satisfy (except for equations of motion)
certain commutation relations in which Poisson brackets
appear: F^G^ - G^F^ º
[F,G] = ih{f,g}; these commutation
relations are an expression of the quantum (Heisenberg) uncertainty
principle.
When quantizing a physical field, the
field equations are usually converted to a wave equation, so that
the field (in some finite region of space) can be expressed as a superposition of plane waves; thus the field is described by
a discrete series of variables - amplitudes and frequencies of
waves. Based on these amplitudes, canonical field
variables are defined - generalized coordinates qA
and momentum pA, which are used to express
Hamiltonian as the sum of independent members of the shape of a
one-dimensional harmonic oscillator corresponding to individual
waves with appropriate wave vectors and polarizations. During a
quantum transition, canonical variables (generalized coordinates
qA and momentum pA) become operators with commutation
relation [^PA ,^QA] = - i h.
The use of these commutation relations to determine the
Hamiltonian eigenvalues leads to discrete
energy levels of the field En = (n + 1/2) h.w.
The application of this canonical method
of quantization to the electromagnetic field is well known
(quantum electrodynamics) and leads to the idea of a free
electromagnetic field as a set of particles - photons, each of
which has energy h.w and
momentum h.w/c. An analogous quantization procedure
for a weak gravitational field within a linearized theory,
performed in 1930-36 [221], [34], [6], leads to the existence of gravitons
as quantum of the gravitational field. Gravitons are particles
with zero rest mass and spin 2 (compare with the mention of the
symmetry of gravitational waves in §2.7), which are transversely
polarized (only the maximum spin values +2 and -2 are realized).
For the general case of nonlinear tensor theory, quantization was
developed by Dirac [70], [6].
Several
variants of canonical quantization of the gravitational field
have been developed. These modifications differ both in the way
of introducing time (as time is taken either directly x0
coordinates or time with respect to certain non-rotating
"normal" reference systems), as well as by choice and
relations between generalized coordinates and momentum (due to the singularity of Lagrangians, there are
certain coupling equations between p and q to reduce the number
of independent canonical variables).
Feynman quantization of path integrals
Quantum physics has achieved impressive
success in explaining the structure and function of atoms, atomic
nuclei, and elementary particles. However, it is by no means easy
to understand the internal causes of the quantum behavior
of microsystems based on our experience with the classical
behavior of the macroworld. Feynman's formulation of quantum theory
[178] is characterized by a very close relationship to classical
physics *) expressed by the principle of least action. In
classical physics (mechanics, electrodynamics, GTR) between a
given initial x1 and final x2 state of the investigated
system, only such a always take movement, for which the integral action S = x1òx2L dt is extreme. On the other
hand, in quantum physics, as is well known, such processes also
takes place that do not comply with this principle and are
impossible according to classical physics - for example, the
tunneling phenomenon.
*) The transition from
classical to quantum physics is so elegant and straightforward
that J.A.Wheeler [277] used this approach to persuade A.
Einstein, but to no avail, to revise his opposition to the
stochastic principles of quantum mechanics.
In Feynman's approach, all trajectories leading from the initial state x1
to the final state x2 are considered equally and
simultaneously, regardless of whether they are permissible or not
according to classical physics. As
if the particle were moving along each imaginary trajectory at
the same time as it traveled between the two states - it
is the set of all virtual trajectories
("all histories"). If the integral x1òx2L dt is calculated for each
trajectory, the probability of transition of the system from the
initial state x1 to the final state x2 will be given by the square of the
quantity
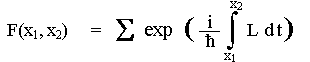 ,
,
obtained as sum and taken through all trajectories - the sum through all possible "histories". It is evident that the largest
contribution to this sum is made by those trajectories that have
a phase coefficient (i/h) ò Ldt almost the same (exponents add up),
while for trajectories with large differences in the exponents
(i/h) ò Ldt in the sum cancel each other
out. The most probable trajectory (corresponding to close values of ò Ldt) will therefore be a classical trajectory
with extreme behavior of the integral of the
action. Trajectory here means "path" in the space of
the given configurations systems; if it is a complex system
described by a large number of parameters, it will be a
trajectory in multidimensional space. Feynman showed that this
formulation is equivalent to the usual Schrödinger and
Heisenberg concept of quantum mechanics. As
with the classical principle of the smallest action, the extreme
of the integral of ò Ldt is not
immediately sought in practice, but Lagrange's equations
of motion are derived, even when using the Feynman
method, the total sum over all trajectories is not directly
calculated.
Feynman's procedure is rather used as a means for
deriving and elaborating quantum theories, as well as their
physical interpretation.
Path quantization of
universes in "superspace"
Misner [277] and deWitt [179] tried to use Feynman's concepts to
quantize the "most classical" object we can imagine: the universe as a whole. They
introduced the so-called superspace - infinite-dimensional space, whose
"points" represent all possible geometries of space
(states of the universe). The line - the trajectory - in this superspace then
represents a certain variant of the
evolution of the universe. It is clear that the practical use of
superspace is possible only under very simplistic conditions.
Misner therefore proposed to study the evolution of a closed
homogeneous universe (generalized Kasner's
models - §5.4) ,
for the description of whose state three parameters are
sufficient; infinitely the dimensional superspace is
reduced here to a three-dimensional "mini-superspace". The superspace of
Fridman's homogeneous isotropic universes is even one-dimensional
- all spatial sections are characterized by the value of the
parameter a(x°). In the framework of superspace is possible also
to mathematically formulate Wheeler quantum geometrodynamics (mentioned above §B4 " Quantum
geometrodynamics ") [275].
Quantum approaches in cosmology, leading
to the hypothesis of more universes, are discussed in §5.5, section "Chaotic inflation",
passage "The emergence of multiple
universes".
Difficulties
and perspectives of quantum gravity
In the case of a
weak gravitational field, it is not necessary to take into
account the geometric character of gravity (curvature of
spacetime) and it can be investigated like any other field
against Euclidean (or other masses curved) spacetime. From this
perspective, gravity can be considered in the context of the
standard field theory of spin 2. In the general case, however, a
number of mathematical and physical problems of quantum theory of gravity
stem from the geometric nature of the gravitational field and its
nonlinearity.
Due to the universality of the
gravitational interaction, expressed by the principle of
equivalence in GTR, the intensity of the gravitational field Gi kl or (canonical) momentum does not form
tensors. The respective commutation relations are then not
covariant and therefore have no direct physical meaning. In §2.8
"Specific features of gravitational
energy",
we showed that the density and flow of energy and momentum tik gravitational field has no tensor
character, energy of the gravitational field is not localizable, of it from here leads to
difficulties in interpreting the gravitational field quanta -
gravitons. The fact that gravity does not have a clearly
localized energy density in the GTR is a major obstacle to the
usual method of quantization. This is because energy is a
quantity that generally plays a key role in the quantization
process.
Due to the covariance of GTR, a larger
number of variables is used than corresponds to the number of
dynamic degrees of freedom. It is therefore difficult to
orientate oneself in the geometric and physical meaning of
superfluous variables and to correctly use arbitrariness in the
choice of coordinates. The nonlinearity of the general theory of
relativity prevents the superposition of individual partial
solutions, which is a significantly different situation than in
electrodynamics. In addition, nonlinearity leads to very complex
relationships between the components of the metric tensor (taken
as the generalized coordinates of the system) and the canonically
associated velocities and momentums.
From the universality of gravity follows another
remarkable and unusual property, which was already highlighted in
§2.5 "Einstein's equation of the
gravitational field" in
deriving Einstein's equations of the gravitational field and in
the following text, it has been discussed many times in the
analysis of gravitational phenomena: it is self- gravity
of the gravitational field. That the gravitational field is able
to generate another gravitational field by its energy. This
causes great difficulties in the quantization process, as both
real and virtual gravitons can emit more virtual gravitons, then
more, etc., which leads to expressions diverging to
infinity *). In other words, there are problems
with the renormalizability of the quantum theory of
gravity.
*) Quantum fluctuations of a vacuum can be
imagined as a pair of particles that are born together at a
certain moment, move separately for a short time, but then meet
again and annihilate each other. The closed loops in the Feynman
diagrams correspond to these virtual particles. According to the
general theory of relativity, the energy of an infinite number of
these virtual pairs would curve space to an infinitesimal
dimension, contrary to reality. Unlike the strong, weak, and
electromagnetic interactions in GTR gravity, this infinity cannot
be eliminated by renormalization because the appropriate
parameters are not available. A possible solution was found in
the so-called supergravity, mentioned below in §B6
"Unification of fundamental interactions.
Supergravity. Superstrings.".
It can be said that at present the main problem is not the construction of a quantum theory of gravity. On the contrary, there are a number of variants of the quantum general theory of relativity, but they show certain ambiguities (eg in the choice of canonical variables, renormalization, physical interpretation, etc.). Further stages of the development of quantum GTR should result in a situation where gravitational and non-gravitational quantum theories will be special cases of general quantum theory. Until 20 years ago, it seemed that the starting point of this unified theory should be the quantum general theory of relativity. Later successes of quantum field theory in elementary particle physics, however, set a new trend: the construction of unitary theories of fundamental interactions, including gravitational (supergravity), on the soil of quantum field theory. Recently, the possibilities of geometric formulation of supergravity unitary theories in multidimensional spaces have been explored (eg generalized Kaluza-Klein theories, superstring theories - see the following §B.6 "Unification of fundamental interactions. Supergravities. Superstrings.").
(no)Possibilities
of experimental verification of quantum gravity
Physics, as a natural science, necessarily requires that every
theory be verified by experiment or observation. And here perhaps
there is even more difficulty than in the actual formulation of
the quantum theory of gravity. The smallest spatial and mass scales
on which it is possible to verify general relativistic
gravitational phenomena in today's experimental technique are of
the order of about 105 km and 1022 kg. At smaller spatial scales (eg kilometers) and for
smaller masses (of the order of kilograms) we cannot
experimentally distinguish between Newton's theory of gravitation
and the general theory of relativity *). And there can be no talk
of experimental analysis of gravity in subatomic microscales in
the foreseeable future! So far, we have had difficulty detecting
gravitational waves from black hole fusion; but there is no hope
of experimental demonstration of their quanta, gravitons.
Quantum theories of gravitation are likely to remain at the level
of experimentally unproven hypotheses for a long
time to come. The only way to confront these theories with
reality for the time being will probably be to observe its
consequences for phenomena in the very beginnings of the
evolution of the universe (similar to that of unitary theories,
such as superstrings) - cf. §5.5 and 5.8.
*) Other interactions, on the other hand,
are experimentally verified on significantly smaller
scales, while not on a larger scale. For weak and strong
interactions, of course, this is on a scale comparable to the
atomic nucleus. Although the electromagnetic interaction has an
unlimited range, it is experimentally directly verified, except
for the microworld, only at scales of the order of kilometers.
Celestial bodies are practically electrically neutral. The only
verification of electrodynamics on a large scale is the
propagation of electromagnetic waves in space.
The question of what role gravity plays in the
structure and interactions of subnuclear elementary particles
will probably remain open for a long time. No role, marginal
or determining role in particle structure? (discussed in §B.6, passage "Superunification
and Supergravity").
Quantum or non-quantum nature of
gravity ?
In current physics, gravity is generally assumed to be quantum
at a fundamental level, just like other interactions. In
principle, however, it is possible to explore the alternative
possibility that gravity is intrinsically non-quantum
("classical"), but the interpretation of some of the
dynamical laws of quantum field theory would be suitably modified
so as to maintain agreement with experiments and observations
while at the same time achieving theoretical correspondences
between GTR and quantum physics.
Quantum superposition of particles and their
gravity
The basis of the understanding of quantum mechanics is the
so-called double-slit experiment, where
individual particles are directed to two very narrow and closely
spaced slits in an otherwise impermeable shielding (described in §1.1, passage "Corpuscular-wave
dualism"). The particles behave as if they pass through both
slits at the same time and on the other side of the partition
they would interfere with themselves and fall
into the places described by the wave function. However, if we
measure which slit the particle passes through, there is no
interference and the particles fall into places opposite the
slits. This works for photons, electrons, and heavier and more
complex particles.
From the point of view of the relationship between
gravity and quantum physics, it may be interesting to ask the
question: "What happens to the gravitational field of a
mass particle when it passes through a double slit?".
If a particle passes straight through, without interference, its
gravitational field will match where it is currently on its
trajectory in front of and behind the slit. A more complicated
situation occurs when a particle passes seemingly through both
slits, with interference on the other side. Does the particle's
gravitational field also split as if it were distributed
according to a stochastic wave distribution and then converge at
the point of positive interference? This would be the case if
gravity were quantum in nature. However, if the particle's
gravity followed a classical trajectory, it would indicate that
gravity is not quantum in nature...?..
We can imagine other implications of a thought
experiment with a particle passing through a double slit that
quantumly interferes behind the slits. If the gravitational field
generated by this particle is classical, we can in principle
measure it with high enough accuracy to determine the position of
the particle without disturbing it. This measurement should make
it possible to reveal which slit the particle passed through.
Would that prevent the particles from superposing? - why? Or
would we violate the quantum uncertainty principle by knowing the
particle's position and momentum with too much precision? The
relations between the structure of spacetime - gravity - and
quantum physics could also show the hidden determinism
lying somewhere deep in quantum physics..?..
No physical experiments of this kind will be
feasible in the foreseeable future, so far these are only
hypothetical thought experiments.
The
mystery of the quantum energy of the vacuum <-> Cosmological constant
According to quantum field theory (§1.2,
passage "Quantum field theory"), even an ideal vacuum is
not a completely empty space, but quantum fluctuations
take place in it - it is filled with virtual quanta,
particles and antiparticles, which are constantly created and
instantly disappear. The vast majority of interactions of virtual
quanta that arise in this way cancel each other out on average,
and the vacuum basically appears as empty space. Quantum physics
requires that the interactions of all possible
quanta and particles be included, giving a sum total of infinite
values, which are removed by renormalization.
From the point of view of the general theory of
relativity, these quantum fluctuations create energy, which due
to universal action is added to the cosmological constant,
considered the immanent energy of the vacuum. Using the
astronomically determined cosmological constant, the energy
density of the vacuum is determined to be approximately 10-9 Joule/m3 (~5 GeV/m3). If we wanted to
explain the cosmological constant as vacuum energy coming from
virtual quantum fluctuations, quantum physics would provide an
incomparably larger absurd value of ~1060
-10113 J/m3 by including a huge amount of quantum fluctuations!
This huge mismatch of up to 120 orders of magnitude is sometimes
metaphorically called a "vacuum catastrophe"...
A completely "meticulous" quantization of
the gravitational field, including the inclusion of virtual
particles of quantum fluctuations that either diverge at Planck
microscales or give a completely unrealistically high vacuum
energy value relative to the cosmological constant, may not be
justified. It is likely that only real particles
created by interactions can contribute to gravity (including dark
energy), not all the virtual ones that could be drawn in Feynman
diagrams. After all, it should be kept in mind that we don't have
(and probably never will have) any experimental data about the
real shape of gravitational action in quantum microscales, it's
all just far-reaching extrapolations from large scales..?..
From a realistic point of view, we can consider the
cosmological constant as another independent
astrophysical constant that no theory can explain.
From another point of view, the vacuum quantum
energy problem is discussed in §B.4, the passage "Giant quantum microfluctuations".
Some new alternative theories related to quantum gravity :
Discrete structure of spacetime
A common denominator of a number of problems with singularities and infinities in nonquantum and quantum field
theory are limit transitions of the type r ® 0,
x ® 0, t ®
0, etc., in which
field values (or even space-time metrics) often diverge. These
limit transitions are made possible by the continuous
nature of
spacetime, in which we can investigate the behavior of physical
fields in principle up to infinitesimal scales of a geometric
point.
But what if, however, the continuity of
space-time is the same illusion, as it was until the 19th century
the continuity of matter? As modern physics has come to know
about the discrete quantum structure of matter, the hypothesis is
offered that space-time is also
quantized - consists
of a huge but numerous number of very small, indivisible
elementary "cells", of a kind of "space-time
dust". If these hypothetical "quantum
geometries"
are small enough, e.g. of the order of Planck's length 10-33 cm, spacetime appears to be completely
continuous, as no physical processes investigated so far can
distinguish finer distances than about 10-15 cm.
Note: We have
already encountered the quantum structure of spacetime in the
previous §B.4 in the field of quantum geometrodynamics. However,
it was an "induced" quantum structure
created by using the laws of quantum physics on gravity as a
curved spacetime. However, this is the primary one,
an axiomatically postulated discrete structure of spacetime
itself (so to speak "from God").
In such a quantum geometry with a discrete spacetime structure, there are no limit transitions
to zero spatial distances and time intervals, so infinite
divergent values of fields and non-physical singularities of
spacetime should not arise.
This idea could be important for quantum field theory
in general, as the energy of quantums is inversely proportional
to the wavelength of the respective "wave ball". If the
wavelengths cannot be less than a certain lower limit, because a
shorter length simply does not exist, then the energy of
the quanta is limited from above - quanta with infinite
energy, which cause such difficulties in quantum field theories,
are precluded.
Loop quantum gravity
On the development of the above-mentioned ideas about the nature
of space for discrete connection with quantum field theory is
based so called loop quantum
gravity theory [...]. Since the rotational momentum -
spin plays an important role in
quantum physics, not Cartesian coordinate networks were used to
quantify spacetime, but it is modeled using the so-called spin network . ....
The founder of loop quantum gravity is
Abhay Ashketar, a physicist of Indian descent who works at the
University of Pennsylvania. The theory originated and developed
from the 1980s and 1990s and T.Jacobson, L.Smolin, C.Rovelli,
J.Baez, Ch.Isham, M.Boyowald and other pioneers of loop quantum
gravity work on it together with Ashtekar.
A. Ashketar first expressed the
3-dimensional space metric using new variables using the SU(2)
(or SO(3)) formalism of the calibration field symmetries. His
collaborators then showed that the Hilbert space of the quantized
calibration field SU(2) can be generated by so-called spin networks, based on the twistor
theory *) of
R.Penrose [...]. These spin networks are
taken as basic fundamental elements in loop
theory creating a structure of space that thus becomes discrete.
It can be imagined as a kind of "skeleton" or
"kit" of one-dimensional fibers (graphs). The spin
network does not exist in some space into which it would be
nested, but the space itself creates
(or creates what we perceive as space on a larger scale). At the
submicroscopic level, space is no longer homogeneous, but has a
fine-grained structure - it consists of countless interconnected
"rings" or "loops" of Planck's dimensions
.
*) We did not introduce twistors
in our book, the author is not convinced of their importance...
Otherwise, however, we used and discussed a number of other ideas
and concepts of the excellent relativistic physicist R.Penrose.
The development of the spin
network over time creates a kind of "spin foam",
which can be put into the context of the above-mentioned quantum
approach Feynman path integrals.
................
.....? ...... here comes a more specific outline of the
methodology of loop gravity ....? .....
.........
The loop quantum theory of gravity is considered to be a certain alternative approach, to some extent competitive with
the theory of superstrings (briefly
outlined at the end of the following §B.6 "Unification
of fundamental interactions. Supergravity. Superstrings.").
Ashketar's loop quantum gravity does not aim to unify the four
basic interactions - electromagnetic, strong, weak and
gravitational, but "only" to unite quantum theory with
gravity as space-time physics. Therefore, we have included a
brief mention of it in this §B.5 on quantum gravity, while
superstrings in the following §B.6 on unitary field theories ...
The real contribution of the loop theory
of gravity is the concept of a discrete
structure of spacetime. However, the current specific formulation of
"spin foam", with its excessive mathematical complexity
and "artificiality", probably disqualifies it as a credible theory of the
real physical nature of gravity and other fields (in the spirit of the principle of simplicity
of fundamental knowledge)..?..
Entropic nature hypothesis of gravity? Probably not !
In §4.7 "Quantum
radiation and the thermodynamics of black holes" were from the point of
view of thermodynamics and information statistics were analyzed
the connection between entropy and gravity
of a black hole, which in the 70s and analyzed
J.D.Bekenstein and S.Hawking is added concepts of quantum evaporation of black holes. This created the "thermodynamics of black holes". All this was within the
curved spacetime of the general
theory of relativity, against which the processes of quantum field theory were analyzed. Entropy S (defined as the ratio of
the heat dQ supplied to the system to the absolute temperature T:
dS = dQ/T) here it
was considered to be an important quantity, which, however, arose
secondarily from specific interactions of
quantums and particles with each other and with the gravitational
field - as a close analogy.
From the completely opposite
side to this issue came up the Dutch physicist Erik
Verlinde [E.P.Verlinde: On the Origin
of Gravity and the Laws of Newton; arXiv: 1001.0785 (2010)] , which was based on the
well-known fact that with each macroscopic process in a
continuous environment, entropy
changes from
a thermodynamic point of view (discussed in
more detail in §1.1 "Atoms and Atomic Nuclei", passage
"Thermals and Thermodynamics", entropy - "Maxwell's
Demon"). E.g. when we stretch the spring or
rubber band, it tends to return to its original length - we feel an elastic force
(macroscopically described by Hooke's law), whose physical origin is in the
electromagnetic interaction between the atoms of matter. At the
same time, from a thermodynamic point of view, it is accompanied
by a change in entropy: a stretched spring or rubber
band has a lower entropy than in the equilibrium
contracted state, into which it tries to get in accordance with
the 2nd act of thermodynamics. The energy balance during
stretching by Dx can be expressed here by the
entropy S using the relation :
F. Dx = T. DS,
where F is
the elastic force, T is the thermodynamic temperature. The product T.DS is in thermodynamics the increase of thermal energy DQ due to the work F.Dx
performed when the spring is stretched by Dx.
When this analogy is logically
reversed, the
elastic force can be considered as a consequence
of the growth of entropy - a kind of "entropic
force".
It was this logical inversion that E.Verlinde used in 2010 for
his peculiar hypothesis about the origin of gravity. Verlinde
declared entropy to be the primary
very fundamental quantity whose growth causes the "entropic force that is the essence
of gravity.
So there is no gravity ! *) - we observe it only as an apparent force, a macroscopic manifestation of entropy growth with random statistical behavior of
microscopic particle-quantum field systems. The
entropic force causes the motion of bodies, which leads to
mechanical work dA = F.dx. This is manifested by heat leading to
a change in entropy: T.dS = F.dx (ie F
= T. grad S) .
*) This concept is heuristically somewhat
similar to LeSage's hypothesis of the mechanical origin
of gravity, discussed in §1.3 "Mechanical
LeSage hypothesis of gravity",
according to which gravity as a separate force also does
not exist, is caused by impacts of small moving
particles ...
The second basic starting point of
Verlinde theory is a holographic
principle
(see §4.7, passage "Loss of information in a black
hole. Holographic principle."):
information - entropy - is located on the border
of the
investigated system - holographic
projection screen. This made it possible to
"derive" Newton's law of gravity of inverted squares in
a simple spherical model with a material body in the middle :
A brief outline: Around the
central body mass M to define a spherical surface of
radius R. This area in Verlinde theory serves as a holographic
projection screen, which is located all the information on
the bodyM. To the surface of this sphere can then in this
model formally assign thermodynamic temperature
T = Mc2/(2.N.kB), where kB is Boltzmann's constant, and N is the number of
particles - the body of information bits M. The density of
information bits on the projection screen is inversely
proportional to the size of the screen, i.e. R-2, so T ~ M/R2. We insert a test
particle of mass m into the investigated sphere. When
we move it in the radial direction by a distance Dx, the entropy of
the sphere changes by DS = m.Dx. Substituting these relations into the above-mentioned
Verlind relation F Dx = T.DS for the entropic
force we get the ratio F ~ mM/R2, which corresponds to the standard Newton's law
of gravity inverted squares of distance. Newton's law of
gravitation "emerged" from these thermodynamic
considerations without assuming the existence of a gravitational
force at the microscopic level ...
In 2016, E.Verlinde further
incorporated quantum fluctuations of vacuum into
his entropic hypothesis as another source of entropic force. This
created another contribution to the "entropic force -
gravity", which generally does not decrease with the square
of the distance. Verlinde, using his appropriate modeling, tries
to alternatively explain the problem of dark matter ("The future evolution of the universe.
Hidden matter") - this would be caused by quantum fluctuations inside
the holographic projection surface, and dark energy ("Accelerated expansion
of the universe? Dark energy?") in space - caused by quantum fluctuations outside this
surface and in the whole space [Verlinde E
.: Emergent Gravity and the Dark Universe ; arXiv:
1611.02269v2 (2016)] ..?..
Opponents'
frequent objections focus on the spherical
symmetry of
Verlinde's models, which are not concise for the actual
distribution of matter in space; but this
could be addressed in further generalizations. However, the fundamental objection against to Verlind's theory is physico-gnoseological: a change in entropy is not the cause gravitational or other forces in physical
systems, but only one of the consequences
of specific physical
interactions taking place in the system. And besides, the second
basic postulate, the holographic
principle, is
only an unconfirmed hypothesis (theoretically
based only on the horizons of black holes, see §4.7). So it's actually
the opposite: the changes in entropy are caused by, among
other things, the gravitational force...
So with that gravity it will
probably be different..!..
| B.4. Quantum geometrodynamics | B.6. Unification of fundamental interactions. Supergravity. Superstrings. |
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||