Versatility - a basic property and key to understanding the nature of gravity

2.2. Universality - the basic property and the key to understanding the nature of gravity

Law of free fall, inertia and gravitational mass
In §1.2 "Newton's law of gravitation" we have shown that the combination of the laws of classical mechanics with the law of general gravity results in a remarkable property of universal action of gravity on the motion of bodies, independend of their mass (which disappears from the equation of motion - it will be shortenes). Thus, Galilei already had the basic key to understanding the nature of gravity in its law of free fall, according to which all bodies fall to the ground with the same acceleration regardless of their composition and weight. This specific property of gravity, now called universality, has long remained virtually unnoticed. Only Albert Einstein understood that it is the universality of gravitational action, that is the most important property of gravity, and he drew the appropriate physical consequences from it and thus built his general theory of relativity as the physics of gravity and the properties of space-time.
The mass of a body manifests itself in physical phenomena in essentially three ways, and we can distinguish three types of mass accordingly :

According to Newton's law of action and reaction, in Newton's theory of gravity, the active and passive gravity are the same. Here so far we notice only the inertial and passive gravitational masses; we will consider the gravitational field as given, already"finished" (the question of excitation of the gravitational field will be discussed in §2.5 "Einstein's equations of the gravitational field").
The material test particle will move in the gravitational field according to the equation

In other words, the universality of gravitational action here says that for each body the inertial and gravitional mass are the same: m_i = m_g (more precisely, these masses are proportional and the unit proportionality constants, ie the equality of both masses, is achieved by a suitable choice of units). The masses in equation (2.4) are then truncated and the motion in the gravitational field is given by the equation d²r/dt² = grad j , which in accordance with the criterion of universality does not contain any individual characteristics of the moving body.

Experience and accurate measurements (see below) show that the inertial and gravitational mass is actually the same for all bodies. Such equality does not follow from Newton's theory, from its point of view it is a remarkable coincidence that cannot be explained or justified in any way. In Newton's theory, gravitional mass describes in fact a completely different property of bodies than inertial mass. Gravitational mass expresses the ability of a given body to gravitationally attract to other material objects, while the inertial mass characterizes the "resistance" of a given body against to mechanical acceleration with respect to an inertial system. Only Einstein's general theory of relativity, based on the properties of spacetime, explains this equality of inertial and gravitational mass in a completely natural way.

Composing inertial and gravitational forces
The fact that gravitational and inertial forces have the same physical nature and can be composed together can be clearly illustrated by a simple imaginary experiment (which can be realized in practice without any problems). We will prepare a railway wagon with a perfectly flat floor and ceiling, with closed doors and windows. With the help of a locomotive, we will run it on a straight smooth track at a constant speed (for example, 80 km/h). We place a heavy billiard ball on the floor of the wagon and release a balloon filled with hydrogen or helium. As long as the wagon is moving at a constant speed, the ball will lie in a certain place on the floor and the balloon will float above it in a certain place on the ceiling. When the wagon starts to brake, the ball it begins to move forward on the floor due to the inertia. Surprisingly, we see that the balloon began to move in the opposite direction across the ceiling, backwards against the movement of the wagon. However, this is not because the law of inertia does not apply to the balloon. The reason is that the inertial forces created by braking combined with the gravitational forces from the Earth - a "sloping" gravitational field was created, as if the wagon were tilted forward. In this resulting (changed) gravitational field, the balloon is lightened, according to standard Archimedes' law, not vertically upwards, but in a somewhat oblique direction, and begins to move backwards. If we performed this experiment in a vacuum, of course, the balloon would move in the same direction as the heavy sphere (and he did not float to the ceiling, but he was rolling on the floor...) .

Gravity and kinematics of motion
Thus, in a gravitational field, all bodies move with the same acceleration, regardless of their composition and mass. Different bodies thrown from the same point with the same (vector) velocity will move along exactly the same trajectories. This versatility, as noted by Einstein, is strikingly similar to the universality of kinematics. We will shed light on this key aspect of gravity in the imaginary experiment according to Fig.2.3. Imagine for a moment that there is no gravity and freely through space (engine off) moves rocket, in whos cabin one observer performs mechanical experiments; the second observer it watches from the outside through the transparent wall of the cabin.
If the indoor experimenter places, for example, a lead ball and a feather motionless next to each other at a certain "height" above the cabin floor, the two bodies will always "hang" next to each other at rest relative to the rocket floor; the same will be seen by the outside observer. However, if the engines is ignites and the rocket starts to move with constant acceleration, the situation will change. The inner observer will feel the "weight" and will see that all the bodies fall to the cabin floor. If he doesn't know about the rocket engines running, he says: "There's a force field in my cabin in which all the bodies fall with the same acceleration". The feather and the lead ball hit the cabin floor exactly at the same time, although their composition and weight are very different. He will recalls the Galileo's law of free fall and says: "This force field is a gravitational field. Probably my rocket is on the surface (or leaning against the surface - the situation in Fig.2.4) of a planet that is the source of the gravitational field that I observe.".

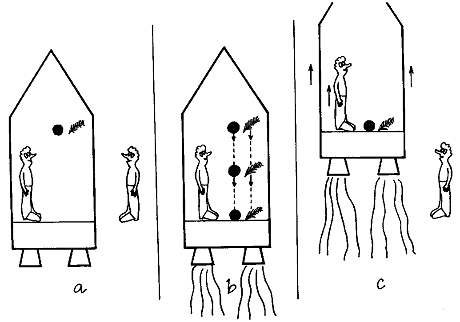
Fig.2.3. An imaginary experiment showing the "imitation" of a gravitational field in an accelerated frame of reference.
a) In the cabin of a rocket moving freely in space without gravity, Newton's law of inertia applies.
b) After turning on the rocket engines, the experimenter will feel heavy inside the cabin and all bodies (metal ball and feather) will fall to the floor with the same acceleration - from the point of view of the internal observer, there is a gravitational field in the cabin.
c) From the point of view of an external observer, however, there is no "real" gravitational field in the cabin, the equally accelerated movements of all bodies relative to the floor and walls of the cabin are a kinematic effect in the non-inertial frame of reference.
Note: In this imaginary experiment, of course, we assume that there is a vacuum in the free space and inside the cabin (the spacesuit is not drawn); the same in Fig.2.4.

However, the outside observer laughs at him because he has a different explanation: "There is no gravitational field inside the cabin! The inside observer feels the weight because it is accelerated with the cabin by the force of rocket engines. The lead ball and feather remain in place but the floor began to move against them with acceleration. That the ball and the feather collide with the floor at the same time is from a kinematic point of view evident. No gravity, but a non-inertial frame of reference in which an apparent field of inertial forces acts. "

We can imagine even the opposite situation (Fig.2.4), when the rocket cabin is supported by a longer rod on the surface of a planet. The experimenter inside the cabin will again observe that all bodies fall to the floor with the same acceleration and may consider this a consequence of the presence of a gravitational field with universal effects. However, if he recalls a dispute with an outside observer in the previous case, he may submit also other justification: "My rocket is in free space without gravity, but the rocket engines are turned on, that the entire rocket uniformly accelerating. The heaviness which I feel is the inertial resistance of my body weight against acceleration, falling bodies with the same acceleration is kinematic effect in non-inertial system. "

Compared to the previous case, however, there is a certain difference, which is still insignificant, but will play an important role in the next. The second explanation will be physically equivalent to the first explanation only locally, within a sufficiently small cabin. The gravitational field around the planet is inhomogeneous - its intensity decreases with height above the surface and the direction is always to the center of the planet. Therefore, if the cabin were too large, the inside observer would find that bodies at a higher height above the floor fall with slightly less acceleration than bodies closer to the floor, and the direction of fall of bodies in one corner of the cabin is somewhat different from the direction of fall in the opposite corner of the cabin. This behavior would no longer be explained by the accelerated movement of the cabin without gravity. Under the term "locally" will be understood in the following "in a sufficiently small region of spacetime, where the given gravitational field can be considered homogeneous".

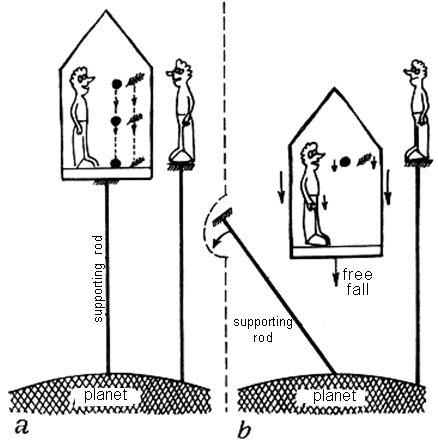Fig.2.4. An imaginary experiment showing the local indistinguishability of inertial and gravitational forces.
a) An observer inside a cabin supported by a fixed rod against the surface of a gravitational planet will observe a gravitational field with universal effects, in which both the lead ball and the light feather will fall with the same acceleration and fall to the floor at the same time. However, he could explain the same with the rocket engines running and the accelerated movement of the cabin; however, the outside observer will not agree.
b) After removing the support rod, the cabin with all objects inside will start to fall freely, there will be a state of weightlessness. The outside observer, of course, explains this by a free fall in a gravitational field, while the inner observer with the same right can be consider his cabin to be inertial without gravity.

If we remove the supporting rod in Fig.2.4, the rocket will start to fall to the surface of the planet in a free fall. Because all bodies, regardless of their composition and weight, fall in the gravitational field with the same acceleration, their mutual acceleration in the cabin will be zero - a state of weightlessness will be created. A feather and a lead ball remain motionless "hang" side by side at the same height above the vabin floor. The inner experimenter declares: "My cabin is an inertial system that moves freely in space without gravity." However, an outside observer (connected to the planet) has a different explanation: "The rocket's cabin and all its bodies inside fall freely in the planet's gravitational field. Because the gravitational field gives the same acceleration to both the feather and the lead ball and to the entire cabin, they will always fall side by side and together with the cabin, so that they will be at rest against its floor and walls." A cabin falling freely in a gravitational field is inertial to the inner observer, but again only locally inertial, because the gravitational field is inhomogeneous and thus inertiality is achieved in different places by somewhat different accelerations of free fall *).
*) All the above conclusions will also apply to (the fate of the inner observer far more favorable!) Variant, where instead of free fall to the surface, we choose the orbital motion of the 1st cosmic velocity around the planet. Such a state of weightlessness, caused by the universal compensation of gravitational and centrifugal forces, was personally tried all cosmonauts.

Which of the two observers described in the imaginary experiments is right? Internal or external? Whatever will perform any local (within the cabine) mechanical experiments, it is possible to completely equally explain how the presence of the gravitational field, or by the action of inertial forces in a non-inertial frame of reference. In such a non-inertial frame of reference (eg in the cabin of an accelerating rocket) we observe a field of "inertial forces", which for the external observer is of purely kinematic origin (and therefore "apparent"), but for the internal observer it is a real field having all the properties of the gravitational field - a universal effect on all phenomena. Conversely, a real (ie, excited by some matter, eg around a planet or star) gravitational field has locally the same properties as an inertial force field in a non-inertial system.

Equivalence principle - the universality of gravity
Inertia and gravity are therefore in a sense, two pages of the same coin: what one observer considers as inertia, for another observer is gravity, and vice versa. Gravitational and inertial forces cannot be distinguished from each other by any local experiment (there is no "local indicator" for them). We can thus express the so-called principle of equivalence :

The principle of equivalence can also be formulated as :
The trajectory of a body when moving in a gravitational field depends exclusively on its initial position and velocity, not on its structure, composition or other properties .

The consequence of the principle of equivalence is the indistinguishability between gravitational and inertial phenomena: acceleration and gravity are manifested in the same way, so the theory of accelerating systems (which is a general theory of relativity in the narrower sense) is also a theory of gravity. The fact of the equivalence of inertial and gravitational mass, which for a long time was considered a coincidence, was elevated by Einstein to the basic law of gravity and the basis of his general theory of relativity.
Comment: Sometimes differentiate two or three levels of the equivalence principle :
- Weak equivalence principle- the gravitational action of bodies does not depend on their mass and composition, the gravitational and inertial mass of bodies is equivalent (it is mutually proportional, with a suitable choice of units it is identical) .
- Strong principle of equivalence applies not only to mechanical, but also to electromagnetic processes. The mass corresponding to the energy of the electromagnetic field (as well as other interactions) should also have gravitational effects, see below.
At the beginning of the construction of GTR, A.Einstein proceeded from the weak principle of equivalence, and then gradually switched to its extension to electromagnetic processes. The current GTR is based on the strong principle of equivalence.
The principle of equivalence expresses the effect of the "already finished" gravitational field on material objects. In 2.5 "Einstein's equation of the gravitational field" we generalize it to the universality of excitation of the gravitational field by all matter-energy, regardless of its composition and nature. This completes the general theory of relativity as the physics of gravity and (curved) spacetime.

An important question arises as to whether the universality of gravitational action is limited to mechanical phenomena or applies to all physical processes. An indirect indication in favor of the second possibility is already given by the fact that bodies of very different composition fall in a gravitational field with the same acceleration. This finding of Galileo was verified by experiments by Eötvös (at the beginning of 20. century) with an accuracy of 10^-8, Dicke et al. (in1963) with an accuracy of 10^-11 [220] and Braginsky et al. (1977) with an accuracy of 10^-12 [31]. Bodies of different composition have different representations of electrons, protons and neutrons, different proportions of mass, eg of electromagnetic origin. Thus, if we measure the same inertial and gravitational mass for bodies of different composition, we can say that the gravitational field has the same effect on protons, neutrons, electrons and on the electromagnetic field itself. The effect of the gravitational field on light, resp. on electromagnetic waves, was also directly experimentally verified - gravitational spectral shift (§2.4 "Physical laws in curved spacetime", passage "Gravitational frequency shift" ) and curvature of light rays in the gravitational field ( §4.3 "Schwarzschild static black holes", passage "Deflection of particles and light in the Schwarzschild field").
The inertial mass of atoms is given mainly by the following components :
a) The rest mass of protons and neutrons; b) Rest mass of electrons; c) The binding potential energy of protons and neutrons in the atomic nucleus caused by strong nuclear interactions; d) Potential electrostatic energy of electrons and electrostatic energy of the nucleus; e) Kinetic energy of electrons, protons and neutrons; f) Effects related to vacuum polarization (formation of virtual particle-antiparticle pairs); g) Energy of weak interactions between nucleons in nuclei; h) Gravitational energy.
The contributions of strong, electromagnetic, weak and gravitational interactions to the mass of an object are approximatelly in the ratio :
- for an atom about 1 : 10^-2 : 10^-12 : 10^-40 ; - for macroscopic bodies about 1 : 10^-2 : 10^-12 : 10^-29 ; - for a star with the mass of the Sun 1 : 10^-2 : 10^-12 : 10^-16 .
By measurements of Eötvös, Dicke and Braginsky proven (with an accuracy of 10^-12) equality of inertial and gravitational mass for platinum (78 protons and electrons, 117 neutrons) and aluminum (13 protons and electrons, 14 neutrons) shows in a more detailed analysis, that the principle of equivalence is verified for the rest mass of protons and neutrons with an accuracy of 10^-11 and for an electron mass of about 10^-8. For the mass related to the nuclear binding energy of nucleons, the kinetic energy of nucleons in the nucleus (related to the Pauli principle) and the electrostatic energy of the nucleus, the verification of the principle of equivalence with an accuracy of ~10^-9 to 10^-10 applies. For the potential an kinetic energy of electrons is achieved the accuracy of 10^-6 to 10^-7.
Antimatter: gravitates or antigravitates ?
The basic pillar of Einstein's GTR principle of equivalence says that the action of gravity does not depend on the composition and structure of matter. The gravitational interaction between matter and antimatter should be identical. An object made of antimatter will thus fall in the gravitational field with the same acceleration as a body made of matter (here on the surface of the Earth its fall will take place with a known value of the gravitational acceleration of 9.81 m/s²). The law of free fall and the principle of equivalence are very accurately verified for ordinary matter composed of atoms consisting of electrons, protons and neutrons. Logically, we conclude that it also applies to individual elementary particles - ordinary (electrons, protons, neutrons), and probably also exotic (neutrinos, mesons, hyperons, ...). However, direct experimental verification of gravitational properties of individual isolated particles is very difficult (if not impossible), because these particles move at high speeds and show electromagnetic and strong interactions with the environment, much stronger than gravitational (discussed in the section "Antiparticles - antiatoms - antimatter - antisworlds", passage "Artificial production of antimatter" in the book "Nuclear physics and physics of ionizing radiation") .
But how is the case with antiparticles (positrons, antiprotons, antineutrons), "antiatoms" composed of them and in general in antimatter *)? We know from experiments on accelerators that particles and antiparticles have the same inertial mass. But will antimatter gravitate or antigravity ? The analysis of the probabilities of short-term existence of virtual electron-positron, proton-antiproton and other particle pairs ("vacuum polarization") shows that the results of Eötvös, Dicke and Braginsky measurements confirm the validity of the principle of equivalence for common antiparticles (such as positron and antiproton) with accuracy 10^-5 to 10^-6. So certainly for antimatter can not expect "antigravity" - no "falling up"! Antimatter will normally gravitate - so far it is not exactly measured whether with the same or slightly different gravitational constant than ordinary matter..?..
*) On the issue of antimatter see §1.5, passage "Antiparticles - antiatoms - antimatter - antisworlds" in the book "Nuclear physics and physics of ionizing radiation".
Experimental uncertainties about the gravitational properties of antiparticles and antimatter leave some room for hypotheses with a slightly different gravitational force of antimatter from ordinary matter. In some alternative or generalized theories of gravity, other fields and interactions are introduced (eg in Kaluza-Klein's 5-dimensional unitary theory of gravity + electromagnetism - §B.2, part "5-dimensional gravity-electromagnetism"), which in the quantum approach can be related to intermediate quantum-particles. In addition to the standard "tensor" graviton with spin 2, there is a "vector" graviphoton with spin 1 and also a "graviscalar" with spin 0. These contributions can be a source of violation of the equivalence principle. The consequence would be that the gravitational potential between two static mass objects m₁ and m₂ at a distance r would have an anomalous course :
V(r) = - G . ^m1 ^.^m2 /_r. (1+ F . e^-^r/d) ,
where in addition to the standard Newtonian gravitational potential G.m₁ .m₂ /r, the Yukawa potential e ^-^r
/d with range d also appears. F is the scaling constant of this complementary interaction, which could hypothetically differ slightly "+/-" for matter and antimatter..?..
It can therefore be said that the principle of equivalence is with relatively high accuracy proven for strong and electromagnetic interactions. With weak interaction, the contribution to the total mass of the body is relatively very small (of the order of about 10^-12), the accuracy of these experiments is not sufficient to completely reliable verification of the equivalence principle, however some indications in favor of its validity for weak interactions, exist here[105]. Regarding the principle of equivalence for the gravitational interaction, these experiments do not provide any information on the gravitational properties of gravitational energy (ie whether gravitational energy contributes equally to inertial and gravitational mass), because its share in the total mass of conventional macroscopic bodies is negligible (~10^-30). However, with increasing weight and compactness, the relative contribution of gravitational energy to the total mass of the body increases. For large planets like Jupiter it is already 10^-8, for the Sun 10^-6; for massive compact formations such as white dwarfs or neutron stars is even significantly higher. Comparison of real astronomically observed trajectories of such bodies with orbits predicted by celestial mechanics, or relativistic astrophysics, confirm the validity of the equivalence principle for gravitational energy, so far not with very high accuracy...

Cosmic verification of the law of free fall
The current space technology makes it possible, at least in principle, to verify the principle of equivalence in direct relation to Galileo's experiments with free fall. Instead of a very short track from the legendary Leaning Tower of Pisa, however, a very long "free fall" would be used at orbit the spacecraft around Earth many times. Ideologically, the principle of such an arrangement can be seen from Figure 2.3a above. In the cabin of a satellite orbiting freely in a gravitational field around the Earth, two test specimens of different compositions are freely placed in a weightless state. If the principle of equivalence applies, both bodies will orbit in the same geodetic path, their mutual position will not change even after a large number of cycles. For accurate verification, of course, the arrangement could not be as trivial as in Fig.2.3a, where an asymmetric gravitational attraction between the test specimens, objects in the cabin and with its walls would be manifested. The arrangement would have to be exactly symmetrical - concentric or coaxial, the position of the test specimens would be evaluated not visually, but by electronic sensing.
An experiment of this kind was designed in 1972 by experts from the University of Stanford under the leadership of P.W.Worden under the name STEP (Satellite Test Equivalence Principle). Using precision technology and sensitive methods of sensing the position of test specimens, the principle of equivalence could be verified in this way with an accuracy of up to 10^-18. So far, only a model of the device has been created, the actual experiment in orbit will hopefully be carried out after 2000.
As accurate as possible verification of the validity of the principle of equivalence for all kinds of interactions and in the widest possible range of physical situations is very important, because the whole general theory of relativity as the physics of space-time and gravitation, is based on the very exact validity of the principle of equivalence for all physical phenomena (ie absolute universality of gravitational interaction). The slightest reliably detected deviation would shake this theory in the very foundations..!..

Gravity - the only absolutely universal force
Gravity acts on all bodies, but also on energy - on all fields, because the physical fields has energy and thus also mass that can "gravitate". So gravity is the only universal force that acts on absolutely everything in this world!
The universality of gravitational action is a basic property that distinguishes gravity from all other types of forces in nature. The fields of gravitational and inertial forces are equivalent for all physical processes, the same physical laws apply to them and are therefore completely indistinguishable from each other locally. From the point of view of the general theory of relativity, it can be said that the inertial and gravitational forces have the samethe (common) physical nature; in the following paragraphs we will see that this common essence is the geometric properties of spacetime.
The versatility of gravity allowed us to convert gravity to kinematics. Kinematics is an expression of the geometric properties of space and time. Thus, we can expect in advance that if gravity changes the kinematics, it will also change the geometric properties of space and time. The statement about the universal action of gravity on all physical phenomena, expressed in Einstein's principle of equivalence, thus has far-reaching consequences and is the basis of Einstein's general theory of relativity.

General theory of relativity and the essence of gravity
The question of whether the general theory of relativity explains the essence of gravity cannot be answered other than: yes and no ! The general theory of relativity converted gravitational action into inertial motion - it combined gravity and inertia, identifying them with the geometric properties of spacetime. It converts the laws that govern gravity into the laws that govern space-time. Thus, unifying relationships between previously separated phenomena were discovered. To the question of the cause of gravitational action, the general theory of relativity answers with curved spacetime, but does it not explain why bodies in their vicinity curve spacetime? The general theory of relativity shows how, but not why. The only complete answer (but from the opposite side) could perhaps be given by a consistent unitary field theory - see the individual chapters of Appendix B "Unitary field theory". To the deepest foundation of all "why?" and "how next?" but we probably won't work out anyway..?..

Gravity, black holes and space-time physics :
Gravity in physics	General theory of relativity	Geometry and topology
Black holes	Relativistic cosmology	Unitary field theory
Anthropic principle or cosmic God
Nuclear physics and physics of ionizing radiation
AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy


2.1. Acceleration and gravity from the point of view of special theory of relativity		2.3. Local principle of equivalence

Universality of gravity - general theory of relativity - essence of gravity