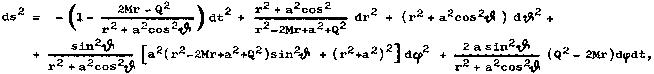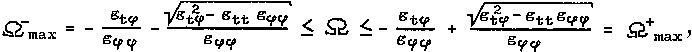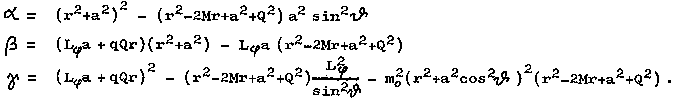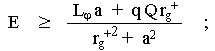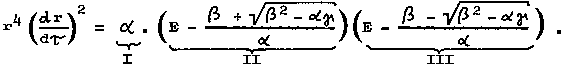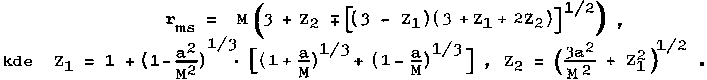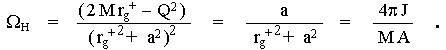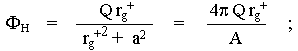Rotating black holes - energy extraction, portals in space
and time?
Chapter 4
B L A C K H O L E S
4.1. The
role of gravity in the formation and evolution of stars
4.2. The
final stages of stellar evolution. Gravitational
collapse
4.3. Schwarzschild
static black holes
4.4. Rotating and electrically charged Kerr-Newman black holes
4.5. The
"black hole has no hair" theorem
4.6. Laws
of black hole dynamics
4.7. Quantum
radiation and thermodynamics of black holes
4.8. Astrophysical
significance of black holes
4.9. Total
gravitational collapse - the biggest catastrophe in nature
4.4. Rotating and
electrically charged Kerr-Newman black holes
In the previous
chapters, it was gradually analyzed how by the
the complete
gravitational collapse of a spherically symmetric star (spherical non-rotating and electrically uncharged) creates a Schwarzschild black
hole. However, the conditions of exact spherical symmetry are
almost never actually met, with most stars rotating
in particular. The
question arises whether a black hole can also be caused by the
collapse of a rotating star, or whether the accelerating rotation
(centrifugal force) is able to prevent collapse? In Newtonian
physics, even the initially slow rotation of the star would
eventually prevail and stop the collapse. However, in the general
theory of relativity, it is shown that even with the collapse of
a rotating star, a black hole can eventually form, albeit in a
more complex way [222], [215], [227].
Collapse of a rotating star
A rotating star,
which is always "flattened" due to centrifugal force,
compresses into a disk-shaped formation (Fig.4.14a), a rapidly
rotating "pancake", during collapse (due to constantly
accelerating rotation due to maintaining angular
momentum), whose
diameter may exceed its thickness several times. If the angular momentum
is not too great (compared to the mass of the star), the collapse
can continue also in the equatorial plane and a black hole
is formed without further complications - a
rotating black hole.
A more complex situation occurs when the angular
momentum is large,
eg greater than the critical value J = M2 (see §3.6). In such a case, the
constantly accelerating rotation can tear the disc-shaped
"pancake" into several parts *) - see Fig.4.14c. Some parts that receive a high angular momentum will fly
away (and accordingly reduces the remaining
angular momentum of the system), but most will be gravitationally bound
and orbit around a common center of
gravity. During their circulation, these fragments will emit
gravitational waves (the system
has a large quadrupole moment rapidly changing with time) carrying away the rotational
energy and thus they will brake and converge (Fig.4.14c, d), until they
gradually merge (Fig.4.14 e) and creates the resulting rotating black hole with angular
momentum J <M2.
First, large fragments are slowed down and merged, because they (according to formula (2.82) ) emit the most intense gravitational
radiation.
*) Theoretically, there is
also the possibility of forming a rotating structure having the
shape of a toroid, in which the collapse would take place first
along a smaller radius and then (if the "longitudinal"
density of mass ~ energy is sufficient) or collapse along a
larger radius. In reality, however, it can be expected that in
such a toroid, immediately upon its formation, there will be
certain inhomogeneities and deformations, which will then grow
with time - the toroidal formation will disintegrate into several
fragments and further evolution will then proceed as
described above in the text (and the lower part of Fig.4.14).
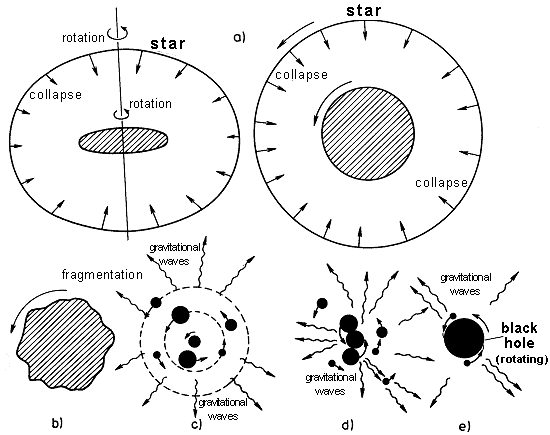
Fig.4.14. Gravitational collapse of a rotating star.
a) When a rotating star collapses, it compresses
into a sharply rotating disk-like formation. If the rotation is
not fast enough to stop the equatorial plane collapse, Kerr's
black hole will form.
b) With a
large angular momentum due to
the constantly accelerating rotation, instabilities may be
transported and the disk-shaped structure may be torn into
several parts.
c , d) The individual
fragments then revolve around a
common center of gravity, brake by the emission of gravitational
waves, gradually converge and connect.
e) Eventually,
this fragments are absorbed
and a rotating black hole is formed with a correspondingly
reduced rotational angular momentum.
Kerr-Newman geometry
However, a black hole created by the collapse of a
rotating star will no longer be spherically symmetric due to
rotation, but can only be axially
symmetric. The so-called Kerr-Newman space-time geometry is
considered to be a general solution for an axially symmetric
rotating and electrically charged black hole (for the reason see the following §4.5), which we described from a geometric point of view in
§3.6 "Kerr and Kerr-Newman geometry". Kerr-Newman
geometry is a generalization of Schwarzschild geometry roughly in
the sense that Schwarzschild geometry is spherical, while
Kerr-Newman geometry is generally elliptical. Some aspects of Kerr-Newman
geometry have been discussed in the aforementioned §3.6; here we
will continue this analysis in order to study the properties of rotating and electrically charged black holes,
whose spacetime is described by this geometry.
The element of the space-time
interval of Kerr-Newman geometry (3.41) in Boyer-Lindquist
coordinates was given in §3.6; we will
write it again here :
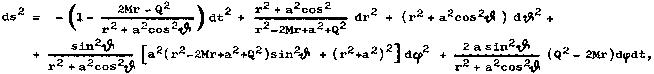 |
(4.25) |
where M is the total mass , Q is the
electric charge , J is the rotational angular momentum of the axially symmetric source of this
geometry; a = J / M is the specific rotational angular momentum
per unit mass of the black hole. The event
horizon r = rg+ has a radius
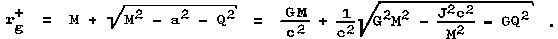 |
(4.26) |
The radius of the
horizon is thus smaller than that of an uncharged
non-rotating black hole of the same mass (for
this case of the Schwarzschild black hole, relation (4.26) passes
into relation (3.14), ie rg = 2M). In conventional spherical coordinates a horizon of a
rotating black hole flattened ellipsoid shape (like the rotation centrifugal force deforms the Earth
into a slightly flattened shape with a diameter of about 20km
difference between the equator and poles; see also notice on
Fig.4.16) and thus significantly, the
faster the black hole rotates - for the higher angular momentum J.
The question arises as to whether a rotation too fast could tear
the horizon by "centrifugal force"
(similar to what would happen with an
excessively fast spin, such as a grinding wheel or a circular
saw). In §4.6 "Laws
of black hole dynamics"
it will be shown that a black hole cannot be rotated
above a certain maximum "allowed" or
"insurmountable" speed of the so-called extreme
Kerr black hole, when M2 = J2/M2. If we try to throw a body into
a black hole rotating at almost extreme speed, which would spin
it even more, centrifugal forces will prevent this body from
penetrating close enough to the horizon, fly out and not be
absorbed; see also the commentary on inequality below (4.36).
For
the physics of black holes are especially interesting the areas
of space r ³ rg+
above the outer horizon - event horizon *). Everything
that takes place below the horizon r = rg+ is causally
separated
from the rest of the universe and has no effect. This applies even to the
inner horizon r = rg - = M - Ö(M2
-a2 -Q2) as well as the annular singularity around r = 0, described in §3.6 "Kerr
and Kerr-Newman geometry".
*) In §3.5 and 3.6, the analytical extension inside r = rg + was
discussed . However,
this internal solution below the horizon does not
seem to have physical significance. On the one
hand, this area is filled with the interior of the collapsing
body. In addition, the analogy of Birkhoff's theorem does not
apply to collapse with rotation (§3.4, theorem 3.3); Kerr's
metric does not describe the outer spacetime during the collapse,
but the asymptotic shape of the metric after the end of all
dynamic processes. Other reasons why the complex internal
geometric-topological structure of spacetime inside a rotating
black hole is not realized are discussed below in the section
"Black holes -
bridges to other universes? Time machines?", Fig.4.19.
Influence
of black hole rotation. Ergosphere.
To clarify the nature of the physical
phenomena that can take place around the Kerr-Newman black hole (and we will see that very interesting effects can be
expected here), we
will first look at the motion properties of the test particles.
The properties of the orbits of the
test particles in the field of the Kerr-Newman geometry
of a general black hole are considerably more complex than in the
case of the Schwarzschild geometry of a non-rotating uncharged
black hole. However, for qualitative knowledge of some basic
aspects of motion it is not necessary to solve complicated Carter equations (3.44), we will suffice with metric
coefficients in the space-time element (4.25).
Therefore, according to Fig.4.15a, let us
have a test particle (uncharged) in a place with specified
coordinates r,J , which moves only in the j direction; such a motion is called stationary because the space-time geometry around
the particle does not change. We will be
interested in the angular velocity with respect to the asymptotically rest
frame of reference W s dj /dt = (dj/dt)/(dt/dt) = uj/ut , where uj and ut are the respective components of
the four-velocity (we investigate the stationary motion, ie only
in the direction j, so uJ = ur = 0). This
angular velocity cannot be arbitrary, only values of W are permissible for which the 4-velocity u lies inside the light cone of the future :
u 2 = g
tt u t u t + 2 g t j u t u j + g jj u j u j <0
,
which, expressed by W, gives: gtt (ut)2
+ 2 gtj W (ut)2
+ gjj W2 (ut)2 < 0, i.e.
| g tt + 2 W g t j
+ W 2 g jj
< 0 . |
(4.27) |
Thus, the geometry of
spacetime "dictates" to a body located at a location
with given r and J a permissible angular velocity in
the range
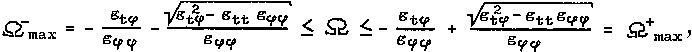 |
(4.28) |
where W-max is the maximum angular velocity of circulation
against the direction of rotation and W+max is the maximum velocity of circulation in
the direction of rotation of the black hole. For large distances r
from a black hole (or at its small angular momentum J®0) is W-max
» -1/r, W+max » 1/r, so the particle velocity u =
W .r Î <-1, +1> can be at most
equal to the speed of light, both in the direction of rotation
and against it, as is the case in the plane space-time STR
(movement allowed inside the light cone). As
you approach to the black hole, the value W-max increases, so the body
must move more slowly against the direction
of rotation of
the black hole, than if the rotation of the black hole were not (Fig.4.15a).
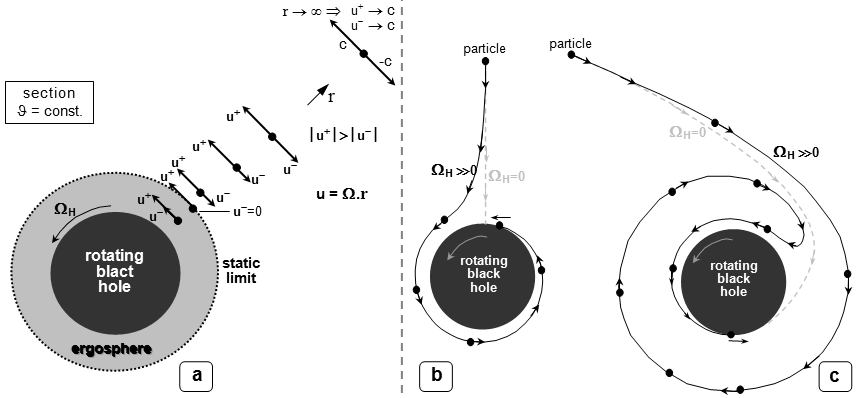 |
Fig.4.15. Tearing down
the motion of bodies near a rotating black hole.
a) The effect of dragging of local inertial
systems (tilting of light cones in the direction of
rotation of a black hole) leads to a gradual limitation
of the maximum possible speed u- movement
of bodies against the direction of rotation of a black
hole when approaching a black hole. Far from the black
hole (for r®¥) is u+ = c, u-
= -c, in finite distances outside the ergosphere it is u+ > 0, u-
<0, | u- | <| u+ |. On the static limit, however, u-
= 0, in the ergosphere even u- > 0 Þ
the body must necessarily move
in the direction of rotation of the black hole.
b) Pparticles free-falling on a rotating
black hole first move in the radial direction, but as
they approach the horizon, the movement turns in the
direction of rotation around the black hole; on the
horizon the particle "falls" in the tangential
direction and remains rotated along with the horizon.
c) A particle thrown at a black hole in
the opposite direction to the rotation of the black hole,
when approached the horizon, is forced by the entrainment
effect to change the direction of orbit and land on the
black hole as co-rotating - just like the particle in
Fig. b).
In Fig. b), c) the particle
trajectories for the case of non-rotating (Schwarzschild)
black holes ( WH = 0) are
plotted in dashed lines for comparison . |
Rotation black hole with
the outer geometry of space exhibits dragging
(entrainment) local inertial system, who free body forces perform a rotational movement about a black hole, and the more
so the nearer they are to the rotating black hole *). This is similar to a ball rotating in a viscous liquid
entraining the liquid near its surface. The "space-time
entrainment" effect of rotating gravity (by angular momentum) allows a
certain amount of energy to be obtained from a black hole, which
is related to its rotation (see "Extraction
of rotational energy"
below).
*) The effect of entrainment of inertial
systems in the gravitational field of a rotating body (not just
black holes) leads to a kind of "spin-orbital
interaction" between the rotation ("spin") of the
central gravitational body and the angular momentum of orbiting
bodies: motion of bodies, eg their energy (see relation (4.39)),
depends on the mutual orientation of the angular momentum of the
black hole and the orbital moment of the body.
In the gravitational field of rotating bodies, there is also a
"spin-spin interaction" with bodies that have their own
rotation. For example, a gyroscope in the gravitational field of
a body rotating at an angular velocity W will perform a precessional
motion with respect to an asymptotically inertial system - its
axis of rotation having an angle j will rotate at an angular
velocity w º dj/dt » W .rg+/r. This phenomenon is called the Lense-Thirring
effect according to the authors who first studied it
[248], see §2.5, passage "Rotating
gravity".
It can be said that Kerr-Newman
geometry in a sense rotates together with a black hole *) -
spacetime light cones are tilted in the direction of rotation
of the black hole. An observer located at a site with
coordinates r, J is at rest with respect to local
geometry, and the directions +j and -j are equivalent for it, only when it rotates (orbits) around a black hole at an
angular velocity
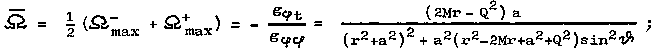 |
(4.29) |
such an observer is
called locally non-rotating.
*) For common rotating bodies (macroscopic objects, planets,
ordinary stars), the Lense-Thirring gravitational-rotational
effects are negligible, mostly at the limits of measurability (it
is discussed in §2.5, section "Rotating
gravity", passage "Possibilities
of verifying the effect of rotation"). However, an
intense gravitational vortex similar to a
massive tornado is created in the vicinity of a
rapidly rotating black hole ! The rotation of the black hole
carries the surrounding space with it and forces it to rotate in
a "vortex" depending on the speed of rotation of the
black hole and the distance from it. At a greater distance from
the rotating black hole, the space rotates very slowly, the
observer does not even feel it (similar to
far from a tornado, air flows only slowly).
As you approach the horizon, the space rotates faster and
"dragging" the observer in the direction of rotation (similar to increasing wind speed near a tornado). At the horizon, space rotates at the same speed as the
horizon itself, each observer is relentlessly drawn into the
vortex of rotation.
The effect of
entraining the motion of bodies near a rotating black hole has a
significant effect on the motion of particles and bodies falling
into a black hole. In Fig.4.15b,c the trajectories of two test
bodies falling into a rotating black hole (from the point of view
of the coordinate system of an external static observer) are
schematically drawn. The particle in Fig.4.15b moves in a free
fall in the radial direction towards the black hole. If only the
black hole did not rotate (static
Schwarzschild black hole), the particle
would move in a straight line to the horizon (initially faster and faster, close to the horizon it
would stop its fall from the point of view of an external
observer and would remain permanently "frozen" at a
given place on the horizon - discussed in § 4.2, passage "Two different views of gravitational collapse
- external and internal"). However, the rotation of the black hole causes the
particle's motion to turns in the direction of rotation around
the black hole as it approaches the horizon. The particle
"hits" the horizon in an almost tangential direction
and remains rotated with the horizon (from
the point of view of an external observer, the particle again
"freezes" on the rotating horizon forever; from the
point of view of the particle itself, it reaches the horizon in a
short time of its own time, flies through it and heads towards
the center of a black hole...). The second
particle in Fig.4.15c is thrown at the black hole in the opposite
direction to the rotation of the black hole. As you approach the
horizon, the effect of entrainment gradually forces you to
reverse the direction of orbit and lands on the black hole as a
co-rotating - it ends up in the same way as the particles in case
b).
Because real bodies can only move inside
the light cone, this tilting of the space-time light cones limits the maximum possible speed of movement of
the body against the direction of rotation of the black hole, from the
original value equal to the speed of light to a value the lower
the closer it is to the black hole (as shown above). On the surface given by the equation
| r = r S =
M + Ö (M 2 - a 2 cos 2
J - Q 2 ) |
(4.30) |
the maximum possible speed of the stationary
observer against the direction of rotation of the black hole is
already zero. This surface (in the shape of a
rotating ellipsoid, Fig.4.16), on which no object can move
against the direction of rotation of the black hole (gt j = 0), is called the static limit;
outside this limit there may be static (immobile with respect to
infinity) bodies, inside not. The area spread between the static
boundary and the horizon is called the ergosphere.
Inside the ergosphere, the entrainment is already so strong that
no body can remain still here; it is inevitably drawn
into rotation and its rotation around the black hole is
not prevented by any force - the light cones are completely
turned in the direction of rotation of the black hole. The
ergosphere (which only rotating black holes have) is the largest
in the "equatorial" region and narrows towards the
poles, where the static limit r = rS touches the horizon r = rg+ (Fig.4.16).
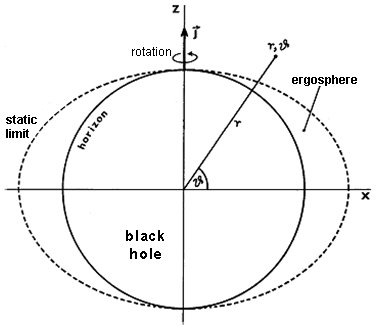 |
Fig.4.16.
Schematic drawing of
the horizon, static limits and region of the ergosphere
of a rotating Kerr-Newman black hole with a rotational
angular momentum J in the direction of the Z axis. This is a "side"
view - from the equator side; the "top" view
(from the pole side) is in Fig.4.17.
Note: The r, J coordinates marked in the figure
for better orientation are not common spherical
coordinates! Near a rotating black hole, the coordinates
r, J differ from the spherical
coordinates because they are "elliptical"
(spheroidal) Boyer-Lindquist coordinates (§3.6). In
common spherical coordinates, the horizon of a rotating
black hole has a flattened ellipsoidal shape. |
In the ergosphere, there are orbits on which
the particles have a negative total energy
with respect to infinity - the binding energy exceeds the proper
mass of the particle *). When passing over the static limit r = rS, the time component
of the metric tensor goo changes sign and becomes negative. Therefore, the
energy E = m gik uk
= m(goou°
+ goaua) a
particle of mass m moving at the velocity ua may become negative for some orbits of the test
particle. Such a particle with negative energy cannot leave the
ergosphere and, when absorbed by a black hole, brings negative
energy below the horizon with respect to infinity - it reduces
the weight of the black hole. Negative energy geodesics are
completely enclosed within the ergosphere, so that no free-moving
particles from the outer region can enter the negative energy
orbit; to achieve a negative energy orbit, the body inside the
ergosphere must be given additional (non-gravitational)
acceleration - see the Penrose process below.
*) From the analysis of the relation (4.34 ") for energy of
particles in the Kerr-Newman field implies that for the E <0
it is necessary an orbit with opposite-direction motion (Lj <0),
whose parameters r,.r,Lj meet a certain (generally relatively complicated)
inequality [8]; it follows from this inequality that the boundary
of the region containing negative energy orbits is precisely the
static limit given by equation (4.30).
Rotational
energy extraction:
Penrose process ; Superradiation; Blandford-Znajek process
Gaining a certain amount of energy
from a black hole related to its rotation is generally made
possible by the effect of "entrainment of space-time"
(local inertial systems) by the angular momentum of a rotating gravitational
field. The ergosphere
has the interesting property (and hence its
name - Greek ergos = work ) that it is possible to obtain from the
black hole the part of energy (~ matter) that is related to
rotation. Penrose [205] investigated the following effect
(Fig.4.17): if body A enters the ergosphere and disintegrates here into two parts B and C so
that one part, such as B , enters the opposite-direction orbit with negative energy and
is absorbed by a black hole, the second part C
can recoil and fly out of ergosphere with greater
energy than
the original body, while reducing the rotational angular momentum
of the black hole. This phenomenon, which makes it possible to
extract rotational energy and angular momentum from a black hole, is
now called the Penrose process.

Fig.4.17. Penrose's process of obtaining energy from the
ergosphere of a rotating black hole. Body A flies into the
ergosphere and there, at the appropriate time, splits into two
bodies B and C so that body B enters an
orbit with negative energy (with respect to infinity) and is
absorbed by a black hole. The second part C then flips
from ergosphere with more energy than the original body A
.
If the body A
had (with respect to infinity) the total energy EA
and the absorbed body B the energy EB <0 (got into orbit with
negative energy), the change in the mass of the black hole when
absorption will be DM = EB
<0. Total energy balance then it will look like this:
| E C = E A - D M
> E A ; |
(4.31) |
therefore, the total energy
obtained in this process is
| D E = E C - E A
= - D M > 0
. |
(4.31 ') |
The balance of kinetic
energy is also interesting; for this purpose, we divide the total
energy of the body into the kinetic energy Ekin and the rest mass: EA
= EAkin + mA.c2, EC = ECkin + mCc2. The obtained kinetic energy DEkin
= ECkin - EAkin = EC - mCc2
- EA +mAc2 then after substituting from (4.31) and mA = mB + mC it comes out
| D E kin = m B . c 2
- D M ; |
(4.32) |
in other words, all the
rest mass of the absorbed body B and, in addition, part of the
mass of the black hole were converted into the kinetic energy of
the flying body C.
A black hole, if it has a maximum
(extreme) rotational speed, can theoretically store up to 42% (of
mc2) of its mass in the form of rotational energy. This energy is contained in a rotating
gravitational field outside the horizon, so it can in principle be drawn.
Regarding the practical
(astrophysical) significance of the Penrose process, various
mechanisms and arrangements have been proposed for obtaining
energy from rotating black holes [204],
[205] *) .
*) Penrose even designed a curious
sci-fi project "black hole power plant" using energy
obtained by throwing waste into a rotating black hole. Waste
containers are thrown into a black hole, the lid opens inside the
ergosphere and the waste is "poured" into a path with
negative energy. The containers thus gain considerable kinetic
energy through the Penrose process, they fly out of the
ergosphere quickly and can impact the turbine blades connected to
the electric generator.
However, a more detailed analysis of the
motion of bodies in the Penrose process by Bardeen, Press and
Teukolský [8] showed, that the decay of a body within the
ergosphere would have to take place with a very
high mutual speed of both fragments - at least c/2. Therefore,
for macroscopic bodies, the Penrose process is unlikely to be
astrophysically significant; we do not know the physical
processes that could give such great mutual velocities to
macroscopic material objects. For charged particles, however,
such a mechanism may be a strong magnetic field around a black
hole - the so-called Blandford-Znajek
process
outlined below.
Another
possibility would be to inject unstable particles (eg
mesons m, p or K, see "Elementary particles and their properties") into the ergosphere, which
would decay into muons, electrons and neutrinos inside the
ergosphere. These secondary particles would fly from each other
at relativistic velocities (> c/2), so that they could be
accelerated by the Penrose process due to the rotation of the
black hole. However, the "practical use" of the kinetic
energy of these accelerated particles flying out of the
ergosphere would be very difficult (cf.
"Antiparticles - antiatoms -
antimatter - antiworlds").
Superradiation
The wave (radiation) similar to Penrose's
process is the effect of so-called superradiation
[287], [8],
when a wave incident on a rotating black hole is - if it has a
suitable wavelength - amplified
by a black hole at
the expense of the rotational energy of a black hole. Let us have
a (monochromatic) wave of a classical field with frequency w, angular momentum (axial quantum number) l and possibly an electric charge q, which
hits (from infinity) on a black hole. In a stationary axially
symmetric Kerr-Newman field, such a wave will be described by the
function (solving the wave equation of the respective field) y(t,r,J,j) =
F(r,J) e -i w t e i l j ; for scalar and electromagnetic fields it
is possible to separate variables, ie F(r,J) can
be written in the form of the product of two functions: F(r,J) = R(r). S(J)
[43], [246]. Because the Kerr-Newman black hole is stationary and
axisymmetrically, the quanties w and l will be integrals of motion. Part of the
wave will be absorbed and after interacting with the black hole,
the "scattered" wave, which will have the same
frequency w,
will continue to move, but generally a different
amplitude. Changes in the mass, charge, angular
momentum, and area
of a black hole during this interaction are bound by the 1st law of Black Hole Mechanics (see §4.6, equation (4.50)) :
d M = ( k / 8 p ) d A + W d J + F d Q
.
The ratio of energy
flow, angular momentum and charge (generally admit that
the wave can also carry an electric charge q) in the incident and
scattered wave is equal to w : l : q, so thanks to the conservation of
energy and angular momentum, changes in the relevant
parameters will be black in the same ratio holes dM : dJ : dQ = w : l : q . The first law of black hole
dynamics then gives
d M ( 1 - W l / w - F q / w ) = ( k / 8 p ) d A
.
Because according to the
2nd law of black hole dynamics (see §4.6; we assume that the
considered wave satisfies the energy condition (2.60) of
non-negative local energy density for each observer) is dA> 0, the inequality will apply
d M ( w - l W - q F ) ³ 0 .
If it is
w < l W + q F
(sufficiently low wave
frequency), the change in the mass of the black hole dM <0 will be negative, so that the
black hole will give energy to the
waves.
Thus, as such a wave interacts with a black hole, its amplitude
increases: even if the wave is partially absorbed, the scattered
portion may receive more energy from the black hole than the
incident wave had - the wave amplifies at the expense of the black
hole's rotational energy. It can be compared to a gravitational
"maser". The effect of superradiation could have some
astrophysical significance *); for black holes of stellar masses
of frequency w satisfying the condition of
superradiation fall into the field of radio waves. Superradiation
can also lead to one interesting effect for black hole physics.
At the end of the last paragraph, it was shown that the orbits of
the particles around the Schwarzschild black hole are always
unstable due to losses by gravitational radiation. However, the
effect of superradiation amplification of gravitational waves
allows the existence of some "floating
orbits"
near the rotating black hole, on which the losses by radiating
gravitational waves are compensated by the energy obtained from
the black hole by the superradiation scattering of these radiated
gravitational waves [210] .
*) Based on the effect of
superradiation, some thought projects [210] have also been
proposed to allow highly developed civilizations to draw large
amounts of energy from rotating black holes, as well as the
"black hole bomb" mechanism: when a black hole is
surrounded by a spherical mirror, the electromagnetic waves will
be reflected many times to the black hole and amplified by
superradiation ("positive feedback" will be created),
so that their intensity (energy) will increase avalanche until
the explosion.
This is how the process of
superradiation for "boson" classical arrays with
integer spin takes place. In the case of "fermion"
classical fields, it turns out that superradiation does not
occur. This is caused by the fact that the energy-momentum tensor
of the classical field does not meet the half-integer spin energy
conditions (2.60), and therefore can not be applied mechanics 2.law black
holes, and from a quantum viewpoint, Pauli principle allows the
presence of only one particle at a time for a given frequency of scattering
wave, so that the scattered wave cannot be stronger than
the incident wave. Quantum aspects of superradiation and the
related effect of quantum evaporation of black holes will be
discussed in §4.7, section "Mechanism of quantum radiation".
Electromagnetic extraction of
rotational energy - Blandford-Znajek mechanism
Another interesting modification of the Penrose process, with the
participation of a strong magnetic field, was discussed by R.Blandford and
R.Znajek in an extensive work [20].
However, the charged particles swirling in the plasma of the
accretion disk around the black hole, represent an effective
electric current generating a magnetic field.
It turns out that an external very strong
magnetic field around a rotating black hole by its force
acting can the fast-moving charged particles to
introduce into negative energy orbits in the
ergosphere of a rotating Kerr black hole, which could lead to the
extraction of rotational energy (and angular momentum) from black
hole by the Penrose process. The extracted energy in the
ergosphere would be transmitted to an electromagnetic field,
which could then accelerate other charged particles. Such the Blandford-Znajek
mechanism could work inside accretion disks around
rotating black holes, where it could contribute to the energy of
relativistic jets from quasars and active galactic nuclei, see
§4.8 "Astrophysical significance of black holes", part "Thick
accretion disks. Quasars".
When a plasma of charged particles
orbits a rotating black hole, it creates a strong poloidal
magnetic field by rotating toroidal currents flowing in the
equatorial plane. The entrainment of space, and thus of magnetic
field lines by the rotation of a black hole (magnetic
power lines twist into a spiral), then induces
an intense electric field,
acting on the charged plasma particles in the direction along the
axis of rotation of the black hole. It accelerates these
particles at relativistic speeds - a powerful electric
generator is formated in the form of a stream of charged
particles. Some of them enter orbits with negative energy in the
ergosphere and fall into a black hole, while the extracted energy
strengthens the electromagnetic field. Other charged particles
are then electromagnetically accelerated by the extracted
rotational energy and transfer this energy to the plasma in the
jets by magnetohydrodynamic effects. Such a "gravito-magnetic
dynamo", driven by the rotation of a black hole,
could supply a considerable amount of energy to the jets
from the accretion disk.
Thus, the above mechanisms show
that rotating black holes are "alive" unlike "dead"
Schwarzschild black holes, from which no energy can be obtained (if we do not take into account accretion discs and
quantum phenomena).
This "liveliness" of rotating
black holes can have considerable astrophysical
significance (in
§4.8, section "Accretion
disks around black holes"
- "Thick accretion disks. Quasars"
will be discussed) .
The
motion of particles in the field of a rotating black hole
The motion
of test particles in the Kerr-Newman field of a general black
hole is given by equations (3.44). From equations (3.44a) and
(3.44b) we get for a particle with rest mass mo,
electric charge q, energy (with respect to infinity) E
and axial component of the angular momentum Lj (with respect to the axis of rotation of
a black hole) the relation
 |
(4.33) |
For the coefficients at
individual powers of energy E (which are functions of the
place and parameters of the test particle and the black hole),
introduces the designation [43] :
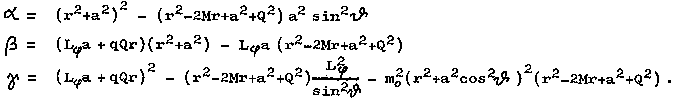 |
(4.33a)
(4.33b)
(4.33c)
|
The above equation then has the form
| (r2 + a2 cos2 J) [ (dr/dl)2
+ (dJ/dl)2 ] = a E2 - 2 b E + g . |
(4.34) |
If we express energy
from here
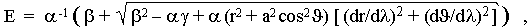 |
(4.34 ') |
is seen (given that a > 0 everywhere outside of the horizon)
that satisfies the energy inequality
| E
³ |
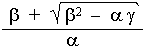 |
. |
(4.35) |
On the horizon r = rg+ is a = (rg+
2 + a2)2,
b = (Lj a + q Q rg+)(rg+
2 + a2),
g = (Lj a + q Q rg+)2, so the relation (4.35) is simplified here to :
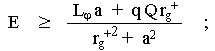 |
(4.36) |
only if this condition
is met can the particle reach the horizon and be absorbed.
Inequality (4.36), which from below limits the amount of energy
brought below the horizon when absorbing a body with charge q and
angular momentum Lj , plays an important role in the dynamics of black holes - see §4.6 "Laws
of black hole dynamics", where the relation (4.51) follows directly
from it.
The analysis of the
motion of test particles in Kerr-Newman geometry according to
Carter's equations (3.44) is generally quite complicated [228],
[48] , [237]. We achieve a certain simplification if we
investigate only the motion of particles in the
"equatorial" plane of a rotating black hole. Equatorial orbits in the Kerr-Newman black hole field are
at the same time the most interesting, the most characteristic
and the most important for practice. Due to the effect of dragging of
local inertial systems, for example, the accretion disk around
the rotating black hole (§4.8) is rotated into the equatorial
plane and the actual accretion takes place mainly from the
equatorial orbits. At great distances from the black hole, the effect of its rotation is small again and the trajectory of the particles here
does not depend too much on in which plane and
in which direction with respect to the axis of rotation of the
black hole the particle moves (the motion of the particle at
great distances is similar to that in the Schwarzschild field of
a non-rotating black hole).
The equation of the radial
component of motion in the equatorial plane of the Kerr-Newman
geometry is obtained from equation (4.34) by substituting J = p/2 and dJ/dl = 0 :
| r 4 ( dr / d t ) 2 = a E 2
- 2 b E + g . |
(4.37) |
a, b, g are
again denoted by quantities according to (4.33a,b,c), where,
however, sin2 J = 1 and cos2 J = 0. This equation can also be rewritten
in the form
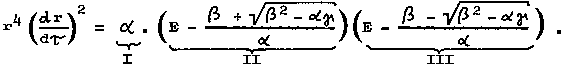 |
(4.37 ') |
The only factor that can
change the sign here is factor II; factors I and III are positive
(if energy E is positive). Quantity
| V
(r) = |
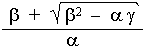 |
|
(4.38) |
here, therefore, it
plays the role of an effective
potential
for the radial component of the motion. A particle with energy E
can only get to places where V(r) £ E
in accordance with the general relation (4.35). The places where
V(r) = E are the turning points where the radial component of
the motion changes its direction. Circular
orbits are
(together with the condition V(r) = E) given by the condition
dV(r)/dr = 0. Thus, circular orbits are at the extremes of the
potential V(r), while the minima V(r) correspond to stable circular orbits. The conditions V(r) = E and
dV(r)/dr = 0 lead to the relations (for movement in the
equatorial plane, Lj = L)
 |
(4.39) |
wher` E º E / mo and` L º L / mo are the energy and the angular
momentum per unit mass of the test particles [8], [81]. The
angular and orbital velocities in orbit (from the point of view
of a distant observer) are equal
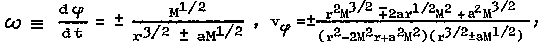 |
(4.39 ') |
which is a
generalization of 3.Kepler's law for circular equatorial orbits
in the Kerr metric of rotating black holes. Formulas (4.39) are
given for simplicity only for the Kerr black hole, ie for Q = 0
(otherwise the rest mass mo could not be included in E
and L and in addition would depend on the
specific charge q/mo of the test
particles). The upper signs applies to the movement in the
direction of rotation of the black hole (L.a> 0),
the lower signs for orbits against the direction
of rotation (L.a <0).
From relations (4.39) it can be seen that circular orbits can
exist only at such distances from the black hole for which the
condition is met
| r 3/2 - 3
M r 1/2 ± 2 a .M 1/2
> 0 .
|
(4.40) |
The photon circular orbit (on which` E = ¥,` L = ± ¥) in
the equatorial plane of the Kerr black hole r = rf , which is also the innermost
(boundary) circular orbit, has a radius rf given by the equation r3/2 - 3 M r1/2 ± 2 a.M1/2 = 0, ie.
| r f = 2m [1 + cos 2 / 3
arccos (± a / m)] . |
(4.41) |
For a = 0 we get rf = 3M in accordance with the relation (4.5) for the photon
sphere of the Schwarzschild black hole, for the extreme black
hole a = M is rf = M for the co-rotating
orbits and rf = 4M for the opposite photon
paths. As in the Schwarzschild field, not all circular orbits are
bound here: for orbits close enough to the boundary photon orbit,
the energy value (4.39) becomes greater than one (` E º E/mo > 1) - particles on such a
circular orbit E is not tied to a black hole and,
under the influence of the slightest upward perturbation, flies
out of this orbit into the infinity.
Bound
circular orbits exist only for r ³ rmv , where
r mv = 2M + 2M (M ± a) 1/2 ±
a
is the boundary radius
of the bound orbit corresponding to E/mo = 1. This radius rmv is also the minimum
"perihelion" of all parabolic orbits (ie orbits with
E/mo = 1, eg bodies falling from infinity);
every parabolic trajectory of a body that penetrates closer than
rmv ends at a black hole. For a = 0 we get rmv = 4M (compare with Fig.4.6 on the left),
for a = M it is for the co-rotating circular paths rmv = M, resp. rmv = 5.83 M for opposite orbits. In
order for a circular orbit to be stable to radial perturbations
(even all bounded circular orbits are not stable!), it must
correspond to the minimum effective potential, ie the condition
d2V(r)/dr2 L 0 must still be met, leading to
inequality
| r
2 - 6 M r ± 8 a Ö (M r) - 3 a 2 ³ 0 . |
(4.42) |
Only for radii
satisfying this inequality can there exist stable circular
orbits, where the equation v (4.42) corresponds to the innermost (lowest, limit) stable
circular orbit r = rms [8] :
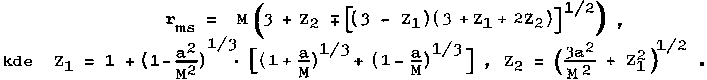 |
(4.42 ') |
For a = 0 we again get
the radius of the innermost stable circular orbit rms = 6M in the Schwarzschild geometry, for
an extremely rotating black hole a = M the correspondingly co-rotating
innermost stable circular orbit has a radius rms = M, while for the innermost stable opposite circular orbit
it is rms = 9M.
At large distances r
from the rotating black hole, the parameters (binding energy,
specific angular momentum, velocity of circulation) of the
co-rotating and counter-rotating orbits
are almost the same. Approaching the black hole (with decreasing r ),
however, increases the influence of the angular momentum of a
black hole - the binding energy of the
co-rotating orbits increases, while the
binding energy of the opposite orbits
decreased in
comparison with Schwarzschild orbits. The most striking difference
motion of test particles compared to the Schwarzschild geometry
will be near the extreme Kerr black hole (a = M), where the trajectories of particles moving in the
direction and against the direction of rotation of the black hole
will also differ the most. This is markedly reflected in the
parameters of boundary stable circular orbits. The innermost
stable circular orbit around the Schwarzschild black hole had the
following characteristics (see §4.3): radius r = 6M, specific angular momentum` L = 2Ö(3) M, energy E = mo
.8/9 and binding energy of particle Ebind = mo - E = 5.72% mo.
For the extreme Kerr black hole, according to formulas (4.42) and
(4.39), the innermost stable co-rotating orbit will have a radius r = M,
a specific angular momentum` L =
2M/Ö3, energy E = mo/Ö3
and the binding energy of the particle will be Ebind = 42.26% mo; in circulation against the
direction of rotation of the black hole is the innermost
stable circular orbit in the equatorial plane have a radius r = 9M, specific
angular momentum of` L = 22M/Ö27 , energy E
= 5M/Ö27 and the binding energy of the particle
will only Ebind = 3.77% from
mo.
If we compare this with the
results obtained in the previous §4.3 (passage
"Emission of gravitational waves
when moving in the field of a black hole"),
specifically with relation (4.21), the most remarkable is that a
body orbiting in a circular orbit (co-rotating) in the equatorial plane
extreme Kerr's black holes glow
out in the form of
gravitational waves more than 40% of its rest weight! This value of the binding energy at the marginal stable
co-rotating orbit is also of great importance for assessing the
potential efficiency of energy release in accretion disks around
black holes - see §4.8, section "Accretion disks".
Light
propagation in the field of a rotating black hole
Similar to
the trajectories of test particles, the rotation of a black hole
also affects the propagation of light in its field - it affects
photon orbits. The angle of deflection of the photons by a
spherically symmetric Schwarzschild black hole depends only on
the impact parameter, not on the direction from which they come
to the black hole. There is only one photon sphere around
Schwarzschild's black hole, on which photons can move at all
angles accordig on the direction from which they reached.
However, if the black hole
rotates, the situation is more complicated - the geometry is not
spherically symmetrical, but only axially symmetrical, so that
for rays coming from different directions, spacetime appears
differently curved. The angle of deflection of the rays (and the
whole character of their trajectory) can significantly depend on
the direction of movement of the photons with respect to the
direction of rotation of the black hole. In general, rays directed against the direction of rotation are deflected
more than photons going in the direction of rotation - Fig.4.18.
These differences are most pronounced for photons passing in close proximity to a black hole. Indeed, from relation (4.41)
it can be seen that there are two photon circular orbits in the
equatorial plane around a rotating black hole: an opposite
circular photon orbit with a larger diameter than Schwarzschild
photon sphere, and a co-rotating photon orbit lying lower than for a non-rotating
black hole. The total effective cross-section of the
gravitational capture of photons by a rotating black hole does
not differ much from the corresponding value (4.15) for the
Schwarzschild black hole. However, the capture angle is asymmetric - photons going in the opposite direction
of rotation are captured with a larger effective cross section
than photons coming along the direction of rotation - Fig.
4.18b.
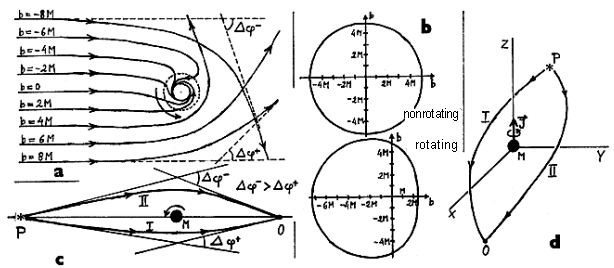
Fig.4.18. Light propagation in the gravitational field of a
rotating black hole.
a) Light
geodesics in the equatorial plane of the Kerr black hole. The
angle of deflection Dj- of
a photon moving against the
direction of rotation is (at the same collision parameter)
greater than the angle Dj+ of deflection of a photon along the direction of rotation of a black
hole. The co-rotating photon orbit r = rf+ has a larger radius than the opposite
photon orbit r = rf-. b) The effective cross-section of capturing
photons (as well as other particles) by a rotating black hole is
asymmetric - counter-moving photons are captured more efficiently
than photons going in the direction of rotation. c
, d) Rotating (Kerr) gravitational lens: c
- asymmetrical beam path in
equatorial plane; d
- deflection of rays in the general
plane.
Winding the light into
the spiral by the black hole's rotation
In §2.5, the passage "Rotating gravity", we showed that the space-time
around a rotating body also rotates in a certain sense - the
Lense-Thirring effect of entrainment of local inertial systems in
the direction of rotation of the source. The space-time around
the massive rotating body is deformed not only in the radial
direction, but the resulting potential well also twists in the
direction of the source's rotation. In the vicinity of rotating
black holes, this effect is very pronounced and is also visible
in light. The angular momentum of a rotating black hole should
generally cause the electromagnetic wave to spiral in the
direction of rotation. Astrophysically, this effect of
"twisted" space-time could be most evident in the
radiation emitted by the accretion disk in the equatorial plane :
-> This light would not travel to us from
the black hole in a straight line, but initially along a curved
path.
-> When an electromagnetic wave passes
through rotating space-time near a black hole, its wavefront will
be deformed. Phase of the wave - alternation of maximum and
minimum - with the influence of entrainment by rotating gravity.
they will move through the field and acquire a helix shape along
the beam, they will form a spiral. It would be a kind of "rotating,
twisting or spiraling light",
the polarization of which would be different from the usual
circular one. If it hits charged particles, it causes, among
other things, their rotation around the direction of propagation
of the beam, which can be considered as a manifestation of the
angular momentum of this radiation. So it behaves like a wave
with orbital angular momentum - cf. §1.5, passage "Intrinsic and orbital angular momentum of
electromagnetic waves".
Parameters of the Kerr-Newman black
hole
In addition
to the expressions (4.26) and (4.30) for the horizon and the
ergosphere, we present other important relationships between the
quantities characterizing a general black hole. The horizon area of the Kerr-Newman black hole is
A
= r=2M,nt=const.|gJJ gjj|1/2 dJ dj = 4p (rg+2
+ a2) =
= 4p [
2 M2 - Q2 + 2M Ö(M2 - Q2 - a2) ]
|
(4.43) |
in geometrodynamic units; in ordinary units, the area of the
horizon is given by the formula
| A
= 4pG/c4 [ 2 G M2 - Q2 + 2 Ö(G2 M4 - J2 c2 - G M2 Q2 ) ] . |
(4.43 ') |
The angular velocity of a black hole horizon (which is the angular
velocity with which a locally non-rotating observer orbits on the
horizon with respect to infinity) is calculated from (4.29) by
placing r = rg+ (which can be further adjusted
by substituting from (4.26) and (4.43) for rg+ and area A ) :
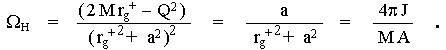 |
(4.44) |
It can be seen that this
angular velocity is the same at all points on the horizon (the
black hole rotates like a "solid body"), so WH is defined as the angular velocity of the black hole.
For completeness, we will also state the electrical
potential of the horizon :
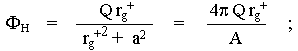 |
(4.45) |
the four-potential of the electromagnetic field Ai(r,
J) around the Kerr-Newman black hole at the
location with the coordinates r, J is
(in the Lorentz calibration Ai ;
i = 0) given
by
| A t =
Q r / (r2 + a2cos2 J) , A
j = - a Q r sin2 J / (r2 + a2cos2 J)
;
|
(4.46) |
(due to stationarity and axial symmetry, the
potential does not depend on time t and on angle j and its other components are equal to
zero).
The surface gravity k on the horizon (see §4.3), which is the
gravitational force acting on the test particle on the horizon
and having the same angular velocity WH as the horizon (ie on the
locally non-rotating particle on the horizon) is equal to
 |
(4.47) |
It can be seen at first
glance, that for an extreme black hole (for which rg+ = rg- = M) the surface gravity is zero
(!).
It is useful to define the
so-called irreducible mass of
a black hole Mired (the meaning of this quantity and its
name will be shown in §4.6 in connection with the laws of
dynamics of black holes), which is the mass that would have
Schwarzschild black hole with the same surface of the horizon - 16p Mired = 4p(rg+ 2 + a2) :
| M
ired º Ö (A / 16 p )
= 1 /
2 Ö (r g + 2 + a 2 ) .
|
(4.48) |
For a black hole of
total mass M , the quantity M ired is limited by inequality
M / Ö 2 £ M ired £ M
,
where the upper limit
corresponds to a Schwarzschild black hole and the lower limit to
an extreme black hole. From (4.48), (4.43) and (4.44) the
following relations can be deduced :
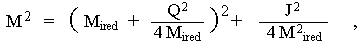 |
(4.49) |
| W H =
a / (4 M 2 ired ) = J /
(4 M . 4 M 2 ired ) . |
(4.44 ') |
The physical significance of the important
relationship (4.49) will be discussed in §4.6 "Laws
of black hole dynamics"
in connection with the 2nd law of Black Hole Dynamics
.
Classification
of black holes
In general
Kerr-Newman geometry, which in the next paragraph we will show is
probably the most general space-time geometry of a general
stationary black hole, we can distinguish some significant
special cases (we can compare with the
classification of Kerr-Newman geometry in §3.6) :
- a) Especially for Q = J = 0
we get the Schwarzschild
geometry of a centrally symmetric non-rotating
uncharged black hole.
- b) For Q = 0, 0 <J <M2 it is Kerr's
geometry of axially symmetric rotating uncharged black holes.
- c) For J = 0, 0 <Q <M
we obtain the Reissner-Nordström
geometry of non-rotating centrally symmetric electrically charged black holes.
- d) At M2 = Q2 + J2/M2 it will be the
Kerr-Newman geometry of the so-called extreme black hole - the fastest possible
rotation (or the largest possible electric charge) of the
black hole with respect to its total mass M; the horizon
has a radius rg = M, surface gravity on
the horizon k = 0.
- e) Finally, in the case of Q2 + J2/M2 > M2, Kerr-Newman geometry no
longer describes a black hole having a horizon
(expression (4.26) becomes imaginary), but the so-called
Kerr naked singularity without horizon (properties of naked singularities and their
existence we discussed in §3.9 "Naked
singularities and the principle of "cosmic
censorship" ").
Kerr-Newman geometry has
a horizon (and thus describes a black hole) only if the condition
M2 l Q2 + J2/M2 is met, ie if it "does not
rotate too fast" or is not "too electrically
charged" compared to its total mass M.
Rotation (intrinsic angular momentum J)
plays an important role for the geometry of spacetime
around a black hole formed by gravitational collapse, because
most stars are rotating and angular momentum of the rotation due
to the law of conservation of angular momentum during the collapse
would not change significantly (unless the case shown in Fig.4.14 occurs,
where a considerable part of the angular momentum can be carried away by
gravitational waves; however, only the "excess" angular
momentum is carried away, the
remaining rotational momentum is still considerable). However, it is different with the electric
charge of black holes :
Electrically
charged black holes? - no !
The electric charge Q is probably not important
for black holes in space. In order for an electric charge to
leave a noticeable mark on the space-time metric, it would have
to have a huge value comparable to the total mass M (in
geometrodynamic units). Because stars are usually electrically
virtually neutral, the creation and maintenance
of such a large charge is very unlikely; in addition, such large
electrical repulsive forces would probably prevent collapse to
dimensions of ~ 2M, because in areas r>2M these electrical
repulsive forces would be completely dominant. Even if a highly
electrically charged black hole formed, it would soon
"discharge" in a real situation. If there is a material
environment around the black hole (interstellar matter), opposite
charges (particles, ions) will be attracted and captured from the
surroundings by the charged black hole - by this selective
absorption(accretion) of oppositely charged particles with
the charge neutralizes the black hole quickly *). But even when a
heavily charged black hole is in a vacuum, quantum
electron-positron pair formation processes in a strong electric
field will play a neutralizing role, repelling black-hole charges
and attracting and absorbing opposite charges through the black
hole. The electric charge of a stationary black hole is therefore
practically zero . The reason why we dealt with
the influence of charge and Reissner-Nordström geometry here and
in §3.5 was rather theoretical - to show interesting (and at
least physically possible in principle) properties of spacetime.
*) If a rotating black hole is immersed in
an environment with a strong magnetic field, a certain
equilibrium very small value of electric charge, determined by
the speed of rotation and the intensity of the external magnetic
field, may persist even in the steady state.
The electric
charge is therefore irrelevant for black holes - black
holes are electrically uncharged, Q = 0 .
Black
holes - bridges to other universes? Time machines?
Rotating or electrically charged black holes have a complex
geometric and topological structure of spacetime (as we have shown in §3.5 "Reissner-Nordström
geometry" and §3.6 "Kerr and
Kerr-Newman geometry"); there has been speculation that they could serve as bridges
- tunnels or portals - to other universes, or tunnels
between distant places or various times
in the same universe. We will try to critically
assess these possibilities from a physical point of view.
Wormholes
Hypothetical "tunnels" in space-time that connect the
shorter route two remote sites in the same space, or two places
in various otherwise separate universes, are called "worm
holes" - according to the similarity with
connecting paths that a worm biting through an apple.
A worm that is
located on the surface of an apple and has to get from one side
to the other can do this in two ways. If it considers its space
to be two-dimensional (the surface of the apple), it must crawl
over the entire circumference of the apple. However, if he
perceives the apple as a three-dimensional object, he can choose
the path inside it and bite through to the desired opposite place
along a much shorter path (or also longer in the case of a
crooked corridor ...). It does not travel two-dimensionally on
the surface of the apple, but uses the three-dimensional shortcut
in the way - "wormhole".
The wormhole in the apple allows only a
slight shortening of the path between the two places on the
surface-peel. However, with a suitable geometric-topological
structure in space, a wormhole could represent an absolutely
fundamental shortening of the path between very distant places in
space (eg from many light-years to hundreds of meters or
kilometers)! An observer who passes through a wormhole does not
exceed the limiting speed of light c anywhere, but can
still cover the distance between the starting point and the
destination much faster than a light beam flying straight.
Hypothetically, wormholes could thus represent peculiar shortcuts
not only in space, but also in time - enabling "time
travel" (cf. the passage "Closed
world lines and time travel"
in §3.3 and "Time travel: fantasy or physical reality?").
According to this analogy with the worm, we intuitively
imagine that the shortcut path between different places or
universes takes place through another, higher dimension,
through hyperspace. In mathematical topology
(§3.1 "Geometric-topological properties of spacetime"), however, a space (manifold) can be multiply
connected by its internal structure, so there
is no need to use additional dimensions to "travel"
between different parts.
Something that could be a forerunner of
the worm hole model, was first described in 1935 by A.Einstein
and N.Rosen as the so-called Einstein -Rosen bridge (see
§3.4 "Schwarzschild geometry",
Fig.3.18) in Schwarzschild's solution of the centrally symmetric
gravitational field.
 |
Fig.3.18. a) Schematic
representation of the
geometric structure of the section (spatial hyperplanes)
v = t = 0, J = p/2
Schwarzschild spacetime in the form of nesting into auxiliary three-dimensional
Euclidean space. This auxiliary three-dimensional space
has no physical significance (it is only a means of
representation); only the internal geometry of the nested
surface, which shows the two asymptotically planar
regions A and A' connected by the
Einstein-Rosen bridge, is relevant.
b) A topological tunnel between two
places in the same universe. c)
"Wormhole" between two places in the same
universe. |
The name "worm hole"
was proposed in 1957 by J.A.Wheeler. The mouth or gullet of a
wormhole would look like a two-dimensional sphere. Unlike the
spherical horizon of a black hole, which allows only a
"one-way path without return", mostly to perdition,
however, the estuary of a wormhole is a bidirectional through
surface (at least in principle). The wormhole has an entrance and an exit,
we can pass them both inside the wormhole and out into the outer
universe. If a hypothetical astronaut penetrates a wormhole, he
could find himself in another place in space and
at a different time, in the future or in the
past (depending on the values of the metric
tensor in both mouths).. Possibly, even in
another causally separated universe (according
to the global topology of spacetime)..?..
The wormhole has no direct connection with the black hole, but in
many mathematical models of black holes there is also a wormhole
inside.
From a geometrical-topological point of view, a wormhole
can be defined as a compact region of spacetime, whose spatial
boundary is topologically equivalent to a simple sphere S3, but whose interior
is topologically connected to places outside
this initial region. It is thus a compact region W in asymptotically
flat spacetime, whose topology has the form W ~ R ´S, where R is the
Riemann space and S is a 3-dimensional tube whose boundary has a topology
of the shape ¶S ~ S2
and the hyper-surface S described in space-time has a spatial (space-like)
character.
From a geometric point of view, we have two types of wormholes :
a) Tunnels connecting different separate
universes ; b) Connections between different distant places of the same
universe (ours).
In terms of "throughput", we also recognize
two types of wormholes :
- Traversible - stable, allowing movement
across space (spacetime), wormholes connecting two different and
distant places in our universe or different universes. To stabilize
these wormholes need matter with a negative energy density
(see the discussion below "Can wormholes really exists?") .
- Non -
traversible -
very short-lived, vanishing so fast that no real object can fly
through them without being absorbed by singularity. Such are the
characteristics of wormholes inside black holes (such as the
Einstein-Rosen bridge), connecting various separate universes. Of
course, all virtual worm micro-holes in quantum topological foam
are non-traversible (again discussed below
in the section "Can
Worm Holes Really Exist ?") .
Ordinary tunnel (such
as railway) connects two places in space, a
wormhole connects two places in space-time. If there were a
wormhole, it would theoretically make it possible to bridge two
very distant places in space in a much shorter path.
An observer (astronaut) through a wormhole - even if it does not
exceed the speed of light anywhere - could cover the distance
between the two places much faster than a light beam flying in
the usual straight path (through the space outside the wormhole).
He would reach a distant place before the light. Due to the fact
that the observer "overtakes" light with this shortcut,
from the point of view of the theory of relativity he can
"overcome time" - he can travel in time
to the future and back to the past. The possibilities of
fictitious or real time travel are discussed in §3.3, part
"Closed
worldlines and time travel ",
then systematically in the syllabus "Time Travel: Fantasy or
Physical Reality?".
Can wormholes really
exists ?
Large "wormholes" could occur in space as remnants of
turbulent processes with matter and space-time during the Big
Bang, which cosmic inflation has expanded to macroscopic or even
astronomical sizes. Microscopic wormholes measuring about 10-33 cm everywhere and
constantly created and destroyed as a result of quantum gravity
fluctuations of spacetime metric and topology (see §B.4 "Quantum
geometrodynamics ") - in quantum topological foam.
Wormholes inside black holes they have
a "mayfly" life. In addition to gravitationally dynamic
effects, quantum radiation effects also contribute to this. A
random quantum of radiation falling on a black hole from the
outside will accelerate to high energies due to gravity and will
"bomb" even the esophagus of a wormhole, which will
shrink and close quickly as a result. Any object that would
attempt to pass through such a wormhole during its short life
will disappear at the moment of the wormhole's rupture, along
with it, in the resulting singularity. Due to this extremely
short duration of topological tunnel is problematic even speak of
the existence of wormhole ...
In order for a macroscopic wormhole could
maintain stable and "through - traversible" must be
present or mass field inducing antigravity effects
(material with negative energy density), which would
avoid the tendency of gravity to "necking" in
singularities and the formation of a black hole - by Raychaudhuryho
equation (2.59) deviation geodesics ( §2.6 " deviation and focusing of geodesics ") energy condition opposite
to (2.60) causes expansion of geodesics after passage through the
wormhole. The only hypothetical possibility of stable wormholes
is to "reinforce" them with a
specific type of substance that would have antigravity
effects and thus effectively "push" the walls of
the wormhole apart; in terms of energy-momentum tensor
components, this substance must have a large stress in the radial
direction, exceeding the energy density. Therefore, a mass with a
negative energy density *) is needed to
stabilize the wormholes (violating the weak energy condition
(2.60)), which K.Thorne called "exotic matter".
*) The exotic substance must have a
negative energy from the point of view of the observer or the
light beam passing through the wormhole, not necessarily
from the point of view of the observer who is at rest inside the
wormhole. In the theory of relativity, the energy density can be
negative in one frame of reference, positive in another.
Black holes are (at least at the level of
current astrophysical knowledge) a legitimate
physical consequence of stellar evolution (§4.1.
"The role of gravity in the
formation and evolution of stars" and §4.2, section "Complete gravitational collapse. Black hole.") and their existence is
evidenced by strong astronomical observational data. However,
wormholes are still a mere hypothesis - we do
not know of any natural way in which wormholes in the universe
could form outside the interiors of black holes.
So far there are no observational indications
for wormholes !
Topological
tunnels inside black holes
About the complete analytical extension of the
Kerr-Newman geometry shown in Figs.3.21 to 3.25 and the resulting
geometric-topological consequences can be
said essentially the
same as the extension of the Schwarzschild geometry (see end of
§4.3). Let us first notice Schwarzschild's geometry, for which a
Kruskal diagram was constructed in §3.4 (Fig.3.17) showing the
presence of two mirror-inverted universes - Fig.3.18a. However, in a gravitational
collapse, Schwarzschild's solution describes the geometry of
spacetime only above the surface of a collapsing star. Therefore, most part of the idealized (an extended)
Schwarzschild solution on the Kruskal diagram is therefore not realized - is "cut off" by the inside of
a collapsing star (Fig.4.19a).
In §3.5 "Reissner-Nordström
geometry" and §3.6
"Kerr and Kerr-Newman geometry" we
have shown, that an observer who, during his motion
in Reissner-Nordström or Kerr-Newman spacetime, intersects the
inner (Cauchy) horizon r = rg-, can get into another
"universe". Accordingly, in the event of a
gravitational collapse (of an electrically charged or rotating
mass), there would be a possibility that after crossing the
Cauchy horizon r = rg- the shrinking mass may avoid singularity and begin to expand
again into another region of spacetime ("another universe") -
Fig.4.19b.
The Einstein-Rosen bridge and
analogous structures of Kerr-Newman geometry can be understood as
a "bridges" connecting two different asymptotically planar universes (assuming the usual Euclidean global
topology of each). With a suitable topology, such a bridge could
connect two different places of
the same (multiple conected) universe - Fig.3.18b, c. Such a "worm hole" (as defined
above) could create
a "topological shortcut" between two distant
regions of spacetime. There is even speculation about the
possibility that a certain movement of both ends of the wormhole
could form a closed time curve. From here, it is only a step
towards the sci-fi idea of how a technically advanced
civilization, with technology that allows it to manipulate
(through gravity) a wormhole, triggers a "time machine" ("Time Travel: Fantasy or
Physical Reality?") ...
Such travel
between different universes, or between different distant places in
the same universe, or even time travel, may be an exciting topic
for science fiction, but the reality is probably more prosaic.
The exact Schwarzschild, Reissner-Nordström or Kerr solution
containing "tunnels" between different universes is
valid only under the conditions for which it was derived, ie for
an otherwise completely empty
asymptotically planar universe.
At the end of §3.5, it was noted
that an observer moving so that it intersects the inner horizon r
= rg-, will see during the final
interval of his own time the whole further history of the
"universe" he is leaving. Any body from this universe
would be seen by an observer approaching rg- with a violet shift increasing to infinity. In
connection with this, it has been shown [114], [192] that the
Cauchy horizon r = rg- inside a black hole is unstable to electromagnetic and gravitational
perturbations occurring outside the black hole (classical
instability) *). Analysis of quantum processes of particle
formation in strong fields inside a black hole further shows [192
] (see also §4.7) that there is also a quantum instability of the inner horizon **), which
manifests itself even in the case when the space is empty from
the classical point of view.
*) Figuratively speaking, a
particle that would fly through such a black hole into another
universe would "demolish"
behind it this theoretical
tunnel into other universes.
**) In addition, the existence of closed time worldlines would
allow particles to interfere with their own past through a time
loop. Quantum considerations suggest that the disturbances
resulting from such phenomena would intensify spontaneously and,
with their high energy, would eventually destroy the topological
tunnel...
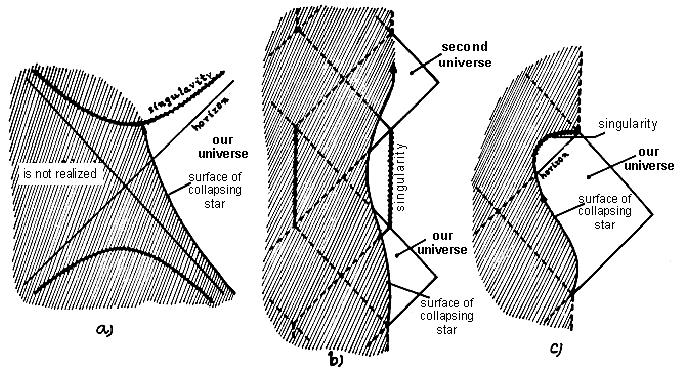
Fig.4.19. The space-time structure of a real black hole.
a) In
Schwarzschild's spacetime of a static black hole created by the
collapse of a (non-rotating) star, a large part of the structure
of the Kruskal's diagram is cut off by interior of
collapsing star.
b) The collapse of a rotating star into a black
hole could theoretically create a space-time structure allowing
it to travel to another universe. The collapsing matter could
then emerge in the second universe in the form of a "white
hole".
c) However,
due to the diverging intensity of the incoming radiation at the
inner horizon and the quantum production of particles around the
singularity, much of the theoretical structure of Kerrr-Newman
geometry (including inner horizons and other universes on the
Penrose diagram) cannot actually be realized. The collapse
creates a singularity that is in the future and takes on a
spatial character, which does not allow any travel to other
universes.
These instabilities (to
perturbations and quantum processes) lead in practice to the destruction and disappearance
of the Cauchy horizon and the emergence of a singularity of the
spatial type - Fig.4.19c. Therefore, it can be expected that in
the real situation the structure of spacetime within the event
horizon r = rg+ will be qualitatively similar to
Schwarzschild's black hole and the complex topological
construction according
to Fig.3.25 will not be realized
(matter would have
to pass through the singular region before).
Again, we come to the conclusion
that the "exotic" possibilities of traveling between
different universes, or time travel, could work at most within
elementary particles (or only a single elementary particle !?) - cf.
with a discussion of closed time curves in §3.3., passage "Closed worldlines and time travel". The individual mechanisms
are described in more detail in the work (syllabus)
"Journeys
through time: fantasy or physical reality?". At
the end of §3.4, the note "Dual
solutions in analytic extension - reality or fiction?", doubts are discussed about the
very physical meaning of the full extensions of Schwarzschild and
Kerr-Newman geometry of spacetime, on which all ideas about
traveling between different universes or in time are
ideologically based..?..
Some related considerations about the direction of time flow are
further outlined in §5.6, section "Time arrow".
Black
holes - "hatcheries"
of new universes ?
In addition to the idea that black holes are portals to other
worlds (universes), an even bolder sci-fi hypothesis has emerged
(recently revived and supplemented by L.Smolin): that new
universes are being born in black holes
. Our entire universe could have been born of a black hole from
another universe; big-bang would really just be a widening of a
black hole in another universe. The idea also emerged that these
emerging universes also carried away the physical laws of the
original ("mother") universe - as if there was a kind
of "cosmic inheritance". This speculative "evolutionary
cosmology of natural selection" would then be
similar in some sense to Darwinian evolutionary biology, as it
said that the most common types of universes would be the ones
that make the most "copies of themselves"; universes
with a large number black holes formed would have a certain
"reproductive advantage" passing on to the next
"generations" of universes...
From the point of view of the sober physical approach of general
relativity and quantum theory, however, these speculative
concepts appear to be unfounded :
1. Black holes do not produce new universes
- from a classical (non-quantum) point of view they do not arise
inside black holes at all (as discussed above ), from a quantum
point of view, spontaneous fluctuations in space-time, which can
potentially lead to the emergence of new universes, are taking
place everywhere and constantly, not just inside
black holes.
2. There is no mechanism by which any particular physical
information can be transferred from one universe to another.
Within classical GTR, this is forbidden by Hawking's and
Penrose's theorems on singularities. In the approach of quantum
cosmology, chaotic quantum field fluctuations and metrics in the
"topological foam" of space-time effectively erase
and randomize any macroscopic physical structure and information
from another (previous) universe..!..
Vojtech
Ullmann