Scary singularities of spacetime

Chapter 3
GEOMETRY AND TOPOLOGY OF SPACE-TIME
3.1. Geometric-topological properties of spacetime
3.2. Minkowski planar spacetime and asymptotic structure
3.3. Cauchy's problem, causality and horizons
3.4. Schwarzschild geometry
3.5. Reissner-Nordström geometry
3.6. Kerr and Kerr-Newman geometry
3.7. Spatio-temporal singularities
3.8. Hawking's and Penrose's theorems on singularities
3.9. Naked singularities and the principle of "cosmic censorship"

3.7. Spatio - temporal singularities
Regular and singular solutions
In classical physics, bodies and fields have the usual and expected physical, geometric and topological properties. They are (relatively) smooth and continuous, have finite dimensions and finite values of their physical quantities. We call such behavior regular. And it can be mathematically modeled using regular imagings , which are simple mutually unambiguous imagings for which unambiguous inverse imagings are available.
  However, in mathematical modeling in theoretical physics, we also encounter situations where the relevant equations diverge and formally give infinite or indeterminate values of physical quantities. A simple example is the idealization of a point electric charge, where according to Coulomb's law there is an infinitely large electric field intensity in a place with zero distance (r = 0) from this charge. Such anomalous behavior of a physical quantity is generally referred to as singular (it is the opposite of regular behavior). And the place or point of anomalous behavior of a physical quantity is called singularity (Latin singularis = isolated, exceptional, unique ) .
  In the analysis of some exact solutions of Einstein's gravitational equations (eg Schwarzschild's solution) we saw that in some places these solutions are not regular. We have seen that some of these "singularities" are caused only by an inappropriate coordinate system and the transition to other coordinates can remove the relevant singular behavior (an example can be pseudosingularity of Schwarzschild sphere). In such cases, therefore, these are not the singularities of spacetime itself (spacetime is regular here).
  However, there are places where singular behavior cannot be removed by switching to another coordinate system, such as the point r = 0 in Schwarzschild geometry. In such a case, it is a real, physical singularity of the spacetime itself (where, for example, the invariants of the curvature tensor reach infinite values). Under the singularities of spacetime in the following we will understand only similar "irremovable" singularities. Here we will clarify some basic features of space-time singularities and try to give a general definition. We will talk about the conditions under which singularities arise in the next §3.8 "Hawking's and Penrose's theorems about singularities".

Physical Unreality of Singularities
In this and other mathematically oriented chapters of our book (§3.4-3.9, §5.3), we deal with singularities "seriously as if they did exist". However, it should be borne in mind that these are only mathematical abstractions. These singularities arise as a consequence of the "straightforward" strict extrapolation of exact solutions of the equations of the general theory of relativity to certain special values of coordinates (eg to t = 0, r = 0).
  Real "physical" singularities, in which real physical quantities would take on infinite values, cannot exist in nature ! We never see true infinity in nature (the analysis of different types of infinity was performed in §3.1, in the section "Infinity in spacetime"). If a theory predicts them, it is its serious shortcoming, indicating either its erroneousness or excessive idealization, or that in a given situation it reaches the limits of its validity. If infinity appears in a theory, we try to remove it (the process of renormalization in quantum theory), at least until the creation of a new more sophisticated theory.
  It turns out that in those "exotic" situations, play an important role the quantum laws of gravity as other kinds of interactions, wich emerge immanently (as a consequence of quantum field fluctuations in vacuum) together with "classical" gravity. The inclusion of these quantum interactions in the general-relativistic gravitational model can remove this singularity  - spacetime does not have to be singular here, it can have a very high but finite curvature, at finite field concentration, finite density and temperature of the gravitational substance. From a quantum point of view, it can be expected that the singularity will "dissolve" in the quantum foam. This is, yet indeterminate, a view of quantum gravity and quantum geometrodynamics (§B.4 "Quantum Geodynamics") .
  Nevertheless, it is useful to investigate mathematically under what circumstances in (non-quantum) theory singularities arise and what properties they have, of which something could "potentially" be applied in practice.

Singularities in electrodynamics and gravity
Let us first compare the situation around singularities in gravity with the corresponding situation in electrodynamics. Singularities also occur in electrodynamics, eg in the place of a point electric charge (classical idealization!) the intensity of the electric field reaches infinite values. However, the metric of Minkowski spacetime, against which (and with the help of) the electric field we monitor (and measure) remains regular everywhere *). In contrast, in the general theory of relativity, we do not have a "non-participating" metric with which we monitor the behavior (and thus possible singularities) of some field. Here, the space-time metric is the same field whose singularities we investigate. Spacetime singularity therefore has much deeper implications than the singularity eg. in clasical electrodynamics. In space-time singularity, where regular space and time cease to exist, all physical laws lose their validity, because all existing physical laws are formulated on the basis of classical space and time.
*) This is the case in STR when we take the electromagnetic field in isolation. In reality, however, the electromagnetic field also evokes a gravitational field (curves spacetime), so that in the place of infinite intensity of electromagnetic field, an infinitely strong gravitational field (infinite curvature of spacetime), and thus spacetime singularity would be created.
  The singular point cannot be considered as a part of the observed space-time manifold, in principle no physical measurements can be performed in it. In order for spacetime to remain a manifold, all singular points of it are necessary exclude ("cut out"). The remaining spacetime will then again be a manifold, where the usual physical laws will apply at each point and where physical measurements can be made. However, the remaining spacetime cannot be declared regular, and we cannot think that we have completely got rid of the singularity. As we will see below, this is remaging spacetime has certain "pathological" properties (related to the fact that some geodesics ends its existence in places "carved" singular points), preventing consider him regulars.
  Let us try to capture the common characteristics of spacetime singularities. In other words: what fundamental "dangers" can they wait for a real observer (moving along world lines of the time or light type) when moving through space-time? For the time being, we will limit ourselves to moving around geodetics for simplicity. We have seen an example of one such danger in the analysis of particle motion in the Schwarzschild geometry of a centrally symmetric gravitational field. If the observer comes under the Schwarzschild sphere, his destiny is sealed - in a short interval of his own time he will necessarily reach the point r = 0, where he will be destroyed by infinite tidal forces.

Coordinate and physical singularities
From a mathematical point of view, in the general theory of relativity, there are basically two types of singularities - the places where the spacetime metric diverges - in principle :
-> Coordinate singularities - apparent
These are points where singular values of the metric arise due to the choice of coordinates, not by a real physical singularity in spacetime.
We can show this in Schwarzschild geometry :
If we calculate the components of the Riemann curvature tensor in the Schwarzschild metric (3.13) based on the connection coefficients (3.15) and transform them into the reference frame of the falling observer, they will be (those of them that are non-zero) proportional to M/r³, e.g.

so that on the Schwarzschild sphere they reach values of the order of 1/M²; similarly, the scalar invariants (e.g. R= R_iklmR^iklm= 48M²/r⁶) of the curvature tensor, which do not depend on the coordinate system. The curvature of spacetime, and therefore the gradients of gravitational forces (tidal forces), are finite on the Schwarzschild sphere - and the smaller they are, the larger the mass parameter M is.
  We thus conclude that the singular behavior of the Schwarzschild spacetime element (3.13) for r=2M does not originate in the singular character of the geometry of spacetime on the Schwarzschild sphere, but is caused by the Schwarzschild coordinates used, which are not suitable for describing the metric at this point. By switching to another suitable reference system, e.g. to the system associated with freely falling test particles, this pseudosingularity on the Schwarzschild sphere disappears.
  We can clearly illustrate how an "inappropriate" coordinate system can cause an apparent singularity using a simple example of a map of the globe. If we trace the spherical surface using coordinates indicating the "geographical" latitude and longitude J and j (Fig. a), all "meridians" will converge at the points of the "north" and "south" poles, so that the longitude is not defined for these points, the metric tensor g_jj is equal to zero here. Or similarly, if we make a map of the globe using a cylindrical projection according to Fig. b, the images P' of the pole P will be at infinity and the metric tensor g_JJ®A. However, the geometry of the spherical surface itself at these poles is completely normal - it is enough to rotate the sphere by a certain angle and the points that appeared singular in the previous coordinate system will be completely regular, and other points, new "poles", will appear singular.

An example of pseudosingularity caused by the coordinate system used. a) A point P on a spherical surface (pole) appears to be singular because the "longitude" for it is not defined in the coordinates used. b) If we make a map of the globe using a cylindrical projection, the pole P will appear singular because its image P' will be at infinity.

The geometry of spacetime itself is completely regular on the Schwarzschild sphere, an observer can freely pass through the Schwarzschild sphere during a finite interval of its own time, will not detect anything special locally and will continue moving. By using other coordinate systems, such as Eddington-Filnkelstein or Krustal-Szekeres coordinates (§3.4 "Schwarzschild geometry"), the singularity at the event horizon can be removed (converted to two consecutive coordinate maps). The peculiarity of the spacetime geometry on the Schwarzschild sphere does not lie in any abnormal local properties of spacetime, but in its global property of the event horizon.
  Coordinate singularities are removed, because they are not connected to any local physical phenomenon *). Coordinate singularities can be removed-transformed by changing the coordinates.
*) This is the case from the point of view of classical physics of the macroworld. In quantum physics, however, event horizons can locally "separate" the emerging virtual particles and antiparticles and thereby cause the physical phenomenon of emission of real particles (§4.7 "Quantum radiation of black holes").
-> Physical singularities - essential
It is different with the second singular place in metric (3.13) - point r=0. Here both the components of the curvature tensor (3.24) and its scalar invariants reach infinite values, so there are infinitely large gradients of gravitational forces. A particle that reaches the point r=0 can no longer continue its movement, is crushed by these infinite tidal forces, literally ceases to exist within the given spacetime. Here we are dealing with a real, essential physical singularity of the geometry of spacetime, which cannot be removed by any choice of the reference frame.
This §3.7 and the following §3.8 and 3.9 are devoted to the properties of real spacetime singularities and the assessment of the possibilities of their existence.
  An illustrative symptom of a physical singularity could therefore be a gravitational singularity of curvature - an infinitely large curvature of spacetime in the vicinity of a singular point. With a bit of exaggeration, we can visually liken a gravitational singularity to a situation where gravity inexorably squeezes us down to an infinitely small point, effectively reducing our existence to nothingness !

How to distinguish between coordinate and physical singularity ?
The spacetime metric is usually expressed using the general quadratic form of the element of the spacetime interval ds² = g_ik dxⁱ dx^k, whose coefficients are the components of the metric tensor g_ik(x⁰,x¹,x²,x³) given as functions of the coordinates - time x⁰ and space x^1,2,3. In the Minkowski planar spacetime STR, (pseudo)Euclidean Cartesian coordinates are used, in which ds² = -dt² + dx² + dy² + dz² - relation (3.3). In polar coordinates (r,J,j) it is ds² = -dt² + dr² + r²(dJ² + sin²J dj²) - relation (3.4). In a curved spacetime in spherical spatial coordinates (r,J,j) with origin r=0, the metric is ds² = -g_tt dt² + g_rr dr² + r²(dJ² + sin²J dj²) with metric coefficients g_tt(r), g_rr(r), g_JJ = r², g_jj = r² sin²J. Specifically, the Schwarzschild metric is (3.13)
From the metric coefficients g_ik, the Christiffel coefficients of the connection Gⁱ_kl , the components of the curvature tensor Rⁱ_klm and the geodesic equations for the motion of test particles are calculated. These data already allow us to fully analyze the properties of the metric under study (§3.2, 3.4, 3.5, 3.6).
  In the functional dependencies of the metric components, we can find places (coordinate values) where the metric exhibits "pathological" properties - divergences, discontinuities, infinities. However, at first glance, we usually do not know whether these are only apparent coordinate singularities or real spacetime singularities. To specify the nature of these singularities, we can proceed in two ways :
-» Explicitly investigate the geodesic motions of test particles - whether at a certain examined coordinate they do not encounter some divergence or infinity that would prevent them from continuing their movement.
-» The numerical values of the metric coefficients and the curvature tensor components depend on the reference system used - the vector basis (which can degenerate near the singularity), but by algebraic combination of the components of the metric tensor g_ik and the curvature tensor Rⁱ_klm, the scalar curvature invariants can be created, the values of which are independent of the coordinate system. They are certain quadratic polynomials - sums of the squares of the components of the curvature tensor and the metric tensor. The basic such scalar curvature invariant is

which arises by restricting the Riemann curvature tensor in all covariant and contravariant components (it is sometimes called the Kretschmann scalar after E.J.Kretschmann, who analyzed it in 1915; later several other curvature invariants were formulated). Such quantities are an effective means for detecting physical singularities. They quantify the degree of curvature of spacetime independently of the coordinate system. If at a certain point this quantity diverges to infinity, it means that the singularity exists there universally - across all coordinate systems.
  For Schwarzschild spacetime (3.13) the scalar curvature invariant is

When reaching r=0, R_Schw is infinite (the curvature becomes infinitely large) - a physical singularity, but at the horizon r=2M it remains finite - a coordinate singularity.

Incompleteness of geodesics
Singularities have one common characteristic: the observer's world line when encountering a singular point (e.g. with r=0 in Schwarzschild geometry) discontinuously ends here after a finite interval of proper time. This geodesic cannot be extended further within the existing manifold, the object describing the geodesic simply ceased to exist for it and can therefore no longer be described by any world point from the given manifold (Fig.3.26) :

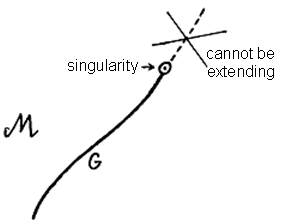Fig.3.26. Incomplete geodtic G, which ends after the finite proper time (or at the finite value of the affine parameter) and can no longer be extended within M, is a sign of spacetime singularity.

We can say that, for example in the Schwarzschild spacetime geodesic there are geodesics (especially, all those geodesics that intersect the Schwarzschild sphere), which have only a finite total length and discontinuously ends after the finite interval of their own time (or at the final value of the affine parameter in the case of isotropic geodesics). Such geodesics are "incomplete". The concept of completeness and incompleteness can be extended from geodesics to general worldlines, while the affine parameter is replaced by a generalized affine parameter *).
*) The generalized affine parameter is introduced as follows [225], [127] :
1. At the point p Î M , through which the curve C passes: x = x (t), the three-dimensional vector base ( e 1, e 2, e 3) in the tangent space is chosen.
2. Parallel transmission along curve C a vector base can be obtained at each point of the curve (for each value of t).
3. The tangent vector V(t) = ( ¶/¶t)_x(t) at each point of the curve can be expressed using the transferred base: V = V^a(t). e_a .
4. The generalized affine parameter is then defined by the integral l = _p ò^x(t) (Vi Vⁱ )^1/2 dt; depends on the point p and on the vector base e_a at the point p .
If x(t) is geodetic, then l is affine parameter on C: x = x(t). Generalized affine parameter l but can be implemented on any curve in M .

In other words, in a complete spacetime M each world lines G(l) of final "length" (as measured by the generalized parameter affine l) has an endpoint in M - is extensible.
  From the example of Schwarzschild geometry (which is obviously singular) it can be seen that geodetic incompleteness - ie the existence of incomplete temporal and isotropic geodesics - is a sufficient condition for the singularity of spacetime. From the physical point of view, we must consider as singular also such spacetime, which is geodetically complete, but in which there exist incomplete time-similar world lines (not-geodetics). The physical significance of incompleteness with respect to spatial-type world lines, on which no real object can move, is not clear, and therefore we will not consider it here.
  Thus, we can finally state the general definition of spacetime singularity : 

The condition "non-extensible" is in definition 3.9 because each extensible spacetime automatically contains incomplete worldlines. For example, if we take only a part of the planar (and of course regular) Minkowski spacetime, there will be incomplete geodesics that will end (or begin) at the "edge" of our defined spacetime. Of course, this phenomenon would not be reasonable consider as a singularity. The first sentence in definition 3.9 can also be equivalently stated as follows :
  Spacetime (M, g) is called singular, if each of its extensions contains incomplete worldlines of the time or isotropic type.
  According to definition 3.9 we have therefore chosen as a sign of the singularity of spacetime the presence of a worldline, which at some point ends in its finite proper time and cannot continue. In the next §3.7 it will be shown under what assumptions such defined singularities in the spacetime of the general theory of relativity arise.

It remains to clarify the physical properties and structure of singularities. It is not easy to build a "physics of singularities", because singularities are in themselves something "non-physical" that must be excluded from the physical manifold M in order for it to remain a manifold. One of the methods of singularity analysis was proposed by Geroch [95] and Hawking [130] and further improved by Schmidt [225]. Each incomplete light line is assigned an appropriate "end point", and those endpoints which belong to such world lines G₁ and G₂ are considered to be identical so that the world line G₂ enters the space-time region formed around the word line G₁ its small variations, and it already remains there (Fig.3.27). Such identification creates classes of equivalence of endpoints of incomplete worldlines, and the set of all these classes of equivalence creates a certain boundary ¶M around the singularity. This boundary is uniquely determined by the structure (M,g), i.e. it can be determined by measuring the non-singular points of M .

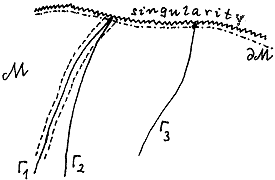Fig.3.27. Around the singularity is constructing the boundary ¶M, consisting of equivalence classes "endpoints" incomplete world lines in M. The endpoints of such worldlines G1 and G2 are considered to be identical (i.e. belonging to the same equivalence class), where G2 enters the dashed area formed around G1 by small variations and no longer leaves it.

That the question of the definition and classification of spacetime singularities is by no means trivial, we can show by a simple example. If we consider only relativistic kinematics, we can imagine a rocket that accelerates so much in ordinary Minkowski spacetime, that its worldline becomes isotropic (the rocket reaches the speed of light) so fast that the total interval in the observer's last time in the rocket will be finite - the worldline will have a finite "length". After the end time expiry, it will no longer be possible to display the rocket by any world point in the given Minkowski spacetime. However, this situation is physically unfeasible because a rocket moving after such a saint would have to have an infinite amount of fuel. However, Geroch [96] constructed spacetime, which is geodetically complete but contains incomplete worldlines of the time type with finite acceleration; from such spacetime it would be possible to "fly away" on a rocket with a finite supply of fuel.
  Intuitively, we expect that the singularity is related to the infinitely large curvature of spacetime. Indeed, definition 3.9 includes this, because one of the reasons why a world line cannot be extended beyond a certain point, there may be an infinitely large curvature of spacetime near this place. However, the incompleteness of spacetime may not always be due to the singularity of the curvature. Examples have been constructed, such as Taub, Newman, Tamburin, and Unti spacetime [188], [127], which satisfies the definition of singularity 3.9 (it contains horizons beyond which some geodesics cannot be extended), but has finite curvature everywhere. The incompleteness of geodesics here has a metric rather than a topological character. However, spacetime of this kind is a purely artificial construction and cannot be used if there is any matter in spacetime. In general, it can be expected that in physically real situations, the singularities of spacetime will actually be caused by infinitely large curvature, or its discontinuity (but let us still keep in mind the above discussion "Physical unreality of singularities"!).

3.6. Kerr and Kerr-Newman geometry		3.8. Hawking's and Penrose's theorems about singularities

Vojtech Ullmann