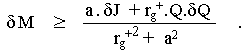 |
(4.51) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 4
B L A C K H O L E S
4.1. The
role of gravity in the formation and evolution of stars
4.2. The
final stages of stellar evolution. Gravitational
collapse
4.3. Schwarzschild
static black holes
4.4. Rotating
and electrically charged Kerr-Newman black holes
4.5. The
"black hole has no hair" theorem
4.6. Laws of black hole dynamics
4.7. Quantum
radiation and thermodynamics of black holes
4.8. Astrophysical
significance of black holes
4.9. Total
gravitational collapse - the biggest catastrophe in nature
4.6. Laws of black holes dynamics
Let us now notice some
general laws in physical phenomena with the participation of
black holes, ie in the interaction
of black holes with the surrounding matter and with each
other. Based on the analysis of specific physical phenomena using
physical laws of gravity, mechanics, electricity and other
fields, as well as geometric-topological methods of studying the structure of space, the general
laws of a global nature applicable to all processes with the
participation of black holes, were derived. These general laws govern the
behavior of some important global quanties describing a black hole and the
surrounding matter. Due to a very close analogy with the
laws of thermodynamics (as will be shown below), these laws are
usually called "laws of black
hole dynamics", or the "laws
of black hole mechanics ", or "thermodynamics".
In the following §4.7 of quantum
processes around black holes to show that this striking
similarity laws dynamics of black holes and the laws of
thermodynamics is not accidental, but has profound physical
meaning.
| Theorem 4.6 ("1st law of black holes mechanics") |
| In all
processes involving black holes, the law of
conservation of total energy (~mass), momentum,
angular momentum and total electric charge of a system of
interacting black holes and other involved objects
applies (ie also interstellar matter, absorbed and
radiated gravitational and electromagnetic waves etc .).
The energy difference dM of the two close equilibrium configurations of
black holes is given by the relation dM = (k/4p).dA + WH.dJ + FH.dQ , (4.50) where dA is the difference of the surfaces of the horizons, dJ is the difference of the rotational angular momentum and dQ is the difference of the electric charges of both black holes (or two close states of the same black hole). WH is the angular velocity of the horizon and FH is the electric potential of the horizon, k is the surface gravity. |
The physical significance of the second and third members in relation (4.50) is the work delivered (or taken) to a black hole to change its rotational angular momentum J and electric charge Q. The meaning of the first member is different and will only arise in connection with the second law of black hole dynamics a from analogy with thermodynamics.
Thus, the first law of
black hole dynamics is simply the law
of conservation of the most important physical quantities
compatible with the "black hole has no hair" theorem
(black holes do not have other conservation laws than the law of
conservation of energy-momentum, angular momentum and electric charge *). The quantities
mass-energy, momentum, angular momentum and charge are measured using its gravitational and electromagnetic effects in the asymptotically
flat spacetime surrouding the studied system (using the Gauss theorem
for integral field flows or by analysing
the trajectories of test
particles).
*) Note that, for example, the law of conservation of baryon
charge (numbers) does not apply to processes with black holes!
The first law of black hole mechanics can be advantageously used in calculations of the motion and interactions of black holes, similarly as it is advantageous to use the laws of conservation of energy and momentum in the calculation of collisions of bodies in mechanics. It is however necessary to include energy, momentum and angular momentum carried away by gravitational waves. For example, in the collision and fusion of two black holes with masses M1 and M2 , the resulting black hole will have the mass M = M1 + M2 - Mwave , where Mwave is the energy-mass carried away by gravitational waves during the process of approaching and merging the two holes; analogously for momentum and angular momentum.
| Theorem 4.7 ("2nd law of black holes dynamics") |
| Let
spacetime e be asymptotically prognostic
(there are no naked singularities and thus the principle
of cosmic censorship is fulfilled) and the energy
condition Rik V i V k ³ 0 applies . Then, in any black hole process, the sum of the areas of all horizons of the black holes involved cannot decrease . |
The second law of black hole mechanics, which plays a fundamental role in black hole physics, was arrived at by various methods on the one hand Hawking [120], [121], on the other hand Carter [43], Christotolou [53], Bardeen [9] and Ruffini [54]. Christodolou and Ruffini studied how the parameters of a black hole change when interacting with the surrounding matter and field, for example when small material objects are thrown into it. The absorption of such a small body changes the mass M, the angular momentum J and the charge Q of the black hole by dM, dJ and dQ. Based on the analysis of the trajectories of these bodies in the field of the Kerr-Newman black hole, Christodolu and Ruffini concluded that the changes dM, dJ, dQ cannot be arbitrary with respect to each other, but only those, that satisfy the inequalities resulting from the relation (4.36), are feasible :
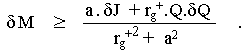 |
(4.51) |
Bodies that have too much angular momentum per unit mass (relative to the center of the black hole) or too much electric charge, the black hole simply does not "receive" - it flies out without crossing the horizon, they are not captured. If we try to throw a body into the maximally rotating extreme black hole, which would spin this black hole even more, centrifugal forces will prevent this body from approaching the horizon and falling into the black hole.
Inequality (4.51) can also be written in the form
| d M ired ³ 0 , | (4.52) |
where Mired = (1/2).Ö(rg+2 + a2) is the irreducible mass of a black hole, which was introduced by relation (4.48) in §4.4. Since, according to Equation (4.48), the area of the horizon is proportional to the square of the irreducible mass (A = 16p Mired 2), dA ³ 0 holds. The inequality (4.52), according to which the irreducible mass of a black hole cannot decrease when any body is absorbed, is a special case of the 2nd law of black hole dynamics; the origin of the name "irreducible mass" can also be seen from here.
However, the general mathematical proof of the second law of black hole dynamics belongs to S.Hawking [120], [121]. According to Penrose's theorem 3.1, the horizon is generated by isotropic (zero) geodesics, which do not intersect anywhere and have no endpoints in the future. Due to the energy condition Rik Vi Vk ³ 0, the following relation holds for the convergence of C geodetics (and thus also zero geodetics generating the horizon): dC/dl ³ C2 ³ 0 (see §2.6). If C were positive at some point (event) P , dC/dl would remain constantly positive and at least as large as at point P, so that after the final interval of the affine parameter l, a focal point would be reached, at which point the isotropic geodetic generators would start to intersect (§2.6). This would create an event through which more than one zero generator passes, which contradicts Penrose's Theorem 3.1. The convergence of isotropic horizon generators must therefore be less than or equal to zero C ³ 0 (their divergence must be non-negative). It follows that the two-dimensional surface the cross sections through which isotropic generators pass cannot decrease over time. Because at the same time, according to Theorem 3.1, no zero geodesics generating the horizon can disappear (they can only be created by new ones - by black hole absorption), this leads to the conclusion that the total horizon area of a black hole can never decrease with time. A necessary precondition, however, is the validity of the principle of cosmic censorship, which guarantees that the horizon cannot meet a (naked) singularity that would absorb and prematurely terminate (otherwise infinite in the future) zero geodesics generating the horizon.
For a general Kerr-Newman black hole, the area of horizon A is equal to
| A = 4 p { [ M + Ö (M 2 - M 2 / J 2 - Q 2 ) ] 2 + J 2 / M 2 } 2 , | (4.53) |
in the special case of the Schwarzschild black hole, A = 16p M2. Based on expression (4.49), the total mass M of a black hole can be divided into three parts :
| M 2 = (M ired + M elmag ) 2 + M rot 2 , | (4.54) |
where Mired is the above mentioned irreducible mass, Melmag = Q2/4Mired is the electromagnetic contribution and Mrot = J/2Mired is the rotational contribution to the total mass.
In connection with the 2nd law of black hole dynamics, we can divide physically possible processes with black holes into two groups (similar to what happens in thermodynamics) :
The actual processes with black holes are irreversible; the reversible process is only a certain idealization, which can only be approached. The situation here is exactly the same as in thermodynamics.
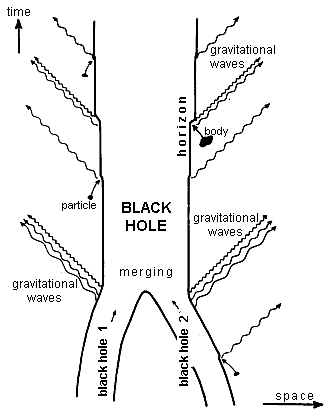 |
Fig.4.21. Schematic representation of the processes of absorption of material bodies by a black hole and the fusion of two black holes. In all similar processes, the total area of the horizon increases . |
The second law of black hole dynamics confirms (in addition to specific calculations of various types of processes) the extraordinary stability of black holes - a black hole cannot "split" or otherwise disintegrate, it is completely indestructible; it can only be increase in size by absorbing of next matter (Fig.4.21). However, we do not consider quantum processes here yet - see §4.7.
An interesting difference
in the growth of the resulting surfaces of black holes and
material bodies
The law of increasing the resulting surfaces of black
hole horizons (according to 2nd law) differs from the behavior of ordinary material
objects. If we take, for example, two identical plasticine small balls,
join them together and knead a new larger ball from them, its
surface will be about 20% smaller than the sum of the surfaces of
both original balls (the volume of the ball is V = (4/3) p.r3, surface of the sphere S = 4pr2, --> S = 22/3.V2/3).
However, for black hole horizons, due to the enormous curvature
of space, after merging, the resulting horizon will be larger than the sum of the two original holes.
| Theorem 4.8 ("3rd law of black hole dynamics") |
| By supplying any finite energy (no finite number of physical steps), a black hole cannot be "spun" at such a speed as to create an extreme black hole (for which J = M2, on the horizon r = M the centrifugal and gravitational forces equalize and the surface gravity k would become zero) . |
As follows again from the relation (4.51), with the angular momentum J the mass M always increases accordingly - the extreme black hole is unreachable, it can only be approached. If it were possible to achieve J = M2 with a finite number of steps, then we would achieve J> M2 with the only other such step - Kerr's naked singularity would arise in conflict with the principle of cosmic censorship. Thus, the 3rd Law of Black Hole Dynamics shows that cosmic censorship cannot be violated by black holes.
Among he laws of black hole dynamics also sometimes include the following statements :
| Theorem 4.9 ("0. Law of black hole dynamics") |
| For a stationary black hole, the surface gravity k is the same at all points on the horizon . |
This "zero" law of black hole mechanics was derived by Bardeen, Carter and Hawking [9]; see also equation (4.47), where k does not depend on the coordinates j and J. The situation here can be compared with conventional gravitational bodies such as planets, where surface gravity k can differ at different points on the surface due to the inhomogeneous distributions of mass density inside the body (§1.2, passage "Surface gravity").
The laws of black hole dynamics (especially the second law in conjunction with the conservation laws that form the content of Law 1) place fundamental restrictions on the magnitude of changes in physical quantities during the interaction of black holes with the surrounding matter and with each other.
Let us have a Kerr black hole of mass M1 and angular momentum J1 = a1 .M1. Let this black hole interact with matter, bodies and radiation during a certain time interval, so that the resulting black hole will have the parameters M2 and J2 = a2 .J2. According to the 2nd law of Black Hole Dynamics, the horizon must increase, so there must be an inequality between the two states of the black hole:
| M 2 [ M 2 + Ö (M 2 2 - a 2 2 ) ] > M 1 [ M 1 + Ö (M 1 2 - a 1 2 ) ] , | (4.55) |
where M and J are determined with respect to the asymptotic planar region, where the laws of conservation of total energy and angular momentum apply. In the case of a1 > 0 (ie when the original black hole rotated), the inequality (4.55) can be satisfied even if M2 is less than M1.
Thus, in principle, it is possible to "extract" a certain amount of energy-mass from the rotating black hole. One way to do this is to take advantage of the entrainment effect of inertial systems by rotating the black hole: a suitable set of bodies is placed around the black hole and the entrainment forces perform the work by means of an appropriare arrangement. An example of such a mechanism was shown in Fig.4.20a where although the rigid frame radiated gravitational waves, but with a suitable arrangement could also perform mechanical work. The second method of extraction of rotational energy from a rotating black hole is the Penrose process described in §4.4, Fig.4.17 (or its superradiation analogy), in which the body flies into the ergosphere, there it is divided into two parts, one of which is absorbed and the other part flies out of the ergosphere with more energy than the original body. By similar processes, in principle, all rotational energy (--> a2 = 0) can be taken away from a black hole ; the limit of the energy obtained is given by the inequality (resulting from (4.55) for a2 = 0)
| (4.56) |
Let us now have two Kerr black holes with the parameters M1,a1 and M2,a2 , which are initially so far apart that their mutual interaction can be neglected. The areas of their horizons will be A1= 8pM1[M1 + Ö(M12 - a12)], A2= 8pM2[M2 + Ö(M22 - a22)]. If these two black holes move towards each other so that they "collide" and merge, during this process a certain amount of energy is radiated in the form of gravitational waves and finally the resulting black hole is stabilized with the parameters M3 and a3 and the area horizon A3= 8pM3[M3 + Ö(M32 - a32)]. According to the 2nd law of Black Hole Mechanics, A3 ³ A1 + A2 , ie.
M 3 [ M 3 + Ö (M 3 2 - a 3 2 ) ] ³ M 1 [ M 1 + Ö (M 1 2 - a 1 2 ) ] + M 2 [ M 2 + Ö (M 2 2 - a 2 2 ) ] .
At the same time, the energy carried away by gravitational waves is (according to the 1st Act - the law of conservation) equal to Ewave = M1 + M2 - M3 ; we could define the "efficiency" of mass conversion to gravitational radiation h = (M1 + M2 -M3) / (M1 + M2). This inequality (ie the 2nd law of black hole dynamics) places a basic upper limit on the magnitude of this radiated energy. For example, in a head-on collision of two non-rotating black holes with masses M1 = M2 = M/2, when the resulting black hole will also be non-rotating (a1 = a2= a3 = 0), we obtain M3 ³ M Ö2, so that the total radiated energy Ewave < M (1 - Ö2) @ 0,293.M and efectivity of conversion of matter into energy gravitational wave is h <1 - Ö2 @ 0.293.
The laws of black hole dynamics, as we have formulated them here, are at first glance similar to the laws of thermodynamics. In order to clearly show and concretize this similarity, we compare the relevant laws of black hole mechanics and the laws of thermodynamics together in a clear table :
| 0. law |
Black holes: For a stationary black hole, the surface gravity k is the same at all points on the horizon. -------------------------------------------------- -------------------------------------- Thermodynamics: At thermal equilibrium, the temperature T of the body is in all places the same. |
Law 1 |
Black holes: d(Mc2) = (kc2/4pG).dA + WH.dJ + FH.dQ -------------------------------------------- -------------------------------------------- Thermodynamics: d E = T.dS + W.dJ + F.dQ for axially symmetric conductive body rotating at angular velocity W , having angular momentum J, total energy E = Mc2 , el. potential F, charge Q, temperature T and entropy S. |
Law 2 |
Black
Holes: The total area A of the horizons of interacting black holes cannot decrease with time. -------------------------------------------------- -------------------------------------- Thermodynamics: The entropy S of an isolated system cannot decrease with time. |
Law 3 |
Black holes: A Black hole cannot be "spun" with a finite number of steps to an extreme black hole for which k = 0. -------------------------------------------------- -------------------------------------- Thermodynamics: The body cannot be cooled to a temperature T = 0 of absolute zero with a finite number of steps . |
The similarity between the laws of mechanics of black holes and the laws of thermodynamics is very tight, and the surface gravity k being analogous to the temperature T and the total area of the horizon A being similar to the entropy S. It can already be seen here that the analogy between the entropy S in thermodynamics and the area of the horizon A in the mechanics of black holes is not only a purely formal similarity of some laws by which these quantities are governed. These quantities also have a similar role: just as in thermodynamics the law of entropy growth forbids the complete conversion of the thermal energy of a heated body into useful work, the law of growth of the black hole horizon area makes it impossible to convert all the mass of a black hole into useful work. In the following paragraphs we will see, that due to quantum processes in the field of black holes, the analogy between the laws of black holes mechanics and the laws of thermodynamics has a deep physical meaning, and black hole can actually be attributed to the thermodynamic temperature and entropy.
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||