When can singularities be expected ?

Chapter 3
GEOMETRY AND TOPOLOGY OF SPACE-TIME
3.1. Geometric-topological properties of spacetime
3.2. Minkowski planar spacetime and asymptotic structure
3.3. Cauchy's problem, causality and horizons
3.4. Schwarzschild geometry
3.5. Reissner-Nordström geometry
3.6. Kerr and Kerr-Newman geometry
3.7. Spatio-temporal singularities
3.8. Hawking's and Penrose's theorems on singularities
3.9. Naked singularities and the principle of "cosmic censorship"

3.8. Hawking's and Penrose's theorems about singularities

From the previous analysis, we have seen that those annoying singularities of spacetime appear in some exact solutions of Einstein's gravitational equations, such as Schwarzschild or Kerr-Newman geometry (see §3.4 and 3.5). The question arises as to whether singularities will occur even in more realistic physical situations. At a certain time (the 1960s), it was hoped that the singularities in the solutions of gravitational equations were the result of assumptions about precise symmetry, and that breaking of symmetry (eg. rotations) could perhaps prevent singularities.

An analogy with classical Newtonian mechanics would also point to this. If we take an exactly symmetrical distribution of small bodies and let them fall by their own gravity, they all "collide" at the same time in the center and create a kind of "singularity" in the distribution of matter (infinite density). However, it is enough to slightly break the exact symmetry (or let the initial state rotate) and the bodies will fly close to the center around each other (or the centrifugal force of constantly accelerating rotation will prevail) without something as bad as singularity happening.

Then singularities would be just an academic question: they would be properties of some idealized and unrealistic models. Because the exact symmetry is never fulfilled in real nature, there would in fact be no sigularitties - they would have no physical significance.

However, Penrose and Hawking's research has shown that in the general theory of relativity (which claims to be the correct physics of gravity) this is not the case - spacetime singularities are a regular phenomenon and occur in solving gravitational equations under very general conditions (even without symmetry), which are probably fulfilled in practice. Penrose and Hawking formulated their results in the form of several existential theorems specifying the conditions, under which spacetime singularities naturally occur. In this section, we will briefly approach these important theorems about singularities.

The first of these theorems is actually a generalization of the well-known fact that in GTR a spherically symmetric collapse below the Schwarzschild radius (see §3.4, 4.2, 4.3) leads to the formation of a singularity. In his theorem, Penrose replaces the Schwarzschild sphere (which is defined for the spherically symmetric case) with a more general object, the so-called trapped surface :

The trapped surface appears when the gravitational field is so strong that even the rays emitted out are "pulled back" by gravity (Fig.3.28). Since nothing can not move at a speed greater than light, the material located within the trapped area is "trapped - imprisoned" in the space area, whose boundary (and thus volume) is shrunk to zero for a finite time interval.

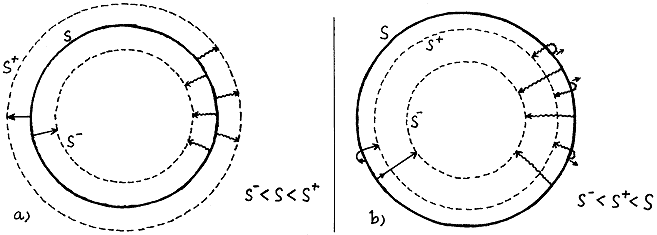
Fig.3.28. Let us have a closed two-dimensional surface S , from which a light pulse is emitted at a certain moment perpendicularly inwards and outwards. The set of points where the light emitted inwards per unit of time will be a closed area S^-, the set of points achieved per unit time by the light emitted perpendicularly outwards will be the closed area S⁺.
a) Under normal circumstances, the area S^- is smaller than the area S and the area S⁺ is greater than S .
b) If S is trapped surface (F), booth the area S^- and the area S⁺ will be smaller than S - even the rays emitted out of S will in fact be drawn inwards.

The Penrose theorem can then be formulated as follows :

We outline the proof of Theorem 3.4 according to Fig.3.29. On the Cauchy hypersurface S we choose a point p_o within the area bounded closed trapped surface F. Here is the convergence of geodesics C ³ C_o > 0, where C_o is some minimum value of convergence. Because according to a) the energy conditions is fulfilled, it will be dC/dl l C_o²/3 > 0 based on Raychaudhuri equation (2.59) (see Theorem 2.5 in §2.6). For l greater than the initial value of l₁ on the surface S, therefore, wil be C l 3/[l-(l₁+3/C_o)] so that the C becomes infinite no further than in the "distance" l_o = 3/C_o from the surface S, namely along each geodesy passing trough the area of the hypersurface S bounded by the trapped area F. Thus, the adjacent geodetics intersect, focal points appear.

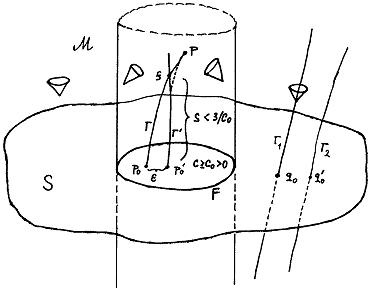Fig.3.29. Proof of the theorem 3.4. In the region of a (three-dimensional) spatial hypersurface S bounded by a two-dimensional trapped surface F, the convergence of geodetics C ³ Co > 0. This causes that geodetic G and infinitely close geodetics G ' to intersect at point f at a distance of less than 3/Co.

Through the point p_o let geodetic G pass, where we choose the point p at a "distance" greater than l_o. The adjacent (infinitely close) geodetic G ' intersects the geodetic G at a point f closer than p. Fractured world lines p'_o- f - p can "straightened" as indicated in obr.3.29 up, which gives the worldline going from the hypersurface S to the point p, which has greater length than geodesy G. And here we come to the first dispute: the time worldline with the greatest length going from the hyperspace S to the point p must be a normal (perpendicular) geodesy; however, if the normal geodesy has a length greater than l_o = 3/C_o, then it is not a worldline of the maximum length going from the hyperplan S to the point p (we have shown the possibility to find a longer worldline). Therefore, if we choose a point p at a sufficiently large distance (greater than 3/C_o along some geodesy) from the hypersurface S, there will be no time worldline of the maximum length going from the hypersurface S to the point p.
According to assumption b), the hypersurface S is a global Cauchy hyperssurface of spacetime M, so that each time worldline in M intersects S (just once). Therefore, since each temporal line passing through the point p intersects the hypersurface S, there between them must be a world line of maximum length going from the hyperplot S to the point p (it should therefore be geodetic).
However, a while ago we showed how it is possible to find a point p, into which it is not possible to lead a worldline of maximum length from the surface S. We thus obtain a logical dispute, which can be satisfactorily resolved only by the fact, that no geodetics from S can get to the point p, which has the above-mentioned controversial properties - no geodesics pointing from the area surrounded by the trapped surface F of the hypersurface S in the future does not have a length greater than 3/C_o. Thus, incomplete geodetics occur in M.

Let us briefly note the meaning and purpose of the individual conditions in Theorem 3.4. We have already outlined condition c) above - it is precisely the basic specific condition that the gravitational field is so strong that not even light can escape from it. Condition a) says according to Raychaudhuri's equation (2.59) that gravity has an attractive character and a focusing effect on geodesics (the derivation of the convergence of geodesics C is non-negative). As shown in §2.6, in order to satisfy the condition R_ik Vⁱ V^k ³ 0, it is necessary that the intrinsic energy density be non-negative for each observer. So it is an energy condition, which is satisfied for all known forms of matter and fields (quantum exceptions will be mentioned below).

More problematic is condition b) - the existence of a (non-compact) global Cauchy hypersurface in spacetime M, which makes theorem 3.4 relatively weak. As we saw in §3.5 and 3.6, some solutions of Einstein's equations (eg Reissner-Nordström or Kerr geometry) lead to spacetime, which does not have global Cauchy hyperfields. Theorem 3.4 actually states that in the presence of a closed trapped surface (eg in the event of a gravitational collapse) there will be either a singularity or a Cauchy horizon; in both cases, the possibility of predicting the future everywhere in M is lost. However, the sentence 3.4 cannot decide between these two eventualities.

When using Theorem 3.4 on the "local" case of gravitational collapse (chapter 4, §4.2-4.4) is also disadvantageous, that we must know the global geometrical structure of the universe (being Cauchy hypersurface is a property not only of the hypersurface, but also the whole spacetime M). It would therefore be useful to get rid of condition b) (the need for the existence of a global Cauchy hypersurface).

When we do, ie. a hypersurface S is only a partial Cauchy hypersurface, will be arguments leading to a sentence of 3.4 apply only in Cauchy area evolution D(S) hypersurface S. The analysis of the situation on the Cauchy horizon H(S) (which is always an isotropic surface) leads to the fact that H(S) must be non-compact in order to satisfy the causality condition for isotropic geodesics. If the energy condition applies and if an trapped surface is present, geodetics that are not complete can be found. The relevant sentence reads as follows :

*) Generic condition (lat. genericus = genus, species; also general, basic ..),
also called a ancestral or type condition, is a somewhat special and abstract requirement (square brackets [..i, j, m, n ..] mean that antisymmetric indices are taken).
Physically, this condition means, that every particle or quantum, moving freely through geodesy, encounters a place throughout its history where space-time is curved by some form of matter or radiation. Under normal circumstances, which may occur astrophysically, it would suffice, for example, R_jklmK^kK^l a 0. The special more complex form of the generic condition is based on the details of the mathematical proof of Theorem 3.5 [130], to exclude some special metrics in which the curvature is nullified in some directions.

Hawking then formulated another sentence :

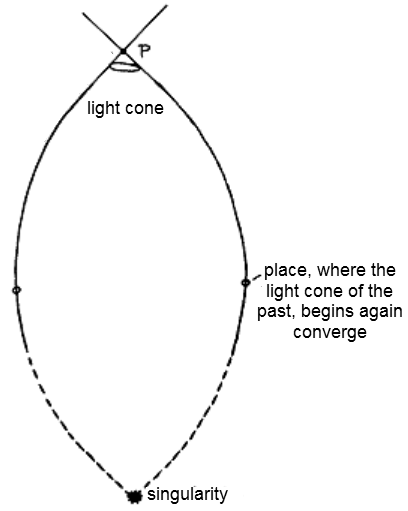Fig.3.30. If we follow the light cone from the point p in the direction of the past and find that its isotropic geodesics begin to converge again (due to the focus of space-time curvatures), we can expect the presence of space-time singularity in the past (eg "big bang" in the space's past) .

Both of these theorems have the advantage that no assumptions need to be made (other than causality) about the global structure of the universe; they are therefore advantageous for the analysis of bounded ("local") phenomena such as the gravitational collapse of stars. Theorem 3.6 is (in the version "in the future") usable for sufficiently homogeneous cases of gravitational collapse (point p corresponds to the center of collapse), but mainly (in the version "in the past") it can be used in cosmological problems (chapter 5). The theorem refers only to the interior and mantle of the light cone past the point p, which are areas that can in principle be observed from p. If we take as a world point p event of our observation of the universe, we can in principle, on the basis of this observation (eg determination of the observed density of matter in the universe) decide whether geodesics have changed the sign of their convergence in the past (Fig.3.30). According to the analysis of Hawking and Ellis [127], [128], the density of the observed relic radiation (which comes isotropically at a temperature of about 2.7 °K) could be sufficient for condition (c) of Theorem 3.6 to be satisfied. Then in the past (according to classical OTR) there should be a singularity of spacetime - the "big bang".

The following theorem is intended especially for singularities in cosmology :

Conditions b) and c) mean that spacetime M is closed and expanding (resp. shrinking) at each point of the hypersurface S .

The above-mentioned theorems 3.4 - 3.7 indicate the presence of spacetime singularities in a wide group of solutions of Einstein's equations under conditions that seem to be fulfilled in nature. This will be shown in Chapter 4 for the gravitational collapse with the formation of a black hole and also in Chapter 5 for the universe as a whole. Hawking's and Penrose's theorems are existential theorems and contain little information about the nature and properties of the predicted singularities - their "dimensions", "shape", "position" in space and time, and so on. In terms of physical importance for the evolution of spacetime, it is also necessary to know the "number" of geodesics incomplete due to singularities: is it just one geodesy, the whole congruence in a certain part of spacetime, or all geodetics (and worldlines in general)? This is possible to get some idea from this existential sentences as well; eg in the case of satisfying the conditions of theorem 3.4 and the absence of Cauchy horizons, no geodesics from the hypersurface S can be extended further than 3/C_o (C_o ³ 0 is the minimum value of convergence to S). If the Cauchy horizon is present, not every geodesy may encounter a singularity, because it may reach an area in which the future cannot be predicted from the S-hypersurface. From the theorems of singularities, it is generally possible to prove at most the existence of a three-dimensional congruence of incomplete geodesics located within the Cauchy region of the evolution of the area S.

The nature of singularities can be determined analytically in the case of exact solutions of Einstein's equations (§3.4-3.6). The role of singularity theorems is different: to show whether singularities are present in such solutions of Einstein's equations, which we cannot describe analytically. And that's certainly not a trivial question. At the same time, we expect that the nature of the singularities in these cases will be at least somewhat similar to those of the exact solutions that are physically close to them.

3.7. Spatio-temporal singularities		3.9. Naked singularities and the principle of "cosmic censorship"

Vojtech Ullmann