| (4.4) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 4
BLACK HOLES
4.1. The
role of gravity in the formation and evolution of stars
4.2. The
final stages of stellar evolution. Gravitational
collapse
4.3.
Schwarzschild static black holes
4.4. Rotating
and electrically charged Kerr-Newman black holes
4.5. The
"black hole has no hair" theorem
4.6. Laws
of black hole dynamics
4.7. Quantum
radiation and thermodynamics of black holes
4.8. Astrophysical
significance of black holes
4.9. Total
gravitational collapse - the biggest catastrophe in nature
4.3. Schwarzschild static black holes
What was qualitatively stated in the previous paragraph about the course of gravitational collapse, is based on a detailed analysis of the simplest model of gravitational collapse, the spherically symmetric collapse. In §3.4 we derived the spacetime geometry corresponding to spherical symmetry - Schwarzschild geometry. With spherical symmetry according to Schwarzschild-Birkhoff theorem 3.3, the geometry of space-time will be Schwarzschild's even in the non-static case. Therefore, if the gravitational collapse take place so that the spherical symmetry is always exactly maintained (i.e. as distridution mass and its motion will be exactly radial), the geometry of the surrounding spacetime will be Schwarzschild during the entire course of gravitational collapse. In the early stages, when the radius of the star is much greater than the gravitational radius, only a part of the Schwarzschild geometry outside the star will be realized, while inside the space time geometry will be different (internal Schwarzschild solution 4.13b, dependent on the internal structure and movement of the mass). In the final stages of collapse, when a star of mass M are compressed under its gravity below its gravitational radius, the surrounding spacetime will already have an (outer) Schwarzschild geometry everywhere (derived in §3.4, the relation (3.13) ) :
| (4.4) |
Schwarzschild's geometry of spacetime thus describes a static spherically symmetric black hole. Some features of Schwarzschild geometry, especially from a geometrical-topological point of view, were discussed in §3.4 "Schwarzschild geometry"; here we will extend this image with respect to the physical properties of the black holes.
What makes a black hole a black hole, is the existence of an event horizon, in this case the Schwarzschild sphere r = 2M, at which the escape ("2nd cosmic") velocity is equal to the speed of light. The possibility of uniform circular motion of the photon in the field of the Schwarzschild black hole is obtained by placing in relation (4.4) for the requirement interval ds2 = 0, dr = 0, J = p/2 and d2j/dt2 = 0 (uniformity). Dividing by dt we get (dj/dt)2 = (1 - 2M/r)/r2 and after further derivation with respect to the requirement d2j/dt2 = 0, we obtain the solution r = 3M = rf . In addition to the Schwarzschild sphere, there is another significant sphere around the black hole - the so-called photon sphere
| r = 3 M = 3 M G / c 2 , | (4.5) |
which is the geometric location of points where the "1st cosmic" velocity is equal to the speed of light, so at this distance photons can orbit around the black hole in circular orbits (Fig. 4.8). These are also the lowest (innermost, boundary) circular orbits (see below); no more circular orbits can exist under the photon sphere, each body must move outwards at high speed here, if it is not to be absorbed by a black hole.
The motion of
particles in the field of a Schwarzschild black hole. Effective
potential.
We can now purposefully continue the analysis of the geodetic
motion of test particles in the Schwarzschild geometry of a black
hole. We will use equations (3.17) - (3.19), which we will write
here again:
| (dr/dt)2 = 1/K2 - (1 - 2M/r)(1 +`L2/r2) , r2 dj/dt = const. def = `L , dt = K(1 - 2M/r) dt . |
(4.6a, b, c) |
In the limit transition r ®¥ is (dr/dt)2 ®1/K2 -1, dt/dt®1/K. The time component of 4-momentum pi = mo.dxi/dt is E º po = mo .dt/dt. The quantity 1/K now has the meaning of the total energy at infinity per unit of the particle's own mass: 1/K =` E¥ ;` L is the angular momentum per unit mass. Thus dt = EA-1.(1-2M/r)dt and equation (4.6a) read
| (dr / d t ) 2 = ` E ¥ 2 - (1 - 2M / r) (1 +` L 2 / r 2 ) , | (4.7) |
which is advantageous to write in the form
| (dr / d t ) 2 = ` E ¥ 2 - V 2 (r) , | (4.8) |
where
| V 2 (r) = (1 - 2M / r) (1 +` L 2 / r 2 ) . | (4.9) |
The derivative (4.8) according to t gives the equation 2.d2r/dt2 = - ¶V2(r)/¶r . The quantity V2(r) therefore has the meaning of the effective potential in the equation describing the dependence between r and t , ie for the radial component of the motion. Substituting dt = (r2/` L) dj from (4.6b) to (4.8), the equation between r and j is obtained :
| (` L 2 / r 4 ) (dr / d j ) 2 = ` E ¥ 2 - V 2 (r) . | (4.10) |
The effective potential
V2(r) consists of three parts :
a) The usual attractive part proportional to
r-1 ;
b) Repulsive part (proportional to r-2) describing the centrifugal barrier ;
c) Another, purely relativistic attractive
part proportional to r-3, creating a "pit" in
the effective potential around r = 0 .
The course of the effective potential for
different values of the angular momentum of the test particle is
shown in Fig.4.6 on the left, where the areas in which the
above-mentioned parts a, b, c dominate are also marked. If we
know the effective potential V(r) and the energy` E¥, we can determine the radial component of
the motion of the test particle based on equation (4.8).

Fig.4.6. Effective potential for test particle motion in the
Schwarzschild black hole field.
Left: The course of the effective potential V(r)
for different values of the specific angular momentum` L of
the particle.
Right: The radial component of movement of the
test particles having a specific energy` E ¥
and angular momentum ` L is
determined by the effective potential VL(r).
The intersections of the line V =` E¥
with the curve V = V(r) are the turning points where the radial
component of the motion changes its direction. Line I has two intersections A and B, which
corresponds to an elliptical orbit with perihelia r = rA and
"aphelia" r = rB. Line II intersects the curve V(r)
only one point C ,
which is a local minimum - this is a stable circular orbit of
radius r = rC. Line III intersects V (r) also at one
point D , which is,
however, the maximum - the corresponding circular orbit with
radius r = rD will be
unstable.
Some significant properties of the orbits of the test particles can be determined without a detailed solution of the relevant equations of motion (4.6). As can be seen from equation (4.8) or (4.10), the radial component of the motion of the test particle changes its direction to the opposite when` E¥2 - V2(r) changes sign. The value of r, for which the effective potential is equal to the energy of the test particle, V(r) =` E¥, is thus the turning point where the approach to the black hole stops and the distance occurs, or conversely, the distance from the black hole changes into an approach.
The various options are illustrated in Figure 4.6 on the right. Line I represents some energy I` E¥ test particle crosses the function V(r) corresponding to said angular momentum` L test particle at two points A and B. The radial component of the motion will then look as if we placed a small ball at the height ` E ¥ (ie at point A or B ) on the appropriate vertically constructed modeled curve V (r ) and let it roll freely in the earth's gravity; the ball would periodically roll between points A and B and its coordinates r would oscillate between the values r = r A and r = R B . Test particles thus rotates along with approximately elliptical orbit "perihelia" r = R A and "aphelia" r = r B . In case that the equation V (r) = ` E ¥ has j en one root, i.e. equality V (r) = ` E ¥ occurs at the point where the function V (r) extreme establish the balance between gravitational and centrifugal by force - it will be a circular orbit . In Fig.4.6 on the right this occurs for lines II and III. Line II intersects the curve V (r) vb o da C of its local minimum. Ball placed in point Cit will still be there (its radial coordinates r = r C does not change) - the test particle will orbit the black hole in a stable circular path (if we do not consider the emission of gravitational waves, see below) . The straight line intersects the curve III, in (R) in point D of the local maximum, j This constitutes again a circular path. However, this circular orbit is not stable, the ball placed at point D will roll down either to the left kr = 2M or to the right due to the slightest deflection. The circular motion of test particles to such an unstable circular orbit is also due to the small P of noise turns in the spiral, either inwardly Cr = 2M (particle is absorbed), or outwards.
From the equation ¶V(r) / ¶r = 0 it follows that at` L> 2. Ö(3) .M the function V(r) has a local maximum and a minimum in points
 |
(4.11) |
In the case of ` L <2. Ö(3) .M there is no minimum or maximum and therefore there is no proper stable circular orbit. Thus, for a particle falling with ` L <2. Ö(3) .M, centrifugal repulsion, which would prevent it from hitting the radius r = 2M, does not apply and such a particle will be absorbed. For` L = 2. Ö(3) .M the maximum and minimum merge into a single inflection point (see Fig.4.6 on the left) at r = 6M - it corresponds to the lowest (innermost) possible stable circular orbit. The maximum of the centrifugal barrier is at the point r = rmax according to (4.11), so if the total energy of the particle is` E ¥ > V(rmax), the centrifugal barrier is overcome and the particle is absorbed by the black hole.
Some types of test particle trajectories in the Schwarzschild black hole field are shown in Fig.4.7. At large distances r >> 2M from the black hole, the situation is not very different from Newtonian mechanics: there are hyperbolic, elliptical or stable circular orbits similar to Kepler (for elliptical orbits there is only a small twisting of the "perihelion", as measured by Mercury, see below).
 |
Fig.4.7.
Basic types of orbits of test particles in the
Schwarzschild black hole field: Trajectories ending on the horizon (the particle is absorbed), parabolic and hyperbolic orbits starting and ending at infinity, "elliptical" and circular orbits corresponding to the orbiting particle around the black hole. There is no capture of the elliptical precession - see their actual shape in Fig.4.12. |
However, in areas close to the black hole (ie at r in the range from 2M to about 10 M), the trajectories of the test particles differ significantly from the Newtonian ones. As indicated above, each of the particles with the angular momentum of `L < 2.Ö(3).M, will be absorbed by a black hole, regardless of their energy` E ¥ (while in Newton's theory at r=0 the centrifugal barrier is infinitely high and only particles with exactly zero angular momentum can fall on the center). For a particle with `L = 2.Ö(3).M existed only one stable circular orbit r = rms, after which the particles (if an adequate energy` E¥) may circulate :
r ms = 6 M = 6 M G / c 2 ;
it is the lowest - innermost stable circular orbit - it is stable only to outward failures, but unstable against inward deflections, see Fig.4.6 on the left (but in fact it is highly unstable due to gravitational wave radiation - see below passage "Gravitational wave radiation when moving in a field black holes") .
The particles with the angular momentum of ` L> 2. Ö ( 3) .M already have all the options of movement, depending on its energy` E¥. On the one hand, they can move in elliptical orbits with the lowest and highest point given by the relation (4.11). Furthermore, for these particles, there are stable circular paths at the V(r) potential minima and labile circular orbits at the V(r) potential maxima. According to formula (4.11) is stable circular orbit radii ranging from R = 6M (for`L = 2.Ö(3).M) to r = ¥ (the` L = ¥) and the radii of circular arcs labile between r = 3M (for` L = ¥) to r = 6M (for` L = 2. Ö(3) .M). Particles arriving from r = ¥ with energies` E ¥ <Vmax , i.e. according to relationship (4.9) of the energy `EA2 < (1 - 2M/r2max)(1 +`L2/r2max), wherein rmax is given by (4.11), they will move along a curved path (at greater distances close to the hyperbolic path), reach "perihelion" and move away into r = ¥ again. However, particles coming from an infinite with energy` E ¥> Vmax , are absorbed by the black hole.
To calculate the period (and angular velocity) of the test particle orbit along a circular path in the Schwarzschild field, we use the relation (4.6b), where we substitute dt = (1/`E).(1-2M/r)dt from (4.6c). We will get
w º d j / dt = (` L / r 2 ) (1 - 2M / r) /` E ¥ .
The condition of circular motion is` E¥ = V(r) and r = rmin (stable circular orbit) or r = rmax (unstable circular path). From relation (4.11) we can easily get `L2 = M2.r2/(M.r - 3.M2) regardless of whether it is a stable or unstable circular orbit. When we substitute these conditions into the relation for dj/dt, we get it after adjustment
w = Ö (M / r 3 ) , ie T = 2 p Ö (r 3 / M) .
Thus, we see that for circular orbits (stable and unstable) in the Schwarzschild field, Kepler's law M = w2 r3, known from Newton's non-relativistic physics , retains its exact validity .
Light
propagation in the Schwarzschild black hole field
When analyzing the motion of photons (as well as other particles
with zero rest mass) we can proceed in basically three ways :
a) Use
either the equation ds2 = 0 with certain given
conditions (so we did it at the beginning of this paragraph when
deriving a photon sphere) ;
b) Or use the geodesy equation (3.16) in
which the parameter ds = dt (= 0 ) is replaced by another suitable
non-zero affine parameter l continuously changing along the
trajectory of the photon (eg l
= t can be taken);
c)
Or finally to investigate the motion of a particle with non-zero
rest mass mo and then
go to the limit mo ® 0 .
In this last method, however, equations (4.8) and (4.10) are not directly applicable, since the variable `EA= EA/mo a `L = L/mo the energy and angular momentum per unit mass of its own are endless. However, the ratio of these quantities, in which mo is truncated, approaches the final value, lim mo®0(` L/` E¥) = b, equal to the collision parameter b defined as the ratio of the angular momentum of the test particle to its momentum :
| b º L / p = L / Ö (E ¥ 2 - m o 2 ) = L / Ö (` E ¥ 2 - 1) . | (4.12) |
The collision parameter b , which is the distance from the center r = 0 at which a straight beam would pass without gravity, determines the behavior of a photon in a given Schwarzschild field of a black hole (the motion of a photon in a gravitational field is given only by its direction and does not depend on its energy).
By combining equations (4.6b) and (4.7) we get after the limit transition mo®0,` L®¥ the equation of the orbit of the photon
| [ (1 / r 2 ) (dr / d j ) ] 2 = 1 / b 2 - (1 - 2M / r) / r 2 . | (4.13) |
The place where 1/b2 = (1 - 2M/r).r2 is here the turning point where the radial component of the motion changes its direction. Therefore, in order for a photon to reach a location with the r coordinate , its collision parameter must satisfy an inequality
| b < r / Ö (1 - 2M / r) . | (4.14) |
The expression on the right side of this inequality (playing a similar role here as the effective potential in equation (4.8)) has a minimum value of 3.Ö(3).M for r = 3M. Thus, only a photon with a collision parameter b <3.Ö(3).M can reach any (arbitrarily small) value of the coordinate r - it is absorbed by a black hole. We get the same result from relation (4.11), in which the limit transition mo®0, ie` L®¥ gives rmax = 3M.

Fig.4.8. Schematic representation of the Schwarzschild sphere
(horizon), photon sphere, output light cones and possibilities of
photon movement in the Schwarzschild black hole field.
Fig.4.8 shows the output light cones (not to be confused with space-time light cones!) at different distances from the black hole. By output cone we mean a cone with a vertex at a given point such that photons emitted in the direction lying inside this cone (light section in Fig.4.8) are not captured and can go to infinity, while light emitted in the direction outside this cone will be absorbed by a black hole (dark hatched slice). At large distances r >> 3M from the black hole, the output cone has a geometry close to 4p. Almost all photons can go to infinity from here, with the exception of photons emitted in the direction of a black hole in a narrow cone at an angle such as the angle of view of which a sphere of radius rz = 3.Ö(3).M appears from a given distance; the orbits of such photons are curved in a gravitational field so that they are absorbed by a black hole. In other words, all photons having a collision parameter less than rz = 3.Ö(3).M are absorbed (Fig.4.9). For photons coming from infinity, the black hole appears as a totally absorbing sphere of radius 3.Ö(3).M. The effective cross section of the photon (and each relativistic particle) capture by the Schwarzschild black hole is therefore equal to
| s r = p r z 2 = 27 p M 2 = 27 p G 2 M 2 / c 4 . | (4.15) |

Fig.4.9. Photons coming to the Schwarzschild black hole with the
collision parameter b < 3.Ö(3).M
are absorbed, photons with
b = 3.Ö(3).M
reach the photon sphere, at b
> 3.Ö(3).M
the photon trajectories are
only curved, but the photons escape from the black hole field.
As you approach the black hole, the output light cone narrows, of course (Fig.4.8), faster than would correspond to a purely geometric view based on the size of the black hole rg = 2M in an otherwise planar space. At a distance of r = 3M (on the light sphere), the output cone has an angle equal to only 2p and narrows rapidly as it approaches the black hole. At a distance r = rg = 2M (on the horizon), the output cone is already completely closed - its angle is equal to zero (not 2p as it would follow from a simple geometric view without taking into account non-Euclidean properties of spacetime). Only a beam radiated exactly perpendicularly "upwards" will not be absorbed here and could theoretically escape, but with an infinite redshift; such photons emitted radially from the horizon outwards remain on the horizon indefinitely, in space-time they still move together with the horizon (the horizon is "generated" by zero geodesics - see theorem 3.1).
Deviation of
particles and light in the Schwarzschild field
The solution of equation (4.10), which is a differential equation
of the orbit shape, leads to elliptic integrals and therefore
cannot be expressed analytically in general. To find an
approximate solution, usable at greater distances from the black
hole (r >> M), it is advantageous to introduce an inverse
radial coordinate u = M/r, which is directly related to the
approximation performed. The effective potential
in the variable u is
V2(r)= (1-2u)(1 + L2u2/M2, the angular momentum is useful
to express by using the collision parameter and velocity at
infinity:`L2 = vA2b2/(1-vA2). Equation (4.10) then takes the
form
| (dr / dj)2 = M2 / b2 + M2(2u - 1).(1 - vA2) / (vA2 b2) - u2 + 2 u3 . | (4.10 ') |
At a sufficiently large distance from the center, the term 2u3 is negligibly small and equation (4.10 ') describes a conic section with the focal parameter p s f/2 = vA2b2/M2(1 - vA2) and the eccentricity e = Ö[vA2(2vA2-1).b2/M3.(1-vA2) + 1]. Additional GTR effects are caused by member 2u3 in equation (4.10 '); at large distances from the center this member causes only slight deviations from the normal Keplerian orbits, but at distances close to the gravitational radius of this member plays a crucial role and the trajectories of the test particles there is diametrically different from the Keplerian.
Let us first examine the hyperbolic movement according to the upper part of Fig.4.10; we will be interested in angle a by which the particles are deflected from its original direction asymptotic. This angle is given by the angle between the asymptotes of the particle orbit: a = j(t=+A) - j(t=-A) - p = 2 [j(r=rm) - j(r=A)] - p/2. If the value of the collision parameter b is high enough, the movement of the test particle will take place at large distances, ie u << 1 will be satisfied in all points of the trajectory. Deriving equation (4.10 ') gives the equation
d 2 u / d j 2 + u - M 2 (1 - v ¥ 2 ) / ( v ¥ 2 b 2 ) = 3 u 2 .
If we neglect the right side 3u2, the solution of this equation will describe a rectilinear motion (zero approximation). Substituting this solution of the zero approximation into the member 3u2 and again solving the resulting differential equation, the trajectory of the particle in the first approximation is obtained, which is already suitable for the given purpose. Angle a then comes out
| a = 2M / b (1 + 1 / v ¥ 2 ) . | (4.16) |
This relation gives the value of the deviation from the linear motion of a test particle moving in the Schwarzschild field at any velocity v¥ (<= 1) with a sufficiently large impact parameter b ; in this case, the collision parameter b is approximately equal to the distance rm of the point of greatest approching of the particle to the center at r = 0. Formula (4.16) also holds for v¥ = 1, so that the angle of deflection of the path of light in the Schwarzschild gravitational field is equal to
| a phot = 4 M / b = 4 GM / (b.c 2) . | (4.16 ') |
For a light beam passing just around the surface of the Sun (b » 7.105 km), this deflection angle emerges aphot » 8,5.10-6 rad = 1,75 '', which was confirmed by observations during a total solar eclipse. In Newton's theory (where a photon is considered to be a particle having in infinity by velocity c), the angle of deflection of the photon's path is half that given by formula (4.16 '). The results of observation clearly confirm the angle value corresponding to the GTR.
Gravitational lenses. Optics of black holes.
The curvature of the light path in the gravitational field leads
to an effect, which is schematically shown in Fig.4.10 b). If
there is a very massive body M near the line between observer O and some light source P (perhaps a star
or quasar), the
light rays from source P will be curved by their
gravitational field on their way to observer O. E.g. the beam III,
which would normally connect the source to the observer, deviates
near the body M and the observer O
will not see it.
Instead, the observer O
is struck by another
suitably curved beam I, so that the source P will appear to the observer projection in
position P1. However, if the dimensions of the object
M are small enough with respect to its mass
or the source-observer distance, light can come to the observer O even after the second path - ray II. In such a case, instead of one of the real
light sources P, the observer will projectively
see two apparent images P1 and P2. But if the source P, the body M and the observer O lies on one line, the point source P will appear as a ring around the OM axis - the so-called Einstein's ring (see figure below);
with a small
deviation from the linear configuration, the source P will then be displayed as an arc.

Fig.4.10. Bending of light rays in a gravitational field.
a) The
trajectory of a photon deviates from the original direction by an
angle a (passing by the angle formed by the
asymptotes of the hyperbolic trajectory of the photon) as it
passes around the material object M. This scheme is also applicable to test
particles of non-zero rest mass. b) Effect lensing due to the bending of light
rays coming from the source P while passing through the gravitational
field of the intermediate body M. The observers O are hit by rays I and II , so that the real source P
appears from there as two
apparent sources Pl and P2 .
If we denote the angle between the lines of the observer O with the source P and the gravitational body M as g, the angle d at which the light source P will appear with respect to the line OM will be given by the equation
d 2 - g d - 4 G M / [x 2 ( x 1 + x 2 ) c 2 ] = 0
valid if all angles
marked in Fig.4.10 b) are small enough. This quadratic equation
has generally two solutions dI and dII corresponding to the two
possible light rays I and II, by which light from the source P can reach the observer O. This interesting phenomenon is called
the gravitational lensing effect, by
analogy with refractive lenses in optics.
Here is the finding derived in
§2.4 (section
"Gravitational electrodynamics
and optics"), that the gradient gravitational
field behaves as an optically
inhomogeneous transparent medium for the passage of
electromagnetic waves. From an optical point of view, a graviting
spherical body with mass M for light appears as a kind of convergent "lens", the optical power of is largest
in the area around the surface of the body (if this is the black hole is at a
distance r = 3.Ö(3).M, for which the image focal
length is 3M) and
decreases to zero at great distances. From an optical point of
view, the gravitational lens has a significant "spherical defect" (spherical
aberration),
but is perfectly achromatic - bends all wavelengths exactly
the same.
 |
Fig.4.11.
Influence of a spherical gravitational lens on a parallel
beam of light rays. a) Behind a body of radius greater than 3M are three areas: the "shadow" area A; area B, where only one ray passes through each point; area C, where two beams pass through each point. b) In the case of a black hole, areas A and B do not exist, at least two rays can pass through each point (the whole space around it is area C). |
Fig.4.11 schematically
shows the situation that occurs when a body or a black hole is
irradiated with a wide parallel beam of light (from infinity). If
a spherical body of mass M has a radius greater than 3M (ie it is
not a black hole), we can divide the space behind such a body
into three optical areas (Fig.4.11a). Immediately behind the
body is the area of the "shadow" A, caused by the light
absorption in the body. In area B , only one ray passes through
each point, while in area C, two gravitationally curved rays
pass through each point (double image ) and interference may therefore
occur. If the body M has a radius of less than 3M
(practically it is a black hole), the area of "shadow"
A and area B are missing here, the whole
space around the black hole for r > 3M
is area C (at least two curved rays pass through
each point) - black hole does not
cast a shadow !
The optics
of black holes is therefore very varied and interesting.
For example, if we illuminate a cone of light from a finite
distance to a black hole, a small part of the photons will return to us: some photons will curve near the
photon sphere by encircling the black hole 180° at a distance
slightly greater than 3.5.M and they will
come back to the place from which they were emitted (some possibly even after multiple orbits near the
photon sphere) - the
effect of a kind of "gravitational
retro lens".
From this point of view, therefore, a black hole in
"reflected light" does not appear as absolutely
"black" as might be expected. In any case (whether we
see black hole on either side relative to the light
source) around the black hole illuminated by
a sufficiently
intense stream of light we will see a kind
of "halo"
- a glowing ring with a radius slightly less than 3.(Ö3).M * ); in fact, it will be a series of
concentric rings corresponding to a simple, doubling
and multiple of photons runs around a black hole near
the photon sphere, ie. photons deflected by a black hole by angles Dj = jo + 2k.p , k = 1,2,3,... ( jo is the angle between the source and the
observer). However, the intensity of this ring is very small
compared to the intensity of the primary source. Another
interesting fact is that an observer in the photon sphere (if he could exist there) he would see his own back in the
distance in front of him.
*) The effect is a bit like the light "halos" in water
drops irradiated by sunlight.
 |
The view of the starry sky towards the black hole shows a series of condensed images of a whole set of stars in the sky, stacked in the form of ever narrower rings around the black hole. |
This strong curvature of
the light rays near the black hole would have a very strange
effects on the appearance
of the starry sky for an observer near the black hole. The
black hole, which is an optically absorbing black body, appears
like a dark disk against the starry sky, but does not overshadow anything - the observer still sees all
the stars in the sky, including those "behind" the
black hole. Only their positions in these directions appear to be
substantially altered - scattered and thickened around the ring r
= 3. (Ö3).M around a black hole.
In addition, each star could be
seen many times in different
directions
- the observer would see not only one sky, but (in principle) an
infinite number of its shrunken images, pressed into concentric circles
around a black hole. The "zero", the basic sky, is made up of rays that go from the
light source directly to the observer. 1.
image of the
sky, formed by rays that made one orbit around the black hole on
the way to the observer, is shown in an annulus with a radius of
about 5.2.M around the black hole. The 2nd image of the sky is visible as another
narrower ring inside the first and corresponds to the rays that
circled the black hole twice. And so on, every other gravitational image of the sky is formed by a contiguous
narrower (and darker) annulus, lying closer to the photon sphere
r = 3.M.
The brightness of these images is
very small overall, and the dimensions of the rings are in the
order of kilometers (for black holes in stellar masses), so that
this bizarre optical effect would be visible only to observers
close enough to the black hole; for distant observers - including
our astronomers - multiple images would be completely indistinguishable .
Strong, weak, and diffuse
gravitational lenses in space
Each mass gravitationally bends the path of
photons and light rays around it - creating a gravitational
lensing effect, causing coordinate shifts and
deformations of background objects caused by the gravity of
objects in the foreground. In most cases, however, these are very
weak effects, on the verge of measurability. The
effect of a gravitational lens can generally be divided into two
categories :
× Strong gravitational
lensing
creating multiple images and large arcs, caused by the massive
gravity of compact objects or the huge accumulation of matter in
galaxies and galaxy clusters.
× Weak gravitational
lensing
causing only small angular deflections of radiation. This can be
caused by two circumstances :
1. Objects of relatively small masses such as stars and
planets, causing the gravitational "microlens"
effect mentioned below.
2. The passage of radiation around
very mass diffusely distributed systems at great distances from
them.
Weak gravitational lensing can be manifested by two effects :
- Convergence of rays increases the angular size
and brightness of the background objects ;
- Gravitational shear beam is manifested by the
tangential blurring of the source image around the
"lensing" object.
Gravitational lenses in
space
Although the effect
of a gravitational lens has long been a well-known consequence of
the general theory of relativity, it was first observed only
recently. When observing stars, the curvature of the path of
light by the gravitational field of other stars is negligible and
the effect of the gravitational lens is practically not manifested,
because the gravitational field of ordinary stars is relatively
weak and decreases rapidly with distance. Therefore, to achieve a
noticeable effect, the two stars would have to lie almost exactly
on a line passing through the observer; the probability of such a
close alignment of two differently distand stars on one line is very small.
Effective gravitational lenses can be galaxies (which have a mass of the order
of ~ 108 -1012 -times larger than the average
star), but the light source on which the lens effect is observed
must then be a very distant object in order to have a certain
probability that light will pass close enough around such a
material galaxy on its way to us. Thus, a massive galaxy or
cluster of galaxies, with its gravitational curvature of
electromagnetic rays, acts like a huge "lens" through which we look into a more
distant universe (see below "Gravitational
lenses - massive astronomical telescopes?"). As a result, the image of a given very
distant galaxy can be amplified, multiplied, or altered into arcs
or rings by the gravity of a vastly massive object that lies
almost exactly on the connecting line
between us and the
observed distant galaxy.
Indeed, in 1979, an unusual pair
of quasars QSO 0957 + 561 A, B (angular
distance between them 5.7'') was discovered at the Kitt Peak
Observatory in Arizona (D.Walsh et al.), which have the same redshift z =
1.41, practically identical spectra and also slightly different
brightness; moreover, the brightness ratio of objects A
and B is the same in all observed wavelength
regions - radio, infrared, optical and ultraviolet []. A natural
explanation for these unusual context is that we observe not
two different quasars, but one quasar, whose image is split into two components by gravitational
lens. This
explanation is further strengthened by the angular distance of
0.8'' from the object B were found giant elliptical galaxy (whose
weight is estimated to be ~2.1011 M¤) redshift of about
z @ 0.4. This intermediate
galaxy is
probably the gravitational lens causing the quasar's apparent
bifurcation. During astronomical observations, there were some
other cases where the system of similar quasars can be explained
as multiple imagings of a single quasar by an intermediate
galaxy as a gravitational lens (eg the triple quasar QSO PG 1115
+ 08).
 |
Left: A gigantic radiant arc - an incomplete Einstein ring - in the Abell 370 cluster of galaxies. Right: |
| Left: Almost complete Einstein ring MG 1131 + 0456. Right: |
|
| Examples of astronomically observed Einstein arcs created by the effect of a gravitational lens. | |
In these cases, when the
gravitational lens is a galaxy with a non-spherical gravitational
field, the imaging is significantly more complicated than
according to Fig.4.10b in the Schwarzschild field - multiple
splitting occurs *). In addition, it is a rotating gravitational
lens (galaxies rotate), which can cause other effects of
asymmetry and inconsistency of emerging images, see §4.4.
*) An odd number of images (often
a triple image ) are observed
radio astronomically, because the intermediate galaxy is
transparent to radio radiation. In the optical field, no direct
ray is observed, it does not pass through an opaque intermediate
galaxy.
The nature of the observed image
carries some information about the course of the gravitational
field of the "lens", so that a detailed analysis of the
structure of the images can provide some data on distribution of matter in the intermediate galaxy -
both radiant and hidden
matter
(non-radiant, dark matter; for this important but still
mysterious component of matter in the universe, see §5.6 "The
Future of the Universe. Arrow of Time. Hidden Matter.", section "Dark
Matter"). From the analysis of images
created by gravitational lensing, it is potentially possible to
read interesting information about the distribution of matter in
space, including dark matter, which we do not see with
astronomical instruments.
The observed multiple imaging of
quasars by the gravitational lensing effect of intermediate
galaxies is, in addition to further confirmation of Einstein's
general theory of relativity, also proof that the quasars really
lie at cosmological distances (and that therefore their great
redshift is the cosmological Hubble redshift).
Gravitational lenses -
powerful astronomical telescopes ?
A gravitational lens is a "connecting lens", so that in addition
to changing the position of the image relative to the object (and
possibly splitting the image), it also manifest
itself in the fact that a distant object may appear larger and brighter to the observer than it actually
is. The brightness gain can be 10 or more times. This effect can
have great astronomical-observational
potential:
a giant gravitational lens can function as an optically very
powerful "objective" and our conventional
astronomical telescope as an "eyepiece" of this hybrid telescopic system. The focal length of such gravitational-optical telescope here can reach unimaginable
values of thousands or millions of light years!
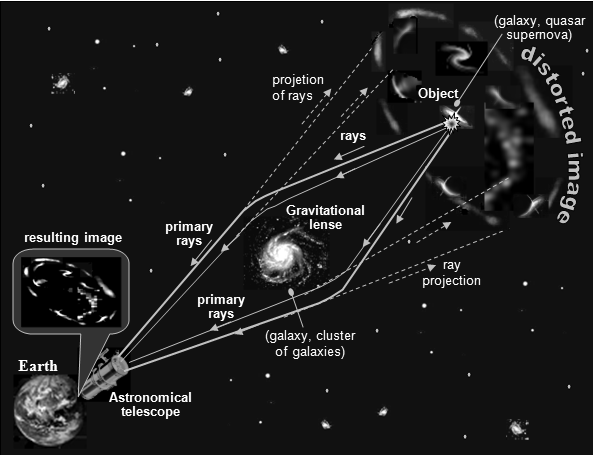 |
Schematic representation of a hybrid
gravitational-optical astronomical "telescope".
A very distant glowing object (galaxy, quasar or supernova) is first imaged by a gravitational lens, which can be an intermediate galaxy or a cluster of galaxies. The bent light rays then enter the classical astronomical telescope (which can be optical or radio astronomical - depending on whether we observe in the optical or radio region), where the resulting image is created. With a bit of exaggeration, the telescope serves as the "eyepiece" of this cosmic imaging system. |
However, in terms of potential astronomical
use, gravitational lenses have two main disadvantages :
1. They are randomly
distributed in different specific places and directions from the
observer, with different sizes and gravitational-optical
properties. They cannot be adjusted in any way, unlike classic
astronomical telescopes, which can be easily oriented in any
direction. However, in a vast universe filled with millions of
galaxies and clusters of galaxies, there are likely to be a large
number of suitable configurations that can act as gravitational
lenses.
2. Gravity lenses are not able
to provide sharp images. Even a precisely spherical mass with a
Schwarzschild gravitational field has a significant
"spherical defect" or spherical aberration in optical
terminology (as shown above); in addition, galaxies have a complex inhomogeneous
distribution of matter. Different parts of a gravitational lens
therefore have different "optical power", leading to blurred
and distorted images composed of different spots and
arcs (as indicated above in the image). However, it is to be hoped that future advanced
computer image processing will be able to correct this to a large
extent and make it possible to reconstruct
important data on distant gravitationally displayed objects.
Large clusters of galaxies
can be particularly massive gravitational lenses. Such a cluster
of galaxies can act as a huge cosmic- cosmological
gravitational lens, which, given the right
constellation, could help to look into the farthest depths of
space, and thus into the most ancient past ...
In addition to an enhanced and
magnified view of the farthest space objects, gravitational
lenses also offer other unique possibilities. Probably the most
notable of these is the ability to monitor the dynamics
of rapid explosive processes such as supernova
explosions. A gravitational lens can create multiple
images of the same object with different time
lags, as these images are created by curved rays with
different paths on the way to the observer. In these split images
of the supernova, which are shifted relative to each other in
time, we can observe practically simultaneously different phases
of the supernova's flare.
Astrometric
significance of gravitational lenses
Gravitational lenses can also have a remarkable astrometric
significance. In general,
they allow the measurement of the masses of astronomical objects
without the need for assumptions about their composition and
dynamic properties. The beam paths I and II in Fig.4.10 are not
the same length, so that any change in the brightness of the
source P will be
reflected in the images P1 and
P2 with a different delay.
Therefore, if we measure the time difference of the changes in
the brightness of the images P1 and P2, then the distance of the
source P from the
observer can be determined by trigonometric analysis of the
angles g, d1, d2. Gravitational lenses thus allow
relatively accurate absolute measuring the
distances of quasars,
independently of indirect astronomical methods. Of great
importance would also be the observation of the effect of a
gravitational lens induced by a massive concentration of hidden (dark
non-radiant) matter (§5.6) in
galaxies and galaxy clusters.
As mentioned above, gravitational
lenses can provide multiple images of distant
objects such as quasars or supernova flares, and these images may
have different time delays due to different beam paths to the
observer. If it is possible to determine the distances of the
participating objects - supernova or quasar and the intermediate
gravitational lens (by measuring the respective redshifts), then
by analyzing two or more split images of the same distant object
(quasar or supernova) we can determine the mass of the
intermediate galaxy - gravitational lens. From these time
differences and distances it is then possible to derive the value
of the Hubble constant H of the expansion
of the universe (§5.1 part "Dynamic expansion of the universe"); it is an independent
determination .
Gravitational "microlenses"
This is sometimes called the gravitational
bending phenomenon of bodies many orders of magnitude smaller
than galaxies or clusters of galaxies - stars or
even planets. In the introduction to this part
of the "Gravitational Lens in Space",
it was mentioned that the probability of a sufficiently close
"matching" of two differently spaced stars on a
straight line with an observer is very small. However, the stars
move at relatively high speeds in random directions, so we
observe relatively strong transverse movements of the stars in
our Galaxy (and partly also in the
neighboring Magellanic Clouds). This
sometimes results in close optical eclipses of
distant stars at an angular spacing of less than a millionth of
an arcsecond. With such an overlap due to the effect the gravitational
lens of the closer star causes a transient brightening
of the more distant star *). At the observed transverse
velocities of the stars, the duration of this phenomenon can be
estimated at about 20-40 days. If we plotted the curve of the
brightness dependence of the observed star on time, we would see
a temporary maximum on the otherwise linear dependence (flat peak similar to the Gaussian curve), whose height (or area under the
curve) depends on the mass of the lens and
on the angular distance of the eclipse.
*) A certain problem could be to
distinguish the changes in brightness caused by a gravitational
microlens from the astrophysical variability of the actual
brightness of a star. In addition to the analysis of curve
dynamics, spectrometric analysis could be a reliable method.
Astrophysical eruptions have different courses in different
colors, while gravitational lenses are achromatic, so that the
course of the light curves of microlenses is the same for all
colors (wavelengths).
If a
sufficiently massive planet (exoplanet) orbited
an intermediate (closer) "lensed" star, she too could
contribute to the gravitational lensing effect: a small and short
secondary brightening would appear on the ascending or descending
part of the light curve of the basic microlens. The duration
(width) of this secondary peak would depend on the mass of the
planet, it can be estimated at several hours.
Concluding remark :
The astronomical use of gravitational lenses is
still in its infancy. Most of the effects discussed here are so
far only theoretical (basic effects can
only be observed in galaxies and galaxy clusters), their astronomical potential will hopefully be used in
the coming decades - with the rapid development of observation
technology and evaluation electronics ...
Precession of
the elliptical orbit in the Schwarzschild field
The analysis of circular orbits of test particles (including
photons) in the Schwarzschild field can be performed accurately
without difficulty. Stable orbits different from circular orbits (for
which the radial coordinate oscillates between
"perihelia" and "aphelia", i.e. between the
values r = rA and r = rB
according to figure 4.6 right) we a while
ago marked as an
"elliptical". However, this is not quite true. The
basic new property of elliptical orbits - the twisting of their
main axis - can most easily be shown in the case of an orbit,
which differs very little from a circular one.
For a circular
orbit r = R = const.
of radius R is (dr/dt)|r=R = 0, (d2r/dt2)|r=R = 0,`L2=
M.R2/(R-3M). A weakly elliptical
orbit (differing only slightly from a circular one) can be
considered as a somewhat disturbed circular orbit, so for it we
can write r(t) = R + e(t), where e «R
(ie is e/R« 1) describes weak radial oscillations
between turning points. Substitute this into the equation created
by deriving equation (4.6a) according to dt, decompose it into a
series in powers of e/R and leave only the members of
the 1st order. After the adjustment we get the equation
d 2 e / dt 2 = - (M / R 3 ) (1 - 6M / R). e ,
whose solution is
e (t) = e o . sin { Ö [ (M / R 3 ) (1 - 6M / R) ] . t } .
According to Kepler's law, the period of the basic circular motion (orbital time) is T = 2p.Ö(R3/M). The period of radial oscillations e(t) is Te = 2p.Ö[R3/M(1-6M/R)]. Thus, the motion does not occur after a constant ellipse, because it would have to be Te = T. During one radial oscillation Te , the test particle (orbiting the angular velocity w) will have an angle w .Te ; the difference of this angle from 2p indicates the phase difference between the radial and the orbital motion for one period: Dj = Te.w -2p = 2p(Te/T -1). By this angle Dj, the turning points are shifted (rotated around the center r = 0) for each revolution, and thus also the line connecting the perihelion through the center with the aphelion (Fig.4.12) :
| Dj = 2 p (T e / T - 1) = 2 p [ 1 / (1 - 6M / R) - 1 ] » 6 p M / R . | (4.17a) |
If the periods T and Te do not differ much, we can consider the orbit of the particle as an ellipse, which is not fixed, but whose main axis constantly gradually rotates (around the center r = 0 through which it passes) at an angular velocity (Fig.4.12)
| w' = Dj /Te = w - we = (M/R3) [1 -Ö(1 - 6M/R)] » (3 M / R) Ö(M/R3) . | (4.17b) |
The approximate expressions in (4.17a, b) hold when R >> 6M, ie far enough from the center.
 |
Fig.4.12. Illustration of the actual motion of a test particle along an "elliptical" path in a Schwarzschild field. The movement does not take place exactly along a fixed ellipse, but we can imagine it as a rotation around an ellipse, which itself performs a precessional movement - the main axis of this ellipse slowly rotates in the same direction around the center r = 0. |
The precession of the elliptical path thus results that the "perihelion" of the test particle shifting by the angle given by (4.17a) at each revolution. These displacements add up with a larger number of cycles, so that even if Dj makes only a small angle for one orbit, over a longer period of time (after many orbits) the perihelion displacement can take a measurable value . This is also the case with the orbit of planets in the solar system, where this effect is most pronounced and most easily measured in the planet Mercury (R @ 5.5x1010 m). Formula (4.17a) for Mercury gives Dj @ 6p G.M / Rc2 @ 5.10-7 rad /circulation; because Mercury's orbital period is 0.241 years, the relativistic shift of its perihelion is about 43'' in 100 years. The actual observed shift in Mercury's perihelion is many times greater, but after deducting all the contributions caused by the disturbing influences of the planets, it remains the part 43 '' predicted by the general theory of relativity.
Effective
cross-section of particle capture by black hole
Equation (4.15) gives the effective cross-section of black-hole
capture only for photons and ultrarelativistic particles with mo
«E¥. To calculate the effective
cross section of the capture of non-relativistic particles
through a black hole, we use the effective potential V(r)
according to (4.9). In order for a particle to be captured by a
black hole, its energy must be greater than the maximum of the
effective potential for a given angular momentum:` E¥ > Vmax . A particle with a
non-relativistic velocity at infinity v «1 (near a black hole,
however, the velocity can be relativistic!)
has energy E¥ = mc2 = mo,
ie` E¥ = 1. The condition` E ¥ = 1> Vmax after substituting (4.11) shows
that the particles to be captured must satisfy the inequality angular momentum
` L <4M (see also figure 4.6, where the
line` E
¥ = 1 is higher than maximum
effective potential only if `
L <4M), which is
expressed by the collision parameter is b <4M/v¥ = bk . Particles with such an impact
parameter are absorbed. Thus, the effective cross section of the
capture of nonrelativistic particles by the Schwarzschild black
hole is
s nr = p b k 2 = 16p M 2 / v ¥ 2 = 4p r g 2 / v ¥ 2 = 16p G 2 M 2 / (c 4 v ¥ 2 ) .
Emission of gravitational waves when moving in
the field of a black hole
It should be emphasized that the motion of bodies in the field of
a Schwarzschild black hole would look as we have described it,
only in the idealized case of an infinitesimal test particle
neglecting the emission of gravitational waves. At large
distances from the black hole, this is approximately
met. However, any
body that approaches a distance comparable to ~2M will begin to
emit intense gravitational waves (due to
high acceleration) as it moves (§2.7,
section "Sources of
gravitational waves"). The resulting radiation braking significantly affects the trajectory of
the body. Orbits (especially "low" orbits with r
<10M), which should theoretically be stable, will in fact be unstable - the body will constantly lose energy by
emitting gravitational waves, so it will gradually spiral down to
the black hole and eventually be absorbed by it. The rate at which a particle of mass m («M)
will lose energy by gravitational radiation as it orbits in a
circular path of radius r is according to formula (2.88)
and Kepler's law
| dE / dt = - 32/5 . m2 M3 / r5 . | (4.19) |
Because the kinetic energy of the particle is E = (1/2) m. w2 r2 = (1/2) m.M/r (according to Kepler's law, w2 r3 = M), we get after substituting into (4.19) the equation for the time change of the orbit radius due to gravitational radiation; its solution is
| r = ro [ 1 - 256/5 (m M2/ro4) . t ]1/4 , | (4.20) |
where ro is the current initial radius of the orbit. It can be seen that the stable path r = ro = const. it can only be within the limit of either m®0 (infinitesimal particles) or ro®¥ (far enough from the black hole). In elliptical orbits, gravitational radiation is strongest in the "perihelion", which is why the greatest radiation braking occurs. As a result, the elliptical orbit (in addition to the total reduction) decreases its eccentricity and gradually turns into a circular orbit (if it has "enough time" to do so before its absorption). In terms of gravitational radiation in the movement of the body in orbit around the black hole can be divided into two stages (Fig.4.13). In the first stage, the body radiates energy according to formula (4.19) and gradually decreases in a spiral to the lowest (innermost and most strongly bound) stable circular orbit with radius r = 6M. The total amount of energy emitted by gravitational waves during this first stage (assuming that a body of mass mo has begun to move far from a black hole) is given by the binding energy in an orbit of radius r = 6M :
| E I = mo [1 - V(r=6M)L=2Ö(3)M] = mo(1 - Ö(8/9) ) @ 0,572 mo . | (4.21) |
After reaching the lowest (innermost) stable circular orbit r = 6M, the body is already very quickly absorbed by the black hole, while sending an intense impulse ("flash") of gravitational radiation - the second stage. The energy emitted by this "flash" of gravitational waves is approximately equal to [289], [62]
| E II » 0.01. m 2 / M . | (4.22) |
 |
| Fig.4.13.
The time course of the frequency and intensity of
gravitational radiation of body m orbiting around a Schwarzschild black hole M
. A body that begins its orbit at some large radius r0 at time t = 0 descends in a spiral and continuously emits weak gravitational waves first, but with ever-increasing intensity and frequency (stage I). After reaching the radius r = 6M, the body is quickly absorbed, emitting a short intense flash of gravitational waves (stage II). The resulting black hole M + m is rotating and relaxes to the stationary configuration of Kerr's black hole by emitting damped gravitational waves. |
The total amount of energy that a body of mass mo << M can radiate in the form of gravitational waves when it falls on a Schwarzschild black hole, ie E = EI + EII , while the decisive part is radiated in the first stage. However, if the body impinges on the black hole directly (radially - without multiple orbits), the first stage will not be there and the radiated energy will be approximately given by (4.22). It can be seen from equations (4.21) and (4.22) that the efficiency of the conversion of the rest mass of a body into the energy of gravitational waves is relatively high, ~ 5.7% - it is about five times higher than the efficiency of thermonuclear reactions (the binding energy at the innermost stable circular orbit of a black hole is significantly higher than the binding energy of nucleons in the atomic nucleus) ! As we shall see in the following §4.4, passage "Particle motion in the field of a rotating black hole", for rotating black hole this efficiency may be even larger.
Horizon area
and surface gravity of a black hole
The area of horizon
r=2M of a
Schwarzschild black hole is
| A = r=2M,nt=const.|gJJ gjj|1/2 dJ dj = 16p M2 = 16p G2 M2 /c4 . | (4.23) |
By deriving equation (4.7) according to t, it is easy to find that the acceleration d2r/dt2 of the test particle in the radial direction is given by
d 2 r / d t 2 = - 2M / r 2 + L 2 / r 3 - 3M L 2 / r 4 .
For a radially moving particle (L = 0), its acceleration d2r/dt2 reaches a value on the horizon (d2r/dt2)|r=2M = -1/4M. The "gravitational acceleration" on the surface of a black hole (ie on the Schwarzschild sphere) is called the surface gravity of the black hole k ; for Schwarzschild's black hole is surface gravity
| k = 1 / 2r g = 1 / 4M = c 2 / 4GM . | (4.24) |
Surface gravity k, which is a measure of the intensity of the gravitational field on the horizon of a black hole, plays an important role in the thermodynamics of black holes and determines the rate of Hawking quantum evaporation of a black hole, as we will see in §4.6 and 4.7.
Extension of
Schwarzschild geometry and black hole
Regarding the geometric constructions from §3.4, only part A
and B of the Kruskal diagram of Schwarzschild geometry
according to Fig.3.17 and 3.19 relate to the real black hole
created by spherical gravitational collapse. By extension
formed part A' and B' are actually replaced with the
interior of collapsing star (where solution is
different) and thus not implemented.
Much of the full extension of
Schwarzschild geometry has nothing to do with the black hole
created by gravitational collapse, because the actual geometry of
spacetime is Schwarzschild's only outside the collapsing star and
moreover in the asymptotic future (see also Fig.4.18a at the end
of §4.4). The complete extension of Schwarzschild's geometry
could only describe a hypothetical so-called eternal
black hole,
which did not form by gravitational collapse, but always existed
as part of the initial conditions of the universe
[]..?..
| 4.2. Stellar evolution. Gravitational collapse | 4.4. Rotating and electrically
charged Kerr-Newman black holes |
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||