| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 4
B L A C K H O L E S
4.1. The
role of gravity in the formation and evolution of stars
4.2. The
final stages of stellar evolution. Gravitational
collapse
4.3. Schwarzschild
static black holes
4.4. Rotating
and electrically charged Kerr-Newman black holes
4.5. The "black hole has no hair" theorem
4.6. Laws
of black hole dynamics
4.7. Quantum
radiation and thermodynamics of black holes
4.8. Astrophysical
significance of black holes
4.9. Total
gravitational collapse - the biggest catastrophe in nature
4.5. The "black hole has no hair" theorem
In previous chapters, we
have shown how the gravitational collapse of sufficiently massive
stars creates black holes. But what specific "shape" do black holes have? The collapse
of a spherical non-rotating star creates a spherical (spherically
symmetrical) Schwarzschild black hole, the collapse of a rotating
star creates an axially symmetric Kerr or Kerr-Newman black hole.
However, these are all idealized
cases. The
question arises, what black hole will be created by the collapse
of a real star? At first glance, it might seem
that the collapse of a "deformed" star, whach may have a "bump" on the surface (protuberances, trace of planetary impact or gas
accretion), could
result in a "deformed" black
hole with a
"bump" on its horizon. As we will see below, according
to the laws of the general theory of relativity, this cannot happen: either no black hole is formed at all, or
an exactly symmetrical black hole is created.
Simply put, a black hole shows no trace of
whether it formed from a star of round or deformed irregular
shape.
The only thing the black hole manifests on the outside - the only thing left for the outside world from a collapsed object - is the outer field. It turns out that compared to the object before the collapse, the black hole has a very simple structure :
| Theorem 4.1 ("black hole has no hair") |
| After the "completion" of the gravitational collapse (ie after the formation of the horizon and the disappearance of all gravitational and electromagnetic waves), the external electromagnetic and gravitational field of a stationary black hole in vacuum is completely determined by only three independent parameters : total mass M, electric charge Q and intrinsic rotational angular momentum J, regardless of what and how the black hole was formed from. |
Metaphorically, this is
expressed by the sentence "a black
hole has no hair", ie it has no other specific independent
characteristics other than mass, charge and rotational angular momentum
*). We substantiate the statement
"black hole has no hair" first by physical arguments,
then we mention some geometric-topological theorems of
uniqueness, on which the general mathematical proof is based, and
finally we show the far-reaching physical consequences of this
theorem.
*) The metaphorical wording
"black hole has no hair" comes from J.A.Wheeler.
By "hair" is meant here some specific symptoms that emerge from the horizon and
show the individual characteristics of the matter from which the
black hole originated. More precisely, we should say "a
black hole has almost no hair", only weight, angular
momentum and electric charge.
The "hairless" theorem he was just a
hypothesis for several years, for which as evidenced by a number
of physical arguments and findings from Zeldovich, Novikov,
Ginzburg, Price, Israel, and Carter, but general proof was
lacking. The definitive completion of the proof of Theorem 4.1
was performed in the works of B. Carter [44], W. Israel [142], S.
Hawking [121] and D. Robinson [219].
Preservation
of interaction with matter absorbed by a black hole
Mass, charge and angular
momentum
are the only conserving quantities (which do not change with time
during collapse), which are associated as sources with long-range force fields (mass and angular momentum with gravitational
field, electric charge with electromagnetic field) on which they
leave a unambiguous "reflection" or
"trace". With the help of these unambiguous reflections
(preserving integral flows over closed areas), these
fields then continue to
hold - maintain the values of these three quantities also after
the horizon has been formed, even if their own sources
disappeared below the horizon or were even perhaps already
destroyed in singularity (in terms of their proper time). The
creation of the horizon is therefore a decisive moment here: whatever then
happens to the resources below the horizon,
this cannot be reflected in any way in the external fields, which
therefore retains its value corresponding to the
resources just before crossing the horizon. This also justifies the use of Gauss's theorem for integral flows of external fields
through closed surfaces, because we do not have to worry about
possible unacceptable topological behavior (eg multiple
connection or singularity) of spacetime inside the horizon. Therefore we can eg
integral
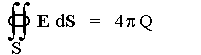
of intensity
of electric field E over a closed surface S,
surrounding a black hole at a sufficient distance, to be
considered as its electric charge Q, even if this real charge
(its carriers) disappeared irreversibly below the horizon, was
absorbed by singularity, or it emerged in another universe or
another place in the same universe (all
this, however, makes no sense to an outside observer, because it
would take place in the absolute future). It is similar with the gravitational
field and its source, mass M.
Thus, if we have two distant bodies or particles A
and B , which are in mutual gravitational or
electromagnetic interaction, after the absorption of one of them
(for example A) this interaction does not
disappear with a black hole. After radiating of dynamic
components of fields arising during collapse or accretion, the
long-range interaction with partner B remains.
However, it will no longer be an interaction with the original
individual body or particle A, but particle B will
interact with the total field of the black hole
of which the absorbed object A has become a part. And this
field is determined by the total mass M, the rotational
angular momentum J and the electric charge Q. It can be
said that the particle A , even with its field, seems to
"dissolve" in the total field of the black hole.
This mechanism also provides an
answer to a frequently asked paradoxical question: "How
can the gravitational force get out from under the horizon of a
black hole and act on outer bodies? - when the horizon does not
let anything out! ". However, the
gravitational field does not have to "penetrate" from
the inside across the horizon. This field is
already in that given external place and was there
before the star collapsed or the body fell into a black hole. And when collapse or absorption body this field does not
expire, but maintains that value it had just
before the act of collapsing or absorption.
Note
: The above
response is in terms of the classical
field theory . In quantum theory of fields
(§1.1 "Atoms and nuclei" passage "Quantum field theory" in the monograph "Nuclear physics and
ionizing radiation") the interaction is modeled by
means of intermediate particles, which are
constantly exchanging interacting bodies (particles). These
should not be"let go" by the horizon
of the black hole . The answer can be seen from two aspects :
1. It is only a model that is
useful for dynamic processes between microparticles (discussed in
the passage "Virtual particles or real?"
mentioned link); for a static force-field action between
macroscopic bodies, it is probably irrelevant .
2. Intermedia particles are virtual,
so for them to "ban" the passage of the horizon in
principle does not apply. As will be shown in §4.7 "Quantum
radiation and thermodynamics of black holes", the laws of quantum physics allow near the
horizon of generation (Hawking) radiation by the effects of the
quantum tunneling phenomenon of virtual pairs of
particles.
Multipole
radiation
The way in which a black hole "loses hairs" during a collapse can
best be understood by analyzing the gravitational collapse, which
differs from the symmetric case by only a small deviation
(perturbation). The external field can then be
decomposed into components related to multipole
moments.
During the collapse, the individual multipole moments will change over time, which will be accompanied by
the emission of waves. It is the radiation
of waves that is the
mechanism that changes the value of some physical quantities during the
collapse. Possibly asymmetries of electric charge cause the
emission of electromagnetic waves during the
collapse. More
important, however, is the emission of gravitational
waves (§2.7 "Gravitational waves", part "Sources of gravitational waves in
space"), which carry away any initial asymmetries in the distribution of mass in a collapsed object.
According to the theory of
radiation [166] can emit only the multipole moments, the
"multi-polarity" is greater or equal to the spin of the respective field *), while the component
with the smaller multipolarity is preserved and do not contribute
to the radiation.
*) The spin of field here is
sufficient to consider classically as a measure of symmetry in
the plane wave of the field: the field has spin s, if its plane wave is invariant to rotation
by an angle of 2p/s around the
direction of propagation.
If the multipole moments, that are "allowed"
to radiate completely, the resulting limit field will be fully
characterized only by the remaining conserving multipole moments,
whose multipolarity is less than the spin of field (and which
cannot therefore radiate). For an electromagnetic field with a spin
of s=1, all multipoles of the charge distribution are radiated in
the form of electromagnetic waves, starting with the dipole
moment, and only the monopole part - the total electric charge - is preserved. For a gravitational field
with spin s=2, all mass distribution multipoles, starting with a
quadrupole moment, are emitted in the form of gravitation
waves; only the monopole part is preserved - the total mass, and the dipole part related to the own
rotational angular momentum in the center of gravity system.
For a (model) scalar field with spin s=0, no part would be preserved,
everything will radiate.
A detailed analysis of the weakly
perturbed gravitational collapse shows that before the formation
of the horizon, all the higher multipole moments allowed are actually radiated. Price [212], showed that for
contributions of such higher multipole fields there are no solutions
with physically permissible asymptotic properties (either infinite on the horizon or divergent for
infinite distances).
"Quantum Hair" ?
Quantum physics results in other
conserving quantities associated with quantum fields. After
forming a black hole, they could persist in the form of some
"quantum hair". However, these are
quantum fields short range; "quantum hair"
could affect the properties of evaporating quantum black
micro-hoes (such microholes are
discussed in §4.7 "Quantum radiation and
thermodynamics of black holes"). However, for macroscopic black holes, possible quantum
micro-hairs have no consequences, because quantum physics is not
applied at macroscopic scales. Extending the analysis to strong
interactions [245] and weak interactions [116] shows that a
macroscopic black hole cannot show the strengths
of weak or strong interactions from leptons and baryons absorbed
in the hole [10], [244].
Theorems about unambiguity
Thus, there are strong physical arguments in favor of
the "black hole has no hair" theorem. However, since a
detailed analysis of the course of gravitational collapse is
possible only in considerably simplified cases, this does not
prove the validity of theorem 4.1 for a general black hole. General matematical proof of
the theorem "black hole has no hair" is based on a
global geometric-topological methods to study the structure of
space-time, through which you can get some
information about the global structure of spacetime on the basis
of certain general assumptions, without necessity
of detailed
solutions gravitational equations. Using these methods, some
important theorems on the
uniqueness of solutions in empty stationary
asymptotically prognostic spacetime were derived.
The simplest
"prototype" of such theorems on unitarity can already
be considered Schwarzschild-Birkhoff theorem 3.3
(derived in §3.4 "Schwarzschild
geometry") , according to which vacuum asymptotically planar
spacetime with spherical symmetry has Schwarzschild geometry and
is thus described by only one parameter M regardless of
how, for example, the mass is distributed radially (if spherical
symmetry is maintained). The relevant more general sentences on
unambiguity are the following :
| Theorem 4.2 (Israel [141]): |
| Each empty (Tik = 0) static spacetime, in which there is a regular event horizon with a sphere topology, has a Schwarzschild geometry (and is therefore centrally symmetric and characterized only by the parameter of the total mass M ). |
| Theorem 4.3 (Israel [142]): |
| Every static spacetime, which contains only a static electromagnetic field and which has a regular event horizon with a sphere topology, has a Reissner-Nordström geometry (it is thus centrally symmetrical and characterized by a total mass M and an electric charge Q ). |
| Theorem 4.4 (Hawking [120], [121]): |
| The stationary black hole must be either axially symmetrical or static (with the event horizon having a sphere topology) . |
If the black hole were not axially symmetrical, it would emit gravitational waves (time-varying quadrupole moment) during rotation and would therefore not be stationary; only an axially symmetrical black hole can rotate and be stationary at the same time.
To illustrate theorem 4.4, imagine the trought experiment according to Fig.4.20. We surround the rotating axially symmetrical black hole at a sufficiently large distance from the horizon with a mass with a fixed axially non-asymmetrical distribution - for example, we make a rigid material frame around it (for example from iron bars), Fig.4.20a. The gravitational action of the frame causes the metric to no longer be axially symmetric. However, this is not a violation of theorem 4.4, because if the black hole rotates, the situation according to Fig.4.20a will no longer be stationary. Due to the entrainment by the angular momentum, the frame begins to rotate in the same direction as the black hole. Since the frame is axially asymmetrical, it will emit gravitational waves during this rotation and thus lose the kinetic energy of the rotation. Finally, the rotation of both the black hole and the frame brakes by radiation; the black hole becomes non-rotating (static) in accordance with Hawking's theorem 4.4. A somewhat more complicated situation would be if the material frame were not free, but fixed (by some non-gravitational forces) so that it could not begin to rotate and emit gravitational waves - Fig.4.20b. Even in this case, theorem 4.4 can be defended. The gravitational action of the frame deforms the horizon. However, the horizon rotates and the deformation of the horizon as it moves will emit gravitational waves (inside the hole), which will slow down its rotation. Finally, the rotation of the black hole to brake again.
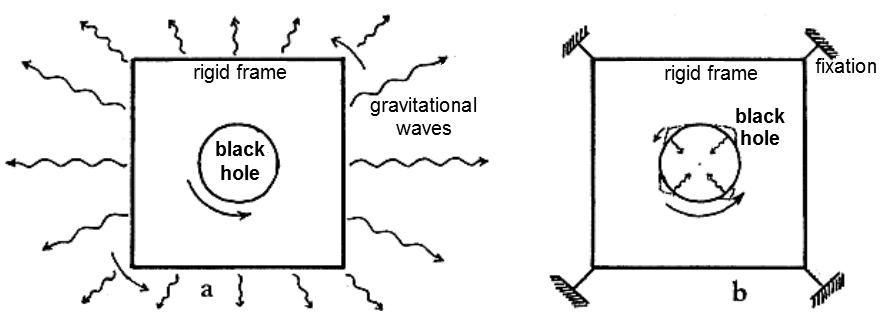
Fig.4.20. Imaginary experiment to physically illustrate the
theorem 4.4.
a) A rigid material
frame is freely placed around the rotating black hole. Due to the
entrainment of the rotation of the black hole, the frame will
spin, gravitational waves will be emitted and the whole system
will be radiation braked. This arrangement is also one of the
ways to obtain energy from a rotating black hole (see §4.4).
b) Rigid material frame fixed around a black hole by
external forces.
| Theorem 4.5 (Carter [44]): |
| For an empty (Tik = 0) stationary axially symmetric spacetime in which there is a regular event horizon with a sphere topology, there are two different groups of solutions, each of which depends on only two parameters; as these parameters we can take the total mass M and the rotational angular momentum J . |
One such group of solutions is Kerr's geometry at a2 £ M2; as Robinson showed, no other distinct group of solutions already exists. Carter's theorem 4.5 was further generalized in the works of Robinson [219], Bose and Wang [24] to the case of the presence of an electromagnetic field (ie for an electrically charged black hole), whereby the Kerr-Newman geometry of spacetime is obtained as a general solution (analyzed in §3.6 "Kerr and Kerr-Newman geometry") .
By combining these
(partially overlapping) theorems 4.2 to 4.5, we conclude that
(if the gravitational field of matter outside the horizon can be
neglected) all stationary black holes must be axially symmetric
and the geometry of spacetime is generally expressed by Kerr-Newman's solution, which is described only three free parameters: mass
M, rotating angular momentum J and the electric charge
Q. And this
is theorem 4.1 "a black hole
has no hair".
Thus, it turns out that in
addition to mass, charge and angular momentum, all other
characteristics (which would not be deducible from these three
parameters) - such as inhomogeneities and asymmetries of mass
distribution and charge of the body before collapse, magnetic
fields, currents, pressures, turbulence, etc. - completely "radiates" in the form of gravitational and
electromagnetic waves, part of which expands into space, part is
absorbed by a black hole. This radiation will carry away the
"hair" of the black hole. Inhomogeneities, as well as
any other phenomena occurring already below the horizon, do not
affect the external field, because information about them (in the
form of appropriate disturbances and waves) of the space-time
geometry does not let to the external observer.
Uniformity of black holes
Black holes of different origins are indistinguishable from each other if they have the
same mass, charge and rotational angular momentum. It is not recognizable
whether the black hole originated from hydrogen or iron, from
ordinary matter or from antimatter, from protons, electrons,
neutrons and in what proportion *). Thus, black holes are very uniform compared to the great variety of
different species and types of stars. All black holes are similar, like eggs with eggs:
almost all of them are Kerr's variously fast rotating
(elliptical), sometimes a Schwarzschild (spherical) hole may
appear between them (probably
not electrically charged). Other qualitative differences between
black holes are not, are only differences in their
"size". With the formation of a black hole, are disappearing almost all the information about what
this black hole came from; only the total weight, angular momentum
and electric charge can be detected.
*) In principle, it is possible, for example, to achieve such a
concentration of light that part of its electromagnetic energy
succumbs to gravitational collapse and forms a black hole. Or
similarly, part of the (non-local) gravitational energy may
succumb to gravitational collapse with sufficient concentration
of gravitational waves (see §2.7 "Gravitational waves" and B.3 "Wheeler's geometrodynamics. Gravity
and topology."). Such a "purely
electromagnetic" (or "purely gravitational") black
hole will then be indistinguishable from the black hole created
by the collapse of an (electrically neutral) star with the
appropriate mass and angular momentum.
However, the conditions for such a massive concentration of gravitational or electromagnetic waves could probably
arise only in the initial stages of the universe's evolution
after a hypothetical "big bang", or perhaps during the
gravitational collapse of entire galaxies...
Black holes are the only macroscopic objects that are very
simple. After the completion of the gravitational
collapse and the departure of the radiation that carries away
their "hair", a very simple object is created in the
final state, which can be precisely and completely
describe with only three parameters and a few mathematical
formulas - without any idealization or limitation of simplifying
models! We do not encounter this anywhere else in the macro world
*). It has an analogy only in the microworld of
"elementary" particles, which can also be completely
described by a few of their quantum numbers (§1.5 "Elementary
particles and accelerators" in
the book "Nuclear Physics and Physics of Ionizing
Radiation") .
*)
It is wonderful and
paradoxical that such a mysterious and exotic object as a black
hole is, from a physical-theoretical point of view, the best
described and explored "body" in nature ..!..
Loss of determinism? - An
information paradox ?
Deterministic laws of classical physics make it possible to predict the state of a system at any time in the future
and in the past, based on knowledge of the complete set of state
conditions of a given system at a certain moment (on Cauchy's spatial type hypersurface
). However, if black
holes are present in the universe, even on the basis of a perfect
knowledge of its state at a certain point in time, it is not
possible to determine the state that was in the past, because the
properties of the matter from which the black hole formed (and also the matter that was at
any time in the past absorbed by a black hole), almost nothing can be detected;
the black hole not only engulfed this matter, but also engulfed all the information about it with
the exception only
of summary mass, charge and angular momentum. The presence of a
black hole - its property of "not
having hair"
- thus, even within classical physics, in principle limits the possibility of reconstructing the past on
the basis of the best knowledge of the present state; it is only
possible to predict the future (and only in
the outer asymptotically planar region of spacetime - see §3.5). This "information paradox" thus leads to a partial loss of determinism. But as we will see in §4.7
"Quantum radiation and
thermodynamics of black holes", the effect of quantum radiation of
black holes even takes us (at least in
principle) this last
deterministic ability..!.. From the point
of view of quantum physics, the "paradox of information
loss" is discussed in §4.7, passages
"Quantum
evaporation: return of matter and information from a black hole?" and "Paradox of information loss?".
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||