| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 2
GENERAL THEORY OF
RELATIVITY
- PHYSICS OF GRAVITY
2.1. Acceleration and gravity from the point
of view of special theory of relativity
2.2. Versatility
- a basic property and the key to understanding the nature of
gravity
2.3. The
local principle of equivalence and its consequences
2.4. Physical
laws in curved spacetime
2.5. Einstein's
equations of the gravitational field
2.6. Deviation and focusing of geodesics
2.7. Gravitational
waves
2.8. Specific
properties of gravitational energy
2.9.Geometrodynamic system of units
2.10. Experimental
verification of the theory of relativity and gravity
2.6.
Deviation and focusing of geodesics
Now, that we already have available to Einstein's equations of
the gravitational field, we still return for a moment to the
question of the influence of the gravitational field on the
motion of bodies, which we began in §2.4. The homogeneous
gravitational field can be "filtered out" in the whole
space by transition to a global inertial system. Even in
inhomogeneous gravitational field according to the equivalence
principle can introduce local inertial system, in which all the
physical phenomena take place (local) under the laws of special
relativity. Therefore, since the gravitational field does not exist locally, the question arises, how does the real
(inhomogeneous) gravitational field actually affect
physical processes? Or otherwise: how
the curvature of
spacetime manifests itself in the laws
of physics? How do
we distinguish the effects of gravity from the influence of the
frame of reference? It is clear that locally
in no way.
Therefore, a non-local approach must be used to study the
effect of gravity. E.g. instead of one test particle (which can
always be considered locally free and which therefore tells us
nothing about the curvature of spacetime), we will observe the
difference in behavior of the two test particles.
Gravitational
force gradients, deviations of geodesics
Let us have two test particles, one of which is located at the
point xi (here we will consider it as a reference)
and the other at the near point xi + ei , where ei is a four-vector space-time
"distance" of these two test particles. If we let these
two adjacent test particles "fall" freely together in
the gravitational field (Fig.2.17), they will move along the
world lines xi (l) and
xi (l) + ei (l) (the four-vector ei (l)
connects the points of both trajectories with the same l), which are geodesics :
![]()
If we subtract these equations from each other and omit the higher order members in ei (we mean the limit transition ei ® 0), we get
![]()
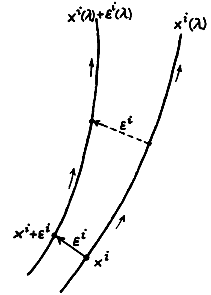 |
Fig.2.7. Two close test particles loosely "falling" next to each other in a gravitational field (curved spacetime) will move along geodesics that will not be completely parallel, but will deviate from each other (deviation of geodesics). |
We are interested in the difference in the motion of both test particles (deviation of both geodesics), ie the covariant derivative of their deviation ei. Using equation (2.15) for the covariant (absolute) derivation of the vector along the curve, we get the final result
| D2 e i
dxk
dxm -------- - Riklm ----- ----- el = 0 , dl2 dl dl |
(2.57) |
which is the so-called equation of deviation of geodesics. According to her, two bodies falling freely next to each other in an inhomogeneous gravitational field will approach or move away from each other (their geodesics will deviate from each other), while the mutual acceleration of both particles D2e i /dl2 is proportional to the curvature tensor Ri klm. The components of the curvature tensor thus describe the gradients of gravitational forces (tidal forces). In planar spacetime, all components of the curvature tensor are equal to zero - there is no deviation of geodesics.
To obtain a more complete picture of the influence of gravity on the motion of matter, let us now move from a pair of nearby geodesics to the whole congruence of such geodesics. We can imagine this as a point test particle is placed at each point in space and their worldlines form this congruence of geodesics in space-time - a certain geodesy passes through each point (event) of space-time. If we determine a unit tangent vector Vi for each geodetic at each of its points, we get the whole field of tangent vectors Vi(xk) for the congruence of geodetics. The divergence ("running away") or convergence ("gathering on each other") C of geodesics in a given congruence is determined by the covariant four divergences of the vector field V i :
| C = def V i ; i . | (2.58) |
The convergence of the congruence of time-type geodetics follows the important Raychaudhuri differential equation [127], [203]
| d C / ds = R ik V i V k + 2 s 2 + (1/3) C 2 , | (2.59a) |
where s describes the mutual "slip" of the geodetic (we do not consider rotation here; if the congruence of the geodetic rotated, the term -2 w2 would still be on the right side). An analogous equation also applies to the convergence of light (zero) geodesics :
| d C / d l = R ik V ik V k + 2 s 2 + 1/2 C 2 , | (2.59b) |
where V i are isotropic tangent vectors.
Energy
conditions
Let us now notice some general properties of equations (2.59a,
b). The last two terms on the right-hand sides of both equations
are nonnegative, so the final sign of the convergence changes is
decided by the term RikVi
Vk. In order for this
term even to be nonnegative, according to Einstein's equations
(2.50b), the gravitational field must be excited by an energy-momentum
tensor satisfying the inequality
| (Tik - 1/2 T gik ) Vi Vk ³ 0 | (2.60a) |
for all vectors of V i time type, resp. inequality
| T ik V i V k ³ 0 | (2.60b) |
for isotropic vectors V i (for which gik Vi Vk = 0). For the energy-momentum tensor of the shape of an ideal fluid (1.108), this is satisfied when the density and pressure satisfy the relations
| r ³ 0 , r + pa ³ 0 , resp. r ³ 0 , r + a=1S3pa ³ 0 . | (2.61a, b) |
This so-called weak energy condition (2.60) is fulfilled for all yet
observed forms of matter, because the
energy density is non-negative and a large negative pressure p *) would be
needed to disturb the energy condition.
*) However, a weak energy
condition would not be met, for example, for a hypothetical C-field
in the "steady-state"
model of the universe (mentioned in Chapter 5), which has
a negative energy density Too,
or for a "false vacuum" field in inflationary expansion of universe (see
§5.5). And also not for the hypothetical so-called exotic
mass used for antigravity
"reinforcement" of traversible wormholes (.......).
In practice, an even stronger condition of
so-called energy dominance is probably met: for each vector
Vi of time type is Tik Vi Vk ³ 0, and the vector Tik Vk is of time or isotropic type, ie
the local energy density is non-negative and in addition, the
local energy flow takes place only inside or on the mantle of the
light cone. Thus, T°°> = |Tik| applies, ie energy "dominates" over the other components
of the energy-momentum tensor. For the most common type of
energy-momentum tensor (1.108) this is satisfied when r ³ 0 , - r £ pa £
r (a = 1,2,3), ie when the pressure
does not exceed the energy density, the speed of "sound" does not
exceed the speed of light.
Note: A total of 4 energy conditions
are sometimes discussed in the literature (....., ....,).
However, for our analysis of the geometry of spacetime around
black holes, as well as global cosmological geometry, a weak
energy condition and a condition of energy dominance will
suffice.
Focusing of geodetics
We see, therefore, that the member RikVi Vk
in equations (2.59a, b) is also nonnegative when reasonable
energy conditions (2.60) are met, so that the inequality holds
for the rate of change of convergence of geodetics
| d C / d s ³ 1/3 C2 ³ 0 , | (2.62) |
according to which convergence grows monotonically along the congruence of geodesics. We can thus declare the statement :
| Theorem 2.5 (focusing of geodesics) |
| If the energy conditions
(inequalities) for the energy-momentum tensor are
satisfied, such that according to Einstein's equations R ik V i V k ³ 0 applies for each vector V i time resp. isotropic type, gravity has an attractive character and on geodesics of the time resp. isotropic type has a focusing effect . |
The statement about the focus of geodesics is of great importance for the geometric- topological logical structure of spacetime - it is used, for example, in proving the 2nd law of black hole dynamics (§4.6) or in proving theorems about the existence of singularities of spacetime (§3.8).
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||