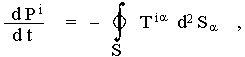 |
(2.86) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 2
GENERAL THEORY OF
RELATIVITY
- PHYSICS OF GRAVITY
2.1. Acceleration and gravity from the point
of view of special theory of relativity
2.2. Versatility
- a basic property and the key to understanding the nature of
gravity
2.3. The
local principle of equivalence and its consequences
2.4. Physical
laws in curved spacetime 2.5.
Einstein's equations of the
gravitational field
2.6. Deviation
and focus of geodesics 2.7.
Gravitational waves
2.8. Specific properties of gravitational energy
2.9.Geometrodynamic system of units
2.10. Experimental
verification of the theory of relativity and gravity
2.8. Specific properties of gravitational energy
Gravitational
binding energy
Energy is an important physical quantity in
dynamic processes in physical systems (in relativistic physics,
the resting energy-mass of particles also appears here). In the
field of gravity, we encounter energy in everyday life, as well
as in the astronomy of planets and stars. It is the potential
energy Ep of bodies in the
gravitational field and the associated gravitational binding
energy, and during the motion of bodies their kinetic
energy Ekin.
If we have individual objects very far
apart in the resting system of material bodies or particles (theoretically at infinite distance), so that the mutual gravity does
not act between them, their mass-energy is given by the sum of
the rest masses of individual particles and is somewhat greater
than when we approach these objects at a shorter distance, where
gravitational forces act significantly. During this approach (eg
contraction of a gas dust cloud into a protostar, see §4.1), the
bound gravitational energy is released (gravitational force works
along the approach path), so that the resulting mass-energy of
the bound system is slightly lower than the sum of initial masses
and energies of individual particles. On the contrary, when
moving bodies away (eg launching a rocket
from Earth to space), we must exert force and perform mechanical
work against gravitational attractive forces. The binding
gravitational energy is negative, there is a kind of
gravitational " mass defect " in gravity - bound
systems *). For ordinary macroscopic bodies, this defect is
completely insignificant and unmeasurable, less than about 10 -30 , for large planets it is of the order of
10 -8 , for stars about 10 -6 .
*) The situation is analogous for the
electrical binding energy of atoms and nuclear binding energy.
The kinetics of chemical reactions are based on
the pumping of the binding energy of atoms in the field of
attractive Coulomb forces. The release of part of the binding
energy of nucleons in the potential field of attractive strong
interactions is a source of nuclear energy. For
atomic nuclei, the mass defect is relatively high, so that by
fissioning heavy uranium nuclei, about 0.1% can be obtained and
by combining light nuclei about 1% of energy from the ideal limit
E = m.c2.
In §4.8 "Astrophysical significance of black holes" we will see that in gravitationally collapsed
compact formations, especially black holes, an even greater
efficiency of "squeezing" energy from matter can be
achieved.
In all these cases of macroscopic bodies, planets and stars for the determination of the gravitational binding energy Ep we suffice with classical Newtonian mechanics and the gravitational law (§1.2 "Newton's law of gravitation", or §1.4 for electricity): for each particle or mass element Dm we determine its product j.Dm with the gravitational potential j at a given place (calculated using the relation (1.26b)) and we integrate over all elements of the system. For the most common case of a spherical body of radius R with density of matter r (r) we can use central symmetry and divide the body into spherical shells of radius r and thickness Dr, whose mass Dm=4pr2.r.Dr we always multiply by the gravitational potential j(r) = m(r)/r, given by the total mass m(r) = p. 0 ò r r2.r dr contained inside a sphere of radius r . Then we integrate from 0 to R: E p = 0 ò R [m(r)/r] dr. For a simplified model example of a homogeneous spherical body of mass M and radius R ( r = M/[(4/3)p R3] = const.), the gravitational potential binding energy is :
E p = G. M 2 / R .
For an inhomogeneous
sphere we can use a modified relation Ep
= [GM2
/ R] . f , where the
coefficient f depends on the density distribution in the
body. If the density
of matter in the inner part is greater than in the peripheral
parts (as is the case with stars), f > 1
- the binding
gravitational energy is slightly higher.
Only in the case of massive gravitationally very strongly bound
compact structures such as white dwarfs, but especially neutron
stars and black holes, it is necessary to use the laws of the
general theory of relativity for the analysis of energetic
processes. The gravitational mass defect is already very
significant here.
Interactive -
configurational binding gravitational energy is very important
for many astrophysical processes, especially the formation of
stars and planetary systems (§4.1 "The
role of gravity in the formation and evolution of stars"), the formation of
large-scale structure of the universe (§5.4
"Standard cosmological model. Big Bang.
structures of the universe."), galaxies, star clusters, dynamics of accretion disks
around black holes (§4.8 "Astrophysical
significance of black holes"). In this chapter, however, we will deal with the issue
of energy of the gravitational field itself .
Gravitational
field energy
In the previous §2.7 it was shown that the commotion in the
gravitational field propagates at a finite
speed
(equal to the speed of light). This fact logically leads to the
conclusion that the gravitational field must have energy and momentum.
Because if one material system causes a disturbance in the
gravitational field, which spreads to the other system and gives
it some energy, the question arises: where is the energy and
momentum in the time interval between its "sending" by
one body (system) and its "receiving" by
the other system? The only satisfactory answer is that the field itself must have those conserving
characteristics of matter (integrals of motion), whose
transmission it mediates - energy, momentum,
angular (rotational) momentum - just like ordinary bodies and material
environments.
As was explained in §1.6, the distribution of energy and momentum in a physical system is expressed in STR using the energy-momentum tensor Tik ; the total energy E , the momentum P = (Pa) (a=1,2,3) and the four-moment Pi º (E, Pa) composed of them, is then given by the volume integrals
| E = xo=const.òT°° d3x , Pa = xo=const.òT°a d3x , P i = xo=const.òT i° d3x . | (2.84) |
The law of conservation of energy and momentum then has a differential form
| ¶ T ik T ik,k º ----------- = 0 , ¶ x k |
(2.85) |
which in three-dimensional transcription is analogous to the continuity equation j k , k º ¶r / ¶ t + div j = 0, where j k º (r, j) is the four-current, r º j ° is the charge density and j is the current density.
If we surround the observed system with an imaginary closed surface S , the transition from volume integrals (2.84) to area integrals using Gauss's theorem and differential law (2.85) we get the laws of conservation of energy and momentum in integral form
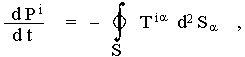 |
(2.86) |
where d2 Sa are components of the (normal) vector of the surface element. This law states that the rate of change of energy and momentum in a spatial region is equal to the total flow of energy and momentum through the closed area S bounding this volume. An analogous law also applies to the angular momentum. For an isolated system, the right-hand side (2.86) is zero, so P i = const. - energy and momentum do not change over time.
According to the principle of equivalence, the generalization of the above-mentioned local law of conservation (2.85) of energy and momentum to the presence of a gravitational field (curved spacetime) is a tensor relationship (see §2.4).
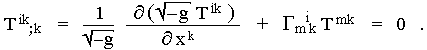 |
(2.87) |
In this form, however,
this equation no longer expresses any local law of conservation,
because due to the presence of the second term in (2.87) it does
not allow the transition between area integral flows and volume
integrals using the Gaussian theorem (as it was possible between
the differential (2.85) and integral (2.86) laws of
conservation). Thus, in the curved spacetime of the general
theory of relativity, the laws of conservation of energy and
momentum of material systems generally do
not apply! It is related to the fact, that the energy and momentum must be preserved not only
of the sources themselves, but including the energy and momentum
of the gravitational field, which, however, is not included in Tik *). Curvature of spacetime is a
certain specific contribution to energy and momentum, that must
be accounted for in order to obtain the correct (exact) law of
conservation. From the equation Tik ;
k = 0, in
general, only an approximate integral law of conservation of
energy and momentum of the source can be obtained, if we
integrate it over an area of small dimensions in comparison with
the components of the curvature tensor Ri
klm ;
then a vector base can be introduced that will be almost
covariantly constant in this region and obtain an approximate
integral law of conservation of energy and momentum.
*) As in Newtonian mechanics, the kinetic
energy itself is generally not preserved, but only the sum of the
kinetic energy and the potential energy of the system in the
respective force field.
From a purely theoretical point of view, the violation of the laws of conservation of energy and momentum in the general theory of relativity is not as "tragic" as it might seem at first glance. In fact, every problem in GTR can in principle be solved using Einstein's equations without the need to apply conservation laws. Nevertheless, energy and momentum are so important and practical concepts of physics that their loss would be very unpleasant. We can compare this with other areas of physics, such as the classical theory of collisions of elastic bodies. Even without the use of conservation laws, their movements can in principle be calculated using a detailed analysis of the deformations of the colliding bodies. However, such a calculation is difficult and requires specific data on the material properties of the individual bodies. The benefits of using the laws of conservation of energy and momentum are evident here. Likewise, in the general theory of relativity, it is reasonable to try to introduce the laws of conservation of quantities interpretable as energies and momentum of investigated systems.
To obtain the laws of conservation, it would be useful to express the "obstructice" term in (2.87) as an ordinary four-divergence of some quantity, which we denote as t ik :
G i mk T mk = ¶ t ik / ¶ x k .
It is clear that the quantity t ik cannot have tensor transformation properties; it acts as a tensor only in linear transformations - it is called a pseudotensor. For Tmk we can substitute from Einstein's equations, so it will be
¶ t ik /¶ xk = 1/8p Gimk G mk . (2.88)
Solving equation (2.88) is not unambigous, there are many different variables tik satisfying this equation (for this see below).
The tensor law (2.87) can therefore be adjusted to the shape
| (T ik + t ik ) , k = 0 , | (2.89) |
where in t ik are used Einstein's equations, so that in this t ik featured only the gravitational variables g ik. Equation (2.89), which contains (at the cost of loss of tensor character) already common partial derivatives, allows transition between volume and area integrals and therefore expresses the law of conservation of the sum of energy-momentum tensor Tik of bodies and nongravity fields and so-called pseudotensor of energy-momentum t ik of gravitational field, which should determine the density and flow of energy and momentum of the gravitational field itself. By integrating equation (2.89) we get
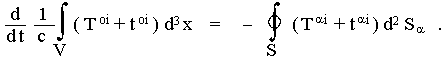 |
(2.90) |
The quantities P i = (1/c) ò (Toi + toi ) d3 x, which in a situation without a gravitational field in the inertial system (tik = 0) change into a common 4-momentum òToi dV of the system, can be interpreted as the total 4-momentun of the system including both the source and the gravitational field. The components T0 i + t 0 i then express the respective current of energy and momentum. Therefore, the integral law of conservation of the four-vector applies
| P i = (1/c) S ò (T ik + t ik ) dS k | (2.91a) |
the total energy and momentum of the system including the gravitational field. It integrates here over the entire spatial-type hyperplate S; if it is a hyperfplate xo = const., it will be
| P i = (1/c) V ò (T io + t io ) dV . | (2.91b) |
The position and role of the pseudotensor of energy - momentum of the gravitational field t ik in Einstein's equations can be clarified (and at the same time obtain one of the variants of its construction) by writing the metric again in the form (2.63)
g ik = h ik + h ik
without claim that the hik are small everywhere. Einstein's equations can then be rewritten in the form
| Rik(1) - 1/2 h ikR(1) = (8pG/c4) (Tik + t ik) , | (2.92) |
where Rik(1) = 1/2 (hli;kl - h;ik - hik;ll + hlk;il) is part Ricci curvature tensor Rik linear in hik and
| t ik = (c4/8pG)(Rik - 1/2 gikR - Rik(1) + 1/2 hikR(1) . | (2.93) |
Since the variables Rik(1) applies linearized variant Bianchi identities (Rik(1) - 1/2 hikR(1)), k = 0, it follows from the field equations (2.92) differential conservation law Tik + tik º hilhkm(Tlm + tlm) :
| (T ik + t ik ) , k = 0 . |
It can be seen from equation (2.92) that the source of the field h ik are the quantities Tik + t ik , for which the differential conservation law applies (2.89); t ik determined by the relation (2.93) is therefore energy-momentum pseudotensor of gravitational field.
The differential law of preservation shape (2.89) will be identically fulfilled when Tik + t ik can be expressed as a four divergence
| (T ik + t ik ) = U ikl , l | (2.94) |
of the so called superpotential Uikl = -Uilk antisymmetrical in the last two indices. Expression (2.94) allows the volume integrals v (2.91) for the quantities P i to be converted by means of a Gaussian theorem to area integrals over a closed surface S surrounding the investigated system :
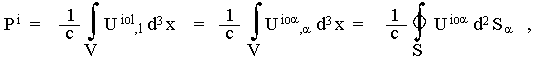 |
(2.95) |
where dSa = na r2 dW is an element "carved" on a closed surface S spatial angle dW = sin J dJ dj with vertex at the origin of coordinates, na = xa/r is the outer normal vector to the surface dSa . When constructing pseudotensor t ik by (2.92) and (2.93) the corresponding superpotential is given by equation
| R(1)ik - 1/2 hikR(1) = (c4/8pG) ¶ U ikl /¶ xl , |
which is met at
Uikl = hmm,k hil - hmm,i hkl - h,mmk hil + h,mmi hkl + hkl,i - hmli,k .
For the total energy of the system inside the closed surface S it then follows from the relation (2.95)
| E º P° = (c4/8pG) Sò( hab,a - haa,b ) dSb , | (2.96a) |
which expressed by gik = hik + hik gives
| P° = (c4/8pG) Sò( gab,a - gaa,b ) dSb . | (2.96b) |
Therefore, to determine the total energy, momentum, and angular momentum of each finite system, it is sufficient to know the asymptotic behavior of the metric at great distances. If tik, and therefore also Tik + tik is symmetric, the differential law of conservation of angular momentum applies
| ¶ J mik / ¶ x m = 0, J mik º x i (T km + t km ) - x k (T im + t im ) , | (2.97) |
according to which the total 4- angular momentum
| Jik º ò(xidPk - xkdPi) = (1/c) Sò[xi(Tkm + tkm) - xk(Tim + tim)] dSm = = (1/c) Vò[xi(Tko + tko) - xk(Tio + tio)] dV |
(2.98) |
is maintained, i.e. it is constant if the values J aik are equal to zero on the surface S bounding the integrated volume V. Quantities Joik describe the density and thus Jaik current angular momentum. With the help of the superpotential, the total angular momentum (whose most important components J23 = J1 , J31 = J2 , J12 = J3 form the usual vector J º (J1, J2, J3) of the angular momentum with respect to the "center of gravity" T of the system xaT =òxa(T°°+t°°)dV/ò(T°°+t°°)dV) is also expressed by means of area integrals over the distant closed surface surrounding the whole system (like the relationship (2.96)) .
Such a description of gravitational energy was basically performed more than 50 years ago by Einstein himself. However, it soon became apparent that the physical significance of Einstein's pseudotensor was somewhat questionable. It was found that when using it, for example, even in a flat space without gravity, it is possible to achieve a non-zero energy density and infinite total energy of a (non-existent) gravitational field by simply switching to spherical coordinates. This absurd result is sometimes called Bauer's paradox. In addition, the four equations (2.88) for the 16 components tik do not unaquivocally determine the functional dependence of tik on the components of the metric tensor gik and its derivatives. Likewise, there are infinitely many superpotentials, because every other set of quantities U' ikl, which in the asymptotically planar region are equal to the components of the superpotential U ikl, give the same values for the area integrals of P i (2.96).
In the 1950s and 1960s, a number of different expressions were constructed for gravitational energy density - let's name at least the pseudotensor Landau and Lifšic [166] (which is symmetrical and contains only the first derivatives of gik) or the pseudotensor of 1958 by Mickevich and Moller [177]. There is possible to create many different expressions for the density of the gravitational energy (in which the total energy-momentum tensor would give conserved quantities when integrated over dV and would change to Tik when the gravitational field disappears), and it is unclear which of them to prefer - which (and if any at all?) is correct. In connection with these and some other problems are experts in relativity and gravity in the fifties and sixty years they divided it into three groups: the first believed that the energy of the gravitational field could be located and it was only necessary to find a "magic" formula for the density of gravitational energy that would suit all aspects; others that although the gravitational field has energy, but it fundamentally non-localizable; the third finally doubted the existence of gravitational energy at all - they considered the gravitational field to be a purely geometric manifestation. We will analyze these three different views.
First, we can be done with the third view (denying gravitational energy): this view is clearly erroneous and arose as a result of misinterpretation in the analysis of component properties of some expressions for pseudotensors of energy-momentum of the gravitational field [241]. The existence of gravitational field energy is evidenced by very strong physical arguments. Gravitational energy can be studied using methods that do not require the application of pseudotensors (or at least not their explicit form) - direct application of Einstein's equations, which lead to retarded potentials (2.65) and hence to a final velocity (equal to the speed of light) of propagation of changes in the gravitatioanal field and to the the existence of gravitational waves, that detach from the source and carry with them part of its energy, momentum and angular momentum even without the presence of any "receiver" these waves (see below). Because the propagation of changes in the gravitational field is associated with the transmission of energy, the final velocity of this of propagation indicates, that the gravitational field itself is the carrier of energy (see the arguments at the begining of this paragraph). Even more sugestivelly, the existence of gravitational energy is demonstrates by some of the experimental aspects mentioned at the end of this paragraph.
Thus, there can be no doubt about the existence of gravitational energy, it only remains to clarify how the concept of energy in the general theory of relativity agrees and how it differs from the properties of energy in non-gravitational physics. Great merits in the field of gravitational energy research has C.Moller (who for a long time held the first opinion about the localizability of gravitational energy), who constructed a number of expressions for gravitational energy [182], [177] and formulated five requirements that a correct energy-momentum pseudotensor of gravitational field should meet :
Moller further showed that when using the components of the metric tensor as field potentials, not all of these conditions can be met at the same time (and therefore, for example, the tetrad formalism is sometime used [182], [177]). It is also related with difficulties in consistently covariant description of the gravitational field using the metric tensor components such as potentials, because the metric field is covariantly constant and therefore does not make sense to investigate the dependence of quantities on covariant derivative potentials, which at the same time serves as the basis of the metric structure.
Nonlocalizability
of gravitational energy
Efforts to find suitable relationships for the density of local
gravitational energy have not led to unambiguous results. Even in
a very strong gravitational field, it is possible to cancel all tik at each point using a locally inertial
frame of reference, where G i kl = 0 ; and vice versa, even in flat
spacetime without gravity it is possible to obtain non-zero
values of t ik using suitable curvilinear
coordinates (Bauer's paradox mentioned above). Thus, it is in
principle impossible to introduce the energy density of the
gravitational field independent of the choice of the coordinate
system, even if the total energy is clearly defined. Therefore,
it does not make sense to talk about some particular localization
of the energy of the gravitational field in space, ie whether or
not there is gravitational energy in a given place (and how
large).
At present, the most widespread view is that the localization of gravitational energy is not possible, the energy of the gravitational field is a global phenomenon, not local, and only integral values of energy, momentum and angular momentum have (and not always!) physical significance. This view is in full conformity with the versatility gravitational interaction, i.e. with principle equivalence, whereby at any point can be implemented locally inertial reference system - locally "eliminate" the gravitational field and thus local gravitational energy. Local gravitational energy does not figure as a source on the right-hand side of Einstein's equations, so it does not curve space-time, has no "weight" and is not measurable. Gravitational energy has reasonable physical properties only in a non-local sense.

Fig.2.13. The analogy between the nonlocalizability of the energy
of the gravitational field
and the nonlocalizability of the beauty of the painting over the
surface of the image.
To better understand the non-localizability of gravitational energy, it will be useful to use analogies with a completely different area - with fine arts. Let's take a nice artistic painting (for example "Mona Lisa" by Leonardo da Vinci - Fig.2.13) and examine its beauty. The beauty of painting is a very vague and subjective concept, but most people will certainly agree that this masterpiece of the great renaissance master is beautiful. However, if we begin to study the "density" with which the beauty of the painting is distributed over the surface of the image, problems begin. If we divide the area of the image into relatively large areas (say, tens of centimeters in size), we can still roughly say that in some fields more beauty is concentrated than in others. E.g. in the area A1 (where the face of Gioconda is) there is certainly more beauty concentrated, than in the area A2 (from a foggy, albeit masterfully conceived background - fig.2.13 top right). However, if we refine the division, such an assessment will soon cease to be possible. If we take, for example, areas B1 and B2 (with dimensions of about 3x3 cm), we do not even recognize on them or where they come from and their beauty can no longer be talked at all (we can see them enlarged in Fig.2.13 at the bottom right) - they will actually we see only the details of applying and drying the paint. So we see that it makes no sense to investigate the density with which the beauty of a painting is distributed across the canvas of a painting: the beauty of a painting is a global quantity, not a local one, it is a property of the composition of the whole painting. And just as a beautiful image is a system of ugly spots, an energetic gravitational field is a system of local areas without gravity and without energy.
The laws of conservation of energy, momentum and angular momentum are a consequence of the homogeneity of time, homogeneity and isotropy of space. In this sense, the concepts of energy, momentum and angular momentum are related to the structure (symmetries) of spacetime. In the presence of gravity, spacetime generally has no symmetry, so serious difficulties with conservation laws can be expected. The law of conservation of energy and momentum remains valid only in a locally inertial frame of reference. The nonlocalizability of gravitational energy then corresponds to the nonlocal character of gravity as such. Concept of gravitational energy as well as gravitational forces are just a way of interpreting the curvature of spacetime using concepts to which we are accustomed in the plane spacetine of nongravitational physics.
In the general theory of relativity, we must say goodbye to the local symmetries of spacetime, and thus to the localization of gravitational energy. However, there are cases where we can replace them with global symmetries and at least preserve the concept of total energy. If spacetime has certain properties of symmetry (eg spherical, axial or plane symmetry) expressed by the existence of the respective Killing vectors x k (introduced in §2.4), then the vector P i = T ik x k can be constructed, for which thanks to the Killing equations the relation Pi;i = Tikxk;i = (1/2)Tik(xk;i + xi;k) = 0 expressing the law of conservation P i holds. Depending on whether the Killing vector x i of temporal or spatial type, this can be interpreted as the law of conservation of energy or momentum.
Gravitational
radiation of an island system
The most important case of a physical system capable of emitting
gravitational waves is an island
physical system *) in asymptotically planar spacetime, ie a
situation where the investigated system is spatially limited (it is still located near the origin of the coordinates)
and at a
sufficiently large distance the spacetime becomes planar. Here we
can relate the total energy and momentum of the system to the
invariance with respect to temporal and spatial shifts with
respect to the observer at infinity (asymptotic symmetries).
*) The most important island systems of
this species are binary stars or multiple star systems.
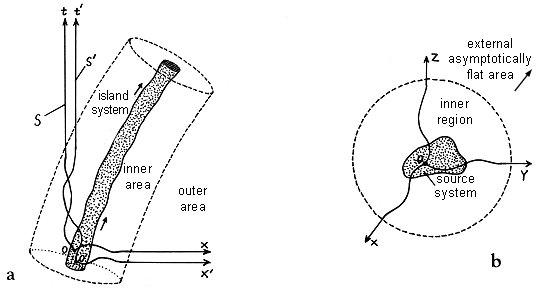
Fig.2.14. Spacetime (a) and space (b)
around the island physical system can be divided into three parts
:
l. The area of the own source (dotted), where in addition to the
strong gravitational field is Tik ¹ 0.
2. A near (but vacuum) "inner" region where the
gravitational field and the curvature of spacetime can still be
strong.
3. Distant asymptotically planar outer region, where the
gravitational field is very weak (spacetime almost flat) and
where an asymptotically inertial frame of reference can be
introduced.
If we use in the island system the asymptotically Galilean
reference systems, we get a clear expression for the total
energy-momentum P i of the system, which is
maintained, is independent of the choice of the coordinate system
in the inner region and behaves as a four-vector with respect to
asymptotically Lorentz transformations.
Indeed,
despite the ambiguity of the expressions for the energy-momentum
pseudotenzor gravitational field, it is possible to obtain from
them an unambignous expression for the total four-vector energy and momentum
P i = (1/c).ò(Toi +toi)dV of such an island system,
which has good physical properties in the sense of Moller's
requirement no. 3,4,5. In an asymptotically flat space, we can
define such a large spatial area around the island source system,
that the gravitational field outside it is negligible (Fig.2.14).
To calculate the energy and momentum of the field, it is then
necessary to take the coordinate system (with begin inside or
somewhere near the source) such that in the outer asymptotic
regions (where there is no field according to the assumption) it
passes into the Galilean system in which r®¥lim gik(x) ® hik + O(1/r), ie. gik(¥) = hik and all components t ik also disappeared here. In the inner
area (near sources), the coordinate system can be chosen
arbitrarily without affecting the values of P i . Although the quantities T ik + t ik do not generally form a tensor
and P i is not a vector in general, the total
energy and momentum are invariant with respect to such
transformations of the coordinates xi ® x'i= xi + ei (x), which
are asymptotically identical, ie r ® ¥lim ei(x) = 0.
It follows easily from the law of conservation for Pi. Taking two coordinate system S
and S' different in the inner area, but passing asymptotically
into the same Galileo system S . To compare the values of Pi
and P'i in these two systems at certain times t
and t', it is possible to imagine another
(imaginary) auxiliary "variable" coordinate system
S", which in the inner region at time t coincides with the systemS
and at time t' with a system S'; in the outer region does not
change and always coincides with the same S. Since, thanks to the
conservation law dPi/dt = 0, the quantities Pi
in each frame of reference are constant and independent of time,
this also applies to the system S'', so that Pi(t)
= P''i (t') = P''i(t') = P'i(t'). This invariance is indeed
also directly visible from the surface integral (2.96) applied to
the closed area lying in the asymptotic region, because no
coordinate-changing transformations only within a bounded spatial
region not can affect the global values of these integrals across
distand surfaces. The total energy and momentum of the island
system is thus not only preserved, but is also independent on the
choice of the coordinate system, if it asymptotically transitions
into a given Galileo system. Since tik are tensor with respect to
linear transformations, the components of the Pi
form a four-vector with respect to linear transformations, i.e.
also with respect to linear transformations converting one
asymptotically Galilean reference frame to another.
At sufficiently large distances from the static island system, the influence of the mass distribution details on the gravitational field gradually disappears and the field there can be considered as spherically symmetric, given by the exact Schwarzschild solution (3.13). For r ®¥ this solution has an asymptotic shape (2.56c)
![]()
where M is the total mass of the system. Substituting the appropriate components of the metric tensor into the relation (2.96) and integration through the sphere of radius r we get P ° = M.c 2 . Moller's requirement No.5 is therefore also met.
To show the real existence of gravitational field energy and at the same time delve deeper into the specific nature of gravitational energy, let us return to the question of the emission and transmission of energy by gravitational waves, as we promised in the previous paragraph. According to Newton's theory, an isolated system exciting a time-varying gravitational field, such as a rotating rod or a binary system according to Fig.10, it will not lose any energy by gravity - both bodies would orbit around a common center of gravity forever with a constant period. The possibility of extracting energy from such a system through gravity is eg place a suitable inelastic body nearby; the changing gravitational field in it causes time-varying tidal deformations, which are converted into a heat heating the body (thermal energy can be dissipated or radiated into space by infrared radiation). However, this takes place in the induction zone of the system. In the general theory of relativity, however, even in an isolated system, the mutual movement of gravitational bodies causes gravitational waves to carry energy from the system - in the wave zone.
Standard (and the late
sixties actually the only) method to calculate the energy
transmitted by gravitational radiation, ie. the amount of energy
taken away from the source by gravitational waves, is to
determine the flow of energy through an imaginary closed surface
surrounding the source far enough in the wave zone, using energy-momentum pseudotensor tik of the rippling gravitational
field. It is assumed that the energy of the source decreases with
the same rate at which the energy calculated in this way is
carried away by the gravitational waves.
We therefore surround the
source system meant
by a closed surface S lying at a sufficient distance
(and thus in the wave zone). According to (2.90), the amount of
energy carried away from the source by gravitational waves is
given by the flow of gravitational energy through this closed
surface S (on the area S we assume a vacuum, ie Tik=0) :
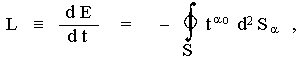
To calculate the energy current ta°, it is necessary to determine the gravitational field in the wave zone, ie at distances R >> c.T, large in comparison with the length of the emitted waves. We start from the general solution (2.65)
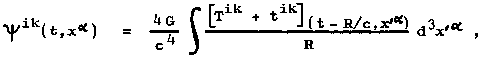 |
(2.65) |
describing metric coefficients, retarded t-R/c from of individual places of the source system. We will assume that the velocities of the bodies in the source system are small, enough that the wavelength is much greater than the dimensions of the source. Only areas lying inside and in the immediate vicinity of the source will then contribute significantly to the retarded integrals (2.65). If we place the origin of the coordinates somewhere inside the source, then from the point of view of each sufficiently distant point, all places of the effective zone of the source will be approximately at the same distance R as the origin of the coordinates. The retarded potentials in the wave zone can thus be expressed in shape
| y ik = (4G / c 4 R) V ò (T ik + t ik ) (tR / c, x ' a ) dV . |
For a given purpose, only the spatial components yab given by the distribution of the total stress tensor Tab + tab are needed. However, using the conservation laws (2.90), which are actually the equations of motion of the source, the quantities yab can be expressed using the integrals of the mass-energy distribution T°°+t°°, because
| V ò (T ab + t ab ) dV = (1/2) d2/dt2 V ò (T oo + t oo ) dV . |
If the source is non-relativistic (ie almost Newtonian) in nature, the gravitational contribution to the total energy can be neglected (t°° << T°°), so we get
| y ab = (2G / c 4 R) d 2 / dt2 K ab (tR / c, x ' a ) , | (2.99) |
where
| K ab = Vò T oo(t,x) xa xb dV = c2 Vò r(t,x) xa xb dV | (2.100) |
is the quadrupole moment of the mass distribution of the source.
Equation (2.99) is a famous quadrupole
formula,
indicating the amplitude
of gravitational
waves at a distance R from a source with a
time-varying quadrupole mass distribution (the
retardation variable t-R/c is irrelevant in practice).
Note: An alternative derivation of the quadrupole
formula consists in distributing Tik(t-R/c, xa) in the formula (2.65) into a power series,
leaving the members in the 2nd order and substituting the formula
for the quadrupole moment.
We can now calculate the pseudotensor t°a and wave gravitational energy. At
great distances from the source, gravitational waves can be
considered (in not too large areas of
space) to be practically planar, in which the field
changes only along one (radial) direction in space. If we orient
the coordinate system so that the propagation direction will be
the x1 axis, the gravitational wave will be
determined only by components h23 and h22 = -H33 and the non-zero component
pseudotensor will only T01, for which from the
definitions of Tik we get
| t 01 = (c2/16pG) [.h23 + 1/4 (.h22 - .h33 )2 ] | (2,101) |
(all quantities are a function only (t-xl/c)). Substituting for h23 = y23, h22 = y22 and h33 = y33 from (2.99) we get for the energy radiated per unit time over the unit area perpendicular to the xl axis the relation
| c. t 01 = (G/32pR2) [...K23 + 1/4 (...K22 -...K33 )2 ] , | (2,102) |
from which follows the above quadrupole formula (2.79) for the intensity of gravitational radiation in the general direction n. The energy loss of the system per unit time, given by the total gravitational radiation in all directions flowing through the sphere of radius R, then gives
dE/dt = - (G/45c2) ...Kab2 ,
which is an important quadrupole formula (2.77) for gravitationally radiated performance. The importance of these formulas is shown in §2.7 "Gravitational waves", passage "Sources of gravitational waves in space".
Gravitational
waves energy
However, due to (legitimate) reservations about the physical
significance of the gravity field energy-momentum pseudotensors,
such a calculation may not be entirely convincing in itself. E.g.
the fact that by suitable choice of the coordinate system it is
possible to cancel the tik at any
point in space [241] has sometimes been interpreted as meaning
that gravitational waves do not transfer energy and do not really
exist. Although agains these objections can be argued that the
total radiated energy does not depend on the coordinate system or
the pseudotensor used, the correctness of the standard procedure
for calculating radiated gravitational energy must be
substantiated by methods that do not require the direct use of
pseudotensors. And indeed, they were found two such ways.
Firstly, Isaacson [140] constructed a tensor (not a pseudotenzor)
of the energy-momentum of gravitational waves propagating against
a background of curved spacetime, whereas this Isaacson tensor (2.76) turned out to be equal to t ik pseudotensor averaged over several waves. This proved
the accuracy of the results obtained by the standard method using
a pseudotensor for the energy of gravitational waves.
Furthermore, direct calculations of Thorne [249], Burke [36],
Chandrasekhar and Esposito [47] showed that the braking of motion in the
source system due to a feedback of an excited variable field
correspond exactly to the energy
carried away by gravitational waves and calculated by standard methods using
pseudotensors. We will briefly mention both methods.
For better illustration, we will again present Fig.2.9 showing Isaacson's method of analyzing the energy of gravitational waves by averaging over several wavelengths :

Fig.2.9. In the Isaacson shortwave approximation, the global
curvature of spacetime ("background") can be
distinguished from the local fluctuations of gravitational waves
if the wavelength is much smaller than the characteristic radius
of curvature of spacetime. This separation is performed by
averaging over a region of several wavelengths using a suitable
standard weighting function W(z) converging to zero with
increasing distance.
In a gravitational wave, it is not possible to locate energy and momentum in an area smaller than the wavelength - so it is not possible to determine what part of the energy is transmitted by the top, valley or "slope" of the wave. However, it can be said that a certain well-defined amount of energy (and momentum) is contained in a given sufficiently large region with dimensions of several wavelengths. This follows from Isaacson's formalism (briefly explained in the previous §2.7), which by dividing the metric into rapidly and slowly changing parts allows not only to investigate gravitational waves in curved spacetime (ie their motion in the field of gravitational bodies or on the global background of a curved universe in cosmology), but also captures the inverse effect, ie the curvature of space-time caused by the effect of energy contained in gravitational waves. This curvature of spacetime by gravitational waves is described by equations (2.75)
| Rikglob
- 1/2Rglob gikglob
= |
having the form of normal Einstein's equations, where the source on the right is the Isaacson's tensor of effective smoothly spread out energy-momentum defined by relation (2.76)
| T ikwave º - (c4/8pG) (<Rikwave> - 1/2 gikglob . <Rwave>) . |
In addition, it turns out that this Isaacson tensor is equal to the space-time average over several wavelengths of the energy-momentum pseudotensor t ik of the gravitational field in the wave :
| T ik wave = < t ik wave > | (2,103) |
(specifically, the calculation was performed for a pseudotensor in the form of Landau and Lifšic [166]). If we are not in a vacuum and in addition to gravitational waves, there are bodies and other non-gravitational fields described by the total energy-momentum tensor Tik H , equations (2.75) will have the form
| G
ikglob
º Rikglob - 1/2Rglob
gikglob = (T ik H + T ikwaves
) . |
(2,104) |
When averaging the
pseudotensor t ik across several wavelengths, we
get the tensor of energy and momentum Twavesik of gravitational waves, which
has a very good physical significance (but in a non-local sense).
According to (2.75) and (2.104), this tensor can serve, among
other things, as an equal-legal source (together with the
energy-momentum tensor of bodies and non-gravitational fields) on
the right side of Einstein's gravitational equations, and thus
contributing to global curvature of space. In principle, it is
even possible to achieve such a concentration of gravitational
waves, that due to their "self-gravity" a part of the
gravitational energy succumbs to gravitational collapse and forms
a black hole; such a "purely gravitational" black hole
will have, thanks to the "black hole has no hair"
theorem, exactly the same properties as a black hole created by
the collapse of ordinary matter, such as a star - see §4.5.
Another example of a purely gravitational object *) is Wheeler's
gravitational geon - a hypothetical metastable formation of
gravitational waves held together by its own gravity (§B.3 "Classical
geometrodynamics. Gravity and topology.", passage "Geons").
*) In a plane gravitational
wave, energy and momentum are related by the relation p = E/c -
the speed of gravitational waves is equal to the speed of light,
the rest mass of gravitons is zero. When two waves of different
directions meet, their momentums p = p1 + p2 add up vectorally,
while the energies E = E1 + E2 add up scalar, so that E/c > p
- superposition of waves of different direction effectively has a
non-zero rest mass.
Isaacson's formalism thus confirms the
correctness of the global results of the calculation of energy
and momentum of gravitational waves by standard methods using
pseudotensors. To determine the energy of gravitational waves,
the basic requirement of the asymptotic Euclidean metric can also
be somewhat weakened, because it is sufficient to investigate a
finite volume with dimensions significantly exceeding the
wavelength.
When studying
gravitational radiation, it is automatically assumed that the
source loses energy (and momentum) at exactly the same rate as
the energy is carried away by the gravitational waves. However,
the methods of calculating the energy of gravitational waves and
the conservation laws on which this assumption is based are not
always as unambiguous in the general theory of relativity as in
classical physics. Therefore, it is especially valuable that the
energy loss of the source can be determined by direct
calculations of the effect of the excited field near the source -
by analyzing the feedback
of the gravitational
field to the radiating system. This
analysis leads to the conclusion, that a small variable component
of the space-time curvature (gravitational field) is formed
inside and near the source with a phase different from the main
variable component; this
member causes a braking force in the source.
Calculations (again based on the relation
(2.65), resp. (2.99)) show, that the main part of this additional
component "re" causing braking can be expressed in the
form
| h oo re = (2G / 15c 5 ) ( d 5 / dt 5 K ab ) x a x b , |
so that the respective braking by the feedback of the emitted waves can even be outlined by modifying the Newtonian potential :
| j = j New + j re , j re º - 1/2 hoore = (2G/15c5) (d5Kab/dt5 )xa xb , | (2.99) |
where jNew is the Newtonian potential and jre is the potential of the braking force caused by the radiation reaction. The acceleration of each test particle at this potential j will be aaº d2xa/dt2 = - j,a = - j New,a- j re,a and the braking force acting on the mass particle m will be equal to m.j re, a . This braking force will lead to a loss of energy inside the source
d E / d t = V ò r . a a v a dV = - V ò r . j re, a v a dV ,
where va is the velocity of the corresponding element rdV (the component jNew does not apply here, because in Newton's theory the energy of the source is preserved and the change can be caused only by the part corresponding to j re). The average speed at which the energy of the system decreases due to braking by the reaction of radiation
< d E / d t > = - V ò r . j re,a v a dV = (G / 45c 5 ) < ( d 3 K ab / dt 3 ) 2 >
comes out the same as the velocity at which energy is carried away by gravitational waves according to the quadrupole formula (2.77). However, this result is obtained here in an independent way, in no way related to the energy contained in the gravitational waves !
Conversions
of gravitational energy
So far, we have analyzed
the properties of gravitational energy (and
the justification of its existence) on a theoretical level. The second line of
argument in favor of the existence of gravitational field energy
turns to experiment - to study the conditions under
which gravitational forces can perform
work and the conversion of gravitational energy into other forms of
energy can occur.
One such "gravitational
engine"
can be considered, for example, the sea
tide, which,
through gravity, converts part of the kinetic energy of the
orbiting moon into heat and mechanical energy on the Earth's
surface. However, the whole process takes place deep inside
"inductive" zone of system (practically
in the middle), so
that any effects of retardation and final velocity of
gravitational action will not be manifested in any way due to the
slow orbital period - energy transfer can be described here in
the context Newtonian theory.
As for gravitational waves, already in the fifties years H.Bondi [21] proposed a very simple and illustrative imaginary experiment, the arrangement of which is shown in Fig.2.15. On a smooth rod, two massive rings can move almost freely, with sufficiently low friction. Gyroscopes at the ends of the rod prevent its (local) rotation. The whole system moves freely in space (center of gravity after geodesy) and gravitational waves move the rings apart and towards each other due to the deviation of geodesics. Due to friction agains the rod, part of the energy of gravitational waves is thus converted into heat, which can take from the rod. Possibly if the rings were connected to the dynamo via levers and a suitable gearbox, the energy of the gravitational waves would be converted into electrical energy. From an energetic point of view, we can consider gravitational wave detectors (briefly described in the previous paragraph) with a bit of exaggeration as a kind of "microelectric power plant" with a small power, using the energy of gravitational waves. Perhaps there can be no more convincing argument that gravitational waves have energy than that, with the help of a suitable arrangement, this energy can in principle be taken and converted into another type of energy..!..
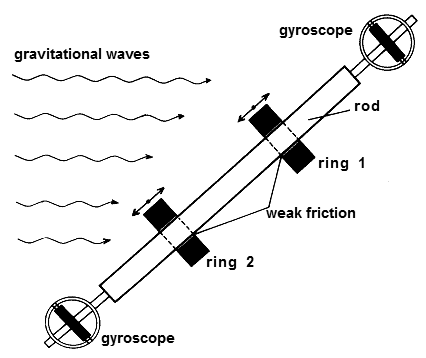 |
Fig.2.15. A simple arrangement for converting the energy of gravitational waves into heat. |
Thus, the general theory of relativity clearly implies the existence of gravitational waves, which detach from the source and carry with them into space part of its energy, momentum and angular momentum, even without the presence of some "receiver" of these waves. The integral law of conservation (2.86) of energy and momentum, when gravitational radiation is included, changes to shape
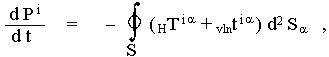 |
(2,106) |
where the surface S lies in the asymptotically planar spacetime (and thus in the wave zone of the system). These equations in asymptotically flat spacetime surrounding the investigated system, which no longer contains non-tensor quantities, say that the rate of change of energy and momentum of the system is equal to the current which is through the closed surface surrounding system transferring energy and momentum substance medium (solid, gas, particles etc.) + non-gravitational fields (eg electromagnetic radiation) - "H", and gravitational waves - "waves". Thus, we see that in the analysis of the behavior of each physical system in an asymptotically plane space-time, we can take advantage of the common laws of conservation of energy, momentum and angular momentum (gravitationally measured), while we must also take into account the energy carried away (or absorbed) by gravitational waves.
During the research, the question of the sign of gravitational energy and the total energy of the physical system in general remained open for a long time. In Newtonian physics, the total energy of a material system and a gravitational field is given by an integral
E = Vò [ r . v2/2 - (grad j)2/(8pG) ] d V ,
wherein the energy density of the gravitational field itself w = -(grad j)2/(8pG) is negative here. The relevant calculation with using the Einstein pseudotensor gives positive energy density of the gravitational field; when using some other terms for the pseudotensor t ik (eg Landau-Lifšic pseudotensor) the gravitational energy density is negative. The energy density of gravitational waves (averaged) is positive . These discrepancies arising from the different distribution of the total energy on the energy source, the energy of the gravitational field and the interaction energy, however, due to the non-localizability of gravitational energy they are not important. However, the sign of the total energy , which is related to the stability of the system, is of fundamental importance. In relativistic theory of nongravity fields, the expression for field energy is explicitly positive. However, the expressions for the energy of the gravitational field neither for the total energy of the physical system in the GTR no longer have this property; the numerical value and the sign of the total energy can only be decided by analyzing the field equations. Such an analysis was performed in the works of Schoen and Yau [230], [231] and Witten [282], who proves that the total energy of the gravitational field and the source system (with a positive energy-momentum tensor) is positive, as it corresponds to the basic physical requirements.
To the above-discussed question "Does the gravitational field have energy?", we can therefore answer positively in the final summary of the specific properties of gravitational energy in the general theory of relativity :
| Theorem 2.6 (gravitational energy) |
|
In comparison with classical physics, there is a certain degradation of the concept of energy in the general theory of relativity. Not only does energy density lose its local significance (so the illustrative notion of energy as a certain "substance" continuously and unambiguously distributed in space is no longer justified), but the total energy can be defined only if special geometric and topological assumptions are met. Only in asymptotically planar spacetime with the Euclidean topology do the quantities of global energy and momentum of the island physical system have a well-defined meaning. If there is no asymptotically flat region of spacetime, there is no invariance with respect to space-time shifts, to which energy and momentum could be related. Figuratively speaking, there is no reasonable "platform" on which to place and "weigh" a given system. Such a situation probably occurs for the universe as a whole, as shown by contemporary cosmology (Chapter 5, §5.2). Energy, which in classical physics is a fundamental concept and basic attribute of matter, thus becomes an ordinal quantity (generally without illustrative physical meaning), which in certain situations (thanks to its law of conservation) describes some properties of matter. However, in light of the connection between the laws of conservation and the symmetries of spacetime, this may not surprise us too much. Degradation of the concept of energy is closely related to the revision of the concepts of space and time in the general theory of relativity, which were overthrown from the throne of absoluteness and immutability and became dynamic elements closely related to the distribution and motion of matter.
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||