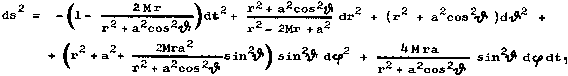 |
(3.37) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 3
GEOMETRY AND
TOPOLOGY OF SPACE-TIME
3.1. Geometric-topological properties of
spacetime
3.2. Minkowski
planar spacetime and asymptotic structure
3.3. Cauchy's
problem, causality and horizons
3.4. Schwarzschild
geometry
3.5. Reissner-Nordström
geometry
3.6. Kerr and Kerr-Newman geometry
3.7. Spatio-temporal
singularities
3.8. Hawking's
and Penrose's theorems on singularities
3.9. Naked
singularities and the principle of "cosmic censorship"
3.6. Kerr and Kerr-Newman geometry
If the body that is the
source of the gravitational field rotates, the excited external
gravitational field will no longer be centrally symmetrical, but
can only be axially symmetrical (if the
mass-energy distribution in the rotating body is symmetrical with
respect to the axis of rotation). In §2.5,
passage "Rotating gravity", we
derived in the approximation of the weak field the effect of the
rotation of a gravitational body on the external excited
gravitational field. We have seen that the rotation of the source
leaves characteristic "traces" in the form of non-diagonal members on the external gravitational field (ie on the space-time metric), causing the outer bodies to be entrained by the
rotating gravitational field in the direction of the source
rotation (so-called Lense-Thirring
effect).
The exact solution of Einstein's equations
(in vacuum) for such an axially symmetric case was found by
R.Kerr [152] in 1963; this solution was then generalized by
E.Newman to the case of the presence of an electric charge [186].
Kerr geometry
Kerr geometry is a generalization of
Schwarzschild geometry roughly in the sense that Schwarzschild
geometry is "spherical", while Kerr geometry is
generally elliptical. In the so-called Boyer-Lindquist coordinates (which
are an elliptical generalization of Schwarzschild coordinates) [28], the space-time element of
Kerr's geometry has the form
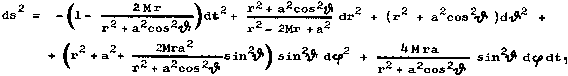 |
(3.37) |
where M is the total mass (weight parameter) and a = J/M is
"specific angular momentum" - total rotational angular momentum J divided by the total mass M. From the expression for the space-time element
(3.37) it is clear (and this is confirmed by the calculation of
the components of the curvature tensor Ri
klm and its scalar
invariant) that Kerr's geometry has a physical
singularity given by the relation
| r 2 + a 2 cos 2 J = 0 . |
This is not a point singularity as in the Schwarzschild solution, but the ring singularity, which is in a plane perpendicular to the axis of rotation of the shape of a circle with radius a .
Similarly as in
Reissner-Nordström geometry are distinguished here three special
cases of differing global space-geometrical structure: a2
< M2 , a2 = M2 , a2 > M2. Kerr geometry is of particular
importance for the case M2 > a2, where it describes the external
field of stationary rotating
objects,
especially black holes *). When R.Kerr derived the
solution [152], he certainly had no idea how this
"algebraically special" solution would prove important
and general; in light of Theorem 4.1, a "black hole has no
hair", any stationary uncharged black hole will have a Kerr
geometry of spacetime.
*) This is exactly true for a
black hole, where Kerr's geometry is a vacuum solution of
Einstein's equations. However, finding a material source of exact
Kerr geometry, leading according to Einstein's equations to a
smooth transition of the inner metric to the outer Kerr metric,
is by no means easy. The shape
of such an ellipsoidal rotating source and the distribution of
matter in it must satisfy certain very special conditions [82].
The gravitational field around the rotating material bodies
(planets, stars, galaxies) is therefore only approximately Kerr.
Outer and inner horizon
In most important case a2 <M2 there are two values of r ,
for which in the denominator of the spatial part of the metric in (3.37) r2
-2Mr + a2 is equal to zero :
| r g + = M + Ö (M 2 - a 2 ) , r g - = M - Ö (M 2 - a 2 ) . | (3.38) |
Thus, again (similarly to the Reissner-Nordström geometry) there are two horizons on which the metric (3.37) is pseudosingular. The outer horizon r = rg+ is the event horizon (with similar properties as the Schwarzschild horizon). To reach the horizon rg+, each object needs an infinitely long coordinate time (but a finite interval of its own time) and also an infinite angle (j ®A) - due to the entrainment of inertial systems by rotation (see §4.4) it must make an infinite number of orbits around the horizon. The inner horizon r = rg- is a Cauchy horizon with complex causal relationships (it is discussed in §3.3 "Cauchy problem, causality and horizons" and in §3.5 "Reissner-Nordström geometry"). Similar to Reissner-Nordström geometry, the inner Cauchy horizon is unstable to external perturbations.
Rotating gravity,
ergosphere
An important property here is the effect of entrainment
of spacetime by
the rotation of the source object (§2.5
"Einstein's equations of the gravitational field", passage "Rotating
gravity"). This rotating gravity forces
each particle, that comes close, to orbit in a consistent
direction. Above the horizon there is an area called the ergosphere, bounded by an elliptical surface called
the static limit given by the equation r = rS = M+Ö(M2 - a2 cos2 J). Within this area, each body
must orbit in the direction of rotation of the source. Through
the ergosphere, it is theoretically possible to draw the energy
of rotating gravity (from black holes). It is discussed in more
detail in §4.4 "Rotating and electrically charged
black holes",
section "Influence of black hole
rotation. Ergosphere", passage "Extraction
of rotational energy. Penrose process.".
Analytical extension of
Kerr geometry
To remove coordinate pseudosingularity (ie
to analytically extend the metric across these areas) the
transition to Kerr coordinates [127], [41] (v+,r,
J,j~+) is used by transformations
| dv+ = dt + [(r2+a2)/(r2-2Mr+a2)].dr , dj~+ = dj + [a/(r2-2Mr+a2)].dr . | (3.39) |
This transformation performs an infinite "compression" of the coordinate time t and an infinite "untwisting" of the angular coordinate j around the horizon. The metric (3.37) then has the form in Kerr coordinates
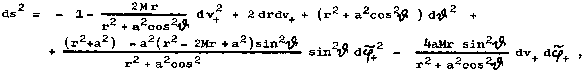 |
(3.40) |
which is already regular in
r = rg+ and r = rg-. The complete
analytical extension is obtained by combining this metric in coordinates (v+,r,
J,j~+) and analogous metrics in coordinates (v-,r, J, j~- ) given by transformations
dv- = dt -
[(r2+a2)/(r-2Mr+a)].dr ,
dj~- = dj - [a/(r2-2Mr+a2)].dr .
A conformal spacetime diagram of this complete extension of Kerr geometry is shown in
Fig.3.25a. The
global structure here is similar to the structure of the
Reissner-Nordström spacetime (compare with Fig.3.21 in the previous §3.5) *), but the nature of the real
singularity r = 0 is somewhat different. It turns out that in
Kerr space-time this singularity has an annular
structure
and it is possible to extrapolate the geometry through it to
negative values of the radial coordinate r
[43], [28].
*) There is also an infinite number of
"universes" between which it is possible to
theoretically (by model) "travel". A critical assessment of similar
possibilities will be in §4.4, section "Black
holes - bridges to other universes?".
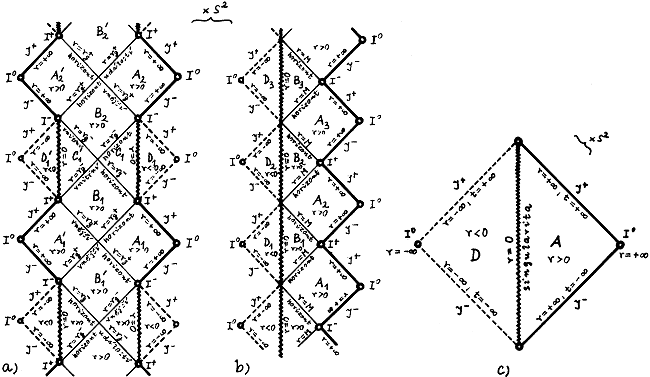
Fig.3.25. Conformal spacetime diagram of the complete extension
of Kerr geometry along the axis of symmetry.
a) Case M2 > a2 > 0.
b ) Case M2 = a2
(extreme Kerr geometry). c ) Case a2 > M2
(Kerr's naked singularity).
In the case of M2
= a2 is rg+ = rg- = M , the inner and outer horizons merge together.
The full extension of this metric shown in Fig.3.25b again has a
similar structure to the Reissner-Nordström geometry at M2
= Q2, with the difference that
analytical extension through the ring singularity to negative r is
possible. The Kerr metric in this case describes the spacetime
geometry of the extreme Kerr black hole with the maximum
possible rotation speed (§4.4).
For a2 > M2, the metric (3.37) is singular
only for r = 0, which is true
singularity
with an annular structure. Through the interior of this annular
singularity, the solution can be analytically extended to negative values of r (Fig.3.25c). There is no horizon and the
singularity can therefore "communicate" in both directions with
the whole surrounding spacetime - it is Kerr's
naked singularity (see §3.9 and §4.4).
Kerr - Newman geometry
We get another
generalization if we consider the presence of an axially
symmetric electromagnetic field, ie a rotating axially symmetric
source will have an electric charge, which is also axially
symmetrically distributed. The geometry of spacetime around such
an object is called Kerr-Newman geometry [186]; it is in fact a combined
Kerr and Reissner-Nordström geometry. The space-time interval
element (in Boyer-Lindquist coordinates) has the form
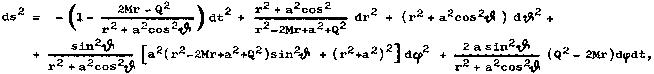 |
(3.41) |
where Q is the total electric charge measured by a distant observer - either by the flux of the electric intensity vector E through the closed surface, or by analysis of the trajectories of the charged test particles. As with Kerr's solution, the geometry of spacetime is stationary and axially symmetric. The outer horizon r = rg+ (event horizon) and the inner horizon r = rg- (Cauchy horizon) have radii
| (3.42) |
Note: The event horizon r =rg+ is also sometimes referred to as the Killing horizon, because the Killing vector field x o º¶/¶t (introduced in §2.4), its time component, here changes the space-time characteristic: outside the horizon it is of the time type while within the horizon it acquires a spatial character.
The global geometric
structure of Kerr-Newman spacetime is analogous to the Kerr
geometry described above. There are again three special cases :
a 2 + Q 2 <M 2 ( black hole ) ,
a 2 + Q 2 = M 2 ( extreme
Kerr-Newman geometry) ,
a 2 + Q 2 > M 2 ( naked
singularity ) .
Carter [43] showed that in the vicinity of an annular singularity there is a region in which gjj<0; here the axial Killing vector ¶/¶j acquires a temporal character, so that closed worldlines of the time type appear here (eg circle t = const, r = const, J = const). In these areas around the singularity, therefore, causality may be violated. The assessment of the physical significance of some aspects of the complete extension of the Kerr-Newman geometry for black holes is in the conclusion of §4.4, for naked singularities in §3.9. The great significance of Kerr-Newman geometry lies in the fact that it is the most general solution for stationary axially symmetric asymptotically planar spacetime which has an event horizon, ie the most general solution describing a black hole - in the spirit of the "black hole has no hair theorem" , see §4.5 "The "black hole has no hair" theorem".
Trajectories of test
particles
The motion of test particles (generally charged) in general
Kerr-Newman spacetime is significantly more complicated than in
Schwarzschild geometry. Even in the special case, when the motion
will take place only in the equatorial plane and we do not
consider the electric charge, the trajectory of the test particle
near the horizon (especially in the ergosphere, see §4.4) will
decisively depend, among other things, whether
the angular momentum
of the particle has a coincident or opposite direction with
respect to the angular momentum J - i.e. if the particle moves in the direction or against
the direction of rotation of the Kerr field source.
The movement of charged test particles due to the action
of electromagnetic forces will generally no longer take place
after geodesics; on the right side of the geodetic equation, instead of zero, the Lorentz force will appear :
| (3.43) |
where q is the electric
charge of the test particle and Fik is the tensor of the
electromagnetic field co-acting as the source of the given
Kerr-Newman geometry.
Analysis
of the motion of test particles in the Kerr-Newman field is
mostly done not from the basic equation (3.43), but had
equivalent using the Hamilton-Jacobi equations [165], [43] which
is easier to determine the symmetry of the integrals of motion.
The resulting equations of motion of a test particle with charge
q, rest mass mo, energy E with respect to infinity, axial
component of angular momentum Lj and component pJ of momentum were
derived by Carter [43], [181] :
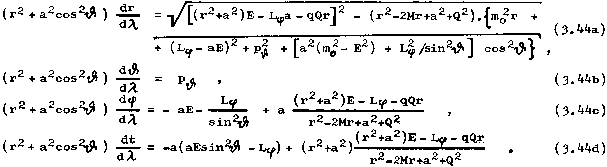
Since the gravitational and electromagnetic fields are stationary and axially symmetric (ie both components of the metric gik and the four potential Ak do not depend on t and j ), the following quantities will be constants (integrals) of motion when moving the test particle: energy E with respect to infinity, axial component L .. angular momentum with respect to the axis of symmetry, electric charge q of the particle and its rest mass mo (which at each point of the trajectory is related to the four-momentum of the particle by the relation mo=(-gikpipk)1/2). Another integral of motion that does not follow from the above symmetries was found by Carter [43]:
| C = P J 2 + a 2 (m 2 - E 2 ) + (L j 2 / sin 2 J) .cos 2 J ; | (3.45) |
because we will not need
this quantity in the next, we did not introduce
it into the
equations of motion (3.44).
We will not perform a general analysis of
particle motion in Kerr-Newman spacetime based on equations
(3.44) here, the interested party can find details eg in [8],
[81], [237]. However, we will use some of the consequences of
equations (3.44) for the motion of particles in Kerr-Newman
spacetime in §4.4 "Rotating
and electrically charged Kerr-Newman black holes", where we discuss the most
physically important aspects of Kerr-Newman geometry (such as the
effect entrainment - dragging of local local inertial systems,
existence of ergosphere, Penrose process, superradiation, etc.)
in connection with the properties of black holes.
Kerr-Newman geometry with nonlinear
electrodynamics
At the end of the previous §3.5, devoted to Reissner-Nordström
spacetime with centrally symmetric electric charge, we briefly
mentioned the possibility of generalization for the case of nonlinear electrodynamics - the passage "Reissner-Nordstrom solution with nonlinear
electrodynamics". An analogous generalization can be
made for Kerr-Newman geometry. When using Born-Infeld
nonlinear electrodynamics ( §1.6, passage
"Nonlinear
electrodynamics") with the parameter nonlinearity b in
the space-time interval (3.41):
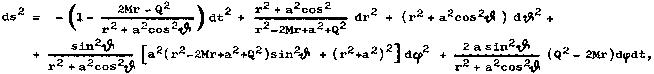 |
(3.41) |
instead of a simple square of the charge "Q2 " there will be more complex functions "f(r, Q)"
analogous to metric (3.36), containing elliptic integrals
where "F(...)" is the Legender's
elliptic function of the 1st kind and "2F1(...)" is the so-called hypergeometric function
(more complex power series from Q2b2/r4) .
For this "Kerr-Newman-Born-Infeld " metric, due to the
excessive computational complexity, it has not yet been possible
to find a completely general analysis of the motion of the test
particles. Trying to approximate
solutions
against slow rotation (a <<
1), using methods perturbation analysis . ............
...............
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||
Vojtech Ullmann