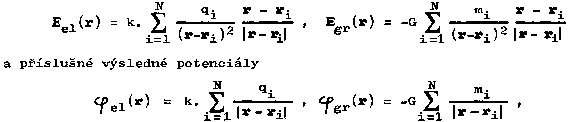 |
(1.25a, b) (1.26a, b) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 1
GRAVITATION AND ITS PLACE IN PHYSICS
1.1. Development of knowledge about nature,
universe, gravity
1.2. Newton's law of gravitation
1.3. Mechanical LeSage hypothesis of the
nature of gravity;
1.4. Analogy between gravity and electrostatics
1.5. Electromagnetic field. Maxwell's
equations.
1.6. Four-dimensional
spacetime and special theory of relativity
1.4. Analogy between gravity and electrostatics
Newton's law of gravitation
| m l . m 2 Fgr = - G . ------------ . r° , r° = r / r , r 2 |
(1.20a) |
on the mutual force attraction of two bodies of mass m l and m 2 at a distance r from each other, with its shape of its formula, very similar to another fundamental law of classical physics - Coulomb's law of electrostatics
| q l . q 2 Fel = - k . ------------ . r° , r 2 |
(1.20b) |
which expresses the
interaction of two (point) electric charges q1 and q2 placed in a vacuum at a distance
r from each other. The value of the
constant k depends on the system of units used. In
fundamental physics, k = 1 is assumed (which naturally defines
the unit of electric charge by its force acting on the unit
distance *), in the SI system k = 8,988.109 N m2 C-2 and the unit of electric charge
is 1 Coulomb (C) . Coulomb's law in the in
the form (1.20b) also apply in an electrically homogeneous and isotropic
material environment, while the proportionality constant k is
expressed in the form k = 1/4p.e
, where e is the permittivity (dielectric constant)
of the given material environment.
*) Unfortunately, the historical
development of physics has led to the fact that in the system of
SI units the charge is not primarily quantified by its electrical
force effects, but only indirectly by the magnetic effects of
electric current (Ampere unit ; one Coulomb is
then defined as 1A . 1s).
Note: The development of knowledge
about electricity and magnetism is briefly outlined in §1.1, the
passage "Electrodynamics,
atomic physics, theory of relativity, quantum physics".
So it is worth watching, how far the analogies between electricity and gravity go. Newton's and Coulomb's law have exactly the same shape, so the masses m1 and m2 of two gravitational bodies can be called their "gravitational charges". All conclusions about the motion of bodies under the influence of gravity made in §1.2 "Newton's law of gravitation" will also apply to the movements of charged bodies under the influence of Coulomb's electrostatic field. Here, too, the electric charges move along Kepler trajectories - they orbit along ellipses, approach and move away along hyperbolas or parabolas (we do not yet take into account the radiation effects caused by the emission of electromagnetic waves during the uneven movement of electric charges).
However, right here we come across the first important difference. While electric charges can have both positive and negative signs (q> = <0) and the electrostatic force between them can be both attractive (between dissenting charges) and repulsive (agreeing charges), the mass exhibiting in Newton's law is always positive (resp. non-negative m ³ 0) and the gravitational force is always attractive. This fundamental property of gravity, which according to Einstei's new equations is fulfilled also in the general theory of relativity (in all physically real situations where the energy-momentum tensor is positive definite - §2.6 "Deviation and focusing of geodesics"), plays a crucial role in such areas as is the physics of black holes (2nd law of black hole dynamics - see §4.6 "Laws of black hole dynamics") or cosmology (theorems on singularities - §3.8 "Hawking and Penrose theorems on singularities", §3.9, chapter 5 "Relativistic cosmology") .
Just as in electrostatics it is useful to introduce the concept of electric field for the interaction of electric charges, it is also advantageous in gravity to describe the interaction of material bodies using the term gravitational field. According to this concept, each material body creates a gravitational field around itself, and this field then shows force effects on every other body that enters it.
Electric
and gravitational fields
Each physical field is characterized by its action on test
particles. In electrostatics, the test particles are electrically
charged bodies, in gravity they are sufficiently small bodies,
which by their own effects do not significantly affect the
investigated gravitational field and its sources. Similar to the
electrostatic field, we quantify by the vector of electric
intensity Eel , which is the force acting on
the unit test charge, ie.
| F el = q. E el , | (1.21a) |
the gravitational field can also be described by the field intensity vector Egr indicating the gravitational force acting on the test particle of unit weight, i.e.
| E gr = m. E gr . | (1.21b) |
Coulomb's law can be expressed by the intensity of the electric field Eel excited in the space around the point electric charge Q :
| E el = k. Q / r2 . r ° . | (1.22a) |
Newton's law of gravitation then states that a point body of mass M excites a central gravitational field of intensity around it
| E gr = - G. M / r2 . r ° . | (1.22b) |
The fact that both the electrostatic and gravistatic fields are conservative makes it possible to express the field intensity using the scalar potential j :
| E el = - grad j el , E gr = grad j gr | (1.23a, b) |
For the central field of a point charge Q or a body M is
| j el ( r ) = k. Q / r , resp. j gr ( r ) = - G. M / r . | (1.24a, b) |
Experience teaches that for the force action of a system of a large number of electric charges or gravitational bodies, the law of superposition applies, according to which the effect of a system of objects (on a given test particle) is equal to the sum of the effects of each object separately, ie for a system of N point charges or mass bodies the electric or gravitational field strength will be
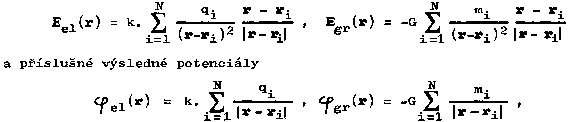 |
(1.25a, b) (1.26a, b) |
where r is the position vector of the point in which we determine the field and ri are the position vectors of the individual point charges q i or bodies m i .
However, the later development of the science of gravity has shown that there is a second essential difference between gravity and electricity. For electromagnetic phenomena, the principle of superposition applies exactly even to the largest charges and strongest fields. But for gravity applies the superposition principle with sufficient accuracy really only in the context of Newton's law, while at large acccumulation mass and strong gravitational fields it is no longer met. This nonlinearity is related to the universality of the gravitational interaction, as will be shown in §2.5 "Einstein's equations of the gravitational field".
Just as it is often useful instead of a system of a large number of discrete electric charges to consider a continuous distribution of an electric charge with a spatial density rel = dQ / dV, ie to express the amount of charge Q contained in a given spatial region V in the form
| Q = V òòò rel(x, y, z) dV , | (1.27a) |
the density of the continuous mass distribution r = dm/dV is usually introduced in mechanics and gravity, so that the total mass M contained in the spatial region V is then expressed by the integral
| M = V òòò r (x, y, z) dV . | (1.27b) |
The relationship between the model of the system of point charges q i and the idea of a continuous charge distribution is expressed by Dirac's d -function: r el ( r ) = i = 1 S N q i . d ( r - r i ). Analogous to weight. For a continuously distributed charge with density rel (r) or for a continuously distributed mass with density r (r) then, due to the principle of superposition, the resulting electric or gravitational field will be
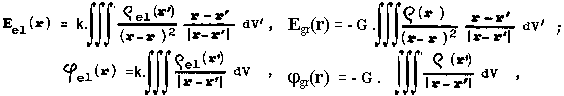 |
(1.25'a, b) (1.26'a, b) |
where r' is the position vector of the integration volume element dV'.
Gauss's theorem of
electrostatics and gravity
Coulomb's and Newton's law can be formulated in the form of Gauss's theorem (Fig.1.3a)
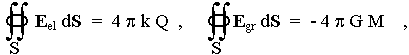 |
(1.28a, b) |
according to which the flow of the field intensity vector E over the closed surface S is given by the total charge Q, resp. the total mass M, contained within this area. By expressing charge and mass using integrals of their density and using Gauss's theorem of vector analysis, relations (1.28a, b) can be rewritten in differential form
| div E el = 4p k r el , div E gr = - 4p G r , | (1.28'a, b) |
which states that the outflow of the field strength vector from the unit volume is given by the local charge density or mass. Expressing the field strength using the potential gradient (1.23) gives a second order Poisson differential equation for the potential :
| Dj el = - 4p k r el , Dj gr = 4p G r , | (1.28''a, b) |
where D º ¶2 / ¶ x2 + ¶2 / ¶ y2 + ¶2 / ¶ z2 is the Laplace differential operator.
Newton's equation of motion of the body of mass m and electric charge q in an electric field has the form
| d2 r / dt2 = (q / m). grad j el , | (1.29a) |
while when moving in a gravitational field, the mass on both sides is shortened (on the equality of inertia and gravity, allowing this shortening, see §2.2 "Versatility - a basic property and the key to understanding the nature of gravity") :
| d2 r / dt2 = grad j gr . | (1.29b) |
The main difference between motion in electric and gravitational fields is that in electric field different bodies move differently according to the value of their specific charge q/m, while in gravitational field the trajectory of a body does not depend on any individual characteristics of a moving body - it is universal properties of the field alone jgr(r). The equation of motion (1.29b) is thus an expression of the universality of gravitational action, which will play a key role in the next relativistic description of gravity.
Gravitoelectromagnetism ?
The electrostatic field is a special case of the general electromagnetic field (see the following §1.5 "Electromagnetic field. Maxwell's
equations") , which rules in our surrounding nature,
everyday life, chemistry, atomic and nuclear physics, and to a
large extent in astrophysics. This raises the question of whether
the analogies between Newtonian gravity and electrostatics
continue into the field of dynamic
manifestations of electricity - electromagnetism ? Within the general theory of
relativity we will show that there really are some formal analogies between the equations of electromagnetism
(Maxwell's equations) and special approximations of Einstein's gravitational equations in GTR. This analogy is called gravitoelectromagnetism - some specific kinematic
effects of gravity are analogous to the magnetic effects of
moving charges. This is mainly the effect of entraining bodies in the direction of rotation of
the source of the
gravitational field (Lense-Thirring
effect - §2.5, passage "Rotating gravity"),
which is somewhat reminiscent of magnetism. For these gravidynamic effects, a certain analogy can be traced with magnetism in electrodynamics. Using special
"purposeful" transformations, Einstein's gravitational
equations can be modified into the form of electromagnetism
equations.
From an objective point of view, however,
these analogies are only formal, with little physical
significance. Phenomena seemingly reminiscent of magnetism are of
the second and higher order in comparison with the primary
gravitational ("gravistatic") action. The actual
physical magnetism caused by the interaction of the
moving "charges" - field sources - in gravity is not contained ...
Note .: For
magnetism in gravity they could be considered well known
to the Coriolis force Fc = -2 m. [ v
´ w ] , which resemble
the magnetic Lorentz force Fm = (1 / c) .q. [ v ´ B
] applied when electric charge q moving speed of the magnetic
field intensity (induction) B . However, these
forces are in fact a kinematic effect in a rotating
frame of reference (angular velocity w ), which
also occurs within the framework of classical Newtonian mechanics
...
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||