Phantoms, phantom and physical measurements in radionuclide scintigraphy
PHANTOMS and
phantom measurements in nuclear medicine
1. Introduction - the essence of phantoms, types of phantoms
2. Phantoms of organs
3. Phantoms for gamma
camera testing
3.1. Testing and calibration of
scintillation camera image homogeneity
3.2. Measurement of the positional
resolution of the camera
3.3. Gamma Camera Imaging Linearity
Analysis
3.4. Tomographic
phantoms for SPECT, PET, CT
4. Dynamic phantoms
4.1. Modeling of periodic cardiac
pulsation
4.2. Modeling of central hemodynamics
4.3. Phantom measurement of esophageal
passage dynamics
1.
Introduction - what are phantoms
Radiological imaging methods (X-ray
diagnostics, nuclear medicine - scintigraphy, NMRI magnetic
resonance imaging, ultrasonography) examine the structures and
processes hidden inside the organism . The
question therefore arises as to whether the relevant images
capture these invisible structures precisely and
objectively and are happening inside the body? For
experimental testing of these aspects of imaging diagnostics, as
well as for measuring physical parameters, imaging properties and
for calibration of used devices, special precisely and
reproducibly made aids, so-called phantoms, are used
.
The word phantom
(Greek phantasm = vision, spirit, ghost) has a number of
common meanings: delusion, ghost, vision, deceptive phenomenon -
imaginary, fictional. Here we will use a somewhat special meaning
of this word - an artificial fact , a model
.
The main task
of radionuclide measurements and imaging in
nuclear medicine is the analysis of structures and processes in
the body through external detection of gamma
radiation emanating from the body after the application of a
suitable radio indicator - Chapter 4 " Radionuclide
scintigraphy ". A number
of side effects can be used to detect this g radiation and to evaluate
the results, such as: statistical fluctuations, imperfect camera
resolution, tissue absorption in the tissue, Compton scattering
of g radiation,
the influence of the tissue background (mostly inhomogeneous),
the difference between the actual dynamics of the studied
processes in the organism from the mathematical model, etc. These
circumstances may adversely affect the accuracy of the measured
parameters and the whole scintigraphic diagnostics. What are the
details of the actual structures of the tissues and the actual
course of the dynamics of events deep within the organism , a
priori we do not know. The same is true for other imaging
methods.
Phantoms can play an important role
in the exact approach to the development and verification of some
radiological imaging methods (especially scintigraphic or X-ray).
By phantom here we will understand an artificial
modelof a given system, which simply expresses certain
important anatomical features, the distribution of the radio
indicator in the organism, or the dynamics of movement and time
changes. Compared to the real organism, in which we investigate
complex, variable and previously unknown anatomical conditions or
distribution of the radioindicator, the phantom has two basic
advantages for study purposes:
- Simplicity and reproducibility
.
- Accurate knowledge of the
geometric arrangement of the phantom in space and the
actual parameters of the geometric distribution
of radioactivity or the dynamics of radionuclide
movement, and these parameters can usually be set
and changed.
In phantom measurements, we can then compare
these actual parameters and structures of the phantom with the
images and with the values ??obtained by analysis of phantom
radionuclide measurements. A necessary (unfortunately
not sufficient) condition for the
correctness and exactness of each measuring method is
that it must work well on the relevant
phantom ! Only then can other secondary effects in a
given biological situation be considered. Otherwise, it would be
just empiricism , with the possibility of
erroneous results ....
Types of phantoms
Phantoms in nuclear medicine can basically be divided into three
groups: a) static phantoms of specific organs; b)
phantoms for calibration and measurement of physical
parameters of imaging devices (gamma camera, X-ray CT); c) dynamic
phantoms .
2.
Phantoms of organs
These phantoms mimic some typical
anatomical shapes and distributions of a radioinducer in a given
organ, in a physiological or pathological situation. The best
known is the phantom of the thyroid gland ,
which is a vessel in the shape of a thyroid gland containing
protrusions and depressions inside simulating cold and hot
nodules. The vessel is filled with a solution of the appropriate
radionuclide ( 99m Tc or 131 L) and imaged with a scintillation camera. We then
assess how faithfully the individual details of the inhomogeneity
of the radioindicator distribution in the phantom are captured in
the scintigraphic image. At the same time, we try to achieve such
conditions (camera settings, collimator, image matrix,
accumulated number of pulses, image modulation) that the
recognizability of even small lesions is as good as possible.
 |
 |
 |
Fig.2.1.
Phantom of the thyroid gland |
Phantom of the thyroid
gland
(thyroid Picker phantom) |
Scintigraphic image of a
thyroid phantom filled with
99m Tc
solution using a gamma camera |
The same phantom
displayed using a
motion scintigraph |
|
 |
| Fig.2.2. Scintigraphic image of the
thyroid phantom accumulated with different preselection
of the number of pulses - with different number of gamma
photons |
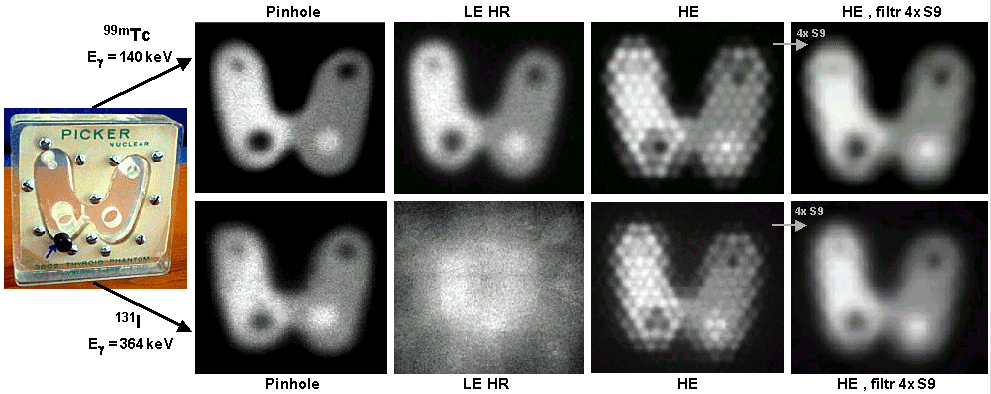
Fig.2.3. Scintigraphic images of a thyroid
phantom filled with 99m Tc ( top ) and 131 I ( bottom ), imaged using a Pinhole
collimator , Low Energy HR and High Energy . A more detailed discussion is in §4.2, section " Scintigraphic collimators ".
Phantoms of other organs - liver, brain, heart
are based on a similar principle ... An interesting option are tomographic
phantoms in the form of anatomical inserts imitating
brain or heart structures, which are inserted into tomographic
test phantoms of the Jasczak type (see
" Tomographic phantoms "
below) in place of the original test rods
and beads.
3.
Phantoms for Gamma Camera Testing
Nuclear medicine, as a field of
measurement and imaging, cannot do without control and
calibration methods and aids. The category of phantoms in nuclear
medicine also includes aids and radiation sources used for calibration
and testing of imaging properties of
scintillation cameras. Parameters quantifying the imaging
properties of scintillation cameras are defined and discussed in
Chapter 4 " Radionuclide scintigraphy ", §4.5
" Physical parameters of scintigraphy - quality control and
phantom scintigraphic measurements
" of the book " Nuclear physics and ionizing
radiation physics ".
The simplest "phantom" a point source
(emitter) of a suitable radionuclide (most often 99m Tc, or 57 Co, 131 I, 18 F), which is placed
in the appropriate place of the camera's field of view; when
placed at a sufficient distance from the gamma camera crystal
without a collimator, it functions as a source of homogeneous
radiation. They also use various other geometric structures -
tubes, balls, cylinders filled with radionuclides. Important test
phantoms are planar homogeneous sources - see below .
3.1. Testing and calibration of
scintillation camera image homogeneity
The physical-technical parameter
of camera image homogeneity is defined and
discussed in more detail in §4.5 " Physical
parameters of scintigraphy - image quality and phantom
measurements " in the section " Homogeneity (uniformity)
of camera field of view
". Two methods are used to test and calibrate the
homogeneity of the gamma camera :
1. Internal
homogeneity - point source
To test the internal ( intrinsic ) homogeneity
of the camera's field of view and its calibration, remove the
collimator and point source from the camera (in practice it can be solution 99mTc with an activity of several MBq of small volume in a
bottle or small syringe) is placed as far
as possible (approx. 2 meters) in the middle under the camera *) - Fig.3.1.1 left. The
camera crystal is thus irradiated practically homogeneously
from this gamma radiation source , so that the resulting
scintigraphic image should also be homogeneous. In the image, we
can then assess (or quantitatively evaluate) any deviations from
the homogeneous distribution. In case the homogeneity of the
field of view is not satisfactory, in this arrangement we can calibrate
the homogeneity of the scintillation camera display
(tuning of photomultipliers and creation of a correction matrix),
for which modern digital cameras have the appropriate software
procedure.
*) The distance of the point source from the camera
crystal - Geometric correction
Intensity I g
-radiation activity from a point source A
at a distance r is given by the general relationship I (r)
= G . A / 4 p r 2 , where the coefficient G indicates the
number of gamma quanta emitted by the radionuclide during one
radioactive transformation. Therefore, if we place the point
source at a distance h from the center of the
scintillation crystal of the gamma camera (which we choose as the
beginning of the planar coordinate system [x, y]), the crystal
will be irradiated with intensity I (x, y) at each of its
coordinates coordinates (x, y). = G . A / [4 p ( h2 + x 2 + y 2 )] (follows from the
trigonometric analysis of the distances between the emitter and
the x, y sites of the crystal) . The places
of the crystal farther from the center will therefore be
irradiated a little weaker than the central
part. If the distance h is many times greater than the
dimensions of the crystal, this effect is practically negligible
- the crystal is irradiated almost homogeneously
(as mentioned above) .
However, at smaller distances h of the
point source, for accurate measurement and calibration of
homogeneity it is necessary to make a correction
in the obtained image by the coefficients K (x, y) = ( h 2 + x 2 + y2 ) / h 2 . This is used with some SPECT cameras when calibrating
homogeneity using a point source, inserted between both detectors
only about 80 cm apart.
Note: Using a point source, we can also
measure the overall resolution of a camera with
a collimator: we draw a section (profile) of the
image of the point source and evaluate its half-width FWHM on the
resulting PSF curve, which is expressed in millimeters. However,
a line source is more suitable for this purpose - see below
" Measuring the positional resolution of the camera ".
 |
Fig.3.1.1.
Two basic ways of measuring the homogeneity of the field
of view of a gamma camera. |
| Testing and calibration
of the internal homogeneity of the field of view of a
scintillation camera without a collimator using a point
source located at a sufficiently large distance. |
Measurement of the
overall homogeneity of a scintillation camera with a
collimator using a flat homogeneous source. |
Double-sided area
homogeneous source 57 Co for testing the homogeneity of a 2-detector
SPECT camera |
2. Total homogenity -
planar source
To control and test the overall ( extrinsic
) homogeneity of the field of view of the
scintillation camera with collimator , planar
homogeneous sources with radionuclide cobalt 57
Co (T 1/2
= 272 days; emits gamma radiation with
energy 122keV) are often
used . , close to 140keV 99m
Tc) , which have the same radionuclide
distribution density over their entire area (surface
homogeneity should be better than 99%, total activity is 200-400
MBq)
- fig.3.1.1 in the middle. The dimensions of the source
must ensure full coverage of the field of view of the gamma
camera (the dimensions of the source should
be at least 2 cm larger than the field of view) . With this source we can quickly and
operatively check the homogeneity of the camera's field
of view with the collimator. The advantage is that we do not have
to take off the collimator and we get a picture of the overall
(resulting) homogeneity, on which we can also recognize a
possible defect of the collimator - mechanical
deformation in the septa. Only when the homogeneity is
unsatisfactory will we recalibrate the camera's photomultipliers
using a 99m
Tc
point source as mentioned above.
Flat cobalt <- versus -> " box
" homogeneous sources
Previously used "box" homogeneous sources
filled with an aqueous solution of 99m Tc are now
rarely used in larger workplaces. Their disadvantages were
considerable laboriousness in filling them, risk
of contamination, higher radiation load during preparation,
difficult mixing of the solution to be truly homogeneous and the
possibility of inhomogeneous absorption of radionuclide on the
phantom walls, which can disrupt homogeneity - in other words
" for a lot of money (effort)
little music "..! .. The
disadvantage of cobalt 57 Co homogeneous sources is the relatively higher
purchase price - with a larger number of scintigraphic
examinations, however, they form only a small fraction of the
price for radiopharmaceuticals ... If the workplace does not have
a flat cobalt source, we recommenduse only method 1. with a point source 99m Tc (removing the collimator is
much easier than filling the "box" source with a
radionuclide solution) .
 |
Fig.3.1.2. Some typical
images of the homogeneity of the field of view of a
camera with a surface source or a point emitter (after application of a correction matrix)
.
a) Normal image of homogeneity. b)
Peripheral photomultiplier failure.
c) Totally detuned photomultipliers or photopeak
set outside the analyzer window. d)
Cracked scintillation crystal.
It is discussed in more detail in §4.2,
section " Technical failures of
scintillation cameras
" |
Double-sided homogeneous sources
Previously manufactured (until the
end of the 1990s) flat homogeneous sources 57 What were one-sided
: the exact homogeneity of the radiation field was guaranteed
only from one - "front-front" wall, from the opposite
"back" side the homogeneity was only approximate.
Therefore, when measuring homogeneity in dual-head SPECT cameras,
it was necessary to perform the acquisition for each detector
separately. Nowadays, double-sided flat
homogeneous sources are produced , which can be inserted between
the heads of the SPECT camera and measure the homogeneity of both
detectors at the same time - Fig.3.1.1
on the right.
Radionuclide purity of homogeneous sources?
First homogeneous area sources 57Co, which began to be produced in the late 1970s,
sometimes contained radionuclide impurities 56 Co (t 1/2 71 days, E g 511, 847, 1038, 1238, 1771, 2598, 3253 keV) and 58 Co (t 1/2 79 days , E g 511, 811 keV) , which could cause
artificial image inhomogeneities due to the emission of higher
gamma energies. There was even a recommendation not to use
"fresh" sources, but only by the age of about 6-8
months from their acquisition (due to
shorter half-lives than 272 days 57 Co, the content of radionuclide impurities will be
significantly reduced) .
Now all this is pointless,
as newer sources have a high radionuclide purity
directly from production (max. content of
radionuclide impurities <0.1-0.2%) .
Note .: If we in
the spectrometric measurements of cobalt-57 in addition to the
basic power 122 + 136keV found higher 692keV gamma peak, not a
radionuclide impurities but the actual legitimate gamma peak of
radiouklidu - see spectrum measured 57 Co .
Inhomogeneity
correction
By measuring the image of a homogeneous source, a matrix
of correction coefficients g ij can be created in a computer , which multiplies the
uncorrected values ??of scintigraphic images a ij in individual pixels
(i, j), thus creating a corrected image a *ij :
 |
Fig.3.1.3. Computer correction of
gamma camera image inhomogeneity.
Left: The uncorrected image and
ij homogeneous source,
having considerable inhomogeneity.
Middle: Matrix of correction
coefficients g ij .
Right: Multiplying by
correction factors produces a corrected image * a ij that is already
homogeneous.
Note: Instead
of the usual luminance modulation , an isometric
display is used here , where the height of the
elements (pixels) above the base is proportional to the
number of pulses contained. The curves at the top are cross-sections
, taken through the center of the images. |
Virtually all disturbances and anomalies in the
imaging properties of the camera are most sensitive
to the homogeneity of the field of view. Therefore, regular
homogeneity testing is required to ensure quality
scintigraphic imaging . Testing time intervals are recommended at
least once a week, with impaired stability of the camera's
electronic circuits every day (individual
camera types have their own recommended testing intervals) . And of course after every electronic intervention in
the circuits of photomultipliers, amplifiers and ADCs. In the
case of impaired homogeneity, it is necessary to adjust or
recalibrate the photomultipliers (tuning) and create a new correction matrix, in the case of gross
abnormalities, electronic intervention or repair.
How the homogeneity of the camera is quantified,
calibrated and corrected is given in
§4.5 " Physical parameters of scintigraphy ",
section " Homogeneity
(uniformity) of the camera's field of view ". Dependence
of the field homogeneity on the physical conditions
The
homogeneity of the gamma camera display depends (in addition to the mechanical, detection, optical and
electronic properties of the device) also
on a number of physical conditions and setting
parameters . Hence the principles that must be followed when
performing correct phantom measurements to correct homogeneity.
We will illustrate them on scintigraphic images of experimental
measurements:
Note:
In brightness modulated images, very sharp
brightness modulation is used to emphasize subtle
differences - - LT 80%, UT 95%. The differences in
homogeneity are in fact much milder ...
- Statistics - number of pulses in
the image
If a sufficient number of accumulated pulses in the image
(information density) is not achieved, statistical
fluctuations can also manifest as inhomogeneity . Of
course, these disturbing statistical fluctuations also affect the
homogeneity correction matrix if it is accumulated with an
insufficient number of pulses. It can be seen in the figure that
an insufficient number of correction matrix pulses (eg 200
imp./pixel) can very adversely affect the static scattering of
the corrected image and thus impair the recognizability of the
lesions. The correction matrix should therefore be recorded with
as many pulses as possible, min. 1000, optimally 5000 imp./pixel
:

Fig.3.1.4 Influence of statistical fluctuations of the correction
homogeneity matrix on the correction result. The image of a
homogeneous 99m Tc source with an HR collimator (uncorrected on the
left) is gradually corrected by matrices stacked with different
numbers of pulses / pixels - information densities ID.
- Used collimator
Classic collimators with parallel holes HR, HS,
HE (properties of different types of
collimator are described in §4.2, section " Scintigraphic
collimators ") , if they do not have a mechanical defect, they do not
in principle affect the homogeneity of gamma
camera display. For divergent / convergent collimators
the homogeneity is already somewhat different, for Pinhole
they differ significantly; however, the correction of this
difference is usually not performed. Just make a correction for
the internal inhomogeneity of the detector .

Fig.3.1.5. Influence of collimator on homogeneity. In the upper
half there are uncorrected images of the homogeneous source 99m Tc obtained with
different collimators, in the lower half these images are
corrected by the matrix for the collimator HR.
- Frequency of pulses during camera image acquisition
The dependence of the camera image homogeneity
on the frequency of registered pulses is relatively small. A more
significant effect begins to manifest itself at a registered
frequency higher than about 30,000 imp./sec. And with a very high
flux of gamma photons (high activity of the
measured object, order GBq) incident on the
camera crystal, the camera detector and its electronic circuits
are flooded , there is a shift, an increase in dead
time . When recording the correction matrix, the
activity of the source used should be such that the pulse
frequency does not exceed about 10,000 cps.
 |
Fig.3.1.6. Influence
of pulse frequency on homogeneity.
In the upper half, there are uncorrected images of a
homogeneous 99m Tc source obtained at different frequencies of
registered pulses, given the activity of the source.
In the lower half, these images are corrected by a low
frequency matrix (1000 cps). |
- Gamma radiation energy of the used radionuclide
Scintillation in the crystal, registration of the photomultiplier
and positional coding of the generated pulses depend on the
energy of gamma photons. It can be seen from the images in our
experimental measurements that the homogeneity of the field of
view depends on the gamma energy, so it is generally recommended
to correct each scintigraphic image with a matrix obtained for
the same gamma radiation energy. However, small differences in
energies do not have a significant effect on homogeneity, so for
example images with technetium 99m Tc or gallium 67 Ga can be corrected by a matrix for cobalt 57 Co - which is
commonly done (as mentioned above) .
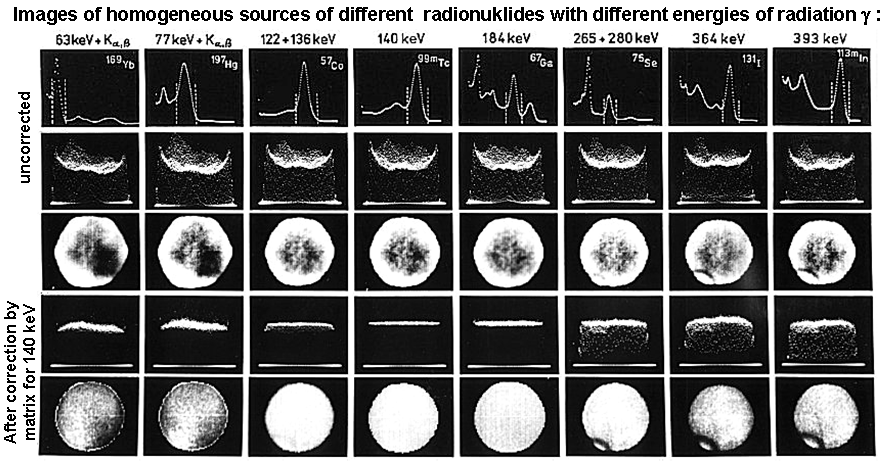
Fig.3.1.7. Influence of gamma radiation energy on the homogeneity
of the camera's field of view. In the upper part there are
uncorrected images of homogeneous sources of different
radionuclides with different energies of emitted gamma radiation.
Below, these images are corrected by a matrix for 140 keV
technetium 99m Tc.
The spectrometric "detuning" of
one of the peripheral photomultipliers can be seen at the bottom
left of the field of view.
- Spectrometric adjustment of the
analyzer window to the photopeak -
its width and symmetry
The adjustment of the analyzer window affects not only the
detection efficiency and the proportion of Compton scattered
radiation, but also the homogeneity of the image. With the window
set asymmetrically to the total photopeak, a slightly different
part of the local photopeak can be detected or cut off for
individual photomultipliers , which leads to local
differences in detection efficiency - image inhomogeneity
. However, small differences in the spectrometric setting (up to
5%) do not have a significant effect on the homogeneity and the
correction result.

Fig.3.1.8. Influence the homogeneity of the camera's field of
view by setting the analyzer window. In the upper part there are
uncorrected images of a homogeneous 99m Tc source with different window settings (width 20%) on
the photo peak. Below, these images are corrected by a matrix for
symmetrical window adjustment to 140 keV technetium 99m Tc.
- Time factor - instrument instabilities
The homogeneity of the gamma camera can also change over
time due to instabilities in the detector and electronic
circuits. The correction matrices must therefore be checked from
time to time and renewed if necessary (disagreement).

Fig.3.1.9. Example of measuring time stability and changes in the
homogeneity of the camera's field of view. The image of the
homogeneous source 99m Tc is gradually corrected by a "differently
old" matrix - at different times between the creation of the
correction matrix and the acquisition of the image for
correction.
The instability of one of the peripheral
photomultipliers can be seen at the bottom left of the field of
view.
Technical Note:
Physical measurements of homogeneous sources and correction
matrices from which the above images are derived were performed
in 1975-78 (as part of the research report " Computer
Data Processing in Nuclear Medicine ") on a
PhoGamma HP Nuclear Chicagogamma camera from 1973.
(picture .... left). The pictures show a certain detuning and
instability of some photomultipliers (especially the peripheral
photomultiplier at the bottom left) for a specific
"piece" of the camera.
The details of the design and electronic circuits have since
undergone considerable technical development. However, the basic
physical and technical principles still apply.
3.2. Measurement of the spatial resolution
of the gamma camera
The physical-technical parameter spatial
resolution of the camera is defined and discussed in
more detail in §4.5 " Physical
parameters of scintigraphy - image quality and phantom
measurements " of the passage " Spatial resolution ", here we present only the basic picture :

Fig.4.5.1 Spatial
scintigraphic resolution - analysis of point source images that
appear as "blurred" scattering circles.
More detailed discussion in §4.5, passage
" Spatial
resolution ".
To test the positional resolution of a gamma camera and the
linearity of the image (see below "Analysis of
linearity imaging") is used to either point and a line
source, or so Bar-phantoms .
For practical determination of resolution
is preferable to use a line source. Compared
spot has a line source is preferably that the image may lead
independently multiple profiles, respectively. These profiles add
- lead a wider section-profile (about 5-10 pixels), which gives a
summed LSF curve with smaller statistical fluctuations
(Fig.3.2.1).
The line source is used for quantitative physical
measurement of the positional resolution of the camera .
be larger than approx. 0.5-1 mm *), which we fill with a
radionuclide solution (most often 99m Tc) and display using a camera with a
collimator. We then draw sections - profiles -
through the image of the line source and on these LSF
( Line Spread Function ) curves we determine the width
at half height - FWHM , which expressed in
millimeters indicates the total positional resolution of the
camera for a given distance from the collimator front -
Fig.3.2.1.
*) If the test point or line source fails
to make a sufficiently small (thin), a quadratic
correction is required for objective evaluation of the
spatial resolution :
FWHM = [FWHM m 2 - D 2
] 1/2 ,
where FWHM m is the measured (uncorrected) half-width, D is the
diameter or thickness of the point or line source, and FWHM is
the resulting actual (corrected) resolution.
For detailed
physical analysis, the so-called modulation transfer
function of the MTF camera can be calculated from the
profile curve of the line source , which gives the contrast of
the model cosine distribution of radioactivity depending on the
spatial frequency - see " Modulation
transfer functions " in the chapter " Mathematical algorithms
of scintigraphy " .
 |
 |
 |
Fig.3.2.1
Measurement of spatial resolution by a line source |
We keep a suitable profile (section) by painting the line
source |
The half-width D 1/2 of the
profile curve of the line
source indicates the positional resolution FWHM |
The modulation transfer
function can be calculated from the profile curve of the
line source |
For precise measurement of the positional
resolution of gamma cameras (in planar mode), it is suitable to
incorporate the line source into the following simple phantom
: we attach our own thin capillary in the middle
to a plexiglass plate, in which two small holes with a
diameter of about 1 mm are excavated at the sides at a distance
of 10 cm . Using a syringe with a thin needle, inject a column of
radionuclide solution into the capillary, eg 99m Tc - this is the line
source itself . We drip the same solution into the
excavated wells in the same way - two point sources
are createdat a precisely known distance, to determine the scale
of the display. We place the phantom in the field of view of the
camera equipped with the required collimator and take
scintigraphic images at different distances. When evaluating, we
keep transverse profiles (sections) of the image
in the places of point sources - from the distances of the pixels
of their maxima we determine the scale of the display
, by which we multiply the horizontal coordinates in the graphs
of profiles. From the profile via the image of the line source - LSF
- we then determine the spatial resolution of the FWHM
(or the MTF modulation
transfer function ) :
 |
Fig.3.2.2. One way to accurately
measure the spatial resolution of a gamma camera.
Left: A simple phantom with a
line source (capillary) and two point sources for
measuring the positional resolution of a gamma camera.
Middle, right: The measurement
was performed with a charge of 99m
Tc at distances of 0, 5, 10, 15 and 20 centimeters from
the front of the collimator of the HR camera Nucline TH.
The degradation of FWHM resolution with distance can be
seen in the images and profile curves. |
Transmission so-called bar-phantoms are used
for a simple visual assessment of the resolution
(and possibly also linearity) of the camera. The bar-phantom consists of a
plastic plate with a system of sealed lead absorbent
strips of various widths. There are gaps between the
lead strips (the width of the gaps and
strips is the same) ; under the camera, the
bar-phantom is placed over a semi-homogeneous source. The lead
strips then absorb radiation from a homogeneous source, while
gamma radiation passes freely through the gaps to the camera
collimator. In the scintigraphic image, we observe which width of
the strips is still distinguishable - the actual positional
resolution is then approximately given by 1.75 times the
narrowest still resolved stripe):
 |
 |
 |
Fig.3.2.3.
Gamma camera resolution testing using bar-phantom. |
Transmission bar-phantom
with stripes
in 4 segments |
An image of a bar-phantom
with stripes in
4 segments |
An image of a bar-phantom
with horizontal stripes of different widths. |
3.3. Gamma Camera Display Linearity Analysis
Linear line sources are used to analyze the linearity of
the image or image distortion (as well as
the resolution - see below) . Deviations
from the linear shape can be assessed on the image of
such a line source (§4.5 " Physical
parameters of scintigraphy ", passage " Linearity of the camera's field of
view ") .
We display line sources in different places of the camera's field
of view and also in different angles, especially in two mutually
perpendicular directions. In principle, the above-mentioned bar
phantoms can also be used to evaluate linearity . However,
the most perfect phantom for analyzing the linearity of
scintillation camera imaging is Cartesian linear
grid . It consists of a regular network of parallel and
perpendicular thin tubes (hoses with a diameter of about 1 mm),
placed at equidistant distances (eg 2 cm). The tubes are filled
with a solution of the appropriate radionuclide, usually 99m Tc, with a suitable
activity (total approx. 100MBq).

Fig.3.3.1 Cartesian linear lattice filled with 99m Tc radionuclide
solution .
The phantom is placed in the field of view of
the camera, the basic measurement is close to the front of the
collimator. For different types of collimator (especially for
convergent or Pinhole), the display is also performed at different
distances to evaluate the effect of distance on the
display scale and on the linearity or distortion of the image:

Fig.3.3.2 Scintigraphic images of a linear rectangular grid with
different types of collimators, taken at different distances.
In a collimator with parallel
holes (such as LE HR, left) we get a linear
representation of the grid everywhere , while for greater
distances from the front of the collimator, the spatial
resolution deteriorates (blurred grid). With a convergent
collimator (such as a SmartZoom with a convergent center
portion), the image of the center portion increases
with increasing distance . With the Fan Beam
collimator (which is convergent in the transverse direction,
parallel in the axial direction), the grids increase only
in the transverse direction with increasing eye distance
, they remain the same in the axial direction .
The Pinhole collimator shows the most
significant dependence on the object distance : we get the image
many times close to the foreheadmagnified , with
increasing distance the zoom decreases and for distances above
about 20cm the image is already reduced . The
pictures also show a general trend of deteriorating resolution
(and thus contrast in the image) with the distance from the front
of the collimator.
If the lattice
phantom is precisely executed and the inner diameter of the tubes
does not exceed 1 mm, it can be advantageously used to measure local
spatial resolution in different places of the field: at
the desired location of the image height to peak (FWHM), which is
the resolution at a given location. Possibly. the regional modulation
transfer function MTF for a given image location can also be
calculated .
Note:
We assembled the first such linear grid at our
nuclear medicine office in Ostrava-Poruba in 1975. It consisted
of a long thin plastic tube with an inner
diameter of 1 mm, which was intertwined with equidistant
grooves (in two perpendicular directions), cut in a
polystyrene board. Using a syringe, it was filled
with a solution of the desired radionuclide, especially 99m Tc. It had
dimensions of 30 ´ 30cm and was used for Pho Gamma 3, HP cameras
with parallel collimators, Pinhole convergent and divergent,
Slant Hole, and then for MB9100,9102 cameras . The
current phantom (in Figure 3.3.1) is made with the same
technology, but has larger dimensions - 52 times46cm to cover the field
of view of current SPECT cameras .
3.4. Tomographic phantoms for SPECT, PET, CT
For physical analysis of basic imaging
properties of tomographic cameras, point or
linear sources can be used, similar to planar scintigraphy.
Special cylindrical phantoms , mostly of the Jasczak
or Venstra type, are used for visual
assessment and testing of tomographic imaging properties of SPECT
and PET cameras in clinical scintigraphy . These are
Plexiglas cylinders, which are filled with a solution of the
appropriate radionuclide (for SPECT mostly 99m Tc, for PET 18 F) . Inside they contain a systemrods and beads of
various sizes, where the radioactivity does not get and which
therefore simulate " cold lesions
" - Fig.3.4.1 above. Another variant is refillable
containers , into which we can inject a solution of a
radioindicator with a suitable specific activity to simulate
" hot lesions " and their
quantification ( SUV , see below) .
Phantom Jasczak folded (top)
and unfolded (bottom) |
 |
 |
Tomographic SPECT images of the upper and lower parts
of the Jasczak phantom |
| |
 |
68 Ge / 68 Ga cylindrical phantom as
a source of annihilation gamma radiation 511keV for
testing and calibration of PET cameras |
| Fig.3.4.1
Two types of tomographic phantoms for SPECT and PET |
We perform a tomographic acquisition
and on the images of cross sections, after reconstruction, then
we monitor the resolution of the lesions
depending on the size. We can test the influence of various
aspects of acquisition (number of
accumulated impulses, number of projections, distances,
displacements of the center of rotation, etc.) and evaluation (reconstruction
algorithm - rear projection or iterative reconstruction, used
filters) on lesion resolution or artefacts.
Phantoms with refillable lesions can also be used to calibrate
the SUV parameter (described
in §4.2, section " Scintigraphic image quality and
detectability of lesions
"), especially for PET imaging. In
addition, at the end of the phantom, there is still free space
filled with a homogeneous distribution of the radionuclide, which
is used to test tomographic homogeneity . As
already mentioned above, special anatomical inserts
imitating the structures of the brain, heart, liver, kidneys and
the like can also be placed in the space of the cylindrical
phantom .
In addition to phantoms operatively
filled at the workplace with a solution of radionuclides (mostly short-term - 99m Tc, 18 F) , solid
(closed) phantoms containing suitably distributed long- lived radionuclides are also used
for gamma camera testing . Most often they are planar
homogeneous sources with a radionuclide57 Co (their
use was described above in the section "
Testing and calibration of scintillation camera image homogeneity "). Closed so-calledgermanium
phantoms, emitting annihilation gamma radiation of 511
kV,are often used for calibration and testing of PET cameras.
They are filled with the parent radionuclide
68 Ge , which with a half-life of 271 days is converted by
electron capture to the short-termpositronradionuclide
gallium 68
Ga . The source of 511 kV
annihilation radiation, detected by a PET camera, is daughter
gallium-68(formed by the interaction of
positrons emitted by68Ga with the electrons of the material), maternal germanium does not participate in radiation.
Point and line sources (mostly also
germanium) are rarely used . The positron
radionuclide 22
Na with a half-life of 2.6
years can also be used for PET phantoms (however,
a certain disadvantage here is the high proportion of hard gamma
radiation 1274keV) .
Simple improvised phantom for measuring the
imaging properties of SPECT and PET cameras
For measuring the basic imaging properties of PET cameras - resolution,
detection sensitivity, astigmatism - I made a very
simple " phantom " -
Fig.3.4.2. From a 5 cm thick polystyrene foam board for door
insulation, I cut a rectangle 20 x 70 cm at the cottage at the
weekend , to which I glued small plastic conical cuvettes
*) to the center r = 0 and at distances of 10,
20, 30 and 34 cm . At the KNM workplace, I then injected
small droplets of fluoride radionuclide solution
18 F onto the conical bottom of the
cuvettes using a micropipette about exactly the same activities (for a specific measurement in the picture it was
1.85MBq) - this created radially
distributed point sources . I then placed this
"phantom" exactly symmetrically inside the detection
ring of the PET camera.
*) This "primitive" solution was
forced by the circumstances: During the general reconstruction of
our workplace in 2011, we lost a relatively well-equipped
electronic and mechanical workshop with all devices, mechanical
tools (lathe, vertical drill, scissors, ...) and tools. .
Therefore, the mechanically perfect design was already difficult
for me to access. However, even this simple solution was completely
satisfactory from a functional point of view ...

Fig.3.4.2
A simple improvised phantom for measuring the imaging
properties of PET and SPECT cameras.
After the acquisition (10 min.), a PET image of
these point sources was created , on which we evaluated the spatial
resolution and detection efficiency
depending on the position r in the PET detection
ring using ROI and profiles -
cf. §4.3, part " Positron emission tomography of PET ", passage " Spatial resolution
of PET ". The effect of
radial " astigmatism " of PET imaging for
greater distances from the center of the PET ring was also well
seen there (it is discussed in the
mentioned passage "Spatial resolution
of PET" in §4.3) and also a slight decrease in the detection efficiency
towards the peripheral areas.
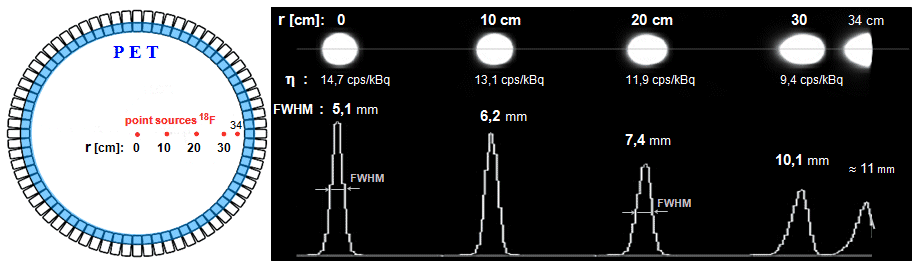 |
Fig.3.4.3 PET images of point sources 18 F located at different
distances r from the center of
the detection ring. By analyzing the ROI and profile
curves with these images, the values ??of detection
efficiency h
and spatial resolution FWHM were
measured (we measured on a GE
Discovery PET camera at KNM FN Ostrava) .
At the last peripheral point source at a
distance of r = 34 cm, part of its image was already cut
off by the edge of the field of view. |
For comparison, we placed a similar
phantom (0-20cm, according to the typical
dimensions of SPECT, eg chest) , with point sources filled
with 99m
Tc , between the circulating SPECT
cameras . In the reconstructed cross-sectional tomographic image,
we guided the profiles through point source
images in an analogous manner and determined the spatial
resolution and detection efficiency for
individual distances r from the center of
rotation :

Fig.3.4.4
SPECT images of 99m Tc point
sources located at different distances r
from the gantry center.
The worse spatial resolution of SPECT imaging is due to
the relatively large distance from the front of the
collimator (22 cm) - it is typical for SPECT chest; in SPECT
brain (distance of lesions from collimators
approx. 10 cm) the resolution is approx.
9-10 mm. Overall, a somewhat better resolution for PET
is given by electronic collimation
(§4.3, passage " Spatial resolution
of PET ") . This is also the reason for the many times better
detection efficiency (sensitivity) of PET
.
Testing and correction of the center of
rotation SPECT cameras
When tomographic SPECT scintigraphy orbiting
detectors, cameras weighing hundreds of kilos around the object
to be examined. If the bearings and arms
in which the detectors are mounted in the gantry show mechanical
play , gravity forces cause the detectors to swing and
shift, so that the rotation does not occur exactly around a fixed
axis - the center of rotation ( COR
) moves . These unwanted
mechanical shifts and fluctuations degrade the quality of the
reconstructed tomographic images (and could
possibly lead to artifacts). For basic
testing of the center of rotation, we place a point source in the
field of view of the camera and start its SPECT scintigraphy. The
relevant program then evaluates the deviations of the
resulting pattern from the circular motion and determines the displacements
of the axis of rotation depending on the instantaneous
angle of the detector. Another place with the risk of unwanted
mechanical movements of the camera detectors during rotation are
their own bearings on which the detectors are mounted. To test
these events. axial fluctuationsa single point
source is not enough - several (eg 3-5) point sources distributed
in specified places of the field of view are used. Appropriate
sensing and correction are done using special acquisition
software for modern SPECT cameras. For cameras with two or more
detectors ("heads"), a more complex measuring procedure
is used, called MHR (Multiple Head
Registration) , where concurrency is also
measured and calibrated - matching the position of images from
individual detectors (cf. the section
" Geometric
matching of CT images
" below) with SPECT and PET images ") ; a larger number of
point sources is used here, approx. 10.
Based on the above measurements, the appropriate correction
coefficients are stored for each angle of rotation. ,
which, when acquiring patient studies, perform appropriate image shifts
in the X and Y directions so that deviations from the center of
rotation and axial oscillations of the detectors are eliminated
.
Note: In
PET positron emission tomography with stationary
detection rings without mechanical movements, of course, this
unfavorable effect does not exist and
corrections of the center of rotation and MHR are not
performed .
Tomographic phantoms for CT
In addition to testing and calibrating the scintigraphic part (as
described above), the SPECT / CT and PET / CT hybrid systems also
measure and test the imaging properties of the CT part
- homogeneity, image contrast, positional resolution, noise.
Basic measurements for daily check of the correct function of the
X-ray machine and opposite detectors (" check-up
") are performed without a phantom - "
through the air ". Further
measurements and testing of specific CT imaging properties are
then performed using cylindrical water and plate phantoms
(there are several types recommended for
different types of CT devices) . These
phantoms contain a part homogeneously filled with water,
in the next part there are suitable absorbent structures
- plastic rollers and strips of various sizes, or metal wires (approx. 0.1 mm tungsten) -
fig.3.4.5. Phantoms are inserted between the X-ray machine and
the detectors into the center of the CT, transmitted by
transmission, the transverse sections reconstructed, and the
densities of the individual parts are displayed and quantified
using Hounsfield units .
The homogeneity and
noise test is performed using a basic part of a
cylindrical phantom filled only with water. Positional resolution
and contract CT images are measured on images of
absorption rollers and strips (different distances) located in
other parts of the phantom, respectively. using LSF and MTF from
wire images. The new CT devices have special programs for
evaluating the image quality.
 |
Fig.3.4.5
Example of two types of tomographic phantoms for testing
CT imaging properties. |
Geometric alignment of CT images with SPECT
and PET images
When merging functional scintigraphic SPECT or
PET images with anatomical CT images, it is important that the
structures shown in both modalities are geometrically
overlapped - displayed in the same image location (image
fusion,
hybrid tomographic systems ). For the
process of this geometric alignment of images, the not very apt
name of registration or normalization
of images is sometimes used ... Scinticraphic +
is used for this calibration of
precise alignment of the positional concurrency of the
displayed SPECT <--> CT or PET <--> CT structures on
hybrid instruments . CT imaging of point sources
filled with mixtures of radionuclide ( 99m Tc or 18 F) and contrast
agent . The radioactive substance in these samples is
"seen" by the SPECT or PET gamma camera, the contrast
agent is "seen" by CT. In the simplest case, it
improvises 2ml. syringes, optimally placed in special cuvettes
filled with about 0.1-0.2 ml. a radiolabelter solution mixed with
a contrast agent. Several (usually 5-10) such point sources are used, regularly distributed in
the field of view of the device - they are inserted into the
holes of a simple plate phantom.
This system of point sources,
containing both radionuclide and contrast agent, is
simultaneously - in-line - displays scintigraphically on
a gamma camera (SPECT or PET) and density on CT. The calibration
program uses cross-correlation of scintigraphic and CT images to
determine the map of the respective mutual displacements - scale
and affine transformations, so that all point sources on SPECT or
PET and CT images are exactly geometrically covered
. This map is then automatically used for clinical SPECT / CT or
PET / CT image fusions.
4.
Dynamic phantoms
These are phantoms that model
various dynamic processes in the body, such as
heartbeat, blood flow in blood vessels, filtering activity of the
kidneys or liver, lung breathing, swallowing of the esophagus.
Mathematical evaluation of dynamic scintigraphic
studies provides a number of quantitative parameters of
the dynamics of investigated biological processes, whose
actual values a prioriunknown and which may be affected
and distorted by some influences, such as statistical
fluctuations, geometric influences, absorption of radiation in
the tissue, inaccurate definition of areas of interest,
inadequacy of the mathematical model used, individual variability
in patients, etc. For the exact analysis of these influences and
for the development of methods and algorithms for the calculation
of quantitative parameters, the need arose for the most complex
types of phantoms, which are dynamic phantoms. These
phantoms model the temporal dynamics of changes
in the distribution of the radioindicator in the relevant organs
and their parts. The advantage is that the actual values ??of the
parameters of this dynamics are known - they are
provided by the construction of the phantom, or can be precisely set
.
Such a dynamic phantom can be useful in three
stages of research and application work in the field of nuclear
medicine:
- During the development of a
new measuring method, selection and tuning of the correct
mathematical model and algorithm for
evaluating the measured data.
- When calibrating the
measuring method and determining the correct calibration
or regression coefficients when evaluating the measured
data.
- When authentication and
"training" has been developed and used methods.
Here we will briefly describe several dynamic
phantoms that we developed (and constructed
either on our own or with the help of a specialist workshop) at the Department of Nuclear Medicine in Ostrava during
research and development work in the field of
physical-mathematical analysis and computer evaluation of
scintigraphic studies.
Our simplest dynamic phantom was the
phantom of the periodic event realized in 1973 by a rotating
turntable carrying a radioactive source (see below). In 1976,
when developing algorithms for mathematical analysis of
radionuclide ventriculography (including the geometric method of
calculating the absolute volume of the heart chamber), we used
various pulsating balloons connected by a tube to a large-volume
calibrated syringe, the piston of which we moved manually - see
picture:

We then used the experience gained with this simple phantom to
develop our motor-driven flexible dynamic phantom of
cardiac activity, which allows us to model both
ventricular pulsation and central hemodynamics. Finally, we
describe our phantom for modeling the dynamics of the swallowing
act of the esophagus, including reflux and antiperistaltics.
Rotating
phantom of the periodic process
A characteristic feature of
cardiac activity is its periodicity . The model
of the periodic event is a circular motion (oscillating motion is not very suitable here) . Our first dynamic phantom consisted of a gramophone
, on the plate of which point sources were placed - containers
with a 99m Tc solution . A turntable with rotating
point sources was placed in the field of view of the
scintillation camera. This phantom played an important role in
the development of the methodology of scintigraphic scanning and
analysis of fast periodic events - it was at a
time when scintigraphic systems could not yet scan gated studies.
An aperture was attached to the edge of the
turntable interrupting the light beam into the phototransistor -
this simulated the R-wave of the ECG . We
designed electronic circuits (in cooperation with Ing. Dubrok),
which implemented these "R-wave" pulses from the
"ECG" into the scintigraphic data flow and developed
software that reconstructed the data from LIST-mode into
scintigraphic images and constructed a phase dynamic
study of one cycle synchronously composed
of many running cycles of the periodic process. Thus, the
methodology of gated radionuclide ventriculography
was developed on the CLINCOM device and put into practice .
 |
Dynamic scintigraphy of
the phantom of a fast periodic event - 3 point sources of
99m Tc placed on a
turntable rotating at a speed of 78 rpm.
a) Record of the scintigraphic study in
LIST mode; E - gating pulses from the phototransistor
simulating the R-wave RKG.
b, c, d, e) Images reconstructed into
Frame-mode with different time resolution.
f) Definition of the area of ??interest
in the summary picture.
g) Common resource flow curves -
Significant statistical fluctuations are seen.
h) The same curves created by the
synchronous composition of 60 common cycles -
fluctuations significantly reduced. |
Flexible dynamic phantom of cardiac activity for
radionuclide ventriculography and angiocardiography
Dynamic scintigraphy of cardiac
activity analyzes two important aspects :
- Heart rate pulsation dynamics
(motility of individual heart wall segments, ejection
fraction, ventricular volumes, cardiac output, phase
ratios, etc.) - radionuclide ventriculography is used for
this;
- Central hemodynamics of
blood pumping by the heart (transit times, minute cardiac
volume, intracardiac shunts, in co-production with
ventriculography also the regurgitation fraction, etc.) -
bolus radiocardiography is used for this.
During research and development work on
mathematical analysis and computer evaluation of dynamic
scintigraphic studies of radionuclide ventriculography and
radiocardiography, we have developed and in cooperation with the
mechanical workshop of VŽKG Ostrava made a comprehensive
dynamic phantom of cardiac activity - Fig.1. This
phantom can be used both for radionuclide ventriculography, where
it models heart chamber pulsation, and for bolus
angiocardiography, where it models cardiac pumping activity. All
parameters, such as ejection fraction, heart rate volume,
residual volume, end-diastolic volume, ejection and filling
rates, heart rate, minute heart volume, phase shifts of
"gating" pulse transmission, can be continuously changed
and precisely set in a wide range. This phantom
thus enables a very complex analysis and
verification of radionuclide cardiological methods and their
precise calibration .
Phantom drive unit
The basis of the entire phantom is a calibrated working
cylinder (glass), in which the piston
moves . The displacement of the piston is mechanically secured
via a rod (connecting rod) from a disk with an eccentrically
located joint driven via a gearbox by an electric motor -
Fig. 1a. The eccentricity of the joint position on the drive disk
can be precisely adjusted, which defines the stroke of
the piston - pulse volume . The frequency
can also be changed continuously using the motor speed controller
movement of the piston in the cylinder - heart rate
. Phase sync pulses ("ECG gain
pulses") are sensed photoelectrically. A diaphragm
is mounted at a suitable location around the circumference of the
rotating drive disk , which obscures the flow of light from the
bulb as it passes around the phototransistor. The generated
electrical impulses are conducted via a normal cardiomonitor to
the computer - they simulate the R-wave of the ECG
. The diaphragm can be freely moved around the circumference of
the drive disk and thus change and precisely set the phase
of the periodic process in which the gating pulses will
be transmitted - it can be used, among other things, for Fourier
phase-amplitude analysis . The entire working cylinder is
located on the support, by the displacement of
which any residual volume can be set
continuously, regardless of the size of the piston stroke.
The described phantom of cardiac activity can
work in two basic modes :
- Pulsing balloon mode with
closed system (Fig.2).
- Flow piston pump mode
(Fig.4).
The drive unit and the control part of the
phantom, including the working cylinder, are common to both
modes.
 |
 |
Fig.1a. Detail of the drive part of
the phantom with a drive disk and a scale for adjusting
the stroke volume and with an aperture and a
photoresistor emitting synchronization pulses.
|
Fig.1b. A general view of the phantom
in a mode modeling the pumping activity of the heart.
|
Phantom of
the pulsating heart chamber
To model the pulsation of the heart chamber
during gated ventriculography (§4.9.4
" Radionuclide gated ventriculography ") , the phantom works in
the arrangement according to Fig.2. In this mode, the phantom is
suitable for testing the calculation of ejection fraction
, cardiac volume, ejection and filling rates, time intervals of
significant cycle phases, Fourier phase-amplitude pulsation
analysis, verification and calibration of methods for calculating
absolute ventricular volume, some aspects of background and
correction on tissue background.
 |
| Fig.2. Dynamic phantom of
heart activity in pulsating balloon mode. In this
variant, the phantom is used to model the pulsating heart
chamber during radionuclide ventriculography. |
A rubber balloon is placed in the field of view
of the camera, which is connected by a hose to the working
cylinder of the phantom. The closed system (working cylinder -
balloon) is filled with an appropriate amount of radioactive
solution of 99m Tc of equilibrium concentration, the volume and
activity of which can be easily changed via the filling valve.
The motor-driven oscillating movement of the piston to the left
and right leads to the periodic filling and emptying of the
radioactive jaw from the balloon - the balloon thus pulsates
similarly to the heart chamber. By changing the stroke volume of
the piston, its speed of movement and the initial position, it is
possible to easily and accurately set any value of ejection
fraction, heart rate and residual volume, heart rate, and thus
minute heart volume (here imaginary). The geometric configuration
also results in the value of the maximum and average ejection and
filling speed.
The balloon pulsates in the aquarium below the level of the
radioactive solution, which represents the absorbing tissue and
the tissue background. The depth of the balloon placement and the
specific activity of the background solution can be easily
changed.
The thus pulsating balloon is
scanned by a scintillation camera, and with the help of gating
pulses emitted by the diaphragm and the phototransistor, a phase
dynamic study of one cycle is synchronously composed of
a large number of running cycles as in ventriculography. In the
mathematical analysis and computer evaluation of this study, they
are then compared calculated values ??of dynamic
parameters with their actual values ??set on the phantom. Part of
such an evaluation of a phantom study of ventriculography using
the VENTR program in our OSTGAM system on the GAMMA-11 instrument
is shown in Fig. 3; good agreement was recorded between the
calculated and actual parameters.
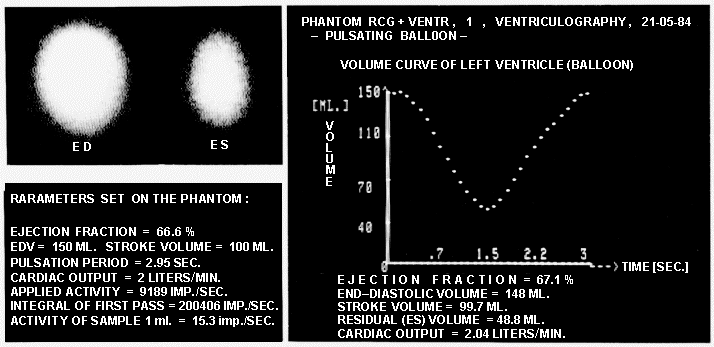 |
Fig.3. Part of the
results of a complex evaluation of phantom radionuclide
ventriculography of a pulsating balloon using the VENTR
program on a Gamma-11 device.
Left: Scintigraphic images of the
balloon in end-diastole and end-systole and table of
actual set values of phantom parameters.
Right: The balloon volume curve,
generated from the activity time curve after background
correction and volume normalization using the
geometrically calculated absolute ED of the balloon
volume, together with the calculated dynamic parameters. |
Phantom of
Central Hemodynamics
Figure 4 schematically shows an arrangement in which the phantom
models the pumping activity of the heart in
central hemodynamics. This mode is mainly used for analysis and
testing of bolus angiocardiography - calculation
of cardiac volume, transits, volumes (§4.9.4
" Dynamic radiocardiography ") .
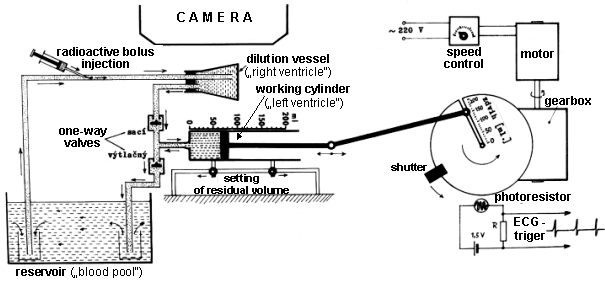 |
| Fig.4. Arrangement of a
dynamic phantom for modeling the pumping activity of the
heart for radionuclide angiocardiography. Note:
The scintillation camera actually "looks" at
the working cylinder and the dilution vessel
perpendicular to the drawing. |
The "left ventricle" in this case is
a working cylinder, which is located together with another
dilution vessel (representing the "right ventricle +
lungs") in the field of view of the camera. From the storage
tank (reservoir with a volume of about 5 liters - can be
changed) representing the total blood volume, when moving the
piston to the right draws (sucks) through the dilution vessel and
one-way suction valve water into the working cylinder, when the
piston moves opposite, the suction valve closes and water it is
pushed through the tube back into the storage container via the
open second one-way valve. The valves alternately close and open,
so the phantom works here as a piston pump with continuously
adjustable parameters. The product of the stroke and heart rate
fraction indicates the flow rate of the pump, ie
"minute heart volume".
A radioactive bolus (approximately
100MBq 99mTc in 1 ml) is injected into the rubber suction tube at
the appropriate time and a dynamic radiocardiography (RKG) study
is started. The bolus quickly proceeds first to the dilution
vessel ("right chamber"), from where it is, partially
diluted, sucked into the working cylinder and from there -
already completely diluted - expelled in parts into a storage
vessel. The time course of radioactivity in the dilution vessel
and in the working cylinder is thus the same as in the right and
left heart chambers during bolus radiocardiography: a sharp
increase with bolus arrival, a slight exponential decrease due to
dilution leakage, then systemic recirculation of the
radioindicator concentration of radioactivity in the system.
 |
| Fig.5. After injecting a bolus into the phantom
suction tube, we see in the sequence images the gradual
passage of radioactivity through the dilution vessel and
working cylinder, from where it is gradually expelled
into the storage vessel with constant dilution, after
which part of the radio indicator returns by system
recirculation. significantly weaker). In the next course,
the radio indicator is homogeneously diluted throughout
the system (these images are no longer captured here). |
The resulting phantom dynamic study is then
processed by the RKG program for the evaluation of
radiocardiography. The gamma-functions and exponential functions
are interleaved with the curves of the time course of
radioactivity in the respective areas of interest (bolus arrival,
dilution vessel, working cylinder), which represent the passage
and dilution of the radioactive bolus in individual parts of the
pumping system, transit times, volumes and cardiac output.
"similar to angoicardiography; the calculated parameter
values are confronted with the actual parameters set on the
phantom. In Fig.6. part of the evaluation of such a bolus phantom
study using our RKG program is shown. The calculated parameters
again agreed very well with the actual parameters of the phantom.
 |
Fig.6. Verification of
the operation of the RKG program for complex evaluation
of bolus radiocardiography using phantom measurement in
the arrangement according to Fig.4.
Left: Images of some stages of the
passage of radioactivity through the phantom; below is a
table of actual phantom set parameters.
Right: Part of the results of the
evaluation of the phantom study by the RKG program
(version on Gamma-11). |
With the described phantom, a number of
measurements were performed both in the pulsating balloon
arrangement of Fig. 2 and in the flow pump mode of Fig. 4. The
phantom has played an important role in the development
of methods and algorithms for dynamic methods of nuclear
cardiology, as well as in the creation of appropriate software
that is still successfully used (VENTR and RKG programs).
In the pulsating balloon mode, the agreement of all parameters
calculated in radionuclide ventriculography ( VENTR program ) was verified and an accurate calibration of
the geometric method for determining the end-diastolic volume of
the heart chamber was performed; a proportional
geometric-analytical method for determining the absolute volume
of the heart chamber was also developed and verified.
In the flow pump mode, the dynamics of flow and dilution were
analyzed and the accuracy of the determination of minute heart
volume and various aspects of combined radiocardiography +
ventriculography were verified.
Another planned addition of a
"short-circuit" tube with adjustable flow, connected
between the left and right ventricles, unfortunately did not take
place - it would be possible to test methods for quantification
of intracardiac short circuits.
In comparison with the phantoms
developed so far, the described phantom has an original concept
and the advantage of greater flexibility and more complex use.
Even some later phantoms (such as the
"Vangerbild Cardiac Phantom" Amersham) did not reach such complexity, even though they were
mechanically made professionally.
Colleagues from the Department of Nuclear
Medicine in Olomouc also made a very nicely mechanically executed
phantom of a pulsating balloon and also performed a number of
measurements with it.
4.3 Phantom measurement dynamics esophageal
For the purpose
of development of the methods of mathematical analysis and
evaluation of complex dynamic scintigraphy of esophagus and
stomach (§4.9.3
" scintigraphy esophagus ") , as well as for testing the correctness
of the program results OESOGAST, we designed a simple ý dynamic phantom modeling passage of tracer marked bite by
esophagus with the possibility of simulating anomalies, including
antiperistaltics or gastro-oesophageal reflux.
The phantom is shown in the
figure on the left. It consists of a longer shaft-helix (length
about 60 cm), into the thread of which fits a housing with a
holder for gamma radiation sources. The shaft is built vertically
in the field of view of the scintillation camera and rotates
using an electric motor with the possibility of changing the
direction of rotation. When the shaft rotates, due to the
threads, the housing with the radioactive emitter also moves
in the field of view of the camera in the vertical direction up
or down - depending on the direction of rotation of the electric
motor. The downward movement simulates the passage of the bite
through the esophagus during the swallowing act, the upward
movement of any reflux or antiperistaltics.
 |
 |
| Dynamic phantom of a radiolabel passage through the
esophagus. |
Simulation of reflux using two emitters. |
During our own phantom
measurements, we place a source of radiation g - a syringe or an ampoule with a
radionuclide 99mTc with an activity of about 50 MBq -
in the holder (connected to the case on the helix) . We can use
one or two ampoules (see below). Move the case to the upper
position, then start the electric motor in the appropriate
direction and start a dynamic scintigraphic study. A number of
phantom measurements have been performed with various
modifications of this arrangement. The basic phantom measurement
models the normal case , ie fast and
uniform passage of the radioindicator through the
esophagus during the swallowing act. Place one container with a
radio indicator in the holder set above the upper edge of the
camera's field of view, start the downward movement and start a
scintigraphic study of this uniform (linear) movement of the
radio indicator. We then stop the movement of the radio indicator
at a suitable stage (it represents the attainment of the
stomach), but let the scintigraphic study run for a while. The
result of the evaluation of the normal phantom study program
OESOGAST is shown in Fig .A . The curves of the passage of
the radio indicator of the upper middle and lower part of the
"esophagus" have the same height and width, while the
calculated transit times agree with the actual times of movement
of the source along the helix, measured by the stopwatch. Also,
the transport functions and fused images M and
her exactly linear
in shape.
 |
 |
 |
| A. Normal steady motion |
B. Movement with
retention simulation |
C. Motion with
antiperistaltic simulation |
The result of another
phantom measurement is shown in FIG. It differs from the previous
normal experiment in that at a certain stage of the downward
movement of the radio indicator, the movement was temporarily
stopped for 2 sec. This anomalous movement of the radioindicator
is again very well visible in the results of the computer
evaluation - the curve of the middle part of the
"esophagus" is extended by 2 sec. transit time,
condensed image and tra n sports functions also faithfully
reflect the trajectory of movement.
During the next phantom
measurement, the direction of rotation of the motor was
temporarily changed during the downward movement, so that the
radio indicator changed after 2 sec. he moved upwards, after
which, after switching again, the movement continued evenly
downwards. This uniform "swallowing" movement with
temporary return is also faithfully represented and quantified on
a computer processing of a scintigraphic study - Fig.C.
Another modification of the phantom measurement coincided with
the normal experiment of even swallowing for most of its course,
but at the end during the stationary phase of the radioindicator
resting in the "stomach" the motor was started again in
the opposite direction (upward movement),
so that the radio indicator returned to the
"esophagus", after changing direction,
which it dropped back to the "stomach" position. The result of the evaluation can
be seen in Fig. D as a simulation of complete gastro-oesophageal
reflux.
 |
 |
| D. Movement with simulation g.-e. reflux 100% |
E. Simulation of gastro.-esophagus. reflux 50% |
The last type of phantom
experiment uses two g
radiation
sources located in a phantom holder (see figure above right).
The course of the measurement is similar to that of a normal
experiment - uniform movement of two closely spaced sources (they
are not distinguished in scintigraphic images, there is one
source with total activity). However, after reaching the lower
resting position of the "stomach", we move one of the
sources upwards for a while (manually to the defined position),
leave it here for a while and then lower it again into the case
next to the other source. This simulates gastro-oesophageal
refluxparts of
the radio indicator from the "stomach" to the
"esophagus". The result of the evaluation can be seen
in Fig. E, where it can be clearly seen from the condensed image
how part of the radio indicator "swung" temporarily
from the "stomach" to the lower part of the
"esophagus"; Quantitative analysis gave a value of
51.5% at reflux in good agreement with reality (both sources j e have
the same activity, so that the actual "reflux" was
50%).
Phantom measurements of this kind are original and have not yet
been reported in the literature (known and available to us). It
was very useful in the development of individual algorithms for
mathematical analysis of radioindicator transport through the
esophagus (analysis of curves, construction of transport function
and condensed image) and verification of the correctness of the
evaluation results by the OESOGAST program
(Dynamic
scintigraphy of the esophagus and stomach).
Note: Inspired by our work, they constructed a similar
phantom of esophageal dynamics at the Department of Nuclear
Medicine of the Army Hospital in Krakow. Instead of a threaded
shaft, they used a toothed belt, the phantom looks very good -
congratulations!
 |
 |
 |
| Scintigraphy |
|
Computer evaluation |
Vojtech Ullmann














































