| (3.32) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 3
GEOMETRY AND
TOPOLOGY OF SPACE-TIME
3.1. Geometric-topological properties of
spacetime
3.2. Minkowski
planar spacetime and asymptotic structure
3.3. Cauchy's
problem, causality and horizons
3.4. Schwarzschild
geometry
3.5. Reissner-Nordström geometry
3.6. Kerr
and Kerr-Newman geometry
3.7. Spatio-temporal
singularities
3.8. Hawking's
and Penrose's theorems on singularities
3.9. Naked
singularities and the principle of "cosmic censorship"
3.5. Reissner-Nordström geometry
Previous spherically
symmetric case can be generalized somewhat while maintaining the
spherical symmetry, that the excitation body will consider the electrically charged with charge Q. In order to
preserve symmetry must be distribution of electric charge also
spherically symmetrical, because the gravitational field
is generated not only source body material,
but also by the energy-momentum tensor of the electromagnetic
field. An asymmetrical charge distribution would lead to an
asymmetric electric field, which would excite an asymmetric
gravitational field.
The space-time interval element will again have the same
spherically symmetric basic shape (3.10)
ds 2 = g tt dt 2 + g rr dr 2 + r 2 (d J 2 + sin 2 J d j 2) .
The difference from the previous Schwarzschild solution is now that the external solution will not be a solution of Einstein's equations without the right side, but the right side here will be the energy-momentum tensor of the electromagnetic field Tikelmag (1.118). In this case, it is a Coulomb centrally symmetric electrostatic field with intensity E = E(r). er , where er is the unit base vector of the radial direction. Because the Schwarzschild radial coordinate R retains the meaning that the surface of a sphere centered at the point of symmetry, having a radius r , is equal to 4p.r2, according to Coulomb's law (Gauss's theorem), E(r) = Q/r2. The energy-momentum tensor of this electric field is then (non-diagonal components are zero)
Tttelmag = -Trr = TJJ = Tjj = E(r)2/8p = Q2/8p.r 4 ;
this we substitute into Einstein's equations Rik - (1/2) gik R = 8p Tik elmag and for spherically symmetric metrics (3.10) we get again two independent differential equations by a similar procedure as when deriving the Schwarzschild solution
dgtt/dr = (1/r) gtt (1 + grr - grr.Q2/r2) , dgrr/dr = -(1/r) grr (1 + grr - grr.Q2/r2) .
The solution to this system is
gtt = C1(1 - C2/r + Q2/r2) , grr = (1 - C2/r + Q2/r2)-1 ,
where for the same reasons as in Schwarzschild's case the integration constants must be C1 = 1 and C2 = -2M. The final expression for the element of the space-time interval of a spherically symmetric gravitational field excited by a spherically symmetric body of total mass M and an electric charge Q thus has the form
| (3.32) |
in geometrodynamic units; in common units it is
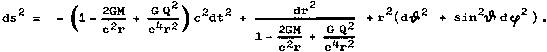 |
(3.32 ') |
This geometry is called Reissner-Nordström geometry (RN). Here, the parameter M again has the meaning of the total mass, the parameter Q the meaning of the total electric charge measured by a remote observer using the Gaussian integral fluxes of the vector E, resp. by analyzing the motion of charged test particles. In the case of 0 < Q2 < M2, the RN field could theoretically describe an electrically charged black hole (§4.4 "Rotating and electrically charged Kerr-Newman black holes").
Derivation
of the gravitational-electric solution from the principle of
least action
The general derivation of the space-time
structure in the presence of a combined gravitational
+ electromagnetic field is sometimes performed using the
variational principle of least action using the combined
Lagrangian of gravitational L G and
electrodynamic L EL :
L
= LG + LEL = (R - 2L) - FikFik
......,
where R is the Ricci scalar curvature, L is the cosmological
constant, Fik is an
electromagnetic field tensor.
The variational principle of least action, then gives the Einstein-Maxwell
equations of gravitational and electromagnetic fields :
Gik
+ Lgik
= 1/2 gik.................... ..
...........................
............... ........ ...........
Properties
of the Reissner-Nordström field
RN geometry with space-time metric (3.32) is a static spherically
symmetric solution of Einstein-Maxwell gravitational equations.
This geometry is asymptotically planar and its horizon has a
spherical topology. It is characterized by the mass M
and the electric charge Q and is singular at the beginning r = 0
of the radial coordinate.
According to the mutual ratio of M
and Q values, we can distinguish four significant cases with
different global geometric structure in Reissner-Nordström spacetime :
a ) At Q =
0, M> 0 we get the Schwarzschild geometry from the previous
§3.4 ;
b ) 0 < Q2 < M2 ;
c ) 0 < Q2 = M2 ;
d ) Q2 > M2 > 0.
Outer and inner horizon
First, we analyze the case 0 <Q 2 <M 2 , which is the most physically
interesting. The Reissner-Nordström metric (3.32) is very
similar to the Schwarzschild metric (3.13), but differs in that
the expression
1 - 2 M r + Q 2 / r 2
is in the case of 0 < |Q| <M equal to zero for two "roots" r = rg+ and r = rg- :
| r g + = M + Ö (M 2 - Q 2 ) , r g - = M - Ö (M 2 - Q 2 ) . | (3.33) |
In ordinary units, these are values
| rg+ = (G/c2) [M + Ö(M2 - Q2)] , rg- = (G/c2) [M - Ö(M2 - Q2)] . | (3.33 ') |
Thus, there are two "horizons" in RN geometry where the metric (3.32) is not regular - " outer" horizon r = rg+ and "inner" horizon r = rg-. The outer horizon r = rg+ has a similar meaning as the Schwarzschild sphere in Schwarzschild spacetime - is the horizon of events, causally separating the inner region from the outer one; from (3.33) we see that in the presence of an electric charge the gravitational radius rg+ is less than rg = 2M in the Schwarzschild case. Under r = rg+ the light cones are turned inwards toward r = 0 (because gtt > 0) and it would seem that every object that gets there will necessarily end up in the singularity r = 0. However, on the inner horizon r = rg- the light cones begin to straighten again (the time component of the metric tensor changes the sign again: gtt <0) - it is therefore possible to move the particle so as to avoid singularity (Fig.3.20). However, it cannot get across the outer horizon (ie the horizon of events) back to the original space-time, but necessarily to the "other universe" that lies with the original in the absolute future (see below).
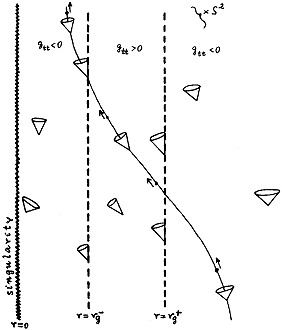 |
Fig.3.20 Kerr space-time diagram of Reissner-Nordström geometry (the situation will look similar in Kerr and Kerr-Newman geometry - §3.6). The outer horizon r = rg+ is the event horizon (the light cones below it face are inwardly towards r = 0). Below the inner horizon r = rg-, however, the light cones begin to "straighten" again, so that the world-line of a body that has penetrated below the horizon r = rg+, does not necessarily end in the singularity r = 0. |
The singular behavior of the metric (3.32) in the standard coordinates on these horizons is again only apparent and can be removed by transition to more suitable coordinates similar to Kruskal's. With the help of the modified coordinate r*
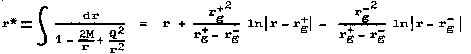 |
(3.34) |
similarly to the extension of Schwarzschild geometry, we introduce isotropic coordinates p = t + r*, q = t - r*. We then further transform these in order to remove the singular coefficient in the metric :
| (3.34 ') |
When introducing new temporal and spatially coordinates of u = (q'- p')/2 and v = (q'+ p')/2 the Reissner-Nordström metric has form
| (3.35) |
After a conformal transformation (analogous (3.5) in §3.2) in order to more clearly present the asymptotic structure, the Reissner-Nordström geometry will be described by the interval
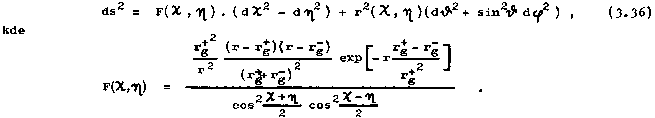 |
(3.35´) |
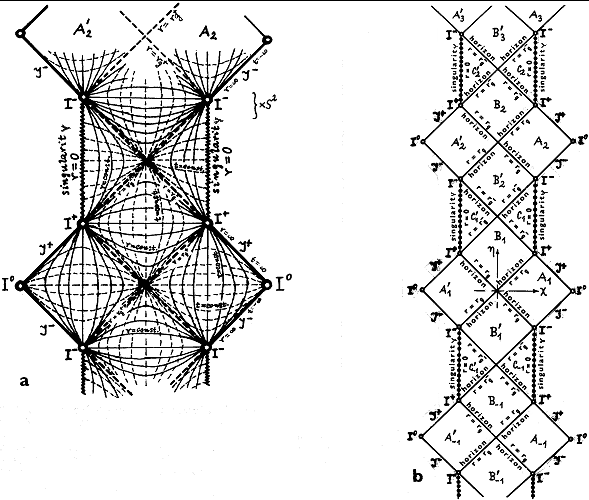
Fig.3.21. Penrose conformal space-time diagram of the complete
extension of the Reissner-Nordström geometry for the case Q2 <
M2 .
a )
Coordinate network - hypersurfaces r = const. and t = const.
b ) Global geometric
structure - infinitely many periodically recurring outer regions
("universes") A..., - 1,1,2,
.., inner regions B..., - 1,1,2, .. and C..., -
1,1,2, .., horizons and
singularities.
Traveling to other
universes ?
The space-time diagram of the conformal image of RN geometry for
the most physically probable case 0 < |Q| <M is shown in Fig.3.21.
The geometric structure of this complete
extension of the Reissner-Nordström solution is unexpectedly complex. An
infinite number of periodically recurring "universes"
(separate asymptotically planar outer regions A…,-1,1,2,…), horizons and singularities appear here.
In contrast to Schwarzschild geometry (Fig.3.19), where
singularities are spatial type (and therefore inevitable for
every object in area B), singularities
of Reissner-Nordström geometry according to Fig.3.21 are of time type - they are, so to speak, "time-limited" and can be
avoided.
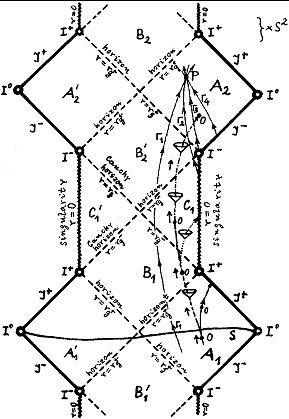 |
Fig.3.22. The O observer moving in the outer asymptotically
planar region A1 of the
Reissner-Nordström spacetime has three possibilities. Either it will constantly move in A1 (solid line), so it will reach infinity I+ or Á+ in the limit. However , if the observer penetrates below the horizon r = rg+ (dashed trajectory) into the inner region B1, he also passes through the horizon inner r = rg- into the region C1, where he has two possibilities: he either encounters singularity (dotted path) where it is absorbed and destroyed, or it can avoid singularity (dashed trajectory) and reach another asymptotically planar outer region A2. The situation in this next "universe" A2 is not completely determined by the initial conditions on the Cauchy hypersurface S , as can be seen, for example, at the point p Î A2 . |
Let us observe the fate
of the observer (as indicated in Fig.3.22), who, during his
movement in Reissner-Nordström spacetime, penetrated below the
outer horizon r = rg+. Because it has fallen below the
horizon of events, it can no longer return to the original outer
space (area A1) and has basically two
possibilities. First, to reach a
singularity, where its world line (and thus its existence within
the considered manifold) will definitely end. However, this is not (unlike
Schwarzschild spacetime) unavoidable, the observer can avoid
the singularity and move further until it
appears in the second asymptotically planar region A2, in the second
"universe",
which lies with respect to the initial A1 in the absolute future. Thus, we
see that a real material object moving in RN geometry within a
light cone can in principle "travel" between individual
"universes" *) without having to go through a
singularity (unlike Schwarzschild geometry,
where the Einstein-Rosen bridge could pass only at superlight
speed).
*) It should be noted that
this "travel between different universes" (and the very
existence of these other universes) is possible only
theoretically in an extremely idealized model of an
asymptotically planar universe without other bodies and fields,
with precise Reissner-Nordström or Kerr geometry. A critical
assessment of similar possibilities will be in §4.4, section
"Black
holes - bridges to other universes?".
If we look at the Causal
relationship of this second universe with respect to the original, we
see that the inner horizons r = rg- are also Cauchy horizons. If we take some
event P in the region A2 and observe how it can be
influenced in principle, we see that although it can be
influenced by geodesics (eg G1)
coming from the region A1 (and given the initial
conditions for suitable Cauchy hypersurface in A1), but new information can also
come there "uncontrollably" by geodesics (eg G2 , G3 , G4) from areas of infinity of the
past I- , Á - and from the singularity, that can
be "seen" from here. This information may undermine any prediction made on the basis of the
initial conditions in area A1. Thus, the observer emerged in
the region of spacetime (another "universe"), which is
not unambiguously determined by the initial conditions for any
Cauchy hypersurface in the original region A1.
Let us confront this
with the deterministic idea of classical (non-quantum) physics, which Laplace had
already formulated: If at certain time
moment we found all
physical quantities in all parts of the universe (ie the
instantaneous state of the universe - the complete set of initial
conditions on Cauchy's hypersurface) and knew the physical laws by
which all these quantities are governed,, we could indefinitely to predict the evolution of the universe, ie its state at any time in the
future (or even the past). However, in the complete extension of
the Reissner-Nordström geometry, this is not fulfilled, there
are Cauchy horizons (and therefore not
exist global Cauchy hypersurfaces) and there are therefore regions, whose
state is not unambiguously determined by any set of initial
conditions. Only in the outer asymptotically planar region can
the future be unambiguously "predicted" from partial
Cauchy hypersurfaces. Thus, even in the classical physics
(on which the Reissner-Nordström geometry, as a solution to Einstein
equation, is based) the
possibility of predicting the future may be limited not only by
the practical unavailability of physical quantities in all parts
of the universe at a certain point in time, but in principle also
by the global geometric-topological structure of spacetime...
Instability of the inner Cauchy
horizon to perturbations; "Mass inflation"
?
The above scenario of the possibility of an observer traveling
through the inner Cauchy horizon to another asymptotically flat
universe assumes that this inner horizon is stable
at roughly constant parameters of the black hole (here mass and charge). However,
pertubation analysis has shown that it can exhibit instability
and even divergence. Even a simple analysis of the incident radio
waves shows that these waves become denser on their way to the
interior of the black hole and exhibit strong gravitational and
Doppler frequency blue-violet shifts. This amplification in the
direction of the inner Cauhy horizon continues to infinity,
leading to its instability even against a small
external perturbation. And more detailed perturbation analyzes
confirmed that this exponential divergence can lead to a
singularity. So the falling traveler will not survive
the encounter and passage through the inner Cauchy horizon..?..
Or another argument: In Fig.3.21, each point of area B
between rg+ and rg- (where the areas r = const. are of the
spatial type) represents a two-dimensional spherical surface,
which is a closed absorbing (trapped)
surface (see definition 3.10). Observer O, as he passes through the surface
r = rg- (Fig.3.22), will see the whole further
history of the asymptotically planar outer region A1,
which he leaves, for the finite time. Therefore, each body from
this area will be visible with an infinitely increasing purple
shift. It follows that the Cauchy horizon r = rg- is unstable to perturbations of
initial conditions on the initial spatial hypersurface S
[192]. It is clear that the "cosmological" questions of
the evolution of the "universe" A1, which the observer is leaving,
will be very important to him. If the universe A1
may collapse in the future, even observer O will not avoid this fate; on the
horizon r = rg- it encounters an infinite density of
matter ~ energy, that is, in the end,
with a singularity.
This mass instability of the inner Cauchy horizon is
sometimes misleadingly called "Mass inflation",
with an analogy to the inflationary expansion of the universe.
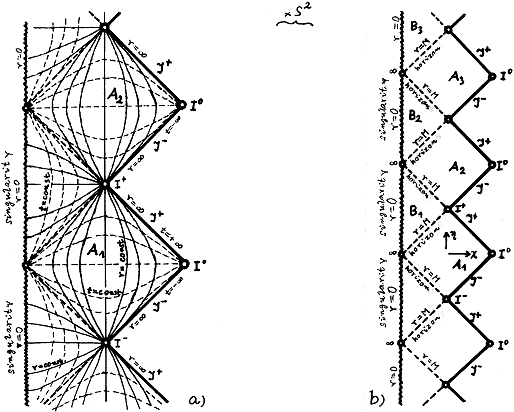
Fig.3.23. Penrose conformal space-time diagram of the complete
extension of the Reissner-Nordström geometry for the case Q2 = M2 .
a ) Hypersurfaces (coordinate lines) r = const.
and t = const.
b ) Global geometric structure - infinitely many
periodically repeating external areas A and the inner
regions B .
Extreme R-N geometry
For the case Q = M, the corresponding conformal space-time
diagram of the complete extension of the Reissner-Nordström
geometry has the shape shown in Fig.3.23. Again, an infinite
number of periodically recurring "outer" regions A (M
<r < ¥) and inner regions B (0
<r <M) can be seen. The outer and inner horizons coincide (rg- = rg+ = M), this is a special case of an extreme
black hole (see §4.4).
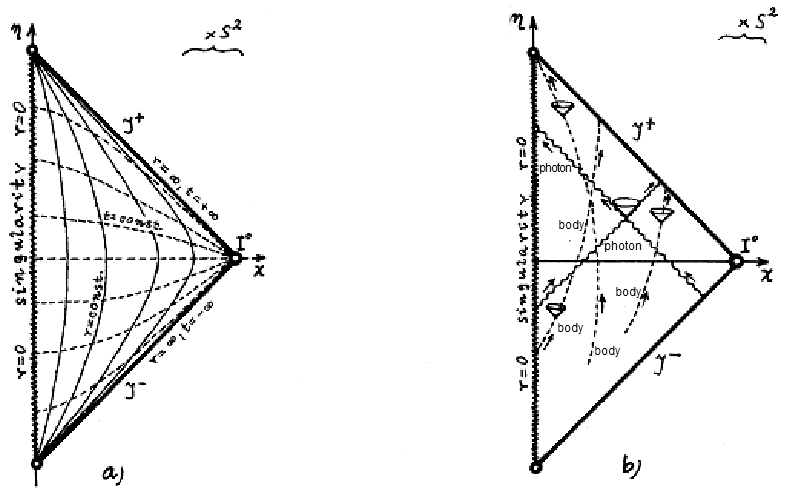
Fig.3.24. Penrose conformal space-time diagram of
Reissner-Nordström geometry in the case of Q2 > M2 .
a )
Coordinate lines - hypersurfaces
r = const. and t = const.
b ) Global
geometric structure - shapes of light cones and radial motion of
bodies and photons. There are no horizons, the singularity r = 0
is "naked" (it is visible from
any point) .
R-N naked singularity
In the case of Q2 > M2, no extension needs to be
sought, because spacetime is non-extensible already in the
original coordinates; is regular everywhere except the point r =
0 - irremovable physical
singularities of spacetime. A conformal space-time diagram
for this case is shown in Fig.3.24. The
horizon of events is not here, it is a naked singularity
(see §3.9 and §4.4).
Generalized Reissner-Nordström
solution in nonlinear electrodynamics
In §1.6, the final passage "Nonlinear electrodynamics", the theoretical possibility was discussed that
the electric field would not behave exactly linearly at extremely
high intensities according to the laws of standard Maxwell
electrodynamics, but there could be fundamental boundaries -
maximum possible electric field strength Emax. This alternative
option could significantly (with
interesting consequences) applied in
Reissner-Nordström solutions, as well as the Kerr-Newman geometry (§3.6) -
and generally black holes (event.
also in other compact objects such as neutron stars and
their special cases magnetars) with
very strong electric and magnetic fields (§4
..., § .....) .......
If we substitute Reissner-Nordström electro -gravitation solution (3.32), to
which this §3.5 is devoted, standard Maxwell's electrodynamics
by nonlinear Born-Infeld electrodynamics (1.120)
- either using the Lagrangian (1.119) or the momentum energy
tensor electromag. field, we get a generalized
Reissner-Nordström solution :
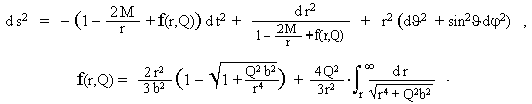 |
(3.36) |
The function f(r, Q) expresses the effect of
the electric field on the metric. The intensity of the electric
field in BN electrodynamics depends on the radial coordinate r
according to the law E(r) = Q/Ö(r4 + Q2.b2). At b = 0, ie without
electrical nonlinearity, f(r, Q) = Q2/r2 - we get the basic RN geometry (3.32) with Coulomb
electric intensity E(r) = Q/r2. The integral contained in the function
f(r, Q) can be explicitly expressed using two kinds of special
functions
| (3.36´) |
where "F (...)" is the Legender
elliptic function of the 1st kind and "2F1(...)" is the so-called hypergeometric function
(more complex power series from Q2b2/r4). Specific
values of these complex functions can be found for physical
calculations in special tables, recently there are also computer
programs for them.
This spacetime of
the generalized RN solution with metric (3.36), which is a
solution of Einstein-Born-Infeld equations, is characterized by
three parameters: mass M, charge
Q and Born-Infeld nonlinearity parameter
"b" (whose inverse value
indicates the final value of the electric field intensity at the
origin of the coordinates r = 0). Even with
b> 0 at larger distances r> 0, it asymptotically
transitions into an RN solution.
......................
It is interesting that in the solution of nonlinear
electrodynamics, zero (isotropic) geodesics represent only the
orbits of (hypothetical-model) gravitons, but generally not
photons ! The paths of photons here can be influenced by
"self-interaction" with a nonlinear electromagnetic
field ...
........... ........... ....... .. .. ................
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||
Vojtech Ullmann