Forbidden nude singularities without horizon

Chapter 3
GEOMETRY AND TOPOLOGY OF SPACE-TIME
3.1. Geometric-topological properties of spacetime
3.2. Minkowski planar spacetime and asymptotic structure
3.3. Cauchy's problem, causality and horizons
3.4. Schwarzschild geometry
3.5. Reissner-Nordström geometry
3.6. Kerr and Kerr-Newman geometry
3.7. Spatio-temporal singularities
3.8. Hawking's and Penrose's theorems on singularities
3.9. Naked singularities and the principle of "cosmic censorship"

3.9. Naked singularities and the principle of "cosmic censorship"

The theorems mentioned in the previous §3.8 predict the existence of singularities in a number of physically real situations. Many exact solutions of Einstein's equations, some of which have been discussed in §3.4-3.6 (eg Schwarzschild or Kerr-Newman geometry), have singularities. Singularities inside black holes have the important property that are surrounded by the event horizon, which prevents them from "seeing" and disable any influence of the rest of the universe by a given singularity.

The question arises as to whether there can be "naked" singularities without a horizon ? For example, by formally placing Q² + J²/M² > M² in the expression (3.37) for Kerr-Newman geometry we get the so-called Kerr naked singularity without horizon.

According to today's knowledge, it is highly probable that such a naked singularity cannot arise, every singularity is "dressed" to the horizon, which R.Penrose metaphorically called the principle of cosmic censorship [202], [204] (here is a its brief wording) :

The principle of cosmic censorship is actually a hypothesis that is not generally proven. On the one hand, the analysis of gravitational collapse testifies to this, where for spherical collapse we get this directly analytically, and with small deviations from symmetry, it can also be shown by pertubation methods that collapse does not lead to naked singularity [211], [246]. Above all, however, the principle of cosmic censorship is a reasonable physical requirement. The presence of naked singularity would lead to a violation of the determination of the further evolution of spacetime *). To the individual places of spacetime M would from such a naked singularity (which is not an element of M !) new information could come uncontrollably through geodetics that do not continue into the past; the situation here is somewhat similar to that in Fig.3.10a. So there would be no Cauchy hypersurface. In the full extension of the Kerr-Newnam geometry, there are also Cauchy horizons, but only in the "inner" region below the event horizon, while in the outer asymptotically planar region the future can be unambiguously predicted from a suitable Cauchy hypersurface. However, naked singularity would make this impossible everywhere, nothing definite could be said about the further evolution of spacetime. And this is against the deterministic spirit of classical physics.
*) A naked singularity without a horizon could, figuratively speaking, "infect" the surrounding universe with its "pathology" - the unpredictability of physical phenomena, the violation of causality. If, for example, even somewhere at a greater distance in space, a planet orbited a star according to Newton-Keppler laws, a naked singularity could randomly send stronger gravitational waves that could disrupt and unpredictably change this orbit.

In addition to its independent physical-philosophical importance, the principle of cosmic censorship have also of key importance in the physics of black holes, eg for the 2nd Law of Black Hole Dynamics (see §4.6).

The hypothesis of cosmic censorship is probably fulfilled in the classical general theory of relativity in all physically real situations (except, of course, with the assumed initial singularity of the universe during the Big Bang, which would be obviously naked - see Chapter 5). However, in §4.7 on the quantum evaporation of black holes, we show that quantum effects can lead to failure to fulfill the hypothesis of cosmic censorship and to violation of the determinants of space-time evolution. There will also be a violation of the classic second law of black hole dynamics, the validity of which requires compliance with the principle of cosmic censorship. At the final stage of quantum evaporation of a black hole - its quantum explosion - a naked singularity then appears (for a moment) directly (§4.7).

The most frequently discussed type of nude singularity is Kerr-Newman nude singularity mentioned in §3.6; tThere we noted that near the annular singularity of the Kerr-Newman geometry, causality may be violated (there are a closed time curve). In black holes, this "pathological" region is separated from the rest of spacetime by the event horizon, so that outside the black hole, there is no disruption of causality. However, in the case of naked singularities, two-way communication is possible between the outer asymptotically planar region and the causal disorder region; closed time curves can be "stretched" to pass through any point of such spacetime [43]. A particle sent from a remote location could return to the starting point before it was sent...

Imagine that for a moment the principle of cosmic censorship was violated and in some way a naked singularity was created. The question then is whether such a naked singularity would still remain naked, or whether eventually the "cosmic censor" then the word would come in the person of a certain physical process and would additionally "dress" this singularity into the horizon? It turns out that two kinds of physical phenomena can play the role of a "cosmic censor", create a horizon around the naked singularity and thus turn it into black hole.

The first "cosmic censor" is purely classical: it is the accretion of the surrounding matter to a naked singularity, in which the ratio of J/M and Q/M is constantly decreasing until a horizon is formed. During accretion, rotational energy is efficiently extracted [205] and any electric charge is discharged (singularity attracts oppositely charged particles).

The second mechanism, functioning even in the absence of surrounding matter as a "cosmic censor", is quantum effects in a strongly inhomogeneous field around the naked singularity. The pair production of particle-antiparticles in the field of naked singularity leads to the flow of quantum radiation from it, whereby the singularity loses mass and rotational angular momentum. The mechanism of quantum radiation is somewhat different from that of black holes (cf §4.7) and depends on the specific spacetime structure naked singularity (where individual partners in a particle-antiparticle pair can "tunnel", Fig.3.32). Quantum radiation of naked singularity leads to its "dressing" to the horizon, ie to the transformation into a black hole.

If we look at the Penrose diagram of the complete extension of the Reissner-Nordström or Kerr-Newman geometry (Fig. 3.21, 3.22, 3.25), we see that the singularity, which in one universe is part of a rotating or charged black hole and thus "shrouded" by the horizon, is for another "universe" (lying in the future) naked. Similarly, if we accepted the bizarre space-time topology (mentioned in §3.5) corresponding twisting and gluing the Penrose diagram cut from paper into a cylindrical surface, it appeared to be a naked singularity in "our universe" as well; similar topological variation leading to time loops and "time machines", however, we have already excluded in §3.1. In §4.4 will show a cosmic censor that cuts off most of the structure of the Penrose diagram at both the classical and quantum levels, thus preventing the transition of a black hole to a white hole accompanied by a naked singularity in another universe (see Fig.4.19).

By nude singularities subject to cosmic censorship, we have so far understood the "globally" nude singularities visible from infinity. Although the principle of cosmic censorship in the formulation of Theorem 3.8 prevents singularities from uncontrollably influencing physical processes "at infinity" (at a sufficient distance from the singularity), it does not say anything about a situation close to the singularity itself. But this is a somewhat "selfish" view, because if an observer moving near a singularity (perhaps inside the horizon of a black hole) "saw" that singularity before being absorbed by it, he would encounter the same unpredictability as we described for a nude singularity. So it would be a "locally naked" singularity. For singularities inside the black holes of stellar masses, it can although be argued that any observer that penetrates below the horizon will be destroyed in a fraction of a second and will therefore not have time to make any observations or experiments in which the possible effect of singularity could manifest itself. In the general theory of relativity (which is a scale-invariant theory) may in principle be a giant black hole in which the observer (astronaut that there flies) is available for days or even months of time when not feel the effect of large tidal forces and can unhurriedly perform experiments and observations and analyze the consequences of uncertainty brought about by the action of singularity. The extended (objectively understood) principle of cosmic censorship should therefore prohibit even these locally naked singularities.

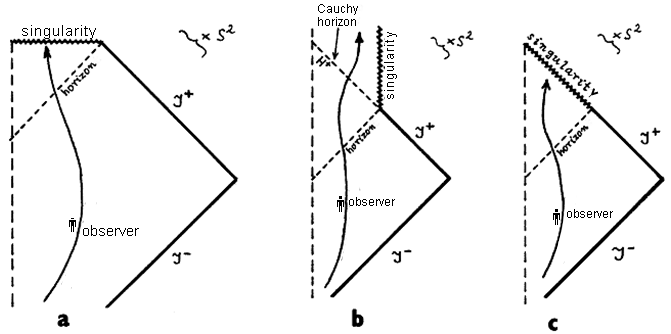
Fig.3.31. Instability of the space-time character of singularity in Schwarzschild's and Kerr-Newman's solution to perturbations in relation to the principle of cosmic censorship.
a) For a precisely spherically symmetric case (without perturbation), in the corresponding Schwarzschild solution, the singularity has a spatial character everywhere, so that no observer can see this singularity before colliding with it - the extended principle of cosmic censorship is fulfilled.
b) The addition of even a slight angular momentum or electric charge leads to a Kerr or Reissner-Nordström solution, in which the singularity takes on a temporal character. An observer below the inner (Cauchy) horizon can see such a singularity - it is locally naked .
c) Cauchy (inner) horizon H⁺ fron Fig.b), however, is unstable to perturbations in the outer area: signals from the infinitely distant areas S will acquire an infinitely large violet shift on H⁺, so that weak field of perturbations will diverge on H⁺- in the place of H⁺ a singularity of curvature will be created, which will be of the isotropic type (nonlinear effects in the field of large curvature could even lead to the emergence of a singularity of the spatial type - compare with Fig.4.19). The principle of cosmic censorship would thus also be fulfilled.

Let's see how the singularities we encountered in §3.4-3.6 withstand the simplest exact solutions of Einstein's equations from this point of view. The singularity r = 0 in Schwarzschild's spherically symmetric spacetime probably conforms to the extended principle of cosmic censorship, because it has a spatial character everywhere (Fig.3.31a), so the lokally naked singularity is not there (singularity cannot be seen before colliding with it). However, Schwarzschild's singularity is unstable: the supply of even a slight angular momentum or electric charge leads to a Kerr or Reissner-Nordström solution, where the singularity ceases to be spatial, but is of a temporal type (Fig.3.31b). It can be seen from Fig.3.31b that such a singularity is locally naked, because, for example, an observer whose worldline is marked can see it without colliding with it; in Fig.3.22 we have even seen a situation where the observer can completely avoid being absorbed by the singularity and penetrate into another "universe", for which the said singularity will be globally naked (it will also be visible here at infinity). For the structure of spacetime, however, the decisive factor here is the inner horizon r = r_g^-, which is the Cauchy horizon of every spatial hypersurface extending to spatial infinity. An observer passing through this inner H⁺(S) horizon, will see the whole future history of the outside world condensed into a single point in time.

If any perturbations (of a general nature - eg some weak fields) are present on the Cauchy hyperfsurface S in the initial conditions, then the signals from the distant S regions will reach an infinitely large "violet shift" at the H⁺ horizon, leading to divergence along H⁺. The inner horizon is therefore unstable to perturbations at spatial infinity, so in the general case (ie in reality) a singularity of curvature can be expected at the H⁺ place, which will be of the isotropic type (Fig.3.31c); nonlinear effects in the field of large curvature could also lead to a singularity of the spatial type, as indicated in Fig.4.19. Thus, the extended principle of cosmic censorship seems to be fulfilled in asymptotically flat spacetimes GTR.

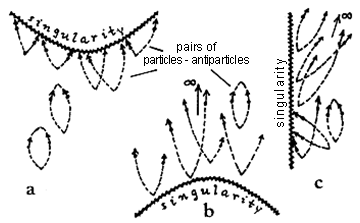Fig.3.32. Possibilities of quantum production of particles and antiparticles in a strong gravitational field near the singularity. a) If the singularity is of the spatial type and is in the future, these particles have nowhere to fly away and are always absorbed by the singularity. b, c) If the singularity is in the past or is of the temporal type, there are temporal or isotropic worldlines along which these particles and antiparticles can move away from the singularity.

A characteristic feature of locally naked singularities is a "time limitations": the existence of such a time- type curve (world lines along which the observer could move), on which there are points A and B such that the singularity lies in future of point A and in the past of point B . Thus, as for the all-encompassing cosmological singularity of the "big bang", the principle of cosmic censorship does not actually apply to it; it is not a locally naked singularity, because there was no observer before the Big Bang ...

3.8. Hawking's and Penrose's theorems about singularities		4. Black holes in space

Vojtech Ullmann