 |
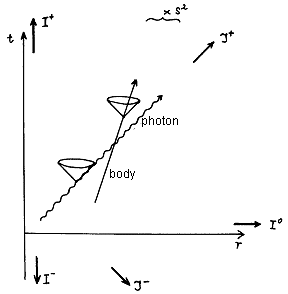
Fig.3.6. Spacetime diagram of Minkowski spacetime in spherical coordinates t, r, J, j with omitted J and j . The arrows are heading to the individual types of infinity. |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 3
GEOMETRY AND
TOPOLOGY OF SPACE-TIME
3.1. Geometric-topological properties of
spacetime
3.2. Minkowski planar spacetime and asymptotic structure
3.3. Cauchy's problem, causality
and horizons
3.4. Schwarzschild
geometry
3.5. Reissner-Nordström
geometry
3.6. Kerr
and Kerr-Newman geometry
3.7. Spatio-temporal
singularities
3.8. Hawking's
and Penrose's theorems on singularities
3.9. Naked
singularities and the principle of "cosmic censorship"
3.2. Minkowski planar spacetime and asymptotic structure
The most important group of spacetimes are asymptotically planar spacetimes, which (as we said in §3.1) model reality well almost everywhere, except cosmology. The simplest such spacetime is planar (everywhere, not just asymptotically) Minkowski spacetime. In Minkowski spacetime we simply show its asymptotic properties; the acquired knowledge about this asymptotic structure will then apply to every asymptotically flat spacetime and we will therefore use it often in the next.
Minkowski planar spacetime, which is the spacetime of the special theory of relativity, is the simplest trivial solution of Einstein's gravitational equations (without the cosmological term) for vacuum at zero boundary conditions. In Minkowski spacetime there is a global inertial (Galilean) frame of reference in which a metric in Cartesian coordinates has the form
| ds2 = - (dxo)2 + (dx1)2 + (dx2)2 + (dx3)2 s -dt2 + dx2 + dy2 +dz2 . | (3.3) |
So the metric tensor is here
| g ik = | / | -1 | 0 | 0 | 0 | \ | º h ik ; | (3.3 ') |
| | | 0 | 1 | 0 | 0 | | | |||
| | | 0 | 0 | 1 | 0 | | | |||
| \ | 0 | 0 | 0 | 1 | / |
all components of the curvature tensor Ri klm are equal to zero. Geodesics are straight lines, tidal forces are zero, gravity in the usual sense does not exist here.
When using spherical spatial coordinates r, J, j, the metric (3.3) of Minkowski spacetime takes the form
| ds 2 = - dt 2 + dr 2 + r 2 (d J 2 + sin 2 J d j 2 ) . | (3.4) |
The space-time diagram of Minkowski space-time in these coordinates is shown in Fig.3.6. The two dimensions associated with J and j are omitted; however, the dimension j could be obtained by rotation about the axis t . In radial motion, isotropic (zero, light) geodesics are lines forming an angle of 45° with the vertical time axis t, geodesics of the time type are also lines forming an angle of less than 45° with the t- axis (lying inside the light cone).
 |
Fig.3.6. Spacetime diagram of Minkowski spacetime in spherical coordinates t, r, J, j with omitted J and j . The arrows are heading to the individual types of infinity. |
Areas of infinity in
spacetime
Assuming
the usual Euclidean topology, in the asymptotic analysis we can
consider the region infinity t ® ± ¥ , r ®¥ of Minkowski
spacetime as a set of limit ("end") points of
congruence of geodesics going from r = 0 to all sides (they will
be geodesics of all three types - temporal, isotropic and
spatial). The equations of such radial geodesics will have the
form r = |v.t + C|, where v ³ 0
is "velocity" and C ³
0 is a finite
constant indicating how r the given geodetic passes at
time t = 0. For v <1 it is a time-type geodetics, for v = 1 it
is an isotropic (zero or light) geodetics and for v> 1 it is a
spatial-type geodetics. The asymptotic
behavior of
these geodesics will be determined by the limits of the
quantities r, r + t and r - t at t ® ± ¥.
For a sufficiently large positive t (distant future) we can write
r = v.t + C , r + t = (v + 1) .t + C , r - t = (v-1) .t + C , (t >> 0)
and for a sufficiently large negative t (distant past) is
r = -v.t - C , r + t = (1-v) .t - C , r- t = - (1 + v) .t - C , (t << 0) .
For worldlines of time type (0 <v <1) will be
t ® ¥ Þ r ®¥ , r + t ®¥ , r - t ®-¥ ;
t ®-¥ Þ r ®¥ , r + t ® ¥ , r - t ® ¥ ;
for the special case v = 0 the same applies, only instead of r ®¥ is r = C. For spatial type worldlines (v> 1) :
t ® ¥ Þ r ®¥ , r + t ®¥ , r - t ®¥
;
t ®-¥ Þ r ®¥ , r + t ®¥ , r - t ®¥ .
For isotropic geodesics (v = 1) will be
t ® ¥ Þ r ®¥ , r + t ®¥ , r - t = C ;
t ®-¥ Þ r ®¥ , r + t = -C , r - t ®-¥ .
In connection with this, in the asymptotic analysis of the infinity region of Minkowski spacetime (as well as any other asymptotically flat spacetime) can be divided into three basic types, as indicated by the arrows in Fig.3.6 :
Since each asymptotically flat spacetime has an asymptotic structure identical to Minkowski spacetime, the above classification of regions of infinity will generally apply to asymptotically planar spacetimes.
For clearly illustrate the asymptotic structure of Minkowski spacetime, it is useful to use the Penrose conformal method mentioned in §3.1. We perform a conformal transformation using the arctangent function applied to the quantities t+r and t - r, determining the type of asymptotic regions :
| h = arctg (t + r) + arctg (t - r), c = arctg (t + r) - arctg (t - r) . | (3.5) |
This is a transformation from the original time t and spatial radial r coordinates to new coordinates h and c , which have a final value even for infinite t and r . After this conformal mapping, the metric (3.3) has the form
| ds2 = {1/(4cos2[(h+c)/2].cos2[(h-c)/2])} (dc2 - dh2 ) + r2(dJ2 + sin2J dj2) , | (3.6) |
where r(h, c) = (1/2) [tg (h+c/2) - tg (h-c/2)].
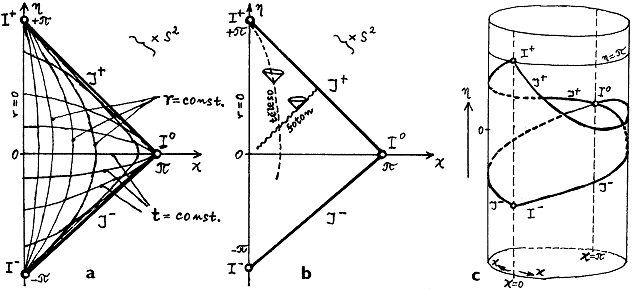
Fig.3.7. Conformal (Penrose) space-time diagram of Minkowski
space-time with omitted coordinates J and j .
a ) Coordinate lines in relation to the original
coordinates t and r .
b ) Shapes of light cones and isotropic and temporal
geodesics.
c ) A conformal image of Minkowski spacetime on
a cylindrical surface (which can represent a static Einstein
model of the universe).
The conformal spacetime diagram of Minkowski spacetime in coordinates h and c is shown in Fig.3.7. The whole infinite Minkowski spacetime is plotted on a finite region bounded by a triangle (so in fact the "double cone") with vertices h = ±p , c = p. The individual area of infinity are displayed on the vertices and sides of the triangle (ie on the vertices and mantles of the cones) - the boundaries of the conformal image :
| I+ s (c = 0, h = p) , I-
s (c = 0, h =
-p) , I° s (c = p, h = 0) Á+ s (c , h | c+h = p, -p < h - c < p) Á- s (c , h | c-h = -p, -p < h + c < p) . |
(3.7) |
The structure of said conformal image of Minkowski spacetime is even better captured in Fig.3.7c in the form of two triangles according to Fig.3.7a,b such that their vertices I° are identified. If the restrictive conditions - p < h + c < p , - p < h - c < p were not imposed on the coordinates h and c, we could consider equation (3.6) as the equation of a cylinder. Relevant restrictions then indicate, that it is a part of a cylindrical surface as shown in Fig.3.7c.
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||