Filters and filtering of scintigraphic data in nuclear medicine

FILTERS and FILTRATION in nuclear medicine

1. Introduction - essence and motivation of filtration, spatial and temporal filtration
2. Methodology of filtration - in spatial and frequency domain, Nyquist frequency
3. Filtration in back projection in SPECT tomographic scintigraphy
4. Types of filters in frequency domain
4.1 Low-pass filters - smoothing
4.2 Bandpass filters - focusing
5. Filter- mania: Which filter is the best?

1. Introduction

What is filtration?
By filtration, we generally mean the process by which a certain part of a given system is leaked and another part is retained or weakened. The tool for this filtration procedure is called a filter .
A simple example is the sieving of noodles, where a strainer-filter passes water and retains the noodles. In chemistry and other technical applications, different coarse or fine filters are used for different solutions - up to microfilters or "molecular sieves", which retain even the finest particles. In politics and the media, information is commonly "filtered" (or censored) in order to manipulate public opinion ... By data filtering we mean a nonlocal mathematical process that transforms  
  data in such a way that it strengthens structures of a certain character and weakens or suppresses others. With nonlocality mentioned here generally exists an inverse ( reverse) transformation , which would be capable of fully filtered data to reconstruct the primary data - there is a loss of information .

Why filter?
Scintigraphy, in spite of all its advantages, constantly faces two basic problems:

1. Imperfect resolution
   Unfortunately, for gamma radiation, there is no real "optics" (refractive or reflective) that would create an optical image based on refraction or reflection of rays, as is the case with visible light; only collimation can be used for display . The openings in the collimator and the partitions between them cannot be infinitely thin - already due to the radiation g radiation . Also, the evaluation of the flash position in the thin large-area scintillation crystal of the camera fails with a scattering of less than about 3 mm. The total resolution of the scintillation camera is thus in practice around 6 - 10 mm.
2. Statistical fluctuations (noise)
   Only a very small part of the radiation g (only those photons that fly exactly parallel through the holes of the collimator) is used for imaging, while the vast majority of the radiation escapes uselessly. The number of photons forming the scintigraphic image is thus relatively low, which due to the quantum-statistical nature of the radiation and detection of photons leads to statistical fluctuations of the detected image-forming pulses.

  Scintigraphic images are therefore (compared to, for example, photographic images) relatively poor quality - they are "blurred" and "noisy". Filtration is used to at least partially correct these adverse effects.

Spatial and temporal filtering
From the spatio-temporal point of view, we can basically perform two types of filtering of scintigraphic data:

• Spatial filtering - it is the actual filtering of scintigraphic images in spatial x, y coordinates. We will deal with this in this work.
• Time filtering - it is the smoothing and averaging of data in the time direction in dynamic studies. The simplest case is the simple summation of two or more consecutive images of a dynamic study, where we have more impulses and thus smaller static fluctuations in the resulting image. Furthermore, it is the smoothing of the curves of the time course of the distribution of the radio indicator in the areas of interest in order to suppress the statistical fluctuations of the points of the curves - to obtain "smoother" curves. We will not deal with this type of filtration here.

Spatial filtering of scintigraphic images has two basic goals:

• Smoothing - suppresses or reduces statistical fluctuations in the image. This is the overriding reason for extermination.
  Note: However, we can already mention one danger here : together with the suppression of disturbing statistical fluctuations, some factual and diagnostically valuable details of the image can be erased with stronger filtration!
• Design adjustments - increasing local contrast, improving resolution ("reconstruction" or focusing the image). Below we will see that achieving this goal is relatively difficult - it is only possible if the best possible statistical image quality is met.

2. Filtration methodology
In terms of the mathematical procedure of the filtration procedure, we distinguish two basic methodologies:

Spatial filtering
Each point of the image is "averaged" with its surrounding points, and the resulting value is stored back to the starting point. This reduces statistical fluctuations at each point of the image (given by the square root of the accumulated number of pulses) - a smoothed image is created. After smoothing, the value of the number of pulses of a given middle pixel partially adapts to the values ??in the surrounding pixels. In this procedure, the contents of the individual elements of the image are multiplied by appropriate weighting factors (the starting center point has the highest weight, the weight of the surrounding points decreases according to their distance from the center point), all values ??are added , divided by the sum of weights and stored back to the default center point. point. Filterthen we call the mentioned weighting matrix of averaging. A typical example is the well - known 9-point smoothing with a weight matrix:

Frequency domain filtering
The use of the frequency domain is based on the Fourier theorem , according to which each function f (x) can be decomposed into the sum of cosine and sine harmonic functions A.cos (2 pn x) (and similarly for sine) , where A is the amplitude harmonic function and n is its frequency (inverse of the period). The relevant graphs and formulas are shown in Fig. 1a. 2. Filtering in the frequency domain consists of 3 stages :

1. The image is first converted to the frequency domain i by the Fourier transform - it decomposes into harmonic functions (mostly cosine ones are used) - a frequency spectrum is created . It is graphically represented by a curve, where the horizontal axis shows the spatial frequency (in units of cycle/centimeter or cycle/pixel) and the vertical axis shows the amplitude of the corresponding harmonic function of this frequency.
2. In the frequency domain, this spectrum of the image is multiplied by a suitable function called a filter , which results in a local increase or decrease (or even cancellation) of the amplitudes of the respective harmonic functions - a filtered spectrum is created.
3. This filtered spectrum is converted back to the spatial region by the inverse Fourier transform - a filtered image is created .

   Fig.1. Mathematical procedure of filtration in spatial and frequency domain. Upper part: Methodology of filtration in the spatial domain by convolution with a filter. Lower part: Methodology of filtration in the frequency domain by filter multiplication.

  It can be shown mathematically (this follows from the formulas applied in Fig. 1) that both filtering methods - in the spatial and frequency domain - are equivalent and give an identical result if the frequency domain multiplication filter is a Fourier image of the convolutional filter in the spatial domain. Filtering in the frequency domain, although it is mathematically more complex (but the user does not know it - the computer will take care of it!), Has some advantages, which will result from further explanation. Here we will only state that the filters in the frequency domain can be flexibly changed by means of their form-factors, while according to the shape of the filter curve it is clear what effect it will have - which noises or details in the image it will eliminate.

The frequency domain is sometimes called the Nyquist region, according to the prominent Swedish-American expert Harry Nyquist ( ¶ 7.2.1889 in Sweden, V 4.4.1976 in Texas), who dealt with the issue of filtration in the field of electrical circuits - LRC filters composed of capacitors, inductances and resistors, filtering electrical signals as a function of frequency.

  The transition from the spatial domain to the frequency domain by means of the Fourier transform is shown in more detail in Fig.2. There are schematic images of two different structures: on the left is a large compact structure (lesion) with a gradual round shape, on the right a small structure (lesion) with a sharp profile. Below each of these images, its profile curve is shown. If we perform a Fourier transform, the large structure on the left will be dominated by low spatial frequencies of harmonic decomposition, while high frequencies will be represented only slightly (ie with low amplitude). For a small structure with a sharp profile (right), the relative proportion of higher harmonic frequencies will be much higher.

Fig.2. Transition from the spatial region to the frequency domain using the Fourier transform for the case of a large compact lesion (left) and a small sharp lesion (right).

If we plot graphically the representation of the amplitudes of individual harmonic functions depending on the frequency, a spectrum is created , which in the frequency domain represents the Fourier image of the original structure from the spatial domain.

Frequency K-space
In the spatial region , the usual Euclidean space - R-space - the image of the displayed quantity F is described by a distribution function , or field, F (x, y, z). In vector notation, by introducing the spatial vector r , this function is F ( r ). The general Fourier transform gives a new distribution function ^{^} F ( k ) = ò _V F ( r ) .exp [2 p i ( kr )] d r , where k = (k ₁ , k ₂ , k ₃) is a new frequency vector , scalar product kr = xk ₁ + xk ₂ + xk ₃ ; integrated over the spatial region V . The distribution function ^{^} F ( k ) is defined in a new linear 3-dimensional vector space. Both the spatial F ( k ) and frequency ^{^} F ( k ) distribution functions carry the same information and are related by a direct and inverse Fourier transform.
  From a mathematical point of view, from the common metric Euclidean R-space, the Fourier transform creates a new "frequency" space, sometimes referred to asK-space ( K-space - the name originated from the fact that after the Fourier transform the new independent variable is a "wave" vector which is used to denote k , it is generally complex). An abstract K-space is in a sense "reciprocal" to the usual physical R-space.

  Thus, in the lower part of Fig. 2 we see that a large compact lesion has a spectrum ending at low spatial frequencies, while the spectrum of a small sharp lesion also contains high spatial frequencies. This pattern has a general character: the more fine details are in the image, the higher the frequencies of the harmonic functions are represented in the frequency domain. The finest details in a scintigraphic image are statistical fluctuations ( noise ) that change chaotically from pixel to pixel - these correspond to the highest spatial frequencies in the Nyquist region. Therefore, if we use a filter that suppresses high frequencies, we remove disturbing noise from the image - this is smoothing using the so-called low-passfilters. The basic "art" here is to choose a filter that would suppress disturbing noise while preserving as many useful details in the image as possible.

  How to achieve such optimal filtration ? The regularities shown in Fig.3 can be a guide to us. The question is answered here: what highest frequencies in the Nyquist region can still express the real details of the distribution of the radio indicator shown by the camera, and what reflect only the interfering noise?

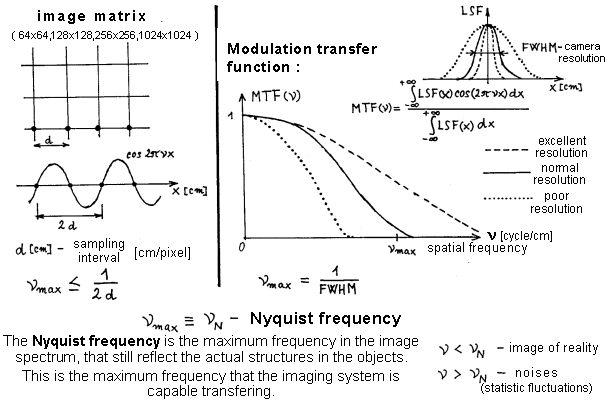Fig.3. To define the Nyquist frequency for a scintigraphic image.

The resolution of a scintigraphic image is in principle limited by two factors.

1. Image matrix
The fineness of the used matrix of scintigraphic image (whether we use the matrix 64x64, 128x128, 256x256, etc.) limits us how fine details we will be able to display with it. In the left part of Fig. 3 it is shown that if the pixel size of the matrix used is d (cm), then the highest frequency of the harmonic function that can be displayed in such a matrix is n _max £ 1 / 2d.

2. Camera resolution
The basic factor limiting the resolution in scintigraphy is the spatial resolution of the camera. Fig. 3 in the upper right shows the profile curves of the LSF image of a point radioactive source, displayed by a gamma camera with excellent resolution (dashed line), medium resolution (solid line) and poor resolution (dotted curve). The FWHM camera resolution is defined as the half-width of the profile curve of the PSF image of a point (or line) source. Two points shorter distances from each other than the FWHM resolution will no longer be recognized by the camera and will be displayed as one point in the scintigraphic image. From this point of view, the highest frequency of harmonic distribution of radioactivity (model), which the camera would still display, would be n_max £ ~ 1 / FWHM - at higher frequencies the individual waves of the (co) sine wave would already merge. The Fourier transform of the profile curve PSF(x) of the point source image produces a spectral curve called the modulation transfer function MTF(n), which shows with what relative amplitude the camera is able to display (transmit) the model harmonic distribution of radioactivity depending on its frequency n . The place where the MTF drops to zero then defines the maximum spatial frequency n_max , which the camera is still able to display.
  

We can therefore make the following statements and definitions at the same time :

  Thus, the Nyquist frequency is also the maximum frequency in the Fourier spectrum of the image, which still reflects the actual structures of the object. Frequencies lower than Nyquist reflect reality in the image , while frequencies higher than n _max no longer have their origin - they are the result of static fluctuations (noise) and can be removed without the risk of losing useful details in the image.
  The value of the Nyquist frequency can help us to optimize the "strength" of the filter: using form-factors (see below), we shape the filter graph so that it approaches zero just for the value of the Nyquist frequency. There is no point in maintaining a higher frequency in the image, because they cannot reflect any real structures, they only express disturbing noise.

Wavelet ( wavelet ) transform
Fourier harmonic analysis is the basis for advanced processing and design modifications signals measured závisloszí and images. Using the Fourier transform , it decomposes the analyzed signal or image into harmonic functions sine and cosine with different amplitudes and frequencies (Fig. 1 and 2), which it then suitably modifies and subsequently backwards (inversely) transforms. The Fourier transform provides information about frequencies which are in the signal (and their representation), but not about their location - time position at the signal or in the spatial (coordinate) place at the image. It is therefore especially suitable for the description of stationary signals or relatively uniform graphs and images without discontinuities and sharp fluctuations. For filters to eliminate interfering static fluctuations (noise), the main problem is the trade-off between the noise suppression rate while maintaining useful detailed information in the images (as mentioned above and will be discussed below in the " Low-frequency smoothing filters " section) . Stronger filtering effectively suppresses noise, but also leads to the risk of smoothing out smaller details in the image.
  The common denominator of these difficulties is the fact that the basis functions of the Fourier transform, sine and cosine, have non-zero periodic values ??in the whole spatial domain ("from - to + infinity") . Therefore, in Fourier filtering, any change in the frequency domain is reflected in the whole image (in the spatial domain): if we try to suppress or cut off certain higher spatial frequencies during filtering in order to reduce noise at the desired image location, it can be reflected in deterioration of spatial resolution throughout image.
Preferred generalization and improvement of standard Fourier transform is called. Wavelet ( wavelet ) transform  That instead of sine and cosine for the decomposition of the analyzed signal uses a special basis functions called wavelets or ripples that are more localized spatial coordinates and rapidly dwindling into infinity. Base functions have a limited length - compared to large sine waves they are only short "ripples" - and with variable frequency (scale) they can move over the entire spatial area of ??the signal: the analysis can be local with differently strong filtering at different points in the signal or image. A number of wavelet functions were created (some of them are in the picture - b, c, d). E.g. The Morlet wavelet is a cosine function multiplied by a Gaussian function with a suitable width.

Above: a) Cosine base function of Fourier transform. Bottom: Wavelets: b) "Mexican hat". c) Morlet. d) Meyer's

  When filtering scintigraphic images, wavelet transforms are so far used only sporadically and experimentally, but with promising results. In the following text, we will focus on standard filtering procedures using the Fourier transform.

3. Back projection filtration in SPECT tomographic scintigraphy
The general principles mentioned above have some specifics when applied to SPECT tomographic scintigraphic images reconstructed by back projection (treatise " Scintigraphy ", part " Tomographic scintigraphy ") . Fig. 4 schematically shows in the upper left part how the back projection of the unfiltered profile of the point source image projected at several angles (from which the point source was scanned during SPECT) creates a star artifact from the projection rays around the resulting image .

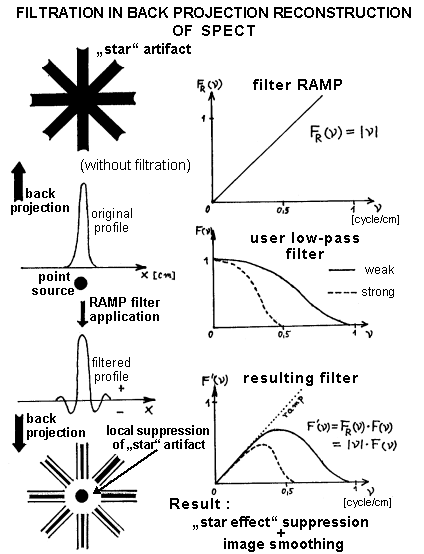Fig.4 Filtration for SPECT rear projection

  If we apply a suitable filter to the profile function of a point source in the spatial region such that at both edges of the curve there is an artificial "oscillation" into negative values (the magnitude of these negative values ??is directly proportional to the magnitude and speed of positive growth) , then the rays with the negative edges are superimposed so that at the intersection they again create a reconstructed "dot" image, but in its vicinity the negative half-waves locally disturb the rays of the star artifact. At greater distances from the point source image, the traces of the projection beams remain, but in principle it does not matter - they "mix" with other projection traces and create a common continuous background.
  In the right part of Fig. 4, this type of filtering is shown in the frequency domain.it suppresses the star effect locally , here it has a linear shape and is called a RAMP filter . The RAMP-filter is a necessary implicit part of every procedure for SPECT reconstruction by the back projection method *), but at the same time it amplifies higher spatial frequencies in the image - fluctuations, noise. If we also apply a user low-pass filter to suppress statistical fluctuations, the resulting filter is given by the product of the RAMP filter with the user filter (shown in the lower part of Fig. 4) - such a filter then suppresses the star effect and smooths the image .
*) The RAMP filter is not used for the iterative reconstruction method.

Fig. 5 schematically shows the whole procedure of acquisition, filtration and rear projection in scintigraphy by SPECT method.

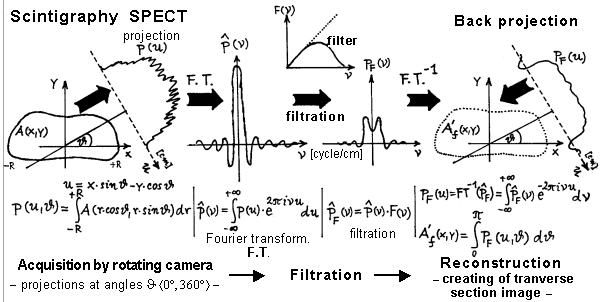
Fig.5. Acquisition, filtration and rear projection procedure in scintigraphy using the SPECT method.

  The examined object (patient), whose cross-section has the distribution of the radio indicator A (x, y), is captured by the camera in a series of projections at different angles J , thus creating images of projections p (u). These images are then Fourier transformed into the frequency domain, and the spectrum P ( n )) is multiplied by a filter comprised of a ramp-filter and the filtered spectrum user filtru.Výsledná P _F ( n ) is then inverse Fourier transform are converted back into the spatial area (the filtered result projection images p _F (u)), after which with back projection (at the same angles J ) it creates the resulting cross-sectional image A´_f (x, y).

4. Types of frequency domain filters
As follows from the previous explanation, frequency domain image filtering consists in multiplying the amplitude of each harmonic function (on which the image has been decomposed) f ( n ) by a certain coefficient, which decreases or amplifies its amplitude depending on frequency n . The set of these coefficients forms a specific filter. Each filter is implemented by a certain mathematical function F ( n ), which for each value of the spatial frequency n generates a coefficient F ( n ), which will multiply the amplitude of the corresponding harmonic in the image spectrum f ( n ). Functional prescription of filter F ( n) usually contains certain optional parameters - ie. form-factors , which together with the mathematical function determine the specific shape of the filter and thus the strength of the filter . Each type of filter has its specific form-factors, but one of the form-factors is common to all filters : it is a so-called " cutoff ", indicating the maximum frequency from which all higher harmonics will be cut (canceled) upwards.

4.1 Low-pas filters - smoothing
Scintigraphic images, especially reconstructed transverse sections of SPECT, often have a large scatter (fluctuation) in individual voxels - image noise. For a better evaluation of these images, it is desirable to reduce this noise - smoothing the image, suppressing statistical fluctuations. The individual structures in the scintigraphic image can be simply divided into three groups in the frequency domain:
- Low frequencies are given by the uniform activity of larger structures and backgrounds.
- Medium frequencies express changes in the number of pulses given by different distributions of the radio indicator in the displayed organs in the range of units up to tens of pixels - useful diagnostic information.
- The highest spatial frequencies express statistical noise - random changes in the number of pulses in adjacent pixels.
  In the frequency domain, we achieve image smoothing (reduction of statistical fluctuations) by attenuating or suppressing high- frequency harmonic functions - multiplying the spectrum by a suitable filter, which for low frequencies has a value close to 1 (leaves changes in the number of pulses corresponding to the structures of the displayed organ) and for high frequencies is approaching zero (suppresses statistical fluctuations in changes in neighboring or nearby pixels) . Such smoothing filters are called low-pass- they transmit mainly low frequencies and reduce (suppress) the amplitude of higher frequencies, ie statistical fluctuations in the number of pulses in adjacent pixels. However, in real images, the spatial frequencies of changes for individual structures usually partially overlap, so that suppression of high frequency noise can lead to the smoothing of real fine structures that also have higher spatial frequencies.
  The individual filters are characterized by a frequency curve, the course of which in different cities determines their action. Figure 6 shows the shapes and equations of the most commonly used low-pass filters. For some of them, a weaker filter is marked with a solid line, and a thicker filter with a dashed line.

Fig.6. The most commonly used smoothing (low-pass) filters.

The simplest filter is to simply cut off (cancel) the harmonic functions of frequencies higher than a certain maximum frequency n _N called "cutoff". The graph of such a filter has the shape of a rectangle - it leaves all frequencies up to n _N = cutoff with unchanged amplitude, while all harmonics higher than "cutoff" are cut off (canceled). The smaller the value of the form factor "Cutoff" = n _{N is} entered, the stronger the filter effect will be.
  The cosine function filter is also shown , which decreases continuously from the value F = 1 for the zero frequency n = 0 to the value F = 0 for the maximum frequency n _N (value "0" is then assigned to all higher frequencies). Thickness of the filter is again higher, the lower the value the form-factor of the "cutoff" = n _N enter.
  Other occasionally used filters are Hamming and Parzen (middle part of Fig. 6). Type filter is a modified Hamming cosine filter, and besides the parameter "cutoff" has one parameter and which controls the "steepness" with which the filter is close to zero in the vicinity of frequencies N ~ N _N . A Parzen filter is a combination of two polynomial functions: a faster descending function is used in the middle of the range, which is then smoothly followed by a slower descending part; the form factor is again a "cutoff".
  The most commonly used low-pass filter is Butterworth shown in the lower part of Fig.6. It has two form-factors - a cutoff indicating the spatial frequency of the cut *) and an order (" order ") regulating how steeply the filter drops from values close to 1 to zero. It is this high "ductility" that makes the Butterworth filter so popular.
Note: The " cutoff " value for the Butterworrth filter here is not arithmetically equal to the cut-off frequency, as is the case for other filters. For n = cutoff, the value of the filter is equal to 0.5, the Butterworth filter reaches exactly zero even in the limit for n ® ¥ . Effectively, the filter approaches zero for n values= 2 ´ "cutoff", the higher the "order" of the filter.
Filtration power
What are the common patterns of using low-pass filters? What determines their "strength"? In Fig. 7, the same scintigraphic image of the brain is filtered by a progressively thicker and thicker filter.

........ without filter ........................ weak filter .............. ........... medium filter ..................... thick filter .............. ..... very strong filter

. ........ without filter ........................ Buttw, ord = 13, cutoff = 0.82 . ..... Buttw, ord = 4, cutoff = 0.5 ........ Buttw, ord = 4, cutoff = 0.26 .... Buttw, ord = 4, cutoff = 0.15

Fig.7. The result of filtering an image of the brain using filters of different strengths

The sooner the filter goes to zero (at lower spatial frequencies), the stronger the filtering effect. The following theorem holds :

Note that this is exactly the opposite of the spatial region , where the filtration force is directly proportional to the area under the convolution filter graph! Advanced reconstruction algorithms for SPECT and PET also use more sophisticated methods that perform differently strong filtering at different points in the image (cf. " Wavelet transform ") .

4.2 Bandpass filters - focusing
Filtering in the frequency domain allows not only smoothing of images by reducing higher harmonic frequencies. Conversely , if we amplify their amplitudes for a certain part of the higher harmonic frequencies , we can increase the local contrast and " sharpen " some details in the image that have been "blurred" due to imperfect camera resolution. Such bandpass filters amplify the mid frequencies and attenuate the high and low frequencies, increasing the contrast of the objects in the image.

Is it possible to completely reconstruct reality by artificially focusing an image?
The image is created by the convolution of the original distribution (object) and the response function of the imaging system. From a theoretical point of view, using an inverse procedure - image deconvolution - it should be possible to completely reconstruct all the details of the original object, even those that are smoothed in the image by imperfect spatial resolution (this procedure is called " resolution recovery ").
  The following image shows the testing of this method at our workplace in 1977 on a Pho Gamma Nuclear Chicago scintillation camera with a Clincom evaluation device and its own software. Radioactive sources (one 2.5 cm diameter dish and 4 1 cm balls) filled with a ^99m Tc solution with different specific activities were placed under the scintillation camera - the profile of their actual activity is in the picture on the top right "Original distribution".  Long-term acquisition (approx. 12 hours) gave a very smooth scintigraphic image (profile on the right in the middle), without visible statistical fluctuations, on which the details of the sources are not visible due to poor resolution (scanned 20 cm from the collimator front). The modulation transfer function MTF (  
      
n) of the camera and the Fourier transform FT of its inverse value 1 / MTF ( n ), the reconstruction filter R (t) in the spatial region was calculated (bottom left figure). By convolving the scintigraphic image with this filter R (t) in the spatial area, I obtained a reconstructed image (bottom right profile), on which the initial original distribution is almost perfectly reconstructed in detail. On closer inspection, however, we see tiny "ripples", especially in flat areas. These do not correspond to reality - they are artifacts created by the amplification of hidden statistical fluctuations. Due to very good "statistics", unattainable in practice, these artifacts are minor. However, it will be shown below that in practice these artifacts are a limiting factor focusing and "reconstruction" of images.

  Filters that, in addition to smoothing statistical fluctuations, are able to focus and highlight details in the image are shown in FIG. and are referred to as bandpass filters (behaving differently in different frequency bands) .

Fig.8. Band focus filters

They differ from low-pass filters in that they do not decrease from F ( n = 0) = 1 monotonically to zero, but consist of two parts :

1. The initial ascending part , which leads to the amplification of higher frequencies and thus to focusing - "focusing" on details in the image.
2. It is continuously followed by a decreasing part (analogous to low-pass filters), ensuring the suppression of higher harmonics - and thus the smoothing of statistical fluctuations (noise).

  The two most commonly used bandpass filters - the Metz type and the Wiener type - are largely similar. The ascending part is derived from the inverse value of the modulation transfer function MTF and provides according to the theory of scintigraphic imaging optimal reconstruction ( deconvolution - image correction to convolutional "blur" by imperfect camera resolution) and image focus - so-called resolution recovery RR , " resolution recovery " - see. treatise "Scintigraphy", passage " Adverse effects of scintigraphy " .
  Form factor " k " (" order") allows you to continuously adjust the relative representation of the ascending (focusing) component of the filter, while the usual parameter" cutoff "determines the representation of the descending (smoothing) component of the filter. part is missing - low value of parameter "k" - "order", the filter only smoothes similarly to any other low-pass filter (first part fig.9).

..... Metz, cutoff = 1, ord = 3 . ......... Metz, cutoff = 1, ord = 10 ....... Metz, cutoff = 0.74, ord = 30 ..... Metz, cutoff = 1.8, ord = 90

Fig.9. Filtration by a band focus filter of various strengths

  However, the focus of the image cannot be increased indefinitely - with a high proportion of the ascending focusing part of the filter, artifacts begin to appear in the image - false structures caused by the amplification of statistical fluctuations; when attempting high focus, the image eventually disintegrates into a system of islands, many of which are not related to the actual distribution of the radio indicator (last part of Fig. 9).
We must therefore point out that :

Note: Filters of this type are also used in photo image processing programs (such as Photo Shop) in the "Sharp" function. Statistical fluctuations are usually low here (visible light photons are 3-6 orders of magnitude more than gamma photons), but for example night images may have similar problems as a scintigraphic image and additional focus may unacceptably increase the "graininess" of the image.

5. Filter - Mania: Which filter is the best ?
In the literature, various authors often recommend certain filters (filters of certain names), which gives readers the general impression that some filters are a priori better than others. They then embark on laborious experiments with filters and literature searches, hoping to find some guaranteed best " miracle " filter that will produce perfect images for them. Here we show that all this is just a deceptive appearance .
  For an objective analysis, it is necessary to realize that it does not filter the name of the filter , or even its mathematical equation - it only generates coefficients by which for individual spatial frequenciesn will multiply the amplitude of the corresponding harmonic function in the spectrum in the Nyquist region. Therefore, if we set different filters - with different names and different functional expressions - using form-factors so that their graphs converge, the result of the filtering will be identical .
Note: I do not list the relevant image here - it would be an uninteresting series of identical images. However, everyone can try that eg Sheep-Logan-Hamming filters with parameter cutof = 1.0, Parzen with cutof = 1.2, Hamming with cutof = 0.9, a = 0.5 and Butterwoth filter with parameters cutof = 0.4, order = 1.5 have almost the same graphs and give the same results when applied to scintigraphic images .
  This rule goes even further. In Fig. 10, the same brain image is filtered by three different filters - filters of different names and different shapes of its graph - but chosen so that the area under the filter curves is approximately the same ; this can be achieved by targeted tuning of form-factors. We see that the result of filtration is almost identical , despite the considerable differences in functional regulations and the shape of the graphs of individual filters.

.... Band-Lim, cutoff = 0.51 . ......... Cosine, cutoff = 0.80 .... ....... GenHann, cut = 0.97, a = 0.5 . ... Butt, cutoff = 0.49, ord = 5

Fig.10. Filters of different names and shapes give almost the same result if they have the same area

  These interesting laws are not generally known (nor are they described in the literature) and seem surprising at first glance; however, they are consistent with the theoretical analysis. The lesson is that "filter mania" has no justification , at least for low-pass filters.
  So to the question " Which filter is the best? ", Asked in the title of this paragraph, we can easily answer: None! With each of the used low-pass filters we can achieve practically the same result by suitable setting of their shaping parameters , it only requires experience and critical thinking.

  And finally, I would like to take one more piece of advice *): Let's not try to change the filters often during the practical evaluation of scintigraphic images! - this would impair the reproducibility of the images, especially when comparing in repeated examinations. When starting work with a new system, it is best to start with certain recommended or previously proven filters (eg Butterworth, order = 3, cutoff = 0.4) , try them out properly (and possibly modify them) and then use them for a long time . Only when there is a serious reason (change in methodology, equipment, sufficient accumulation of experience, etc.) , it is reasonable to change the filter used for the examination. And of course we can purposefully try different filtration when we are looking for some atypical anomalies in the image ...
*) Perhaps I can afford to give some modest advice - I am probably the oldest "witness" of the filtration of scintigraphic images in the field of nuclear medicine in our country. From a physical-mathematical point of view, I actively dealt with the issue of filtration around 1976 in connection with the theory of scintigraphic imaging and modulation transfer functions .

Risks and pitfalls of image filtering
Once again, a warning about image filtering:
An old Czech proverb says: " Where there is nothing, the devil doesn't take it ".
For our example, this proverb paraphrase as follows:
" Where there is nothing, there the devil can deliver - an artifact !
" - the devil, in the person of excessive filtering , highlighting the statistical fluctuations adds artifacts -
And where something is , there's the devil can muster :
An exaggerated filtration smooth out the details in the picture !

This work was lectured at seminars and symposia of the Czech Society of Nuclear Medicine and is a regular part of postgraduate courses and seminars for the field of nuclear medicine within the IPVZ at KNM in Ostrava.

Computer evaluation		Complex programs

Vojtech Ullmann