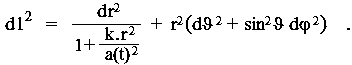 |
(5.21) |
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | Gravity, black holes and physics |
Chapter 5
GRAVITATION
AND THE GLOBAL STRUCTURE OF THE UNIVERSE :
RELATIVISTIC COSMOLOGY
5.1. Basic
starting points and principles of cosmology
5.2. Einstein's
and deSitter's universe. Cosmological
constant.
5.3. Fridman's dynamic models of the universe
5.4. Standard
cosmological model. Big
Bang.
5.5. Microphysics
and cosmology. Inflationary
universe.
5.6. The
future of the universe. time
arrow. Dark matter. Dark
energy
5.7. Anthropic
principle and existence of multiple universes 5.8.
Cosmology and physics
5.3. Fridman's dynamic models of the universe
Obviously, the real universe, at least at its current stage of development, cannot be described by any of the models based on the assumption of static, because in Einstein's model there is no redshift of light from distant galaxies, and in de Sitter's model space cannot contain any matter or radiation. To model the real universe, it is therefore necessary to abandon the assumption of static (which is incompatible with current astronomical knowledge) and create a more general time - dynamic cosmological model.
Metrics of
a non-stationary homogeneous isotropic universe
We will therefore consider a homogeneous isotropic universe,
which will generally not
be stationary. The metric of three-dimensional space (ie the spatial part of the interval) in such a case will again have a
homogeneous isotropic general shape (5.4), but the radius of
curvature a here will generally be a function of time
a(t) :
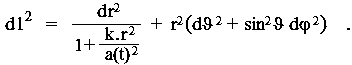 |
(5.21) |
Recall that originally in relation (5.4) we
marked the value of the curvature of the space "R" (R :
->
a) as "a". However, in an application to a dynamically
expanding universe, a(t) will become important as a scale
expansion factor. The length element (5.21) is sometimes
modified to a shape in Cartesian
coordinates, in
which it is proportional to the corresponding Euclidean
expression (however, this is for
illustration only, it is not relevant for cosmological analysis). This can be done by
introducing a new coordinate r
using the transformation r ®
r/(1 + r2/a2). The spatial metric (5.21) then has the form
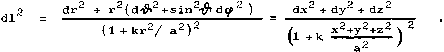 |
. |
It is natural to choose a spatial reference system to reflect the isotropy of space as well as the distribution and motion of matter. Thus, the most suitable is a locally "parallel - concurrent" reference system moving in each place of space together with the matter contained therein. The coordinates are "carried - drifting" along with the expansion. The local velocity of matter in such a system is thus zero everywhere, the reference system is formed by the matter filling the universe itself. All motion of mass is expressed by deformation of reference system (cosmological "mollusc"). It is therefore appropriate to transform the spherically symmetric coordinate system by replacing the original radial coordinate r with a parallel (concurenz) coordinate: r(t) ® r(t).a(t). Or, because the radius of curvature a can be used as a natural unit for distance measurement, it is advantageous to introduce new dimensionless coordinates r ® r/a, in which the length element has the shape
| (5.21 ') |
The distance dl
between any nearby points is thus proportional to the a(t) - scale factor, so that increase or decrease a(t) over
time means increasing or decreasing all distances in the system -
expanding or shrinking all matter carried by space (cf. discussion in §5.4, passage
"What expands during the
expansion of the universe? (And what does not expand)").
It is advisable to choose the
time coordinate so that the space metric is the same at all
points and in all directions at all times. In
order for all
directions to be equivalent, the components goa of the metric tensor must be zero in this
reference frame. The space-time metric will therefore have the
form ds2 = goo dx°2 + dl
2. The
coefficient goo is a function of only x°, so goo = -1 (= -c2) can be achieved by a suitable
choice of the time coordinate. The time coordinate x°, which we
can denote by t , then gives its own time at each point
in space. The space-time interval here will have the simple form
ds2 = -c2 dt2 + dl
2.
The spacetime
geometry of a homogeneous isotropic universe
can therefore be generally written in the form of the so-called Robertson-Walker-Fridman metric
:
| (5.22) |
where a(t) is the scale factor, k is a
parameter of the type of curvature of space and r is the
radial coordinate in the above-mentioned
"parallel-concurent" reference system, in spherical
coordinates (r,J,j) with the
origin r=0 at any point. All time dependence - the evolution of
the universe - is contained here only in the scale factor a(t).
As early as
the mid-1930s, H.P.Robertson and A.G.Walker showed, that the
expression of type (5.22) is the most general metric
that can describe an expanding homogeneous and isotropic
universe.
To determine the time evolution of a (t), we use
Einstein's equations, where we substitute the necessary
components of the Ricci curvature tensor Rik and scalar
curvature R, which we calculate from metric (5.22) (using the methods from §2.4).
The non-zero components here are :
Rtt = -3.ä/a ; Rrr = [(a.ä + 2..a2)/c2 + 2k]/(1-kr2) ; RJJ = r2.[(a.ä + 2..a2)/c2+ 2k] ; Rjj = r2.[(a.ä + 2..a2)/c2+ 2k].sin2J ;
R = 6.[ä/(c2.a) + .a2/(c2.a2) + k/a2] ,
where each dot above a represents a derivative according
to time t .
Fridman´s equations of
universe evolution
Equation of evolution of the
universe resulting
from general Einstein equation (5.7) Rik - 1/2 gik R - L.gik = 8pTik , where we substitute
the components of the tensor of
energy-momentum Tik, the components of metric
tensor gik and the Ricci curvature tensor Rik for metric (5.22) (calculated
above). The
energy-momentum tensor Tik of the
cosmological "gas" (3.3) in everywhere locally
quiescent reference system has non-zero components only Too = r. c2, T11 = T22 = T33 = -p , where in a homogeneous and
isotropic universe the density r and
pressure p can be functions only of time t. Einstein's equations (5.7) for
the metric (5.22) then lead to two differential equations after
adjustment - they are important
| Fridman's equations : |
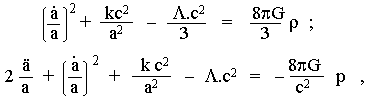 |
(5.23a) (5.23b) |
which are the basis of relativistic cosmology. Together with the equation of state p = p(r) of a cosmological substance (gas, liquid, plasma, radiation), these equations make it possible to determine a, p, r as a function of time t , ie to determine the evolution of the universe. Each dot above a denotes the derivative by time. Both of these equations are related by identity
| d ( r .c 2 a 3 ) / dt = - p. d (a 3 ) / dt , | (5.23c) |
which is an expression
of the local law of conservation of energy .
Orthographic note
:
In the literature, the author's name is usually written "Friedmann",
but the Petersburg's author of cosmological equations was
actually written "Fridman" (![]() ).
).
The basic cosmological equations (5.23) are also given under the
abbreviation FLRW (Fridman–Lemaitre–Robertson–Walker)
equations, after the names of the authors who in the years
1920-30 dealt with the analysis of the dynamics of relativistic
cosmological models.
Fridman's equations
(5.23) are an exact solution of Einstein's
equations of general relativity for a homogeneous and isotropic
universe with Robertson-Walker metric (5.22), filled with a
substance with density r, showing pressure p (according
to the corresponding equation of state),
with energy-momentum tensor (5.3).
In relativistic cosmology, instead of absolute values of time changes of the scale factor . a = da/dt, ä = d2a/dt2, relative quantities derived from them are often introduced, which can be (at least in principle) directly measured from astronomical observations. The Hubble constant H *) is used as a measure of the relative rate of change of the radius of curvature, i.e., the rate of expansion (or hypothetically also compression); a more apt name should be Hubble speed parameter :
| H =def .a(t) / a(t) . | (5.24) |
*) The quantity H is called a "constant" only in the sense that it is the same for all places (it does not depend on the coordinates); in general, however, is a function of time H(t). A more apt name is therefore the Hubble speed parameter. The current value of the Hubble constant Ho was estimated mostly in the range Ho ~ (50 ¸ 100) km s-1/megaparsec. Newer astronomical measurements give a more precise value :
| H 0 ~ 70 km s -1 / megaparsec . | (5.24´) |
In addition to the "classical" Hubble constant H, the so-called reduced dimensionless Hubble constant h, normalized to a speed of 100 km s-1/Mpc, is sometimes used :
| h = def H 0 / 100 km s-1 / Mpc . | (5.24´´) |
The Hubble constant H was already
introduced in §5.1, relation (5.2), as a coefficient of
proportionality in Hubble's law of expansion, which
determines by how much the velocity [km/s] of a distant cosmic
object (galaxy) increases when its distance increases by 1
megaparsec.: v = H . r, where r is the
distance and v is the retraction speed. The velocity of
the distance is astronomically measured on the basis of the
Doppler effect using the redshift z = Dl/l - the relative
increase of the wavelength l
of radiation of this galaxy: for z <1 it
is approximately v ~ c . z; the exact
relationship between the retraction speed and the redshift is v =
c . [(z+1)2 -1] / [(z+1)2 +1].
Furthermore, the so-called deceleration parameter q is introduced
| q = def a. ä / . a 2 | (5.25) |
characterizing the slowing or acceleration of expansion or contraction. Using the quantities H and q, Fridman's equations (5.23a, b) can be expressed in the form
| k.c2/a2 = 8pGr/3 - H2 + L.c2/3 , k.c2/a2 = (2 q - 1) H2 + L.c2 . | (5.23'a, b) |
Dynamics
and evolution of cosmological models
Using Fridman's equations, it is possible to analyze the dynamics of the expansion of
a(t) of the universe, depending on the mass density of matter r, its equation of state p(r) and the cosmological constant L. Let us first notice the simpler case L = 0 , without the cosmological constant :
From equation (5.23'a) it can be
seen, that the sign of 8pG.r/3 - H2, ie the relationship between
mass density and expansion rate, decides which of the variants k =
1, 0, -1 can be realized.
The case k
= 1
corresponding to a closed universe occurs when 8p G.r/3 > H2, ie when the mean mass density r in space is greater than a certain "critical density" rcrit
| r crit = 3 H2 / 8p G . | (5.26) |
Based on currently
observed galaxy distance rates (Hubble constants), this critical
density is approximately 8.10-30 g/cm3, which corresponds to only about
5 hydrogen atoms per 1 m3.
If r <
rcrit => k = -1 - it is an open
universe,
in the boundary case r = rcrit we have k
= 0 - it
corresponds to the Euclidean
universe,
which is also open. Equation (5.23b) shows that the equivalent
criterion for the curvature character of the Fridman universe is
the value of the deceleration parameter q: in a closed universe it is q>
1/2, in an open universe q <1/2 and in the Euclidean universe
it corresponds to q = 1/2. These variants will be analyzed in
more detail below.
In the limit case r = rcrit will be k = 0 , the universe has an infinitely large radius of curvature - it is a model of an open universe with flat space (Euclidean). Spacetime metrics have a simple shape here
| ds 2 = - c 2 dt 2 + a 2 (t) . (dx 2 + dy 2 + dz 2 ) , | (5.27) |
whereas the time-varying
coefficient a(t) does not express the curvature of space, but is
only a scale factor.
It should be noted
that although the Euclidean metric of three-dimensional space is obtained for the r
= rcrit , the whole four-dimensional
space-time is not flat here! Only certain special sections (hypersurfaces) of spacetime are flat, corresponding to
the same proper time of all particles filling the
universe.
Fridman's equations have an
accurate analytical solution in the case of a universe filled
with an "ideal fluid" with the equation of state
| p = w. c 2 . r , | (5.28) |
where p is the pressure, r is the mass-energy density of the fluid (in a locally quiescent reference frame) and w is the state constant. The energy-momentum tensor Tik was given in §5.1, relation (5.3). The time dependence of the scale function a(t) is then obtained by substituting p into Fridman's equation (5.23a). In our case k = 0 has a simple form
| a (t) = a 0 . t 2 / [3 (w + 1)] , | (5.29) |
where a0 is the corresponding integration constant depending on
the initial conditions. We can distinguish two basic cases here :
w = 0 corresponds to incoherent dust that does not create any pressure, p = 0. The
universe is controlled by matter, where the pressure is
negligible due to the density of matter - it corresponds to the
late stages of evolution. Then it follows from the general
solution (5.29) that the distance between every two points increases with time according to the law
| a (t) = a 1 . t 2/3 , a 1 = ...... | (5.30) |
w = 1/3 - radiation dominant universe. In the early stages of the evolution of the universe, which is to be considered the maximum pressure p =r.c 2 /3 of (5.29) for the expansion we get the time dependence of the shape
| a (t) = a 2 . t 1/2 , a 2 = ...... | (5.31) |
In both cases space with dominant agent or radiation at r = rcrit dependence a = a(t) here has the shape of a parabola (Fig.5.3) - radius of curvature a increases monotonically from zero (a singularity!) at t = 0 to infinity when t®¥.
If r > rcrit , is k = 1 - this is the closed universe. Equation (5.23a) for k = 1 , L = 0 has the form .a2 + 1 = a2.8p G.r/3. If the universe is filled with incoherent dust, ie p = 0, it follows from equation (5.23c) r.a3 = const.; since the volume of a closed universe is V = 2p2 a3, the sum of mass in the whole space is constant:
| r . 2 p 2 a 3 = M = const. = 2 p 2 a o 3 r o , | (5.32) |
where ao and ro are the radius and density of the mass of
the universe at some fixed point in time to.
The function a (t) is often
expressed in parametric form. After introducing a new
"time" variable h, by substituting dh = a.dt, the solution of equation (5.23a)
can be written in parametric form
| a = (4GM / 6 p c 2 ). (1 - cos h ) , t = (4GM / 6 p c 2 ). ( h - sin h ) . | (5.33) |
The graphical representation of the time dependence a = a(t) is thus a cycloid (Fig.5.3a), which describes a fixed point on a circle of radius
| a max = 4GM / 3 p c 2 | (5.34) |
when rolling along a
straight line (time axis t); the parameter h is the rolling angle. The density of the
mass changes according to the law r =
3/a2max(1 - cos h)3 = 6H2/8pG(1+cos h). In Friedman's model of a
closed universe filled with dust with density r > rcrit , evolution looks so (Fig.5.2)
that at the beginning t = 0 the universe is
based on an initial singular state a = 0 with zero volume and infinite mass
density, gradually expanding to to dimension a = amax , and then shrinks again to the
point a = 0 - terminal
singularities.
According to the left part of Fig.5.2, the evolution of the
universe is often modeled by an inflating balloon
(and then shrinking), on the surface of which galaxies or
clusters of galaxies are drawn. In such an inflation of the
balloon, all points of its surface move away
from each other at a speed proportional to their distance from
each other, in accordance with Hubble's law (5.2). A critical
assessment and refinement of this model will be discussed in the
following §5.4, passage "What is actually
expanding?".

Fig.5.2. Temporal evolution of a closed universe.
Left : The closed Fridman universe can be
imagined as a three-dimensional sphere that gradually
"inflates" from zero radius (initial singularity at
time t = 0) to a certain maximum radius, and then shrinks back to
a point (final singularity). All distances Dl between any
objects (galaxies or clusters of galaxies) increase or decrease
in proportion to the radius of curvature as the universe expands
or contracts.
Middle : A space-time diagram of a closed universe
nested in a fictional five-dimensional space.
Right : An illustration of expanding and
contracting matter during the evolution of the universe.
However, in the stages a ® 0, ie at the beginning and at the end of evolution, the assumption of the equation of state of incoherent dust is not realistic. Conversely, a substance are inevitably becomes ultrarelativistic, so closer to reality is the state equation p = r.c2/3. Equation (5.23c) then gives r .a4 = const. and the solution of equation (5.23a) is here
| a = a ~ . sin h , t = a ~ . (1 - cos h ) / c |
(the graph is a semicircle), where a ~ = Ö(8p G. r. a4/3c4) = const. = Ö(8p G.ro ao4/3c4) . The global nature of evolution will be the same as in the previous case - no pressure of matter filling the closed universe is able to prevent singular points a = 0.
If r < rcrit , then k = -1 - it is an open universe. If it is filled with dust, the solution of equation (5.23a) is
| a = â. (cosh h - 1) , t = â. (sinh h - h ) / c , |
where â = 8p G. r a3/3c2 = const. = 8p G. ro ao3/3c2). The dependence a = a(t) here has the shape of a hyperbola (Fig.5.3a) - the radius of curvature a grows monotonically from zero (singularity!) at t = 0 to infinity at t®¥. A similar picture is obtained when the effect of pressure is included; the extreme case p = r .c2/3 is a solution
| a = a ~ . sinh h , t = a ~ . (cosh h - 1) / c . |
Thus, Friedman's open universe also has a singularity, but only one thing - the initial one.
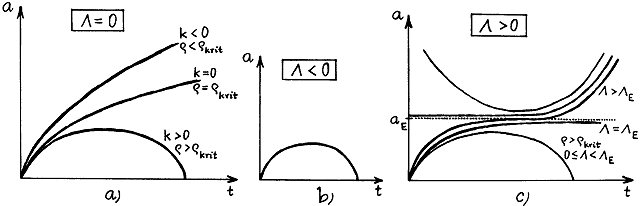
Fig.5.3. Evolution of cosmological models (time course of radius a
of space) depending on the value of
the cosmological constant L and the density of mass distribution r .
(aE and L
E in the figure on the right denote the
values of the radius of the universe and the cosmological
constant corresponding to Einstein's cosmological model)
In addition, when a non-zero cosmological constant L is included, a certain additional force appears in the universe (repulsive for L > 0 and attractive at L <0), which accelerates or slows down
the expansion or contraction of the universe. This force does not
depend on the weight and increases with distance. From the point
of view of the global evolution of the universe, the effective energy of the vacuum, generated by the cosmological
member, has an important property (different from the material
form of matter) - it does not
dilute or thicken during the expansion or contraction of
the universe, it maintains a constant value. The solution of equations
(5.23) then at L ¹ 0 leads to the following
possibilities :
If L <0 , gravity always ultimately prevails and the evolution of the
universe has a course according to Fig.5.3b at any mass density r. This variant probably does not apply in space. More varied possibilities of
space evolution arise at L
>
0 - are shown in Fig.5.3c :
- If the cosmological constant L <
LE
is less
than the Einstein value (5.15) L E = 4p G.r/c2, for supercritical density r > rcrit evolution of the universe to
proceed roughly (qualitatively) as for L = 0.
- At L > LE the a(t) increases from zero to
infinity, but at a certain stage the expansion slows down significantly for a time - there is a
kind of "quasi-static the phase" during which the attractive
forces are balanced by the repulsive ("indecisive" universe);
later dominated by the repulsive force *). The duration
Tst of this quasi-static phase, during
which the radius of curvature of the universe is maintained
approximately at the value of the radius of the Einstein static
model (5.16) a = aE, is longer
the smaller the difference L -
LE
: Tst ~ ln [L/(L - LE)].
- With L®LE
, the
universe enters the state of Einstein's static universe mentioned
in the previous paragraph. However, this Einstein model is unstable because the slightest perturbation of
density will lead to expansion.
For r > rcrit and L = LE there are two other solutions :
1. In the infinitely distant past t®-¥ was a = aE, in the future unlimited
expansion (unlikely variant) ;
2. The
universe come out of the state a(0) = 0 at time t = 0, after which it expands and asymptotically (at infinitely
distant future t®¥) reaches a radius a®aE.
For L > 0 exists, in
addition to the special
possibilities mentioned, there is also solution, according to which
at t = -¥ universe was infinite radius,
then the contraction took place up to a
certain minimum
value of amin, after which unbounded expansion occurs (an unlikely scenario).
The mentioned peculiarities of
cosmological models with non - zero cosmological constant are used from
time to time in attempts to overcome the supposed or real
difficulties of relativistic cosmology (internal difficulties and
inconsistencies with the results of observations) - cf. §5.5 "Microphysics and Cosmology.
Inflation Universe.", or §5.6, section "Dark
energy and accelerated expansion of the universe".
Three basic dynamics of
the scale factor - summary
For the astrophysically plausible scenario of evolution of our
universe (according to the standard model of physical cosmology -
§5.4), three basic dynamics should be applied in individual
stages of evolution - three time dependences of the scale factor
a = a(t), resulting from solving of Fridman equations (5.23) :
- The
era of radiation - radiation dominant plasma ,
when the material content of the universe is dominated by
radiation and relativistic particles, arousing pressure p=r.c2/3. The time dependence of the scale function a(t) is then
a(t) ~ t
1/2 .
This situation was in the early hot universe (after inflation expansion) and
lasted (in "pure form") for about 50,000 years.
- The
era of matter ,
when the energy density of a substance (non-relativistic
particles, gas, dust) is greater than the
energy of radiation. The time dependence of the scale function
a(t) is here
a(t) ~ t
2/3 .
Both of these dependences have a similar parabolic shape
according to Fig.5.3a (k >= 0). Proportionality coefficients depend on the specific
substance content. The era of matter in the universe is still
going on now ...
- Vacuum
energy stage - cosmological constant
when the density of matter and radiation is negligible compared
to the vacuum energy generated by the cosmological member L.gik in the gravitational
equations. The time dependence of the scale function a(t) is then
exponential
a(t) ~ e H . t ~ e Ö(L/3) . t
and in fact corresponds to the special case of de Sitter's
model. In §5.5 "Microphysics and Cosmology.
Inflation Universe." we
will see that this situation probably occurred in a very early
universe, just after the Big Bang in a time range aprox. 10-36 ÷ 10-32 sec. - inflationary
expansion of the early universe. And then it may happen
again in the very distant future - accelerated expansion
of the universe, when the density of matter and
radiation drops to very low concentrations due to the expansion
of the universe and "dark energy", generated
by the cosmological constant, begins to dominate (§5.6, section "Dark
energy and accelerated expansion of the universe ").?..
Relative Omega - parameterization of
cosmological models
Instead of absolute values of mass density and cosmological
constant, their dimensionless relative
ratios W with respect to their respective
significant (critical) values are often used to model the
evolution of the universe. The ratio of the actual value of the mass density r with respect to the critical density is
introduced :
| W M = def r / r crit (= r . 8 p G / 3 H 2 ) | (5.36) |
and the ratio of the actual value of the cosmological constant L to the Einstein value :
| W L = def L / L E (= L. c 2 / 3H 2 ) . | (5.37) |
Fridman's equation (5.23a) expressed by the parameters W is as follows :
| k.c 2 / H 2 a 2 = W M + W L - 1 . | (5.38) |
The deceleration parameter q, introduced by equation (5.25), is expressed by the parameters W :
| q = W M / 2 - W L . | (5.39) |
For WL = WM/2 the expansion takes place at a constant speed, at WL < WM/2 the expansion slows
down, at WL > WM/2 the expansion accelerates.
Using dimensionless W
values, it is easier to test the evolution
of a cosmological model. E.g. for a flat model, WM + WL = 1. It
is also possible to construct clear graphs of the behavior of
cosmological models in coordinates, on the axes of which the
values WM and WL are
plotted .
Sometimes an even more detailed W- parameterization of the
cosmological model is introduced. The general mass density r (rM) is divided into a substance formed by non-relativistic
particles rm (especially baryons - also
denoted by rB) and relativistic particles and radiation rrad
(in the early stages of the universe it is high-energy gamma
radiation, also denoted by rg). With W -option further expresses
the curvature parameter k . The basic Fridman equation
(5.23a) for the rate of expansion of the universe is then written
in the form :
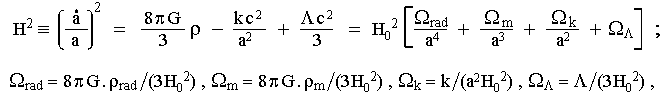 |
(5.40) |
where Wxxx are the contributions of the individual components of matter ~ energy to the dynamics of expansion: Wrad from relativistic particles and radiation, Wm from non-relativistic matter, Wk from the curvature of space and WL from the cosmological constant - "vacuum energy". The parameter H0 » 67 km s1 /Mpcs is the current value of the Hubble constant.
--------------------------------------------------
---
Current note:
According to recent astronomical observations of distant
supernovae, there are some indications that the expansion
of the universe is currently accelerating,
that in addition to ordinary and dark (non-radiant) matter, there
is also so-called dark energy in universe, which
shows "antigravity". Thus, the evolution of the
universe seems to follow the curve in Fig.5.3c, the case of L > LE (see §5.6 "The Future of the
Universe. The Arrow of Time.", the passage "Dark
Energy and the Accelerated Expansion of the Universe"),
corresponds to WL > WM/2 ...
| 5.2. Einstein's and deSitter's universe. Cosmological constant. | 5.4. Standard cosmological model. Big Bang. |
| Gravity, black holes and space-time physics : | ||
| Gravity in physics | General theory of relativity | Geometry and topology |
| Black holes | Relativistic cosmology | Unitary field theory |
| Anthropic principle or cosmic God | ||
| Nuclear physics and physics of ionizing radiation | ||
| AstroNuclPhysics ® Nuclear Physics - Astrophysics - Cosmology - Philosophy | ||