Back: List of complex programs
3.2 Comprehensive evaluation
of radionuclide angiocardiography
Using radionuclide
angiocardiography, we examine the dynamics of blood flow
through the central circulation , ie through the heart
cavities, large vessels and lungs. The examination consists of
scanning the transit and dilution of the radioactive bolus with the right heart, lungs, left heart and
systemic circulation with a scintillation camera . Computer
processing creates images of significant phases of bolus flow and
curves of time transit and bolus dilution in the ventricles and
lungs. On scintigraphic image we can visually monitor the flow of
radioactive bolus different parts of the heart and lungs, and
thus recognize any serious abnormalities in the central cicirculation
and some anatomical abnormalities. Mathematical processing and
dilution curves pass bolus chambers of the heart and lungs will
receive a number of quantitative parameters of central
hemodynamics, enabling detailed examination and detection of
subtle pathological deviations. By comparing the curves from
the right and left heart, the value of cardiopulmonary mean transit
time is obtained . By mathematical analysis of the curve from
the lungs (pulmogram) we can quantify the LP
shunt (calculate
the short-circuit flow and the Qp/Qs value). By analyzing the
relevant curves, it is possible to further quantify PL short
circuits, calculate the values of the right ventricular ejection
fraction, cardiac volume , cardiopulmonary blood volume,
in combination with radionuclide ventriculography also
regurgitation fraction .
Data storage
Under le indication for examination or
executing. premedication with inactive Sn-pyrophosphate (see
below) and the scintillation camera detector are placed above the
precordium area in the anterior or modified LAO projection.
Prepare about 400-600
MBq (for children about 7MBq / kg) 99m Tc in a volume of max. 1ml for
the syringe . and insert the needle into the internal jugular
vein or an anecubital vein. We start saving the dynamic study and
then quickly apply the contents of the syringe. By rapid
application of a small volume of concentrated radioindicator, a
compact discrete bolus of radioactivity
will move through the bloodstream towards the heart , the passage
of which through the central circulation and gradual dilution
will be mapped by the camera *).
*) The condition for quality images and especially the correct
analysis of the curves is that the radio indicator actually
enters the heart as a short compact
bolus. With
normal application to the anecubital vein, the bolus in the
venous circulation is often prolonged (in up to 25% of cases), or
even divided and fragmented. Such a deformed bolus can greatly
distort the analysis of central hemodynamics (eg a fragmented
bolus can simulate a short-circuit wave on a pulmogram).
Additional mathematical corrections (eg by the deconvolution
method) usually fail here. For reliable and
greater provision of
a quality bolus, there is an anatomically appropriate route of
bolus administration - administration to the internal jugular vein. It is also recommended to apply a
bolus in inspiration.
Recommended selection
of dynamic study storage :
Matrix 64 ´ 64 , 16 bit
Group 1: 100 images after 0.2 sec. (for slower cardiac operation 0.5 sec./frame)
Group 2: 50 frames after 1 sec.
Group 3: 10 images after 30 sec.
(If the acquisition program
cannot group, a higher number of frames must be preselected, eg
300 frames after 0.3 sec.)
If the value t only the first flow (usually for the
diagnosis of congenital heart defects) do not perform
premedication inactive Sn-pyrophosphate and charging
scintigraphic studies will terminate once it has been evident for
several seconds recirkulce system (watch for perzistent
oscilloscope or computer screen). If we want to calculate the
minute heart volume, then we save the study until the end. In
this case, it is necessary to premedicate with inactive
Sn-pyrophosphate about 20 minutes before bolus administration, or
use another intravascular indicator o r labeled with 99m Tc (erythrocytes labeled in vitro,
labeled plasma proteins). In addition, to calculate the minute
heart volume, we insert the patient's weight in [ kg ] in the comment ., height in [ cm ] and blood volume
in [ ml.
] . We determine the volume of blood either
by the dilution method or we read it empirically from the tables
according to the height, weight and sex of the patient. To
calculate the right ventricular ejection fraction, it is
necessary to monitor the heart rate during the first bolus
transit and record this value for use in evaluation.
Data evaluation
After invoking the
appropriate radiocardiographic scintigraphic study using the
basic OSTNUCLINE system (if
the individual groups are recorded as separate studies, we will
invoke them all using the command "Next" - combine for
evaluation in one study) run a
comprehensive program RKG - bolus angiocardiography (its first part ).
Visual evaluation of bolus
passage images
We begin the
evaluation of a dynamic radiocardiographic study by visually
monitoring the flow of a radioactive bolus through individual
parts of the heart and lungs on scintigraphic images. We can thus
identify possible more serious abnormalities in the central
circulation and some anatomical deviations. The display will show
a series of sequential images properly nasumovaných passage of
tracer c e ntrální circulation, together with the
corresponding time intervals. This series of paintings is offered
for preliminary visual evaluation . If we do not find any
pathology in the images, we can use the implicitly built-in text
of the standard normal evaluation , eg:
"After bolus injection of
the radiolabel, unexposed cavities of the right heart are imaged,
followed by filling of the unexpanded lung and pulmonary artery,
which are emptied reasonably rapidly into the normally configured
left heart and aortic cavities.
At the same time, this
preliminarily generates a standard formulation of a normal
conclusion:
"Conclusion: We do not
observe pathological changes in central hemodynamics in the
visual evaluation of sequential scintigrams of bolus passage
through the small circulation or in the quantitative analysis of
circulation curves."
however, which can be
modified during further evaluation (see below). In the
pathological case, we choose a non-standard
variant of verbal evaluation, in which we enter free
text into the
marked box using the keyboard ; with this variant, no standard
formulation of the conclusion is generated either. A series of
images, including verbal evaluation, can be printed for
documentation (it is important only for more significant
pathologies).
Designation of areas of
interest
For the
quantification of central hemodynamics, an important initial act
is the designation of areas of interest (ROI) of
individual parts of the central circulation. Using the arrows or
the slider below the image, we step through the images in the
study and gradually make the individual structures through which
the radioactive bolus flows visible. Areas of interest are drawn
in the order:
ROI 1 ......... bolus
arrival site
ROI 2 ......... right ventricle
ROI 3 ......... right atrium (for assessment of LP shunt location)
ROI 4. ........ lungs
ROI 5 ......... left ventricle
ROI 6 ......... aorta (only for quantification of PL
shunt)
When drawing the ROI
from the right ventricle, make sure that the part of the right
ventricle adjacent to the septum is not included. When defining
the ROI of the lungs (usually on the left), the area of large
branches of the lung must not be included, the medial border must
be away from the aorta and the left ventricle. When marking left
ventricular we pay attention, we did not work and the right part
of the chamber (on the appropriate image-filled stage left Komrat
is because the right ventricle has been emptied and n measurement
to see) - we recommend marking the moment when the arrows or
return rider image filled the right ventricle.
ROI 3 of the right
atrium is optional and we mark it when we want to assess whether
or not. The LP shunt is at the level of the ventricular or atrial
septum. The ROI 6 of the aorta is also optional and we only mark
it if we want to quantify the PL shunt.
Hemodynamic curves
Curves (histograms) of the time course of activity (ie bolus
passage and dilution) in these areas of interest are constructed
from these areas of interest, which are corrected for the dead
time of the camera-computer system (for a given system the
effective dead time is about 6 m sec .). You can also set
the appropriate compression or expansion of the timeline scale
curves so that the curves are optimally displayed for each
patient regardless of the flow time. One step of expansion or
compression represents about 20% of the current length of the
curve. To capture the dynamics of the first pass of the bolus, it
is appropriate to perform such an expansion that, in addition to
the entire primocirculation peak, the beginning of the
recirculation wave is displayed. To capture the dynamics of
system recirculation, it is necessary to have the entire
recirculation wave displayed with reserve. The program sets the
optimal time scale automatically, so manual modifications of
expansion and compression are usually not necessary.
Mathematical
model of bolus passage and dilution dynamics
Quantitative
analysis and determination of hemodynamic parameters is performed
on the basis of a mathematical model that captures the main features
of the passage of a radioactive bolus through the heart cavities
during gradual dilution. The most basic model is shown in
Fig.3.2.1a.
 |
Fig.3.2.1.
a) The simplest model of passage and
dilution of the bolus through the heart (dilution)
chamber.
b) Time course of radioactivity in the
dilution chamber measured by an external detector (scint.
camera) after injection of a radioactive bolus into the
inflow tube. |
It consists of a flow
tube which opens into a dilution chamber of volume V and
flows out of it again. We assume that there is an immediate and
perfect mixing of the inflowing and outflowing liquid in the
chamber. Let the flow through this system be equal to Q [ ml./sec. ] . Inject a small drop (bolus) of
radioactive solution with activity A 0 into the inflow tube . Upon
arrival in the dilution chamber, the droplet is immediately diluted
to the entire volume V and begins to gradually wash
out with the inflowing and outflowing liquid . The activity in
the dilution chamber (measured by the appropriate external
detector, eg camera) will have a time course A (t) according to
Fig.3.2.1b. The law of conservation of activity gives the
equation.
A(t)
A(t+dt) = A(t) - --- . Q . dt ,
(3.2.1)
V
or
A(t)
dA(t) = - --- . Q . dt
. (3.2.2)
V
If we choose the moment
of arrival and stirring of the bolus as the beginning of the time
reading, the solution is the differential equation (3.2.2)
.... ...............
...............-(Q/V).t
...... ..........A(t) = A0 . e .... .........,...........t ³ 0 . ..................(3.2.3)
The decrease in chamber radioactivity will
therefore be exponential . According to our idealized model, the
rise should be instantaneous, but in reality it will have the
shape according to Fig.3.2.1b (so-called gamma-functions are
often used for interleaving, see below). From the functional
relation (3.2.3) by integration we easily obtain the size of the
area under the curve A (t) :
.....................¥
...... ..........ó ..................................V
...... ..........ô
A(t) dt.... =.... A0 ... ¾
¾ . .......(3.2.4)
...... ..........õ ..................................Q
...... ..........0
This important
relationship can be expressed by the sentence :
The area (integral) under
the time course curve of the bolus flow through the dilution
chamber is directly proportional to the input activity A 0
and the volume of the chamber V and indirectly
proportional to the flow Q through this chamber.
This theorem is sometimes
referred to as the Steward-Hamilton principle.
A more complex model of
the heart chamber is shown in Fig. 3.2.2a. Dilution chamber of
the same features as the previous model, is connected in a
closed circuit , which begins and ends in the reservoir
representing vasculature containing
complete blood Volume V B .
 |
Fig.3.2.2.
a) A more realistic model of the heart
chamber is a dilution chamber ("pump")
connected in a closed circuit with a reservoir
representing the total blood volume in the vascular
system.
b) The time course of radioactivity in the dilution
chamber connected in this way after the injection of the
radioactive bolus. |
After injecting a bolus
of activity A 0 into the inlet tube, the
radioactivity in the dilution chamber will change with time
according to the graph in Fig.3.2.b. The dilution curve will
initially be the same as in the previous model, but will not go
to zero later, but due to recirculation through the bloodstream, the
radioactivity in the chamber will approach a certain asymptotic
value A¥ given by the dilution principle
by diluting A0 activity in
whole blood volume V B :
V
A¥ = A0 .
--- .
(3.2.5)
VB
The relation therefore
applies to the volume of the dilution chamber
A¥
V = VB . --- .
(3.2.6)
A0
In order to be able to
use the relation (3.2.4) now, it is necessary to separate from
the actual curve of the time course of radioactivity in the
dilution chamber the part that corresponds to the primocirculation of the bolus without systemic
recirculation. Therefore, we define the function A *
(t), which arises by exponential extrapolation of the peak of the function A (t)
corresponding to the first bolus flow (dashed curve in Fig.
3.2.2b). For this function A *
(t) without recirculation, relations (3.2.3) and (3.2.4 ) will
apply . Substituting
for the unknown volume of the dilution chamber V
from (3.2.6) to (3.2.4) we obtain an important relation
A¥
Q = VB . ---------
, (3.2.7)
¥
ò A*(t)
dt
0
according to which the flow
Q can be determined by multiplying the total blood volume V B by the ratio of the asymptotic value of the
activity A ¥ of the dilution chamber and the area
(integral) under the curve of the first flow A *
(t) through this chamber. Equation (3.2.7) has the remarkable
property that it applies not only to the whole chamber, but also
to any part of it (if A (t) ®
kA (t), then also A ¥ ® kA ¥ and A *
(t) ® kA
* (t), so
the corresponding coefficient k is truncated in a fraction). The
prerequisite here is, of course, a perfect dilution. Equation
(3.2.7) is the basis for determining blood flow through the heart
- minute volume of heart - cardiac
output.
The curves of the
passage of the radioactive bolus through the individual parts of
the central circulation begin with a significant peak of the
first pass and continue with a less pronounced recirculation plate (in addition to the always present
systemic recirculation, it can also be a short-circuit
recirculation). Towards higher times, the descending part of the
peak of the first pass is superimposed with this recirculation. Two
methods are used to separate the "pure" peak of the
first flow. The first of these was described above - it is an
exponential fit of the fast part of the descending arm of the
peak and extrapolation to longer times, thus creating the curve A
* (t). The second method is the
interpolation of the so - called gamma
function (in
fact, it is an integrand of the function G), which has a general shape
G(t) = Rl . (t-R0) R2 . e R3.(t-R0) , R2 ³ 0, R3 < 0 .
(3.2.8)
The fitted gamma
function is also extrapolated outside the interleaved section and
replaces the primocirculation peak - a "pure" first
flow curve is created .
The four parameters of
the gamma function fit so that this function best captures the
dynamics of the first passage of the bolus through the heart
chamber or lungs. Parameter R0 expresses the time shift related
to the time interval between the start of the dynamic study and
the start of the bolus arrival at the site. The parameter R1 is
related to the radioactivity of the bolus A 0 . The parameters R2 and R3 are
the velocity coefficients of the ascending and descending parts
of the curve. The usefulness of gamma-functions lies in the fact
that they are able to fit even asymmetric
peaks due to the
fact that they are composed of two parts: the coefficient (t-R0) R2 describes the exponential increase at the
bolus entry, while the coefficient e R3
(t-R0)
describes the exponential decrease in radioactivity during bolus dilution
and completion.
In the RKG program, the
fit of gamma-functions is used both for the curves from the right
and left heart in determining the mean transit time of the
central circulation, and for the pulmogram in the quantification
of short circuits. Section of the curve, which has the gamma
function interleave is determined automatically (with manual
modification) - the starting point via the maximum second
derivative, the endpoint for the downlink leg is defined by the
condition defined by decrease decrease rate (usually 80% of the
maximum rate of leaching of radioactivity ones)
.
Cardiac output
The
determination of volume of cardiac output (CO) is optional in the
RKG program. If the answer is yes, we determine the value of the
patient's total blood volume when asked by the program . This
value is either determined by the dilution method and inserted at
the request of the program, or (more often) the program
determines it by an empirical formula
from the height , weight and sex of the patient. Next, we choose
from which curve we want to calculate the minute volume - we
recommend either from the left ventricle or from the whole heart.
The start and end point of the section of the descending
(dilution) part, which intersects the exponential function, is
then automatically defined (with the possibility of manual
modification) on the curve selected in this way. Custom
"pure" curve A *(t) of the first flow rate is
then obtained by joining the section of the original curve A (t)
from zero to the point of maximum rate of descent, and at this
point the subsequent exponential function extrapolated to fusion
with the horizontal axis. Next, the equilibrium point is defined , where the
radioindicator is already evenly mixed in the bloodstream.
Based on the ratio between the asymptotic activity ou A ¥ in equilibrium and the area
(integral) under the curve of the first flow, calculate the
minute heart volume according to the relation (3.2.7) derived in
the previous paragraph. The calculated value is offered for
approval, so that the calculation of the minute volume can be
repeated arbitrarily for different curves and differently
selected dilution sections on these curves.
Regurgitation fraction
Under normal
circumstances, virtually all blood expelled by left ventricular
systolic contraction becomes part of the systemic circulation.
However, in some cardiopathies (mitral or aortic valve
insufficiency), some of the expelled blood returns to the left ventricle during
diastole - regurgitation occurs . To quantify this
disorder, which reduces the effective performance of the heart,
an important parameter is the so-called regurgitation fraction
RGF , which indicates the percentage of heart rate that
returns to the ventricle :
SVtot
-
SVef
RGF = --------- . 100 % ,
(3.2.9)
SVtot
where SV tot is the total heart rate expelled by the heart
chamber in one stroke, SV ef is
the effective
heart rate volume actually sent in one stroke to the systemic
circulation.
To determine the
regurgitation fraction, it is necessary to first perform a bolus radiocardiography including the equilibrium phase (during
the first transit we monitor the heart rate) and then equilibrium
ventriculography . First, we evaluate the ventriculography,
from which we use the value of heart
stroke volume SV ventr to determine regurgitation , which indicates the total ( apparent ) heart
rate volume **) : SV tot = SV ventr
. Then we evaluate the bolus radiocardiography, which will give
us the value of the minute volume of heart CO [ liters / min ] - from the principle of the method it
follows that it is a real (effective) flow drawn by the
heart into the systemic circulation, regardless of possible
regurgitation. If the heart rate at the first transit was f [ beats / min. ] , is the effective stroke
volume SVef = CO / f [ ml. ] -
does not include the regurgitation fraction. The value of the RGF
regurgitation fraction is already directly based on the above
relationship.
**) Total stroke volume expresses the amount
of blood expelled from the heart during systole, regardless of
whether part of this blood flows back into the atria during
systole (mitral regurgitation) or subsequently returns to the
ventricle in diastole (aortic regurgitation). Thus, the total
heart rate includes the regurgitation fraction.
The question whether to
count the regurgitation fraction appears in the RKG program when
the minute heart volume was calculated. We then insert the heart
rate read at the first bolus transit and the heart rate value
obtained from the ventriculography.
According to our
experience, a regurgitation fraction of around 10% can be
considered a physiological limit, values ??of up to about 25% are
assessed as mild regurgitation, above about 50% as severe
regurgitation. In any case, it should be borne in mind that the
result of the calculation may be affected by the quality of the
bolus and the accuracy of the determination of the absolute
volume of the ventricle.
Right ventricular ejection fraction
When a radioactive bolus flows through the
pulsating (pumping) dilution
chamber, the rate of decrease of the descending part of the
primocirculatory peak is proportional to the heart rate and
pulsed ejection fraction. Thus, by analyzing the dilution curve,
it can in principle be used to determine the ejection fraction
of the chamber. This is because there is a clear relationship
between the ejection fraction EF and the average flow Q through
the separation chamber
VED
Q .= EF . VED .
f. = EF . ---- , (3.2.10)
T
where V ED is the
end-diastolic volume of the heart chamber, f is the heart rate
and T is the period of the heart cycle. Substituting the flow Q
from there into the basic exponential function (3.2.3) describing
the dilution curve from the chamber, we get
EF.VED
.f . t
- --------
. t
V
A(t) =
A0 . e
,
(3.2.11)
where V is the average volume of
the chamber during pulsation. The exact relationship between the
average volume of ventricle V and its end-diastolic volume
m V ED depends on the
specific shape of the volume curve, but under a justified
assumption of roughly cosine course of the cardiac cycle
(symmetrical ejection and filling) we can consider V as the
average between end-diastolic and end- systolic chamber volume:
VED
+ VES VED
+ (VED-EF.VED)
2 - EF
V =
------- = -------------- = VED .
----- .
2
2 2
Substituting the last expression for V
into (3.2.11), V ED is truncated
and the equation describing the descending dilution section of
the curve will read
2.
f . EF
- ------
. t
2
- EF
A(t) = A0 . e . (3.2.12)
Thus, if we interpolate the
descending arm of the peak of the first pass of the bolus through
the heart chamber, the exponential function is intersected
- R .t
A(t) = A0 . e ,
then from the rate coefficient R
of radioactivity leakage from
the chamber determined in this way, we can determine the ejection
fraction of the heart chamber :
2
. R 2
. R
EF = -----
. T = ------- , (3.2.13)
2
+ R (2+R)
. f
where T is the period of the
heart cycle and f is the heart rate.
In the practical implementation
of this method, it should be taken into account that formula
(3.2.13) applies only if the perfect dilution is fulfilled and
that the input function is Dirac's d- function , ie the radio indicator came into the chamber as a perfect
compact bolus . The condition
for entering a perfect bolus is (partially) met for the right
ventricle, but certainly not for the left ventricle. The method
is therefore (limited) only applicable to the determination of
the right ventricular ejection fraction.
The optional calculation of the
right ventricular ejection fraction in the RKG program begins by
defining a descending (dilution) section on the right ventricular
curve through which the exponential is intersected. We enter the
heart rate (which was read on the cardiomonitor during storage
when the right ventricle was filled with a bolus) and the program
calculates its ejection fraction based on the rate coefficient of
the exponential function of radioactivity leakage from the right
ventricle. The calculated EF value is displayed together with the
right ventricular curve and is offered to agree or repeat the
calculation (for example, with a modified section for exponential
fitting).
Cardiopulmonary mean transit
time
The mean transit time of the central
circulation MTT is the time it takes
for an element of blood to pass from the right ventricle through the central
circulation through the lungs to the left ventricle. The simplest
way to determine the cardiopulmonary transit time is to determine
the time difference between the peaks of the primocirculation
curves of the right and left ventricles ("peak to peak"
method). However, since these curves are not symmetrical (the
ascending part of the peak is significantly steeper than the
descending part), the time difference between the peaks may
differ somewhat from the actual transit time. A more accurate
method of determining cardiopulmonary transit time is to
determine the time difference between the centers of gravity
(centroids) of the peaks of the first flow on the left and
right ventricular curves. Time coordinate of the center of
gravity (centroid) t C is defined by the requirement
that the area (integral) below the fitted gamma function to the
left and right of the center of gravity be the same :
tC ¥
ò G(t) dt = ò G(t) dt .
0
tC
The average transit time
of the cardiolulmonary circulation MTT is then given by the
difference of the time coordinates of the centers of gravity
(centiodes) of the fitted gamma-functions of the left and right
ventricles: MTT = t C (LK) - t C
(PK) - in seconds.
If we have quantified
the cardiac output Q, we can determine another parameter of
central hemodynamics based on the MTT transit time - cardiopulmonary blood volume V K-P
indicating the total volume of blood in the central circulation:
V K-P = MTT. Q. In order for this volume to come out
in milliliters, the MTT must be kept in seconds and the Q must be converted from
the usual [ liters / min. ] to [ milliliters /
second ] .
The determination of the
transit time of the central circulation in the RKG program
consists in the fact that the gamma-functions are interleaved by
the primocirculation peaks on the curves of the right and left
ventricles and the mean cardiopulmonary transit time (MTT) is
calculated from the time difference of their centers of gravity
(centroids). At a normal heart rate (approx. 60-80 beats / min.),
The normal MTT values ??for adults are around 6-8 sec, in
children (where there is a higher heart rate) around 3-5 sec.
Rooms with d at an earlier stage was quantified
evaluation minute volum heart, and calculates the total volume of
blood in the pulmonary circulation in [ mL. ].
Normal values ??in adults here are around 500-800 ml. The
calculated value of MTT and possibly also cardiopulmonary blood
volume is displayed together with the curves from the right and
left heart and is offered to agree or repeat the calculation (we
can, for example, modify sections for gamma-function fit on the
primocirculatory peaks of these curves).
Quantification
of intracardiac shunts
Under normal circumstances (without the presence of a
shunt), the radioactive bolus is carried (with gradual dilution)
by blood from the right heart through the pulmonary circulation
to the left heart (Fig. 3.2.3). On the pulmogram curve, in
addition to the significant peak of the first bolus flow, it
appears after about 30-50 sec. only a lower peak
of systemic recirculation caused by the return of considerably
diluted activity through the systemic circulation back to the
heart and lungs.
 |
Fig.3.2.3.
a) Schematic representation of the route
of passage of the bolus of the radio indicator of the
central circulation.
b) Manifestations of short circuits in
the circulation curves of the passage and dilution of the
bolus in the heart chambers, lungs and aorta. |
However, in some
disorders (atrial or ventricular septal defect) part of the blood
flows from the left heart cavities to the right heart cavities
and then into the pulmonary circulation *)
- there is a left-right (LP) shunt and thus premature recirculation of
blood in the pulmonary circulation.
*) Rarely, a short circuit between the aorta
and the lungs ("tube") can occur, in which the
short-circuit recirculation takes place only through the lungs
and omits the right ventricle .
This short-circuit flow carries with it part of the bolus
activity. On the pulmogram curve, the LP short circuit manifests
itself by the fact that soon after the peak of the first flow
another wave appears, reflecting the premature recirculation of
blood in the lungs caused by the short circuit - Fig.3.2.3b,
Fig.3.2.4a. The magnitude of this recirculation wave relative to
the magnitude of the primocirculation wave is a measure of the
severity of the LP short circuit. The central hemodynamics the
Schemes and matically illustrated in obr.3.2.3a. Under
normal circumstances, the pulmonary flow rate Qp is equal to the
systemic flow rate Qs. In the presence of an LP short circuit,
the lung flow Qp is formed by the sum of the system Qs and the
short-circuit Qz flow: Qp = Qs + Qz. It follows that Qz = Qp - Qs
and Qs = Qp - Qz.
 |
Fig.3.2.4.
a) Quantification of L.-P. short circuit
by pulmogram decomposition
b) Quantification of P.-L. short circuit
by decomposition of the aortic passage curve of the
radioindicator. |
Primocirculation,
short-circuit recirculation and system recirculation partially
overlap in time and intersect. To quantify the short circuit, it
is necessary to decompose the pulmogram into a part
corresponding to the first bolus flow and a part representing
premature (short-circuit) recirculation - Fig.3.2.4a. The first
part of the pulmogram (from the beginning of the primocirculation
peak to the point of maximum decrease) first interpolates the gamma function and extrapolates to higher times until it
merges with the horizontal axis. This gamma function represents
the first bolus flow through the pulmonary circulation and the
area S1 below it (its integral) is proportional to the pulmonary
flow Qp . This fitted first flow curve is then subtracted
from the original pulmogram. This creates a difference curve,
on which there is no longer a peak of the first flow, there is
only recirculation both systemic (late) and possibly short -
circuited (premature). Our task now is to separate the pure
short-circuit wave from the system recirculation on the
difference curve, with which it partially intersects. For this
purpose, a broad peak of the differential system recirculation to RivCo
proložíme more gamma function and extrapolate it to the left
into shorter times, which may be precisely superimposed
recirculation system with short circuit (early) recirculation. By
subtracting this extrapolated curve (gamma-function) of the system recirculation from the original difference curve, we
already get a "pure" curve of premature
(short-circuit) recirculation. The area S2 (integral) below it is
proportional to the flow Qz by the short circuit. The
difference of areas S1 - S2 is proportional to the system flow Qs
- Fig. 3.2.4a.
Two parameters are used
to quantify the LP short circuit . The
first is the shunt
flow rate Qz expressed as a percentage of the
total lung flow rate Qp :
Qz S2
---- = --- . 100 [ % ] ( ³ 0 ) .
Qp S1
Without the presence of
a short circuit, this parameter is close to zero, the normal
limit is about 12%. The second parameter used to quantify the LP shunt is the ratio of lung and system flow Qp /Qs :
Qp
S1
---- = ------
( ³ 1 ) . *)
Qs S1
- S2
Without the presence of
a shunt, the parameter Qp /Qs is close to one, the limit of the
normal is about 1.15.
*) This relationship is only valid when no
right-left (PL) short circuit is present. If a PL short circuit
occurs, the fraction given by the PL short circuit flow rate must
be subtracted from the primary circulation area S1: S1 * (Qz P-L / Qs), where Qz P-L is the PL short circuit flow, Qs
is the system flow. Thus, the general relationship for the
pulmonary to systemic flow ratio will be Qp
/ Qs = S1. (1-Qz P-L / Qs) / (S1 - S2).
Unfortunately, the
system recirculation subtraction method is not always applicable.
Sometimes the wave of system recirculation is not well expressed
on the pulmogram curve and therefore cannot be well interpolated,
extrapolated and subtracted. In such a case, we are forced to try
to extract the short-circuit recirculation wave from the initial
section of the rise .fixed part of the difference curve. A
suitable chosen part of this section of the difference curve is
interpolated by the least squares method, the ascending speed of
which is given by the gradient of the initial growth of the
difference curve, but the velocity coefficient of the descending
part (which is covered by system recirculation and is not
visible) is assumed to be the same as in the previous gamma
-function of the first flow. The gamma function is then
considered as a short circuit and a recirculating wave area S2
below is used to quantify shunt flow Qz. The method without
subtracting systemic recirculation is called the Maltz and Treves
method. The accuracy and reproducibility of this method is
usually not very good. It is quite difficult to determine a
section here which is not yet strongly affected by systemic
recirculation. V our the RKG program, the end point for
short-circuit recirculation fitting is determined automatically
as the first maximum convexity of the difference curve, of course
with the possibility of manual shift.
In any case, the method
without subtracting the system recirculation more or less overestimates the short circuit. For normals or weak
shorts, this error would be significant and would prevent us from
making a reliable decision on the presence and magnitude of such
a (suspicious) short circuit. Fortunately, in these cases, the
systemic recirculation wave is usually well expressed, and
therefore the correct method with subtraction of systemic
recirculation can be used. Recirculation system can not subtract
space and especially for any major faults, the wave recirculation
system is covered by a superposition gradually abolished repeated
and still íce blurred waves of short-circuit
recirculation. In these cases, however, the first short-circuit
recirculation wave is substantially larger than the part of the
system recirculation that could event. intervene, so by not
subtracking of systemic recirculation we do not make of
significant mistakes (if we set cautiously ascending section of
the differential curve for fiting shunt -gamma function).
Right-left shunt
Demonstration and quantification of left-right (LP) short-circuit
is the most common indication for bolus radiocardiography. Less
common are disorders (mostly of congenital origin), in which part
of the blood flows pathologically from the cavities of the right
heart directly into the cavities of the left heart without going
through the pulmonary circulation (Fig.3.2.3) - there is a right-left (PL) shunt and thus premature recirculation of
non-oxygenated blood in the systemic circulation. During
radiocardiography, this shunt flow carries with it part of the
bolus radioactivity. This results in the left ventricle appearing
prematurely at about the same time (or earlier) as the
lungs, so that the left ventricle appears premature (in short ,á) wave
in front of the main primocirculatory peak, approximately at the
time the bolus reached the lungs. In a similar way, the PL short
circuit is reflected in the time course curve of radioactivity in
the aorta - a premature circulating wave caused by a short
circuit appears in front of the main primocirculatory peak -
Fig.3.2.3b below. The magnitude of this premature wave in
relation to the magnitude of the main wave of the systemic
circulation is a measure of the severity of the PL shunt - Fig.
3.2.4b.
As with the LP shunt,
the shant and system circulation partially overlap and intersect.
Therefore, to quantify the short circuit, it is again necessary
to decompose the curve from the aorta into a portion
corresponding to the main bolus flow and a portion representing
the premature (short circuit) circulation. The main
primocirculatory peak of the aortic curve intersects the gamma
function and is extrapolated in both directions. This gamma
function represents the normal first bolus flow through the
systemic circulation and the area S1 (integral) below it is
proportional to the physiological fraction of the systemic flow
Qs. By subtracting the fitted and extrapolated to this gamma
function from the systemic circulation pùvo d From the
aortic curve, a difference curve is created, on which there is no
longer a peak of systemic circulation, there is only a premature
circulation wave, and towards higher times, the curve of normal
systemic recirculation rises. This premature circulation wave
represents a short circuit and the area S2 (integral) below it is
proportional to the flow Qz P-L
by a right-left shunt . The total area S1 + S2 under both waves
is proportional to the total system flow Qs. The ratio of shunt
and system circulation flows is used to quantify the PL short
circuit :
QzP-L S2
------ = ------ 100 [ % ] .
Qs S1 +
S2
This parameter indicates
the flow QzP-L by a right-left shunt expressed as a
percentage of the total system flow - Fig. 3.2.4b.
It should be noted that
on the statistically highly fluctuating curve of the aorta,
gamma-function interleaving and separation of circulating waves
are quite problematic, so that the quantification of the PL short
circuit is considerably more difficult and less accurate
than for left-right shunts.
We will now briefly
describe how the quantification of the LP short circuit is
implemented in the RKG program. The start point of the main peak,
the peak and the end point of the primocirculation peak are
automatically defined on the lung-pulmogram curve (with the
possibility of manual modification). The end point of the
primocirculation peak is defined on the descending part of the
curve at the point where the descent speed begins to decrease (so
as not to include part of the short-circuit circulation). If we
suspect that the automatically defined end point is somewhat to
the right, we recommend moving it manually to a location just
after the steepest descent of the curve. The gamma- f is first
interspersed with the section of the main peak defined in this
way function and subtracted from the original
pulmogram. A difference curve is created capturing both systemic
and possible short-circuit (and thus premature) recirculation.
You will be asked if system recirculation can be read. We answer
in the affirmative when both the system recirculation and the
recirculation wave are clearly expressed on the pulmogram curve
(we must not confuse short-circuit and system recirculation!). In
this case, additional gamma functions are interleaved by the
automatically defined wide system recirculation peak and
subtracted from the original difference curve. Vz n ikne
curve by the short-circuit recirculation from whose surface
(integral) defined section (peak) is calculated the value of a
short circuit, i.e. Qp / Qs and the percentage of short-circuit
flow of blood. If the systemic recirculation is not clearly
visible, we will answer in the negative. In the initial section
of the difference éThe starting point of the short-circuit
recirculation and the end point for the interpolation of the
gamma function are then automatically defined (with the
possibility of manual modification). The gamma function is then
interleaved by the initial section on the difference curve
defined in this way in the manner described in the theoretical
part of this paragraph, the area (integral) of which quantifies
the short circuit.
| Mathematical analysis of LP short
circuit in the evaluation of radionuclide
angiocardiography |
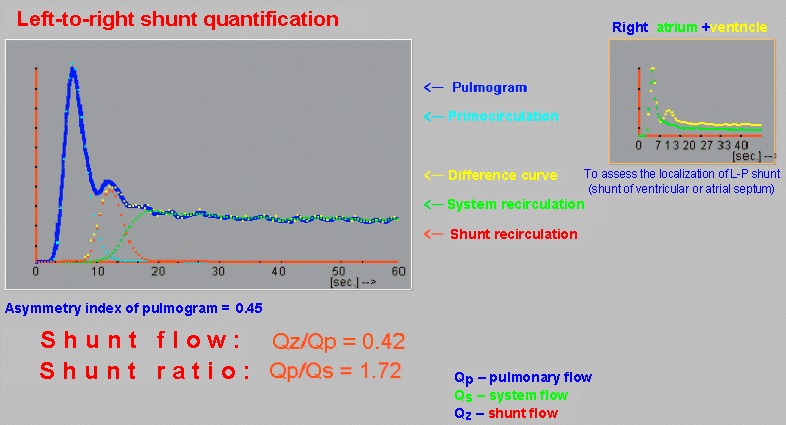 |
| By
decomposing the pulmogram curve into primary circulation,
systemic recirculation and premature recirculation, we
observe a hemodynamically significant left-right
shunt . A comparison of the bolus passage curves
through the right atrium and ventricle indicates a short
circuit at the level of the ventricular septum. |
At the end of the
calculation, the pulmogram curve, divided into primocirculation,
system and short-circuit recirculation curves, is displayed on
the screen simultaneously (with color differentiation), together
with the values of the most important calculated parameters of
central hemodynamics; for documentation we can print.
Final protocol
Finally, the
display shows a summary image containing the curves of the
arrival of the bolus, right heart, pulmogram and left heart,
images of the right and left heart as the bolus passes, along
with the values of the calculated quantitative parameters. In the
lower part, the texts of the verbal evaluation for the final
editing (addition, reformulation) in confrontation with images,
curves and values of quantitative parameters are displayed. At
this point we also insert the final evaluation , or we
will check and modify the automatically generated conclusion
formulation. The resulting report prepared in this way is then
printed on the printer in the required number of copies - Fig.
3.2.5.
| Mathematical analysis and complex
evaluation of radionuclide angiocardiography |
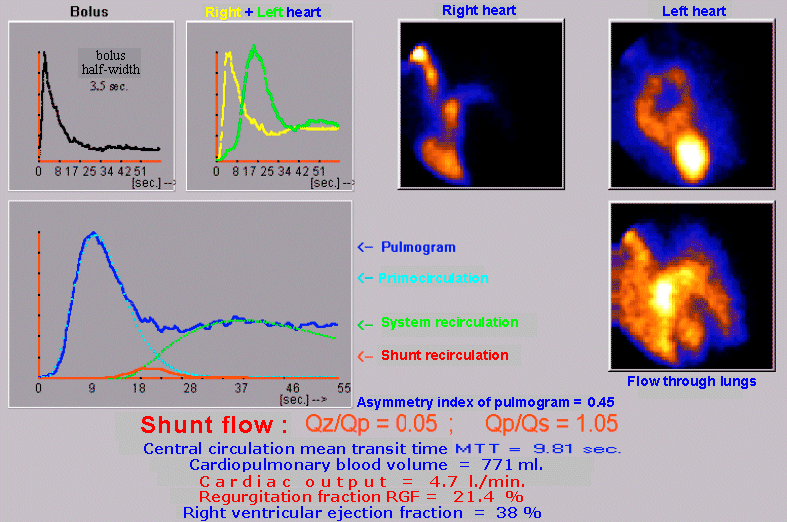 |
Visual
assessment: After
intrajugular bolus injection of the radiolabel, the
unexposed cavities of the right heart are imaged,
followed by filling of the unexpanded lung and pulmonary
artery, which are emptied reasonably rapidly into the
normally configured cavities of the left heart and aorta.
During the passage of the bolus through the left heart,
we do not observe a premature occurrence of a
radioindicator in the right heart and lungs.
Conclusion: In the visual evaluation of sequential
scintigrams of the passage of the bolus through the
cardiac circulation, nor in the quantitative analysis of
circulation curves, we do not observe pathological
changes in central hemodynamics.
|
Program structure
The RKG program consists of the following parts
(capable of independent function):
RKG1 - display of a
series of images, visual evaluation, marking of ROI, creation of
curves
RKG2 - mathematical processing of curves: correction for dead
time, expansion and compression of the scale, calculation of
cardiac output and ejection fraction of the right ventricle
RKG3 - mathematics. processed curves: cardiopulmonary
calculation. transit time (MTT) and shunt
quantification
RKG4 - display of
results, editing of verbal description and printing of report
At the same time, this
structure shows how to proceed when the program is interrupted or
restarted in order to repeat a certain part of the calculations.
For example, if we want to change only the verbal evaluation,
just run RKG4. To re-quantify the short circuit or MTT, we start
from RKG3. If we want to perform the whole m and thematic
processing of curves again, we run the program from RKG2. Only if
we want to mark the ROI differently, it is necessary to run the
program from the beginning, ie from RKG1.
Occupancy of SAVE
AREA after the end of the program :
SA1,2,3 - time course
curves of radioactivity in marked ROIs
SA10 - image of left heart
SA12 - image of right heart
Back: List of complex programs





