Back: List of complex programs
3.4. Comprehensive evaluation
of dynamic renal scintigraphy
Radioisotope methods of
kidney examination are among the most frequent procedures in
nuclear medicine. In comparison with already practically almost
deserted renography easily by using a pair of collimated
scintillation detectors using scintillation cameras provides the
opportunity to visually assess Scintigraphic images of the
kidneys and a detailed and comprehensive analysis of the kinetics
of the administered radiopharmaceuticals le d
trespasses, parts
and urinary tract. Dynamic scintigraphy of the kidneys therefore
serves to qualitatively and quantitatively evaluate the functional
ability of the kidneys , their perfusion
and the kinetics
of the upper urinary tract . A
comprehensive mathematical evaluation of this dynamic study
includes the following main points :
- Visual evaluation of images of radioactivity
distribution in the kidneys at different stages of
indicator passage by the uropoietic system.
- Quantitative processing of first flow indicator
curves and determination of perfusion
parameters
- Evaluation and quantitative processing of nephrographic curves .
- Determination of renal function,
both global and separate for each kidney. It can
be used to determine glomerular
filtration (labeled DTPA) as well as to
determine the tubular function
TER resp. effective
plasma flow ERPF (labeled hippuran and MAG3).
- Construction of transit functions (curves) and
determination of transit times of
passage of a radioindicator through the kidneys and their
parts (crust and hollow system).
- Printing of a comprehensive
final protocol containing all the
necessary data, images of significant phases, curves,
quantitative parameters and verbal interpretations,
including a concisely formulated conclusion.
Radio indicator
application and data storage
Investigations carried
out either sitting or lying down, the detector scintillation
camera fitted with a corresponding collimator (by energy gamma
radionuclide used) is attached to the back of the patient so that
the kidneys were just under half of the field of view (in the
upper part of the visual field is then sufficient margin to be
displayed n in the blood pool). Prepare an appropriate
radio indicator with an activity of approx. 100-300 MBq for 99mTc-DTPA or MAG-3 in the syringe , or about
15-20 MBq for 131I-hippuran. The position of the
detector is specified by applying a syringe with prepared
activity above the proc before application. xyphoides - on a
monitor or persistent oscilloscope screen, the syringe should be
displayed at the cranial border of 1/3 to 1/4 of the midfield.
For precise positioning (especially for atypical placement of the
kidneys), the method of d and pre-application of a small
amount of radioindicator (2-3 MBq - does not significantly affect
the dynamic study itself), which makes the kidneys visible on the
camera monitor after 2-4 minutes , which we then set to the field
of view without any problems. We then quickly
apply the indicator (we recommend rinsing the syringe with
saline - a three-way valve is advantageous) and start accumulation of dynamic scintigraphic
study *) .
*) If we want to determine the absolute
value of kidney function (clearance or glomerular filtration) by blood sampling , measure the syringe with a radio
indicator in a suitable standardized way (eg calibrated
scintillation detector - see note) - - we obtain the value of
applied activity in relative units [number of pulses / unit of
time]. Measure the activity remaining in the syringe after
application (including the background) and subtract it from the
applied activity. During the examination, we will take one or two
blood samples in the twentieth to thirtieth minute. After
centrifugation, measure the activity of 1 ml. plasma by the above
detector in the same relative units (see note). After the end of the dynamic
study, we insert into the commentary to the study the measured
relative value of the applied activity, the remaining activity
after application, the measured activity of 1 ml. plasma together
with time data of the sampling time from the application and the
time interval between the measurement of the applied activity and
the 1 ml sample. plasma.
Note: To
measure the applied activity and the activity of a 1 ml sample.
plasma, we recommend using a well scintillation detector (eg NKG
314) equipped with a suitable lead collimation insert (hole
diameter approx. 4 mm) and a crossbar. The syringe with the
activity for application is measured on a crossbar at a height of
approx. 4O-50 cm above the detector with the collimation insert
fitted. In the same arrangement, we measure the syringe with the
remaining activity after application. Sample 1 ml. plasma
measured in a test tube inserted é into the well of the
scintillation detector. Between measurements of activity in both
of these diametrically different geometric arrangements, a
conversion factor of high value (of the order of tens of
thousands) applies. This factor is best determined by dilution
measurement: Draw a suitable radionuclide activity into the
syringe (eg approx. 20-50 MBq 99m Tc) and measure the number of
pulses on the crossbar via the collimation insert. Then we mix
this activity perfectly in a larger volume (preferably in 10
liters) of water. Then take a 1 ml sample. and measure the number
of pulses in the well of the scintillation detector. The
conversion factor F is then determined from the relation F = VN o / N 1 , where V is the
volume of water in ml., N o is the number of syringe pulses on the
crossbar and N 1is the number of sample pulses
of 1 ml. in the detector well. If we keep the geometry of the
measurement, this factor will apply in the long run - we
recommend recalibrating it about twice a year. However, it is
advisable to perform a simple check of the detection efficiency
of the measuring system before each series of measurements.
Recommended storage
mode :
180 images after 10 sec. , 64 x 64 matrix , 16 bit.
If we need to quantify
perfusion, we store in two groups:
Group 1: 60 images for 1 sec.
Group 2: 174 frames after 10 sec.
The recommended storage
time is 30 minutes. However, if we see a sufficiently fast
passage of the radio indicator on the display during storage and
we do not need an accurate determination of the global function,
the examination can be terminated earlier, eg in the 20th minute.
Conversely, when we observe the retention of the radioindicator,
it is appropriate to apply a diuretic (furosemide) in the
15th-20th minute (we will write down the time of diuretic
application) and continue to save until 30.m i n. When
evaluating the study, we then evaluate the response of retention
to the diuretic. If necessary, we can also make static
scintigrams of late phases, which can then be evaluated
simultaneously with the dynamic study.
Study evaluation
After invoking a scintigraphic study in the
basic OSTNUCLINE system, we will launch a comprehensive program RENDYN
- dynamic scintigraphy of the kidneys .
Visual evaluation of sequential
images
First, a series of
appropriately absorbed images (together with the values ??of the
respective time intervals) is created on the screen, capturing
the distribution and course of accumulation of the radioindicator
in the kidneys and its gradual excretion into the bladder. This
sequence of images to our modulation objectively reflect the
dynamics of tracer concentration, we can set scaling individually
characterized ch images to a common maximum (usually
chooses the most out of the picture in 3 to 5 min.) According to
these images, select the pre-verbal assessment , both implicit standard formulation of normal
evaluation ,
e.g.
“After intravenous administration of
the radioindicator, the kidneys of the usual
shape, size
and placement
are displayed , without focal changes. The
nephrographic curves of both kidneys have a normal course, we do
not observe a slowdown of drainage or retention
of the radioindicator in the hollow kidney system.
Conclusion:
Visual evaluation with equivalent scintigrams as well
as quantitative analysis of
nephrographic curves indicate good function of both kidneys,
rapid
transit through the parenchyma and free drainage of the hollow
system.
Signature: MUDr. ” ,
thus inserting non-standard text describing the relevant pathology. A
series of images together with a verbal evaluation can be printed
for documentation (Fig.3.4.0), but this is usually not necessary,
as images of significant phases are included in the resulting
protocol.
Designation of areas of
interest and creation of curves
The following areas of interest are characterized
for the quantitative analysis of dynamics :
Bloodstream .........
ROI 1
Left kidney ........... ROI 2
Right kidney .......... ROI 3
Optional (if
retention):
Left renal cortex ...... ROI 4
Right kidney cortex ..... ROI 5
Tissue background
.......... RO I 6
For the area of interest
of the blood pool, we will use the images immediately after the
arrival of the activity. As ROI1, we mark the perfused structures
above the kidneys here, it is desirable to include the heart area
if it is in the field of view. The areas of interest of the
kidneys are marked in the following images of the parenchymatous
phase. If we are interested in the transit functions and times of
the parenchyma and pelvis separately, we mark the ROI of the
cortex of the right and left kidneys in the images in the
excretion phase. These ROIs will be moon-shaped, with the inner
part avoiding the pancreas and the urinary tract, the outer
part running along the ROI2 or ROI3 of the whole kidney. When
(optional) marking the ROI6 of the tissue background, we must
take care to avoid the kidneys, strongly perfused areas and
urinary tract (we recommend mlunar-shaped areas far enough
from the outer lower side of the kidneys). The program creates
curves of the time course of radioactivity from the marked areas
of interest, which eventually corrects on a tissue background.
Before the actual
mathematical processing of dynamic curves ,
the program asks what kind of sequential scintigraphy of the kidneys it
is: whether it is an examination of glomerular filtration (using 99mTc - DTPA), an examination of tubular
function (using 99mTc - MAG 3), an examination using
131I - hippuran. Furthermore,
whether it is a native study or after exposure to captopril. According
to these answers, the execution of calculations is adapted, the
respective Save Area is installed and the terminology of the
calculated parameters is generated.
The mathematical processing of the curves follows .
At all stages of processing below, the program first asks if we
want to execute them, and they are executed only if the answer is
yes. This saves evaluation time in cases where we are only
interested in some parameters, or only visual and qualitative
data.
Kidney
perfusion analysis
If a fast group of images capturing the
perfusion phase has been recorded, the renal perfusion can
be (optionally) analyzed. Displays the initial (i.e. perfusion)
phase curves of both the kidney and can set the display scale in
the horizontal direction (compression-expansion) for optimal P r ezentaci
perfusion dynamics. On perfusion curves of both kidneys is then
automatically (with manual correction) feature points of arrival
radiotracer top of the first pass of the bolus and
"valley" plata separating perfusion and parenchymal
phase of nefrografic to curve. For the left and right kidneys,
indices quantifying perfusion are calculated: Washida's
perfusion-flow index, which, based on the ratio between the
descending and ascending arms of the peak of the first bolus
pass, quantifies the part of the blood - borne radio indicator
that flows through the kidney and continues through the
bloodstream, in contrast to the second part that is filtered by
the kidney (Fig.3.4.1a). Furthermore, the relative
perfusion index
is calculated , which, based on the proportion of integrals
(areas) of the ascending parts of the perfusion curve of the left
and right kidneys, calculates in percent the relative blood flow of the left and right kidneys
(Fig.3.4.1b).
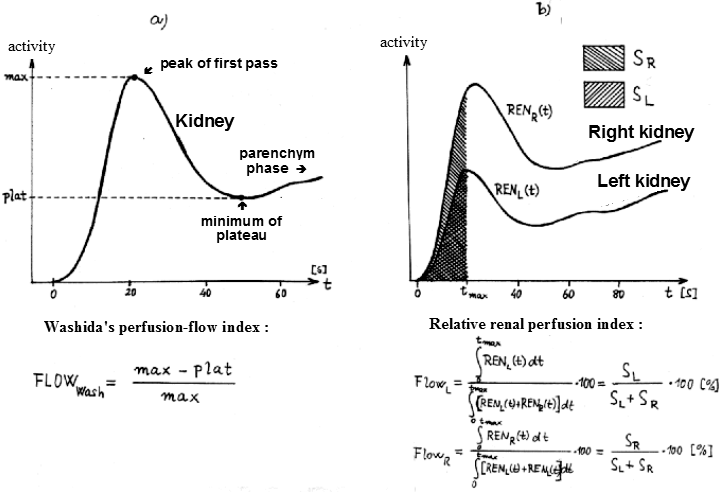 |
Fig.3.4.1. Quantification of renal
perfusion by analysis of the first-pass bolus of the
radiolabel of the radiolabel.
a) Washida's perfusion-flow
index quantifies the ratio of filtration and perfusion of
the kidney.
b) Relative renal perfusion is
quantified by the ratio of the areas under the perfusion
onset curves. |
Perfusion curves
together with the calculated perfusion parameters are displayed
and can be printed graphically (however, we do not normally
perform this printing, relative perfusion indices will be
included in the final report).
Quantification of the excretion
phase of nephrographic curves
Important parameters for
the assessment of renal excretory activity are the time at which
the maximum is reached and the
value of the excretion
half-life of the radioindicator from the kidney. On the
nephrographic curves of the left and right kidneys (generated
from ROI1 and ROI2), the maximum point and the start and end
point of the section for quantification of kidney excretion are
automatically defined (with the possibility of manual
modification). Exponential functions are interpolated by this
least squares method and gr and f fitings are plotted. The
maximum time and half-life of the radiolabel excretion from the
kidney are calculated. If a diuretic was administered during the
study, the excretion half-lives can be calculated separately for
the descending sections of the curves before and after diuretic
administration - by comparing these half-lives, we can quantify renal response to diuretics .
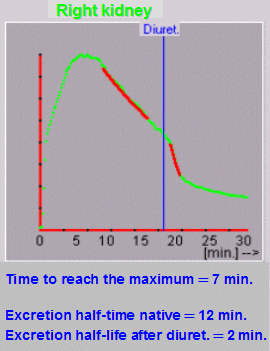 |
Fig.Exkr0.
From the interpolation of the exponential function by the
excretory sections of the nephrographic curve before and
after the application of the diuretic, a good reaction of
the kidney can be seen here - the half-life of the
excretion is from the slowed value of 12 min. shortened
to 2 minutes. |
Note: Quantification of the
maximum and excretion phase is optional - if one of the
nephrographic curves (or both) is constantly rising, we will not
perform this calculation and the resulting protocol will use Tmax
instead of parameters. and T1 / 2 (or T1 / 2nat., T1 / 2diur)
prints "Excretion not quantified".
Analytical
method for calculating the separated function
The separated renal function, ie the
determination of the relative share of the left and right
kidneys in the total (global ) renal clearance, can be determined by
analyzing the ascending (parenchymatous, secretory) sections of
the nephrographic curves corrected for blood background. *)
The analytical method , developed within the framework
of our research task 1985-90, is schematically outlined in
Fig.3.4.2.
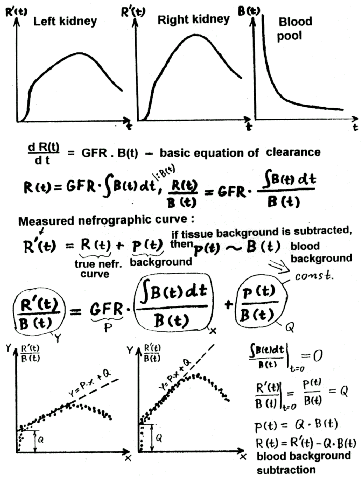 |
Fig.3.4.2.
Analytical method for calculating the separated renal
function.t - time,
R(t) -real nephrographic curve,
R´(t) - measured nephrographic curve,
B(t) - bloodstream curve,
p(t) - tissue background,
GFR - kidney function
|
To calculate, we have
nephrographic curves R(t) of both kidneys and a curve of the time
course of radioactivity in the blood pool (blood pool) B(t). We
start from the basic differential equation of radiolabel
secretion in the kidney, according to which the instantaneous rate of increase of radioactivity in the kidney is
directly proportional to the instantaneous concentration
of radioactivity B(t) in the bloodstream with the GFR
coefficient characterizing the kidney clearance
:
d
R(t)
ľľľ =
GFR. B(t).
dt
By integrating this
equation and dividing both sides by the concentrations of B (t)
of the radio indicator in the blood pool,
we get the transformed equation
R(t)
0nt B(t) dt
---
= P . -------- ,
B(t) B(t)
which after transformation [ ň
B(t) dt ] / B(t) ® x, R(t) / B(t) ® y is the equation
of the line y = P. x in the transformed variables x and y,
whose P direction indicates the paired GFR function of the kidney. Thus, this
transformed equation describes a linearized initial section of the
nephrographic curve.
However, the measured
nephrographic curve R˘(t) consists of the actual
nephrographic curve R (t), on which the background p (t) is
superimposed: R˘(t) = R(t) + p(t). We can make a
fairly reasonable assumption that in the initial ascending phase
of the nephrogram, the background in the kidney area consists
mainly of the radioactivity of blood contained in the vascular
system of the kidney ( (t), where Q is a constant. By integrating
and modifying the equation of the measured nephrographic curve,
we obtain a transformed equation
R?(t)
0nt B(t) dt
----
= P . --------
+ Q ,
B(t)
B(t)
in which the last term Q
= p(t) / B(t) is constant due to the assumption of the
vascular nature of the background p(t).
After the transformation [ ň
B(t) dt ]
/ B(t) ®
x, R˘(t) / B(t) ® y, this equation
is then the equation of the line y = Px + Q in the transformed
variables x and y, whose direction P gives separated clearance of
GFR of the given kidney and the parameter Q
indicates the fraction of blood background in the kidney (details of
derivation are given in Fig.3.4.2).
According to this
theoretical derivation, we determine the separated kidney
function as follows: We transform the nephrographic curve of each
kidney by dividing it by the blood pool curve and at the same
time transform the time coordinate **)
. We obtain the so-called linearized nephrographic curve ,
which always contains a significant and clearly visible linearly
ascending section, beginning shortly after the arrival of
activity in the kidney and ending at the moment when excretion
begins. The beginning and end of a linear section are quite well
defined both manually (or visually) and automatically.
**)The total time course of the concentration
of the radio indicator B(t) in the bloodstream is composed of
several exponential components, but during a relatively short
period of linear rise of the transformed nephrographic curve, B
(t) can be considered practically monoexponential: B(t) @ B. e - l
.t . Then [ ň B(t) dt ] / B(t) @ l .t is
linear and the time coordinate transformation does not need to be
performed.
With this line segment
we interpolate the linear regression function by the least
squares method, thus obtaining its parameters P and Q. The slope
parameter of the line P represents a separate kidney function.
The parameter Q, which is the intersection of the fitted line
with the vertical axis at the moment of arrival of radioactivity
indicates the fraction of blood background in the kidney, i.e.,
the coefficient which j e multiply the curve of blood
pool in order to get the curve of the blood background in the
kidney. By subtracting the blood pool curve thus multiplied from
the measured nephrographic curve, we obtain a "pure"
nephrographic curve corrected for blood
background . Separate the valuetherefore, the clearance is determined
without the need for correction on the vascular background. Blood
background correction is a welcome "by-product" of
calculating separate clearance; All other calculations,
especially deconvolution and construction of transit functions
and determination trance and ther times, so they can run
longer on a "clean" nefrografických curves.
We will now return to
the implementation of this analytical method of calculating the
separated function in our RENDYN program for complex mathematical
evaluation of dynamic renal scintigraphy. The stage of
quantification of the separated function begins with the
simultaneous display of both nephrographic curves and the
question of whether we want to calculate the separated function.
In the positive case,
transformed (linearized) nephrographic curves created by dividing
the original nephrographic curves by the blood pool activity
curve and coordinate transformations are created and displayed
for the left and right kidneys, respectively. Curve so formed
possess the important property that they always include the well
defined linear segment corresponding own secretion radioin d diacetylated
monoglycerides in the kidney. The beginning of the linear section
corresponds to the interface of the venous and secretory phase,
when an equilibrium mixing of the radioindicator in the
bloodstream has already taken place. The end of the linear
portion corresponds to the situation where the secretory phase
will be influenced beginning excretion from kidney and linear curve
starts to bend.
The program
automatically defines this linear section on the first run and
interpolates the linear regression function with it using the
least squares method. The fit graph, the equation of the linear
function and the question of whether we agree with the
interpolation are displayed. We answer in the affirmative when
the line passes well through the linear section of the curve. In
the case of not entirely accurate fitting, the interpolation can
be repeated, while the program offers the possibility of manual
modification of the start and end point for interpolation of the
linear function.
In this
way, the curves from both kidneys are processed. Separated
clearance is calculated based on the guidelines of linear
functions interspersed with the respective linear sections of the
transformed curves of both kidneys. The analytical method used,
based on the differential equation c of the
kidney learance, in
addition to calculating the separated function, also performs an
exact correction of nephrographic curves on the venous
background, as described above.
The step of determining the separated function ends with the
display of both "pure" nephrographic curves (corrected
for background) together with the results of the determination of
the separated function (in% of the total function). The
calculation can be repeated as required.
*) Why a
mathematically more complex analytical method?
The hitherto standard method of determining the separated renal
function is outlined in Fig ..... The point of the interface of
the perfusion and secretion phase is first determined on the
nephrographic curves. It is assumed that the activity in the
kidney in this phase is given only by its blood circulation and
at this point the time course of the radioactivity in the
bloodstream is drawn. Furthermore, the second important point is
determined on the nephrographic curve (approximately in the 2nd
minute) before the onset of the peak, where there is already
sufficient secretion of r and dioindicator in the kidney,
but we assume that excretion from the kidney has not yet
occurred. The ratio of the areas enclosed by the nephrographic
curves and the interleaved blood background curves between the
two significant points then indicates the separate function of
the right and left kidneys .
However, this
method has two pitfallsrelated to the definition of
both significant points on the nephrographic curve. The first
significant point - the interface between the perfusion and
secretory phases - is often not clearly expressed on the
nephrographic curve, which makes it impossible to define it
precisely and can introduce a significant error in the
subtraction of the blood background. Defining the second required
point can also be problematic, as we do not have a clear control
on how early before the peak of the nephrographic curve the excretion of the radioindicator from the
kidney begins to be applied secretly . Both
of these difficulties are eliminated by the analytical method for
determining the separated kidney function implemented in our
program. It can therefore be considered more objective and exact.
Its further contribution stems from the basic text.
Kidney
excretory fraction - output efficiency
For an objective
assessment of renal drainage , the analysis of the
nephrographic curves themselves can sometimes be misleading. The
shape of the nephrographic curve is constantly influenced by the
mutual "balance" of the function (accumulation) of the
kidney and its drainage (excretion). Especially when there is
impaired renal function and an overall flat nephrographic curve,
it is difficult to assess the degree of obstruction of the ducts.
To some extent, deconvolution transit analysis (described below)
can help. However, the combined mathematical analysis of
nephrographic curves with the curve from the bloodstream
according to Fig.3.4.2 offers yet another possibility to quantify
the excretion of the radioindicator from the kidneys. If we
multiply the linear function y = Px + Q (fitted by a straight line of the
transformed nephrographic curve) by the curve of the blood pool
B(t), we get a pure accumulation
curve Ac(t), expressing the
accumulation of the radioindicator in the kidney under
hypothetical situation, if there were no drainage-excretion:
this is what the nephrographic curve of the given kidney would
look like in case of total obstruction - see Fig.Excr1.
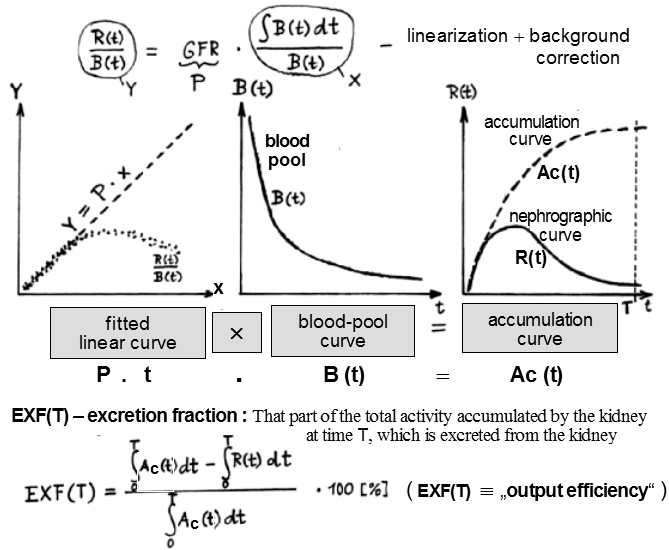 |
| Fig. Excr1. Calculation of the
excretion fraction of the kidney (follows on from the
Fig.3.4.2.). |
Kidney excretion can now be assessed by
comparing the calculated accumulation curve Ac(t) with the actual
nephrographic curve R(t); we will use the areas under both curves
for this. The excretion fraction EXF(T) is the
part of the total radioactivity accumulated by the kidney
at time T that is actually excreted from the
kidney. We calculate it so that the difference between
the areas under the accumulation curve Ac(t) and the
actual nephrographic curve R(t) is expressed as a percentage of
the area under the accumulation curve - Fig. Excr1. The value of
the excretion fraction quantifies the efficiency of kidney
excretion - output efficiency - of the kidney.
The reference time T for which the excretion
fraction is calculated is customary to take T = 30min.
For a kidney with well-functioning drainage, the excretion
fraction is above 80%. In Fig. Excr2 we see the results of the
excretion analysis in the case where the left kidney showed
normal drainage, while in the right kidney there was a serious
drainage disorder - obstruction of the excretory tract.
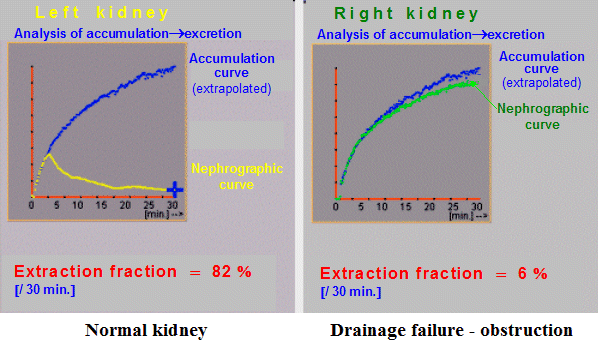 |
| Fig. Excr2. Intermediate results of kidney drainage
analysis. |
The kidney excretion curve can
also be useful for assessing renal drainage - it arises by plotting
the difference between the value of the accumulation
curve Ac(t) and the value of the actual nephrographic curve R(t).
In Fig. Excr3, the excretion curves of the pathological case from
the previous figure are plotted.
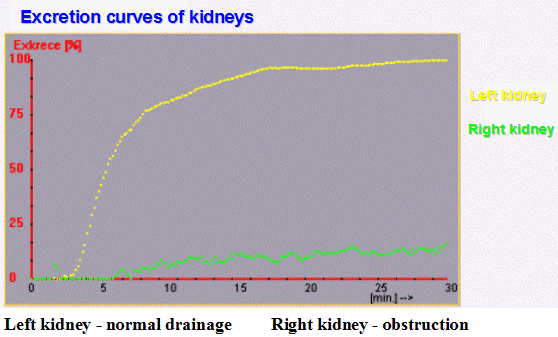 |
| Fig. Excr3. Excretion curves of boot kidneys . |
Blood-pool
curve processing and determination of global function
By mathematical analysis of the rate of
decrease of the concentration of nephrotropic radioindicator in the bloodstream, it is
possible to determine the total clearance
of the kidneys,
ie GFR, TER resp. ERPF - depending on the radiopharmaceutical
used.
The time course curve of the radioindicator concentration in the
bloodstream (from ROI1) has a typical shape (Fig.3.4.2).
Immediately after the application, it reaches the maximum value
almost abruptly (when applying the radioindicator in the form of
a discrete bolus, oscillations corresponding to primocirculation
and recirculation in central hemodynamics may occur at this
maximum for our problem). Then the curve decreases relatively
quickly mainly due to the distribution of the
radioindicator into the extracellular space. The rate of decline
decreases until after about 20 minutes it reaches a steady
monoexponential course given by the clearance of the
radioindicator from the bloodstream due to the actual filtration
activity of the kidneys. And it is the rate of this
monoexponential decline that is proportional to the global
functional fitness of the kidneys - their clearance.
The course of the blood
pool curve in the first approximation can be approximated by a
biexponential - the sum of two exponential functions, the first
of which has a high velocity coefficient in the exponent and
corresponds to the initial sharp decline, the second slower
exponential has a significantly lower velocity coefficient given
by total kidney clearance. However, in a more detailed analysis,
we find that the initial sharp decline s is not exactly monoexponential,
because it involves more compartments of the distribution
dynamics of the radiopharmaceutical. We have found that the shape
function is well suited for accurate modeling of the leakage
curve of a radiolabel from the bloodstream.
B(t)
= R1 . e -[R2/(1+
tR3)] .
t
+ R4 . e -R5 . t ,
which we call
"multiexponential". It is actually a combined
exponential function with a continuously decreasing rate
coefficient R2 / (1 + t R3) at the first exponential term, which asymptotically
transitions into a monoexponential function (second term) with a
constant rate coefficient R5, which is determined by the global
renal clearance GFR:
R5
= GFR / VD ,
where VD is the distribution volume of the
radio indicator used.
In our program, we
process the curve of the time course of radioactivity in the
bloodstream (from ROI1) as follows:
At the beginning of the
curve, shortly after the arrival of the activity in the place
where the possible chaotic course of the curve has already
stabilized on the monotonic descent, the starting point of the
fit is defined. The end point of the fit is defined at the very
end of the curve (around 30 minutes). Automatically defined
points can be modified manually.
This is followed by an
iterative interpolation of the multiexponential function by this
section of the blood-pool curve. First, the program uses a
suitable algorithm to determine the point in time (ie the point
of the curve) where the faster unbalance components have
disappeared and starting from which the curve has a virtually
monoexponential course (the faster unbalance phase is indicated
by dots below the curve). The monoexponential function R4.exp
(-R5.t) is interpolated with this slower component, it is
subtracted from the primary blood pool curve and the exponential
function R1.exp (-R2.t / (1 + tR3)) is interpolated by the
resulting difference curve . with variable rate coefficient R2/(1
+ tR3). The resulting interpolated function is
given by the sum of both exponential functions. A fit graph is
plotted and the clearance half-life value T1/2 = ln2 / R5 is displayed below, which
basically indicates how long it takes the kidney to cleanse half
the volume of distribution of a given substance.
Next, the program asks
if we want to calculate the global function. According to the
above relation, the global renal clearance is given by the
product of the rate coefficient R5 of the asymptotic exponential
and the distribution volume of the radio indicator VD :
GFR
= R5 . VD .
We have calculated the
value of R5 fitace curve of blood-pool, we need more value
distribution volume VD
. In the program we
can choose two methods for determining the volume of distribution
of a radiopharmaceutical: calculation based on the value of
applied activity and measured activity of a blood sample, or
determination (or estimation) of volume of distribution by
empirical formula from patient height and weight .
In the first method, the
program measures the required measured data: the value of the
applied activity and the residue in the syringe after
application, the calibration factor between the measurement of
the applied activity and the activity of the blood sample (check
the default value of the calibration factor), the activity value
of 1 ml. plasma sample, time interval between application and
collection and time interval between measurement of applied and
collected activity (for correction for 99mTc decay ). Based on the
interpolated multiexponential function of the decrease in
radioactivity in the bloodstream, the activity of the sample
taken was 1 ml. plasma at a defined time after application along
this function extrapolates to the moment of entry of activity,
there it is related to the value of applied activity, which
calculates the distribution volume VD
and thus the value of global clearance in [ ml./sec. ] .
The above-described
sample method for determining global kidney function is correct,
but not every workplace has the ability to accurately measure the
activity of blood samples taken and applied activity. In
addition, taking a blood sample is burdensome for the patient,
and sampling methods in general are often too complicated for the
current routine operation of nuclear medicine facilities.
Therefore, most offices prefer somewhat less accurate but much
easier way to quantify f esterification global renal
function when volum distribution of radiopharmaceuticals is
determined using an empirical formula of
height and weight patient without the need for sampling and
knowledge of the applied activity. The empirical formula, which
is part of our program, contains parameters whose numerical
values were obtained by correlation analysis of a number of
examinations, in which the global function was determined at our
workplace by both the sample method (taken as a reference) and
the empirical method of determination VD
from height and weight.
The empirical formula for the distribution volume VD
depends, of course, on the type of radiopharmaceutical used, in
our program it is implemented for MAG3 and for DTPA.
If a separate function
has been calculated, the absolute global function is calculated
for the left and right kidneys in [ml./sec.] . The results of the global and separate
functions are shown on the display, along with color-coded
nephrographic curves and a bloodstream curve (can be printed for documentation).
Calculation
of transit functions and transit times
Qualitative evaluation
of renal function is normally performed on the basis of assessing
the shape of nephrographic curves. Also, most quantitative
parameters of renal function are determined by mathematical
analysis of nephrographic curves. Nefrografická curve, however,
is determined not only the function of the le d guilt,
but also depends on the way in which the tracer
in the kidneys gets. The kidneys are "saturated" with
radioactivity from the blood pool, as shown in the upper left
part of Fig.3.4.3. Radioactivity in the bloodstream changes
significantly over time (in which the kidneys also participate).
The scanned nephrographic curve is then the result of a certain composition
of the kidney's own response function -
the so-called transit function- and time course curves of radioactivity
in the bloodstream. From a mathematical point of view, the
nephrographic curve is created by the composition, the so-called convolution, of the kidney's own transit function and
the course of radioactivity in the bloodstream. It is interesting
and useful to extract the hidden self-response function of the
kidney - the transit function - simulating the hypothetical
situation shown in the picture in the middle left, when we would
apply the bolus of the radioindicator directly to the renal
artery and monitor its transit through the kidney. The typical
shape of such a transit function is drawn next to the right:
after the arrival of the bolus, the radioactivity increases
abruptly, maintains a constant value during transport by the
parenchyma, and after penetrating the hollow system leaves the
kidneys.
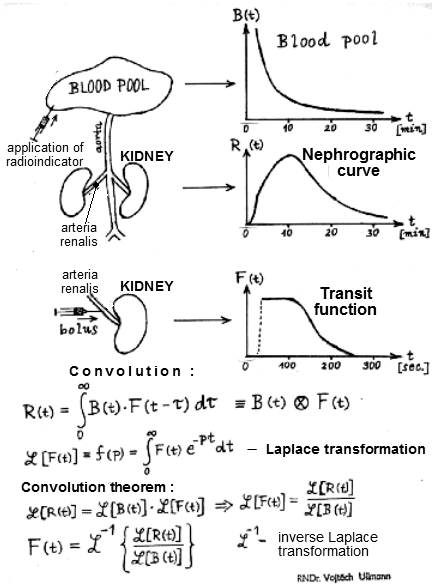 |
Fig.3.4.3.
By deconvolving the nephrographic curve with the curve of
the concentration of the radioindicator in the
bloodstream, we calculate the transit function, which
models the passage of the bolus of the radioindicator in
the hypothetic situation if we applied it directly to the
renal artery. |
The lower part of
Fig.3.4.3 briefly outlines the mathematical method of calculating
the transit function. First, the convolution integral expressing
the formation of the nephrographic curve R(t) by composing the
kidney's own transit function F(t) and the time-varying
radioactivity in the bloodstream B(t) as an input function is
given. The extracted transit function can be used with an
appropriate functional transformation m ation of all three stakeholders
such functions for which it is valid so. Convolution theorem
: convolution of two functions is equal to the product of
paintings both functions. In our case, the Laplace transform is
used. It follows from the convolution theorem that the desired
"extraction" of the transit function F(t), ie the
deconvolution of the nephrographic curve, is achieved by the
following procedure: *)
- We apply the
Laplace transform to the nephrographic curve R(t) and to
the bloodstream curve B(t).
- The obtained
Laplace image of the nephrographic curve is divided by
the image of the bloodstream curve B(t).
- We apply the
inverse Laplace transform to the resulting fractional
function, thus obtaining the transit function of the
kidney F(t).
*) We developed the method and program at our
workplace in the years 1980-82 and included it in the program for
a comprehensive analysis of dynamic scintigraphy of the kidneys
on the GAMMA-11 device. It later became part of the OSTNUCLINE
system on a PC.
From the transit
functions we can subtract three significant time moments,
characteristic for the dynamics of the passage of the
radioindicator through the kidney:
The minimum transit time (beginning of
the decrease in the transit function) indicates that the radio
indicator has already passed through the kidney (or parenchyma)
and is starting to leave. The mean transit time (at the
point where the transit function is halved) indicates the time
taken for half of the input amount of the radio indicator to pass
through the kidney (or parenchyma). The maximum transit time (the
point where the transit function drops to practically zero)
indicates the time during which all the input radio indicator has
already passed through the kidney or a given part of it.
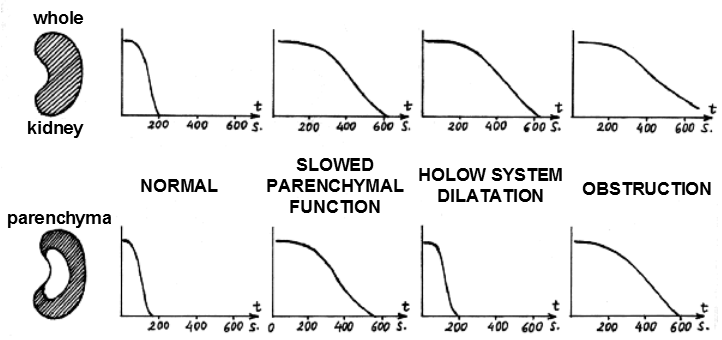 |
| Fig.3.4.4. Typical forms of transit functions of the
whole kidney (top) and parenchyma (bottom) for different
types of nephropathy. |
Transit function and times are useful to calculate
for the whole kidney as well as for the parenchyma and pelvis of
both kidneys. It allows to assess whether any extension of
transit tracer kidney is already at the level of glomerular and
tubular, or is caused by dilation Fri n lid or an obstruction of urinary
tract. In Fig.3.4.4 we have in the upper part the transit
function always from the whole kidney, at the bottom below the
corresponding transit function only of the parenchyma. We can
distinguish about four cases, always listed above the vertical
pair of transit functions:
- Normally
functioning kidneys with fast transit, where the
transit function of the whole kidney ends around 200 sec.
and in the case of the parenchyma it is even slightly
shorter (transit through the non-dilated pelvis
represents only a few seconds - usually 5 - 20 sec.).
- With reduced
parenchymal function, there is a marked
prolongation of the transit time both for the parenchyma
and subsequently for the whole kidney.
- If the transit
times for the whole kidney are prolonged, but the
parenchyma shows normal transit (max. Transit time up to
about 300 sec.), This indicates dilatation of the
pelvis, through which the flow lasts a longer time.
- When obstruction of urinary tract, is a
result of prolonged transit (and usually very much) as
the entire kidney, and parenchyma filtered and against
the pressure from the breach.
In this context, it
should be noted that careful delineation of the ROI of the
parenchyma so that no part of the hollow system is included
should be considered, especially in distopic or rotated kidneys.
In our experience, transit functions and the resulting transit times are very sensitive parameters of kidney function. There is a
big difference between normal and pathological values of transit
times. Regional analysis for the whole kidney, parenchyma and
pelvis can be a valuable aid in the differential diagnosis of the
causes of nephropathy.
The calculation of
transit functions and transit times of the passage of the
radioindicator through the kidneys and their parts is optional in
our program. Transit functions are constructed using the
above-mentioned Laplace deconvolution of nephrographic curves
(corrected for tissue and intravascular background) with an
interpolated exponential bloodstream curve, which is taken as the
input function. The resulting transit function reconstructs the
situation in which the tracer would be administered as a bolus
injected Přím of arterial renal artery. The points of
minimum, mean and maximum transit time are automatically defined
on the transit curves (with the possibility of manual
modification). If renal parenchymal ROIs have been marked,
transit curves and times are calculated for t yit curves,
from the differences indirectly for the pans. We can thus assess
whether the possible extension of transit occurs at the level of
the parenchyma or the hollow system.
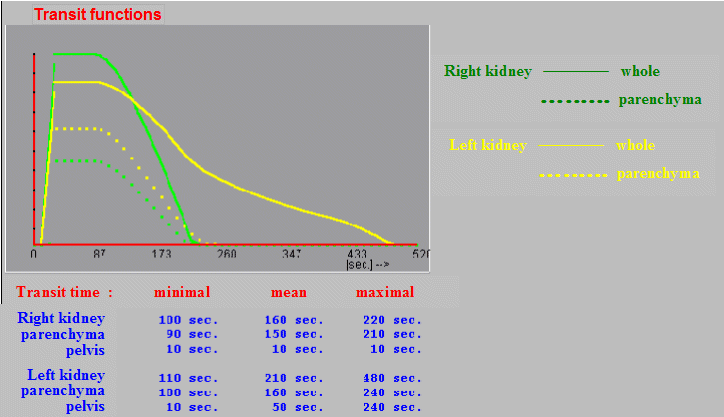 |
| Fig.3.4.5. Intermediate results of transit functions
and transit times in deconvolution analysis of dynamic
renal scintigraphy. |
After processing all
transit curves, these curves are displayed together in a clear
graph (Fig.3.4.5) together with the values of transit times, from
which we can infer a possible absolute and mutual extension of
the radioindicator transit through the kidneys and their parts
(for documentation we can print).
Evaluation of
significant images and nephrographic curves
On the b Ada analysis of sections of curves in
calculating the separated functions and half-excretion is
nasumují relevant images and thus create images of renal
perfusion, secretory and early and late excretory phase, wherein
the bottom of the screen offering to review and edit text and visual
slope evaluation of these paintings. If still images, eg of later
phases, have been stored and pre-selected before starting the
RENDYN program, they will also be displayed and can be evaluated
visually.
For the same purpose,
nephrographic curves are displayed together with a query about
or. application of diuretics. If the diuretic has been applied,
enter the time of its application. On the display, the
color-differentiated nephrographic curves of both kidneys are
enlarged in a common graph, and if the areas of interest of
parenchymes (ROI3 and 4 ) have been marked , the curves
of the time course of radioactivity in parenchyms are also
plotted in dotted lines. A significant vertical line indicates
the moment of diuretic application. In the text, visual
assessment, which is offered for editing in the bottom of the
screen, we can assess the shape nefrogra f ical waveform including
eventually. diuretic responses.
Assessment of the renovascular
origin of hypertension
In renal
artery stenosis
, the affected kidney increases production in the
renin-angiotensin system and thus increases the filtration
pressure. In this way, the body tries to correct
kidney function, but at the cost of systemic hypertension . With simple (native)
functional renal scintigraphy, even with significant renal artery
stenosis (due to the above correction mechanism), the result may
be practically normal or only non-specifically reduced. The
situation is different if we administer an ACE inhibitor before
dynamic functional scintigraphy. ACE
inhibitorsthey
inhibit the conversion of angiotensin and lower systemic blood
pressure. There is a release of vas efferens and thus a reduction
in filtration pressure at the glomerular level in the kidney
affected by renal artery stenosis, while in the other kidney with
a normal blood supply there are only slight changes. Thus, after
administration of an ACE inhibitor, there is a change in the
transport of the applied nephrotropic radioindicator through this
kidney, which is reflected in a change in the shape of the
nephrographic curve .
If we perform dynamic
sequential scintigraphy of the kidneys in a native pair - after
administration of captopril (which is the most commonly used
ACE-inhibitor), then in the subsequent evaluation of both studies
(but it is necessary to enter the study specifications correctly)
it is possible to display a native nephrographic curve captopril
always for the left and right kidneys, which allows you to
compare the effect of this drug on kidney function. In the text
of the visual evaluation at the bottom of the screen, we can talk
about the event. renovascular origin of hypertension .
Note on the order
of the two studies :
The first dynamic scintigraphy
should be performed after administration of Captopril, as it is
no longer necessary to repeat the test under native conditions if
the result is normal. If the result of functional scintigraphy
after premedication with an ACE-inhibitor is not completely
normal, then another native examination (ie without premedication
with an ACE-inhibitor) will be performed at the appropriate time
interval (preferably at least 24 hours) under the same conditions
(especially hydration of the patient).
The resulting protocol
Finally, a summary image
is displayed on the screen containing images of the kidneys in
significant phases of the dynamic study (images of the perfusion
and parenchymatous phases, early and late excretion phases),
nephrographic curves and levin transit functions. Below them is
an overview of the most important quantitative parameters
calculated by the program. At the bottom of the screen is the
text of the verbal evaluation, which can be modified and
supplemented. The same applies to the text of the
"Conclusion" if its standard wording has been generated
; otherwise we will insert the text of the
final evaluation here, including the doctor's signature. Finally,
a final report is printed (in the
required number of copies) containing significant images, curves,
calculated parameters and verbal evaluation, including the
conclusion and signature of the doctor (Fig.3.4.6) :
Department
of Nuclear Medicine, University
Hospital Ostrava Date:
.............. Name of patient: ....................... . Birth
certificate number: .........................
|
| Mathematical
analysis and complex evaluation of dynamic functional
scintigraphy of kidneys - MAG3 |
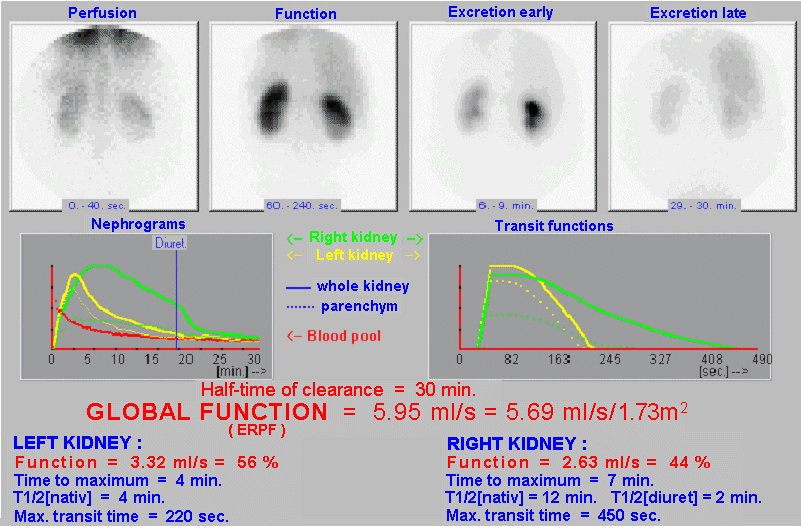 |
| Evaluation:
After intravenous administration of the radioindicator,
the kidneys of the usual shape, size and placement are
displayed, without focal changes. The nephrographic curve
of the left kidney has a normal course, on the curve of
the right kidney we observe a slowdown of drainage and
retention, disappearing after diuretics. Conclusion: Visual
evaluation of sequential images and quantitative analysis
of nephrographic curves indicate good function of
both kidneys, rapid transit through the parenchyma and
free drainage of the hollow system. In the right kidney,
a slight slowing of dilatation- type
drainage .
|
Department
of Nuclear Medicine, University
Hospital Ostrava
Date:
.............. Name of patient: ....................... . Birth
certificate number: .........................
|
| Mathematical
analysis and complex evaluation of dynamic functional
scintigraphy of kidneys - MAG3 |
 |
Evaluation:
After intravenous administration of the radioindicator, a
well-accumulating left kidney of the usual shape and size
was displayed, without focal changes. The right kidney
appears late as markedly hypofunctional
and inhomogeneous - only the narrow margin of the
functional parenchyma around the markedly dilated
excavated hollow system with significant retention
is preserved . The nephrographic curve of the left kidney
has a physiological course. The nephrogram of the right
kidney has a markedly flat shape with a low functional
segment, the curve has a permanently ascending course,
unresponsive to the application of a diuretic in the 17th
minute.
Conclusion:
Visual evaluation of sequential images and quantitative
analysis of nephrographic curves indicate good left
kidney function, but severely hypofunctional
right kidney with marked renal parenchymal
atrophy. Left renal drainage
physiological, right obstructive drainage
disorder , no response to diuretic. Global
kidney function is almost normal due to age.
|
Structure of the RENDYN
program
The RENDYN program consists of the following
parts:
RENDYN 1 - display of a series of images,
verbal evaluation, ROI marking, creation of curves
RENDYN 2 - mathematical processing of curves, quantification of
global and separated functions
RENDYN 3 - Laplace deconvolution, calculation of transit
functions and times
RENDYN 4 - summation of images of secretory and excretion phase,
verbal evaluation
RENDYN 5 - comparison of native and after captopril
curves RENDYN 6 - display of results, text editing, report
printing
At the same time, this structure shows how to
proceed when the calculation is interrupted or when the program
is restarted in order to repeat a certain part of the
calculations. E.g. to change the texts of the verbal evaluation,
just run RENDYN5, to repeat the calculation of the parameters of
the global and separate functions, run RENDYN2 (after which
RENDYN3 and 4 can be omitted and continue by running RENDYN5).
Occupancy of SAVE AREA after the end of the
RENDYN program :
SA 1,2,3 - ROI, curves
SA 10 - image of perfusion phase
SA 11 - image of secretory phase
SA 12 - image of early excretion phase
SA 11 - image of late excretion phase
Back: List of complex programs










